the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Evanescent acoustic-gravity modes in the isothermal atmosphere: systematization and applications to the Earth and solar atmospheres
Oleg K. Cheremnykh
Alla K. Fedorenko
Evgen I. Kryuchkov
The objects of research in this work are evanescent wave modes in a gravitationally stratified atmosphere and their associated pseudo-modes. Whereas the former, according to the dispersion relation, rapidly decrease with distance from a certain surface, the latter, having the same dispersion law, differ from the first by the form of polarization and the nature of decrease from the surface. Within a linear hydrodynamic model, the propagation features of evanescent wave modes in an isothermal atmosphere are studied. Research is carried out for different assumptions about the properties of the disturbances. In this way, a new wave mode – anelastic evanescent wave mode – was discovered that satisfies the dispersion relation . Also, the possibility of the existence of a pseudo-mode related to it is indicated. The case of two isothermal media differing in temperature at the interface is studied in detail. It is shown that a non-divergent pseudo-mode with a horizontal scale can be realized on the interface with dispersion ω2=kxg. Dispersion relation at the interface of two media is satisfied by the wave mode, which has different types of amplitude versus height dependencies at different horizontal scales kx. The applicability of the obtained results to clarify the properties of the f-mode observed on the Sun is analyzed.
- Article
(979 KB) - Full-text XML
- BibTeX
- EndNote
Acoustic-gravity waves (AGWs) in the Earth's atmosphere have been studied theoretically and experimentally for more than 60 years. The linear theory of AGW (Hines, 1960; Yeh and Liu, 1974; Francis, 1975) admits the existence in the atmosphere of a continuous spectrum of freely propagating waves, consisting of acoustic and gravity regions on the dispersion plane, as well as of evanescent modes, which can only propagate horizontally.
The freely propagating AGWs effectively transfer the energy and momentum between various atmospheric layers and thus play an important role in the dynamics and energy balance of the atmosphere. These waves are generated by various sources (both natural and technogenic ones), which are accompanied by a significant energy output into the atmosphere. Further, when the AGWs propagate upward, the energy conservation compensates for the decrease in the atmospheric density with the height by exponentially increasing amplitude. Therefore at a certain height the waves become nonlinear. Significant progress in the development of the nonlinear theory of AGWs was achieved by a number of authors, in particular, Belashov (1990), Nekrasov et al. (1995), Kaladze et al. (2008), Stenflo and Shukla (2009), and Huang et al. (2014). Numerical modeling of the freely propagating AGWs in the realistic viscous and heat-conducting atmosphere is an important area of modern studies of these waves (i.e., Cheremnykh et al., 2010; Vadas and Nicolls, 2012).
Satellite observations of AGWs in the Earth's polar thermosphere indicate a prevailing presence of waves with oscillation periods concentrated around the Brunt–Väisälä period and of horizontal scales of about 500–700 km (Johnson et al., 1995; Innis and Conde, 2002; Fedorenko et al., 2015). Azimuths of the propagation of these AGWs demonstrate the close connection with the directions of background winds in the thermosphere. Moreover, the amplitudes of the waves depend on the speed of headwind, but do not depend on height (Fedorenko and Kryuchkov, 2013; Fedorenko et al., 2018). These experimental results cannot be sufficiently explained by the theory of freely propagating AGWs. They may indicate waveguide or evanescent (along a horizontal surface) propagation of at least part of the observed waves.
As well as freely propagating AGWs, evanescent wave modes also play an important role in atmospheric dynamics of the Sun and planets. Evanescent waves propagate horizontally in an atmosphere, vertically stratified by gravity, subject to the presence of vertical gradients of parameters. The energy of these waves should decrease both up and down from the level at which they are generated. Therefore, evanescent waves are most effectively generated in areas of presence of significant vertical gradients of temperature and density or strong local currents. For example, in the solar atmosphere suitable conditions for realization of evanescent modes occur at the boundary between the chromosphere and corona. This follows from the analysis made by Jones (1969) for the so-called non-divergent modes of solar oscillations. In the Earth's atmosphere, such waves can be efficiently generated at sharp vertical temperature gradients, for example, at the base of the thermosphere or at the heights of the tropopause and mesopause. Also, evanescent wave modes can emerge in the presence of strong inhomogeneous winds, for example, in the region of the polar circulation of the thermosphere.
The study of evanescent waves traditionally gets less attention than the study of freely propagating AGWs. The most known of them are the horizontal Lamb wave and vertical oscillations with Brunt–Väisälä (BV) frequency (Beer, 1974; Waltercheid and Hecht, 2003). In hydrodynamics, physics of terrestrial and solar atmosphere, the surface gravity mode with dispersion ω2=kxg, is also well studied (Tolstoy, 1963; Jones, 1969). In particular, it was shown that it is the fundamental mode (f-mode) of oscillations in the solar atmosphere (Jones, 1969). Experimental f-mode observations are used to study flows, refinement of the solar radius, and other parameters of the Sun (Ghosh et al., 1995; Antia, 1998). In the Earth's atmosphere, evanescent waves are often observed at altitudes near the mesopause using ground-based instrumentation (Shimkhada et al., 2009).
In this paper, different types of evanescent acoustic-gravity modes characteristic of an isothermal atmosphere are investigated using a set of linearized hydrodynamic equations. In particular, the possibility of the existence of a new type of evanescent acoustic-gravity mode with the dispersion is proved in the assumption of anelasticity of the disturbance. Also, the possibility of realizing the evanescent modes in the model of a thin temperature gap is studied.
Consider an unbounded ideal isothermal atmosphere, stratified in a field of gravity. Linear perturbations in such a medium satisfy a set of four first-order hydrodynamic equations (Hines, 1960). These equations are convenient to bring to a set of two second-order equations for the perturbations of the horizontal Vx and vertical Vz particle velocities (Tolstoy, 1963):
where ρ0, γ, and g denote background atmosphere density, ratio of specific heats, and acceleration of gravity, respectively; is the sound speed, is the density-scale height, T is the temperature, k is the Boltzmann constant, and m is the molecular mass of the atmospheric gas.
Solutions to Eqs. (1) and (2) are searched for in the form
where ω and kx are cyclic frequency and horizontal component of the wave vector, respectively; parameter a sets the vertical scale of the change in the amplitude of velocities, Vx and Vz, with the height, z. For brevity, we will refer to a as the stratification of the corresponding mode.
Equations (1) and (2) admit, similarly to Hines (1960), on the existence on the “frequency–wave number” plot of regions of freely propagating gravity and acoustic waves, in which and kz is the vertical component of the wave vector. Also, from Eqs. (1) and (2) we get the solutions in the form of evanescent wave modes with real a and propagating horizontally (Waltercheid and Hecht, 2003). Solutions in the form of evanescent modes are usually obtained by imposing additional conditions on the perturbation properties.
2.1 Non-divergent and pseudo-non-divergent modes
Let us note the well-known hydrodynamics approximation of perturbations incompressibility (see, e.g., Ladikov-Roev and Cheremnykh, 2010), for which
In frames of this approximation, we obtain the following equations from Eqs. (1) and (2):
After substituting Eq. (3) into Eqs. (5) and (6), we find that
This yields a dispersion equation for incompressible wave modes in the form
Given the dispersion found, we obtain an expression for the polarization of the incompressible modes:
Further, from the condition (Eq. 4) and polarization (Eq. 8) we get a=kx. Insofar as a is a real value, then non-divergent (ND) wave mode has no periodic vertical solution and is horizontally propagating.
Let us show that the dispersion relation (Eq. 7) is also satisfied by another wave mode. After using this relation in Eqs. (1) and (2), we get
which implies that there are two solutions to this equation:
The first solution in Eq. (11) corresponds to the non-divergent (ND) wave mode, and the second one we call pseudo-non-divergent mode (NDp). The expression for polarization NDp is obtained from Eq. (9) and has the form
Also for this mode, the following equation holds:
which shows that for the NDp mode divV=0 only when .
2.2 Anelastic and pseudo-anelastic modes
Let us show that Eqs. (1) and (2) indicate that another wave mode, not previously studied, may exist. To do this, we introduce, according to Bannon (1996), the anelastic linear perturbations, which satisfy the condition
In the isothermal atmosphere with barometric density distribution we have
therefore, for such anelastic perturbations, the following equation holds:
Substituting Eq. (13) into Eqs. (1) and (2), we get
Thus, given Eq. (3), this should be
Then the dispersion equation for anelastic (AE) modes takes the form
With the resulting dispersion, polarization follows from Eqs. (14) and (15):
Further, taking into account Eq. (13), we obtain . Consequently, the AE mode also does not have a solution periodic vertically and can only propagate horizontally.
After substituting the dispersion (Eq. 16) into Eqs. (1) and (2), we get
whence we get a pair of values a identical to Eq. (11). Consequently, there is another wave solution that satisfies Eq. (16): we call it the pseudo-anelastic (AEp) mode. The first value in Eq. (11) corresponds to the AEp wave mode, and the second to the AE one.
Polarization of the AEp mode has the form
Let us prove that the different types of evanescent modes characteristic of an isothermal atmosphere are related. We substitute Eq. (3) into Eqs. (1) and (2) without additional conditions that were imposed in Sect. 2 when deriving ND and AE modes. As a result, we get
where is the square of the Brunt–Väisälä frequency.
From Eqs. (20) and (21) we obtain the dispersion equation
Expressions ω2=N2 and are well-known dispersions of Brunt–Väisälä oscillations with and Lamb waves (L) with ; in addition to these known modes, dispersion (Eq. 22) also admits the existence of additional solutions in the form of BV pseudo-modes (BVp) with ω2=N2, and Lamb pseudo-modes (Lp) with , (Beer, 1974; Waltercheid and Hecht, 2003).
Then represent Eq. (22) in the form of a quadratic equation with respect to a:
The solution to this equation is
from which it follows that for modes with dispersions and ω2=kxg there are two possible values: a=kx and . The first value corresponds to modes ND and AEp, and the second to NDp and AE.
Thus, each evanescent mode can be associated with a pseudo-mode which satisfies the same dispersion relation but differs in polarization and dependence of the amplitude from the height, i.e., in its stratification. Table 1 presents the properties of different evanescent modes characteristic of the isothermal atmosphere: BV oscillations, Lamb waves, non-divergent and anelastic modes, along with associated pseudo-modes: BVp, Lp, NDp, AEp. Table 1 shows that for all pseudo-modes, the polarization changes depending on the value of kx. Wave modes AE and ND at completely coincide with AEp and NDp, respectively.
The location of the dispersion curves for anelastic and non-divergent modes relative to gravity and acoustic regions in the (ω,kx) plane is shown in Fig. 1. The mode touches the gravity region of freely propagating AGWs at the same value at which the ω2=kxg curve touches the acoustic region (see Fig. 1). In this case, the dispersion curves of AE and ND modes are symmetric relative to the “characteristic” curve (see Beer, 1974), which separates the AGW acoustic region from the AGW gravity region. In fact, the characteristic curve is the geometric mean of the dispersion curves of AE and ND modes with .
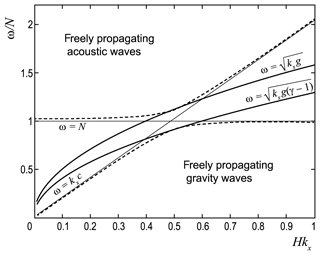
Figure 1Dispersion dependencies ω=f(kx): (1) boundaries between acoustic and gravity regions for freely propagating waves (dashed lines); (2) evanescent modes: (upper solid curve) and (lower solid curve), ω=N (thin horizontal line), and ω=kxc (thin sloping straight line).
From Fig. 1 we see that the dispersion curves of different evanescent modes have intersections at separate points. A Lamb dispersion curve with intersects the BV curve with ω2=N2 at the point . However, these modes cannot interact with each other by reason of different polarizations and values of a. At the same time, the pairs Lp-BV and L-BVp completely coincide in these properties and are indistinguishable at the intersection points.
Dispersion curves ω2=kxg and intersect with the Lamb curve and the BV curve at points , . In addition, the ND mode curve intersects with the Lamb curve at the same value kx at which the AE mode curve intersects with the BV curve (see Fig. 1). ND and AE modes cannot interact with the Lamb mode and BV oscillations due to different polarizations (Table 1). Pseudo-modes NDp and AEp, at the points of intersection with the Lamb wave and the BV oscillations, have the same polarization and values of a. Similarly, ND and AE are indistinguishable at the points of intersection with Lp and BVp. Table 2 shows all evanescent modes that coincide with each other at the points of intersection of the dispersion curves, and between which interaction is possible. The cases of ND and AE mode curves intersection with curves (, which separate the area of freely propagating AGWs from the evanescent area, are not presented in Table 2.
Table 2The coincidence of the evanescent mode properties at the intersection points of the dispersion curves. Note: the bottom rows show the modes that are indistinguishable from the corresponding mode of the top row at the point of intersection of the dispersion curves.

3.1 The energy of evanescent modes in an isothermal atmosphere
In Sects. 2 and 3, we considered a model of an unbounded isothermal stratified atmosphere to determine which types of evanescent modes can satisfy the initial system of Eqs. (1) and (2). However, in an infinitely extended medium, the necessary condition for the existence of evanescent modes is the absence of unlimited growth of oscillation energy above and below the height level at which they are generated. It is easy to verify that in an isothermal infinite atmosphere, none of the modes listed in Table 1 satisfy this condition.
Suppose further that an evanescent wave is generated at a certain altitude level z=0. The kinetic energy density of waves should decrease both up and down from the level z=0. When the energy density , if , and E→∞, if . When the energy density E→0, if , and E→∞, if . Based on these considerations, it is not difficult to understand how the energy density varies with height for different types of evanescent modes in an infinite isothermal atmosphere (see Table 3). Therefore, for the realization of such modes, it is necessary to have boundaries in the medium at which the condition for reducing energy in both directions from this boundary can be satisfied.
Table 3The change in energy density of evanescent modes with height in an infinite isothermal atmosphere.

The presence of boundaries is not the only condition that can limit the energy of the evanescent mode. If the equality holds for these modes, then their energy does not vary with height in an isothermal atmosphere. For an infinite atmosphere, this solution does not seem to be physical, but it can make sense for a real atmosphere of finite height. As follows from Eq. (11), for the ND and AE modes, as well as their pseudo-modes, the condition performed at the point . Also, at this point, the ND mode is identical to the NDp mode, and the AE mode completely coincides with AEp. In addition, when these evanescent modes adjoin the border of regions of freely propagating AGWs (see Fig. 1).
Consider some features of the energy balance for the evanescent modes. It follows from Eq. (20) that
Combining Eqs. (22) and (24) gives the relation
The average density of the kinetic energy of the perturbations is , and of the potential energy it is (Yeh and Liu, 1974; Fedorenko, 2010). Therefore, from Eq. (25) it follows that for the evanescent modes Ek≠Ep. At the same time, for freely propagating AGWs, the equality Ek=Ep is always fulfilled (Yeh and Liu, 1974). At the point where evanescent modes on the plane (ω,kx) in Fig. 1 are adjacent to areas of freely propagating AGWs, the equality holds. Taking this circumstance into account, from Eq. (25) we obtain
that is, at this point Ek=Ep.
Let us consider the possibility of realization of evanescent modes in the atmosphere at a thin interface between two isothermal half-spaces of infinite extent, which differ in temperature T. Let the boundary be localized at some altitude level z=0. In the lower half-space (z<0) we have T=T1, while in the upper half-space (z>0) we have T=T2 and it is assumed that T2>T1. Note that a similar model was considered by Rosental and Gough (1994). We will search for solutions to Eqs. (1) and (2) in the form of for the lower half-plane and in the form for the upper half-plane. Substituting these dependencies into Eqs. (1) and (2) yields
Here indices 1 and 2 denote the values in the lower and upper half-spaces, respectively.
The density of the kinetic energy of evanescent waves should decrease from the level z=0 both up and down. This condition limits the possible values of a1 and a2. In the upper half-space (z>0), when , the energy density if . In the lower half-space (z<0), when , the energy density if . Therefore, it is necessary to take in Eq. (27) for a1 the solution with a “+” sign and in Eq. (28) for a2 with a “−” sign, so that the energy decreases on both sides of the interface.
It is also necessary to consider that the possible values of a1 and a2 must satisfy the boundary condition (Tolstoy, 1963; Rosental and Gough, 1994), arising from Eqs. (1) and (2):
where ρ1 and ρ2 are the densities on both sides of the boundary. The procedure for deriving equality (Eq. 29) is exactly the same as in the papers by Cheremnykh et al. (2018a, b). When obtaining Eq. (29) we require continuity of the vertical velocity component (kinematic condition) and perturbed pressure (dynamic condition). In the barometric atmosphere we have ρc2=γp0, where p0 is the equilibrium pressure, which must be continuous across the interface. Therefore, when γ1=γ2, Eq. (29) can be written as
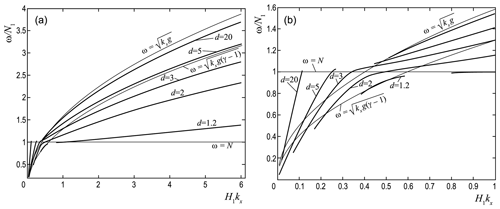
Figure 2Dispersion dependencies ω=f(kx) at the boundary of the discontinuity for different values of the parameter d. General dependence (a), long-wave part in more detail (b).
Dispersion dependencies of ω=f(kx) calculated numerically by means of Eq. (30) are shown in Fig. 2a for different values of the parameter . On each of these curves, the condition for decreasing energy up and down from the interface is satisfied. The long-wavelength part of the spectrum, where the most interesting features appear, is shown in more detail in Fig. 2b. Also shown in these figures are the dispersion curves and for the ND and AE wave modes. The discontinuities of the ω=f(kx) curves, as well as their cut-off for smaller kx values, are due to requirements and . Some features of the behavior of ω=f(kx) will be discussed below.
As shown by Miles and Roberts (1992), the dispersion Eq. (30) can be rewritten to a polynomial form suitable for analysis:
Non-physical solutions (Miles and Roberts, 1992) arising from quadratic expressions under the radicals were excluded from consideration while obtaining Eq. (31) (see Eqs. 27 and 28). Solutions of Eq. (31) can be analyzed by studying their asymptotic behavior.
If , then from Eq. (31), we get
It follows from this expression that
Equation (32) contains an interesting dependence of the frequency on the parameter d. In the limit d→∞, the dispersion ω2≈kxg of the ND (NDp) mode, independent of the properties of both environments, follows from Eq. (32). With d→1 and using Eq. (32), we obtain the dispersion of the BV (BVp) mode with the parameters of the lower medium, that is, . The indicated asymptotic features are visible on the curves shown in Fig. 2 below.
In the long-wave limit, i.e., at kx→0, from Eq. (31) it follows that
Hence we find that
For the considered small kx, for different values of d, from Eq. (33) we obtain the family of Lamb-type acoustic modes (see Fig. 2b). For large values of d, using Eq. (33), we obtain the expression ; i.e., the oscillation frequency is determined by the characteristics of the medium in the upper half-space.
The evanescent modes' frequencies lie on the (ω, kx) plane between the acoustic and gravity regions of freely propagating AGWs determined for upper and lower media separately (see Fig. 1). It is necessary to take into account when considering evanescent modes at the boundary of two isothermal media with different temperatures that the evanescent regions are different in the upper and lower half-planes. On the (ω, kx) plane, these regions are shifted more relative to each other the more the value of d is. At the same time, the wave modes at the interface of the media should remain evanescent in both media, and their dispersions should be enclosed within the overlap region of two evanescent regions. The cut-off curves for evanescent regions in the media under consideration are obtained in the case of the null expressions under the radicals in Eqs. (27) and (28). Gaps on the ω=f(kx) dispersion curves are due to the evanescent areas of the two media not matching (see Fig. 3).
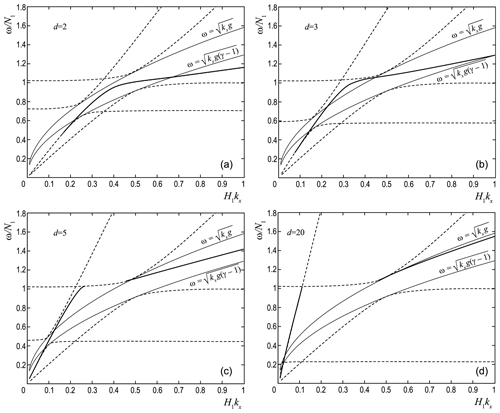
Figure 3Dispersion dependencies of the ω=f(kx) type at the temperature discontinuity boundary for d=2 (a), d=3 (b), d=5 (c), and d=20 (d). The dashed curves represent the boundaries of the areas with free propagation of AGWs in the upper and lower half-spaces, respectively.
Note that the dispersion curves ω=f(kx) for values d≤4 are mostly inside both evanescent regions (see Fig. 3a, b), except for the longest waves. When d≥4, the dispersion curve ω=f(kx) breaks into two separate branches (see Fig. 3c, d). The long-wave branch is acoustic, and another branch with kx≥0.4H1 is surface gravity by its physical nature.
In an unlimited isothermal medium, evanescent modes are separate “pure” solutions of hydrodynamic equations. At the interface between two isothermal media with different temperatures, dispersion of the evanescent modes has a combined character, comprising different types of “pure” modes, depending on the value of the parameter d and spectral properties ω (kx).
For some values of d, the curves of the dispersion Eq. (30) approach fairly closely the curves ω2=kxg and , and also intersect them at different points. These intersection points correspond to the specific value of kx at which the dispersions of the ND and AE modes are realized, in the model under consideration, in a “pure” form. Let us now examine these cases in more detail. For this purpose, we substitute the dispersion relations ω2=kxg and directly into Eqs. (27) and (28), and then into the boundary condition (Eq. 30).
As was shown in Sect. 2, for the dispersion relations ω2=kxg and , the values of each of the parameters a1 and a2 are the same for both relations and are determined by Eq. (11). Consider the valid values of a1 and a2 for these dispersions with regard to the requirement of energy decay in both directions from the interface and .
5.1 Dispersion of the form ω2=kxg
For a dispersion of the form ω2=kxg, we first analyze the stratification of the ND mode with a1=kx, a2=kx. In order for the energy of this mode to decay in both directions from the discontinuity, the following inequalities must be satisfied, i.e., H1>H2. Therefore, the ND mode can be realized at the discontinuity if the ambient temperature in the upper region is less and the density is greater than they are in the lower region. This situation corresponds to the unstable state of the atmosphere (see Roberts, 1991).
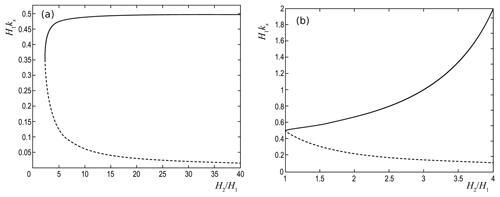
Figure 4Horizontal scales kxH1, on which the modes with the dispersions ω2=kxg (a) and (b) are realized, depending on . (See text for details.)
Take the stratification of the NDp modes in the form of , . The energy in this case decreases both ways from the discontinuity, if , i.e., when H2>H1. This condition corresponds to the stable state and the case under consideration. For the NDp mode from the dispersion Eq. (30) we get
From Eq. (34) it follows that
Figure 4a shows values of kx for which the dispersion curve ω2=kxg intersects with the calculated dispersion curve ω=f(kx) depending on the parameter d. The upper solid curve in this figure corresponds to the solution (Eq. 35) with the sign “+” before the radical and shows the points of intersection with the shorter wavelength branch. The lower dashed curve corresponds to the solution with a sign “−” and represents the points of intersection with the long-wavelength branch. For the upper curve when d→∞. For d<2.5, there are no intersections of the curve ω=f(kx) calculated numerically from Eq. (30) with the curve for the dispersion ω2=kxg.
When combining the stratifications for ND modes as a1=kx and for NDp modes as , Eq. (30) yields the only possible value of . For a combination of stratifications (NDp), a2=kx (ND) we get . Both of these cases do not satisfy the condition of energy decrease with height.
Thus, consideration of the possible values of a1 and a2 leads to the conclusion that on the interface of two isothermal media with H2>H1, the NDp mode can only be implemented with a dispersion ω2=kxg and a specific scale .
5.2 Dispersion of the form
For the AE stratification of the form , and for the AEp stratification of the form a1=kx, a2=kx, from the dispersion Eq. (30) follows the identity H1=H2. Therefore, such modes are not realized at a temperature discontinuity. Apparently, to study the conditions of realization of AE and AEp modes, it is necessary to consider atmospheric models in which height profile H(z) is continuous.
It should be noted that for the dispersion of the form , cases of combined mode stratifications are possible, satisfying the condition of decreasing energy on both sides of the boundary. So, for the combination of stratifications a1=kx (AEp), (AE) from Eq. (30), we obtain the relation
whence . In this case, the inequality must be satisfied. When we get the following restriction: d<5. Given this limitation and condition , we find that a mode with a dispersion of and stratification of AE type for the upper half-space and of AEp type for the lower half-space can propagate at the boundary in the range and for . For the stratifications (AE), a2=kx (AEp) from Eq. (30) we obtain the relation
It implies the ratio , in which the parameter d can take any values with d>1, and the horizontal wave number is limited by the inequality . Features of the behavior of the mode at the discontinuity, depending on the scale kx, are shown in Fig. 4b.
Let us dwell on some of the results in terms of their use for the analysis of experimental data.
With the f-mode observed on the Sun, one should identify the mode that we classify as the ND mode, for which ω2=kxg, Vz∼exp (kxz) and divV=0 (Roberts, 1991). In the framework of the considered temperature discontinuity model, it was shown that with T1<T2 (corresponding to the chromosphere–corona interface) the condition for decreasing amplitude with height to both sides of the interface is satisfied only by the NDp mode with ω2=kxg, and divV≠0. When the ratio d→∞ (i.e., , the NDp mode with asymptotically approaches the ND mode. On the interface between the chromosphere and the solar corona, d is large but of finite magnitude: d∼50 (Jones, 1969; Athay, 1976). Therefore, the condition of the presence of a free surface, which is required for the realization of the ND mode, is fulfilled only approximately. Therefore, in the framework of the temperature discontinuity model, the f-mode observed on the Sun should not be associated with the non-divergent ND mode, but with non-divergent pseudo-mode NDp.
For the Earth's atmosphere, the maximum possible value of d is observed at the interface between the thermosphere with T2∼800–1500 K (depending on solar activity) and the underlying atmosphere with T1∼300 K. When d=5, the dispersion (Eq. 30) asymptotically tends to with kx→∞. Therefore, it can be expected that evanescent modes in this case will be close to .
In other layers of the Earth's atmosphere we have d≤1.3 (Jursa, 1985). As follows from Eq. (33), for small values of d≤1.3 and for the wavelengths in the interval , the relation ω2→N2 is satisfied (see Fig. 2). Therefore, it can be expected that at small positive temperature gradients in the atmosphere, waves with a frequency close to the frequency of Brent–Väisälä should prevail. These conclusions experimentally confirm (Shimkhada et al., 2009) the results of observations of short-period evanescent waves with small wavelengths at altitudes near the mesopause.
In the paper, different types of evanescent acoustic-gravity modes characteristic of an isothermal atmosphere are investigated. A new mode was derived in the form of anelastic acoustic-gravity wave mode with the dispersion equation . The main properties of the AE mode are presented in Table 1 in comparison with other known evanescent modes. It is shown that for both anelastic and non-divergent modes there are pseudo-modes that satisfy the same dispersions but have different polarization and the dependence of the amplitude of the disturbances on the height.
For AE and ND evanescent modes, the value of sets a special scale (wavelength) at which these modes are identical to their pseudo-modes AEp and NDp. In addition, at the same point they are adjacent to the boundaries of the continuous spectrum (AE mode to the gravity region and ND mode to the acoustic region, respectively).
The features of the evanescent modes' realization at the interface of two isothermal media are considered. It is shown that in this case, dispersions of evanescent modes are combined, merging the features of different types of modes characteristic of an unbounded isothermal atmosphere. This effect is most pronounced in the following asymptotic cases: (1) when d→∞, we obtain the dispersion for the ND (NDp) mode in the form ω2≈kxg; (2) when d→1, for scales kx∼H1, a mode with is realized; (3) for kx→0, a Lamb wave with a dispersion relation of the form is obtained, which depends only on the parameters of the medium in the upper half-space.
It was demonstrated that on the interface of two isothermal media with T2>T1, the NDp mode with the dispersion ω2=kxg and the selected scale is realized. At the same time, the ND mode does not satisfy the condition of decreasing energy on each side of the interface. Dispersion on the interface of two media is satisfied by the wave mode, which has different types of amplitude versus height dependencies at different horizontal scales kx. When , the height dependence of AE amplitude for z>0 and AEp amplitude for z<0 satisfy the condition of decreasing energy from the interface. By contrast, when , this condition is satisfied by AEp amplitude for z>0 and AE amplitude for z<0.
It is important to note that according to our analysis in the framework of the temperature discontinuity model, (1) the f-mode observed on the Sun should not be associated with the non-divergent (ω2=kxg, divV=0) mode, but with its non-divergent pseudo-mode (ω2=kxg, divV≠0). (2) At the interface between the Earth's thermosphere and the underlying atmosphere it can be expected that evanescent modes with short wavelengths will be close to the new mode (. (3) Oscillations with a frequency close to the frequency of Brent–Väisälä should prevail at altitudes near the Earth's mesopause.
No data sets were used in this article.
This article has been prepared by the authors with equal contributions.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Solar magnetism from interior to corona and beyond”. It is a result of Dynamic Sun II: Solar Magnetism from Interior to Corona, Siem Reap, Angkor Wat, Cambodia, 12–16 February 2018.
This publication is based on work supported in part by Integrated Scientific Programmes of the National Academy of Science of Ukraine on Space Research and Plasma Physics.
This paper was edited by Sergiy Shelyag and reviewed by Tamaz Kaladze and one anonymous referee.
Antia, H. M.: Estimate of solar radius from f-mode, Astron. Astrophys., 330, 336–340, 1998.
Athay, R. G.: The Solar Chromosphere and Corona: Quiet Sun, Reidel, Dordrecht, the Netherlands, 504 pp., 1976.
Bannon, P. R.: On the anelastic approximation for a compressible atmosphere, J. Atmos. Sci., 53, 3618–3628, 1996.
Beer, T.: Atmospheric Waves, John Wiley, New York, USA, 300 pp., 1974.
Belashov, V. Yu.: Dynamics of nonlinear internal gravity waves at ionosphere F-region heights, Geomagn. Aeron+., 1990. 30, 637–641, 1990 (in English).
Cheremnykh, O., Cheremnykh, S., Kozak, L., and Kronberg, E.: Magnetohydrodynamics waves and the Kelvin–Helmholtz instability at the boundary of plasma mediums, Phys. Plasmas, 25, 102119, https://doi.org/10.1063/1.5048913, 2018a.
Cheremnykh, O. K., Selivanov, Yu. A., and Zakharov, I. V.: The influence of compressibility and non-isothermality of the atmosphere on the propagation of acoustic-gravity waves, Kosm. nauka tehnol., 16, 9–19, https://doi.org/10.15407/knit2010.01.009, 2010.
Cheremnykh, O. K., Fedun, V., Ladikov-Roev, Y. P., and Verth, G.: On the stability of incompressible MHD modes in magnetic cylinder with twisted magnetic field and flow, Astrophys. J., 866, 86, https://doi.org/10.3847/1538-4357/aadb9f, 2018b.
Fedorenko, A. K.: Energy Balance of Acoustic Gravity Waves above the Polar Caps According to the Data of Satellite Measurements, Geomagn. Aeron+., 50, 107–118, 2010.
Fedorenko, A. K. and Kryuchkov, Y. I.: Wind Control of the Propagation of Acoustic Gravity Waves in the Polar Atmosphere, Geomagn. Aeron+., 53, 377–388, 2013 (in English).
Fedorenko, A. K., Bespalova, A. V., Cheremnykh, O. K., and Kryuchkov, E. I.: A dominant acoustic-gravity mode in the polar thermosphere, Ann. Geophys., 33, 101–108, https://doi.org/10.5194/angeo-33-101-2015, 2015.
Fedorenko, A. K., Kryuchkov, E. I., Cheremnykh, O. K., Klymenko, Yu. O., and Yampolski, Yu. M.: Peculiarities of acoustic-gravity waves in inhomogeneous flows of the polar thermosphere, J. Atmos. Sol.-Terr. Phy., 178, 17–23, https://doi.org/10.1016/j.jastp.2018.05.009, 2018.
Francis, S. H.: Global propagation of atmospheric gravity waves: A review, J. Atmos. Terr. Phys., 37, 1011–1054, 1975.
Ghosh, P., Antia, H. M., and Chitre, S. M.: Seismology of the solar f-mode, I. Basic signatures of shearing velocity fields, Astrophys. J., 451, 851–858, 1995.
Hines, C. O.: Internal gravity waves at ionospheric heights, Can. J. Phys., 38, 1441–1481, 1960.
Huang, K. M., Zhang, S. D., Yi, F., Huang, C. M., Gan, Q., Gong, Y., and Zhang, Y. H.: Nonlinear interaction of gravity waves in a nonisothermal and dissipative atmosphere, Ann. Geophys., 32, 263–275, https://doi.org/10.5194/angeo-32-263-2014, 2014.
Innis, J. L. and Conde, M.: Characterization of acoustic-gravity waves in the upper thermosphere using Dynamics Explorer 2 Wind and Temperature Spectrometer (WATS) and Neutral Atmosphere Composition Spectrometer (NACS) data, J. Geophys. Res., 107, NoA12, https://doi.org/10.1029/2002JA009370, 2002.
Johnson, F. S., Hanson, W. B., Hodges, R. R., Coley, W. R., Carignan, G. R., and Spencer, N. W.: Gravity waves near 300 km over the polar caps, J. Geophys. Res., 100, 23993–24002, 1995.
Jones, W. L.: Non-divergent oscillations in the Solar Atmosphere, Sol. Phys., 7, 204–209, 1969.
Jursa, A. S.: Handbook of geophysics and the space environment, Vol. 1. Hanscom Air Force Base, MA: Air Force Geophysics Laboratory, Air Force Systems Command, United States Air Force, 1040 pp., 1985.
Kaladze, T. D., Pokhotelov, O. A., Shah, H. A., Khan, M. I., and Stenflo, L.: Acoustic-gravity waves in the Earth's ionosphere, J. Atmos. Sol.-Terr. Phy., 70, 1607–1616, 2008.
Ladikov-Roev, Y. P. and Cheremnykh, O. K.: Mathematical Models of Continuous Media, Naukova Dumka, Kyiv, 552 pp., 2010 (in Russian).
Miles, A. J. and Roberts, B.: Magnetoacoustic-gravity surface waves, I. Constant Alfven Speed, Sol. Phys., 141, 205–234, 1992.
Nekrasov, A. K., Shalimov, S. L., Shukla, P. K., and Stenflo, L.: Nonlinear disturbances in the ionosphere due to acoustic gravity waves, J. Atmos. Terr. Phys., 57, 732–742, 1995.
Roberts, B.: MHD Waves in the Sun, in: Advances in solar system magnetohydrodynamics, edited by: Eric R. Priest, E. R., Wood, A. W., Cambridge University Press, Cambridge, UK, 105–137, 1991.
Rosental, C. S. and Gough, D. O.: The Solar f-mode as interfacial mode at the chromosphere-corona transition, Astrophysical J., 423, 488–495, 1994.
Simkhada, D. B., Snively, J. B., Taylor, M. J., and Franke, S. J.: Analysis and modeling of ducted and evanescent gravity waves observed in the Hawaiian airglow, Ann. Geophys., 27, 3213–3224, https://doi.org/10.5194/angeo-27-3213-2009, 2009.
Stenflo, L. and Shukla, P. K.: Nonlinear acoustic-gravity waves, J. Plasma Phys., 75, 841–847, https://doi.org/10.1017/S0022377809007892, 2009.
Tolstoy, I.: The theory of waves in stratified fluids including the effects of gravity and rotation, Rev. Mod. Phys., 35, N1, https://doi.org/10.1103/RevModPhys.35.207, 1963.
Vadas, S. L. and Nicolls, M. J.: The phases and amplitudes of gravity waves propagating and dissipating in the thermosphere: Theory, J. Geophys. Res., 117, A05322, https://doi.org/10.1029/2011JA017426, 2012.
Waltercheid, R. L. and Hecht, J. H.: A reexamination of evanescent acoustic-gravity waves: Special properties and aeronomical significance, J. Geophys. Res., 108, D114340, https://doi.org/10.1029/2002JD002421, 2003.
Yeh, K. S. and Liu, C. H.: Acoustic-gravity waves in the upper atmosphere, Rev. Geophys. Space. GE, 12, 193–216, 1974.
- Abstract
- Introduction
- Evanescent modes in the isothermal atmosphere
- General properties of evanescent modes
- Evanescent modes at the interface of isothermal media
- Characteristic scales of ND and AE evanescent modes on the discontinuity
- Discussion
- Main results
- Data availability
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- Review statement
- References
- Abstract
- Introduction
- Evanescent modes in the isothermal atmosphere
- General properties of evanescent modes
- Evanescent modes at the interface of isothermal media
- Characteristic scales of ND and AE evanescent modes on the discontinuity
- Discussion
- Main results
- Data availability
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- Review statement
- References






