Fine structure and motion of the bow shock and particle energisation mechanisms inferred from Magnetospheric Multiscale (MMS) observations

This study presents new observations of fine structure and motion of the bow shock formed in the solar wind, upstream of the Earth's magnetosphere. NASA's Magnetospheric Multiscale (MMS) mission has recorded data during 11 encounters with a shock oscillating with frequency of 1 mHz. Shocks move with a speed of 4–17 km s⁻¹; have thickness of 100 km, i.e. an ion gyroradius; and represent cascades of compressional magnetic field and plasma density structures of increasing frequencies or smaller spatial scales. Induced density gradients initiate chains of cross-field current-driven instabilities that heat solar wind ions by the stochastic $\stackrel{\mathrm{̃}}{E}\times B$ wave energisation mechanism. The theoretical ion energisation limits are confirmed by observations. We have identified the ion acceleration mechanism operating at shocks and explained double-beam structures in the velocity space. The nature of this mechanism has been revealed as a stochastic resonant acceleration (SRA). The results provide for the first time a consistent picture of a chain of plasma processes that generate collisionless shocks and are responsible for particle energisation.

1 Introduction

Collisionless shocks in solar wind plasma are associated with non-linear steepening of low-frequency magnetosonic waves (Sagdeev, 1966; Tidman and Krall, 1971; Friedman et al., 1971; Biskamp, 1973), which leads to broadband turbulence, particle heating and acceleration. It has recently been demonstrated that ion and electron heating in collisionless shocks are related to electric fields of drift instabilities triggered by shock compression of plasma (Stasiewicz, 2020; Stasiewicz and Eliasson, 2020a, b, 2021; Stasiewicz et al., 2021; Stasiewicz and Kłos, 2022). The cross-field drift instabilities involved in plasma energisation include the lower hybrid drift (LHD) instability (Yamada and Owens, 1977; Drake et al., 1983; Zhou et al., 1983; Gary, 1993; Daughton, 2003) in the frequency range f_cp–f_lh, the modified two-stream (MTS) instability (Wu et al., 1983; Winske et al., 1985; Muschietti and Lembége, 2017) in the frequency range f_lh–f_ce and the electron cyclotron drift (ECD) instability (Forslund et al., 1972; Lashmore-Davies and Martin, 1973; Janhunen et al., 2018) around the harmonics of the electron cyclotron frequency nf_ce. Here, f_cp is the proton cyclotron frequency, and $f_{\text{lh}}\approx (f_{\text{cp}}{f}_{\text{ce}}{)}^{\mathrm{1}/\mathrm{2}}$ is the lower hybrid frequency. The electric fields of these instabilities have amplitudes ranging from $\stackrel{\mathrm{̃}}{E}\sim$ 10 mV m⁻¹ in frequency range f_cp–f_lh to $\stackrel{\mathrm{̃}}{E}\sim$ 100 mV m⁻¹ at frequencies around the electron cyclotron, f_ce. These waves heat ions and electrons in a stochastic process, and they can also accelerate selected ions by the $\stackrel{\mathrm{̃}}{E}\times B$ wave mechanism to hundreds of kilo-electronvolts (keV) (Stasiewicz and Eliasson, 2021; Stasiewicz et al., 2021; Stasiewicz and Kłos, 2022). The $\stackrel{\mathrm{̃}}{E}\times B$ wave mechanism can accelerate charged particles to the limit corresponding to the $\stackrel{\mathrm{̃}}{E}\times B$ velocity in the wave electric field ${\stackrel{\mathrm{̃}}{V}}_{E\times B}={\stackrel{\mathrm{̃}}{E}}_{⟂}/B$. The energisation capacity implied by this (wave) mechanism is

$$\begin{array}{}\text{(1)}& {\stackrel{\mathrm{̃}}{K}}_{\mathrm{w}}\sim {\displaystyle \frac{m_j}{\mathrm{2}}}\left[v_{⟂j}^{\mathrm{2}}+{\left({\stackrel{\mathrm{̃}}{E}}_{⟂}/B\right)}^{\mathrm{2}}\right],\end{array}$$

where v_⟂j is the initial perpendicular velocity of a particle with mass m_j (j=e for electrons, j=p for protons, and j=i for general ions). This energy corresponds typically to 200 keV for protons and 1 keV for electrons in shocks measured by Magnetospheric Multiscale (MMS) spacecraft. The symbol $\stackrel{\mathrm{̃}}{E}$ is used here for the wave electric field to distinguish it from the convection electric field and the corresponding E×B drift $V_{E\times B}=E_{⟂}/B$.

The $\stackrel{\mathrm{̃}}{E}\times B$ acceleration is similar to the wave surfing (surfatron) mechanism (Katsouleas and Dawson, 1983; Ohsawa, 1985; Ucer and Shapiro, 2001; Kichigin, 2013), which when applied to shocks requires a wide front of coherent waves (Shapiro et al., 2001; Shapiro and Ucer, 2003). In this mechanism the energy for particles is provided by the convection electric field. In contrast, the $\stackrel{\mathrm{̃}}{E}\times B$ wave mechanism can work on intermittent bursty waves in any direction, and the energy is taken from wave electric fields $\stackrel{\mathrm{̃}}{E}\sim$ 10–100 mV m⁻¹, much larger than the convection field E∼ 3 mV m⁻¹. The present mechanism relies on a stochastic condition, which requires sufficiently strong gradients of the electric field to render particle motion chaotic and facilitate heating (Cole, 1976; Karney, 1979; McChesney et al., 1987; Balikhin et al., 1993; Stasiewicz et al., 2000; Stasiewicz, 2007; Vranjes and Poedts, 2010). The threshold for stochastic heating has recently been generalised to the form (Stasiewicz, 2020)

$$\begin{array}{}\text{(2)}& {\mathit{\chi }}_j(t,\mathit{r})={\displaystyle \frac{\text{div}\left({\mathit{E}}_{⟂}\right)}{{\mathit{\omega }}_{\mathrm{c}j}B}}>\mathrm{1}\iff {\displaystyle \frac{N_{\mathrm{c}}}{N}}>{\displaystyle \frac{V_{\mathrm{A}j}^{\mathrm{2}}}{c^{\mathrm{2}}}}\end{array}$$

and applied to electron and ion heating observed at the bow shock (Stasiewicz and Eliasson, 2020a, b). Here, ${\mathit{\omega }}_{\mathrm{c}j}=q_{j}B/m_j$ is the angular cyclotron frequency of particle species with charge q_j, N_c is the number density of excess charges, N is the plasma number density, $V_{\mathrm{A}j}^{\mathrm{2}}=B^{\mathrm{2}}/\left({\mathit{\mu }}_{\mathrm{0}}N{m}_j\right)$ and c is the speed of light. The equivalent formula on the right-hand side of Eq. (2) implies that stochastic heating requires a charge non-neutrality fraction larger than the ratio of the Alfvén speed, V_Aj, to the speed of light squared. The particles are magnetised (adiabatic) for |χ_j|<1, demagnetised (subject to non-adiabatic heating) for |χ_j|  ≳  1 and selectively accelerated to high perpendicular velocities when |χ_j|≫1.

Acceleration of ions in quasi-perpendicular shocks is performed mostly by lower hybrid (LH) waves which have the energisation capacity for protons limited by the wave's phase speed (Stasiewicz and Eliasson, 2021):

$$\begin{array}{}\text{(3)}& K_{\text{LH}}\mathit{\lesssim }\mathrm{1.5}{\left({\displaystyle \frac{m_{\mathrm{p}}}{m_{\mathrm{e}}}}{T}_{\mathrm{e}}{T}_{\mathrm{p}}\right)}^{\mathrm{1}/\mathrm{2}},\end{array}$$

which will also be shown to apply in the analysed case. T_e and T_p are electron and proton temperatures in energy units.

In this paper we shall determine the motion and thickness of shocks and analyse ion distribution functions and magnetic and electric field turbulence measured at quasi-perpendicular shocks, as well as particle heating mechanisms implied by these measurements. We provide for the first time a physical explanation for the multiple-beam structures in the perpendicular velocity plane observed in ion distributions at shocks.

2 Oscillatory bow shock

On 3 January 2020 NASA's Magnetospheric Multiscale (MMS) spacecraft (Burch et al., 2016) were in solar wind at 13:40  UTC at the beginning of the data period shown in Fig. 1. MMS entered quasi-perpendicular shock no. 1 at 13:47  UTC at position (10.8, 13.8, −1.6), or R = 17.6 R_E GSE (geocentric solar ecliptic), and then moved further earthward with a speed of 1.7 km s⁻¹. The variations of the dynamical solar wind pressure that was about 1 nPa caused oscillatory movements of the shock front with speeds of 4–17 km s⁻¹ and have led to 11 shock crossings within 2 h on a distance of 2 R_E, which are labelled in Fig. 1a with nos. 1–11. The first crossing was caused by the outward motion of the shock front with a speed of 15 km s⁻¹ followed by an earthward motion 8 min later of shock no. 2 with a speed of 17 km s⁻¹ in the spacecraft frame. The last shock crossing, no. 11, was at 15:49  UTC, position (9.1, 12.7, −2.0) R = 15.8 R_E, with outward speed of 4 km s⁻¹. The four MMS spacecraft had an average separation distance of 21 km. The velocity of the shock fronts has been determined with inter-spacecraft timing (Schwartz, 1998) of the magnetic field measured by the fluxgate magnetometer (Russell et al., 2016). The motion is outward for all odd shock numbers and earthward for all even shocks.

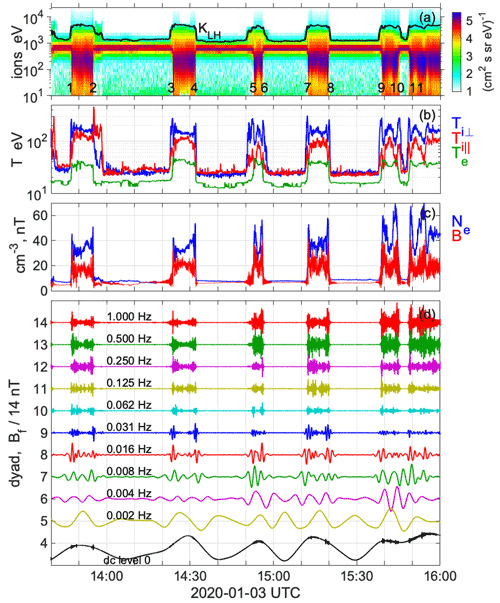
Figure 1 A series of 11 encounters with an oscillatory bow shock by the MMS3 spacecraft on 3 January 2020. (a) Omnidirectional ion flux measured by the Fast Plasma Investigation (FPI) in energy range 10–20 keV. Overlaid is the energisation capacity of lower hybrid waves given by Eq. (3). (b) The ion temperatures T_i⟂ and T_i∥ and the electron temperature T_e = T_e⟂ ≈ T_e∥ derived as moments of the distribution functions measured by FPI. (c) The electron number density and the magnitude of the magnetic field. (d) Multiresolution decomposition of the measured magnetic field in the frequency range 0–1 Hz.

The ion differential particle flux shown in Fig. 1 is measured by the Fast Plasma Investigation (FPI) experiment (Pollock et al., 2016) in energy range 10 eV–30 keV. It exhibits the solar wind beam centred around 700 eV which becomes thermalised in the shock regions while some ions are accelerated to a few kilo-electronvolts. Overlaid is the energisation capacity of lower hybrid waves K_LH given by Eq. (3). This equation exhibits good agreement with MMS measurements in all of ca. 40 quasi-perpendicular shocks analysed by the authors. Figure 1b shows perpendicular and parallel ion temperatures, T_i⟂ and T_i∥, which confirm the known fact that ion heating in shocks is stronger in the perpendicular direction.

The electron temperature in quasi-perpendicular shocks is isotropic, i.e. T_e = T_e⟂ ≈ T_e∥, and obeys a specific relation, which has been found recently (Stasiewicz and Eliasson, 2020a):

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{T_{\mathrm{e}}}{B}}={\displaystyle \frac{T_{\mathrm{e}\mathrm{0}}}{B_{\mathrm{0}}}}{\left({\displaystyle \frac{B_{\mathrm{0}}}{B}}\right)}^{\mathit{\alpha }},\end{array}$$

with $\mathit{\alpha }=\mathrm{1}/\mathrm{3}$. This relation, named quasi-adiabatic, predicts a dip of $T_{\mathrm{e}}/B$, where B has a maximum. It has been derived under the assumption that the perpendicular energy gain, $T_{\mathrm{e}⟂}\propto B$, during compressions of the magnetic field is redistributed to the parallel energy component by scattering on waves, leading to the above temperature relation. At quasi-parallel shocks, we observe a similar relation but with $\mathit{\alpha }=\mathrm{2}/\mathrm{3}$, which also has a theoretical justification. The isotropisation of electrons is due to scattering on high-frequency oblique electrostatic waves with a parallel electric field component (Stasiewicz and Eliasson, 2020b).

Figure 1 shows compressions of the electron number density N_e and the magnetic field B occurring at shocks. To understand the process of non-linear steepening of the magnetosonic waves that leads to the formation of perpendicular shocks, we perform multiresolution frequency decomposition of the measured magnetic field B from Fig. 1c with orthogonal wavelets (Daubechies, 1990). The decomposition shown in Fig. 1d is exact, i.e. the sum of all components gives the original signal, and the orthogonality means that the time integral of the product of any different pair of the frequency dyads is zero. The numbered dyads in this stacked plot represent baselines (zero levels) for the signal B_f/14 nT at the indicated frequency f. The residual “dc” magnetic field is shown as a black line at the bottom with the same normalisation.

The decomposition shows a cascade of waves with the lowest frequency of ∼ 1 mHz seen at the bottom, which cause the spacecraft to exit and re-enter the shock. The compressional waves extend to 1 Hz and above with maximum amplitude co-located with the strongest gradient of B and N. The maximum amplitude of compressions is observed in the 0.5 Hz channel, which can be associated with ion cyclotron waves. The proton cyclotron frequency is 0.1 Hz in the solar wind regions, but it goes up to 0.6 Hz in shock compressions. The Alfvén Mach number for the plasma flow is $M_{\mathrm{A}}=V_{\mathrm{i}}/V_{\mathrm{A}}\approx$ 7 in solar wind regions, and plasma beta is given as β_e≈ 1 and β_i≈ 2. Some additional diagnostic parameters for these shocks can be found elsewhere (Stasiewicz and Eliasson, 2020a).

2.1 Burst data analysis

In this section we focus our analysis on high-resolution burst data measured during time 14:31:36–14:32:22  UTC, which contains shock no. 4 of Fig. 1a. All shocks have similar wave content and heating/acceleration capacity, which can be seen in Fig. 1. However, the magnitude of compression increases slightly in the earthward direction, which can be seen in Fig. 1c. On the other hand, the shock speed decreases in the earthward direction.

Figure 2a–c show reduced one-dimensional distribution functions measured by the FPI instrument. The ion measurements are transformed to a Cartesian coordinate system in which the $\widehat{\mathit{x}}$ axis is along the E×B direction, the $\widehat{\mathit{z}}$ axis is along the magnetic field and the $\widehat{\mathit{y}}=\widehat{\mathit{z}}\times \widehat{\mathit{x}}$ axis is along the electric field, forming the E×B reference system in velocity space $(v_{E\times B},v_{\mathrm{E}},v_{\mathrm{B}})$. We have used the convection electric field $\mathit{E}=-{\mathit{V}}_{\mathrm{p}}\times \mathit{B}$ to construct these coordinates, where V_p is the velocity of the maximum of the distribution function. Colour spectrograms show phase space density $F(v_{E\times B},t)$, F(v_E,t), F(v_B,t) integrated over two other velocities with time resolution of 0.15 s corresponding to the sampling time of the instrument. The vertical lines labelled with A–E mark positions of ion distribution functions shown in Fig. 4. The shock ramp, identified with the B and T_e profiles in Fig. 2d and e, is within blue vertical lines.

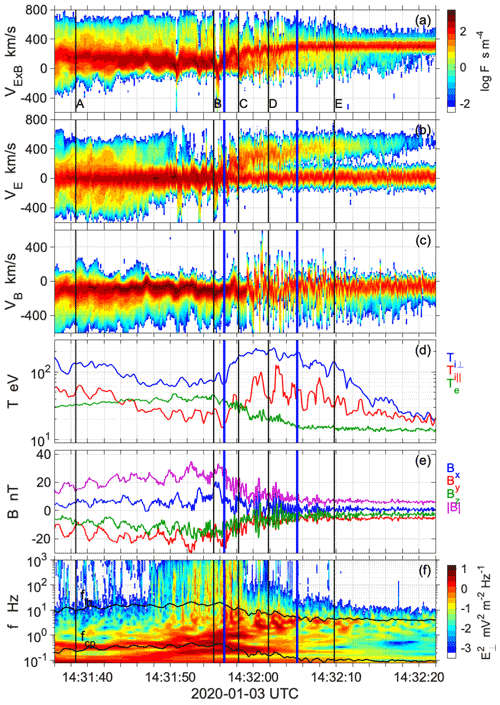
Figure 2 Shock no. 4 in burst mode measurements by MMS3 spacecraft. Panels (a), (b) and (c) show reduced one-dimensional ion distribution functions $F(v_{E\times B},t)$, F(v_E,t) and F(v_B,t), respectively. (d) Ion temperatures T_i⟂, T_i∥ and T_e measured by FPI. (e) Three components and modulus of the magnetic field in GSE system. (f) Time–frequency spectrogram of the perpendicular electric field. Overlaid are the lower hybrid frequency f_lh and the proton cyclotron frequency f_cp. The shock ramp is within two blue vertical lines.

Figure 3 Multiresolution decomposition of the ${\stackrel{\mathrm{̃}}{V}}_{E\times B}$ wave speed for the time interval of Fig. 2. It shows acceleration capacity of waves in the frequency range 1–256 Hz, which can account for the measured velocities of ions shown in Fig. 2a–c. Blue vertical lines mark the shock ramp region.

Electrons are mostly in quasi-adiabatic regime, |χ_e| < 1, which means that the temperature shown in Fig. 2d follows the quasi-adiabatic relation (Eq. 4), i.e. $T_{\mathrm{e}}\propto B^{\mathrm{1}-\mathit{\alpha }}$ at shocks (Stasiewicz and Eliasson, 2020a). On the other hand, ions are in strongly stochastic regime with |χ_p|∼ 50, computed with waves f < 64 Hz. The temperatures T_i⟂ and T_i∥ measured by FPI show the perpendicular ion temperature elevated to 200 eV in the foot and ramp of the shock from the isotropic temperature 20 eV measured in the solar wind. The high perpendicular ion temperatures in the foot of shocks are artefacts of the presence of multiple beams in the perpendicular plane; see Fig. 2b. These beams produce a large velocity spread from the mean velocity, making high temperature from moment computations. Individual beams have lower temperatures than the magnetosheath plasma, whereas Fig. 2d shows the opposite. Secondary beams are produced by the $\stackrel{\mathrm{̃}}{E}\times B$ acceleration, as we will show further in the text.

In Fig. 2f we show the time–frequency spectrogram of the field measured by the electric field double-probe instruments (Ergun et al., 2016; Lindqvist et al., 2016) with sampling rate of 8192 s⁻¹. Overlaid is the lower hybrid frequency f_lh and the proton cyclotron frequency f_cp. Lower hybrid drift waves have been observed in the dayside magnetosphere by many authors (Bale et al., 2002; Vaivads et al., 2004; Walker et al., 2008; Norgren et al., 2012). They can be identified in the frequency range f_cp–f_lh, as discussed extensively in previous papers (Stasiewicz and Eliasson, 2020a, b). This frequency range also contains ion whistler waves, which could originate from mode conversion of lower hybrid waves on density striations (Rosenberg and Gekelman, 2001; Eliasson and Papadopoulos, 2008; Camporeale et al., 2012).

The vertical striations seen in the spectrogram (Fig. 2f) represent cascades of instabilities: LHD → MTS → ECD extending form f_cp up to nf_ce in the range of a few kilohertz. The presence of ECD instability at shocks has been reported in several papers (Wilson et al., 2010; Breneman et al., 2013; Stasiewicz, 2020). Lower hybrid waves generated in the shock propagate upstream in Fig. 2f and appear to be associated with particles in Fig. 2b.

The velocity of the shock in Fig. 2 determined from inter-spacecraft timing is (−12.0, −9.7, 2.1) or 15.6 km s⁻¹ (GSE) in spacecraft frame. Time lags between two signals were determined with the least squares method for the ramp interval. Strong wave activity in the magnetic signal sampled at 64 Hz introduces some uncertainty into the results. We have used multiresolution wavelet decomposition to remove high frequencies which produce jitter. Wavelet decomposition was chosen instead of low-pass filtering to avoid introducing phase distortions. The least squares values were minimised for signals at frequencies f = 0–2 Hz, which were used to determine the shock velocity. The neighbouring frequency level f < 4 Hz gave a velocity difference of ∼2 km s⁻¹, which we assumed corresponds to the error of the analysis. This value also corresponds to the speed of the spacecraft.

The upstream magnetic field was steady, (1, −5, −3) nT, making angle ∠_BN = 71^∘ with the shock-normal direction. The proton gyroradius is 100 km in the solar wind, going up to 200 km in the shock. The ion inertial length is 80 km in the solar wind, going down to 40 km in the shock. The time duration of the shock ramp within the blue vertical lines is 9 s. With the derived shock speed of 15 km s⁻¹, this implies a ramp thickness of 135 km or 1 proton gyroradius (r_p). The shock comprising the ramp and foot would have thickness 2r_p embracing the whole proton orbit, which can be inferred from data presented in Fig. 2 and in particular from the ion temperature in Fig. 2d. These values agree with many other estimates of shocks thickness and motion published by other authors. However, shock thickness scalings based on ion inertial length or the hybrid gyroradius $(r_{\mathrm{p}}{r}_{\mathrm{e}}{)}^{\mathrm{1}/\mathrm{2}}$ are not supported by measurements.

The FPI instrument cannot resolve accurately the small thermal spread of the solar wind beam. Furthermore, the double-beam structure seen in Fig. 2b artificially increases the ion temperature in the ramp and foot of the shock (Fig. 2d), so the values of the ion gyroradius are likely overestimated.

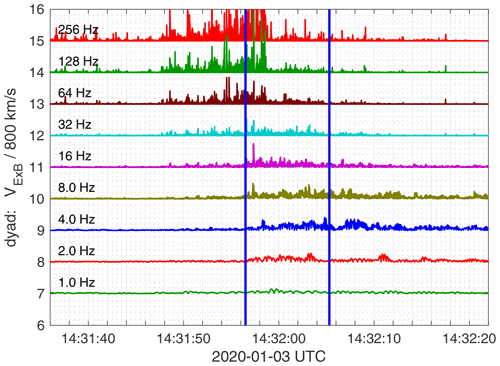
In Fig. 3 we show decomposition of ${\stackrel{\mathrm{̃}}{V}}_{E\times B}$, which corresponds to the energisation capacity of waves in the frequency range 1–256 Hz. The decomposition can be compared with the measured distribution functions shown in Fig. 2a–c. It indicates that the observed ions can be accelerated by the $\stackrel{\mathrm{̃}}{E}\times B$ mechanism. Acceleration capacity of waves increases with frequency and goes well over 1000 km s⁻¹ for f > 256 Hz.

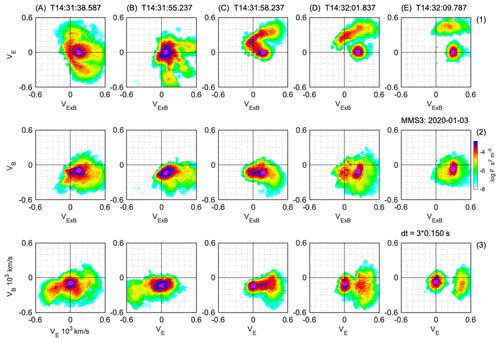
Figure 4 Ion distribution functions measured by the Fast Plasma Investigation (FPI) on MMS3 at times indicated in Fig. 2. The columns correspond to events A–E and show three projections of the ion distribution function. The first row shows a reduced two-dimensional distribution function in the perpendicular plane $F(v_{E\times B},v_{\mathrm{E}})$, the second row shows $F(v_{\mathrm{B}},v_{E\times B})$, and the third row shows F(v_B,v_E), integrated over the remaining velocity. Magenta circles show positions of the primary beam. The distributions are averages of three sampling times of 0.15 s each.

2.2 Ion distribution functions measured at shocks

We shall now inspect the measured ion distribution functions shown in Fig. 4 in columns A–E, which correspond to events marked in Fig. 2. Each picture shows a two-dimensional reduced distribution function in the reference system ($v_{E\times B},v_{\mathrm{E}},v_{\mathrm{B}}$). The distributions are averages of three measurements with sampling time 0.15 s each. Magenta circles mark positions of the primary beam in the measured distributions.

Event A shows partly thermalised ions in the magnetosheath with some remaining non-gyrotropic features. The crescent-like structure in distribution A1 is characteristic for $\stackrel{\mathrm{̃}}{E}\times B$ acceleration, which will be explained further. Event B shows ion distribution downstream of the shock peak, and event C shows the distribution on the upstream side of the peak. Event D is in the middle of the shock ramp, and E is in the foot of the shock.

All distributions are strongly non-gyrotropic and some are with separated beams. Similar distributions with double-beam structures have been reported by many authors (Paschmann et al., 1982; Gosling and Thomsen, 1985; Fuselier, 1994; Mazelle et al., 2003; Kucharek et al., 2004; Wilson, 2016; Johlander et al., 2016) and interpreted usually in terms of “specularly reflected ions, non-specularly reflected ions, gyrating ions, gyro-phase-bunched ions” or simply “shock reflected ions”.

Particularly puzzling are multiple peaks in the perpendicular plane (first row). Ions reflected from magnetic barriers could acquire a different parallel velocity component V_∥. But they are in the same electric field, so they should have the same ${\mathit{V}}_{⟂}\approx {\mathit{V}}_{E\times B}$ velocity component as the original solar wind beam, with possible modifications by temperature-dependent gradient drifts. However, we observe secondary beams in all directions in the perpendicular plane, with similar parallel velocities, which appears to be at odds with standard plasma physics. Ion distribution functions shown in Fig. 2a–c are inconsistent with the concept of reflection, which should produce a reflected ion beam in Fig. 2c (parallel direction) and possibly in Fig. 2a (E×B direction). Instead, the secondary beam is observed in Fig. 2b (E direction), which can be explained by the stochastic resonant acceleration (SRA) mechanism presented in the next section.

2.3 The $\stackrel{\mathrm{̃}}{E}\times B$ wave energisation mechanism

In this section we shall argue that the presented observations are consistent with the $\stackrel{\mathrm{̃}}{E}\times B$ acceleration (Stasiewicz and Eliasson, 2021). First, we should distinguish between the convection E×B drift of ∼ 500 km s⁻¹ used to establish the coordinate system and the wave electric drift ${\stackrel{\mathrm{̃}}{\mathit{V}}}_{E\times B}=\stackrel{\mathrm{̃}}{\mathit{E}}\times \mathit{B}/B^{\mathrm{2}}$ at higher frequencies. For wave amplitudes of ∼ 50 mV m⁻¹ in a magnetic field of 7 nT, the latter is ${\stackrel{\mathrm{̃}}{V}}_{E\times B}\sim$ 7000 km s⁻¹, corresponding to the gyration speed of a 250 keV proton, which can explain acceleration of ions in quasi-parallel shocks (Stasiewicz and Eliasson, 2021; Stasiewicz et al., 2021; Stasiewicz and Kłos, 2022).

Usually, particles do not obey the electric drift in waves with frequencies higher than the gyrofrequency or wavelengths shorter than the gyroradius. In such situations, the effects average to zero over the wave period or wavelength. However, when the electric field gradient ${\partial }_x{E}_x=k_x{\stackrel{\mathrm{̃}}{E}}_x$, with electrostatic waves with wave vector k_x, exceeds the stochastic condition in Eq. (2), the particle can be accelerated to the value in Eq. (1) within a fraction of the gyroperiod.

The mechanism of $\stackrel{\mathrm{̃}}{E}\times B$ acceleration by electrostatic waves can be studied with the Lorentz equation (Stasiewicz and Eliasson, 2020a, b, 2021). The previous model is generalised here for waves propagating in arbitrary direction in the perpendicular plane to the magnetic field ${\mathit{B}}_{\mathrm{0}}=(\mathrm{0},\mathrm{0},B_{\mathrm{0}})$. The position r and velocity v of an ion with mass m and charge q are determined by the equation $m\mathrm{d}\mathit{v}/\mathrm{d}t=q(\mathit{E}+\mathit{v}\times {\mathit{B}}_{\mathrm{0}})$ together with $\mathrm{d}\mathit{r}/\mathrm{d}t=\mathit{v}$. We assume that convection electric field E_y convects plasma into electrostatic wave ${\mathit{E}}_{\mathrm{w}}\sin ({\mathit{\omega }}_{\mathrm{D}}t-\mathit{k}\cdot \mathit{r})$ propagating in the (x,y) plane at angle α to the x direction, with the Doppler-shifted frequency ω_D in the observer's frame. By using dimensionless variables with time normalised by ${\mathit{\omega }}_{\mathrm{c}}^{-\mathrm{1}}$, space by k⁻¹ and velocity by ${\mathit{\omega }}_{\mathrm{c}}/k$ (with ${\mathit{\omega }}_{\mathrm{c}}=q{B}_{\mathrm{0}}/m_{\mathrm{p}}$ being the angular ion cyclotron frequency), the normalised equations of motion for a test ion in a stationary (shock related) frame are

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{\mathrm{d}{u}_x}{\mathrm{d}t}}=\left({\mathit{\chi }}_{\mathrm{w}}\cos \mathit{\alpha }\right)\sin \mathrm{\Phi }+u_y,\text{(6)}& {\displaystyle \frac{\mathrm{d}{u}_y}{\mathrm{d}t}}=\left({\mathit{\chi }}_{\mathrm{w}}\sin \mathit{\alpha }\right)\sin \mathrm{\Phi }-(u_x-{\mathit{\chi }}_{\mathrm{d}}),\text{(7)}& {\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}=u_x;{\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}=u_y.\end{array}$$

Here, $\mathrm{\Phi }={\mathrm{\Omega }}_{\mathrm{D}}t-x\cos \mathit{\alpha }-y\sin \mathit{\alpha }$ is the wave phase with the Doppler-shifted angular frequency ${\mathrm{\Omega }}_{\mathrm{D}}={\mathit{\omega }}_{\mathrm{D}}/{\mathit{\omega }}_{\mathrm{c}}=\mathrm{\Omega }+{\mathit{\chi }}_{\mathrm{d}}\cos \mathit{\alpha }$ with respect to $\mathrm{\Omega }=\mathit{\omega }/{\mathit{\omega }}_{\mathrm{c}}$ in the plasma frame. The normalised amplitudes of the $\stackrel{\mathrm{̃}}{E}\times B$ drift and the convection drift are, respectively,

$$\begin{array}{}\text{(8)}& {\mathit{\chi }}_{\mathrm{w}}={\displaystyle \frac{E_{\mathrm{w}}}{B_{\mathrm{0}}}}{\displaystyle \frac{k}{{\mathit{\omega }}_{\mathrm{c}}}};{\mathit{\chi }}_{\mathrm{d}}={\displaystyle \frac{E_y}{B_{\mathrm{0}}}}{\displaystyle \frac{k}{{\mathit{\omega }}_{\mathrm{c}}}}.\end{array}$$

Please note that χ_w=χ_p represents here the stochastic wave parameter given by Eq. (2). By setting χ_d=0, we obtain equations in the plasma frame of reference.

The most efficient energisation occurs on the acceleration lane (Stasiewicz and Eliasson, 2021), which corresponds to u₀=Ω that matches particle velocity with phase speed of waves. The initial conditions for the here-presented solutions are chosen in such a way that the gyration velocity v₀ at t=0 is aligned with the ($k_x,k_y,\mathrm{0}$) vector or alternatively with the phase velocity of waves so that in the plasma frame we have

$$\begin{array}{}\text{(9)}& u_{x\mathrm{0}}=u_{\mathrm{0}}\cos \mathit{\alpha },u_{y\mathrm{0}}=u_{\mathrm{0}}\sin \mathit{\alpha };\end{array}$$

where $u_{\mathrm{0}}=v_{\mathrm{0}}k/{\mathit{\omega }}_{\mathrm{c}}=k{r}_{\mathrm{c}}$, and $r_{\mathrm{c}}=v_{\mathrm{0}}/{\mathit{\omega }}_{\mathrm{c}}$ is the gyroradius.

Generally the equations have chaotic solutions, because for χ_w>1 the solutions are very sensitive for initial conditions and have positive Lyapunov exponent (Balikhin et al., 1993; Stasiewicz et al., 2000). They are representative of deterministic chaos. The parameters of these equations are the following: Ω, χ_w, χ_d, u₀ and α, which can be varied to fit particular physical conditions.

Figures 5 and 6 show examples of solutions applicable to the foot/upstream region of the shock in Fig. 2e, where the assumption B≈  const. is valid, and we see ions accelerated in the y direction, presumably by lower hybrid waves in Fig. 2f. The frequency Ω=25 is below the lower hybrid frequency Ω_lh≈43, and the ratio ${\mathit{\chi }}_{\mathrm{w}}/{\mathit{\chi }}_{\mathrm{d}}=E_{\mathrm{w}}/E_y=\mathrm{8}$ is realistic.

At time $t=-\mathrm{1}$ the proton in Fig. 5 has initial gyration energy $K_{\mathrm{0}}=u_{\mathrm{0}}^{\mathrm{2}}$ and is drifting earthward with the convection speed $u_x={\mathit{\chi }}_{\mathrm{d}}=\mathrm{5}$. During time $t=\mathrm{0}-\mathrm{0.4}$ it experiences a burst of waves with amplitude χ_w=40. We see that the gyration energy $K=u_x^{\mathrm{2}}+u_y^{\mathrm{2}}$ has increased more than 4 times after a couple of wave periods. The acceleration is in the u_y direction, while u_x is constant, which could correspond to Fig. 4, column E, row 1.

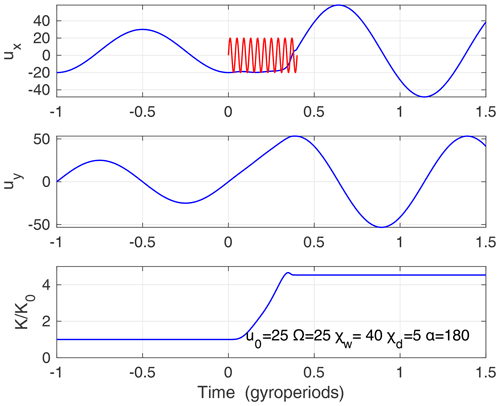
Figure 5 Exact solutions of Eqs. (5)–(9) with a numerical accuracy of 10⁻⁶. A proton with normalised gyration speed u₀=25 is drifting earthward with convection speed $u_x={\mathit{\chi }}_{\mathrm{d}}=\mathrm{5}$. At time t=0 it encounters a burst of waves with frequency f=25f_cp propagating upstream, α = 180^∘, active during time $\mathrm{0.4}{f}_{\text{cp}}^{-\mathrm{1}}$. The particle is accelerated by more than 4 times the initial gyration energy as shown in the lower panel. Acceleration increases u_y while u_x remains constant, which corresponds to the situation seen in Fig. 4, column E, row 1.

The convection electric field E_y is an essential element in the shock surfing (or surfatron) acceleration (SSA) by waves in front of shocks (Shapiro et al., 2001; Shapiro and Ucer, 2003) and in shock drift acceleration (SDA) models based on the magnetic gradient drift. The situation observed in Fig. 2b, where particles are accelerated along the convection electric field E_y, suggests that we may have the surfatron case here.

To illuminate the significance of E_y for acceleration of particles, we show in Fig. 6 similar solutions as in Fig. 5 but with convection switched off by setting χ_d=0. It can be seen that energisation of particles does not depend on the value of E_y, so the positioning of secondary ion beams along v_E in measurements is circumstantial.

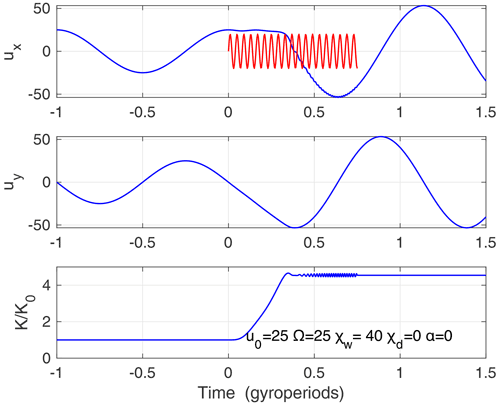
Figure 6 The same as in Fig. 5 but without the convection electric field, i.e. χ_d=0. The waves are active a longer time during $\mathrm{0.75}{f}_{\text{cp}}^{-\mathrm{1}}$, and the propagation direction of waves is reversed, i.e. α=0. Acceleration is the same but in the negative u_y direction.

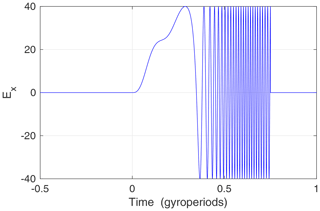
Figure 7 The normalised wave electric field E_x=χ_wsin Φ seen by the proton from Fig. 6. Acceleration occurs only during coherence time 0–0.3 $f_{\text{cp}}^{-\mathrm{1}}$ by means of v_xE_x>0. The energy gain is transferred to v_y by the Lorentz force ${\dot{v}}_y=-(q/m)v_x{B}_z$.

The position of accelerated particles in the perpendicular plane $(v_x,v_y)\equiv (v_{E\times B},v_{\mathrm{E}})$ is controlled by the wave propagation direction. For waves propagating upstream, α = 180^∘ (−x direction) and it is in the positive v_y direction, while for α=0 it is in the negative v_y direction. At time 14:31:50  UTC in Fig. 2b we see ions accelerated in the negative v_E direction, which is most likely due to downstream-propagating waves as in case of Fig. 6. For waves propagating at α =  ± 90^∘, the acceleration is in the v_x or equivalently v_E×B direction, which is also observed in measurements. By changing the wave propagation angle α and the amplitude of waves χ_w, we can reproduce any secondary ion peak which can be found in Fig. 4, row 1. A free gyration after acceleration would produce crescent-like structures seen in most distributions.

It can also be seen that the duration of wave activity is not an essential factor. In Fig. 7 we show the electric field E_x seen by the particle along the trajectory made in Fig. 6. The energisation occurs only during short coherence time after t=0 by means of v_xE_x>0. The work done by the electric field on the v_x component is transferred to the v_y component by the Lorentz force v_xB_z. The mechanism is inherently bursty and works only during short coherence times of a few wave periods. After decoherence, the waves do not affect particles anymore, as can be seen in Figs. 5–7. We can conclude that stochastic particle energisation by waves is performed in a sequence of coherent resonant interactions. This leads to the concept of stochastic resonant acceleration (SRA) as a complementary description of the $\stackrel{\mathrm{̃}}{E}\times B$ wave mechanism. The coherence/resonance is between the wave phase speed $\mathit{\omega }/k_{⟂}$ and the particle initial gyration velocity v_⟂ (not drift velocity) in the plasma reference frame. This resonance should not be confused with a better-known parallel resonance $(\mathit{\omega }-n{\mathit{\omega }}_{\mathrm{c}})/k_{\parallel }=v_{\parallel }$.

The stochastic condition in Eq. (2) is necessary for energisation of particles. When χ_w<1, no acceleration can be produced by Eqs. (5)–(9), irrespective of the values of other parameters. The convection electric field E_y plays no role in the $\stackrel{\mathrm{̃}}{E}\times B$ energisation, which could be anticipated. Indeed, transformation between the plasma frame of reference (where E_y=0, χ_d=0) and the shock fixed frame with the convection electric field cannot involve E_y in particle energisation as both are equivalent inertial systems.

Secondary beams in the perpendicular plane, such as those seen in Figs. 2b and 4 are commonly observed in front of quasi-perpendicular shocks and have been usually described as shock-reflected ions. In shock reflection scenarios it has been usually assumed that the E_x field which makes the cross-shock potential is also responsible for the reflection. Contrary to this popular belief, a strong E_x field does not reflect ions upstream but accelerates them in the y direction through the $\stackrel{\mathrm{̃}}{E}\times B$ mechanism in a stochastic resonant way.

The heating maps published by Stasiewicz and Eliasson (2020a, 2021) show that stochastic heating is most efficient for electrostatic waves in the frequency range (0.1–10) f_cp with the maximum efficiency depending on the value of χ. Kinetic simulations which can resolve frequencies around ∼ f_cp, e.g. Leroy et al. (1982), Lowe and Burgess (2003), Hellinger et al. (2007) and Caprioli et al. (2014), exhibit signatures of ions accelerated by the SRA mechanism. However, these accelerated ions have been described as “shock reflected” by authors being unaware of the SRA mechanism.

3 Conclusions

This research provides confirmation of the plasma heating/acceleration scenario in shocks outlined in earlier publications (Stasiewicz, 2020; Stasiewicz and Eliasson, 2020a, b, 2021; Stasiewicz et al., 2021). Shocks' oscillatory movements and the development of compressions are related to a 1 mHz wave in Fig. 1d. Non-linear steepening of low-frequency magnetosonic waves leads to density gradients that appear to trigger ion cyclotron waves as seen in magnetic waveforms in Fig. 1d and in the electric spectrogram in Fig. 2f. The instability progresses to waves around the lower hybrid frequency (∼ 10 Hz) and further up to a few kilohertz, generating a cascade of instabilities LHD → MTS → ECD mentioned in the Introduction. The significance of these cross-field current-driven instabilities for heating of the solar wind plasma has been advocated earlier by many authors (Forslund et al., 1972; Lashmore-Davies and Martin, 1973; Yamada and Owens, 1977; Wu et al., 1983; Zhou et al., 1983; Winske et al., 1985; Drake et al., 1983; Gary, 1993; Daughton, 2003; Muschietti and Lembége, 2017).

Using only the fundamental Lorentz equation, we have identified the $\stackrel{\mathrm{̃}}{E}\times B$ wave mechanism which explains how waves around the lower hybrid frequency and above accelerate ions to velocities of 800 km s⁻¹, as can be seen in Figs. 2 and 3. We have shown that stochastic particle energisation by waves occurs in a series of coherent resonant interactions. The nature of this mechanism can be described as a stochastic resonant acceleration (SRA). The resonance is between the wave phase speed $\mathit{\omega }/k_{⟂}$ and the particle initial gyration velocity v_⟂. The model is also capable of explaining multibeam ion distributions measured at shocks and shown in Fig. 4. These secondary beams have been described in the literature as “shock-reflected particles”, without physical explanation of the reflection process.

Energisation of particles depends on interaction time with waves. Particles are convected rapidly across perpendicular shocks with thickness of 100 km but can spend considerably longer times in a spatially extended turbulence (a few R_E) of quasi-parallel shocks. The short interaction time in quasi-perpendicular shocks limits the ion acceleration to a few kilo-electronvolts or velocities v_p < 1000 km s⁻¹ as can be seen in Figs. 1a, 2a–c and 4. Waves involved in acceleration are in the frequency range of ∼ f_lh and above, as can be seen in the acceleration capacity shown in Fig. 3. The longer interaction time with higher-amplitude waves at higher frequencies in quasi-parallel shocks makes it possible to accelerate protons to velocities of v_p ∼ 7000 km s⁻¹ that correspond to energies of 250 keV (Stasiewicz et al., 2021; Stasiewicz and Kłos, 2022).

Using exceptional-quality multipoint measurements by MMS, we have made exact determinations of the shock ramp thickness, which is about 100 km, while the ramp and foot combined have a thickness of 2 gyroradii that embraces the whole ion cyclotron orbit (or 200 km). We have also pointed out that high perpendicular ion temperatures measured in front of shocks are mainly the result of secondary beams produced by the wave acceleration process.