the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Ionospheric response to solar extreme ultraviolet radiation variations: comparison based on CTIPe model simulations and satellite measurements
Rajesh Vaishnav
Erik Schmölter
Christoph Jacobi
Jens Berdermann
Mihail Codrescu
The ionospheric total electron content (TEC) provided by the International GNSS Service (IGS) and the TEC simulated by the Coupled Thermosphere Ionosphere Plasmasphere Electrodynamics (CTIPe) model have been used to investigate the delayed ionospheric response against solar flux and its trend during the years 2011 to 2013. The analysis of the distinct low-latitude and midlatitude TEC response over 15∘ E shows a better correlation of observed TEC and the solar radio flux index F10.7 in the Southern Hemisphere compared to the Northern Hemisphere. Thus, a significant hemispheric asymmetry is observed.
The ionospheric delay estimated using model-simulated TEC is in good agreement with the delay estimated for observed TEC against the flux measured by the Solar Dynamics Observatory (SDO) extreme ultraviolet (EUV) Variability Experiment (EVE). The average delay for the observed (modeled) TEC is 17(16) h. The average delay calculated for observed and modeled TEC is 1 and 2 h longer in the Southern Hemisphere compared to the Northern Hemisphere.
Furthermore, the observed TEC is compared with the modeled TEC simulated using the SOLAR2000 and EUVAC flux models within CTIPe over northern and southern hemispheric grid points. The analysis suggests that TEC simulated using the SOLAR2000 flux model overestimates the observed TEC, which is not the case when using the EUVAC flux model.
- Article
(6999 KB) - Full-text XML
- BibTeX
- EndNote
The ionospheric day-to-day variations are mainly controlled by fluctuations of solar extreme ultraviolet/ultraviolet (EUV/UV) radiation responsible for photoionization and photo-dissociation processes, lower atmospheric forcing, and space weather events such as geomagnetic storms. During geomagnetically and meteorologically quiet conditions, the electron density gradually increases after sunrise, with a maximum around 14:00 LT due to photochemical processes, and starts decreasing thereafter due to the combined effect of production and strong recombination, continuing after sunset due to recombination processes.
The solar radiation flux varies at different timescales, including the diurnal cycle, the 27 d solar rotation period, and the prominent 11-year solar cycle. This results in corresponding variations in composition and dynamics of the thermosphere–ionosphere (T–I) system (Hedin, 1984). The T–I system is highly variable with location and time, depending on the solar activity and geomagnetic disturbances.
The photoionization processes in the ionosphere cause different variations, including short-term variability at the timescale of the 27 d solar rotation or seasonal variations. Past studies on the effect of solar radiation variations at different timescales have been based on the total electron content (TEC, frequently given in TECU; 1 TECU= 1016 electrons m−2), peak electron density (NmF2, cm−3), and the corresponding height (HmF2, km) (e.g., Jakowski et al., 1991; Afraimovich et al., 2008; Lee et al., 2012; Jacobi et al., 2016; Schmölter et al., 2018, 2020; Vaishnav et al., 2018, 2019; Ren et al., 2018, and references therein).
The annual contributions to the mean TEC variability have a stronger impact on the Southern Hemisphere, whereas the semi-annual contributions have similar phase and amplitude at conjugate points, suggesting close coupling between the ionosphere and thermosphere (Liu et al., 2009). Mendillo et al. (2002) suggested that both annual and semi-annual variations of NmF2 are largely caused by changes in the neutral composition, which are driven by the global thermospheric circulation.
Solar proxies are frequently used to represent the solar activity. Among them are the F10.7 index, the Mg-II index, and the He-II index. Furthermore, attempts have been made to determine simple proxies for global TEC variability based on these indices (e.g., Unglaub et al., 2011). These proxies have been compared to the ionospheric parameters at the timescale of the 27 d solar rotation. An ionospheric delay of about 1–2 d has been reported (e.g., Jakowski et al., 1991; Jacobi et al., 2016). Using a more precise and higher temporal resolution solar flux, an ionospheric delay of about 17–19 h has been reported by Schmölter et al. (2018). The spatial and seasonal effects on the ionospheric delay have been further investigated in detail by Schmölter et al. (2020) using European and Australian locations. Their study highlighted the role of geomagnetic activity in the ionospheric delay.
To investigate the process associated with the ionospheric delay, Jakowski et al. (1991) used a one-dimensional numerical model between 100 and 250 km altitude with simplifying assumptions. They suggested that a delay of approximately 2 d arises in atomic oxygen at 180 km due to photo-dissociation and transport processes. This hypothesis has yet to be confirmed with comprehensive ionospheric models such as CTIPe (Coupled Thermosphere Ionosphere Plasmasphere Electrodynamics). Ren et al. (2018) investigated the ionospheric delay using observations and modeling. They emphasized the role of the ratio in the ionospheric delay. Vaishnav et al. (2018) suggested the possible role of transport processes in the ionospheric delay.
During the past decades, more improved physics-based T–I models have been developed which are able to characterize ionospheric dynamics. Among them are the Coupled Thermosphere Ionosphere Plasmasphere Electrodynamics model (CTIPe; Fuller-Rowell and Rees, 1983; Codrescu et al., 2012), the Thermosphere–Ionosphere–Electrodynamics General Circulation Model (TIE-GCM; Richmond et al., 1992), and the Global Ionosphere Thermosphere Model (GITM; Ridley et al., 2006). Furthermore, some extended Earth system models like WACCM-X (Liu et al., 2018) and the Ground-to-topside model of Atmosphere and Ionosphere for Aeronomy (GAIA; Jin et al., 2012; Liu et al., 2020) include T–I dynamics. Based on the results of the T–I model, an ionospheric lag against variations of the solar EUV could be identified, whereby the EUV entry in the model was represented by the F10.7 index (Ren et al., 2018; Vaishnav et al., 2018).
The most commonly used solar proxy for ionizing irradiance is the solar radio flux at 10.7 cm (F10.7 index, given in solar flux units (sfu); 1 sfu ) (Tapping, 1987). Most of the T–I models use a modified F10.7 index (e.g., the average of daily and 41 or 81 d averages) to calculate the model EUV spectra based on reference spectra. Several authors have reported that a modified F10.7 index, which includes both short-term and long-term variability, is a better proxy for ionizing irradiance than F10.7 directly (Richards et al., 1994). There are several empirical models available, such as the SOLAR2000 (Tobiska et al., 2000) and EUVAC flux model (Richards et al., 1994), to calculate the irradiance.
Profiles of the delayed ionospheric response dependent on latitude have been calculated in previous studies (Lee et al., 2012; Ren et al., 2018), and the influence of seasonal variations and geomagnetic activity on both hemispheres has also been characterized (Schmölter et al., 2020). The complexity of the seasonal variations and associated anomalies has been investigated in other studies for ionospheric parameters like TEC (Romero-Hernandez et al., 2018). Such seasonal anomalies were observed in the F2 region associated with higher electron density in winter than in summer during daytime (the so-called winter or seasonal anomaly), during equinoxes than during solstices (semi-annual anomaly), and in December than in June (annual or non seasonal anomaly) (Balan et al., 1998; Zou et al., 2000; Romero-Hernandez et al., 2018). However, seasonal variations have not yet been analyzed for the ionospheric delay.
The ionospheric electron density (or ion density) is mainly controlled by the photoionization, the loss through recombination, and transport processes. Transport processes play a significant role in the T–I composition and are responsible for the plasma distribution, possibly leading to the observed ionospheric anomalies. Fuller-Rowell (1998) suggests a possible mechanism associated with the seasonal anomaly through the neutral wind.
This study aims to analyze the ionospheric TEC variations in both the Northern and Southern Hemisphere during a moderate solar activity during the inclining phase of solar cycle 24 (2011–2013). We use GNSS data from 70∘ S to 70∘ N latitude at 15∘ E longitude due to better coverage with ground measurements in TEC maps. The observed TEC is compared with the model-simulated TEC using different solar EUV flux models. The ionospheric delay against solar EUV flux has been investigated by Schmölter et al. (2020) using TEC observations. Therefore, the focus of the present study is laid on the ability to reproduce the ionospheric delay using the CTIPe model at 15∘ E.
In Sect. 2, we introduce the data sources and the CTIPe model. In Sect. 3, we investigate the TEC variability and a possible relationship with F10.7 index variations and compare TEC simulated with the different solar EUV flux models. In Sect. 4, we summarize our conclusions.
2.1 TEC observations
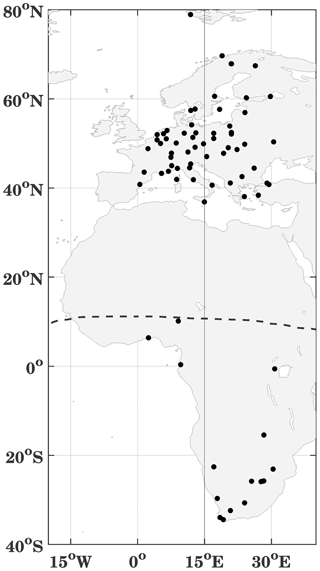
In this paper, we use TEC data from 70∘ S to 70∘ N latitude at 15∘ E from the International GNSS Service (IGS) provided by NASA's CDDIS (Noll, 2010), which are available at 1 h time resolution and with a latitude–longitude resolution of (Hernández-Pajares et al., 2009). The accuracy of IGS TEC maps is given with 2–8 TECU (Chen et al., 2020). There are only few IGS stations in the Southern Hemisphere, but in the Northern Hemisphere (European region), there are several ground stations located around 15∘ E, as shown in Fig. 1.
2.2 Solar EUV radiation
Several solar proxies are available that have frequently been used in previous studies to represent the solar activity level compared to the ionospheric parameters before the space age and due to the unavailability of direct solar EUV measurements. Continuous time series of the solar EUV spectrum itself, however, have been available since the launch of the NASA Thermosphere Ionosphere Mesosphere Energetics and Dynamics (TIMED) satellite mission in 2001. Solar irradiance measurements from the TIMED Solar Extreme Ultraviolet Experiment (SEE) instrument have been available since 22 January 2002 (Woods et al., 2005). The SEE instrument is designed to measure the soft X-rays and EUV radiation from 0.1 to 194 nm, with resolution and accuracy of 0.1 nm and approximately 10 %–20 %. SEE includes two instruments, the EUV grating spectrograph and the soft X-ray (XUV) photometer system (Woods et al., 2000). Here we use daily values of solar irradiance integrated from 1 to 105 nm wavelength. The TIMED SEE observations are used for comparison with the empirical solar flux models, SOLAR2000 and EUVAC.
Furthermore, the Solar Dynamics Observatory (SDO) EUV Variability Experiment (EVE) provides a continuous high-resolution spectrum with a wavelength range from 0.1 to 120 nm, a spectral resolution of 0.1 nm, and a temporal resolution of 20 s. (Woods et al., 2010; Pesnell et al., 2011). The high-resolution EUV observations provided by the SDO EVE satellite have been used to calculate an ionosphere delay in TEC.
Solar proxies are mostly used as a solar activity representation in thermosphere–ionosphere models. Hence, we also use the daily F10.7 index for our analysis.
2.3 CTIPe model
The CTIPe model is a global, first-principle, three-dimensional numerical, physics-based coupled thermosphere–ionosphere–plasmasphere model, which self‐consistently solves the primitive equations of continuity, momentum, and energy to calculate wind components, global temperature, and the composition of neutrals, which is further used to calculate plasma production, loss, and transport. The model consist of four components, namely a neutral thermosphere model (Fuller-Rowell and Rees, 1980), a midlatitude and high-latitude ionosphere convection model (Quegan et al., 1982), a plasmasphere and low-latitude ionosphere model (Millward et al., 1996), and an electrodynamics model (Richmond et al., 1992). The calculations are performed with latitude/longitude resolution. In the vertical direction, the atmosphere is divided into 15 levels in logarithmic pressure at an interval of one scale height, starting from a lower boundary at 1 Pa (about 80 km altitude) to above 500 km altitude at pressure level 15. The high-latitude ionosphere (above 55∘ N or S) and the midlatitude–low-latitude ionosphere–plasmasphere components have been implemented as separate modules.
The numerical solution of the composition equation and the energy and momentum equations describe transport, turbulence, and diffusion of atomic oxygen, molecular oxygen, and nitrogen (Fuller-Rowell and Rees, 1983). To run the model, external inputs are required like solar UV and EUV, Weimer electric field, TIROS/NOAA auroral precipitation, and tidal forcing from the Whole Atmosphere Model (WAM). The F10.7 index is used as an input solar proxy to calculate ionization, heating, and oxygen dissociation processes in the ionosphere. The CTIPe ionosphere results include the major ion species H+ and O+ for all altitudes and other molecular and atomic ions, N2, O2, NO+, and N+, below 400 km. Detailed information on the CTIPe model is available in Codrescu et al. (2008, 2012) and Fernandez-Gomez et al. (2019).
2.4 EUV representation in the CTIPe model
2.4.1 SOLAR2000 model
The SOLAR2000 model is the most recent EUV model version in a series of iterations by Tobiska et al. (2000). SOLAR2000 incorporates multiple satellite and rocket measurements, including the AE-E satellite observations, to specify both a reference spectrum and solar variability. The EUV is calculated using the Lyman-α flux and the F10.7 index with the set of modeling equations. SOLAR2000 determines the EUV irradiance for 809 emission lines and also for 39 wavelength bands.
2.4.2 EUVAC solar flux model
Within CTIPe, a reference solar spectrum based on the EUVAC model (Richards et al., 1994) and the Woods and Rottman (2002) model, driven by variations of input F10.7, is used. The EUVAC model is used between 5 and 105 nm and the Woods and Rottman (2002) model for 105 to 175 nm. Solar flux is obtained from the reference spectra using the following equation:
where fref and A are the reference spectrum and solar variability factor, respectively, and (F10.7 + F10.7A), where F10.7A is the average of F10.7 over 81 d.
The EUVAC model includes solar flux in 37 wavelength bins based on the measured F74113 solar EUV reference spectrum (Hinteregger et al., 1981) and the solar cycle variation of the flux.
2.4.3 Comparisons between empirical EUV irradiance variability models and observations
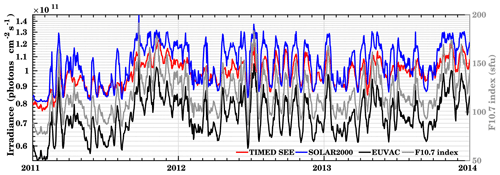
We compare TIMED SEE observations with the two empirical models constructed from direct proxy parameterizations of the EUV irradiance database, which are used to represent EUV in the CTIPe model.
Figure 2 shows the modeled integrated irradiance spectra from 5 to 105 nm calculated by both models, together with the TIMED SEE irradiance from 2011 to 2013. The second y axis shows the F10.7 index used to calculate the spectra in empirical models. In comparison to the SOLAR2000 model flux and TIMED SEE, flux values calculated by the EUVAC model are smaller. There is a significant difference between the flux models and the observed irradiance. The flux calculated by the SOLAR2000 model overestimates the observed flux mostly during the Northern Hemisphere winter months, whereas it is in good agreement during Northern Hemisphere summer months. The observed EUV irradiance during moderate solar activity is comparable to the SOLAR2000 flux, with a difference of about 10 % and 23 % higher than the EUVAC model. The EUVAC flux is about 30 % lower than the SOLAR2000 model. The correlation coefficient of EUV from both the EUV flux models with the observed EUV flux is approximately 0.90 during the study period. In summary, the SOLAR2000 model is in relatively good agreement with the observed flux, while the EUVAC model underestimates SOLAR2000 and the TIMED SEE flux. These results agree with earlier comparisons (Lean et al., 2003; Woods et al., 2005; Lean et al., 2011, and references therein).
Woods et al. (2005) compared the TIMED SEE observations with the flux calculated from different empirical models for 8 February 2002. They reported that the empirical models are within 40 % of the SEE measurement at wavelengths above 30 nm. The EUVAC and SOLAR2000 models agreed best with TIMED SEE, compared to the other models.
Lean et al. (2003) validated the NRLEUV model with different empirical models such as SOLAR2000, HFG (Hinteregger et al., 1981), and EUVAC. In absolute scales, NRLEUV, HFG, and EUVAC have total energies that agree within 15 %, but the SOLAR2000 absolute scale is more than 50 % higher. Their study reveals that long EUV wavelength (70 to 105 nm) energy contributions (about 46 % of the whole flux from 5 to 105 nm) are the main reason for the higher EUV flux in the SOLAR2000 model compared to other empirical models.
In the following sections, we show the results and discuss the TEC observations and their comparison with the modeled TEC at 15∘ E. Furthermore, relations with solar radiation and the delayed response over both the Northern and Southern Hemispheres are presented. Schmölter et al. (2020) have reported on a detailed investigation of the delayed ionospheric response over European and Australian regions. Here, we analyze the delayed response at 15∘ E covering the latitudes from 70∘ S to 70∘ N and compare the response over the southern African region with the European region.
In this study we have addressed the following points:
-
The TEC variations at moderate solar activity of solar cycle 24 are analyzed to compare the input for the delay analysis. A characterization of these differences between observed and modeled TEC is important to derive further relations.
-
We used the periodicity estimation (frequency analysis) to study observed and modeled TEC characteristics in detail.
-
The relation between the F10.7 index and hemispheric TEC has been used to analyze the solar and ionospheric inputs of delay estimation.
-
In our study we focus on the ionospheric delay estimation as a main point of our analysis.
-
The comparison of observed TEC variations with simulated TEC is done by using different flux models. In previous work it has already be shown that the solar activity has the strongest impact on TEC under nominal conditions and is therefore significant for the derived delay.
3.1 TEC variation at moderate solar activity of solar cycle 24
The ionospheric electron density strongly varies from day to night depending on the daily variations of solar radiation.
Figure 3 depicts the 11:00–13:00 LT averaged midday variations in TEC for the moderate solar activity conditions from 2011 to 2013. The figure shows the comparison between the observed TEC and modeled TEC simulated using the EUVAC flux model at 15∘ E longitude. Note that at this longitude, climatological hemispheric differences in TEC are expected due to peculiarities of the magnetic field, in particular the South Atlantic Anomaly, which causes low ionization in the Southern Hemisphere.
The TEC variations highly depend on the level of ionization due to the solar radiation flux. The observed TEC shows such variations compared to the SDO EVE-integrated flux (1–120 nm), as shown on the second y axis of Fig. 3. During 2012, there are continuous 27 d cycles. This kind of regular variation in solar observations enables us to explore the respective ionospheric variations, which are clearly driven by the ionization and recombination processes.
The maximum TEC is observed at the Equator and in low-latitude regions. The TEC level reduces towards the high-latitude regions. In general, the TEC values vary latitudinally depending on the northern and southern hemispheric season. At the Equator, the plasma moves upward and redistributes along the Equator, causing the fountain effect (Appleton, 1946). The thermospheric wind circulations firmly control the plasma movement. The plasma moves from the summer hemisphere to the winter one, causing a decrease in the F peak height, further decreasing the ratio. The TEC values in the Southern Hemisphere are higher than in the Northern Hemisphere.
Figure 3a shows maximum TEC around the Equator during the December solstice, and a minimum of TEC is observed during the June solstice of 2011, which coincides with the minimum solar EUV flux. There are local minima during equinoxes in 2013.
In comparison to observed TEC, the modeled TEC (Fig. 3b) is lower during the spring and summer period in the Southern Hemisphere, while it is in better agreement during the winter season. The bias between the modeled and observed TEC is higher during the spring and summer season in the Southern Hemisphere. In general, the modeled TEC is lower than the observed TEC.
The variations in TEC are not only controlled by the solar radiation, but there are also other factors such as local dynamics or geomagnetic activities due to solar wind variations, which also influence the ionospheric state (Abdu, 2016). Fang et al. (2018) studied day-to-day ionospheric variability and suggested that absolute values in TEC variability at low latitudes are largely controlled by solar activity, while for midlatitudes and high latitudes, however, solar and geomagnetic activities contribute roughly equally to the absolute TEC variability.
A detailed comparison between the observed TEC and modeled TEC simulated using the different solar flux models (SOLAR2000 and EUVAC) during January, June, and December is presented and discussed in Sect. 3.6.
3.2 Periodicity estimation
Solar activity varies at different timescales from minutes to years or even centuries. The periodic behavior in the solar proxies has been studied by various authors to explore the response of the terrestrial atmosphere and especially the T–I region and to investigate the connection between solar variability and ionospheric parameters (Jacobi et al., 2016; Vaishnav et al., 2019). A widely used method to analyze periodicities in time series is the continuous wavelet transform (CWT). The CWT captures the impulsive events when they occur in the time series (Percival and Walden, 2000; Mallat, 2009). However, the CWT also reveals lower frequency features of the data hidden in the time series.
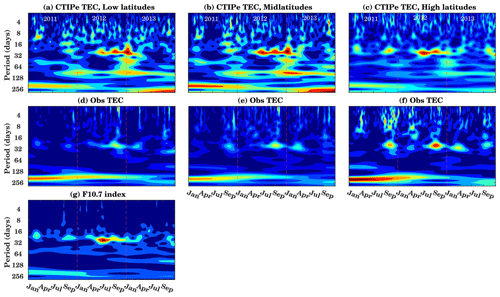
Here, we will investigate and compare the different temporal patterns of observed and modeled TEC. The daily TEC and F10.7 index from 2011 to 2013 are used to analyze the periodic behavior of the T–I system. Figure 4 shows the continuous wavelet spectra of the model-simulated TEC, observed TEC, and F10.7 for low latitudes [], midlatitudes [± (30–60∘)], and high latitudes [± (60–70∘)] from 2011 to 2013. Here averaged TEC is used for the low latitudes, midlatitudes, and high latitudes.
The upper panels (a)–(c) of Fig. 4 show the CWT of modeled TEC, while the middle panels (d)–(f) show the observed TEC, respectively, over the different latitude bands mentioned in the figure title. The lower panel (g) shows the CWT of F10.7.
The CWT of modeled TEC shows the dominant 16–32 d oscillations during 2012. This is, however, not the case during 2011 and 2013. During these periods, the influence of other dynamical processes in the ionosphere (e.g., lower atmospheric forcing) is stronger. During these years, very weak 27 d periodicity is observed. The 27 d period is stronger during December and January. Pancheva et al. (1991) showed that the 27 d variation in the lower ionosphere (D region) is often caused by dynamical forcing (planetary waves), particularly in the winter season under low solar activity. A similar 16–32 d periodicity is observed in the F10.7 index. It is well known that the 27 d periodicity is one of the major and dominant modes of variations in the solar proxies.
As an advantage, the CWT also shows small-scale features. Over low latitudes and midlatitudes, 8–16 d oscillations are observed to be dominant. Furthermore, another high-power region is visible in the 128–256 d period, representing the semi-annual oscillations in both modeled and observed TEC and in the F10.7 index. The semi-annual oscillation is mostly dominant during the period of investigation. Apart from it, in model-simulated TEC, a 64–128 d period is observed during 2012 and 2013. The oscillations are stronger at low-latitude and midlatitude stations compared to high latitudes.
The second row of Fig. 4 shows the oscillations in the observed TEC. Here, a weak 27 d cycle is observed during December, and the 128–256 d period is mostly dominant during 2011 and 2012. There is a weak signature of semi-annual oscillations during 2013. As compared to the periodicity observed in model-simulated TEC, the 64–128 d periodicity is missing in the observations over all the latitudes. Furthermore, shorter period fluctuations can be seen, especially at high latitudes (Fig. 4f), with a preference for the winter season. These may be connected with planetary wave effects from below (e.g. Altadill et al., 2001, 2003).
Figure 4g shows the CWT spectra of the F10.7 index. Here the dominant period is 16–32 d during 2012, and a weak 16–32 d period oscillation is observed during 2011 and 2013.
In general, from the above investigation, it can be seen that 16–32 d periodicity was dominant during 2012. Vaishnav et al. (2019) used cross-wavelet and Lomb–Scargle periodogram techniques to estimate the periodicity of various solar proxies and global TEC during long time series from 2000–2016. They found that the semi-annual oscillation is mostly dominant during the solar maximum years 2001–2002 and 2011–2012.
3.3 Relation between F10.7 index and hemispheric TEC
Solar activity has the strongest effect on ionospheric variations, especially during enhanced solar activity. The last solar minimum was extremely extended, and the following solar cycle was quite weak (e.g., Huang et al., 2016), so that meteorological influences become more relevant. To examine the effect of solar activity on TEC variations during a weak solar cycle, we analyzed the relationship between F10.7 and midday TEC (11:00–13:00 LT). Figure 5 shows the correlation between TEC and F10.7 during 2011–2013 for the Northern Hemisphere (NH; upper panels) and Southern Hemisphere (SH; lower panels), indicating the correlation coefficient (R). In order to represent the NH and SH, daily data of 40∘ N and 40∘ S latitudes at 15∘ E longitude have been used respectively. The mean root mean square (rms) at 40∘ N is 6.92 TECU, and the mean rms at 40∘ S is 7.54 TECU for the whole period.
We have calculated correlations using the observed TEC over the NH and SH. During 2011, the maximum correlation for all the years is observed, which amounts to R=0.71/0.79 for the NH/SH. This suggests that midday TEC values are mainly controlled by solar EUV radiation.
From the current study and past publications (Romero-Hernandez et al., 2018), it is well known that during high solar activity, weak correlations are observed compared to the moderate solar activity conditions. But during the year 2012, the lowest correlation of about 0.06 was observed in the SH, while the correlation was about 0.36 in the NH region. During the year 2013, the correlation is weaker than during 2011, namely about 0.42 for the NH and 0.60 for the SH.
In general, the correlation coefficient is higher in the southern hemispheric region as compared to the Northern Hemisphere during 2011 and 2013, whereas lower correlations are observed during the year 2012. The analysis for 2012 shows some unexpected behavior over these study regions. This unusual behavior could be due to physical and chemical processes that have an impact on the ionospheric state.
3.4 Cross-correlation and delay estimation
The possible relations between solar activity, geomagnetic activity, and ionospheric parameters have been studied by several authors (e.g., Abdu, 2016; Fang et al., 2018; Vaishnav et al., 2019). However, several past studies, due to the unavailability of high-resolution datasets, used only daily resolution. To estimate the ionospheric delay, different ionospheric parameters have been considered using daily resolution data; an ionospheric delay of about 1–2 d against solar proxies has been reported (Jakowski et al., 1991; Jacobi et al., 2016; Vaishnav et al., 2019). Only recently, Schmölter et al. (2020) used SDO EVE and GOES EUV fluxes to calculate the ionospheric delay of about 17 h as a mean value based on hourly time resolution data. This observed delay was also confirmed by numerical physics-based models (Ren et al., 2018; Vaishnav et al., 2018).
Here, we investigate the ionospheric delay using hourly resolution observations and compare it with the model-simulated TEC. Figure 6 shows the cross-correlation and a corresponding ionospheric delay calculated using SDO EVE-observed integrated flux from the 1 to 120 nm wavelength region in comparison with modeled TEC at 15∘ E longitude. The modeled TEC used for these analyses has been simulated using the EUVAC solar flux model and the F10.7 index as a solar input proxy to calculate the input spectra. The cross-correlation was applied on independent monthly datasets from 2011–2013, as the maximum correlation is expected during the solar rotation period. If longer periods are selected, the periodicity is a mixture of lower and higher solar activity. Then the appearance of sunspots at different locations on the solar disk shifts the maximum EUV emissions in relation to coherence with one another, for which the correlation is expected to decrease. Even shorter periods can result in lower correlations due to the reduced sampling size, i.e., a stronger impact of smaller deviations as well. Similar results have been shown by Vaishnav et al. (2019). They studied correlation analysis between TEC and multiple solar proxies for different time periods. Their study revealed that the correlation is lower during shorter and longer periods. Better correlations are only expected during the solar rotation period.
The upper panels of Fig. 6 show the (a) cross-correlation and (c) the ionospheric delay using the observed TEC. The maximum correlation is observed during the year 2012 with about 0.5, while in 2011 and 2013 the correlation is weaker. The lowest correlation is observed during the winter months of 2011–2012. Further, latitudinal variations are also seen in the correlation coefficient.
Figure 6c shows the cross-correlation coefficient calculated using the modeled TEC and SDO-EVE flux. The correlation coefficient is higher than the one seen in the observed TEC. There are several processes that can influence the behavior of the ionosphere and the real observations such as lower atmospheric forcing or geomagnetic activity. But in the model, lower atmospheric variability is not included, except in a statistical sense, which affects the total variability; hence higher correlation is observed in modeled TEC compared to observed TEC.
The analysis suggests that the model can reproduce similar trends and features to those shown in the observations. The overall correlation coefficient in the Southern Hemisphere is higher than in the Northern Hemisphere.
Figure 6b shows the ionospheric delay calculated from the observed TEC against the SDO flux. The ionospheric delay varies strongly with latitude and time. A shorter ionospheric delay is observed during January as compared to other months. For January, the ionospheric delay is about 13–16 h. The maximum delay is about 22 h in the low-latitude region during 2011 and 2012 but about 22–23 h during 2013 in low latitudes and midlatitudes. During 2011 the ionospheric delay is maximum for the winter period at the Equator with about 22 h, while it decreases towards high latitudes. A very low ionospheric delay of about 5–10 h is observed during August 2012 for midlatitudes. An interesting feature that can be noted here is that the ionospheric delay increases with increasing solar activity from 2011 to 2013.
A similar analysis for the estimation of the ionospheric delay has been performed for the model-simulated TEC, as shown in Fig. 6d. The CTIPe model is able to reproduce features seen in the observed TEC (Fig. 6b). The ionospheric delay is higher during December and follows the solar activity.
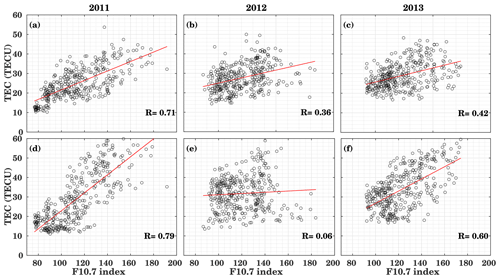
Figure 5Relation between F10.7 index and midday-observed TEC (11:00–13:00 LT) at 40∘ N, 15∘ E (a, b, c) and 40∘ S, 15∘E (d, e, f) for 2011, 2012, and 2013. The red line is the linear fit.
In the higher latitude region (above 60∘ latitude in both hemispheres), the ionospheric delay in the model is smaller than in the observations and amounts to about 5–10 h. Simultaneously, the correlation coefficient is high at the high-latitude regions in the Southern Hemisphere and is about 0.4, as shown in Fig. 6c. This bias is due to the model limitations such as model input, grid resolution, and insufficient physical descriptions (Negrea et al., 2012).
Generally, the ionospheric delay calculated from the modeled TEC is in good agreement with the observed one, and it is about 17 h. Furthermore, the ionospheric delay is always higher in the Northern Hemisphere as compared to the Southern Hemisphere. Partly negative correlation has been observed in both the model and the observations. This negative correlation might be possible due to additional heating sources or unknown factors such as the state of the ionosphere and its dominant physical processes. Another more important factor is lower atmospheric forcing, such as gravity or planetary wave. Gravity waves can influence the upper atmosphere's thermal and compositional structures. These sources might lead to changes in the ionosphere's local dynamics and contribute to additional increase and decrease in the electron density, irrespective of actual solar activity conditions.
The correlation coefficients in the Southern Hemisphere are generally higher than in the Northern Hemisphere.
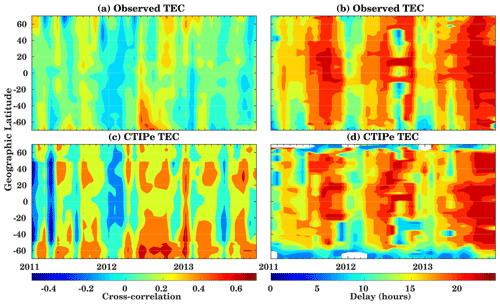
Figure 6Correlation coefficient (a, c) and delay estimation (b, d) using observed (a, b) and model-simulated (c, d) hourly TEC and SDO EVE-integrated flux (1–120 nm).
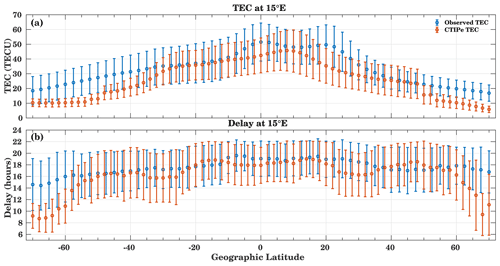
Figure 7(a) Daily mean TEC variations and (b) delay estimation using observed (blue) and model-simulated (red) hourly TEC and SDO EVE-integrated flux. The error bars show standard deviations of mean values.
Furthermore, to understand the mean variations of TEC and its connection with the ionospheric delay, we calculated the latitudinal mean observed TEC with the standard deviations and compare it with the model-simulated TEC from 2011 to 2013 as shown in Fig. 7a. The model-simulated TEC underestimates the observed TEC at all latitudes. As expected, the maximum TEC of about 50 TECU is observed at low latitudes, while model-simulated TEC is about 45 TECU. The maximum bias is observed poleward of 35∘ S and 45∘ N, and this bias increases towards high latitudes. As discussed in the previous sections, there are several problems such as providing inputs for the model, grid resolution effects, and insufficient physical descriptions that need to be addressed in the future to reduce the bias in the model.
To see the mean latitudinal variations of ionospheric delay, we used the monthly delay calculated from 2011 to 2013. The mean ionospheric delay is about 17–18 h in the observations at low latitudes and midlatitudes, while it is about 15 h in the high-latitude regions. As compared to the delay in observations, the model-simulated delay is 1–2 h less in the low latitudes and midlatitudes, but the difference strongly increases in the high-latitude regions. Poleward of 55∘, the ionospheric delay reduces to less than 10 h.
This analysis shows that the model can reproduce the ionospheric delay as seen in the observations and generally produces a delay of about 18 h at middle latitudes.
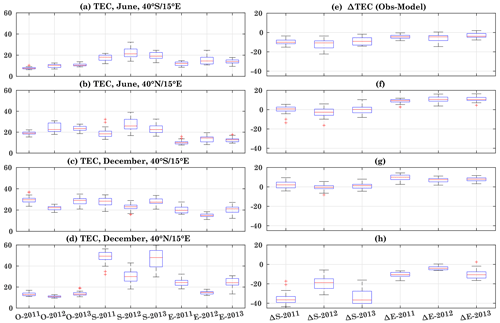
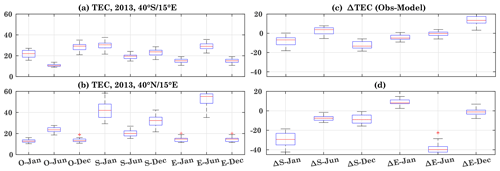
Figure 8Box plots based on daily TEC during June and December 2011–2013 for 40∘ S and 40∘ N. The months and location are mentioned in the figure titles. Here O, S, and E represent observed, CTIPe-SOLAR2000 flux model, and CTIPe-EUVAC flux model TEC, respectively. The left panels show the box plots for the difference between observed TEC with the model-simulated TEC using different flux models. Data points beyond the whiskers are displayed using the “+” sign.
3.5 Observed TEC variations and its comparison to TEC simulated using different EUV flux models
To further visualize the observed daily TEC and its comparison with the modeled TEC at different latitudes, the results are presented in the box-and-whisker plot in Fig. 8 for June and December 2011 to 2013. The box has lines at the lower quartile, median (red line), and upper quartile values. Whiskers extend from each end of the box to the adjacent values in the data. Outliers beyond the whiskers are displayed using the “+” sign.
To analyze the TEC variations at the grid point 40∘ S and 40∘ N, for 15∘ E each in both hemispheres during June and December (left panels, a–d), we compare the observed TEC (O) with the modeled TEC simulated using the SOLAR2000 (S) and the EUVAC (E) flux model for different years. The F10.7 index is used as the primary solar input to calculate the spectra in the model. The box plots have been generated using the daily data of June and December, respectively. The right panels (e–h) show the differences between observed and modeled TEC at different corresponding locations and months (e–h).
The median of modeled TEC using the SOLAR2000 flux model overestimates the observed TEC by about 10, 11, and 7 TECU during June 2011, 2012, and 2013, respectively, at 40∘ S as shown in Fig. 8a, e. A slightly smaller overestimation can be seen using the EUVAC flux model, with a difference of less than about 5 TECU during 2011 and 2013 and 6 TECU during 2012. Hence, both models generally show overestimation of TEC at this latitude and month.
Figure 8b and f show the TEC plot and difference box plot at 40∘ N, 15∘ E during June. At this grid point, the observed TEC values are high compared to the southern hemispheric grid point. The observed TEC is quite comparable with the modeled TEC simulated using SOLAR2000 during 2011 and 2013. However, it shows an overestimation by 2 TECU during 2012. In comparison to SOLAR2000-simulated TEC, the EUVAC-model-based TEC simulation shows an underestimation of about 5–10 TECU. The modeled TEC using the SOLAR2000 flux model is higher than the one simulated using the EUVAC model. A good agreement between the modeled and observed TEC can be seen at the southern and northern hemispheric grid points (Fig. 8e–f), where the bias is less than 10 TECU. The analysis for December is shown in Fig. 8c–d. The difference plot (Fig. 8g–h) shows a different behavior than in June. The modeled TEC simulated using the SOLAR2000 is in agreement during December over 40∘ S, but the modeled TEC simulated using the EUVAC underestimates the observations by about 10 TECU.
Over the grid point 40∘ N, 15∘ E, both flux models result in an overestimation, and the SOLAR2000 flux model produces maximum bias during 2011 and 2013, with about 40 and 20 TECU during 2012. The modeled TEC simulated using the EUVAC model shows an overestimation of about 10 TECU.
The overall difference between the model and observations is larger during December as compared to June. The discrepancy observed in the CTIPe results is possibly due to the various reasons mentioned in the previous section.
Figure 9a–b show the box plots of TEC for January, June, and December during 2013. Here the CTIPe model run used the modified F10.7A index (average of previous 41 d averages with previous day value) as solar input to calculate the spectra in solar flux models. We choose this period to consider different ionizing radiations. Here the difference plots Fig. 9c–d show bias during January, June, and December at 40∘ S, 15∘ E and 40∘ N, 15∘ E.
At 40∘ S, 15∘ E, the modeled TEC simulated using the SOLAR2000 flux model overestimates TEC during January and December and underestimates TEC during June by about 5 TECU. The modeled TEC simulated using the EUVAC model shows quite different behavior. It shows overestimation during January and June but underestimation during December.
In comparison to the southern hemispheric grid point, the TEC over 40∘ N, 15∘ E simulated using the SOLAR2000 shows overestimation of TEC and maximum bias during January by about 25 TECU. In the case of the EUVAC model, it shows underestimation during January compared to observed TEC. During June and December, the modeled TEC simulated using EUVAC shows overestimation with respect to the observed TEC.
Here it is interesting to note that the southern hemispheric grid point shows good agreement compared to the Northern Hemisphere. During January, the SOLAR2000 model overestimated TEC by about 20 TECU, while the EUVAC model overestimated TEC by 5 TECU at 40∘ N, 15∘ E. The observed TEC shows seasonal variations, while the model is not able to capture seasonal behavior.
We performed a similar comparison using F10.7A (average of previous 81 d averages with previous day value) as solar input proxy in the solar flux models (not shown). The results show a similar bias as the one presented in Fig. 9. The flux values provided by EUVAC are smaller than SOLAR2000 results in the photoionization processes, and this results in a decrease in TEC.
Klipp et al. (2019) compared the IGS TEC with the modeled TEC using different flux models (EUVAC and SOLAR2000) over Central and South American regions. They showed different behavior of empirical models during different solar activity conditions.
The large bias observed in the physics-based model is mainly due to the solar EUV flux input and grid resolution. The model needs further improvement regarding the input of solar flux.
Miyoshi et al. (2018) investigated the effects of the horizontal resolution on the electron density distribution using the GAIA model. They showed that fluctuations produced in model-simulated electron density with periods of less than about 2 h and length scales of less than about 1000 km with a high horizontal resolution of , which are in good agreement with observations. These fluctuations are not seen in a low-resolution () simulation. Hence, the model resolution is an important factor for the large bias between observations and model simulations.
We presented a climatological analysis of GNSS-observed and CTIPe-model-simulated TEC during 3 years, 2011 to 2013, of the 24th solar cycle, to investigate and compare modeled TEC with the observed ones, the ionospheric delay, periodicity estimation, and relation of TEC with the solar proxy. Our results show a distinct low-latitude and midlatitude TEC response at a longitude of 15∘ E.
The main results of this study can be summarized as follows:
-
The periodicity estimations over the low latitudes, midlatitudes, and high latitudes show that 16–32 d periodicity was dominant during 2012. As compared to the periodicity observed in model-simulated TEC, the 64–128 d periodicity was missing in the observations over all considered latitudes.
-
While comparing TEC against the F10.7 index, the correlation is higher in 2011 and 2013 over the Southern Hemisphere as compared to the Northern Hemisphere; i.e., there is a hemispheric asymmetry. A similar characteristic has been observed by Romero-Hernandez et al. (2018). The lowest correlation is observed during 2012.
-
The ionospheric delay has been investigated using the modeled and observed TEC against the solar EUV flux. The ionospheric delay estimated using model-simulated TEC is in good agreement with the delay estimated for observed TEC. An average delay for the observed (modeled) TEC is about 17 (16) h. The study confirms the model's capabilities to reproduce the delayed ionospheric response against the solar EUV flux. These results are in close agreement with Schmölter et al. (2020).
-
The average difference between the northern and southern hemispheric delay estimated for observed (modeled) TEC is about 1 (2) h. The average delay is higher in the Northern Hemisphere as compared to the Southern Hemisphere.
-
Furthermore, the observed TEC is compared with the modeled TEC simulated using the SOLAR2000 and EUVAC flux models within CTIPe at the northern and southern hemispheric grid points. The analysis indicates that TEC simulated using the SOLAR2000 flux model overestimates the observed TEC, which is not the case when using the EUVAC flux model. The large bias observed in the physics-based model is mainly due to the solar EUV flux input and grid resolution. Our results show that the model needs further improvement in respect to the solar flux input to further reduce the presented deviation to TEC measurements.
IGS TEC maps have been provided by NASA through ftp://cddis.gsfc.nasa.gov/gnss/products/ionex (CDDIS, 2018). SDO-EVE data have been provided by the Laboratory for Atmospheric and Space Physics (LASP) through http://lasp.colorado.edu/eve/data_access/evewebdata (LASP, 2018a). Daily F10.7 index can be downloaded from http://lasp.colorado.edu/lisird/data/noaa_radio_flux/ (LASP, 2018b).
RV together with CJ and MC performed the CTIPe model simulations. RV drafted the first version of the manuscript. ES, CJ, and JB actively contributed to the analysis. All authors discussed the results and contributed to the final version of the paper.
Christoph Jacobi is one of the editors-in-chief of Annales Geophysicae. The authors declare that they have no conflict of interest.
This research has been supported by the Deutsche Forschungsgemeinschaft (grant nos. JA 836/33-1 and BE 5789/2-1).
This paper was edited by Dalia Buresova and reviewed by Gerhard Schmidtke and one anonymous referee.
Abdu, M. A.: Electrodynamics of ionospheric weather over low latitudes, Geoscience Letters, 3, 11, https://doi.org/10.1186/s40562-016-0043-6, 2016. a, b
Afraimovich, E. L., Astafyeva, E. I., Oinats, A. V., Yasukevich, Yu. V., and Zhivetiev, I. V.: Global electron content: a new conception to track solar activity, Ann. Geophys., 26, 335–344, https://doi.org/10.5194/angeo-26-335-2008, 2008. a
Altadill, D., Apostolov, E., Solé, J., and Jacobi, C.: Origin and development of vertical propagating oscillations with periods of planetary waves in the ionospheric F region, Phys. Chem. Earth Pt. C, 26, 387–393, https://doi.org/10.1016/s1464-1917(01)00019-8, 2001. a
Altadill, D., Apostolov, E. M., Jacobi, Ch., and Mitchell, N. J.: Six-day westward propagating wave in the maximum electron density of the ionosphere, Ann. Geophys., 21, 1577–1588, https://doi.org/10.5194/angeo-21-1577-2003, 2003. a
Appleton, E. V.: Two Anomalies in the Ionosphere, Nature, 157, 691, https://doi.org/10.1038/157691a0, 1946. a
Balan, N., Otsuka, Y., Bailey, G. J., and Fukao, S.: Equinoctial asymmetries in the ionosphere and thermosphere observed by the MU radar, J. Geophys. Res.-Space, 103, 9481–9495, https://doi.org/10.1029/97ja03137, 1998. a
CDDIS: GNSS Atmospheric Products, available at: http://cddis.nasa.gov/Data_and_Derived_Products/GNSS/atmospheric_products.html, last access: 15 August 2018. a, b
Chen, P., Liu, H., Ma, Y., and Zheng, N.: Accuracy and consistency of different global ionospheric maps released by IGS ionosphere associate analysis centers, Adv. Space Res., 65, 163–174, https://doi.org/10.1016/j.asr.2019.09.042, 2020. a
Codrescu, M. V., Fuller-Rowell, T. J., Munteanu, V., Minter, C. F., and Millward, G. H.: Validation of the Coupled Thermosphere Ionosphere Plasmasphere Electrodynamics model: CTIPE-Mass Spectrometer Incoherent Scatter temperature comparison, Space Weather, 6, S09005, https://doi.org/10.1029/2007sw000364, 2008. a
Codrescu, M. V., Negrea, C., Fedrizzi, M., Fuller-Rowell, T. J., Dobin, A., Jakowsky, N., Khalsa, H., Matsuo, T., and Maruyama, N.: A real-time run of the Coupled Thermosphere Ionosphere Plasmasphere Electrodynamics (CTIPe) model, Space Weather, 10, S02001, https://doi.org/10.1029/2011sw000736, 2012. a, b
Fang, T.-W., Fuller-Rowell, T., Yudin, V., Matsuo, T., and Viereck, R.: Quantifying the Sources of Ionosphere Day-To-Day Variability, J. Geophys. Res.-Space, 123, 9682–9696, https://doi.org/10.1029/2018ja025525, 2018. a, b
Fernandez-Gomez, I., Fedrizzi, M., Codrescu, M. V., Borries, C., Fillion, M., and Fuller-Rowell, T. J.: On the difference between real-time and research simulations with CTIPe, Adv. Space Res., 64, 2077–2087, https://doi.org/10.1016/j.asr.2019.02.028, 2019. a
Fuller-Rowell, T. J.: The “thermospheric spoon”: A mechanism for the semiannual density variation, J. Geophys. Res.-Space, 103, 3951–3956, https://doi.org/10.1029/97ja03335, 1998. a
Fuller-Rowell, T. J. and Rees, D.: A Three-Dimensional Time-Dependent Global Model of the Thermosphere, J. Atmos. Sci., 37, 2545–2567, https://doi.org/10.1175/1520-0469(1980)037<2545:atdtdg>2.0.co;2, 1980. a
Fuller-Rowell, T. J. and Rees, D.: Derivation of a conservation equation for mean molecular weight for a two-constituent gas within a three-dimensional, time-dependent model of the thermosphere, Planet. Space Sci., 31, 1209–1222, https://doi.org/10.1016/0032-0633(83)90112-5, 1983. a, b
Hedin, A. E.: Correlations between thermospheric density and temperature, solar EUV flux, and 10.7 cm flux variations, J. Geophys. Res.-Space, 89, 9828–9834, https://doi.org/10.1029/ja089ia11p09828, 1984. a
Hernández-Pajares, M., Juan, J. M., Sanz, J., Orus, R., Garcia-Rigo, A., Feltens, J., Komjathy, A., Schaer, S. C., and Krankowski, A.: The IGS VTEC maps: a reliable source of ionospheric information since 1998, J. Geodesy, 83, 263–275, https://doi.org/10.1007/s00190-008-0266-1, 2009. a
Hinteregger, H. E., Fukui, K., and Gilson, B. R.: Observational, reference and model data on solar EUV, from measurements on AE-E, Geophys. Res. Lett., 8, 1147–1150, https://doi.org/10.1029/gl008i011p01147, 1981. a
Huang, J., Hao, Y., Zhang, D., and Xiao, Z.: Changes of solar extreme ultraviolet spectrum in solar cycle 24, J. Geophys. Res.-Space, 121, 6844–6854, https://doi.org/10.1002/2015ja022231, 2016. a
Jacobi, C., Jakowski, N., Schmidtke, G., and Woods, T. N.: Delayed response of the global total electron content to solar EUV variations, Adv. Radio Sci., 14, 175–180, https://doi.org/10.5194/ars-14-175-2016, 2016. a, b, c, d
Jakowski, N., Fichtelmann, B., and Jungstand, A.: Solar activity control of ionospheric and thermospheric processes, J. Atmos. Terr. Phys., 53, 1125–1130, https://doi.org/10.1016/0021-9169(91)90061-b, 1991. a, b, c, d
Jin, H., Miyoshi, Y., Pancheva, D., Mukhtarov, P., Fujiwara, H., and Shinagawa, H.: Response of migrating tides to the stratospheric sudden warming in 2009 and their effects on the ionosphere studied by a whole atmosphere-ionosphere model GAIA with COSMIC and TIMED/SABER observations, J. Geophys. Res.-Space, 117, A10323, https://doi.org/10.1029/2012ja017650, 2012. a
Klipp, T. S., Petry, A., de Souza, J. R., Falcão, G. S., de Campos Velho, H. F., de Paula, E. R., Antreich, F., Hoque, M., Kriegel, M., Berdermann, J., Jakowski, N., Fernandez-Gomez, I., Borries, C., Sato, H., and Wilken, V.: Evaluation of ionospheric models for Central and South Americas, Adv. Space Res., 64, 2125–2136, https://doi.org/10.1016/j.asr.2019.09.005, 2019. a
LASP: EVE Data, available at: http://lasp.colorado.edu/eve/data_access/evewebdata, last access: 15 August 2018a. a, b
LASP: F10.7 index, available at: http://lasp.colorado.edu/lisird/data/noaa_radio_flux/, last access: 15 August 2018b. a, b
Lean, J. L., Warren, H. P., Mariska, J. T., and Bishop, J.: A new model of solar EUV irradiance variability 2. Comparisons with empirical models and observations and implications for space weather, J. Geophys. Res.-Space, 108, 1059, https://doi.org/10.1029/2001ja009238, 2003. a, b
Lean, J. L., Woods, T. N., Eparvier, F. G., Meier, R. R., Strickland, D. J., Correira, J. T., and Evans, J. S.: Solar extreme ultraviolet irradiance: Present, past, and future, J. Geophys. Res.-Space, 116, A01102, https://doi.org/10.1029/2010ja015901, 2011. a
Lee, C.-K., Han, S.-C., Bilitza, D., and Seo, K.-W.: Global characteristics of the correlation and time lag between solar and ionospheric parameters in the 27-day period, J. Atmos. Sol.-Terr. Phy., 77, 219–224, https://doi.org/10.1016/j.jastp.2012.01.010, 2012. a, b
Liu, H., Tao, C., Jin, H., and Nakamoto, Y.: Circulation and Tides in a Cooler Upper Atmosphere: Dynamical Effects of CO2 Doubling, Geophys. Res. Lett., 47, e2020GL087413, https://doi.org/10.1029/2020gl087413, 2020. a
Liu, H.-L., Bardeen, C. G., Foster, B. T., Lauritzen, P., Liu, J., Lu, G., Marsh, D. R., Maute, A., McInerney, J. M., Pedatella, N. M., Qian, L., Richmond, A. D., Roble, R. G., Solomon, S. C., Vitt, F. M., and Wang, W.: Development and Validation of the Whole Atmosphere Community Climate Model With Thermosphere and Ionosphere Extension (WACCM-X 2.0), J. Adv. Model. Earth Sy., 10, 381–402, https://doi.org/10.1002/2017ms001232, 2018. a
Liu, L., Wan, W., Ning, B., and Zhang, M.-L.: Climatology of the mean total electron content derived from GPS global ionospheric maps, J. Geophys. Res.-Space, 114, A06308, https://doi.org/10.1029/2009ja014244, 2009. a
Mallat, S.: A Wavelet tour of signal processing: the sparse way, 3rd Edn., Academic Press, Burlington, MA, 832 pp., 2009. a
Mendillo, M., Rishbeth, H., Roble, R., and Wroten, J.: Modelling F2-layer seasonal trends and day-to-day variability driven by coupling with the lower atmosphere, J. Atmos. Sol.-Terr. Phy., 64, 1911–1931, https://doi.org/10.1016/s1364-6826(02)00193-1, 2002. a
Millward, G. H., Moffett, R. J., Quegan, S., and Fuller-Rowell, T. J.: A coupled thermosphere-ionosphere-plasmasphere model (CTIP), in: Solar-Terrestrial Energy Program: Handbook of Iono- spheric Models, edited by: Schunk, R. W., Cent. for Atmos. and Space Sci., Utah State Univ., Logan, Utah, USA, 239–279, 1996. a
Miyoshi, Y., Jin, H., Fujiwara, H., and Shinagawa, H.: Numerical Study of Traveling Ionospheric Disturbances Generated by an Upward Propagating Gravity Wave, J. Geophys. Res.-Space, 123, 2141–2155, https://doi.org/10.1002/2017ja025110, 2018. a
Negrea, C., Codrescu, M. V., and Fuller-Rowell, T. J.: On the validation effort of the Coupled Thermosphere Ionosphere Plasmasphere Electrodynamics model, Space Weather, 10, S08010, https://doi.org/10.1029/2012sw000818, 2012. a
Noll, C. E.: The crustal dynamics data information system: A resource to support scientific analysis using space geodesy, Adv. Space Res., 45, 1421–1440, https://doi.org/10.1016/j.asr.2010.01.018, 2010. a
Pancheva, D., Schminder, R., and Laštovička, J.: 27-day fluctuations in the ionospheric D-region, J. Atmos. Terr. Phys., 53, 1145–1150, https://doi.org/10.1016/0021-9169(91)90064-e, 1991. a
Percival, D. B. and Walden, A. T.: Wavelet Methods for Time Series Analysis, Cambridge University Press, Cambridge, UK, https://doi.org/10.1017/CBO9780511841040, 2000. a
Pesnell, W. D., Thompson, B. J., and Chamberlin, P. C.: The Solar Dynamics Observatory (SDO), Sol. Phys., 275, 3–15, https://doi.org/10.1007/s11207-011-9841-3, 2011. a
Quegan, S., Bailey, G., Moffett, R., Heelis, R., Fuller-Rowell, T., Rees, D., and Spiro, R.: A theoretical study of the distribution of ionization in the high-latitude ionosphere and the plasmasphere: first results on the mid-latitude trough and the light-ion trough, J. Atmos. Terr. Phys., 44, 619–640, https://doi.org/10.1016/0021-9169(82)90073-3, 1982. a
Ren, D., Lei, J., Wang, W., Burns, A., Luan, X., and Dou, X.: Does the Peak Response of the Ionospheric F2 Region Plasma Lag the Peak of 27-Day Solar Flux Variation by Multiple Days?, J. Geophys. Res.-Space, 123, 7906–7916, https://doi.org/10.1029/2018ja025835, 2018. a, b, c, d, e
Richards, P. G., Fennelly, J. A., and Torr, D. G.: EUVAC: A solar EUV Flux Model for aeronomic calculations, J. Geophys. Res.-Space, 99, 8981–8992, https://doi.org/10.1029/94ja00518, 1994. a, b, c
Richmond, A. D., Ridley, E. C., and Roble, R. G.: A thermosphere/ionosphere general circulation model with coupled electrodynamics, Geophys. Res. Lett., 19, 601–604, https://doi.org/10.1029/92gl00401, 1992. a, b
Ridley, A., Deng, Y., and Tóth, G.: The global ionosphere–thermosphere model, J. Atmos. Sol.-Terr. Phy., 68, 839–864, https://doi.org/10.1016/j.jastp.2006.01.008, 2006. a
Romero-Hernandez, E., Denardini, C. M., Takahashi, H., Gonzalez-Esparza, J. A., Nogueira, P. A. B., de Padua, M. B., Lotte, R. G., Negreti, P. M. S., Jonah, O. F., Resende, L. C. A., Rodriguez-Martinez, M., Sergeeva, M. A., Neto, P. F. B., la Luz, V. D., Monico, J. F. G., and Aguilar-Rodriguez, E.: Daytime ionospheric TEC weather study over Latin America, J. Geophys. Res.-Space, 123, 10345–10357, https://doi.org/10.1029/2018ja025943, 2018. a, b, c, d
Schmölter, E., Berdermann, J., Jakowski, N., Jacobi, C., and Vaishnav, R.: Delayed response of the ionosphere to solar EUV variability, Adv. Radio Sci., 16, 149–155, https://doi.org/10.5194/ars-16-149-2018, 2018. a, b
Schmölter, E., Berdermann, J., Jakowski, N., and Jacobi, C.: Spatial and seasonal effects on the delayed ionospheric response to solar EUV changes, Ann. Geophys., 38, 149–162, https://doi.org/10.5194/angeo-38-149-2020, 2020. a, b, c, d, e, f, g
Tapping, K. F.: Recent solar radio astronomy at centimeter wavelengths: The temporal variability of the 10.7 cm flux, J. Geophys. Res.-Atmos., 92, 829–838, https://doi.org/10.1029/jd092id01p00829, 1987. a
Tobiska, W., Woods, T., Eparvier, F., Viereck, R., Floyd, L., Bouwer, D., Rottman, G., and White, O.: The SOLAR2000 empirical solar irradiance model and forecast tool, J. Atmos. Sol.-Terr. Phy., 62, 1233–1250, https://doi.org/10.1016/s1364-6826(00)00070-5, 2000. a, b
Unglaub, C., Jacobi, C., Schmidtke, G., Nikutowski, B., and Brunner, R.: EUV-TEC proxy to describe ionospheric variability using satellite-borne solar EUV measurements: First results, Adv. Space Res., 47, 1578–1584, https://doi.org/10.1016/j.asr.2010.12.014, 2011. a
Vaishnav, R., Jacobi, C., Berdermann, J., Schmölter, E., and Codrescu, M.: Ionospheric response to solar EUV variations: Preliminary results, Adv. Radio Sci., 16, 157–165, https://doi.org/10.5194/ars-16-157-2018, 2018. a, b, c, d
Vaishnav, R., Jacobi, C., and Berdermann, J.: Long-term trends in the ionospheric response to solar extreme-ultraviolet variations, Ann. Geophys., 37, 1141–1159, https://doi.org/10.5194/angeo-37-1141-2019, 2019. a, b, c, d, e, f
Woods, T. and Rottman, G.: Solar ultraviolet variability over time periods of aeronomic interest, in: Atmospheres in the Solar System: Comparative Aeronomy, edited by: Mendillo, M., Nagy, A., and Waite, J., American Geophysical Union, Washington, D.C., USA, 221–233, https://doi.org/10.1029/130gm14, 2002. a, b
Woods, T., Bailey, S., Eparvier, F., Lawrence, G., Lean, J., McClintock, W., Roble, R., Rottman, G., Solomon, S., Tobiska, W., and White, O. R.: TIMED Solar EUV experiment, Phys. Chem. Earth Pt. C, 25, 393–396, https://doi.org/10.1016/s1464-1917(00)00040-4, 2000. a
Woods, T., Eparvier, F., Bailey, S. M., Chamberlin, P., Lean, J., Rottman, G., Solomon, S., Tobiska, W., and Woodraska, D.: Solar EUV Experiment (SEE): Mission overview and first results, J. Geophys. Res.-Space, 110, A01312, https://doi.org/10.1029/2004ja010765, 2005. a, b, c
Woods, T., Eparvier, F., Hock, R., Jones, A., Woodraska, D., Judge, D., Didkovsky, L., Lean, J., Mariska, J., Warren, H., McMullin, D., Chamberlin, P., Berthiaume, G., Bailey, S., Fuller- Rowell, T., Sojka, J., Tobiska, W. K., and Viereck, R.: Extreme Ultraviolet Variability Experiment (EVE) on the Solar Dynamics Observatory (SDO): Overview of Science Objectives, Instrument Design, Data Products, and Model Developments, Sol. Phys., 275, 115–143, https://doi.org/10.1007/s11207-009-9487-6, 2010. a
Zou, L., Rishbeth, H., Müller-Wodarg, I. C. F., Aylward, A. D., Millward, G. H., Fuller-Rowell, T. J., Idenden, D. W., and Moffett, R. J.: Annual and semiannual variations in the ionospheric F2-layer. I. Modelling, Ann. Geophys., 18, 927–944, https://doi.org/10.1007/s00585-000-0927-8, 2000. a