the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Influence of the semidiurnal lunar tide in the equatorial plasma bubble zonal drifts over Brazil
Ana Roberta Paulino
Amauri F. Medeiros
Cristiano M. Wrasse
Ricardo Arlen Buriti
Hisao Takahashi
Using OI6300 airglow images collected over São João do Cariri (7.4∘ S, 36.5∘ W) from 2000 to 2007, the equatorial plasma bubble (EPB) zonal drifts were calculated. A strong day-to-day variability was observed in the EPB zonal drifts, which is directly associated with the very complex dynamics of the nighttime thermosphere–ionosphere system near the Equator. The present work investigated the contribution of the semidiurnal lunar tide M2 for the EPB zonal drifts. The M2 presented an amplitude of 3.1 m s−1 in the EPB zonal drifts, which corresponds to 5.6 % of the average drifts. The results showed that the M2 amplitudes in the EPB zonal drifts were solar cycle and seasonally dependent. The amplitude of the M2 was stronger during the high solar activity, reaching over 10 % of the EPB zonal drift average. Regarding the seasons, during the Southern Hemisphere summer, the M2 amplitude was twice as large (12 %) compared to the equinox ones. The seasonality agrees with other observations of the M2 in the ionospheric parameters such as vertical drifts and electron concentration, for instance. On the other hand, the very large M2 amplitudes found during the high solar activity agree with previous observations of the lunar tide in the ionospheric E region.
- Article
(616 KB) - Full-text XML
- BibTeX
- EndNote
Equatorial plasma bubbles (EPBs) appear during the nighttime near the magnetic equator and extend across the tropics along the magnetic field lines (e.g., Weber et al., 1978). EPBs can be understood as a depletion of the plasma density compared to the background ionosphere (e.g., Sobral et al., 1980b).
Airglow emissions from the thermosphere can be used to detect and study the morphology and dynamics of EPBs (e.g., Sobral et al., 1980a; Mendillo and Baumgardner, 1982; Fagundes et al., 1995; Takahashi et al., 2001). Additionally, as the EPBs contain plasma irregularities, radio techniques have also been used to investigate them (e.g., Woodman and La Hoz, 1976; Abdu et al., 1985, 1998; Fejer et al., 1996; de Paula and Hysell, 2004; Chu et al., 2005).
In the equatorial ionosphere, the zonal electric field controls the vertical movement of the F layer. In general, during the daytime the plasma moves upward, while during the nighttime, the motion is downward. However, after the sunset, the pre-reversal enhancement (PRE) can occur, which is a rapid upward movement of the F region before it reverses, i.e., before the motion becomes downward (Farley et al., 1986). The PRE has well-defined temporal dependencies, being more intense during the summer and with high solar activity (Fejer et al., 1991).
Besides the PRE, after the sunset, there is a quick recombination in the ionospheric E region (e.g., Bates, 1988), producing a strong vertical gradient of plasma with high-density levels in the F region. This scenario is very favorable to the Rayleigh–Taylor instability (RTI) development, which has been recognized as the main mechanism for generating EPBs (Dungey, 1956; Haerendel et al., 1992). Even so, the RTI theory requires a seeding process in order to initiate the instability. Although gravity waves, thermospheric wind, post-sunset vortex, large-scale waves, and magnetic disturbances have been pointed out as possible seedings for EPBs (e.g., Kudeki et al., 2007; Abdu et al., 2009; Abalde et al., 2009; Saito and Maruyama, 2009; Takahashi et al., 2009; Paulino et al., 2011a; Huang et al., 2013; Tsunoda et al., 2018), this topic continues to be under scientific investigation (e.g., Fritts et al., 2009, and references therein).
EPBs move zonally eastward under quiet magnetic conditions during the nighttime, reaching high drift values during the evening hours (e.g., Pimenta et al., 2003; Paulino et al., 2011b). Clear seasonal and solar activity dependencies were also observed (e.g., Pimenta et al., 2001; Paulino et al., 2011b). In contrast, during the magnetic storms, this behavior can be totally disturbed; i.e., the drifts can inclusively reverse to the west (e.g., Abdu et al., 2003; Li et al., 2009; Paulino et al., 2010; Santos et al., 2016).
The PRE (vertical motion) and the zonal drifts present a strong day-to-day variability in the equatorial ionosphere (e.g., Liu, 2020; Aswathy and Manju, 2021, and references therein). The understanding of the short-period variability represents one of the biggest challenges in atmospheric and space science (e.g., Tsunoda, 2006). Among the features that can produce day-to-day variabilities, the lunar tide appeared to be relevant after the work by Stening and Fejer (2001), which simulated the effects of the semidiurnal lunar tide (M2) on the vertical motion of the F region and PRE. According to them, the M2 can either change the local time of PRE or its amplitude. The M2 has a period of 12.43 h, and it is the main lunar tide periodicity. It is primarily produced in the lower levels of the atmosphere due to the gravitational interaction of the Sun–Earth–Moon system, and it can propagate upward into the atmosphere–ionosphere (Chapman and Lindzen, 1970). The M2 is composed of migrating components, which follow the motion of the Moon, and non-migrating components, which can propagate to the east or west.
As a direct response to the EPBs and M2 interaction, changes of ∼14 min in the starting time of the EPBs were observed over the Brazilian equatorial region (Paulino et al., 2020) along almost one solar cycle. The present article aims to investigate, for the first time, the M2 effects on the EPB zonal drifts derived from airglow images. It used measurement over São João do Cariri (7.4∘ S, 36.5∘ W) from 2000 to 2007, covering periods of high and low solar activities. In addition, the seasonality is going to be studied as well.
An all-sky airglow imager was deployed at São João do Cariri in September 2000 to observe the nighttime airglow. The OI6300 emissions were used to study equatorial plasma bubbles. This imager operated up to December 2010, and it was equipped with a CCD camera and filter wheel. The CCD had a resolution of 1024×1024 pixels binned on-chip down to 512×512 to enhance the signal-to-noise ratio. The CCD had high linearity (0.05 %), high quantum efficiency, low dark noise (five electrons per pixel per second), and low readout noise (15-electron root mean square – rms). In addition, the optical system had a fisheye lens and a telecentric system of lenses, allowing the record of the OI6300 airglow images, with 90 s of time integration. The filter wheel could select five other emissions, but only the OI6300 filter was used in the present work to calculate the EPB zonal drifts. The observations were made between September 2000 and April 2007, centered at new Moon periods, resulting in 13 nights of data per month. This limitation of the observations is due to the strong brightness of the Moon, which does not allow us to make good-quality images when the Moon is above the horizon.
The collected images were unwarped to the geographic coordinates with a spatial resolution of 512 km × 512 km according to the method described by Garcia et al. (1997). Then, the EPB zonal drifts were calculated using a cross-correlation between two lines of consecutive images. The lag between the lines was assumed to be the displacement of the structures within the time interval recorded between the two images. With this information, it was possible to calculate the EPB zonal drifts across all latitudes covered by the field of view of the unwarped images (see Paulino et al., 2011a, for further details).
Only quiet magnetic nights were used; i.e., the EPB zonal drifts were calculated considering nights when the Dst index is higher than −30 nT and that do not have any characteristics of magnetic storms (Paulino et al., 2011a).
The amplitude of the semidiurnal lunar tide oscillation in the EPB zonal drifts was calculated by converting the solar local time (t) to the lunar local time (τ), i.e., , where ν is the age of the Moon set to be equal to 0 at the new Moon (see Forbes et al., 2013; Paulino et al., 2017, for further details).
To investigate a possible influence of the solar cycle on the strength of M2 in EPB zonal drifts, the period of observation was divided into high solar activity (HSA) and low solar activity (LSA). The classification was done using the F10.7 cm solar flux as a proxy to the solar activity. The nights with solar flux greater than W m−2 Hz−1 were considered to be HSA. In contrast, the nights with solar flux lower than W m−2 Hz−1 were supposed to be LSA. These criteria make the HSA period from September 2000 to December 2002 and the LSA period from January 2006 to April 2007.
Additionally, the summer period includes the months from December to February. The equinox period was set for March, April, May, September, October, and November for the whole period of observations. Please note that during the winter period, the EPBs rarely appear (Sobral et al., 2002), and thus the winter months were not used in these analyses.
Figure 1 shows the hourly binned average of the EPB zonal drifts for the whole observed period as a function of the lunar local time. The error bars indicate the standard deviation, suggesting a strong variability of calculated EPB zonal drifts. The solid line represents the least-square best fit for 12 h oscillation, corresponding to the semidiurnal lunar tide period in lunar time. Although the observations were concentrated around the new Moon period, it can be observed that one entire cycle of the oscillation can be reproduced. In addition, the long period of observations used makes the fit statistically representative. One can see that the solid line fits very well to the data, indicating that the lunar semidiurnal tide was present during the whole studied period, with an amplitude of 3.1 m s−1 corresponding to 5.6 % of the zonal drift average. Another relevant aspect of being considered is that, although the amplitude is relatively small, this oscillation is always present in data producing an interesting day-to-day variability in the dynamics of the EPBs.
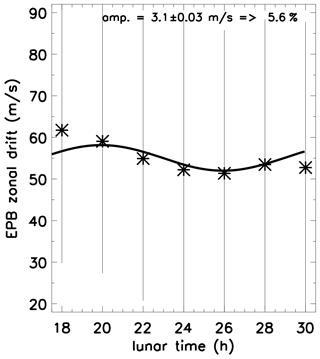
Figure 1EPB zonal drift (stars) obtained from airglow images and semidiurnal lunar tide fits (solid line) as a function of lunar time for the whole observed period. Error bars represent the standard deviation at each hourly bin. The estimated amplitude of a 12 oscillation is shown on the top with its uncertainty.
Figure 2 shows the EPB zonal drift as a function of the lunar time separated by seasons. Again, the solid lines represent the fits for lunar tide. Figure 2a shows the results for the summer period considered in this analysis, the months from December to February for all the studied years. The calculated M2 amplitude was 7.2 m s−1, representing 12.1 % of the zonal drift average. Furthermore, an almost perfect fit to the data was observed, which suggests that M2 is more pronounced in the variability of the EPB zonal drifts during the summer.
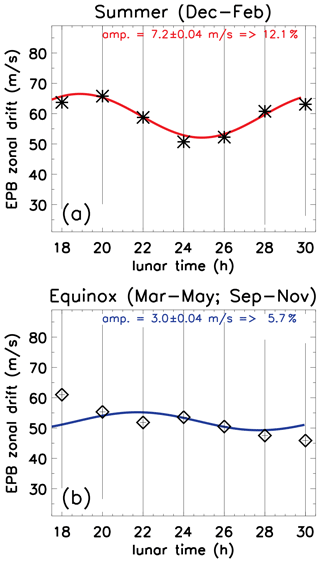
Figure 2EPB zonal drift (stars) for the summer (stars in panel a) and equinox (open diamonds in panel b) obtained from airglow images and semidiurnal lunar tide fit (red line in panel a and blue line in panel b) as a function of lunar time. Error bars represent the standard deviation at each hourly bin. The estimated amplitude and its uncertainty for a 12 h oscillation are shown at the top of each panel.
Figure 2b shows how the M2 acted during the equinox months (March to May for the falls, September to November for the springs). The amplitude of semidiurnal lunar tide oscillation was 3.0 m s−1, which is about 5.7 % of the zonal drift average. The fit was not so good when compared to the summer period as well.
Figure 3 shows the M2 amplitude on EPB zonal drifts considering the (a) HSA and (b) LSA. The M2 amplitude was over 10 % of the zonal drift average for the HSA, i.e., 5.9 m s−1, while for the LSA the amplitude was calculated as 1.2 m s−1 (2.3 % of the average). Additionally, the least-square best fit was better for the HSA activity than for the LSA, which indicates that the M2 found better conditions to propagate in the thermosphere–ionosphere during the high solar activity. It is important to note that the HSA period used 27 months and that the LSA period used 16 months. Even so, the period chosen for LSA is enough to retrieve the M2 from the data.
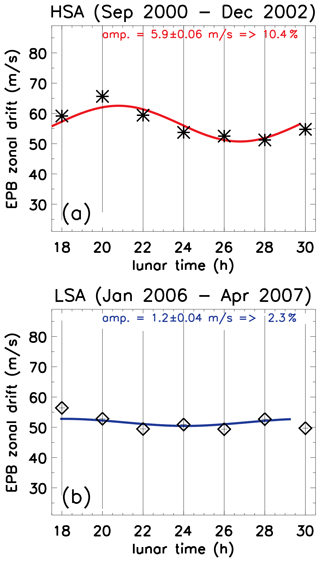
Figure 3EPB zonal drift (stars) for the HSA (stars in panel a) and LSA (open diamonds in panel b) obtained from airglow images and the semidiurnal lunar tide fit (red line in panel a and blue line in panel b) as a function of lunar time. Error bars represent the standard deviation at each hourly bin. The estimated amplitude and its uncertainty for a 12 h oscillation are shown at the top of each panel.
The presence of M2 in the thermosphere–ionosphere system can be understood as a combination of the lunar tide in the E region (geomagnetic tide) and F region (ionospheric tide) of the ionosphere. The former comes from electrical currents in the E region, in this case the neutral wind, primarily due to the tides in the E region, generating polarization electric fields, which can be transmitted to the F region, producing drifts due to the E-region dynamo. The latter is due to the neutral wind variation caused by the wind in the F region which generates polarization electric fields through the F-region dynamo.
Stening et al. (1999) showed the importance of this coupling from simulation in a general circulation model, and Eccles et al. (2011) showed observational results and simulation of the strong connection between the geomagnetic and ionospheric semidiurnal lunar tide. A recent and very comprehensive explanation of the lunar tide in the ionosphere was published by Forbes and Zhang (2019).
During the nighttime near the Equator, in general, the F region of the ionosphere drifts downward and eastward under magnetic quiet conditions. The zonal drift of the plasma is almost equal to the neutral zonal wind because the vertical electric field, which induces the zonal plasma drifts, is driven through the F-region dynamo (e.g., Chapagain et al., 2012). In this case, the contribution of the geomagnetic tide seems to be small, primarily after midnight.
Based on these aspects, it is expected that the results from Fig. 1 will represent mostly the contribution of the ionospheric tide. Thus, the value of the amplitude of ∼3.1 m s−1 should be compatible with the amplitude of the lunar tide in the thermospheric zonal wind. Zhang et al. (2014) showed that the M2 presented an amplitude of a few meters per second around the Equator in the zonal wind measured from the Gravity Field and Steady-State Ocean Circulation Explorer (GOCE) satellite. Additionally, they showed that the contribution of the ionospheric tide to the M2 is larger near the Equator as compared to the geomagnetic contribution from the space perturbations. Forbes (1982), extended in Forbes et al. (2014), showed that the semidiurnal tide can propagate directly into the thermosphere, primarily the components with long vertical wavelengths, which could explain the presence of this oscillation in the thermosphere/EPB zonal drifts.
Regarding the seasonal results retrieved from Fig. 2, i.e., during the summer, the M2 amplitude was larger in the EPB zonal drifts than during the equinoxes. The amplitude of the M2 in the zonal wind from the GOCE was large in January and February in the equatorial zone, and this behavior was also predicted by the Global Scale Wave Model (Zhang et al., 2014). Additionally, the M2 amplitudes have been studied in the vertical plasma drifts in the equatorial region (e.g., Stening and Fejer, 2001; Fejer and Tracy, 2013), and the results showed a similar seasonal dependency, i.e., large amplitudes during the Southern Hemisphere summer.
A full explanation for the seasonal variation in the M2 amplitudes in EPB zonal drift is quite complex due to the complexity of the dynamics involved in the motion of the F-region plasma, which is strictly related to the E-region dynamo, primarily during the daytime. The M2 is mainly composed of the migrating component with a secondary contribution of the non-migrating ones, which can play an important role in the global structure of the lunar tide (Paulino et al., 2013). Maybe better conditions for propagation of some tidal non-migrating components could be the reason for the enhancement of M2 in zonal and vertical drifts. This hypothesis could be sustained by the observed large M2 amplitudes in the mesosphere and lower-thermosphere temperatures (Paulino et al., 2013) and zonal wind (Paulino et al., 2015). Forbes and Zhang (2019) showed large M2 amplitudes in the electron concentration during the summer; however, there were slight amplitudes near the Equator. Stening et al. (1999) also found large amplitudes in the vertical drift during the Southern Hemisphere summer, primarily in the nighttime period.
Furthermore, sudden stratospheric warmings, which are more frequently observed during the Southern Hemisphere summer, have been pointed out as a mechanism capable of enhancing the amplitudes of semidiurnal tides in the equatorial region (e.g., Fejer et al., 2011; Stening, 2011; Forbes and Zhang, 2012; Park et al., 2012; Paulino et al., 2012; Pedatella et al., 2012; Yamazaki et al., 2012; Chau et al., 2015; Maute et al., 2016). During the period of this study, four sudden stratospheric warmings were observed (see Table 2 of Yamazaki, 2014). Thus, it could also contribute to the M2 amplitudes in the F-region drifts during the Southern Hemisphere summer.
Although in the equatorial region, the neutral winds are less dependent on the solar cycle, consequently, one could expect that the lunar tide will not present a reasonable solar cycle dependency. However, the results from Fig. 3 showed the M2 amplitudes in the EPB zonal drifts to be 4 times larger during the HSA. It is expected that our results will have a weak influence on the E region dynamo because during the nighttime the recombination acts quickly to suppress the E region. Complementarily, it is established that the vertical penetration of the semidiurnal lunar tide into the ionosphere from the E region depends on the solar cycle due to the molecular viscosity, which filters some wave components with small vertical wavelengths (Forbes, 1982; Forbes et al., 2014). Yamazaki and Kosch (2014) showed a clear solar dependence of the geomagnetic lunar tide over the last century, and other works have also shown solar dependence of the lunar tide modulation in the equatorial electrojet (e.g., Eccles et al., 2011; Lühr et al., 2012; Yizengaw and Carter, 2017). Additionally, Eccles et al. (2011) showed M2 oscillation modulation parameters of the F region as well. Those results contribute to understanding that the lunar tide is solar dependent in some ionospheric parameters. Thus, these are reasons to believe that the M2 in the EPB zonal drifts can also be solar dependent.
The present work showed that the M2 modulated the EPB zonal drifts in the equatorial region over Brazil from 2000 to 2007, and the main results are summarized as follows.
-
The amplitude of the semidiurnal lunar tide in the equatorial plasma bubble zonal drifts was 3.1 m s−1, which is 5.6 % of the mean drifts.
-
A clear seasonal variability for the M2 amplitudes was observed, with high values during the summer of the Southern Hemisphere when they were compared to the equinox months.
-
The amplitudes of the semidiurnal lunar tide in the equatorial plasma bubble zonal drifts were solar cycle dependent, reaching values 4 times larger during the high solar activity.
The used airglow images can be requested from the corresponding author.
IP wrote the manuscript and did most of the analysis. ARP converted solar time to lunar time and revised the manuscript. AFM revised the manuscript and helped in the calculation of the EPB zonal drifts. CMW and HT revised the manuscript. RAB revised the manuscript and coordinated the observations.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the special issue “From the Sun to the Earth's magnetosphere–ionosphere–thermosphere”. It is a result of the VIII Brazilian Symposium on Space Geophysics and Aeronomy & VIII Symposium on Physics and Astronomy, Brazil, March 2021.
This work has been financed by the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) and the Fundação de Amparo à Pesquisa do Estado da Paraíba (FAPESQ PB) The authors thank the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) for making available, even during the pandemic period, the “Periódicos da CAPES”, which was fundamental for the construction of this paper.
This research has been supported by the CNPq (grant no. 306063/2020-4) and the FAPESQ PB (grant no. 002/2019).
This paper was edited by Luis Vieira and reviewed by Xin Wan, Yuichi Otsuka, and one anonymous referee.
Abalde, J. R., Sahai, Y., Fagundes, P. R., Becker-Guedes, F., Bittencourt, J. A., Pillat, V. G., Lima, W. L. C., Candido, C. M. N., and de Freitas, T. F.: Day-to-day variability in the development of plasma bubbles associated with geomagnetic disturbances, J. Geophys. Res.-Space, 114, A04304, https://doi.org/10.1029/2008JA013788, 2009. a
Abdu, M., Sobral, J., Batista, I., Rios, V., and Medina, C.: Equatorial spread-F occurrence statistics in the American longitudes: Diurnal, seasonal and solar cycle variations, Adv. Space Res., 22, 851–854, https://doi.org/10.1016/S0273-1177(98)00111-2, 1998. a
Abdu, M. A., Kantor, I. J., Batista, I. S., and de Paula, E. R.: East-west plasma bubble irregularity motion determined from spaced VHF polarimeters: Implications on velocity shear in the zonal F region bulk plasma motion, Radio Sci., 20, 111–122, https://doi.org/10.1029/RS020i001p00111, 1985. a
Abdu, M. A., Batista, I. S., Takahashi, H., MacDougall, J., Sobral, J. H., Medeiros, A. F., and Trivedi, N. B.: Magnetospheric disturbance induced equatorial plasma bubble development and dynamics: A case study in Brazilian sector, J. Geophys. Res.-Space, 108, 1449–1462, https://doi.org/10.1029/2002JA009721, 2003. a
Abdu, M. A., Alam Kherani, E., Batista, I. S., de Paula, E. R., Fritts, D. C., and Sobral, J. H. A.: Gravity wave initiation of equatorial spread F/plasma bubble irregularities based on observational data from the SpreadFEx campaign, Ann. Geophys., 27, 2607–2622, https://doi.org/10.5194/angeo-27-2607-2009, 2009. a
Aswathy, R. and Manju, G.: The post sunset equatorial F-region zonal drift variability and its linkage with equatorial spread F onset and duration over Indian longitudes, Adv. Space Res., 67, 1254–1260, https://doi.org/10.1016/j.asr.2020.11.024, 2021. a
Bates, D. R.: Recombination in the normal E and F layers of the ionosphere, Planet. Space Sci., 36, 55–63, https://doi.org/10.1016/0032-0633(88)90146-8, 1988. a
Chapagain, N. P., Makela, J. J., Meriwether, J. W., Fisher, D. J., Buriti, R. A., and Medeiros, A. F.: Comparison of nighttime zonal neutral winds and equatorial plasma bubble drift velocities over Brazil, J. Geophys. Res.-Space, 117, A06309, https://doi.org/10.1029/2012JA017620, 2012. a
Chapman, S. and Lindzen, R. S.: Atmospheric tides; thermal and gravitational, Gordon and Breach, New York, 1970. a
Chau, J. L., Hoffmann, P., Pedatella, N. M., Matthias, V., and Stober, G.: Upper mesospheric lunar tides over middle and high latitudes during sudden stratospheric warming events, J. Geophys. Res.-Space, 120, 3084–3096, https://doi.org/10.1002/2015JA020998, 2015. a
Chu, F. D., Liu, J. Y., Takahashi, H., Sobral, J. H. A., Taylor, M. J., and Medeiros, A. F.: The climatology of ionospheric plasma bubbles and irregularities over Brazil, Ann. Geophys., 23, 379–384, https://doi.org/10.5194/angeo-23-379-2005, 2005. a
de Paula, E. R. and Hysell, D. L.: The São Luís 30 MHz coherent scatter ionospheric radar: System description and initial results, Radio Sci., 39, RS1014, https://doi.org/10.1029/2003RS002914, 2004. a
Dungey, J.: Convective diffusion in the equatorial F region, J. Atmos. Terr. Phys., 9, 304–310, https://doi.org/10.1016/0021-9169(56)90148-9, 1956. a
Eccles, V., Rice, D. D., Sojka, J. J., Valladares, C. E., Bullett, T., and Chau, J. L.: Lunar atmospheric tidal effects in the plasma drifts observed by the Low-Latitude Ionospheric Sensor Network, J. Geophys. Res.-Space, 116, A07309, https://doi.org/10.1029/2010JA016282, 2011. a, b, c
Fagundes, P., Sahai, Y., and Takahashi, H.: Investigation of OI 557.7 nm and OI 630.0 nm nightglow intensity ratios during the occurrence of equatorial F-region plasma bubbles, J. Atmos. Terr. Phys., 57, 929–932, https://doi.org/10.1016/0021-9169(94)00064-U, 1995. a
Farley, D. T., Bonelli, E., Fejer, B. G., and Larsen, M. F.: The prereversal enhancement of the zonal electric field in the equatorial ionosphere, J. Geophys. Res.-Space, 91, 13723–13728, https://doi.org/10.1029/JA091iA12p13723, 1986. a
Fejer, B. G. and Tracy, B. D.: Lunar tidal effects in the electrodynamics of the low latitude ionosphere, J. Atmos. Sol.-Terr. Phys., 103, 76–82, https://doi.org/10.1016/j.jastp.2013.01.008, 2013. a
Fejer, B. G., de Paula, E. R., González, S. A., and Woodman, R. F.: Average vertical and zonal F region plasma drifts over Jicamarca, J. Geophys. Res.-Space, 96, 13901–13906, https://doi.org/10.1029/91JA01171, 1991. a
Fejer, B. G., de Paula, E. R., Scherliess, L., and Batista, I. S.: Incoherent scatter radar, ionosonde, and satellite measurements of equatorial F region vertical plasma drifts in the evening sector, Geophys. Res. Lett., 23, 1733–1736, https://doi.org/10.1029/96GL01847, 1996. a
Fejer, B. G., Tracy, B. D., Olson, M. E., and Chau, J. L.: Enhanced lunar semidiurnal equatorial vertical plasma drifts during sudden stratospheric warmings, Geophys. Res. Lett., 38, L21104, https://doi.org/10.1029/2011GL049788, 2011. a
Forbes, J. M.: Atmospheric tide: 2. The solar and lunar semidiurnal components, J. Geophys. Res.-Space, 87, 5241–5252, https://doi.org/10.1029/JA087iA07p05241, 1982. a, b
Forbes, J. M. and Zhang, X.: Lunar tide amplification during the January 2009 stratosphere warming event: Observations and theory, J. Geophys. Res.-Space, 117, A12312, https://doi.org/10.1029/2012JA017963, 2012. a
Forbes, J. M. and Zhang, X.: Lunar Tide in the F Region Ionosphere, J. Geophys. Res.-Space, 124, 7654–7669, https://doi.org/10.1029/2019JA026603, 2019. a, b
Forbes, J. M., Zhang, X., Bruinsma, S., and Oberheide, J.: Lunar semidiurnal tide in the thermosphere under solar minimum conditions, J. Geophys. Res.-Space, 118, 1788–1801, https://doi.org/10.1029/2012JA017962, 2013. a
Forbes, J. M., Zhang, X., and Bruinsma, S. L.: New perspectives on thermosphere tides: 2. Penetration to the upper thermosphere, Earth Planets Space, 66, 122, https://doi.org/10.1186/1880-5981-66-122, 2014. a, b
Fritts, D. C., Abdu, M. A., Batista, B. R., Batista, I. S., Batista, P. P., Buriti, R., Clemesha, B. R., Dautermann, T., de Paula, E. R., Fechine, B. J., Fejer, B. G., Gobbi, D., Haase, J., Kamalabadi, F., Kherani, E. A., Laughman, B., Lima, P. P., Liu, H.-L., Medeiros, A., Pautet, P.-D., Riggin, D. M., Rodrigues, F. S., São Sabbas, F., Sobral, J. H. A., Stamus, P., Takahashi, H., Taylor, M. J., Vadas, S. L., Vargas, F., and Wrasse, C. M.: Overview and summary of the Spread F Experiment (SpreadFEx), Ann. Geophys., 27, 2141–2155, https://doi.org/10.5194/angeo-27-2141-2009, 2009. a
Garcia, F. J., Taylor, M. J., and Kelley, M. C.: Two-dimensional spectral analysis of mesospheric airglow image data, Appl. Optics, 36, 7374–7385, https://doi.org/10.1364/AO.36.007374, 1997. a
Haerendel, G., Eccles, J. V., and Çakir, S.: Theory for modeling the equatorial evening ionosphere and the origin of the shear in the horizontal plasma flow, J. Geophys. Res.-Space, 97, 1209–1223, https://doi.org/10.1029/91JA02226, 1992. a
Huang, C.-S., de La Beaujardière, O., Roddy, P. A., Hunton, D. E., Ballenthin, J. O., Hairston, M. R., and Pfaff, R. F.: Large-scale quasiperiodic plasma bubbles: C/NOFS observations and causal mechanism, J. Geophys. Res.-Space, 118, 3602–3612, https://doi.org/10.1002/jgra.50338, 2013. a
Kudeki, E., Akgiray, A., Milla, M., Chau, J. L., and Hysell, D. L.: Equatorial spread-F initiation: Post-sunset vortex, thermospheric winds, gravity waves, J. Atmos. Sol.-Terr. Phys., 69, 2416–2427, https://doi.org/10.1016/j.jastp.2007.04.012, 2007. a
Li, G., Ning, B., Liu, L., Wan, W., and Liu, J. Y.: Effect of magnetic activity on plasma bubbles over equatorial and low-latitude regions in East Asia, Ann. Geophys., 27, 303–312, https://doi.org/10.5194/angeo-27-303-2009, 2009. a
Liu, H.-L.: Day-to-Day Variability of Prereversal Enhancement in the Vertical Ion Drift in Response to Large-Scale Forcing From the Lower Atmosphere, Space Weather, 18, e2019SW002334, https://doi.org/10.1029/2019SW002334, 2020. a
Lühr, H., Siddiqui, T. A., and Maus, S.: Global characteristics of the lunar tidal modulation of the equatorial electrojet derived from CHAMP observations, Ann. Geophys., 30, 527–536, https://doi.org/10.5194/angeo-30-527-2012, 2012. a
Maute, A., Fejer, B. G., Forbes, J. M., Zhang, X., and Yudin, V.: Equatorial vertical drift modulation by the lunar and solar semidiurnal tides during the 2013 sudden stratospheric warming, J. Geophys. Res.-Space, 121, 1658–1668, https://doi.org/10.1002/2015JA022056, 2016. a
Mendillo, M. and Baumgardner, J.: Airglow characteristics of equatorial plasma depletions, J. Geophys. Res.-Space, 87, 7641–7652, https://doi.org/10.1029/JA087iA09p07641, 1982. a
Park, J., Lühr, H., Kunze, M., Fejer, B. G., and Min, K. W.: Effect of sudden stratospheric warming on lunar tidal modulation of the equatorial electrojet, J. Geophys. Res.-Space, 117, A03306, https://doi.org/10.1029/2011JA017351, 2012. a
Paulino, A., Batista, P., Clemesha, B., Buriti, R., and Schuch, N.: An enhancement of the lunar tide in the MLT region observed in the Brazilian sector during 2006 SSW, J. Atmos. Sol.-Terr. Phys., 90–91, 97–103, https://doi.org/10.1016/j.jastp.2011.12.015, 2012. a
Paulino, A., Batista, P., Lima, L., Clemesha, B., Buriti, R., and Schuch, N.: The lunar tides in the mesosphere and lower thermosphere over Brazilian sector, J. Atmos. Sol.-Terr. Phys., 133, 129–138, https://doi.org/10.1016/j.jastp.2015.08.011, 2015. a
Paulino, A. R., Batista, P. P., and Batista, I. S.: A global view of the atmospheric lunar semidiurnal tide, J. Geophys. Res.-Atmos., 118, 13128–13139, https://doi.org/10.1002/2013JD019818, 2013. a, b
Paulino, A. R., Lima, L. M., Almeida, S. L., Batista, P. P., Batista, I. S., Paulino, I., Takahashi, H., and Wrasse, C. M.: Lunar tides in total electron content over Brazil, J. Geophys. Res.-Space, 122, 7519–7529, https://doi.org/10.1002/2017JA024052, 2017. a
Paulino, I., Medeiros, A., Buriti, R., Sobral, J., Takahashi, H., and Gobbi, D.: Optical observations of plasma bubble westward drifts over Brazilian tropical region, J. Atmos. Sol.-Terr. Phys., 72, 521–527, https://doi.org/10.1016/j.jastp.2010.01.015, 2010. a
Paulino, I., d. Medeiros, A. F., Buriti, R. A., Takahashi, H., Sobral, J. A. H. A., and Gobbi, D.: Plasma bubble zonal drift characteristics observed by airglow images over Brazilian tropical region, Revista Brasileira de Geofísica, 29, 239–246, 2011a. a, b, c
Paulino, I., Takahashi, H., Medeiros, A., Wrasse, C., Buriti, R., Sobral, J., and Gobbi, D.: Mesospheric gravity waves and ionospheric plasma bubbles observed during the COPEX campaign, J. Atmospheric Sol.-Terr. Phys., 73, 1575–1580, https://doi.org/10.1016/j.jastp.2010.12.004, 2011b. a, b
Paulino, I., Paulino, A. R., Cueva, R. Y. C., Agyei-Yeboah, E., Buriti, R. A., Takahashi, H., Wrasse, C. M., Santos, A. M., Fragoso de Medeiros, A., and Batista, I. S.: Semimonthly oscillation observed in the start times of equatorial plasma bubbles, Ann. Geophys., 38, 437–443, https://doi.org/10.5194/angeo-38-437-2020, 2020. a
Pedatella, N. M., Liu, H.-L., Richmond, A. D., Maute, A., and Fang, T.-W.: Simulations of solar and lunar tidal variability in the mesosphere and lower thermosphere during sudden stratosphere warmings and their influence on the low-latitude ionosphere, J. Geophys. Res.-Space, 117, A08326, https://doi.org/10.1029/2012JA017858, 2012. a
Pimenta, A., Fagundes, P., Bittencourt, J., and Sahai, Y.: Relevant aspects of equatorial plasma bubbles under different solar activity conditions, Adv. Space Res., 27, 1213–1218, https://doi.org/10.1016/S0273-1177(01)00200-9, 2001. a
Pimenta, A., Bittencourt, J., Fagundes, P., Sahai, Y., Buriti, R., Takahashi, H., and Taylor, M.: Ionospheric plasma bubble zonal drifts over the tropical region: a study using OI 630 nm emission all-sky images, J. Atmos. Sol.-Terr. Phys., 65, 1117–1126, https://doi.org/10.1016/S1364-6826(03)00149-4, 2003. a
Saito, S. and Maruyama, T.: Effects of transequatorial thermospheric wind on plasma bubble occurrences, J. Natl. Inst. Inform. Commun. Technol., 56, 257–266, 2009. a
Santos, A. M., Abdu, M. A., Souza, J. R., Sobral, J. H. A., Batista, I. S., and Denardini, C. M.: Storm time equatorial plasma bubble zonal drift reversal due to disturbance Hall electric field over the Brazilian region, J. Geophys. Res.-Space, 121, 5594–5612, https://doi.org/10.1002/2015JA022179, 2016. a
Sobral, J., Abdu, M., Takahashi, H., Taylor, M., de Paula, E., Zamlutti, C., de Aquino, M., and Borba, G.: Ionospheric plasma bubble climatology over Brazil based on 22 years (1977–1998) of 630 nm airglow observations, J. Atmos. Sol.-Terr. Phys., 64, 1517–1524, https://doi.org/10.1016/S1364-6826(02)00089-5, 2002. a
Sobral, J. H. A., Abdu, M. A., and Batista, I. S.: Airglow studies on the ionosphere dynamics over low latitude in Brazil, Ann. Geophys., 36, 199–204, 1980a. a
Sobral, J. H. A., Abdu, M. A., Zamlutti, C. J., and Batista, I. S.: Association between plasma bubble irregularities and airglow disturbances over Brazilian low latitudes, Geophys. Res. Lett., 7, 980–982, https://doi.org/10.1029/GL007i011p00980, 1980b. a
Stening, R. J.: Lunar tide in the equatorial electrojet in relation to stratospheric warmings, J. Geophys. Res.-Space, 116, A12315, https://doi.org/10.1029/2011JA017047, 2011. a
Stening, R. J. and Fejer, B. G.: Lunar tide in the equatorial F region vertical ion drift velocity, J. Geophys. Res.-Space, 106, 221–226, https://doi.org/10.1029/2000JA000175, 2001. a, b
Stening, R. J., Richmond, A. D., and Roble, R. G.: Lunar tides in the Thermosphere-Ionosphere-Electrodynamics General Circulation Model, J. Geophys. Res.-Space, 104, 1–13, https://doi.org/10.1029/98JA02663, 1999. a, b
Takahashi, H., Taylor, M., Sobral, J., Medeiros, A., Gobbi, D., and Santana, D.: Fine structure of the ionospheric plasma bubbles observed by the OI 6300 and 5577 airglow images, Adv. Space Res., 27, 1189–1194, https://doi.org/10.1016/S0273-1177(01)00159-4, 2001. a
Takahashi, H., Taylor, M. J., Pautet, P.-D., Medeiros, A. F., Gobbi, D., Wrasse, C. M., Fechine, J., Abdu, M. A., Batista, I. S., Paula, E., Sobral, J. H. A., Arruda, D., Vadas, S. L., Sabbas, F. S., and Fritts, D. C.: Simultaneous observation of ionospheric plasma bubbles and mesospheric gravity waves during the SpreadFEx Campaign, Ann. Geophys., 27, 1477–1487, https://doi.org/10.5194/angeo-27-1477-2009, 2009. a
Tsunoda, R. T.: Day-to-day variability in equatorial spread F: Is there some physics missing?, Geophys. Res. Lett., 33, L16106, https://doi.org/10.1029/2006GL025956, 2006. a
Tsunoda, R. T., Saito, S., and Nguyen, T. T.: Post-sunset rise of equatorial F layer – or upwelling growth?, Prog. Earth Planet. Sci., 5, 22, https://doi.org/10.1186/s40645-018-0179-4, 2018. a
Weber, E. J., Buchau, J., Eather, R. H., and Mende, S. B.: North-south aligned equatorial airglow depletions, J. Geophys. Res.-Space, 83, 712–716, https://doi.org/10.1029/JA083iA02p00712, 1978. a
Woodman, R. F. and La Hoz, C.: Radar observations of F region equatorial irregularities, J. Geophys. Res., 81, 5447–5466, https://doi.org/10.1029/JA081i031p05447, 1976. a
Yamazaki, Y.: Solar and lunar ionospheric electrodynamic effects during stratospheric sudden warmings, J. Atmos. Sol.-Terr. Phys., 119, 138–146, https://doi.org/10.1016/j.jastp.2014.08.001, 2014. a
Yamazaki, Y. and Kosch, M. J.: Geomagnetic lunar and solar daily variations during the last 100 years, J. Geophys. Res.-Space, 119, 6732–6744, https://doi.org/10.1002/2014JA020203, 2014. a
Yamazaki, Y., Richmond, A. D., and Yumoto, K.: Stratospheric warmings and the geomagnetic lunar tide: 1958–2007, J. Geophys. Res.-Space, 117, A04301, https://doi.org/10.1029/2012JA017514, 2012. a
Yizengaw, E. and Carter, B. A.: Longitudinal, seasonal and solar cycle variation in lunar tide influence on the equatorial electrojet, Ann. Geophys., 35, 525–533, https://doi.org/10.5194/angeo-35-525-2017, 2017. a
Zhang, J. T., Forbes, J. M., Zhang, C. H., Doornbos, E., and Bruinsma, S. L.: Lunar tide contribution to thermosphere weather, Space Weather, 12, 538–551, https://doi.org/10.1002/2014SW001079, 2014. a, b





