GUMICS-4 analysis of interplanetary coronal mass ejection impact on Earth during low and typical Mach number solar winds

We study the response of the Earth's magnetosphere to fluctuating solar wind conditions during interplanetary coronal mass ejections (ICMEs) using the Grand Unified Magnetosphere-Ionosphere Coupling Simulation (GUMICS-4). The two ICME events occurred on 15–16 July 2012 and 29–30 April 2014. During the strong 2012 event, the solar wind upstream values reached up to 35 particles cm⁻³, speeds of up to 694 km s⁻¹, and an interplanetary magnetic field of up to 22 nT, giving a Mach number of 2.3. The 2014 event was a moderate one, with the corresponding upstream values of 30 particles cm⁻³, 320 km s⁻¹ and 10 nT, indicating a Mach number of 5.8. We examine how the Earth's space environment dynamics evolves during both ICME events from both global and local perspectives, using well-established empirical models and in situ measurements as references. We show that on the large scale, and during moderate driving, the GUMICS-4 results are in good agreement with the reference values. However, the local values, especially during high driving, show more variation: such extreme conditions do not reproduce local measurements made deep inside the magnetosphere. The same appeared to be true when the event was run with another global simulation. The cross-polar cap potential (CPCP) saturation is shown to depend on the Alfvén–Mach number of the upstream solar wind. However, care must be taken in interpreting these results, as the CPCP is also sensitive to the simulation resolution.

1 Introduction

The present understanding is that the coupling of the solar wind and the Earth's magnetosphere occurs via magnetic reconnection (Dungey, 1961) and viscous processes (Axford and Hines, 1961) such as the Kelvin–Helmholtz instability (e.g., Nykyri and Otto, 2001) and diffusion (Johnson and Cheng, 1997). Although viscous processes may play a strong role, particularly when the interplanetary magnetic field (IMF) is northward (IMF B_Z>0 nT) (e.g., Osmane et al., 2015), magnetic reconnection on the dayside magnetopause is responsible for the majority of plasma transport across the magnetopause during southward interplanetary magnetic field IMF (IMF B_Z<0 nT), allowing the solar wind to drive activity in the Earth's space environment (Nishida, 1968; Koustov et al., 2009). The intervals of extended periods of strongly southward IMF typically arise when the Earth encounters an interplanetary coronal mass ejection (ICME) (see, e.g., Kilpua et al., 2017b). ICMEs are interplanetary counterparts of coronal mass ejections (CMEs), large eruptions of plasma and magnetic field from the Sun, driving the strongest geomagnetic disturbances (e.g., Gosling et al., 1991; Huttunen et al., 2002; Richardson and Cane, 2012; Kilpua et al., 2017a). The signatures of ICMEs at 1 AU include high helium abundance (Hirshberg et al., 1972), high magnetic field magnitude and low plasma beta (Hirshberg and Colburn, 1969; Burlaga et al., 1981), low ion temperatures (Gosling et al., 1973), and smooth rotation of the magnetic field (Burlaga et al., 1981). While there have been attempts to form a universal set of signatures to describe ICMEs (Gosling, 1990; Richardson and Cane, 2003), they vary significantly such that no single set of criteria is able to describe all the ICME events, and none of them is unique to ICMEs. For example, only one-third to one-half of all the ICMEs have a magnetic flux rope (or a magnetic cloud) (e.g., Gosling, 1990; Richardson and Cane, 2003), whose signatures combine enhanced magnetic field, reduced proton temperature, and the smooth rotation of the magnetic field over an interval of a day (Burlaga et al., 1981). While magnetic clouds are the most studied part of ICMEs due to their significant potential to cause large space storms, their relationship with the entire ICME sequence still poses many questions (e.g., Kilpua et al., 2013). Moreover, if the ICME is sufficiently faster than the ambient solar wind plasma, a shock is formed ahead of the ICME (Goldstein et al., 1998), with a region of compressed solar wind plasma between the leading shock front and the magnetic cloud, referred to as the sheath region.

The sheath and ejecta are the most distinctive parts of ICMEs (see, e.g., Kilpua et al., 2017b), and both can drive intense magnetic storms (e.g., Tsurutani et al., 1988; Huttunen and Koskinen, 2004). However, they have clear differences in their solar wind conditions and, consequently, their coupling to the magnetosphere is different (Jianpeng et al., 2010; Pulkkinen et al., 2007; Kilpua et al., 2017b). ICME sheaths typically include high solar wind dynamic pressure and fluctuating IMF, including both northward and southward orientations within a short time period (Kilpua et al., 2017b). The duration of the sheath is also typically shorter than the following cloud: for example. Zhang et al. (2012) obtained the average values of 10.6 and 30.6 h for sheaths and clouds, respectively. Sheaths are known to enhance high-latitude ionospheric currents (Huttunen and Koskinen, 2004) and they are found to have higher coupling efficiency than clouds (Yermolaev et al., 2012). The clouds typically enhance the equatorial ring current (Huttunen and Koskinen, 2004).

Due to the potential for strongly southward IMF orientation, ICME magnetic clouds drive enhanced magnetospheric activity. Moreover, during cloud events, due to the combination of generally high magnetic fields and low plasma densities, the solar wind Alfvén–Mach number M_A can reach quite low values and even be close to unity. The role of M_A in solar wind–magnetosphere coupling has been highlighted in recent studies (Lavraud and Borovsky, 2008; Lopez et al., 2010; Myllys et al., 2016, 2017). In particular, the role of low M_A conditions typical for ICME magnetic cloud in the saturation of the ionospheric cross-polar cap potential (CPCP) has been a subject of several studies (e.g., Ridley, 2005, 2007; Lopez et al., 2010; Wilder et al., 2015; Myllys et al., 2016; Lakka et al., 2018).

Global MHD models have been used to study the effects of ICMEs on the magnetospheric and ionospheric dynamics. Wu et al. (2015) used the H3DMHD model (e.g., Wu et al., 2007) to examine a CME event on 15 March 2013. They found that the high-energy solar energetic proton time–intensity profile can be explained by the interaction of a CME-driven shock with the heliospheric current sheet embedded within nonuniform solar wind. A recent paper by Kubota et al. (2017) studied the Bastille Day geomagnetic storm event (15 July 2000) driven by a halo CME. They found that the inclusion of auroral conductivity in the ionospheric part of the global MHD model by Tanaka (1994) led to saturation of the CPCP without any effect on the field-aligned currents, thus suggesting a current system with a dynamo in the magnetosphere and a load in the ionosphere. The difficulty in assessing these studies is that they often do not include uncertainty estimate of the model results, while the methods are different for each study. Moreover, while the different MHD simulations are based on the same plasma theory, the approaches are different in terms of the exact form of the equations, the numerical solutions, and the initial and boundary conditions, thus making comparisons of different models difficult. Nonetheless, understanding of the performance limits of the simulations is essential for meaningful comparisons to in situ measurements.

Regardless of the different approaches used in global codes, the performances of the models have been assessed in several studies. Usually such assessments are done through comparisons of the simulation results with in situ or remote observations of dynamic events or plasma processes (Birn et al., 2001; Pulkkinen et al., 2011; Honkonen et al., 2013). This is often not easy, as even small errors in the simulation configuration may create large differences with respect to the observations locally at a single point (Lakka et al., 2017), even if the simulation would reproduce the large-scale dynamic sequence correctly. Moreover, recent studies (Juusola et al., 2014; Gordeev et al., 2015) have shown that none of the codes emerges as clearly superior to the others, each having their strengths and weaknesses. In the absence of uniform code performance testing methodology, validating the results individually is important.

In this study we use the GUMICS-4 (Janhunen et al., 2012) and global MHD simulation and consider two ICME events, one with a significantly stronger solar wind driver than the other. To compare the two events, we use variables that are both particularly sensitive to upstream changes and used extensively in previous studies, and examine how those variables are affected by the two events. The comparisons include the subsolar magnetopause position, the amount of energy transferred from the solar wind into the magnetosphere, the CPCP, and the magnetic field magnitude within the inner part of the magnetosphere, thus including both global and local variables. We especially focus on periods within the magnetic clouds within the ICMEs, by using two different spatial resolutions. We provide an uncertainty estimate (standard deviation and in some cases also relative difference) for each quantity by comparing simulation results to well-established references, which include the Shue model (magnetopause location), the epsilon parameter (energy transferred through the magnetopause), the polar cap index (PCI) (CPCP), and in situ measurements by the Geotail and Cluster spacecraft (magnetic field magnitude). Both uncertainty estimate methods are assessed and they are used if the method is valid for the chosen quantity.

This paper is structured in a following way: Sect. 2 describes GUMICS-4 global MHD code and the simulation setup, Sect. 3 describes characteristics of the two ICME events and the executed simulations, Sect. 4 presents the main results and Sect. 5 includes the discussion followed by conclusions.

2 Methodology

2.1 GUMICS-4 global MHD simulation

The simulations were executed using the fourth edition of the Grand-Unified Magnetosphere-Ionosphere Coupling Simulation (GUMICS-4), in which a 3-D MHD magnetosphere is coupled with a spherical electrostatic ionosphere (Janhunen et al., 2012). The finite-volume MHD solver solves the ideal MHD equations with the separation of the magnetic field to a curl-free (dipole) component and divergent-free component created by currents external to the Earth ($\mathit{B}=B_{\mathrm{0}}+B_{\mathrm{1}}\left(t\right)$) (Tanaka, 1994). The MHD simulation box has dimensions of 32…−224R_E in the X_GSE direction and −64…+64 R_E in both the Y_GSE and Z_GSE directions, while the inner boundary is spherical with a radius of 3.7 R_E. GUMICS-4 uses temporal subcycling and adaptive cartesian octogrid to improve temporal and spatial resolution in key regions, which means that it only runs on a single processor due to difficulties in parallelizing computations with two adaptive grids. The temporal subcycling reduces the number of MHD computations an order of magnitude while maintaining the local Courant–Friedrichs–Levy (CFL) constraint (Lions and Ciarlet, 2000, pp. 121–151). The adaptive grid ensures that whenever there are large gradients, the grid is refined, thus resolving smaller-scale features especially close to boundaries and current sheets.

The ionospheric grid is triangular and densest in the auroral oval, while in the polar caps the grid is still rather dense, with about 180 and 360 km spacing used in the two regions, respectively. The ionosphere is driven by field-aligned currents and electron precipitation from the magnetosphere as well as by solar EUV ionization. Field-aligned currents contribute to the cross-polar cap potential through

$$\begin{array}{}\text{(1)}& \mathrm{\nabla }\cdot \mathit{J}=\mathrm{\nabla }\cdot \left[\mathrm{\Sigma }\cdot \left(-\mathrm{\nabla }\mathit{\varphi }+V_n\times \mathit{B}\right)\right]=-j_{\left|\right|}\left(\widehat{\mathit{b}}\cdot \widehat{\mathit{r}}\right),\end{array}$$

where J is current density, Σ is the height-integrated conductivity tensor, ϕ is the ionospheric potential, V_n is the neutral wind caused by the Earth's rotation, $j_{\left|\right|}$ is the field-aligned current, and $(\widehat{\mathit{b}}\cdot \widehat{\mathit{r}})$ is the cosine of the angle between the magnetic field direction $\widehat{\mathit{b}}$ and the radial direction $\widehat{\mathit{r}}$ (Janhunen et al., 2012). Electron precipitation and solar EUV ionization have contributions to the height-integrated Pedersen and Hall conductivities with solar EUV ionization parametrized by the 10.7 cm solar radio flux that has a numerical value of $\mathrm{100}\times {\mathrm{10}}^{-\mathrm{22}}$ W m⁻². Electron precipitation affects the altitude-resolved ionospheric electron densities and are used when computing the height-integrated Pedersen and Hall conductivities. The details on the ionospheric part of GUMICS-4 can be found in Janhunen and Huuskonen (1993) and Janhunen (1996).

The region between the MHD magnetosphere and the electrostatic spherical ionosphere is a passive medium where no currents flow perpendicularly to the magnetic field. The magnetosphere is coupled to the ionosphere using dipole mapping of the field-aligned current pattern and the electron precipitation from the magnetosphere to the ionosphere and the electric potential from the ionosphere to the magnetosphere. This feedback loop is updated every 4 s.

2.2 GUMICS simulations of two ICME events

We use both 0.5 and 0.25 R_E maximum spatial resolutions as well as varying dipole tilt angles in this study. Two complete ICME periods were simulated using 0.5 R_E resolution by starting with nominal solar wind conditions preceding the events and ending with nominal conditions following the events. To give the GUMICS-4 magnetosphere time to form (Lakka et al., 2017), the simulations were initialized with 2 h of constant solar wind driving using upstream values equal to those during the first minute of the actual simulation ($n,\left|V\right|,\left|B\right|$ values of 4 cm⁻³, 310 km s⁻¹ and 1.1 nT for the 2012 event, and 11 cm⁻³, 300 km s⁻¹ and 1.8 nT for the 2014 event).

Due to computational limitations, using the best maximum spatial resolution (0.25 R_E) covering both ICME events with full length is not feasible due to long simulation physical times (up to 3.5 d) and resulting long simulation running times. Hence, two additional runs were performed with 0.25 R_E maximum spatial resolution in order to gain a more detailed view of the dynamics of the magnetosphere and ionosphere when the ICME magnetic cloud was propagating past the Earth. These runs lasted 6 h each and were executed by restarting the 0.5 R_E runs with enhanced resolution. Table 1 summarizes all four simulation runs related to the study.

Table 1 Summary of the event simulations within the current study.

3 Observations of two ICME events

We use the solar wind data from the NASA OMNIWeb service (http://omniweb.gsfc.nasa.gov, last access: 30 January 2018) and the solar energetic particle data from the NOAA NCEI Space Weather data access (https://www.ngdc.noaa.gov/stp/satellite/goes/index.html, last access: 22 March 2018). Onset times for the ICME sheath (i.e., the shock time) and the magnetic cloud boundary times are retrieved from the Wind spacecraft ICME catalog (https://wind.nasa.gov/ICMEindex.php, last access: 30 January 2018). Figures 1 and 2 show the upstream parameters during both events. For both figures, IMF $X,Y,Z$ components and the IMF magnitude are shown in panel (a), upstream plasma flow velocity $X,Y,Z$ components in panel (b), the upstream plasma number density in panel (c), upstream Alfvén–Mach number (in logarithmic scale) in panel (d), energetic proton fluxes for three GOES-15 energy channels between 8 and 80 MeV in panel (e), and the cross-polar cap potential from the GUMICS-4 simulation in panel (f). Figure 1 includes the time range from 09:00 UT, 14 July to 15:00 UT, 17 July 2012, while Fig. 2 shows the period from 19:00 UT, 28 April to 17:00 UT, 1 May 2014. The time of the ICME shock and the start and end times of the ICME are marked with vertical red lines in both figures. The grey-shaded regions indicate the time periods simulated with the maximal 0.25 R_E spatial resolution. Both IMF and plasma flow velocity components are given in the GSE coordinate system, which is also the coordinate system used by the GUMICS-4 simulation.

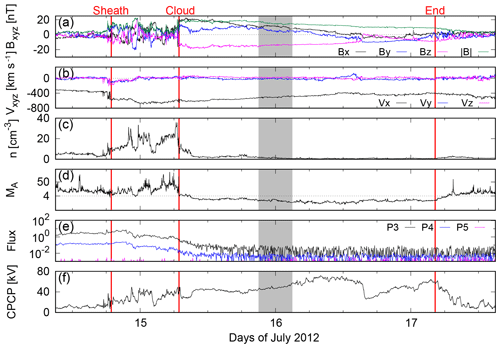
Figure 1 Solar wind and IMF conditions during 14 July 09:00 UT–17 July 15:00 UT, 2012. Panels from top to bottom: (a) IMF components B_X, B_Y and B_Z and the IMF magnitude in nT, (b) plasma velocity components V_X, V_Y and V_Z in km s⁻¹, (c) plasma number density n in cm⁻³, (d) upstream Alfvén–Mach number M_A (M_A=4 is marked with a dotted line), (e) GOES-15 geostationary orbit proton fluxes for three energy channels between 8 and 80 MeV, and (f) the ionospheric cross-polar cap potential from GUMICS-4. Data in panels (a)–(d) are measured by ACE/Wind. Vertical red lines indicate the onset of the ICME sheath/magnetic cloud or the end of the ICME event. Grey background shows the part of the ICME event that is simulated using both 0.25 and 0.5 R_E as a maximum spatial resolution.

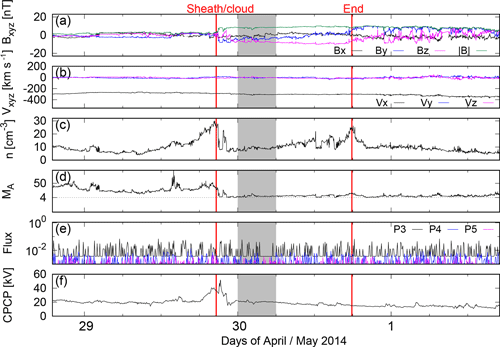
Figure 2 Solar wind and IMF conditions during 28 April 19:00 UT–1 May 17:00 UT, 2014. Panels from top to bottom: (a) IMF components B_X, B_Y and B_Z and the IMF magnitude in nT, (b) plasma velocity components V_X, V_Y and V_Z in km s⁻¹, (c) plasma number density n in cm⁻³, (d) upstream Alfvén–Mach number M_A (M_A=4 is marked with a dotted line), (e) GOES-15 geostationary orbit proton fluxes for three energy channels between 8 and 80 MeV, and (f) the ionospheric cross-polar cap potential from GUMICS-4. Data in panels (a)–(d) are measured by ACE/Wind. Vertical red lines indicate the onset of the ICME sheath/magnetic cloud or the end of the ICME event. Grey background shows the part of the ICME event that is simulated using both 0.25 and 0.5 R_E as a maximum spatial resolution.

Figure 1 shows the arrival of the leading shock at 18:53 UT on 14 July 2012 as the simultaneous abrupt jump in the plasma and magnetic field parameters and the following ICME sheath as irregular directional changes in the IMF and compressed plasma and field. The energetic particle fluxes for the two lower-energy channels increase until after the shock passage, which suggests continual particle acceleration in the shock driven by the ICME. At 06:54 UT on 15 July, the onset of the ICME magnetic cloud is identified by strong southward turning of the IMF. There is significant reduction in the number density and the clear decrease in the variability of the interplanetary magnetic field. During the next 45 h, the IMF direction stayed strongly southward while slowly rotating towards a less southward orientation. We note that in the trailing part of the ICME, the field changes rather sharply to northward, thereafter continuing to rotate southward again. We cannot rule out that this end part is not another small ICME, but as our study focuses on the strong southward magnetic fields in the main part of the ICME we do not consider the origin of this end part further here.

The ICME on April 2014 was slower than the July 2012 ICME, and its speed was very close to the ambient solar wind speed. Hence, no shock nor clear sheath developed ahead of this ICME. The onset of the ICME-related disturbance is marked by the increased plasma number density followed by a rapid decrease and a clear southward turning of the IMF at 20:38 UT on 29 April (Fig. 2). The weaker activity is also evident in the lack of energetic particle fluxes above the background in the magnetosphere. The very early phase of this cloud may contain some disturbed solar wind (the region of higher density and fluctuating field), but we do not identify it as a sheath and focus our study on the effects of the cloud proper.

Both magnetic clouds are characterized by a low Alfvén–Mach number. In the 2012 case, M_A drops even below unity and is 1.9 on average during the cloud structure, while during the 2014 magnetic cloud, the minimum M_A was 3.8 and the average was 5.8.

The 2012 event features generally larger CPCP, with values above 40 kV and reaching 70 kV (Fig. 1f). On the other hand, during the 2014 event the CPCP peaks early at 50 kV and subsequently reduces to 20 kV (Fig. 2f). GUMICS-4 CPCP values depend on grid resolution, and while lower grid resolution may result in substantially lower CPCP values than the observed values (Gordeev et al., 2015), higher resolution leads to higher CPCP values (e.g., Lakka et al., 2018) and thus better agreement with the observations.

The 2012 ICME event is considerably longer than the 2014 event, with 57 h 26 min total duration, of which 12 h 1 min are sheath and 45 h 25 min part of the magnetic cloud passage. The 2014 event lasted 21 h 13 min in total. The 2012 ICME had larger effects on magnetospheric activity, as the solar wind driving was considerably stronger, with the average IMF magnitude and solar wind speed of 14 nT and 490 km s⁻¹, respectively, compared with 8.5 nT and 303 km s⁻¹ of the 2014 event. The maximum IMF magnitude and upstream solar wind speed were also larger during the 2012 event, with 21 (10) nT and 660 (321) km s⁻¹ maximum values measured during the 2012 (2014) cloud. However, while maximum number density was higher during the 2012 magnetic cloud (36 vs. 30 cm⁻³), the average number density was considerably higher during the 2014 event (2012: 2 cm⁻³ vs. 2014: 12 cm⁻³).

During the two ICME events, data from the Cluster 1 (hereafter Cluster) and Geotail satellites were available from the CDAWeb service (https://cdaweb.sci.gsfc.nasa.gov/index.html/, last access: 8 October 2018). Figure 3 shows the orbits of Cluster (blue) and Geotail (green) along with the magnetopause location (black) from the empirical Shue model (Shue et al., 1997) on the XY plane (Fig. 3a and c) and on the XZ plane (Fig. 3b and d) for both events. The magnetopause position is computed for the most earthward magnetopause location during the events, while the orbit tracks include intervals of nominal upstream conditions before and after the ICME events. Start and end points of the time intervals are marked with a cross and a triangle, respectively. Dots mark the points where satellite orbits intersect (located visually) the innermost position of the magnetopause. The variability of the magnetopause position means that between those orbit tracks the S/C may cross to outside the magnetosphere. The used coordinate system is GSE. Based on Fig. 3, the Cluster spacecraft orbits inside of the magnetosphere throughout the 2012 event and for most of the 2014 event. On the other hand, Geotail is outside the magnetosphere an extended period during 16–17 July 2012 as well as during several periods in April–May 2014.

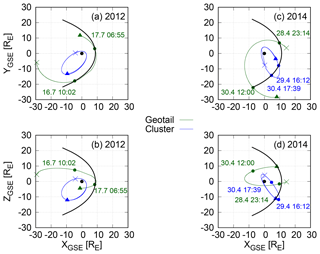
Figure 3 Orbits of Cluster 1 (blue) and Geotail (green) satellites during 14 July 09:00 UT–17 July 15:00 UT, 2012 (a, b) and during 28 April 19:00 UT–1 May 17:00 UT, 2014 (c, d). Orbits are shown on the XY plane in panels (a) and (c) and on the XZ plane in panels (b) and (d). The coordinate system is GSE. The most earthward position of the Shue magnetopause during both time intervals is drawn in black. Start and end points of the time intervals are marked with a cross and a triangle, respectively. The points along the satellite orbits between which the spacecraft may encounter magnetopause crossings are marked with dots.

Figures 4 and 5 show time series of the magnetic field magnitude $\left|B\right|$ along the Geotail (panel a) and Cluster (panel b) orbits during the 2012 and 2014 events. Green (Geotail) and blue (Cluster) curves show the observations, while the black (magenta) curve shows the magnetic field magnitude along the spacecraft orbits in GUMICS-4 simulation using 0.5 (0.25) R_E maximum spatial resolution. The yellow-shaded regions in panels (a) and (b) indicate times when the spacecraft may encounter magnetopause crossings. Note that a logarithmic scale is used for the Cluster data. Panel (c) in both figures shows the radial distance of the spacecraft from the center of the Earth. Note that satellite measurements have been interpolated over long (several hours) data gaps, most notably on 16 July, 12:15–18:45 UT.

Table 2 Average relative difference magnitudes in the magnetopause nose position for a given simulation phase.

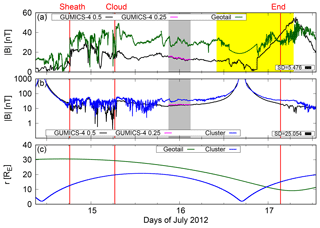
Figure 4 The time series of the magnetic field magnitude $\left|B\right|$ along the orbits of Geotail (a) and Cluster 1 (b) during 14 July 09:00 UT–17 July 15:00 UT, 2012 as measured by Geotail (green) and Cluster 1 (blue) and predicted by GUMICS-4 (black and magenta). Black and magenta curves in panels (a)–(b) show GUMICS-4 results with maximum spatial resolutions of 0.5 (black) and 0.25 (magenta) R_E. (c) Radial distance of both spacecraft from the center of the Earth. Yellow-shaded regions indicate approximate time intervals when a satellite may exit the magnetosphere. Grey-shaded regions show the part of the ICME event simulated also using 0.25 R_E maximum spatial resolution. Standard deviations (SDs) for observation vs. GUMICS-4 (0.5 R_E resolution) datasets are given in panels (a) and (b).

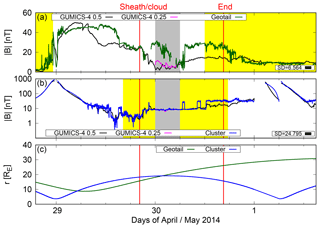
Figure 5 The time series of the magnetic field magnitude $\left|B\right|$ along the orbits of Geotail (a) and Cluster 1 (b) during 28 April 19:00 UT–1 May 17:00 UT, 2014 as measured by Geotail (green) and Cluster 1 (blue) and predicted by GUMICS-4 (black and magenta). Black and magenta curves in panels (a)–(b) show GUMICS-4 results with maximum spatial resolutions of 0.5 (black) and 0.25 (magenta) R_E. (c) Radial distance of both spacecraft from the center of the Earth. Yellow-shaded regions indicate approximate time intervals when a satellite may exit the magnetosphere. Grey-shaded regions show the part of the ICME event simulated also using 0.25 R_E maximum spatial resolution. SDs for observation vs. GUMICS-4 (0.5 R_E resolution) datasets are given in panels (a) and (b).

At the start of the 2012 event, Geotail resides in the plasma sheet but quickly moves to the boundary layer (roughly 14 July, 16:00 UT to 15 July, 06:00 UT), after which it enters the lobe as the cloud proper hits the magnetosphere. At around the end of the data gap at the end of 16 July, the spacecraft moves to the low-latitude boundary layer and the magnetosheath (identified from plasma data not shown here).

At the start of the 2012 event, Cluster is near perigee, recording field values dominated by the dipole contribution. Cluster exits the ring current region around 16:00 UT on 14 July and enters the plasma sheet. A brief encounter in the lobe is recorded between roughly 18:00 UT 15 July and 06:00 UT 16 July. A second period in the inner magnetosphere commences around 12:00 UT on 16 July, with exit to the lobe after 00:00 UT 17 July (identified from plasma and energetic particle data not shown here).

4 Analysis

4.1 Global dynamics

Figures 6 and 7 show the effect of upstream IMF B_Z (panel a) and solar wind dynamic pressure (panel b) on the magnetopause nose (panel c), total energy through the dayside magnetopause nose position (panel d) and the ionospheric CPCP (panel e) during the simulated intervals shown in Figs. 1 and 2. The 0.5 R_E resolution run results are shown in black, and 0.25 R_E resolution results are shown in magenta. The grey-shaded area highlights the 6 h interval simulated using both resolutions. Blue and green curves indicate reference values (see below) and solar wind upstream conditions, respectively.

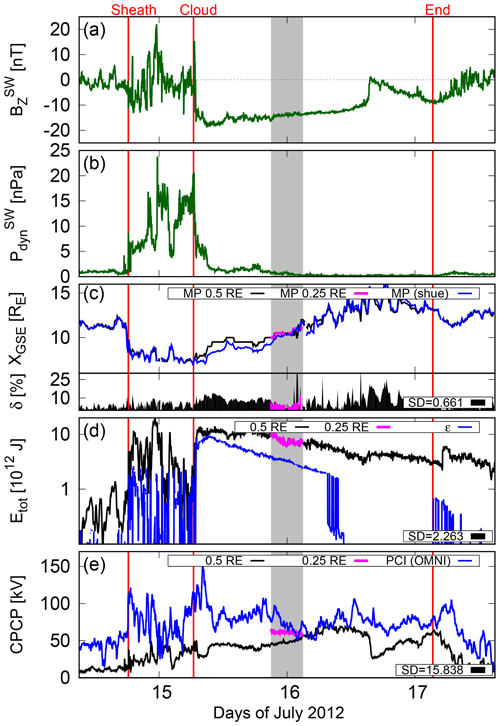
Figure 6 (a) Interplanetary magnetic field Z component, (b) solar wind dynamic pressure, (c) distance to the nose of the magnetopause, (d) energy transferred from the solar wind into the magnetosphere through the dayside magnetopause, and (e) the cross-polar cap potential during 15 July 21:00 UT–16 July 03:00 UT, 2012. Magenta plots in panels (c)–(d) show results with a maximum spatial resolution of 0.25 R_E. Blue curves in panels (c), (d), and (e) show the reference values (the Shue model, the ϵ parameter, the PCI). The relative difference magnitude δ between GUMICS-4 and the reference value is shown in panel (c). SDs for reference vs. GUMICS-4 (0.5 R_E resolution) datasets are given in panels (c)–(e).

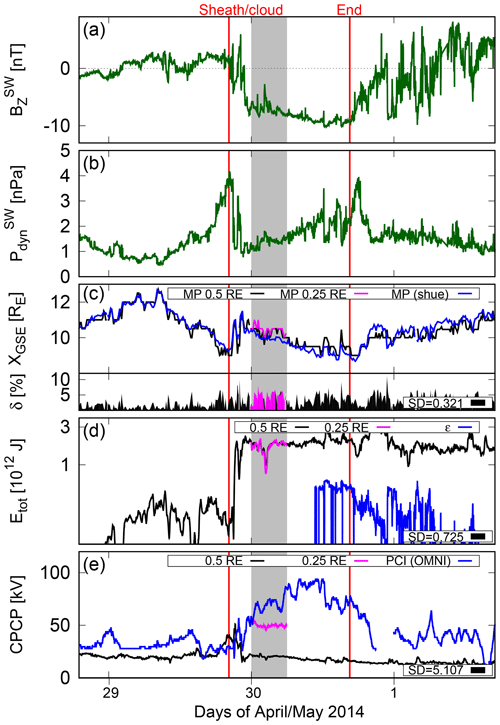
Figure 7 (a) Interplanetary magnetic field Z component, (b) solar wind dynamic pressure, (c) distance to the nose of the magnetopause, (d) energy transferred from the solar wind into the magnetosphere through the dayside magnetopause, and (e) the cross-polar cap potential during 30 April 00:00–06:00 UT, 2014. Magenta plots in panels (c)–(d) show results with a maximum spatial resolution of 0.25 R_E. Blue curves in panels (c), (d), and (e) show the reference values (the Shue model, the ϵ parameter, the PCI). The relative difference magnitude δ between GUMICS-4 and the reference value is shown in panel (c). SDs for reference vs. GUMICS-4 (0.5 R_E resolution) datasets are given in panels (c)–(e).

As a metric for validating the simulation results, we use the magnitude of the relative difference (given as δ in panel c of Figs. 6 and 7)

$$\begin{array}{}\text{(2)}& \mathit{\delta }=\left|{\displaystyle \frac{x_{\mathrm{ref}}-x_{\text{GUMICS-4}}}{x_{\mathrm{ref}}}}\right|,\end{array}$$

in which x is the GUMICS-4 variable and x_ref refers to the reference parameter value of the variable. An average δ value is computed for each ICME simulation phase (nominal solar wind, sheath, cloud) for both 0.5 R_E and 0.25 R_E resolution runs. These percentage values can be found in Table 2. We also compute the standard deviation (SD) for the reference vs. GUMICS-4 results. A single SD value (given in panels c, d and e) is computed for the 0.5 R_E resolution runs to illustrate how similar the temporal evolution is over timescales of days for GUMICS-4 and the reference parameter.

Figure 6a and b show that the IMF B_Z fluctuates approximately between −5…+5 nT during nominal solar wind conditions, while the solar wind dynamic pressure is steady and low. At the onset of ICME sheath, both B_Z and dynamic pressure start fluctuating with increased amplitude. Moreover, after the onset of ICME cloud, the orientation of the IMF slowly rotates from southward to northward, with the solar wind dynamic pressure decreasing rapidly and remaining low until the end of the simulated interval. This behavior is somewhat similar during the 2014 event (Fig. 7a–b), with the exception of missing high-amplitude fluctuations due to the absence of a distinct ICME sheath.

In GUMICS-4, we identify the magnetopause nose position as a single grid point with the maximum value of J_Y along the Sun–Earth line, using 1 min temporal resolution, smoothed using 10 min sliding averages. This value is compared with the Shue et al. (1997) empirical magnetopause model. For simplicity, the nose of the magnetopause is referred to as a magnetopause. Figure 6c shows that at the onset of ICME sheath, the magnetopause moves earthward as a consequence of changing upstream conditions, which is followed by sunward return motion lasting until the end of the ICME event. The average δ is highest during the cloud (8 %) and lowest (2.5 %) during nominal solar wind conditions. During ICME sheath, average δ is 4.5 %. During the 2014 event, the magnetopause starts moving earthward at least 10 h before the onset of ICME cloud (Fig. 7c), as the dynamic pressure increases, with IMF B_Z staying positive. After the onset however the magnetopause moves sunward for a few hours until slowly moving earthward again. The difference in average δ between cloud and nominal solar wind conditions is lower than for the 2012 event, as the respective values are 3.3 % and 2.4 %.

The grey-shaded region in Fig. 6c shows that during the first 4 h of the 6 h run the magnetopause position predictions (black and magenta curves) by GUMICS-4 are within 5 % of the Shue et al. (1997) model (blue curve). During the last 2 h, however, there are more fluctuations in the GUMICS-4 magnetopause position, especially in the 0.5 R_E resolution run. From 15 July, 21:00 UT to 16 July, 01:00 UT the simulation runs agree on the magnetopause location and also with the Shue model, with differences within 10 % all the time of the first 4 h. However, the last 2 h show more variations between the three curves: the finest resolution shows slight outward motion of the magnetopause, which toward the end of the period is less than that predicted by the Shue model. On the other hand, the 0.5 R_E resolution run shows inward indentations followed by outward motion consistent with the Shue model. Overall, the 0.5 R_E resolution run is 58 % of the time within 10 % of the Shue model, and the 0.25 R_E resolution run agrees 67 % of the time within 10 % of the Shue model. Despite the fact that the average relative difference is slightly lower for the 0.5 R_E resolution run (4.9 %) than for the 0.25 R_E resolution run (5.6 %), over the entire 6 h periods, the 0.25 R_E run is within 10 % of the Shue model 92 % of the time, while the 0.5 R_E run reaches within 10 % of the Shue model 89 % of the time due to the 0.5 R_E run being more inclined toward moving more earthward during the last 2 h of the 6 h period.

The time evolution of the magnetopause position during the 6 h period in Fig. 7 is similar for both spatial resolutions, with both simulation runs responding similarly to small upstream fluctuations. Both simulation runs stay within 10 % of the Shue model prediction for the entire 6 h period. The average relative difference is only slightly lower for the higher-resolution run (3.2 %) than for the lower-resolution run (4.5 %).

Overall, the higher-resolution run yielded better agreement with the magnetopause location, especially for a moving magnetopause nose (2012 event), because increasing the spatial resolution sharpens the gradients and allows better identification of the locations of the maxima (Janhunen et al., 2012). Comparison of the runs shows, however, that the results are consistent with each other, indicating that the lower-resolution run provides similar large-scale dynamics to the finer-resolution run. Furthermore, increased δ during the 2012 ICME cloud and overall higher δ during the 2012 event indicate that GUMICS-4 accuracy in the magnetopause nose position prediction is better during weaker solar wind driving. This is further demonstrated by the standard deviation values, which are 0.661 for the 2012 event and 0.321 for the 2014 event (see Figs. 6c and 7c).

Total energy through the dayside magnetopause is computed by evaluating the energy flux incident at the (Shue) magnetopause, and it is evaluated from

$$\begin{array}{}\text{(3)}& \mathbf{K}=\left(u+p-{\displaystyle \frac{B^{\mathrm{2}}}{\mathrm{2}{\mathit{\mu }}_{\mathrm{0}}}}\right)\mathit{V}+{\displaystyle \frac{\mathrm{1}}{{\mathit{\mu }}_{\mathrm{0}}}}\mathit{E}\times \mathit{B},\end{array}$$

where u is the total energy density, p pressure, B magnetic field, V flow velocity and E×B the Poynting flux and its component perpendicular to the magnetopause surface. As is shown in Fig. 6c, the relative difference magnitude δ in the magnetopause nose location can reach up to 30 % values. To avoid underestimating the size of the magnetosphere, we evaluate the magnetopause surface by moving the radial distance of each Shue magnetopause surface value 30 % further away from the Earth. This surface is then used in integrating the energy flux values entering the magnetosphere sunward of the terminator (X>0 R_E). The results are shown for the 2012 event in Fig. 6d for both 0.5 and 0.25 R_E resolution runs along with the computed ϵ parameter (Perreault and Akasofu, 1978):

$$\begin{array}{}\text{(4)}& \mathit{ϵ}={\displaystyle \frac{\mathrm{4}\mathit{\pi }}{{\mathit{\mu }}_{\mathrm{0}}}}V{B}^{\mathrm{2}}{\sin }^{\mathrm{4}}\left({\displaystyle \frac{\mathit{\theta }}{\mathrm{2}}}\right)l_{\mathrm{0}}^{\mathrm{2}},\end{array}$$

where μ₀ is vacuum permeability, B and V are the magnitudes of the IMF and solar wind plasma flow velocity, θ is the IMF clock angle, and l₀ is an empirically determined scale length.

While both resolution runs agree with each other, it is evident that their numerical values are quite far from the reference ϵ parameter. It should be noted however that the ϵ parameter is not scaled to represent the energy input, but the energy dissipated in the inner magnetosphere (Akasofu, 1981). Thus the relative difference is not a good metric to describe the difference between GUMICS-4 and the ϵ parameter, and thus we are not using it in this paper. However, general temporal evolution is similar for most parts of ICME cloud, with both GUMICS-4 and the ϵ parameter reproducing steep increase at the onset of cloud as well as subsequent slow decrease, as is shown by the computed SD value in Fig. 6d (2.263). As in the case of the 2012 event, the two simulation runs using different spatial resolutions are almost inseparable in terms of the incoming solar wind energy during the 2014 event (Fig. 7d). During moderate solar wind driving in 2014, GUMICS-4 is closer to the ϵ parameter, with a considerably lower SD value (0.725) compared with the 2012 event. This is an interesting characteristic of the ϵ parameter warranting further study.

Differences between the simulations executed using different spatial resolutions in local measures, such as the magnetopause nose position, do not show in global variables, such as the total energy through the dayside magnetopause surface. As can be seen in Fig. 6d, the curves of the two different spatial-resolution runs are almost identical. This emphasizes that integrated quantities, such as energy, give a better representation of the true physical properties of the magnetosphere in the GUMICS-4 solution and are not dependent on grid resolution (Janhunen et al., 2012). We acknowledge that using more sophisticated methods for identifying the magnetopause surface from the simulation could potentially lead to some changes in the results. The Shue model was used for its simplicity and computational ease. Our results agree in general with Palmroth et al. (2003), who identified the magnetopause by using plasma flow streamlines from GUMICS-4, indicating that the use of the Shue model does not introduce large errors into the energy estimates.

The magnetosphere–ionosphere coupling, here illustrated by the CPCP time evolution in Fig. 6e, is compared with the polar cap index (Ridley and Kihn, 2004) computed as

$$\begin{array}{}\text{(5)}& \mathrm{PCI}=\mathrm{29.28}-\mathrm{3.31}\sin (T+\mathrm{1.49})+\mathrm{17.81}\mathrm{PCN},\end{array}$$

where T is month of the year normalized to 2π and PCN is the northern polar cap index retrieved from OMNIWeb. The PCI is a very indirect proxy (based on a single-point measurement only) for the CPCP, and thus the comparisons must be interpreted with great care. Also, taking into account that one of the well-known features of GUMICS-4 is lower predicted CPCP values compared with its contemporaries (Gordeev et al., 2015), it is of little importance to report the relative differences in CPCP values with the PCI as a reference. However, in terms of the SD values, GUMICS-4 and the PCI show better agreement in the temporal evolution of CPCP during the 2014 event (SD = 15.838) than during the 2014 event (SD = 5.107). It is apparent that these SD values are clearly the highest of all three (magnetopause nose, energy, CPCP) for both events. This is in part due to the ionospheric (local) processes contributing to the PCI, but is not related to the large-scale potential evolution.

4.2 Saturation of the cross-polar cap potential

Figures 8 and 9 show the CPCP (both the Northern Hemisphere and the Southern Hemisphere) as a function of the solar wind electric field E_Y component for both ICME events. Color-coding marks the IMF magnitude in Figs. 8a and 9a, solar wind speed in Figs. 8b and 9b, and the upstream Alfvén–Mach number in Figs. 8c and 9c. Every data point in Fig. 8 (Fig. 9) is computed from 10 min averages, binned by E_Y with 1.0 (0.5) mV m⁻¹ intervals. The ICME sheath (solid circles) and cloud (solid squares) periods as well as the nominal solar wind conditions (solid triangles) prior to and following the events are analyzed separately. Note that here only the coarse grid (0.5 R_E) simulation results are used, as we analyze the effects during the entire magnetic cloud and sheath periods, including times before and after the event not covered by the high-resolution run.

Figure 8 shows that the response of the CPCP to the upstream E_Y is quite linear during the magnetic cloud (squares) when solar wind driving electric field E_Y is below 5 mV m⁻¹, during nominal solar wind conditions (triangles) and ICME sheath (diamonds). However, the polar cap potential first decreases and subsequently saturates during the cloud when the solar wind driving is stronger (E_Y>5 mV m⁻¹). For the 2012 event, we refer to the E_Y range from 0 to 5 mV m⁻¹ as the linear regime, and from 5 mV m⁻¹ upward as the nonlinear regime.

Figure 8a shows the obvious result that the highest E_Y values are associated with the highest IMF magnitudes. However, it also shows that the largest IMF magnitudes are associated with the nonlinear regime, indicating that strong upstream driving leads to CPCP saturation. In addition, Fig. 8b suggests that the increase in the CPCP in the linear regime is clearly higher for lower velocity values (cloud structure) than for higher velocity values (sheath and nominal conditions). Generally, this agrees with the previous studies utilizing statistical (Newell et al., 2008) and numerical (Lopez et al., 2010) tools. The latter authors suggest that this is caused by the solar wind flow diversion in the pressure-gradient-dominated magnetosheath; faster solar wind will produce more rapid diversion of the flow around the magnetosphere, and thus a smaller amount of plasma will reach the magnetic reconnection site.

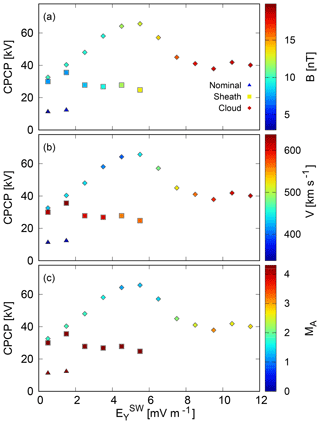
Figure 8 The cross-polar cap potential (CPCP) as a function of the IMF E_Y for the 2012 ICME sheath and cloud periods, with nominal solar wind conditions before and after the ICME event taken into account separately. GUMICS-4 simulation data with 1 min time resolution have been averaged by 10 min and binned by upstream E_Y with 1.0 mV m⁻¹ intervals. Panels (a), (b) and (c) show the magnitudes of the IMF, the upstream flow speed and the Alfvén–Mach number, respectively.

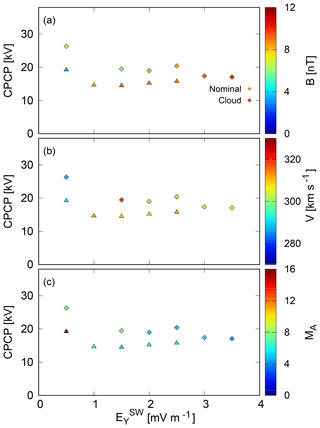
Figure 9 The CPCP as a function of the IMF E_Y for the 2014 ICME cloud period, with nominal solar wind conditions before and after the ICME event taken into account separately. GUMICS-4 simulation data with 1 min time resolution have been averaged by 10 min and binned by upstream E_Y with 0.5 mV m⁻¹ intervals. Panels (a), (b) and (c) show the magnitudes of the IMF, the upstream flow speed and the Alfvén–Mach number, respectively.

Figure 8c shows that the upstream Alfvén–Mach number M_A is at or above 4 (M_A≥4) during the nominal solar wind conditions and during the ICME sheath, while during the magnetic cloud M_A resided below 4 and almost reached unity. This supports the interpretation that saturation of the CPCP depends on the upstream Alfvén–Mach number M_A such that saturation occurs only when M_A values fall below 4. The dependence of the CPCP saturation on M_A is well-known, documented in both measurements (Wilder et al., 2011; Myllys et al., 2016) and simulation studies (Lopez et al., 2010; Lakka et al., 2018).

Figure 9 agrees with the view presented above, as the response of the CPCP to the upstream E_Y during the 2014 event is quite linear regardless of the IMF magnitude (Fig. 9a), plasma flow speed (Fig. 9b), or large-scale solar wind driving structure (ICME cloud or nominal solar wind). This is apparently because solar wind driving is substantially weaker during the 2014 event than during the 2012 event, with the IMF magnitude reaching barely 10 nT and upstream plasma flow speed varying only on the order of 10 km s⁻¹. As a result, the upstream Alfvén–Mach number is M_A>4 throughout the ICME event as well as during the nominal solar wind conditions. The high polar cap potential values for the lowest E_Y bin are associated with the large density enhancement driving polar cap potential increase before the arrival of the cloud proper.

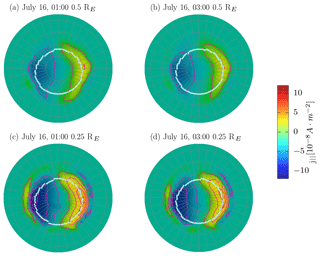
Figure 10 shows the region 1 and region 2 field-aligned current (FAC) system coupling the magnetosphere and the ionosphere (e.g., Siscoe et al., 1991). The four panels show how field-aligned currents are distributed in the Northern Hemisphere ionosphere on 16 July 2012 at 01:00 UT and 03:00 UT at 0.5 R_E maximum resolution (Fig. 10a–b) and at 0.25 R_E maximum resolution (Fig. 10c–d). Current density is shown both as color coding and contours, while the white dotted line depicts the polar cap boundary. The distribution of the FAC does not change much in either of the simulations, thus suggesting that the coupling of the magnetosphere and the ionosphere remains relatively constant. However, as is shown in Fig. 6e, the CPCP shows different temporal evolution based on the used spatial resolution, with increasing (constant) CPCP in the 0.5 (0.25) R_E simulation, thus suggesting that while the magnetosphere–ionosphere coupling is unaffected, the solar wind–ionosphere coupling is affected by enhanced spatial resolution.

Figure 10 The Northern Hemisphere field-aligned current pattern in GUMICS-4 simulation at 01:00 UT (a, c) and at 03:00 UT (b, d) on 16 July 2012. Panels (a) and (b) or (c) and (d), respectively, show the results of the simulation run in which 0.5 or 0.25 R_E maximum spatial resolution was used.

4.3 Local dynamics

Figures 4 and 5 show the time series of the IMF magnitude $\left|B\right|$ in the Geotail and Cluster orbits during the 2012 and 2014 events compared with the GUMICS-4 results along the satellite tracks. The standard deviations are computed using the same methods as in Sect. 4.1, and are given in panels (a) and (b). Since the inner boundary of the GUMICS-4 MHD region is at 3.7 R_E, the times when Cluster is closer than 3.7 R_E to Earth are ignored when computing SD values.

Prior to the arrival of the sheath region in 2012, Geotail enters the plasma sheet boundary layer earlier than predicted by GUMICS-4. During the ICME sheath there are many dips and peaks in both plots, with the difference between measured (both Geotail and Cluster) and predicted values varying, as can be seen from Fig. 4a and b. Also, Fig. 4a shows that starting from 17 July, 06:00 UT, the measured field at Geotail increases as the satellite goes to the magnetosheath proper, while GUMICS-4 prediction decreases as the orbit track in GUMICS-4 approaches the shock region (see Fig. 3a). The 2014 event shows similar features, especially when Geotail enters and exits the magnetosphere at 23:14 UT, 28 April, and at 12:00 UT, 30 April, respectively, with measured (by Geotail) $\left|B\right|$ in the former case fluctuating and rising sharply from 10 to 40 nT, while the GUMICS-4 $\left|B\right|$ increases more steadily from a few to 20 nT as the satellite enters from the magnetosheath to the magnetosphere. In the latter case decrease (increase) in measured (simulated) $\left|B\right|$ occurs several hours after the spacecraft exits the magnetosphere (later yellow-shaded region in Fig. 5a) because of the differences in the moment of exit (and exact location of the magnetopause location). Note that while Cluster makes an entry into the magnetosphere at 16:12 UT, 29 April, GUMICS-4 predicts a position within the magnetosheath and an entry into the magnetosphere only following the end of the cloud.

Note that the Cluster perigee (2 R_E) (Fig. 4c) is below the inner boundary of the GUMICS-4 simulation (3.7 R_E), which causes the simulation field to record unphysical values around the time of the maxima at 09:00 on 14 July 2012 and 15:00 on 16 July 2012, hence the data gaps in GUMICS-4 data plots.

The effect of the ICME sheath is visible after its arrival in Fig. 4, with both measured and predicted $\left|B\right|$ fluctuation. The ICME magnetic cloud proper seems to cause the largest difference in $\left|B\right|$ during the 2012 event, when the driving was quite strong.

The SDs over the simulated time ranges using 0.5 R_E spatial resolutions are considerably lower on Geotail orbit (2012: 5.476, 2014: 6.564) than on Cluster orbit (2012: 25.054, 2014: 24.795).

5 Discussion

In this paper we study (1) how the magnetosphere responds to two ICME events with different characteristics by means of using the GUMICS-4 global MHD simulation and (2) how accurately GUMICS-4 reproduces the effects of the two events. The 2012 event was stronger in terms of solar wind driver, the 2014 event being significantly weaker in terms of both solar wind speed and IMF magnitude. We considered both global and local parameters, including magnetopause nose position along the Sun–Earth line, total energy transferred from the solar wind into the magnetosphere, and the ionospheric cross-polar cap potential (CPCP). Local measures include response of the magnetic field magnitude along the orbits of Cluster and Geotail spacecraft. The two ICME events were simulated using 0.5 R_E maximum spatial resolution. To test the effect of grid-resolution enhancement on global dynamics, we simulated 6 h subsets of both CME cloud periods with 0.25 R_E maximum spatial resolution. As uncertainty metrics we use both relative difference magnitude δ and SD.

Due to stronger solar wind driving, the 2012 event causes the magnetosphere to compress more than during the 2014 event, with the magnetopause moving earthward at the onset of the 2012 ICME sheath and reaching 7 R_E distance from Earth, until moving sunward at the onset of ICME magnetic cloud (see Fig. 6c). Both ICMEs are preceded by low IMF B_Z and solar wind dynamic pressure, with 2014 missing high-amplitude fluctuations before ICME cloud due to the absence of a separate ICME sheath. Despite this, the movement of the magnetopause is similarly earthward prior to the cloud, reaching 9.5 R_E just before the onset of the cloud (see Fig. 7c). During the cloud, however, the orientation of the IMF slowly rotates from southward to northward and the magnetopause is in constant sunward (earthward) motion in 2012 (2014). While the polarity of the IMF changes before the end of the ICME in 2012, it changes from southward to northward only after the end of the ICME in 2014.

The magnetopause nose location in GUMICS-4 is identified as a single grid point from the maximum value of J_Y along the Sun–Earth line. Location deviations in response to solar wind driving in the GUMICS-4 results are dependent on the driver intensity: stronger driving during the 2012 CME magnetic cloud leads to a larger relative difference magnitude δ (2012: 8.0 % δ on average) as compared to the Shue et al. (1997) model, whereas the agreement between the simulation and the empirical model is quite good (3.3 % δ on average) during weaker driving during the 2014 event (Figs. 6 and 7). This view is further supported by SDs: for the full simulation time range, the SD is 0.661 (0.321) in 2012 (2014). Average δ during nominal solar wind conditions is almost identical for both events: 2.5 % for the 2012 event and 2.4 % for the 2014 event.

Comparison of the magnetopause location between the 0.25 R_E (0.5 R_E) resolution run and the Shue model shows that the relative difference between the two is below 10 % for 92 % (89 %) of the 6 h subset in 2012 (Fig. 6c), while corresponding analysis of the 6 h subset in 2014 (Fig. 7c) yielded differences below 10 % for 100 % of the time regardless of the resolution. It should be noted that, despite the relative difference in magnitude being slightly lower for the 0.5 R_E resolution run than for the 0.25 R_E resolution run for both the 2012 (4.9 % and 5.6 %) and 2014 (3.2 % and 4.5 %) events, the 0.25 R_E run reaches better agreement with the Shue model, especially when the magnetopause is moving during high solar wind driving in 16 July, 01:00 UT (Fig. 6c).

When spatial resolution is increased, gradient quantities such as J_Y have sharper profiles and therefore larger values (Janhunen et al., 2012). As it is the maximum value of J_Y that we use to locate the magnetopause nose, the nose position evaluation in the lower-resolution runs is more ambiguous due to the larger spread of the current and due to the larger grid cell size. This may lead to changes in the maximum value of up to several R_E over short time periods in response to upstream fluctuations. In the finer-resolution runs, J_Y distribution is sharper, which leads to lesser fluctuations in the maximum value determination. However, the differences between the two grid resolutions occur only under rapidly varying solar wind or very low solar wind density conditions.

The empirical models developed by Shue et al. (1997, 1998) are based on statistical analysis of a large number of spacecraft measurements of plasma and magnetic field during magnetopause crossings. While the Shue et al. (1997) model is optimized for moderate upstream conditions, the Shue et al. (1998) model targets especially stronger driving periods. However, we computed the difference in the magnetopause position between the two models and found that it is mostly less than 0.1 R_E with a maximum difference of 0.4 R_E, with the Shue et al. (1997) model predicting more sunward magnetopause nose. Because of the small difference at the magnetopause nose, we have only used the Shue et al. (1997) model in our study. Our results agree with previous papers (Palmroth et al., 2003; Lakka et al., 2017), with the latter reporting a 3.4 % average relative difference between the Shue model and GUMICS-4. Moreover, according to Gordeev et al. (2015), global MHD models are very close to each other in terms of predicting magnetopause standoff distance.

Differences in the magnetopause location do not necessarily translate into differences in global measures, as can be seen from Figs. 6d and 7d, which show the time evolution of the energy transferred from the solar wind through the magnetopause surface. The response of the total energy E_tot during both ICME cloud periods is quite similar regardless of the used grid resolution. As an integrated quantity, energy entry is a better indicator of the true physical processes of the GUMICS-4 solution and does not suffer from dependence on grid resolution like the maximum J_Y (Janhunen et al., 2012). Therefore, in analyses of simulation results, it would be better to consider such global integrated quantities, even if they have no direct observational counterparts. This can be seen in Figs. 6d and 7d, with large differences between GUMICS-4 and the ϵ parameter (Perreault and Akasofu, 1978) in energy transferred from the solar wind into the magnetosphere in both 2012 and 2014. However, standard deviations show that GUMICS-4 reproduces the temporal evolution of the ϵ parameter better during low solar wind driving (2014) than during high driving (2012), as the respective SD values are 0.725 and 2.263. Moreover, our results are mostly on the same order of magnitude compared to what was obtained by Palmroth et al. (2003) by using plasma flow streamlines for computing the magnetopause surface from GUMICS-4 results.

In the ionosphere, the cross-polar cap potential value is dependent on the grid resolution, with higher resolution yielding higher polar cap potential values (see Figs. 6e and 7e). In comparison with the PCI (Ridley and Kihn, 2004), standard deviation is considerably lower for the 2014 event (5.107) than for the 2012 event (15.838). Thus, at least two factors contribute to the ionospheric coupling: grid resolution and intensity of solar wind driving. Considering that the SD values are clearly higher than, e.g., the corresponding energy transfer values and that the PCI considers only the Northern Hemisphere, the PCI may not provide the most accurate reference for GUMICS-4. However, both considerable difference between GUMICS-4 and the PCI and the dependence on grid resolution agree with previous studies (e.g., Lakka et al., 2018). Generally, global MHD codes differ from each other in terms of the CPCP values (Gordeev et al., 2015). It is not easy to reproduce realistic CPCP values in a global MHD code, since they are generally prone to close excessive amounts of electric current through the polar cap and thus the CPCP values are either unrealistically large (e.g., LFM model, Lyon et al., 2004), with reasonable auroral electrojet currents, or reasonable accompanied by low auroral electrojet currents (De Zeeuw et al., 2004) (e.g., GUMICS-4 and BATS-R-US model; Powell et al., 1999).

The polar cap structure and the distribution of the FAC do not change much in either of the simulations, thus suggesting that the coupling of the magnetosphere and the ionosphere remains relatively constant. As is shown in Fig. 10a–b, the region 1 currents are clearly visible, while the region 2 currents get stronger only by enhancing the grid resolution in the MHD region (Janhunen et al., 2012). However, the upstream conditions change considerably from 01:00 to 03:00, with the upstream Alfvén–Mach number decreasing from 1.9 to 0.6, suggesting that polar cap potential saturation mechanisms are likely to take place (Ridley, 2007; Wilder et al., 2015; Lakka et al., 2018). Considering that GUMICS-4 reproduces saturation with both 0.5 R_E (this paper) and 0.25 R_E resolutions (Lakka et al., 2018), it is apparent that the FAC influence on the dayside magnetospheric magnetic field does not contribute to the saturation effect. However, to actually prove it is beyond the scope of the current paper. We therefore conclude that the increase in the CPCP during the 0.5 R_E simulation run is caused by processes outside of the magnetosphere, likely in the magnetosheath, and that GUMICS-4 responds differently to low Alfvén–Mach number solar wind depending on grid resolution.

Figures 8 and 9 illustrate the CPCP as a function of the solar wind E_Y component. Color-coded are the IMF magnitude in Figs. 8a and 9a, the solar wind speed in Figs. 8b and 9b, and the upstream Alfvén–Mach number in Figs. 8c and 9c. Nominal solar wind conditions before and after the actual ICME events as well as the ICME sheath and cloud periods are considered separately. We note that only results from the lower spatial resolution (0.5 R_E) runs are included in the figures. Consistent with earlier studies, Fig. 8 shows saturation of the CPCP during high solar wind driving (see, e.g., Shepherd, 2007; Russell et al., 2001): with nominal solar wind conditions or during the ICME sheath period the response of the CPCP to the upstream E_Y is rather linear, while for the ICME cloud period the CPCP saturates when E_Y>5 mV m⁻¹. From Fig. 8a it can be seen that the saturation occurs when B>12 nT and Fig. 8b shows that the increase in the CPCP in the linear regime depends on the upstream velocity in such a way that the increase is clearly higher for lower velocity values (cloud event) than for higher velocity values (sheath event and nominal conditions), as suggested by previous statistical (Newell et al., 2008) and numerical (Lopez et al., 2010) studies. The latter study proposes that this is because of the more rapid diversion of the solar wind flow in the pressure-gradient-dominated magnetosheath under faster solar wind, which leaves a smaller amount of plasma at the magnetic reconnection site.

The saturation of the CPCP is absent in Fig. 9 due to the significantly weaker solar wind driving during the 2014 event (the upstream E_Y is below 4 mV m⁻¹). This in turn leads to the upstream Alfvén–Mach number being on average 5.8 during the ICME cloud event. Lavraud and Borovsky (2008) suggest that when the Alfvén–Mach number decreases below 4 and the overall magnetosheath plasma beta (p∕p_B, where p is the plasma pressure and p_B the magnetic pressure) below 1, the magnetosheath force balance changes such that plasma flow streamlines are diverted away from the magnetic reconnection merging region in the dayside magnetopause (Lopez et al., 2010), which causes the CPCP saturation. However, the CPCP saturation limit of M_A=4 is not necessarily the only governing parameter, as there is both observational evidence with large M_A values (up to 7.3) (Myllys et al., 2016) and simulation results indicating saturation at low but above M_A=1 values (this study). Nonetheless, our results suggest that the saturation of the CPCP is dependent on the upstream M_A in such a way that M_A needs to be below 4 for the saturation to occur.

An interesting aspect is that the CPCP does not reach its maximum simultaneously with E_Y; i.e., the CPCP is largest with moderate E_Y (5–6 mV m⁻¹) (see Fig. 8). As E_Y increases to 11 mV m⁻¹, the CPCP decreases from 70 to 40 kV. This is actually apparent in Fig. 1h as well: the absolute values of both B_Z and V_X reach their maximum values a few hours after the onset of the magnetic cloud, which is at 06:54 UT, 15 July. However, the CPCP is at that time quite moderate, about 40 kV, and does not reach its maximum until 16 July, when both B_Z and V_X have already reduced significantly. Thus the CPCP overshoots in Fig. 8, a feature that was not observed in a GUMICS-4 study by Lakka et al. (2018) using artificial solar wind input consisting of relatively high-density and constant driving parameters.

The performance of GUMICS-4 was put to the test by means of comparing the magnetic field magnitude $\left|B\right|$ to in situ data of the Cluster and Geotail satellites. GUMICS-4 values are mostly lower than those measured by either of the two spacecraft, with GUMICS-4 predictions being closer to Cluster than Geotail. Computed standard deviations reveal that, over the entire simulation periods, the temporal evolution of GUMICS-4 magnetic field magnitude predictions is closer to Geotail measurements (2012: SD = 5.476, 2014: SD = 6.564, equatorial orbit) than Cluster measurements (2012: SD = 25.054, 2014: SD = 24.795, polar orbit) for both events. It should be noted that the times when Cluster is closer than 3.7 R_E to Earth are ignored when computing SD values due to the inner boundary of the GUMICS-4 MHD region, which is located at 3.7 R_E.

During both events, $\left|B\right|$ is increased during ICMEs, especially their magnetic cloud counterparts. During the 2012 ICME sheath both Cluster and Geotail record fluctuating $\left|B\right|$ until the onset of the cloud. While missing a sheath in 2014, magnetic field magnitude measured by Cluster fluctuates as well prior to the cloud. At the same time (29 April, 15:00 UT) $\left|B\right|$ measured by Geotail decreases sharply. The difference between Cluster/Geotail and GUMICS-4 is mostly on the order of 10 % but can reach above 50 % values, especially during the 2012 magnetic cloud event in both Cluster and Geotail orbit. Such a difference seems relatively large, especially since it was shown by Ridley et al. (2016) that all the global MHD models available at the Community Coordinated Modeling Center (CCMC) are close to each other when comparing the ability to reproduce magnetic field components to in situ measurements. While the study used 662 simulation runs, it should be noted that GUMICS-4 was used in only 12 of them. However, GUMICS-4 should predict $\left|B\right|$ closer to in situ measurements at least during moderate solar wind driving, as was shown by Facskó et al. (2016). In his work the difference in $\left|B\right|$ was 10 % or lower on 20 February 2002, when no ICME events were recorded.

With such discrepancy between our results and previous results, we checked some of the simulation runs at CCMC, in which BATS-R-US (Powell et al., 1999) code was used, and searched for runs of either of the two ICME events discussed in this paper, with magnetic field measurements along Geotail and/or Cluster orbit also available. BATS-R-US was chosen since it shares several features with GUMICS-4. We found one simulation run (CCMC run name Tom_Bridgeman_022415_1) in which the 2012 event was simulated, with results along Geotail orbit available. In addition, we simulated the 2014 event (CCMC run name Antti_Lakka_070918_2) to check the results along Cluster path. Consequently, we are able to compare GUMICS-4 and BATS-R-US in both 2012 (Geotail) and 2014 (Cluster), and the results are shown in Fig. 11. Panel (a) shows comparison between the two models during the 2012 event and panel (b) during the 2014 event. In situ measurements by Geotail and Cluster are shown in panels (a) and (b), respectively. Note that the 2012 BATS-R-US run was completed at around 17 July 00:00 UT. By looking at the figure it is apparent that the predictions of both GUMICS-4 and BATS-R-US are quite similar, especially during the magnetic cloud events at both Cluster and Geotail orbits. Actually, GUMICS-4 is mostly closer to Cluster measurements than BATS-R-US in 2014, when Cluster exits the magnetosphere and $\left|B\right|$ measured by Cluster fluctuates between 10 and 40 nT, as was discussed in Sect. 4.3. In 2012 a large difference in $\left|B\right|$ (up to 100 %) during ICME cloud applies to both models. During ICME sheath and nominal solar wind conditions $\left|B\right|$ fluctuates more and the prediction accuracy of the models depends on the time interval under inspection. It is evident that both models are quite equal considering the ability to reproduce $\left|B\right|$ during both 2012 and 2014 ICME events.

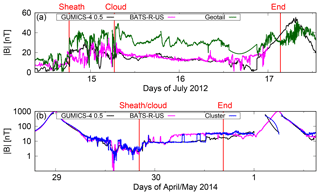
Figure 11 The time series of the magnetic field magnitude $\left|B\right|$ along the orbits of Geotail during 14 July 09:00 UT–17 July 15:00 UT 2012 (a) and Cluster 1 during 28 April 19:00 UT–1 May 17:00 UT 2014 (b) as measured by Geotail (green) and Cluster 1 (blue) and predicted by GUMICS-4 (black) and BATS-R-US (magenta).

The discrepancy between in situ measurements and the two models may not concern only GMHD models, since we computed the magnetic field during the 2012 event at Cluster orbit using the empirical Tsyganenko magnetic field model T89 (e.g., Tsyganenko and Sitnov, 2005). For most parts GUMICS-4 is actually closer to Cluster observations, with the gap between the two models gradually decreasing as Cluster approaches the perigeum on 16 July (not shown). Therefore it is reasonable to assume that something in the ICME event, possibly unusually strong compression, leads to a larger field than predicted by the GMHD models or the Tsyganenko model, and that, e.g., increasing the spatial resolution of the GMHD models would not make a significant difference for the two reasonably similar codes (Janhunen et al., 2012). The negligible effect of enhanced spatial resolution is actually shown in Figs. 4 and 5 for GUMICS-4.

It should be noted that the event is one of the strongest that occurred in 2012 by the mean magnetic field magnitude value during magnetic cloud. On the other hand, in some cases good agreement can be obtained when modeling strong ICMEs. Recently Kubyshkina et al. (2019) studied two events that occurred in 2015 and were the strongest events of solar cycle 24, and achieved reasonable agreement between measurements and different models, such as BATS-R-US with the Rice Convection Model and empirical models including the Tsyganenko T96 model. Mostly the error in the magnetic field magnitude was less than 15 nT, with the error increasing for a short while to more than 50 nT. The reason why some events cause greater errors than other events is however beyond the scope of the current paper and is left for future studies.

We conclude that for both events, $\left|B\right|$ predicted by GUMICS-4 is closer to Cluster observations, which feature high magnetic field magnitude outside the plasma sheet. While the differences between GUMICS-4 and in situ measurements can be quite large, it was shown that the $\left|B\right|$ predicted by GUMICS-4 agrees well with BATS-R-US predictions, and thus the large differences are not model-related but rather related to the upstream conditions during the ICME events. Thus the relative difference in $\left|B\right|$ may not be a good metric when simulating ICME events and evaluating the performance of a global MHD model.

While the agreement between predicted and measured $\left|B\right|$ may depend on the upstream conditions, the overall time evolutions seem to have a better match, and the SD values suggest that GUMICS-4 reproduces temporal evolution of $\left|B\right|$ better at Geotail orbit, which is much further away from the Earth than Cluster and resides mostly in the lobe and on the boundary layer. We computed standard deviations for Cluster orbit when the S/C is both further and closer than 5 R_E away from the center of the Earth. SD for further than 5 R_E is 22.984 (19.666) for the 2012 (2014) event, while for closer than 5 R_E the SD is 106.337 (104.605) for the 2012 (2014) event. If these calculations are repeated for 6 R_E distance, the SD values are 14.390 (15.282) when the S/C is further in 2012 (2014) and 104.618 (88.423) when the S/C is closer in 2012 (2014). Thus, the temporal evolutions agree better when Cluster is further away from the Earth.

The differences are most likely not caused by grid cell size variations due to the adaptive grid of GUMICS-4, because the simulation runs over simulated 6 h stages produce quite similar results for both resolutions. Also, the two runs deviate most from each other during the first hours of the 6 h stage, during which the 0.25 R_E run may not have fully eliminated the effects of simulation initialization, which can prevail for hours (Lakka et al., 2017). Moreover, the adaptive grid of GUMICS-4 is enhanced the most near the dayside magnetopause. Both events show signs of increased deviation from the measurements near the dayside magnetopause (edges of yellow-shaded regions in Figs. 4 and 5), further manifesting inaccuracies in determining the magnetopause in GUMICS-4.

6 Conclusions

The results of this paper can be summarized as follows.

1. Enhancing spatial resolution of the magnetosphere in GUMICS-4 affects the accuracy of the determination of the magnetopause subsolar point. Global measures, such as energy transferred from the solar wind into the magnetosphere, are not affected. The cross-polar cap potential can be affected significantly, with up to over a factor of 2 difference between simulations using different spatial resolutions for the magnetosphere.

2. Our results show signs of cross-polar cap potential saturation during low upstream Alfvén–Mach number. GUMICS-4 responds differently to low Alfvén–Mach number solar wind, which may affect the saturation phenomena. This may lead to grid size effects on polar cap saturation in MHD simulations.

3. Comparison metric choice should be done cautiously. For instance, relative difference in $\left|B\right|$ may not be a good metric when studying ICME events. Due to inaccuracies in the magnetopause subsolar point determination, comparison between GUMICS-4 and in situ data should be done cautiously when the spacecraft is near the magnetopause.