Phenomena preceding major earthquakes interconnected through a physical model

The analysis of earthquake time series in a new time domain termed natural time enables the uncovering of hidden properties in time series of complex systems and has been recently employed as the basis of a method to estimate seismic risk. Natural time also enables the determination of the order parameter of seismicity, which is a quantity by means of which one can identify when the system approaches the critical point (the mainshock occurrence is considered the new phase). Applying this analysis, as an example, to the Japanese seismic data from 1 January 1984 until the super-giant M 9 Tōhoku earthquake on 11 March 2011, we find that almost 3 months before its occurrence the entropy change of seismicity under time reversal is minimized on 22 December 2010, which signals an impending major earthquake. On this date the order parameter fluctuations of seismicity exhibit an abrupt increase. This increase is accompanied by various phenomena; e.g., from this date the horizontal GPS azimuths start to become gradually oriented toward the southern direction, while they had random orientation during the preceding period. Two weeks later, a minimum of the order parameter fluctuations of seismicity appears accompanied by anomalous Earth magnetic field variations and by full alignment of the orientations of GPS azimuths southwards leading to the most intense crust uplift. These phenomena are discussed and found to be in accordance with a physical model which seems to explain on a unified basis anomalous precursory changes observed either in ground-based measurements or in satellite data.

1 Introduction

Almost 8 years have passed since the Tōhoku earthquake (EQ) that occurred on 11 March 2011 in Japan with magnitude (M) 9.0, the largest magnitude ever recorded in Japan. In the meantime, independent research groups reported anomalous precursory variations of quantities like the geomagnetic field (Xu et al., 2013; Han et al., 2015), seismicity upon analyzing it in natural time (Sarlis et al., 2013, 2015; Varotsos et al., 2014), and Earth's surface displacements measured by Global Positioning System (GPS) (Chen et al., 2014). In the 1980s, a short-term earthquake prediction method was introduced based on the observation of seismic electric signals (SESs), which are low-frequency transient changes in the electric field of the Earth preceding EQs (Varotsos and Alexopoulos, 1984a, b; Varotsos et al., 1986). Several SESs recorded within a short time are termed SES activity (Varotsos and Lazaridou, 1991). Major EQs are preceded by intense SES activities accompanied by evident Earth magnetic field variations (Varotsos et al., 2003b) mainly recorded on the z component (Sarlis and Varotsos, 2002; Varotsos, 2005). This method was motivated by a physical model for SES generation, which also foresees that some additional transient multidisciplinary phenomena should be simultaneously generated and ended well before the EQ rupture as schematically shown in Fig. 1a. This was in direct contrast to other proposed precursory mechanisms (Rikitake, 1981) that usually exhibit anomalous behavior becoming more intense upon approaching the EQ failure as seen in Fig. 1b. The scope of the present study is twofold: first, investigate whether the transient phenomena foreseen by this model actually appeared before the M 9 Tōhoku EQ, having been observed by ground-based measurements or by GPS data; second, report other precursory phenomena that appeared before the Tōhoku EQ almost simultaneously with the transient phenomena that were expected on the basis of this model.

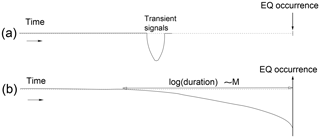
Figure 1 Schematic diagram showing the two distinct approaches proposed for a precursory behavior. (a) The case of the physical model for SES generation, which differs greatly from other suggested mechanisms (Rikitake, 1981) in which the anomalous precursory behavior becomes more intense upon approaching the EQ occurrence (b).

The aforementioned physical model for SES generation, termed the pressure stimulated polarization current (PSPC) model (Varotsos and Alexopoulos, 1986; summarized also in Varotsos and Alexopoulos, 1984a, b, and Varotsos et al., 1993), suggests the following (see Fig. 2): in the Earth, electric dipoles always exist (Varotsos and Alexopoulos, 1986) due to lattice imperfections (point and linear defects; e.g., see Varotsos, 2008) in the ionic constituents of rocks. In the future focal region of an EQ, where the electric dipoles have initially random orientations (Fig. 2c), the stress, σ, starts to gradually increase due to an excess stress disturbance (Fig. 2a). Let us call this stage A hereafter. When this gradually increasing stress reaches a critical value (σ_cr), the electric dipoles exhibit a cooperative orientation (Fig. 2e) resulting in the emission of a transient SES (Fig. 2b) with current density j. We call this stage B. Uyeda et al. (2009b) pointed out that the PSPC model is unique among other models in that SESs would be generated spontaneously during the gradual increase in stress without requiring any sudden change in stress such as microfracturing (Molchanov and Hayakawa, 1995) (or faulting).

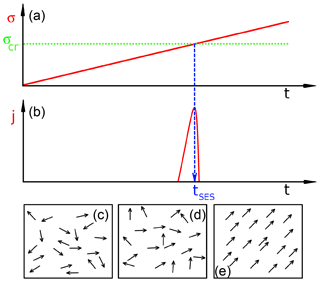
Figure 2 Schematic diagram of the physical model proposed for the SES generation. (a) Before an EQ, the stress σ gradually increases in the focal area versus the time t towards reaching a critical value σ_cr. (b) When σ reaches σ_cr a transient electric signal is emitted that constitutes an SES. (c) Random orientation of the electric dipoles at small stress. (d) Partial orientation at an intermediate stress σ(<σ_cr). (e) Cooperative orientation of the electric dipoles when σ = σ_cr.

Observations of SES activities in Japan (Uyeda et al., 2000, 2002, 2009a), in China (see Huang, 2011, and references therein; for example see the geoelectric field changes depicted in Fig. 2b of Fan et al., 2010, that started almost 50 d before the M_s 8.0 Wenchuan EQ in 2008), and in Mexico (see p. 220 of Ramírez-Rojas et al., 2011) and in California (where magnetic field variations similar to those associated with the SES activities in Greece have been reported; e.g., see Fraser-Smith et al., 1990; Bernardi et al., 1991; see also P. A. Varotsos et al., 2011) have shown that their lead time lies in the range from a few weeks to a few months or so, in agreement with earlier observations in Greece (Varotsos and Lazaridou, 1991; Varotsos et al., 1993) (where the maximum lead time observed is 5.5 months or so; e.g., see P. A. Varotsos et al., 2011). Hence, the SES observations in various EQ-prone areas reveal (P. A. Varotsos et al., 2011) that before the occurrence of major EQs there is a crucial timescale (from a few weeks to around a few months or so), in which the critical stress σ_cr is attained and changes in other associated physical quantities should become also detectable (P. Varotsos et al., 2011).

This paper is structured as follows: in the next section, i.e., Sect. 2, we present the anomalous variations of multidisciplinary nature observed before the M 9 Tōhoku EQ by independent research groups, while our own findings obtained by natural time analysis of the seismicity of Japan are given in Sect. 3. In the subsequent Sect. 4, we investigate whether the observed precursory variations are in accordance with the PSPC model, and in the final section, i.e., Sect. 5, we summarize our conclusions.

2 Anomalous variations of multidisciplinary nature observed by independent groups before the 2011 M 9 Tōhoku EQ

2.1 Earth's magnetic field variations

Xu et al. (2013) found anomalous behavior of geomagnetic diurnal variations mainly in the vertical component at the Esashi station (ESA) located at about 135 km from the M 9 Tōhoku EQ focal zone for about 10 d, i.e., 4–14 January 2011. They analyzed geomagnetic data of a 3-year period, i.e., from 1 January 2010 to 31 December 2012, by computing ratios of diurnal variation range between the target station ESA and the remote reference station Kakioka about 300 km from the EQ epicenter. To validate this finding, further investigations were reported by Han et al. (2015) after analyzing geomagnetic data of 16-year long-term observations in Japanese stations. They again found that the mean values of the ratios of the diurnal variations in the vertical component showed a clear anomaly exceeding the statistical threshold during the aforementioned period, i.e., 4–14 January 2011, and in addition they emphasized that this anomaly is unique in over 16 years. This has been further validated by the most recent study of Han et al. (2016), who analyzed geomagnetic data of long-term observations at 17 stations in Japan. They found that the above unique anomaly in the vertical component has also been observed at a second station at Mizusawa (MIZ) in the Tōhoku region, which is about 20 km southwest of the ESA station. This fact that both ESA and MIZ show clear anomalies at the same time suggests that the anomaly cannot be the result of observation system error or artificial noises (Han et al., 2016). Furthermore, this anomaly cannot be attributed to magnetic storms since it has been observed during a period in which no moderate–strong magnetic storms were recorded.

2.2 Earth's surface displacements

Daily resolution data retrieved from the 1243 GPS stations in Japan were utilized by Chen et al. (2014) to expose surface displacements before the M 9 Tōhoku EQ. They applied the method proposed by Chen et al. (2011) on filtering long-term plate movements, short-term noise, and frequency-dependent (i.e., semiannual and annual) variations from the three-component GPS data for all stations. The N–S and E–W components were utilized to compute the orientations of the horizontal azimuths, termed GPS azimuths.

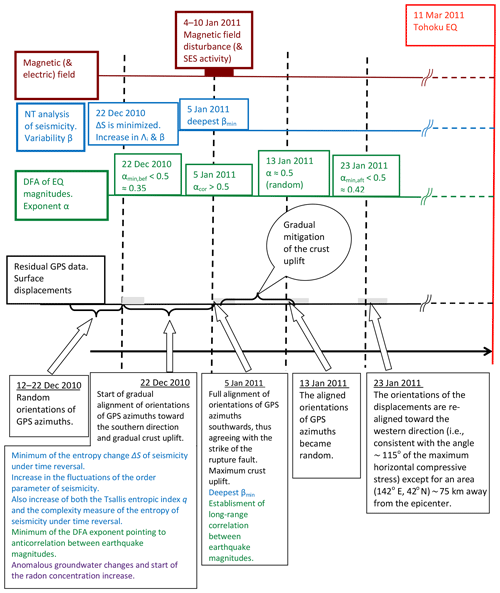
Figure 3 Schematic diagram that compiles the multidisciplinary changes before the Tōhoku EQ. Period of observations: from 12 December 2010 until 23 January 2011. The black text describes the observations by means of residual GPS data, the brown text describes those obtained by means of Earth's magnetic field variations, the green text describes those obtained by detrended fluctuation analysis (DFA), the blue text describes those obtained by natural time analysis, and the purple text describes those obtained by anomalous groundwater and radon changes.

In general, the residual surface displacements are random (Chen et al., 2014, 2011). However, as depicted by black text in Fig. 3, southward movements became evident (Chen et al., 2014) on 5 January 2011, i.e., 65 d before the Tōhoku EQ. Other changes before and after 5 January 2011 have also been observed as follows: while during the period 12–22 December 2010 random orientations of GPS azimuths prevailed, a gradual alignment toward the southern direction started on 22 December 2010 and continued until around 5 January 2011, accompanied with a gradual uplift of the crust. The most intense crust uplift was observed approximately on 5 January 2011 together with the full alignment of GPS azimuths southwards (more details are given in Sect. 4).

2.3 Changes in the level and temperature of confined groundwater

Orihara et al. (2014) reported that anomalous groundwater changes started 3 months before the Tōhoku EQ. In particular, groundwater level and temperature decreased almost simultaneously in a 2000 m well at a spa, Goyo-onsen, in Iwate Prefecture, 155 km northwest of the epicenter. This simultaneous decrease occurred only once in the 3.5-year records when considering that the recordings started in this source since October 2007. Orihara et al. (2014) emphasized that Tōhoku EQ is the only EQ that was preceded by anomalous changes in both water level and temperature. The exact date of the initiation of this phenomenon is not mentioned explicitly by Orihara et al. (2014), because the measurements were not made continuously but were taken intermittently and irregularly (the average interval between them being 8 d). They plotted, however, the consecutive measurements versus conventional time in their Fig. 1 (period 2007–2012) in which one can read that the phenomenon initiated around 20 December 2010, which agrees with what they state, i.e., around 3 months before Tōhoku EQ.

In addition, Orihara et al. (2014) reported that, according to radon concentration measurements (Tsunomori and Tanaka, 2014) in the groundwater in the Izu Peninsula (at a distance about 500 km from the epicenter), an increase started almost 3 months before Tōhoku EQ. This increase occurred only this time during a 35-year observation.

3 Precursory changes observed by means of natural time analysis of Japanese seismicity

Natural time analysis uncovers important hidden properties in time series of complex systems (P. A. Varotsos et al., 2011) and has been recently employed by Turcotte and coworkers as the basis of a new methodology (nowcasting) to estimate the current seismic risk level (Rundle et al., 2016, 2018; Luginbuhl et al., 2018a, b).

3.1 Natural time analysis background

In a time series comprising N EQs, the natural time for the occurrence of the kth EQ of energy Q_k is defined as ${\mathit{\chi }}_k=k/N$. In natural time analysis, we study the evolution of the pair (χ_k,p_k), where

$$\begin{array}{}\text{(1)}& p_k=Q_k/\sum _{n=\mathrm{1}}^N{Q}_n\end{array}$$

denotes the normalized energy released during the kth EQ. Q_k and hence p_k for earthquakes are estimated through the relation (Kanamori, 1978)

$$\begin{array}{}\text{(2)}& Q_k\propto {\mathrm{10}}^{\mathrm{1.5}{M}_k}.\end{array}$$

It is widely accepted (Carlson et al., 1994; Holliday et al., 2006) that the observed earthquake scaling laws indicate the existence of phenomena closely associated with the proximity of the system to a critical point (the mainshock is the new phase). In particular, it has been indicated by Carlson et al. (1994) that it seems possible that systems that operate persistently near a threshold of instability are in some way like thermodynamic systems near critical points (EQ can be regarded as a stick-slip frictional instability of a preexisting fault). The order parameter of seismicity is the quantity by which one can identify the approach of the dynamical system to a critical point (the mainshock is the new phase). It was argued by Varotsos et al. (2005c) that the variance

$$\begin{array}{}\text{(3)}& {\mathit{\kappa }}_{\mathrm{1}}=\langle {\mathit{\chi }}^{\mathrm{2}}\rangle -\langle \mathit{\chi }{\rangle }^{\mathrm{2}}\end{array}$$

of natural time χ weighted for p_k, given by

$$\begin{array}{}\text{(4)}& {\mathit{\kappa }}_{\mathrm{1}}=\sum _{k=\mathrm{1}}^N{p}_k({\mathit{\chi }}_k{)}^{\mathrm{2}}-{\left(\sum _{k=\mathrm{1}}^N{p}_k{\mathit{\chi }}_k\right)}^{\mathrm{2}},\end{array}$$

may serve as an order parameter of seismicity.

The entropy S in natural time is defined (Varotsos et al., 2003a, 2004) by

$$\begin{array}{}\text{(5)}& S\equiv \langle \mathit{\chi }\ln \mathit{\chi }\rangle -\langle \mathit{\chi }\rangle \ln \langle \mathit{\chi }\rangle ,\end{array}$$

where the brackets $\langle \mathrm{\dots }\rangle \equiv \sum \left(\mathrm{\dots }\right)p_k$ denote averages with respect to the distribution p_k, i.e., $\langle f\left(\mathit{\chi }\right)\rangle \equiv \sum f\left({\mathit{\chi }}_k\right)p_k$. Notably, the functional given by Eq. (5) has been shown (Varotsos et al., 2005b) to exhibit positivity, concavity, and experimental stability, which are the three requirements in order to be characterized as entropic functional. Furthermore, note that the entropy S is a dynamic entropy (Varotsos et al., 2004) depending on the sequential order of the events and not simply a statistical entropy (e.g., Shannon entropy) (see Varotsos et al., 2005a). Upon considering time reversal $\widehat{T}$, i.e., $\widehat{T}{p}_k=p_{N-k+\mathrm{1}}$, the value S changes to a value S₋:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{S}_{-}=\sum _{k=\mathrm{1}}^N{p}_{N-k+\mathrm{1}}\left({\displaystyle \frac{k}{N}}\right)\ln \left({\displaystyle \frac{k}{N}}\right)\\ \text{(6)}& {\displaystyle }& {\displaystyle }-\left(\sum _{k=\mathrm{1}}^N{\displaystyle \frac{k}{N}}{p}_{N-k+\mathrm{1}}\right)\ln \left[\sum _{l=\mathrm{1}}^N{\displaystyle \frac{l}{N}}{p}_{N-l+\mathrm{1}}\right].\end{array}$$

The physical meaning of the entropy change $\mathrm{\Delta }S\equiv S-S_{-}$ in natural time under time reversal is discussed in Varotsos et al. (2007) and P. A. Varotsos et al. (2011).

Using a moving window of length i (number of events) sliding through the time series of L consecutive events, the entropy in natural time is determined for each position $j=\mathrm{1},\mathrm{2},\mathrm{\dots },L-i$ of the sliding window. Thus, a time series of S_i is obtained. By considering the standard deviation σ(ΔS_i) of the time series of $\mathrm{\Delta }{S}_i\equiv S_i-(S_{-}{)}_i$, we define (P. A. Varotsos et al., 2011; Ramírez-Rojas et al., 2018; Sarlis et al., 2018b) the complexity measure Λ_i:

$$\begin{array}{}\text{(7)}& {\mathrm{\Lambda }}_i={\displaystyle \frac{\mathit{\sigma }\left(\mathrm{\Delta }{S}_i\right)}{\mathit{\sigma }\left(\mathrm{\Delta }{S}_{\mathrm{100}}\right)}},\end{array}$$

where the denominator has been selected to correspond to the standard deviation σ(ΔS₁₀₀) of the time series of ΔS_i of i=100 events (e.g., Ramírez-Rojas et al., 2018).

ΔS constitutes a key measure that may identify (P. A. Varotsos et al., 2011) when the system approaches the critical point (dynamic phase transition). For example, ΔS has been applied for the identification of the time of an impending sudden cardiac death risk (Varotsos et al., 2007). Furthermore, it has been used (Sarlis et al., 2011) for the study of the predictability of the Olami–Feder–Christensen (OFC) model for earthquakes (Olami et al., 1992), which is probably (Ramos et al., 2006) the most studied non-conservative self-organized criticality (SOC) model. The OFC model originated by a simplification of the Burridge and Knopoff spring–block model (Burridge and Knopoff, 1967) by mapping it into a non-conservative cellular automaton simulating the earthquake's behavior and introducing dissipation in the family of SOC systems. In particular, it was found that ΔS exhibits a clear minimum (P. A. Varotsos et al., 2011) (or maximum if we define $\mathrm{\Delta }S\equiv S_{-}-S$ instead of $\mathrm{\Delta }S\equiv S-S_{-}$; e.g., see Sarlis et al., 2011) before a large avalanche in the OFC model, which corresponds to a large earthquake. For example, by analyzing the seismicity during the period 2012–2017 in natural time in the Chiapas region of Mexico where the M 8.2 earthquake occurred on 7 September 2017, we observed (Sarlis et al., 2018b) that the entropy change ΔS of seismicity under time reversal was minimized almost 3 months before and in particular on 14 June 2017.

3.2 Results from natural time analysis of seismicity

Interesting results have been recently obtained upon analyzing the Japan seismic catalog in natural time and computing the fluctuations of κ₁. To compute the κ₁ fluctuations, we use a sliding natural time window comprising the number i of EQs that would occur on average in a few months or so (Sarlis et al., 2013, 2015; Varotsos et al., 2014). We then calculate the average value μ(κ₁) and the standard deviation σ(κ₁) of the ensemble of κ₁ obtained. The quantity

$$\begin{array}{}\text{(8)}& {\mathit{\beta }}_i\equiv \mathit{\sigma }\left({\mathit{\kappa }}_{\mathrm{1}}\right)/\mathit{\mu }\left({\mathit{\kappa }}_{\mathrm{1}}\right)\end{array}$$

is defined as the variability of κ₁ (P. A. Varotsos et al., 2011). The time evolution of the β value can then be pursued by sliding the excerpt i through the EQ catalog, and the corresponding minimum value is labeled β_min. The following key results have been obtained.

Varotsos et al. (2013) found that the fluctuations β of κ₁ of seismicity exhibited a clearly detectable minimum approximately at the time of the initiation of a pronounced SES activity recorded by Uyeda et al. (2002, 2009a) around 2 months before the volcanic–seismic swarm activity in 2000 in the Izu Islands region, Japan.

Sarlis et al. (2013) analyzed the Japan seismic catalog in natural time from 1 January 1984 to 11 March 2011, and their results showed that the fluctuations β of κ₁ of seismicity exhibited distinct minima β_min a few months before all the shallow earthquakes of magnitude 7.6 or larger that occurred during this 27-year period in the Japanese area $N_{\mathrm{25}}^{\mathrm{46}}{E}_{\mathrm{125}}^{\mathrm{148}}$. Among these minima, the minimum before the M 9 Tōhoku EQ observed at around 5 January 2011 was the deepest. Subsequently, Sarlis et al. (2015) found that the spatiotemporal variations of β_min enable the estimation of the epicentral area of the impending mainshock for all these EQs of magnitude 7.6 or larger.

In addition, Varotsos et al. (2014) focused on the minima β_min preceding all magnitude 8 (and 9) class EQs in the Japanese area from 1 January 1984 to 11 March 2011 and applied detrended fluctuation analysis (DFA) (Peng et al., 1993, 1994) to the earthquake magnitude time series. DFA has been established as a standard method to investigate long-range correlations in non-stationary time series in diverse fields (e.g., see Peng et al., 1993, 1994; Telesca and Lovallo, 2009) including the study of geomagnetic data associated with the M 9.0 Tōhoku EQ (Rong et al., 2012). The results of DFA are described in terms of the so-called DFA exponent (Peng et al., 1993, 1994), hereafter labeled α (α=0.5 means random, α greater than 0.5 means long-range correlations, and α less than 0.5 means anti-correlations). The following three main features have been identified (Varotsos et al., 2014): the minima β_min are observed during periods when long-range temporal correlations between EQ magnitudes have been developed since the corresponding DFA exponent is α>0.5. Before (bef) the minima β_min there exists a stage in which an evident anti-correlated behavior appears showing a minimum α_min,bef in the DFA exponent markedly smaller than 0.5. Finally, after (aft) the minima β_min, the long-range correlations break down to an almost random behavior (α=0.5), possibly turning to anti-correlation exhibiting a minimum α_min,aft with ${\mathit{\alpha }}_{\min ,\mathrm{aft}}<\mathrm{0.5}$. These three main features of temporal correlations between EQ magnitudes can be visualized in Fig. 3 for the case of the M 9 Tōhoku EQ. The deepest minimum β_min was observed around 5 January 2011 during a period in which long-range correlations between EQ magnitudes prevail with a DFA exponent α>0.5. Before this minimum an anti-correlated behavior was identified on 22 December 2010 with ${\mathit{\alpha }}_{\min ,\mathrm{bef}}=\mathrm{0.35}$. After β_min the long-range correlations break down on 13 January 2011 to an almost random behavior with α=0.5, and subsequently the behavior turned to anti-correlation on 23 January 2011 with ${\mathit{\alpha }}_{\min ,\mathrm{aft}}=\mathrm{0.42}$. As explained in the next section, the main features of the temporal correlations between EQ magnitudes obtained by DFA appeared simultaneously with distinct phases of crustal deformation identified by GPS measurements described in the previous section.

Recently we have shown that almost 3 months before the M 9 Tōhoku earthquake, i.e., on 22 December 2010, the following additional facts have been observed: first, the complexity measure Λ_i associated with the fluctuations of the entropy change of seismicity under time reversal exhibited an abrupt increase which conforms to the seminal work by Lifshitz and Slyozov (Lifshitz and Slyozov, 1961) and independently by Wagner (1961) for phase transitions showing that the characteristic size of the minority phase droplets exhibits a scaling behavior in which time growth has the form $A(t-t_{\mathrm{0}}{)}^{\mathrm{1}/\mathrm{3}}$ (Varotsos et al., 2018). It was also found that the increase ΔΛ_i of Λ_i follows the latter form and that the prefactors A are proportional to the scale i, while the exponent (1∕3) is independent of i (Varotsos et al., 2018). Second, the Tsallis entropic index q (Tsallis, 1988) shows a simultaneous increase which interestingly exhibits the same exponent (1∕3) (Varotsos et al., 2018). Third, a minimum ΔS_min of the change ΔS of the entropy of seismicity in the entire Japanese region under time reversal was found by Sarlis et al. (2018a), who also demonstrated that the probability of obtaining such a minimum by chance is approximately 3 %, thus showing that it is statistically significant. In addition, the robustness of the appearance of this minimum on 22 December 2010 upon changing the EQ depth, the EQ magnitude threshold, and the size of the area investigated has been documented (Sarlis et al., 2018a). Such a minimum is of precursory nature, signaling that a large EQ is impending according to the natural time analysis of the OFC model as mentioned in Sect. 3.1. Fourth, studying the fluctuations β of κ₁ of seismicity in the entire Japanese region $N_{\mathrm{25}}^{\mathrm{46}}{E}_{\mathrm{125}}^{\mathrm{148}}$ versus the conventional time from 1 January 1984 until the Tōhoku EQ occurrence on 11 March 2011, we find (Varotsos et al., 2019) a large fluctuation of β upon the occurrence of the M 7.8 earthquake near Chichijima on 22 December 2010. This finding has also been checked for several lengths from i=150 to 500 events, which also revealed the following (Varotsos et al., 2019): upon increasing i it is observed (see Figs. 2b and 4e of Sarlis et al., 2013) that the increase Δβ_i of the β_i fluctuation on 22 December 2010 becomes distinctly larger – obeying the interrelation $\mathrm{\Delta }{\mathit{\beta }}_i=\mathrm{0.5}\ln (i/\mathrm{114.3})$ – which does not happen (see Fig. 4a–d of Sarlis et al., 2013) for the increases in the β fluctuations upon the occurrences of all other shallow EQs in Japan of magnitude 7.6 or larger during the period from 1 January 1984 to the time of the M 9 Tōhoku EQ. Hence, the β fluctuation on 22 December 2010 accompanying the minimum ΔS_min is unique. Its presence is of paramount importance for the validity of the physical model that will be discussed in the next section.

4 Compatibility of the observed precursory phenomena with the PSPC physical model

Let us now discuss the multidisciplinary observations described in the previous two sections (and compiled in Fig. 3) that preceded the M 9 Tōhoku EQ. As we shall see all these observations are directly evidenced from the PSPC model, except probably of the anomalous changes in the level and temperature of confined groundwater.

A striking fact is that around 5 January 2011 the phenomenon of aligned orientations of the GPS azimuths occurred almost simultaneously with two other phenomena, i.e., the initiation of the anomalous Earth magnetic field variations and the minimum β_min of the fluctuations of the order parameter of seismicity. This is strikingly reminiscent of the mechanism of the emission of SES activity (stage B of PSPC model) in which, upon reaching σ=σ_cr, the electric dipoles exhibit cooperative orientation that also reflects alignment of the horizontal GPS azimuths (black in Fig. 3), as expected by P. Varotsos et al. (2011), leading to the most intense crust uplift. Such an SES emission is directly evidenced by the observed anomalous variations of the Earth's magnetic field mainly in the vertical component (brown in Fig. 3). This emission is consistent with the observation of the deepest minimum β_min around 5 January 2011 of the fluctuations of the order parameter of seismicity (blue in Fig. 3) in view of the up-to-date experimental results mentioned above that an SES activity initiates almost simultaneously with both the observation of β_min and the establishment of long-range temporal correlation between earthquake magnitudes.

Another striking fact is that the aforementioned simultaneous appearance of the three phenomena around 5 January 2011 has been preceded by a stage of an evident anti-correlated behavior between earthquake magnitudes since it was found that ${\mathit{\alpha }}_{\min ,\mathrm{bef}}=\mathrm{0.35}$ upon the occurrence on 22 December 2010 of the M 7.8 EQ in southern Japan at 27.05^∘ N, 143.94^∘ E. On the same date, the horizontal GPS azimuths, which were initially random, started to become gradually oriented toward the southern direction probably due to an excess stress disturbance. This may also originate the simultaneous appearance of various phenomena, including the large abrupt increase in the order parameter fluctuations along with an abrupt increase in the complexity measure Λ_i of the change in the entropy of seismicity under time reversal (recall that this change is then minimized); an increase in the Tsallis entropic index q (Tsallis, 1988); and start of groundwater anomalous changes, i.e., groundwater level drop, temperature decrease, and increase in radon concentration. This corresponds to stage A of the PSPC model, according to which an excess stress disturbance starts gradually increasing until reaching σ_cr.

After the occurrence of β_min at around 5 January 2011, the intense crust uplift was gradually mitigated and the orientations of GPS azimuths returned (Chen et al., 2014) to random around 13 January 2011, thus agreeing with the DFA exponent α=0.5 (Varotsos et al., 2014). The behavior turned to anti-correlation around 23 January 2011 with DFA exponent ${\mathit{\alpha }}_{\min ,\mathrm{aft}}=\mathrm{0.42}$, and a shift of earthquake-related stress disturbance was observed (Chen et al., 2014), where westward movements replaced the southward ones; i.e., the orientations of the residual displacements were realigned along the western direction and the crust depressed. After this change on 23 January 2011 the stress disturbance gradually approached the threshold of the fault rupture, and the orientations of the residual displacements became random again (Chen et al., 2014), in agreement with the DFA exponent of the earthquake magnitude time series being close to 0.5 until around 10 February 2011 (see Fig. 5 of Varotsos et al., 2014), which indicates random behavior. This fact that the Tōhoku EQ occurred after the emergence of an almost random behavior did not come as a surprise since it is strikingly reminiscent of similar findings in other complex time series as follows: in the case of electrocardiograms, for example, the long-range temporal correlations that characterize the healthy heart rate variability break down for individuals at high risk of sudden cardiac death (SCD), and this is often accompanied by the emergence of uncorrelated randomness (P. A. Varotsos et al., 2011; Goldberger et al., 2002) (SCD could be viewed as a critical phenomenon; e.g., see Varotsos et al., 2004, 2005a, 2007).

5 Summary and conclusions

Several phenomena of multidisciplinary nature preceded the M 9 Tōhoku EQ that occurred on 11 March 2011. Leaving aside the details, these phenomena were mainly accumulated around two dates, i.e., 22 December 2010 and 5 January 2011, which concur with the two stages A and B of the PSPC physical model, respectively. These phenomena include the following.

• a.

  Around the date 22 December 2010:

  • 1.

    The entropy change of seismicity under time reversal is minimized along with increased fluctuations (since Λ_i increases).

  • 2.

    There is an increase in the fluctuations of the order parameter of seismicity.

  • 3.

    The DFA exponent decreased to the value ${\mathit{\alpha }}_{\min ,\mathrm{bef}}=\mathrm{0.35}$, which is the lowest observed during the period 1984–2011 of our study, pointing to an evident anti-correlated behavior in the earthquake magnitude time series.

  • 4.

    The horizontal GPS azimuths started to become gradually oriented toward the southern direction (while they had random orientations during the preceding period 12–22 December 2010).

  • 5.

    Anomalous changes in the groundwater started (level drop, temperature decrease, and probably increase in radon concentration).

  • 6.

    Increase in the Tsallis entropic index q.

• b.

  Around the date 5 January 2011:

  • 1.

    Unprecedented minimum β_min of the fluctuations of the order parameter of seismicity.

  • 2.

    Anomalous magnetic field variations started (which, according to Maxwell equations, should be accompanied by a strong SES activity).

  • 3.

    Full alignment of the orientations of the GPS azimuths southwards accompanied by the most intense crust uplift.

  • 4.

    Long-range temporal correlations in the earthquake magnitude time series.

All the above phenomena were observed to begin and end well before the M 9 Tōhoku EQ occurrence as schematically shown in Fig. 1a in accordance with the PSPC model (Fig. 2).