the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Magnetotail reconnection asymmetries in an ion-scale, Earth-like magnetosphere
Christopher M. Bard
John C. Dorelli
We use a newly developed global Hall magnetohydrodynamic (MHD) code to investigate how reconnection drives magnetotail asymmetries in small, ion-scale magnetospheres. Here, we consider a magnetosphere with a similar aspect ratio to Earth but with the ion inertial length (δi) artificially inflated by a factor of 70: δi is set to the length of the planetary radius. This results in a magnetotail width on the order of 30 δi, slightly smaller than Mercury's tail and much smaller than Earth's with respect to δi. At this small size, we find that the Hall effect has significant impact on the global flow pattern, changing from a symmetric, Dungey-like convection under resistive MHD to an asymmetric pattern similar to that found in previous Hall MHD simulations of Ganymede's subsonic magnetosphere as well as other simulations of Mercury's using multi-fluid or embedded kinetic physics. We demonstrate that the Hall effect is sufficient to induce a dawnward asymmetry in observed dipolarization front locations and find quasi-periodic global-scale dipolarizations under steady, southward solar wind conditions. On average, we find a thinner current sheet dawnward; however, the measured thickness oscillates with the dipolarization cycle. During the flux-pileup stage, the dawnward current sheet can be thicker than the duskward sheet. This could be an explanation for recent observations that suggest Mercury's current sheet is actually thicker on the duskside: a sampling bias due to a longer lasting “thick” state in the sheet.
- Article
(7085 KB) - Full-text XML
- BibTeX
- EndNote
In the magnetospheres of Mercury and Earth, observations of plasmoids, flux bundles, and dipolarization fronts (DFs) demonstrate a marked asymmetry in their distribution across the magnetotail. At Earth, a number of studies have found magnetotail duskward biases in several magnetic phenomena: flux rope occurrence (Slavin et al., 2005; Imber et al., 2011), dipolarization fronts (Liu et al., 2013), energetic particle injections (Gabrielse et al., 2014), and reconnection (e.g., Asano et al., 2004; Genestreti et al., 2014). Additionally, the current sheet was found to be thinner on the duskside (Artemyev et al., 2011; Vasko et al., 2015). Similarly, at Mercury, Poh et al. (2017b) used MESSENGER data to fit the Harris sheet model to 234 tail current sheet crossings and found a bias towards dusk having thinner current sheets (by ≈10 %–30 %). In contrast, however, other MESSENGER studies (Sun et al., 2016; Dewey et al., 2018) found dawnward biases in dipolarization events and reconnection front locations.
The general existence of tail asymmetry is thought to be a result of sub-ion-scale effects (Lu et al., 2018; Liu et al., 2019), though there is still some uncertainty about the exact manifestation and causes of specific asymmetries. It is debated whether Hall electric fields are sufficient to reproduce this or if other ion-/electron-scale physics are required. Although some authors argue that electron-scale physics is required (Chen et al., 2019), we show in this paper that Hall effects are sufficient to cause an asymmetry in some observed features. Furthermore, it is unknown exactly why Mercury and Earth observe different asymmetries; it is hypothesized that system-size effects (relative to the ion inertial length δi) play a key role (Lu et al., 2016, 2018; Liu et al., 2019).
Several studies have proposed mechanisms to explain how Hall reconnection induces asymmetry in the magnetotail. Lu et al. (2016, 2018) (hereafter Lu+), in studying Earth's magnetotail with global hybrid simulations and localized particle-in-cell (PIC) simulations, showed that the decoupling of ions and electrons within the current sheet (the Hall effect; e.g., Sonnerup, 1979) creates an electric field and associated tail current density. The resulting E×B drift is sufficient to create tail asymmetries and indeed may be the primary cause. The duskside magnetic flux is preferentially evacuated via electron transport dawnward, which leads to a smaller normal Bz and thinner current sheet on the duskside.
In a similar study, Liu et al. (2019) (hereafter Liu+), using local PIC simulations of embedded, thin current sheets, confirmed that the Hall effect creates electron E×B and diamagnetic drifts which transport magnetic flux dawnward within the current sheet. However, they found that, although the preexisting tail Bz initially suppresses the onset of dawnside reconnection, the reconnection Bz drives outflows towards dawn and thins out the current sheet on that side. This creates an “active region” of reconnection on the dawnside, which has a thinner current sheet and stronger tail current jy. After analyzing both these studies, Liu+ proposed that, although the Lu+ model provides a explanation for a duskward bias in the initial reconnection onset, the Liu+ active region provides an explanation for dawnward biases within local, in-progress magnetotail reconnection. We test several aspects of this general picture within this paper.
Unfortunately, simulating large magnetospheres such as Earth (few hundred δi) while properly resolving the small-scale Hall physics requires grid sizes in the billions of cells. Several strategies have been proposed to evade this constraint; one is to embed regions of detailed kinetic physics within large-scale Hall magnetohydrodynamic (MHD) simulations (Chen et al., 2019). This allows for reproduction of kinetic effects within certain regions of the magnetosphere without having to run an expensive, fully kinetic simulation. However, these simulations assume no kinetic effects outside the embedded regions, which are limited to certain regions in the dayside and/or the tail. It is unclear whether or not this methodology, including boundary handling, affects the local-global feedback dynamics in the magnetosphere. Future studies will eventually be needed to compare magnetospheres from Hall MHD, kinetic, and combined kinetic–Hall simulations to ascertain these effects.
Another strategy suggests that we need only set the Hall scale to some length sufficient to capture the essential physics of Hall reconnection without having to fully resolve the physical length scale. In these simulations, the Hall length is set to ≈3 % of the global-scale length (Tóth et al., 2017), which is sufficient to capture the out-of-plane flows and the quadrupolar magnetic field structure induced by the Hall effect. However, recent research in 2D island coalescence (Bard and Dorelli, 2018) suggests that although including the Hall term in MHD simulations is sufficient in itself to generate these signatures of Hall reconnection, the actual reconnection rate depends on resolution and numerical resistivity. Although the Hall term is present, the reconnection itself may be Sweet–Parker-like and slow (unlike fast Hall reconnection). Bard and Dorelli (2018) observed that 20–25 cells per δi was necessary (within the context of their numerical viscosity) in order to observe fast Hall reconnection. This is much greater than the 5–10 cells per δi typically used in simulations (Dorelli et al., 2015; Dong et al., 2019; Chen et al., 2019). This suggests that, although artificially inflating δi allows the Hall effect to emerge and have a global impact, much higher resolution is required to observe the universally fast (∼0.1 vA) reconnection observed in kinetic simulations. Finally, Bard and Dorelli (2018) found qualitatively different behavior for varying ratios of system size to δi: large systems can produce bursty reconnection (with a low average reconnection rate) even when δi is sufficiently resolved to produce “fast”, instantaneous reconnection. Ultimately, the combined requirements of high resolution and large system size create a computational requirement beyond what is currently possible for magnetospheres. Indeed, we are only setting a resolution appropriate to 5 cells per solar wind δi in this work, though local density fluctuations in the tail may allow up to 10–20 cells per δi.
One possible method for dealing with this issue may be to use graphics processing units (GPUs), which have proven to be robust and viable for scientific computing. Indeed, several groups have already utilized GPUs to accelerate plasma simulations throughout heliophysics, astrophysics, and plasma physics (Bard and Dorelli, 2014; Benítez-Llambay and Masset, 2016; Fatemi et al., 2017; Bard and Dorelli, 2018; Schive et al., 2018; Grete et al., 2019; Liska et al., 2019; Wang et al., 2019). GPUs take advantage of parallelism in order to have a higher throughput for floating point operations. Finite-volume schemes are massively parallel: the calculation of how a computational cell evolves from t to t+Δt is independent of similar calculations for other cells. This makes explicit Hall MHD schemes (such as presented in this paper) quite amenable to GPU acceleration.
In this paper, we undertake a numerical experiment designed to assess the role of the Hall effect on global magnetospheric structure and dynamics within a “small” ion-scale magnetosphere, specifically focusing on how it induces asymmetry in the magnetotail. We present a magnetosphere simulation code which accelerates the explicit MHD solver algorithm via GPUs. We simulate an Earth-like analogue magnetosphere which has a similar bow shock–magnetopause distance and magnetotail width as Earth's (relative to the planetary radius); however, δi is artificially inflated to the planetary radius (RE). In other words, we are self-similarly scaling Earth from its current size relative to ion scales (magnetotail width ≈ 600δi) to a size closer to the ion scale (magnetotail width ≈ 30δi). In this “ion-scale Earth”, Hall physics plays a greater role in magnetosphere dynamics, and we are able to more readily observe global Hall MHD effects. We view this work as a first step in the study of the system-size dependence of Hall MHD magnetic reconnection in Earth-like magnetospheres; future system-size studies can be performed by making δi smaller relative to the planetary radius and increasing the resolution to sufficiently cover the ion scales.
This paper is presented as follows: Sect. 2 provides a brief overview of the Hall MHD algorithm as implemented using GPUs; Sect. 3 provides the initial condition and setup of the simulation; and Sect. 4 presents tail asymmetries in the simulation and discusses them in the context of observations and proposed theoretical explanations.
We take a Hall MHD code accelerated by GPUs using the MPI library and the NVIDIA CUDA API (Bard and Dorelli, 2014; Bard, 2016; Bard and Dorelli, 2018) and adapt it to simulate planetary magnetospheres. We review the underlying mathematical equations and algorithms in this section.
Following Tanaka (1994) and Powell et al. (1999), we split the magnetic field vector B into a background component B0 and a perturbed, evolving component B1 such that . The embedded B0 is assumed to be static (), divergence-free (), and curl-free (). This allows for more accurate handling of the magnetic field, especially near the planet where the dipole field is very strong. In order to preserve the divergence-free constraint on the evolved magnetic field, we solve the Generalized Lagrangian Multiplier (GLM) formulation of MHD (Dedner et al., 2002), with an additional Hall term added via Ohm's law.
The ideal MHD Ohm's law is extended with the Hall term such that the electric field E is given by
with c the speed of light, e the elementary charge, n the plasma number density, v the plasma bulk velocity vector, and the current density vector. We note that since the background magnetic field B0 is curl-free in our formulation, the current density is taken to be the curl of the perturbation B1.
We normalize the density (ρ), magnetic field, and length scale to reference values ρ0, Bw, and L0, respectively. v is normalized to , the pressure P to , and the time t to . The normalized plasma beta can be used in place of setting P0 directly; the conversion between the two is β0=2 P0.
This results in the set of equations:
where is the total energy density, γ is the ratio of specific heats (taken to be in all of our simulations), and combines the bulk velocity (v) with the normalized Hall velocity . The ion inertial length is normalized to the reference length such that . The normalized in our simulation is a fixed parameter that can be changed at runtime. We evaluate the normalized current density () at cell centers and linearly interpolate to the cell edges when needed.
ψ is a scalar function whose evolution is designed to be equivalent to ∇⋅B; ch and cp are parameters for the propagation and dissipation of local B divergence errors, respectively. Following Dedner et al. (2002), we set ch as the global maximum wave speed over the individual cells and set cp such that . Although Dedner et al. (2002) recommended , and this value works very well to control the magnetic divergence in non-magnetospheric simulations, we find that some level of tweaking is required because of the accumulation of divergence errors at the inner boundary. To ameliorate further complications caused by this issue, we separate the momentum equation into a non-magnetic flux and a magnetic source term:
which prevents divergence errors from inducing a nonphysical acceleration along magnetic field lines (Brackbill and Barnes, 1980) but with some loss of accuracy across shock jumps.
The overall system is evolved via a time-explicit second-order Runge–Kutta scheme coupled with a simple HLL Riemann solver (Harten et al., 1983; Toro, 1999) and a monotonized central limiter (e.g., Tóth et al., 2008) with the slope-limiting parameter β set to 1.25. For numerical stability, the explicit time step is determined by the global Courant condition: . The Courant parameter is C=0.325, Δxmin=0.2 RE is the smallest cell length in the simulation, and vmax is the maximum wave speed in the simulation. For Hall MHD, is estimated in each grid cell i using the fast magnetosonic (vf) and whistler wave (vw) speeds (Huba, 2003; Tóth et al., 2008):
with the normalized Alfvén speed and the normalized sound speed. The highest value of vmax,i across all cells is used to set the global time step.
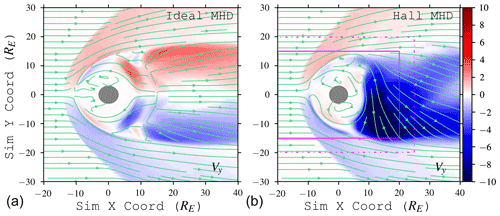
Figure 1Cross-tail velocity Vy in the tail plane perpendicular to reconnection for both ideal (a) and Hall (b) MHD, normalized to v0=97.9 km s−1. Streamlines show in-plane velocity. Purple lines in the right figure surround the highest resolution regions: RE (solid); RE (dot-dashed). A typical Dungey-like, symmetric convection pattern induced by numerical resistivity is clearly demonstrated in ideal MHD. Adding the Hall term induces out-of-reconnection-plane flows, which drives an asymmetric convection pattern; this is similar to what has been simulated for Ganymede (Dorelli et al., 2015; Tóth et al., 2016; Wang et al., 2018).
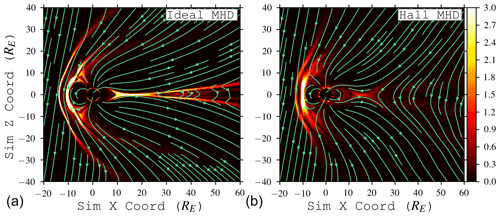
Figure 2Normalized current density magnitude in the simulation xz plane at y=0 for both ideal (a) and Hall (b) MHD. Streamlines show in-plane magnetic field. Adding the Hall term induces out-of-reconnection-plane flows (Fig. 1); the resulting tail convection causes the magnetotail current sheet to vary along the x direction across the tail width (y) (see, e.g., Figs. 7 and 9 for examples of spatial variation in the xy plane).
For our simulation setup, we choose normalized solar wind and terrestrial magnetic field parameters such that the magnetopause standoff distance matches that of Earth's magnetosphere (≈10 RE), the bow shock standoff distance is ≈3 RE beyond the magnetopause, and δi is equivalent to the planetary radius.
These relative distances can be controlled by setting four dimensionless parameters1:
-
, the solar wind Alfvénic Mach number;
-
, the solar wind plasma beta;
-
, the ratio of the dipole field strength at 1 RE to the solar wind magnetic field;
-
, the ion inertial length.
Since only the first three of these parameters control the magnetopause and bow shock standoff distances, we can arbitrarily set δi to control the relative Hall scale. This allows our theoretical magnetosphere to be simultaneously “Earth-like” (in a relative physical sense) and ion-scale (relative to δi).
.
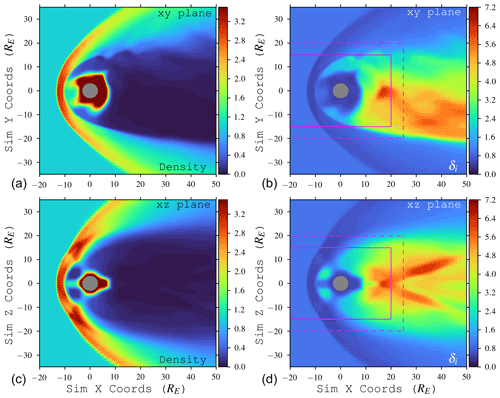
Figure 3Density (a, c) and local value of δi (b, d) calculated via in the xy (a, b) and xz planes (c, d), taken from an example snapshot during the final Hall MHD portion of the run. Density is normalized via and mi=3942 amu; δi is normalized via L0=RE. Purple lines denote same regions as Fig. 1: solid lines denote region with RE; dashed lines denote RE. Most of the near-tail region (within purple boxes; x>0) has >5 cells per local δi
Thus, we choose our reference values as follows: km, n0=5 cm−3, ρ0=min0 with the mass of each ion , and nT. From these, we derive , t0≈65 s, , and RE.
The solar wind is initialized with values ρsw=1 ρ0, km s−1, and wind plasma βsw=0.305 such that Psw=0.1526 P0. The wind magnetic field is initially set to Bsw=(- for a northward interplanetary magnetic field (IMF) with magnitude Bsw=1 Bw; we later flip the IMF by setting .
The planetary background magnetic field (B0) is approximated with a magnetic dipole
with r the position vector from the center at and the planetary dipole moment taken as (0, 0, −3000), such that on the magnetic equator at r=1 RE. This satisfies the requirement that B0 be both curl-free and divergence-free.
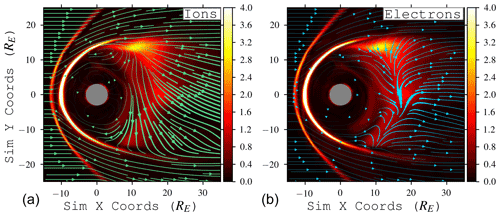
Figure 4Cross-tail convection in the reconnection plane at z=0 for ions (a) and electrons (b), with the background color (orange) illustrating normalized current sheet density magnitude. Blue (green) streamlines indicate direction of electron (ion) velocity (normalized via ), with line sizes proportional to the magnitude of the maximum electron (ion) velocity in the plane. The electron velocity (in normalized units) is calculated from .
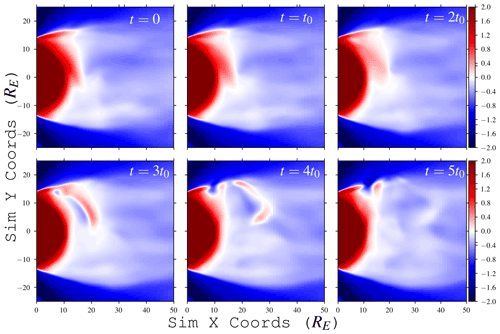
Figure 5Formation and evolution of a global dipolarization over 5 t0≈5.4 min, as seen in the evolution of magnetotail normal magnetic field Bz (red: out-of-page; blue: into page). Displayed times are relative to upper left image; t=0 here corresponds to 6t0 after the start of the 45 t0 Hall MHD simulation period. Bz has been normalized via .
As a summary, the dimensionless parameters for this experimental magnetosphere are MA=4.09; βsw=0.305; ; . For Earth, and the other parameters would be the same. For Mercury, the dimensionless parameters would be, e.g., ; βsw=0.65; ; .
At the inner boundary, we had difficulties with density depletion causing large local Alfvén speeds and small global time steps. We tried several types of inner boundaries, experimenting with different combinations of floating (zero-gradient) and fixing the plasma variables. Ultimately, although the following inner boundary conditions are not entirely realistic, they allow for a stable evolution of the magnetosphere in both the dayside and the tail. We set the inner boundary at a radius of 3 RE; in these ghost cells, we fix the density at 4 ρ0, float the pressure, float the radial magnetic field, set the tangential B to zero, and set the velocity to zero. For the divergence cleaning, we find that simply setting the ghost ψc = 0 works better than having a floating condition. We note that in more realistic magnetospheres, cold plasma from the ionosphere may flow out to the tail and impact the dynamics. We will leave this topic for future studies.
For the outer boundaries, the left edge of the simulation domain fixes the conservative variables to the background solar wind condition; the rest of the box has zero-derivative boundaries for all variables.
The simulation coordinates are defined with −x pointing towards the Sun, z along the planetary magnetic dipole axis, and +y (−y) towards the dusk (dawn) completing the orthogonal set. Although the planet does not rotate, dawn and dusk are used assuming the sun rises in the east. In order to resolve the artificially inflated δi, we choose 5 cells per , giving a minimum resolution of RE. This resolution is set within the range −20 RE < x<20 RE; −15 RE < y, z<15 RE; beyond this the cell length increases by 7 % with each additional cell up to a maximum of 5 RE or until it hits the boundary. The total size of the grid is (just over 18 million cells), covering a domain of −35.6 RE < x<122 RE, −86.4 RE < y, z<86.4 RE.
We start the simulation in ideal MHD () with a northward IMF (Bsw given above) for 120 t0 and then flip Bz,sw for the southward IMF case and run it for another 120 t0. At this point, we turn on the Hall term by setting and run it for another 12 t0 in order to allow the perturbations induced by the abrupt change of physics to settle. From this point on, the simulation was run for 45 t0 under continuous pure southward IMF and with the Hall term on. The main results discussed below come from this final portion of the run with the Hall term enabled.
4.1 Hall-induced asymmetry
Prior to turning on the Hall term, the magnetospheric convection is of Dungey-type. Turning the Hall term on, however, induces an out-of-reconnection-plane E×B force which breaks that symmetry and drives convection in a preferred direction (Fig. 1). This convection also modifies the current sheet structure between ideal and Hall MHD (Fig. 2) and causes it to vary in length along the x− direction across the tail y coordinate. For smaller magnetospheres, this effect was first seen in nonideal MHD simulations of Ganymede (Dorelli et al., 2015; Tóth et al., 2016; Wang et al., 2018); this was later seen in 10-moment and embedded kinetic simulations of Mercury (Dong et al., 2019; Chen et al., 2019). Our simulation supports the idea that this Hall-induced drift is sufficient to produce an asymmetry: kinetic effects are not required, but they may manifest different kinds of asymmetry.
Finally, since our choice of RE is based on the normalized δi=1 RE, we check here that we are able to correctly resolve δi in the tail. As Fig. 3 illustrates, the local value of δi exceeds 1 RE in the magnetotail and may reach up to 5 RE. Thus, we are appropriately resolving the Hall length scales in the tail.
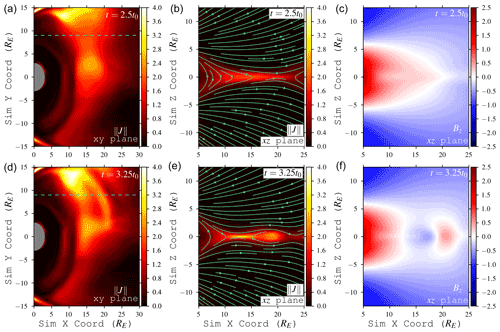
Figure 6Formation and evolution of a global dipolarization due to locally reconnecting magnetic field lines in the xy and xz planes, as seen in the evolution of magnetotail current density () and normal magnetic field Bz. is normalized via ; Bz is normalized via . Displayed times are relative to the sequence shown in Fig. 5. The dashed cyan lines in (a) and (d) mark the y position of the xz cuts in (b), (c), (e), and (f).
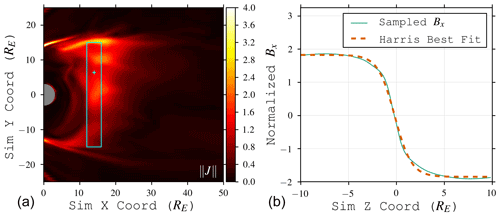
Figure 7Example of Bx sampling and Harris sheet fit (b) as described in text (Eq. 11). χ2=0.004 for this fit. Bx has been normalized via . Panel (a) shows the magnetotail current sheet magnitude (normalized via ) in the simulation z=0 plane; the Bx sampling box domain boundaries are shown in cyan, with the small cross showing the location of the example sample. The box boundaries are and .
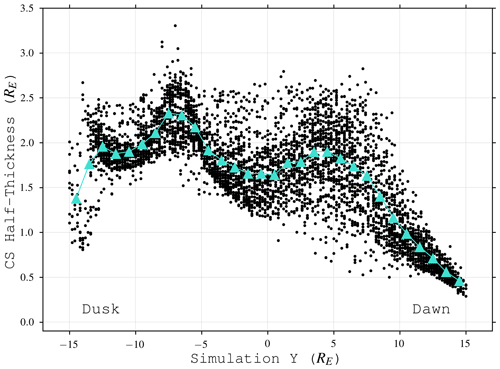
Figure 8Best-fit current sheet half-thicknesses (LCS) derived by fitting Eq. (11) to 5037 cuts of Bx along the z direction. These cuts were randomly sampled in the tail xy plane and over the simulation time period (see text). There is a bias towards the current sheet being thinner on the dawnside. However, the dawnside also sees a larger spread in thicknesses: this is a result of temporal effects (see main text for discussion).
4.2 Dipolarizations
In our simulation, the Hall electric field induced by tail reconnection accelerates ions towards the duskside and the electrons towards dawn. Since δi=RE here, the reconnection current sheet spans a significant fraction across the tail; this means that the ions are decoupled from the magnetic field during much of their in-plane convection duskward (green arrows in Fig. 4). The electrons, being coupled to the magnetic field, carry the reconnected, normal Bz flux dawnward (blue arrows). Because the reconnected magnetic flux originates over a large region within the tail, there is a significant pileup leading to a reconnecting, active region of plasmoid formation on the dawnside. This pileup–reconnection mechanism may be a general cause of dipolarizations in ion-scale magnetospheres (like Mercury, e.g., Sundberg et al., 2012). Although the drifting electrons themselves do not cause dipolarization events, they can affect where events occur. We speculate that increasing the system size relative to δi will limit the extent of dawnward flux transport via current sheet electrons and cause the flux pileup to shift closer to tail center (or duskward). In other words, this type of asymmetry we observe here may be more pronounced in δi-scale magnetospheres and weaker in larger magnetospheres. However, it is unknown how this mechanism will interact with the overall Hall-induced duskward ion convection, which will begin to dominate electron convection at scales ≫δi.
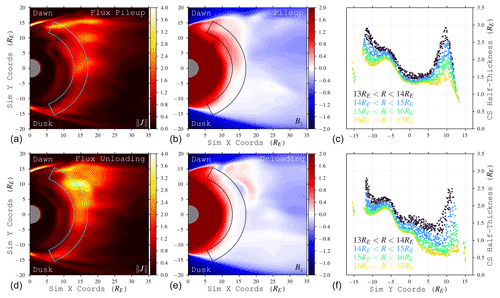
Figure 9Cross-comparison of current sheet density magnitude (a, d), current sheet Bz flux pileup (b, e; same parameters as Fig. 5) and sampled thicknesses (c, f) during (a, b, c) and after (d, e, f) a global dipolarization event. Current sheet fits are sampled from the area within the wedges (13 RE < R<17 RE). The current sheet is thick where the Bz flux has piled up and thin where the flux has been unloaded. There is a 2.25 t0≈2.4 min time difference between the snapshots of the top and bottom rows.
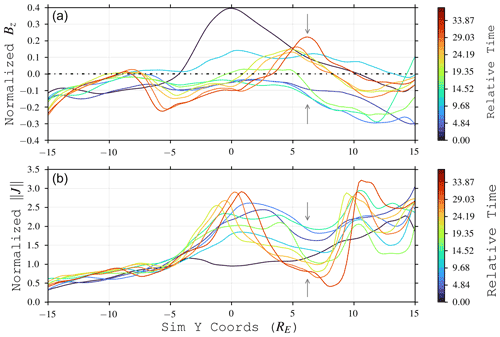
Figure 101D cuts of tail magnetic field Bz (a) and current density magnitude (b) taken from x=15 RE, −15 RE < y<15 RE in the z=0 equatorial plane. is normalized via ; Bz is normalized via . Colors denote times relative to t=0 in Fig. 5 (top left panel). Arrows highlight where local pileup of Bz on dawnside thickens the current sheet, resulting in a lower current density and impeding local reconnection.
During the 45 t0 ≈48 min duration of our simulation, there were seven events visually observed on the dawnside (none on the duskside) which followed the general substorm pattern of a buildup/loading phase followed by an unloading (or expansion/relaxation) phase (Rostoker et al., 1980). For each event, we observed pileup of the normal Bz magnetic flux over a period of several minutes, followed by a burst of reconnection and the subsequent ejection of plasmoids tailward (Figs. 5 and 6). Three of the seven events produced large plasmoids (on the order of 10 RE = 10δi), while the rest resulted in smaller ones (≤5 RE; ≤5δi). The larger ejecta appeared to build up and release on timescales of around 10 min, while the smaller events had shorter timescales of around 5 min. Most events originated at a down-tail distance ≈13–16 RE; after ejection, their resulting plasmoids traveled to about 30 RE down-tail over several minutes before dissipating.
The observed dawnward bias in dipolarization events for our ion-scale magnetosphere corroborates similar dawnward biases found in MESSENGER observations (Sun et al., 2016; Dewey et al., 2018) and global simulations of Mercury (Dong et al., 2019; Chen et al., 2019). It is interesting to note that our results are under a steady, southward solar wind condition. As long as there is Hall-driven convection in the tail, the competition between dawnside Bz pileup and reconnection drives this cycle. At the moment, it is not clear whether this process is unique to our ion-scale Earth, since its strong planetary dipole field means that flux piles up over a large swath of the tail. It is possible that a similar process may occur at Mercury (which has a weaker dipole field), i.e., that its observed dipolarizations are indeed akin to global substorms (Kepko et al., 2015). Further investigation is needed to determine how varying the magnetospheric parameters (as presented in Sect. 3) affects these observations, especially as system size increases relative to δi.
We note that, at Earth, there are additional localized (not global) dipolarization fronts resulting from current sheet instabilities or transient reconnection events (e.g., Runov et al., 2009; Sitnov et al., 2009). We do not see these small-scale fronts in our ion-scale Earth; this may be because we do not have enough down-tail resolution to observe localized current sheet instabilities which form them.
4.3 Current sheet thickness
Another test of the active region picture is the predicted thickness asymmetry of the tail current sheet: Liu+ predicted that the sheet would be thinner on the dawnside. We follow Poh et al. (2017a) and estimate the current sheet thickness in our model by using a Harris sheet (Harris, 1962):
where Ba is the asymptotic lobe field, Z0 is the current sheet center, LCS is the current sheet half-thickness, and the offset allows for asymmetry between the north and south Bx lobes on either side of the current sheet. We take 6000 one-dimensional cuts of Bx along the north–south direction between RE in a volume covering the current sheet from 12 RE < x<16 RE and −15 RE < y<15 RE, randomly sampled across the box plane and during the final 45 t0≈48 min period (example shown in Fig. 7). These cuts are fit to Eq. (11) using the Levenberg–Marquardt least-squares algorithm in scipy.curvefit (Virtanen et al., 2020); instances that do not fit well (χ2>0.01) or that return nonsensical results (LCS<0) are rejected. This results in 5037 samples of the current sheet thickness across the magnetotail (Fig. 8). This distribution shows that the dawnward current sheet is thinner on average than the duskward sheet. However, there is a significant scatter in this result; the dawn sheet covers a wider range of thicknesses. This variation is caused by the dawnside pileup–reconnection mechanism.
The current sheet oscillates with the dipolarization cycle (Sect. 4.2) between a “thick state” due to the Bz pileup and a “thin state” immediately following the flux unloading and plasmoid ejection. This is demonstrated in Fig. 9, where fitted CS thicknesses during both flux loading and unloading stages are plotted along with snapshots of the Bz state. During the loading stage, the piled up flux on the dawnside (5 RE < y<12 RE) fattens the current sheet; here, the sampled dawn thicknesses are comparable to and can exceed the dusk thicknesses. However, after the unloading stage, the current sheet on the dawnside is much thinner where the flux has been evacuated (bottom right plot; R>15 RE). Interestingly, we can see that where the Bz flux remains (R<15 RE), the current sheet continues to be thick. Combining all the sample fits over several cycles of loading and unloading results in the picture shown in Fig. 8: a dawnward current sheet moving between thick and thin states depending on the level of flux pileup. Indeed, this is a common pattern throughout the simulation: where there is flux pileup, the current sheet is thicker, and the current density is lower (e.g., Fig. 10).
This cycle may explain the apparent contradiction between the Liu+ prediction of thinner dawnward current sheets in ion-scale magnetospheres and the Poh et al. (2017b) spacecraft observation of thicker dawnward sheets at Mercury. Even though, on average, the current sheet is thinner dawnward (as Liu+ predicts), the sampling of measurements could be producing the opposite result. As shown in Figs. 8 and 9, the sampled sheet thickness can greatly depend on where and when the craft crosses the tail. In our simulation, the current sheet is continuously morphing between thick and thin states; both types of regions exist simultaneously within the dawnside. Most points in the tail preferentially see thicker sheets over time, though some preferentially see thinner sheets. It is possible that these effects combine to produce a sampling bias in time and space towards thicker sheets. We note that this is speculation and will require more investigation with respect to the various solar wind driving conditions and seasons that MESSENGER experiences at Mercury.
We have simulated a small, ion-scale Earth in which the standoff distance and magnetotail width are akin to Earth's as measured in planetary radii but with the solar wind ion-scale length δi set to 1 RE. The resulting tail plasma behavior was more similar to Mercury's magnetosphere than Earth's. Along with Chen et al. (2019) and Dong et al. (2019), our results support the idea that tail asymmetry is a universal consequence of the Hall effect in ion-scale magnetospheres. Essentially, it is the relative size of the magnetosphere compared to δi, not the absolute size (planetary radii), that controls the importance and influence of Hall-induced consequences. We find that Hall effects are sufficient to generate tail asymmetries in dipolarization, plasmoids, and current sheet thickness. No electron-scale kinetic effects are required, though they may contribute to or modify asymmetries. However, we emphasize that we did not simulate the same magnetosphere as Chen et al. (2019): our ion-scale Earth is smaller relative to δi than Mercury and has different magnetospheric parameters (Sect. 3). There may be additional effects not being considered, especially with regards to how varying the dimensionless magnetospheric parameters affects the manifestation of tail asymmetries.
In general, our simulation appears to corroborate the Liu+ picture of tail asymmetry in ion-scale magnetospheres; however, the Lu+ finding that the transported tail Bz thickens the current sheet is readily manifested here. Although the reconnected Bz does drive outflows and thin current sheets on the dawnside, we see that it can pile up and thicken current sheets. There is a continuous cycle between the dawnward transport of Bz leading to pileup (which thickens the current sheet) and reconnection (which thins the current sheet); this manifests in an oscillating current sheet thickness. On average, we find the current sheet is thinner on the dawnside, but it can occasionally be thicker in some regions depending on the level of flux pileup.
Further study will be required to confirm or contrast this picture for magnetospheres with system size ≫ δi. Since our simulation is of a experimental magnetosphere, several questions concerning more realistic magnetotails remain:
-
How does the weaker, offset dipole of Mercury affect the amount of magnetic flux available for transport/pileup and the resulting plasmoid formation/ejection?
-
Are the observed dipolarizations at Mercury actually “global”, like substorms?
-
How does increasing the system size δi ratio affect asymmetry formation, tail convection, transport of Bz, and plasmoid and DF formation?
-
What other effects (e.g., kinetic, ionosphere) cause asymmetries, and how do they interact with the Hall effect and one another?
We look forward to future studies which will investigate these questions in greater detail.
Observational data were not used, nor created for this research. The model algorithm is described above and in the references, and simulation parameters are given for reproducing the magnetosphere.
CMB developed the code, analyzed the simulation results, wrote the manuscript and produced the figures. JCD edited the manuscript and provided computing resources. Both authors conceptualized the research goals and guided the direction of inquiry.
The contact author has declared that neither they nor their co-author has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Christopher M. Bard thanks Alex Glocer for useful discussions concerning simulation techniques. Christopher M. Bard thanks Ryan Dewey for helpful discussions concerning Mercury tail asymmetries and MESSENGER observations. Plots were created using matplotlib (Hunter, 2007). The authors thank Gabor Toth and the anonymous referee for very helpful comments which improved this paper. Observational data were not used, nor created for this research; the model algorithm and simulation parameters are described above.
Christopher M. Bard's software development has been partly supported by an appointment to the NASA Postdoctoral Program at NASA Goddard Space Flight Center, administered by the Universities Space Research Association under contract with NASA. This research has been supported by the Goddard Space Flight Center (Internal Scientist Funding Model; grant no. HISFM18-0009).
This paper was edited by Minna Palmroth and reviewed by Gabor Toth and one anonymous referee.
Artemyev, A. V., Petrukovich, A. A., Nakamura, R., and Zelenyi, L. M.: Cluster statistics of thin current sheets in the Earth magnetotail: Specifics of the dawn flank, proton temperature profiles and electrostatic effects, J. Geophys. Res.-Space, 116, A09233, https://doi.org/10.1029/2011JA016801, 2011. a
Asano, Y., Mukai, T., Hoshino, M., Saito, Y., Hayakawa, H., and Nagai, T.: Current sheet structure around the near-Earth neutral line observed by Geotail, J. Geophys. Res.-Space, 109, A02212, https://doi.org/10.1029/2003JA010114, 2004. a
Bard, C.: Tools for Studying Magnetospheric-Wind Interactions, PhD thesis, The University of Wisconsin – Madison, 2016. a
Bard, C. and Dorelli, J. C.: On the role of system size in Hall MHD magnetic reconnection, Phys. Plasmas, 25, 022103, https://doi.org/10.1063/1.5010785, 2018. a, b, c, d, e
Bard, C. M. and Dorelli, J. C.: A simple GPU-accelerated two-dimensional MUSCL-Hancock solver for ideal magnetohydrodynamics, J. Comput. Phys., 259, 444–460, https://doi.org/10.1016/j.jcp.2013.12.006, 2014. a, b
Benítez-Llambay, P. and Masset, F. S.: FARGO3D: A New GPU-oriented MHD Code, Astrophys. J., 223, 11, https://doi.org/10.3847/0067-0049/223/1/11, 2016. a
Brackbill, J. U. and Barnes, D. C.: The effect of nonzero product of magnetic gradient and B on the numerical solution of the magnetohydrodynamic equations, J. Comput. Phys., 35, 426–430, https://doi.org/10.1016/0021-9991(80)90079-0, 1980. a
Chen, Y., Tóth, G., Jia, X., Slavin, J. A., Sun, W., Markidis, S., Gombosi, T. I., and Raines, J. M.: Studying Dawn-Dusk Asymmetries of Mercury's Magnetotail Using MHD-EPIC Simulations, J. Geophys. Res.-Space, 124, 8954–8973, https://doi.org/10.1029/2019JA026840, 2019. a, b, c, d, e, f, g
Dedner, A., Kemm, F., Kröner, D., Munz, C.-D., Schnitzer, T., and Wesenberg, M.: Hyperbolic Divergence Cleaning for the MHD Equations, J. Comput. Phys., 175, 645–673, https://doi.org/10.1006/jcph.2001.6961, 2002. a, b, c
Dewey, R. M., Raines, J. M., Sun, W., Slavin, J. A., and Poh, G.: MESSENGER Observations of Fast Plasma Flows in Mercury's Magnetotail, Geophys. Res. Lett., 45, 10110–10118, https://doi.org/10.1029/2018GL079056, 2018. a, b
Dong, C., Wang, L., Hakim, A., Bhattacharjee, A., Slavin, J. A., DiBraccio, G. A., and Germaschewski, K.: Global Ten-Moment Multifluid Simulations of the Solar Wind Interaction with Mercury: From the Planetary Conducting Core to the Dynamic Magnetosphere, Geophys. Res. Lett., 46, 11584–11596, https://doi.org/10.1029/2019GL083180, 2019. a, b, c, d
Dorelli, J. C., Glocer, A., Collinson, G., and Tóth, G.: The role of the Hall effect in the global structure and dynamics of planetary magnetospheres: Ganymede as a case study, J. Geophys. Res.-Space, 120, 5377–5392, https://doi.org/10.1002/2014JA020951, 2015. a, b, c
Fatemi, S., Poppe, A. R., Delory, G. T., and Farrell, W. M.: AMITIS: A 3D GPU-Based Hybrid-PIC Model for Space and Plasma Physics, in: Journal of Physics Conference Series, J. Phys. Conf. Ser., 837, 012017, https://doi.org/10.1088/1742-6596/837/1/012017, 2017. a
Gabrielse, C., Angelopoulos, V., Runov, A., and Turner, D. L.: Statistical characteristics of particle injections throughout the equatorial magnetotail, J. Geophys. Res.-Space, 119, 2512–2535, https://doi.org/10.1002/2013JA019638, 2014. a
Genestreti, K. J., Fuselier, S. A., Goldstein, J., Nagai, T., and Eastwood, J. P.: The location and rate of occurrence of near-Earth magnetotail reconnection as observed by Cluster and Geotail, J. Atmos. Sol.-Terr. Phys., 121, 98–109, https://doi.org/10.1016/j.jastp.2014.10.005, 2014. a
Grete, P., Glines, F. W., and O'Shea, B. W.: K-Athena: a performance portable structured grid finite volume magnetohydrodynamics code, arXiv e-prints, arXiv:1905.04341, 2019. a
Harris, E. G.: On a plasma sheath separating regions of oppositely directed magnetic field, Il Nuovo Cimento, 23, 115–121, https://doi.org/10.1007/BF02733547, 1962. a
Harten, A., Lax, P., and van Leer, B.: On upstream differencing and Godunov type methods for hyperbolic conservation laws, SIAM Rev., 25, 35–61, 1983. a
Huba, J. D.: Hall Magnetohydrodynamics – A Tutorial, in: Space Plasma Simulation, edited by: Büchner, J., Dum, C., and Scholer, M., Lecture Notes in Physics, Vol. 615, 166–192, SAO/NASA Astrophysics Data System, 2003. a
Hunter, J. D.: Matplotlib: A 2D graphics environment, Comput. Sci. Eng., 9, 90–95, https://doi.org/10.1109/MCSE.2007.55, 2007. a
Imber, S. M., Slavin, J. A., Auster, H. U., and Angelopoulos, V.: A THEMIS survey of flux ropes and traveling compression regions: Location of the near-Earth reconnection site during solar minimum, J. Geophys. Res.-Space, 116, A02201, https://doi.org/10.1029/2010JA016026, 2011. a
Kepko, L., Glassmeier, K. H., Slavin, J. A., and Sundberg, T.: Substorm Current Wedge at Earth and Mercury, in: Magnetotails in the Solar System, Geophysical Monograph Series, 207, 361–372, https://doi.org/10.1002/9781118842324.ch21, 2015. a
Liska, M., Chatterjee, K., Tchekhovskoy, A. e., Yoon, D., van Eijnatten, D., Hesp, C., Markoff, S., Ingram, A., and van der Klis, M.: H-AMR: A New GPU-accelerated GRMHD Code for Exascale Computing With 3D Adaptive Mesh Refinement and Local Adaptive Time-stepping, arXiv e-prints, arXiv:1912.10192, 2019. a
Liu, J., Angelopoulos, V., Runov, A., and Zhou, X. Z.: On the current sheets surrounding dipolarizing flux bundles in the magnetotail: The case for wedgelets, J. Geophys. Res.-Space, 118, 2000–2020, https://doi.org/10.1002/jgra.50092, 2013. a
Liu, Y.-H., Li, T. C., Hesse, M., Sun, W. J., Liu, J., Burch, J., Slavin, J. A., and Huang, K.: Three-Dimensional Magnetic Reconnection With a Spatially Confined X-Line Extent: Implications for Dipolarizing Flux Bundles and the Dawn-Dusk Asymmetry, J. Geophys. Res.-Space, 124, 2819–2830, https://doi.org/10.1029/2019JA026539, 2019. a, b, c
Lu, S., Lin, Y., Angelopoulos, V., Artemyev, A. V., Pritchett, P. L., Lu, Q., and Wang, X. Y.: Hall effect control of magnetotail dawn-dusk asymmetry: A three-dimensional global hybrid simulation, J. Geophys. Res.-Space, 121, 11,882–11,895, https://doi.org/10.1002/2016JA023325, 2016. a, b
Lu, S., Pritchett, P. L., Angelopoulos, V., and Artemyev, A. V.: Formation of Dawn-Dusk Asymmetry in Earth's Magnetotail Thin Current Sheet: A Three-Dimensional Particle-In-Cell Simulation, J. Geophys. Res.-Space, 123, 2801–2814, https://doi.org/10.1002/2017JA025095, 2018. a, b, c
Poh, G., Slavin, J. A., Jia, X., Raines, J. M., Imber, S. M., Sun, W.-J., Gershman, D. J., DiBraccio, G. A., Genestreti, K. J., and Smith, A. W.: Mercury's cross-tail current sheet: Structure, X-line location and stress balance, Geophys. Res. Lett., 44, 678–686, https://doi.org/10.1002/2016GL071612, 2017a. a
Poh, G., Slavin, J. A., Jia, X., Raines, J. M., Imber, S. M., Sun, W.-J., Gershman, D. J., DiBraccio, G. A., Genestreti, K. J., and Smith, A. W.: Coupling between Mercury and its nightside magnetosphere: Cross-tail current sheet asymmetry and substorm current wedge formation, J. Geophys. Res.-Space, 122, 8419–8433, https://doi.org/10.1002/2017JA024266, 2017b. a, b
Powell, K. G., Roe, P. L., Linde, T. J., Gombosi, T. I., and De Zeeuw, D. L.: A Solution-Adaptive Upwind Scheme for Ideal Magnetohydrodynamics, J. Comput. Phys., 154, 284–309, https://doi.org/10.1006/jcph.1999.6299, 1999. a
Rostoker, G., Akasofu, S. I., Foster, J., Greenwald, R. A., Kamide, Y., Kawasaki, K., Lui, A. T. Y., McPherron, R. L., and Russell, C. T.: Magnetospheric substorms-definition and signatures, J. Geophys. Res.-Space, 85, 1663–1668, https://doi.org/10.1029/JA085iA04p01663, 1980. a
Runov, A., Angelopoulos, V., Sitnov, M. I., Sergeev, V. A., Bonnell, J., McFadden, J. P., Larson, D., Glassmeier, K. H., and Auster, U.: THEMIS observations of an earthward-propagating dipolarization front, Geophys. Res. Lett., 36, L14106, https://doi.org/10.1029/2009GL038980, 2009. a
Schive, H.-Y., ZuHone, J. A., Goldbaum, N. J., Turk, M. J., Gaspari, M., and Cheng, C.-Y.: GAMER-2: a GPU-accelerated adaptive mesh refinement code – accuracy, performance, and scalability, Mon. Not. R. Astron. Soc., 481, 4815–4840, https://doi.org/10.1093/mnras/sty2586, 2018. a
Sitnov, M. I., Swisdak, M., and Divin, A. V.: Dipolarization fronts as a signature of transient reconnection in the magnetotail, J. Geophys. Res.-Space, 114, A04202, https://doi.org/10.1029/2008JA013980, 2009. a
Slavin, J. A., Tanskanen, E. I., Hesse, M., Owen, C. J., Dunlop, M. W., Imber, S., Lucek, E. A., Balogh, A., and Glassmeier, K. H.: Cluster observations of traveling compression regions in the near-tail, J. Geophys. Res.-Space, 110, A06207, https://doi.org/10.1029/2004JA010878, 2005. a
Sonnerup, B. U. Ö.: Magnetic field reconnection, Solar System Plasma Physics, 3, 45–108, 1979. a
Sun, W. J., Fu, S. Y., Slavin, J. A., Raines, J. M., Zong, Q. G., Poh, G. K., and Zurbuchen, T. H.: Spatial distribution of Mercury's flux ropes and reconnection fronts: MESSENGER observations, J. Geophys. Res.-Space, 121, 7590–7607, https://doi.org/10.1002/2016JA022787, 2016. a, b
Sundberg, T., Slavin, J. A., Boardsen, S. A., Anderson, B. J., Korth, H., Ho, G. C., Schriver, D., Uritsky, V. M., Zurbuchen, T. H., Raines, J. M., Baker, D. N., Krimigis, S. M., McNutt, Ralph L., J., and Solomon, S. C.: MESSENGER observations of dipolarization events in Mercury's magnetotail, J. Geophys. Res.-Space, 117, A00M03, https://doi.org/10.1029/2012JA017756, 2012. a
Tanaka, T.: Finite Volume TVD Scheme on an Unstructured Grid System for Three-Dimensional MHD Simulation of Inhomogeneous Systems Including Strong Background Potential Fields, J. Comput. Phys., 111, 381–389, https://doi.org/10.1006/jcph.1994.1071, 1994. a
Toro, E. F.: Riemann solvers and numerical methods for fluid dynamics: A practical introduction, Springer-Verlag, 1999. a
Tóth, G., Ma, Y., and Gombosi, T. I.: Hall magnetohydrodynamics on block-adaptive grids, J. Comput. Phys., 227, 6967–6984, https://doi.org/10.1016/j.jcp.2008.04.010, 2008. a, b
Tóth, G., Jia, X., Markidis, S., Peng, I. B., Chen, Y., Daldorff, L. K. S., Tenishev, V. M., Borovikov, D., Haiducek, J. D., Gombosi, T. I., Glocer, A., and Dorelli, J. C.: Extended magnetohydrodynamics with embedded particle-in-cell simulation of Ganymede's magnetosphere, J. Geophys. Res.-Space, 121, 1273–1293, https://doi.org/10.1002/2015JA021997, 2016. a, b
Tóth, G., Chen, Y., Gombosi, T. I., Cassak, P., Markidis, S., and Peng, I. B.: Scaling the Ion Inertial Length and Its Implications for Modeling Reconnection in Global Simulations, J. Geophys. Res.-Space, 122, 10336–10355, https://doi.org/10.1002/2017JA024189, 2017. a
Vasko, I. Y., Petrukovich, A. A., Artemyev, A. V., Nakamura, R., and Zelenyi, L. M.: Earth's distant magnetotail current sheet near and beyond lunar orbit, J. Geophys. Res.-Space, 120, 8663–8680, https://doi.org/10.1002/2015JA021633, 2015. a
Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M., Reddy, T., Cournapeau, D., Burovski, E., Peterson, P., Weckesser, W., Bright, J., van der Walt, S. J., Brett, M., Wilson, J., Jarrod Millman, K., Mayorov, N., Nelson, A. R. J., Jones, E., Kern, R., Larson, E., Carey, C., Polat, İ., Feng, Y., Moore, E. W., Vand erPlas, J., Laxalde, D., Perktold, J., Cimrman, R., Henriksen, I., Quintero, E. A., Harris, C. R., Archibald, A. M., Ribeiro, A. H., Pedregosa, F., van Mulbregt, P., and Contributors, S.: SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python, Nat. Method., 17, 261–272, https://doi.org/10.1038/s41592-019-0686-2, 2020. a
Wang, L., Germaschewski, K., Hakim, A., Dong, C., Raeder, J., and Bhattacharjee, A.: Electron Physics in 3-D Two-Fluid 10-Moment Modeling of Ganymede's Magnetosphere, J. Geophys. Res.-Space, 123, 2815–2830, https://doi.org/10.1002/2017JA024761, 2018. a, b
Wang, Y., Feng, X., Zhou, Y., and Gan, X.: A multi-GPU finite volume solver for magnetohydrodynamics-based solar wind simulations, Comput. Phys. Commun., 238, 181–193, https://doi.org/10.1016/j.cpc.2018.12.003, 2019. a
In resistive MHD, there is a fifth dimensionless parameter: the Lundquist number S, which sets the resistive dissipation scale. However, we do not explicitly define resistivity in this code; thus, we will not consider S here and instead leave this for future studies.





