Roles of electrons and ions in formation of the current in mirror-mode structures in the terrestrial plasma sheet: Magnetospheric Multiscale observations

Mirror-mode structures widely exist in various space plasma environments. Here, we investigate a train of mirror-mode structures in the terrestrial plasma sheet on 11 August 2017 based on the Magnetospheric Multiscale mission. We find that bipolar current densities exist in the cross section of two hole-like mirror-mode structures, referred to as magnetic dips. The bipolar current density in the magnetic dip with a size of ∼2.2 ρ_i (the ion gyro radius) is mainly contributed by variations of the electron velocity, which is mainly formed by the magnetic gradient–curvature drift. For another magnetic dip with a size of ∼6.6 ρ_i, the bipolar current density is mainly caused by an ion bipolar velocity, which can be explained by the collective behaviors of the ion drift motions. The current density inside the mirror dip contributes to the maintenance of the hole-like structure's stable. Our observations suggest that the electrons and ions play different roles in the formation of currents in magnetic dips with different sizes.

1 Introduction

Mirror modes are pressure-balanced and compressional magnetic structures (Hasegawa, 1969; Tsurutani et al., 2011; Wang et al., 2016; Zhang et al., 2018). They widely exist in many space plasma regions, such as solar wind (Zhang et al., 2008, 2009; Russell et al., 2009), the planetary magnetosheath (Volwerk et al., 2008; Schmid et al., 2014), the planetary magnetosphere (Vaivads et al., 2001; Rae et al., 2007), and comets (Glassmeier et al., 1993; Volwerk et al., 2016). These structures are believed to be generated by the mirror instability excited in the mirror-unstable environment (Hasegawa, 1969; Southwood and Kivelson, 1993). The plasma perpendicular temperature anisotropy provides free energy to excite the mirror instability (Kivelson and Southwood, 1996). Once the mirror-mode structures are generated, they will be convected with the ambient flow since they are non-propagating relative to the ambient flow (Tsurutani et al., 2011). Due to gradients in the magnetic field and plasma density, the mirror-mode structure may slowly propagate relative to the ambient plasma flow (Hasegawa, 1969; Pokhotelov et al., 2003). It is expected that they will stop to grow or decay when they move into the mirror-stable region. Actually, they are reported to be able to survive in the mirror-stable region in the solar wind and magnetosheath (Balikhin et al., 2009; Russell et al., 2009).

Mirror-mode structures appear not only as quasi-periodic sinusoidal oscillations, but also as local enhancements or decrease in the magnetic field intensity, referred to as magnetic peaks or dips (Tsurutani et al., 2011). Magnetic peaks can only exist in the mirror-unstable environments, while magnetic dips are able to survive in the mirror-stable region (Kuznetsov et al., 2007; Soucek et al., 2008). The typical scales of the mirror-mode structures are 10 s ρ_i in the magnetosheath (Tsurutani et al., 1982; Horbury and Lucek, 2009), where ρ_i is the ion gyro radius. Based on observations of the four Cluster satellites, the longest scales of the mirror-mode structures in the magnetosheath are found to be 2–6 times the lengths of their shortest scales, and their shapes are approximately cigar-like (Horbury and Lucek, 2009). By contrast, magnetic dips with a scale less than 1 ρ_i also exist in the magnetosheath as well as in the plasma sheet, and electron vortices are found inside the structure (Ge et al., 2011; Huang et al., 2017, 2018, 2019; Yao et al., 2017).

In the terrestrial plasma sheet, there also exist mirror-mode structures with several ion gyro radii (Vaivads et al., 2001; Zieger et al., 2011; Li et al., 2014; Wang et al., 2016). The earthward fast flows can result in a magnetic pileup in its leading area, and the ion perpendicular temperature anisotropy in the pileup region is able to make the local plasma conditions mirror-unstable to generate mirror-mode structures (Zieger et al., 2011). Mirror-mode structures accompanied by electron dynamics and whistler waves are also reported to occur during the dipolarization processes (Li et al., 2014; Huang et al., 2018). Dipolarization fronts (DFs), characterized by a sharp enhancement in B_Z in GSM (geocentric solar magnetospheric coordinates, used everywhere unless otherwise stated), are formed ahead of the earthward fast flows (Ge et al., 2012; Wu et al., 2013; Schmid et al., 2016; Xiao et al., 2017). They play an important role in the energy conversion, mass transport, particle accelerations, and wave activities (Fu et al., 2012b; Huang et al., 2012, 2015b). They are able to create a pressure pileup region ahead of the DF when moving earthward (Schmid et al., 2011; Liu et al., 2013). Mirror-mode structures with a scale of ∼4 ρ_i are reported to occur in the pressure pileup region ahead of a DF, and the mirror instability is suggested to be a potential mechanism to generate these structures since local environments are mirror-unstable (Wang et al., 2016). Within a mirror-mode structure there should be an electric current driven by the magnetic gradient and curvature drifts of the ions and/or electrons in order to sustain their stability (Constantinescu, 2002).

In this study, we investigate a train of ion-scale mirror-mode structures in the terrestrial plasma sheet on 11 August 2017 using the Magnetospheric Multiscale (MMS) mission data. Our aim is to figure out whether the main contributor to the current density inside the ion-scale mirror-mode structure is the electron or ion.

2 Observation

The MMS spacecraft consist of four identical satellites, which constitute a tetrahedron with inter-spacecraft distances of tens of kilometers (Burch et al., 2015). In the present study, we use the survey (a resolution of 16 Hz) of magnetic field data obtained by the Fluxgate Magnetometer (Russell et al., 2016) and the survey (4.5 s) of plasma data recorded by the Fast Plasma Instrument (Pollock et al., 2016).

2.1 Overview of a DF event

Figure 1 shows that B_Z sharply increases ∼8 nT within 7 s accompanied by a fast earthward flow with a maximum speed of ∼397 km s⁻¹ at $\sim \mathrm{20}:\mathrm{38}$ UT on 11 August 2017. Also, the local ion beta, the ratio of the ion thermal pressure to the magnetic pressure, is ∼4, and the elevation angle ($\mathit{\theta }=\arctan \left(\frac{B_Z}{\sqrt{B_X^{\mathrm{2}}+B_Y^{\mathrm{2}}}}\right)$) changes ∼50^∘ with a maximum angle of 64^∘ (not shown). These observations satisfy the criteria of the DF from Fu et al. (2012a), indicating that it is a DF event shown as the vertical dotted line at around 20:38 UT in Fig. 1. At 20:40 UT, the MMS spacecraft are located near (−18, 14.6, 2) R_E in GSM. The normal direction of the DF is (0.34, 0.82, −0.46) determined by the minimum variance analysis (MVA) (Sonnerup and Scheible, 1998) using the data in the interval between 20:37:33 and 20:37:42 UT. The ratio of the intermediate to minimum eigenvalues (λ₂∕λ₃) is ∼15, indicating that the estimated normal direction is reliable (Volwerk, 2006; Wang et al., 2014). The estimated normal direction suggests that the MMS spacecraft are located at the duskward side of the DF based on the semi-circle assumption of the DF (Huang et al., 2015a).

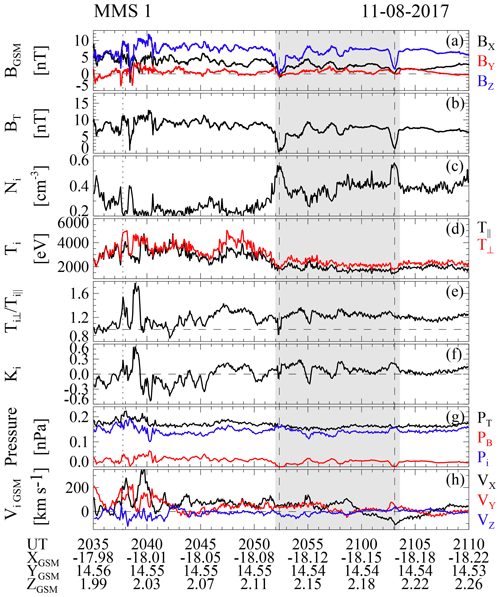
Figure 1 Observations of a DF event by MMS1 on 11 August 2017. From top to bottom: three components of the magnetic field in GSM (a), the total magnetic field (b), ion density (c), ion perpendicular (red) and parallel (black) temperatures (d), ion perpendicular temperature anisotropy (e), the threshold of the mirror instability (f), the magnetic, ion thermal, and total pressures (g), and three components of the ion velocity in GSM (h). The gray shadow indicates several compressional structures. The vertical dotted line indicates the DF, and the dashed lines indicate the trough of two hole-like structures.

Several quasi-periodic compressional magnetic oscillations with a period of ∼2 min are observed in the interval between 20:51 and 21:04 UT shown as the gray region in Fig. 1. The total magnetic field varies in anti-phase with the ion number density during this interval. In addition, the total pressure and sum of the magnetic and ion thermal pressures are almost constant, indicating that they are pressure-balanced structures. The threshold of the ion mirror instability K_i is shown in Fig. 1f, where $K=\frac{T_{\perp }}{T_{\parallel }}-\mathrm{1}-\frac{\mathrm{1}}{{\mathit{\beta }}_{\perp }}$, T_⊥, T_∥, and β_⊥ are perpendicular and parallel ion temperatures and perpendicular ion beta, respectively (Southwood and Kivelson, 1993). Local plasma environments become mirror-unstable and can excite ion mirror instabilities when K_i>0. The maximum K_i in each compressional structure reaches over 0.2, and it tends to decrease to near or below 0 from the center of each structure to its edge. Before 20:51 UT or after 21:04 UT, K_i is near or below 0; i.e., the background environment for these structures is marginally mirror-stable.

The above properties of the compressional structures indicate that they are likely to be mirror-mode structures (Tsurutani et al., 2011). Mirror-mode structures are supposed to be non-propagating structures relative to the ambient flow if there are no significant gradients in the magnetic field and plasma density (Pokhotelov et al., 2003). Burst magnetic field data (a resolution of 128 Hz) are available only between 20:51 and 20:54 UT; thus, we perform timing analysis (Harvey, 1998) to calculate the propagating velocity of the hole-like structure between 20:51:55 and 20:52:56 UT to verify whether these compressional structures are non-propagating. Figure 2a shows the positions of the MMS spacecraft relative to MMS1 at 20:52 UT. The inter-spacecraft distances are ∼13 to 21 km. Before performing the timing, the magnetic field data have been low-pass filtered with a cutoff period of 30 s to reduce the effect of high-frequency fluctuations. Figure 2b shows the cross-correlations between MMS1 and the three other satellites by using B_Z. The maximum correlation coefficients are all almost 1 between MMS1 and MMS2/3/4, with lag times of −0.312, −0.164, and −0.039 s, respectively. The estimated velocity is (71.3, 11.7^∘, −28^∘) in spherical coordinates (r,θ, φ) transferred from the GSM coordinate system, where θ and φ are the longitude and latitude, respectively. By contrast, the average ion velocity is (71.6, 37.8^∘, −28.4^∘) in this interval. Comparing these two velocities, one can find that the compressional structures in Fig. 1 are approximately stationary; i.e., they are mirror-mode structures.

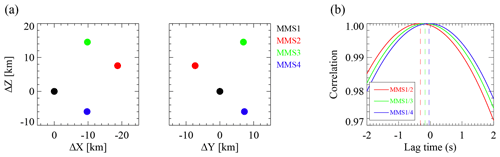
Figure 2 (a) Positions of the MMS spacecraft relative to MMS1 at 20:52 UT in the x–z (left) and y–z (right) planes. (b) The cross-correlations between MMS1 and the three other MMS satellites are calculated by using B_Z in the interval 20:52:55–20:52:56 UT.

The first and last mirror-mode structures as the dashed lines shown in Fig. 1 are hole-like, which are referred to as magnetic dips. We will focus on these two magnetic dips in the rest of the paper, and we mark them as MM1 (20:51:55–20:52:56 UT) and MM2 (21:02:26–21:03:34 UT).

2.2 Plasma properties in MM1

To further look at the plasma properties in the magnetic dips, we transform the ion and electron velocities as well as the magnetic field and current density into the principal axis (LMN) coordinate system as shown in Fig. 3. The principal axis vectors are calculated by MVA using the magnetic field data obtained from MMS1 in the interval between 20:51:55 and 20:52:56 UT. To reduce the effect of the high-frequency fluctuations, the magnetic field data have been low-pass filtered with a cutoff period of 30 s before performing the MVA analysis. The L, M, and N directions are (0.46, 0.27, 0.85), (0.28, 0.86, −0.42), and (−0.84, 0.43, 0.32) in GSM, respectively. The eigenvalue ratio λ₂∕λ₃ is ∼9.

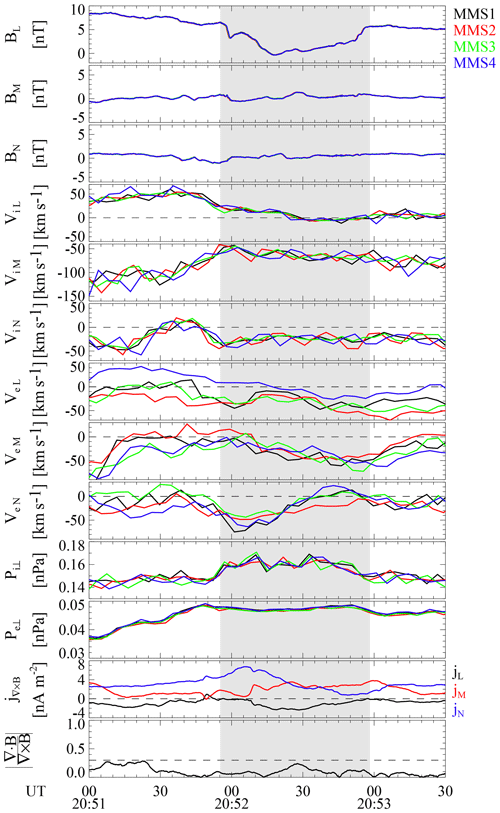
Figure 3 From top to bottom: three components of the magnetic field, ion and electron velocities in LMN, the ion and electron perpendicular thermal pressures, the current density in LMN, and the ratio of $|\mathrm{\nabla }\cdot B|/|\mathrm{\nabla }\times B|$ between 20:51 and 20:53:30 UT. The black, red, green, and blue colors indicate data obtained from MMS1, MMS2, MMS3, and MMS4, respectively. The current density is calculated by the curlometer technique. The gray region indicates the interval of the magnetic dip.

Figure 3 shows that B_L is dominant, while B_M and B_N vary around 0. The angles between the average magnetic field in this interval and the L, M, and N directions are ∼18, 108, and 87^∘, respectively. It indicates that the cross section of MM1 is approximately parallel to the M–N plane and is approximately perpendicular to the ambient magnetic field. The N direction is supposed to be parallel to the above-estimated velocity by timing; however, the angle between these two directions is ∼37^∘. The MVA technique can be affected by waves or noises superimposed on the discontinuity surface (Lepping and Behannon, 1980; Schmid et al., 2019), while the inter-spacecraft distances and configuration of the MMS spacecraft can affect the accuracy of the calculation (Harvey, 1998), which might be a possible explanation for the large difference between the two estimated normal directions. The ion velocity is mainly in the M–N plane during the whole interval, and there are no significant changes in both V_iM and V_iN. By contrast, the N component of the electron velocity V_eN shows a bipolar variation with an amplitude of ∼40 km s⁻¹. To reduce the effect of the high-frequency noise, the electron data have been smoothed within a 30 s window in Fig. 3 as well as in Fig. 4. Interestingly, an enhancement of (a decrease in) V_eN occurs on the left-hand (right-hand) side of MM1; i.e., a bipolar feature appears in V_eN.

The current density in Fig. 3 is calculated by the curlometer technique (Dunlop et al., 2002) using the magnetic field data low-pass filtered with a cutoff period of 30 s. The current density can be regarded as reliable when the ratio $|\mathrm{\nabla }\cdot B|/|\mathrm{\nabla }\times B|$ is less than 0.2 (e.g., Wang et al., 2017, 2019). The N component of the current density j_N shows a bipolar variation similar to V_eN with an opposite trend of change. The correlation coefficient between j_N and V_eN inside MM1 is −0.97. By comparing the variations in the ion and electron velocities, one can note that the bipolar current density inside MM1 is mainly associated with the electron velocity. The peak and trough of the bipolar V_eN tend to occur near the maximum gradient of B_L, while there is no significant change in P_e⊥.

Since the magnetic dips are stationary in the ambient flow, we can estimate their scale in the cross section by

$$\begin{array}{}\text{(1)}& \sqrt{{\left({\int }_{t_{\mathrm{1}}}^{t_{\mathrm{2}}}{V}_M\mathrm{d}t\right)}^{\mathrm{2}}+{\left({\int }_{t_{\mathrm{1}}}^{t_{\mathrm{2}}}{V}_N\mathrm{d}t\right)}^{\mathrm{2}}},\end{array}$$

where V_M and V_N are the M and N components of the ion velocity, and t₁ and t₂ are the start and end times of each magnetic dip. The scale of MM1 is estimated to be $\sim \mathrm{4.1}\times {\mathrm{10}}^{\mathrm{3}}$ km, or ∼2.2 ρ_i, where ρ_i is the local ion gyro radius calculated by the average ion perpendicular temperature and the average B_T in MM1 between 20:51:55 and 20:52:56 UT. Since the spacecraft may not cross the center of the magnetic dip, the estimated scale is the lower limit.

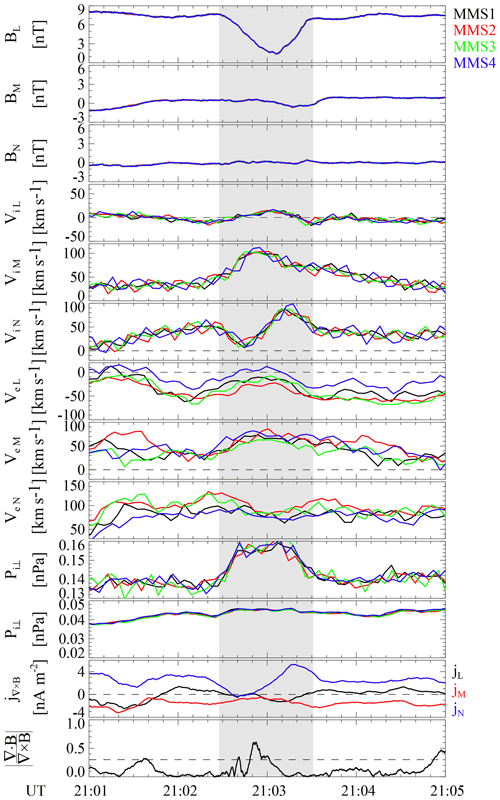
Figure 4 From top to bottom: three components of the magnetic field, ion and electron velocities in LMN, the ion and electron perpendicular thermal pressures, the current density in LMN, and the ratio of $|\mathrm{\nabla }\cdot B|/|\mathrm{\nabla }\times B|$ between 21:01 and 21:05 UT. The black, red, green, and blue colors indicate data obtained from MMS1, MMS2, MMS3, and MMS4, respectively. The current density is calculated by the curlometer technique. The gray region indicates the interval of the magnetic dip.

2.3 Plasma properties in MM2

Figure 4 shows the magnetic field, ion velocity, electron velocity, and current density in LMN between 21:01 and 21:05 UT. The magnetic field data between 21:02:26 and 21:03:34 UT are used to calculate the principal axis vectors by MVA. The ratio λ₂∕λ₃ is ∼6, and the L, M, and N directions are (0.26, 0.1, 0.96), (−0.44, 0.89, 0.02), and (−0.86, −0.43, 0.28), respectively. The angles between the average magnetic field in this interval and the L, M, and N directions are ∼1.5, 89, and 89^∘, respectively. B_L is dominant during the whole interval, while B_M and B_N are very small. Thus, the cross section of MM2 is also approximately parallel to the M–N plane and almost perpendicular to the ambient magnetic field. No large-amplitude fluctuations appear in MM2 compared to MM1. The ion velocities V_iM and V_iN are dominant, while V_iL varies around 0. Interestingly, a bipolar feature in V_iN with a variation up to 80 km s⁻¹ (peak minus trough) can be distinctly found inside the dip, while V_iM tends to increase compared to the ambient flow. V_iN is smaller (larger) than the ambient value on the left-hand (right-hand) side of the dip. The peak and trough of the bipolar V_iN appear when there are significant gradients in the magnetic field and the ion perpendicular thermal pressures. This indicates that the bipolar V_iN could be associated with the magnetic gradient and diamagnetic drifts. The length of MM2 in the cross section is estimated to be $\sim \mathrm{6.4}\times {\mathrm{10}}^{\mathrm{3}}$ km, or ∼6.6 ρ_i.

The current density in Fig. 4 is also determined by the curlometer technique. Before performing the curlometer analysis, the magnetic field data have been low-pass filtered with a cutoff period of 20 s to reduce the effect of the high-frequency fluctuations. One can find that j_N shows a similar bipolar feature to V_iN. The correlation coefficient between V_iN and j_N is 0.92 in the whole interval of MM2, indicating that both parameters have a strong relation. The peak minus the trough of j_N during MM2 is ∼5.6 nA m⁻². By contrast, j_L and j_M have no such clear bipolar feature. The electron velocities show variations with periods larger than 1 min, but no clear bipolar feature appears in any component of the electron velocity during MM2, indicating that the bipolar j_N is mainly determined by V_iN.

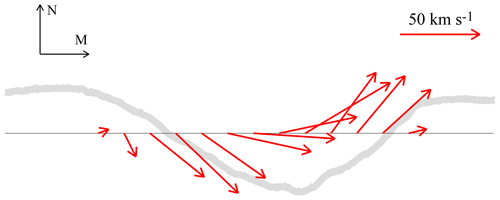
To look at the variations of the ion flow in MM2, we assume that the ion velocity observed during MM2 consists of V_{i_a} and V_{i_md}, where V_{i_a} is the ambient ion velocity and V_{i_md} is the ion velocity inside MM2 relative to the ambient flow. The average velocity 30 s before and after MM2 is selected to be regarded as V_{i_a} with a value of (−2.6, 51.4, 33.4) km s⁻¹ in LMN. Figure 5 shows the deflection of V_{i_md} in the M–N plane. The arrows indicate the direction of the ion velocity, and their lengths indicate the magnitude of V_{i_md} in the M–N plane. The direction of V_{i_md} gradually changes from around −60 to 50^∘ in the M–N plane. Also, the strength of V_{i_md} in this plane gradually increases and then decreases from the left-hand side of the magnetic dip to the right-hand side. In addition, the N component of V_{i_md} changes from negative to positive at just around the center of the structure.

Figure 5 Ion velocities V_{i_md} in the M–N plane during MM2. The arrows indicate the direction of the ion velocities, and their lengths indicate the amplitudes of the ion velocities. The gray line indicates the total magnetic field of MM2.

3 Discussion

Since mirror-mode structures are stationary in the ambient flow, we can estimate the distance of the structures relative to the DF in the Y direction using the average V_Y∼30 km s⁻¹ during the structures. Thus, they are likely to occur dawnside of the MMS spacecraft, with a distance of ∼4 R_E in the Y direction when the spacecraft are crossing the DF at around 20:38 UT. Comparing this distance with the typical size of the DF (∼3 R_E) (Huang et al., 2015a) and the size of the magnetic dips in Fig. 1, the mirror-mode structures might come from the dawnside flank of the DF. Since the DF is considered to be a tangential discontinuity (Schmid et al., 2019) which pushes the background plasma to its flanks (Fu et al., 2012a, b; Liu et al., 2013; Birn et al., 2015), the plasma near the flank is expected to come from the pressure pileup region ahead of DFs. In addition, mirror-mode structures have been reported to be potentially generated in such a pressure pileup region (Zieger et al., 2011; Wang et al., 2016). Thus, the mirror-mode structures in Fig. 1 might originate from the pressure pileup region ahead of the DF.

Based on Ampère's law, there should exist a current in the magnetic dip to sustain the structure's stability (see Constantinescu, 2002). Figures 3 and 4 show that a bipolar current density is observed in both MM1 and MM2. B_L changes ∼5 nT in MM1 between 20:52:30 and 20:52:56 UT, and half of the estimated length of MM1 is 2.05×10³ km in the cross section. Assuming that B_M and B_N are 0 and that B_L changes just along the trajectory of MMS, a current density j_B with a value of ∼2 nA m⁻² in the cross section is necessary to be self-consistent with the magnetic field depression. The amplitude of the bipolar j_N is ∼2 nA m⁻² between 20:52:30 and 20:52:56 UT, almost equal to j_B, indicating that MM1 is a stable structure (Constantinescu, 2002). Similarly, MM2 is also a stable structure.

Significant changes can be found in electron velocities in MM1, while the three components of the ion velocity are almost constant. Therefore, the current density in MM1 is mainly contributed by electrons. The amplitude of the bipolar electron velocity in V_eN is ∼40 km s⁻¹ (see Fig. 3). Three kinds of the electron drift motions are expected to create the current density, i.e., the magnetic gradient drift, the magnetic curvature drift, and the diamagnetic drift. The electron perpendicular thermal pressure P_e⊥ changes ∼0.002 nPa in MM1, the average electron number density is ∼0.4 cm⁻³, and the average total magnetic field is ∼3 nT. Consequently, the estimated electron diamagnetic drift velocity is ∼4 km s⁻¹, much smaller than the amplitude of the bipolar V_eN. The peak of the bipolar V_eN occurs in the time interval between 20:52:40 and 20:52:50 UT, during which there are no significant magnetic field fluctuations. We select this time interval to estimate the velocities of the magnetic gradient and curvature drifts. The total magnetic field changes ∼1.1 nT, and the median total magnetic field is ∼2.2 nT in this interval. The median electron perpendicular and parallel temperatures are ∼680 and 650 eV. The length scale of MM1 is $\sim \mathrm{4.1}\times {\mathrm{10}}^{\mathrm{3}}$ km in the M–N plane and its duration is ∼61 s; thus, the length for the time interval between 20:52:40 and 20:52:50 UT is ∼680 km. Using the data from all four MMS satellites, we can determine the curvature of MM1 by

$$\begin{array}{}\text{(2)}& {\mathit{\rho }}_{cj}=B^{-\mathrm{2}}{B}_{\mathrm{i}}{\mathrm{\nabla }}_{\mathrm{i}}{B}_j-B^{-\mathrm{4}}{B}_j{B}_{\mathrm{i}}{B}_l{\mathrm{\nabla }}_{\mathrm{i}}{B}_l,\end{array}$$

where the indices i, j, and l indicate the three components of the magnetic field, and $B=\left|B\right|$ (Shen et al., 2003). The curvature radius R_C is 1∕ρ_c. Before performing the calculation, the magnetic field data have been low-pass filtered with a cutoff period of 1 s to reduce the effect of the high-frequency noise. The median R_C in this interval is 1.1×10³ km. Thus, the velocities of the electron magnetic gradient and curvature drifts are ∼209 and 262 km s⁻¹, respectively. Since the magnetic curvature drift in MM1 is in the opposite direction of the magnetic gradient drift, the collective velocity of these two velocities is ∼53 km s⁻¹, which is close to the amplitude of the bipolar V_eN. It suggests that the bipolar electron velocity in MM1 is mainly formed by the electron magnetic gradient and curvature drifts.

The size of MM1 is ∼2.2 ρ_i, and its central magnetic field strength is almost 0. Thus, the ion gyro radius is expected to significantly change within one orbit, and ions would randomly jump between neighboring magnetic dips. These ions are referred to as chaotic particles (Büchner and Zelenyi, 1989), which could be one reason why ions do not seem to contribute to the formation of the current in MM1.

No significant changes occur in the electron velocity in MM2; thus, the bipolar current density is mainly contributed by the variations of the ion velocity (see Fig. 4). The size of MM2 is ∼6.6 ρ_i, larger than that of MM1. The trough of the bipolar V_iN is observed at around 21:02:45 UT; meanwhile, V_iM increases ∼50 km s⁻¹ compared to the ambient flow on the left-hand side of MM2. The amplitude of the bipolar V_iN is ∼50 km s⁻¹, i.e., the ion velocity inside MM2 ∼70 km s⁻¹ relative to the ambient ion flow. The ion perpendicular thermal pressure tends to be larger from the edge of MM2 towards its center (see Fig. 4); therefore, an ion diamagnetic drift is expected to be formed (Baumjohann and Treumann, 1997). We use the data in the time interval between 21:02:30 and 21:02:50 UT to estimate the ion thermal pressure and magnetic gradients. Also, the average ion perpendicular and parallel temperatures, average total magnetic field, and average curvature radius in this interval are used to estimate the velocities of the ion drift motions. Consequently, the velocities of the ion diamagnetic, magnetic gradient, and curvature drift motions are ∼17, 33, and 79 km s⁻¹, respectively. By contrast, the velocities of the electron diamagnetic, magnetic gradient, and curvature drifts are ∼5, 14, and 36 km s⁻¹, since the ion diamagnetic and magnetic curvature drifts move almost in the same direction in the M–N plane, while the ion magnetic gradient drift moves in the opposite direction. Thus, the collective drift velocity is ∼63 km s⁻¹, very close to the ion velocity inside MM2 with a speed of 70 km s⁻¹. Thus, one can expect that the bipolar V_iN in Fig. 4 is the collective behaviors of the ion drift motions in MM2.

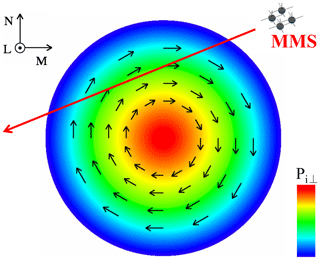
Figure 6 Schematic of MMS1 crossing the magnetic dip in the M–N plane. The colors changing from the center (red) of the magnetic dip to its edge (blue) indicate the decrease in the ion perpendicular thermal pressure as shown by the color bar. The black arrows in the magnetic dip indicate the direction of the ion velocity. The red arrow indicates a possible trajectory of MMS1.

Except for the bipolar V_iN, there is an enhancement of V_iM in MM2. To figure out the variations of V_iM and V_iN in MM2, we analyze the possible trajectory of the MMS spacecraft crossing MM2. Mirror-mode structures in the magnetosheath are found to be cigar-like structures instead of sheets or tubes (Constantinescu et al., 2003; Horbury and Lucek, 2009). To simplify our analysis, we assume that the cross section of MM2 is a circle. To be self-consistent with the magnetic field depression, the ion flow as well as the current are supposed to be clockwise like the black arrows shown in Fig. 6. Based on the normal directions of both half sides of the structure along the spacecraft trajectory and the ambient flow direction, we can get the possible trajectory of the MMS spacecraft in the M–N plane. We calculate the normal directions of the two sides of MM2 by MVA, and the values are (0.03, 0.79, 0.61) and (−0.05, −0.65, 0.76) in LMN for the intervals 21:02:30–21:03 and 21:03:10–21:03:25 UT, respectively. The ratios of the intermediate to minimum eigenvalues λ₂∕λ₃ are 6.4 and 8.5, respectively. The normal directions are almost orthogonal to each other; thus, the maximum length of MM2 in the cross section could be 1.4 times the estimated length (6.6 ρ_i) based on the assumption of a circle. The velocity of the ambient ion flow is (−2.6, 51.4, 33.4) km s⁻¹ in LMN. Thus, a possible trajectory of MMS in the M–N plane can be drawn based on the ambient flow and the above-normal directions like the red arrow shown in Fig. 6. Since the inter-spacecraft distances are very small compared to the scale of MM2, only the possible trajectory of MM1 is shown in Fig. 6. Along the trajectory, V_iN changes from negative to positive from one to another side of MM2, while V_iM is positive, which is in agreement with the deflection of the ion flow shown in Fig. 5. Thus, the variations of V_iM and V_iN are consistent with the prediction of the ion vortex in the cross section. Such a ring-like flow might play an important role in the evolution of the mirror-mode structure or in maintaining the stability of the magnetic dip.

4 Summary

We have studied the ion-scale mirror-mode structures in the plasma sheet on 11 August 2017. We find that a bipolar current density in the magnetic dip with a size of ∼2.2 ρ_i is mainly contributed by an electron bipolar velocity in the cross section. The electron bipolar velocity mainly results from the magnetic gradient and curvature drifts. The chaotic motion of ions might be one significant reason that ions have almost no contribution to the formation of the bipolar current in this magnetic dip. For another magnetic dip with a size of 6.6 ρ_i, the bipolar current is mainly contributed by the ion bipolar velocity, which can be explained by the collective behavior of the ion drift motions. And the variations of the ion velocity in the cross section suggest the potential existence of the ion vortex. We suggest that the scale as well as the magnetic geometry of the magnetic dip are significant for determining the roles of electrons and ions in the formation of the current inside the dip.