the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Hybrid-Vlasov modelling of nightside auroral proton precipitation during southward interplanetary magnetic field conditions
Maxime Grandin
Markus Battarbee
Adnane Osmane
Urs Ganse
Yann Pfau-Kempf
Lucile Turc
Thiago Brito
Tuomas Koskela
Maxime Dubart
Minna Palmroth
Particle precipitation plays a key role in the coupling of the terrestrial magnetosphere and ionosphere by modifying the upper atmospheric conductivity and chemistry, driving field-aligned currents, and producing aurora. Yet quantitative observations of precipitating fluxes are limited, since ground-based instruments can only provide indirect measurements of precipitation, while particle telescopes aboard spacecraft merely enable point-like in situ observations with an inherently coarse time resolution above a given location. Further, orbit timescales generally prevent the analysis of whole events. On the other hand, global magnetospheric simulations can provide estimations of particle precipitation with a global view and higher time resolution. We present the first results of auroral (∼1–30 keV) proton precipitation estimation using the Vlasiator global hybrid-Vlasov model in a noon–midnight meridional plane simulation driven by steady solar wind with a southward interplanetary magnetic field. We first calculate the bounce loss-cone angle value at selected locations in the simulated nightside magnetosphere. Then, using the velocity distribution function representation of the proton population at those selected points, we study the population inside the loss cone. This enables the estimation of differential precipitating number fluxes as would be measured by a particle detector aboard a low-Earth-orbiting (LEO) spacecraft. The obtained differential flux values are in agreement with a well-established empirical model in the midnight sector, as are the integral energy flux and mean precipitating energy. We discuss the time evolution of the precipitation parameters derived in this manner in the global context of nightside magnetospheric activity in this simulation, and we find in particular that precipitation bursts of <1 min duration can be self-consistently and unambiguously associated with dipolarising flux bundles generated by tail reconnection. We also find that the transition region seems to partly regulate the transmission of precipitating protons to the inner magnetosphere, suggesting that it has an active role in regulating ionospheric precipitation.
- Article
(4972 KB) - Full-text XML
-
Supplement
(30534 KB) - BibTeX
- EndNote
The terrestrial atmosphere and ionosphere are known to be affected by the precipitation of particles coming from the magnetosphere and the solar wind. Precipitating protons in the kiloelectron volt energy range produce diffuse auroral emission, principally in the auroral oval and in the cusp region (Hardy et al., 1989). Some emission lines are only produced during proton aurora, namely the Hα and Hβ lines (at 656.3 and 486.1 nm, respectively) and the Lyman-α line at 121.7 nm (Lummerzheim et al., 2001). It is hence possible to distinguish the aurora related to proton precipitation from the aurora produced by electron precipitation.
Contrary to precipitating electrons which may be significantly affected by parallel electric fields in the auroral acceleration region (e.g. Lin and Hoffman, 1982), the acceleration (or deceleration) of auroral-energy precipitating protons by parallel electric fields resulting from a field-aligned potential drop is negligible (Liang et al., 2013). This enables a mapping of the proton aurora in the ionosphere to the magnetospheric region from which the particles originate. Frey et al. (2003) used this property to produce evidence of continuous magnetic reconnection at the magnetopause, as a proton aurora spot was observed persisting for several hours in the cusp region.
Within the auroral region, proton precipitation maximises in the pre-midnight sector in terms of total energy flux, but the mean precipitating energy peaks in the evening sector near 18:00 magnetic local time (MLT), where it can exceed 20 keV (Galand et al., 2001). The most common form of nightside proton aurora is a diffuse arc equatorwards from the electron aurora in the pre-midnight sector (Hardy et al., 1989). In addition, Nomura et al. (2016) have presented recent observations of pulsating proton aurora patches in the evening sector.
On the nightside, precipitating protons mostly originate from the central plasma sheet (e.g. Eather, 1967; Gilson et al., 2012; Spanswick et al., 2017). Proton precipitation is most commonly associated to two mechanisms. First, pitch-angle scattering into the bounce loss cone can take place in regions where the magnetic field curvature radius Rc is within the same order of magnitude as the gyroradius rL of particles, as can be seen near the neutral sheet (Tsyganenko, 1982; Sergeev and Tsyganenko, 1982). This criterion has been formalised as , with (Sergeev et al., 1983). Second, loss-cone scattering of protons can be due to wave–particle interactions. Electromagnetic ion cyclotron (EMIC) waves are the prime candidate for such interactions (e.g. Erlandson and Ukhorskiy, 2001; Sakaguchi et al., 2008; Popova et al., 2018), but more recently, Xiao et al. (2014) suggested that fast magnetosonic waves, also known as equatorial noise, might interact with protons across a broad range of magnetic local times. It has been found, for instance, that the pulsating proton aurora can be produced by non-linear interactions with EMIC waves, which appear as Pc1 pulsations in ground-based magnetometers (Ozaki et al., 2016). On the dayside, it has been found that proton aurora flashes can be observed equatorwards from the cusp in relation to EMIC waves associated with plasma pressure pulses in the magnetosphere (Yahnina et al., 2008). More generally, EMIC waves can be responsible for auroral proton precipitation equatorwards of the proton oval, forming long-lasting spots, arcs and flashes (Yahnin et al., 2018). Besides pitch-angle scattering associated with the κ parameter and with EMIC waves, protons may precipitate because of configurational changes and magnetic reconnection (Mende et al., 2002).
Observations of proton precipitation can be achieved from space using particle detectors aboard spacecraft or from the ground using optical instruments or radars. Low-Earth-orbiting (LEO) satellites comprising particle detectors, such as those of the Defense Meteorological Satellite Programme (DMSP) or NOAA 6, have been gathering electron and proton data in the kiloelectron volt energy range for several decades (Galand, 2001). Other spacecraft, such as the NASA Thermosphere Ionosphere Mesosphere Energetics and Dynamics (TIMED) or Imager for Magnetosphere-to-Aurora Global Exploration (IMAGE), have been measuring auroral emission from space, in particular the hydrogen lines in the ultraviolet range (e.g. Zhang et al., 2005; Frey et al., 2002; Hubert et al., 2003).
From the ground, optical instruments such as meridian-scanning photometers or all-sky imagers can be used to monitor proton precipitation by measuring the auroral emission at the hydrogen lines. Recently, two Forty-Eight Sixty-One (FESO) meridian-scanning photometers, designed to observe the second hydrogen Balmer line (486.1 nm), have been deployed in Canada to provide observations of the proton aurora with enhanced sensitivity and sample rates (Unick et al., 2017). Ground-based optical instruments can be used in conjunction with satellite observations (e.g. Donovan et al., 2008). Besides this, since energetic proton precipitation produces ionisation enhancements in the E region of the ionosphere, ionospheric radars such as incoherent scatter radars can provide indirect observations of proton precipitation (e.g. Lyons et al., 2010).
In numerical studies, two aspects of proton precipitation can be distinguished. First, empirical models describing precipitation fluxes and locations have been developed. One example of these is the Hardy model (Hardy et al., 1989, 1991), which provides the average precipitation patterns as a function of the Kp index obtained by compiling 2 years of DMSP spacecraft data. This statistical model describes proton precipitation in a spatial grid containing 30 bins in corrected geomagnetic latitudes above 50∘ and 48 bins in MLT at seven levels of geomagnetic activity, from Kp=0 to . The model gives the proton precipitation differential number flux in the 20 DMSP energy channels (from 30 eV to 30 keV with regular spacing in the logarithmic scale) as well as the integral number flux, the integral energy flux and the mean precipitating energy. The Hardy model has been used as an input in a number of ionospheric models, e.g. TRANSCAR and IPIM (Blelly et al., 2005; Marchaudon and Blelly, 2015). More recently, the OVATION Prime model (Newell et al., 2014), derived from a combination of DMSP particle data and global ultraviolet imager (GUVI) data from the TIMED spacecraft, has been developed and includes proton precipitation. However, due to the lack of DMSP satellites orbiting in the post-midnight sector, the MLT sectors comprised between 00:15 and 03:30 MLT are described using a linear interpolation.
Second, models based on first principles focus essentially on ionospheric effects of precipitating ions, such as the linear transport model described in Basu et al. (2001). In such approaches, precipitating fluxes are taken as model inputs, and the transport code provides ion production rates and auroral emission intensity profiles in the ionosphere. From a magnetospheric point of view, while simulations of electron precipitation have been achieved with various models (e.g. Palmroth et al., 2006; Raeder et al., 2008), attempts to model proton precipitation are scarce. A few magnetohydrodynamics (MHD) models have addressed the issue of relating particle precipitation characteristics to the magnetotail dynamics (see below; Gilson et al., 2012; Ge et al., 2012); however, currently no global kinetic simulations of the near-Earth environment have undertaken this task.
One obvious aspect through which proton precipitation and magnetotail dynamics can be tied is the relationship between auroral streamers and bursty bulk flows (BBFs). Bursty bulk flows are fast plasma flows propagating in the magnetotail along the Sun–Earth direction, either earthwards or away from the Earth (Angelopoulos et al., 1992, 1994). They are also characterised by an enhanced Bz (northward component of magnetic field) and reduced plasma pressure (e.g. Ohtani et al., 2004). A given BBF may embed several dipolarising flux bundles (DFBs), which are themselves coherent magnetic structures exhibiting a Bz increase of up to a few tens of nanoteslas (Liu et al., 2013), and may play a role in particle energisation in the magnetotail (Runov et al., 2017). Auroral streamers are thin auroral structures oriented in the north–south direction (e.g. Nishimura et al., 2011). They have been associated with BBFs based on observational evidence combining spacecraft data with a ground-based auroral imager, a magnetometer and coherent scatter radar data (e.g. Fairfield et al., 1999; Nakamura et al., 2001a, b; Amm and Kauristie, 2002; Sergeev et al., 2004; Gallardo-Lacourt et al., 2014). Regarding modelling aspects, Ge et al. (2012) reproduced proton precipitation enhancements associated with approaching BBFs with a global MHD model and found good agreement with spacecraft and ground-based auroral observations.
In this paper, we present an overview of nightside proton precipitation in a global magnetospheric hybrid-Vlasov simulation under southward interplanetary magnetic field (IMF) conditions, using the Vlasiator model (von Alfthan et al., 2014; Palmroth et al., 2018). Contrary to previous work in which the main focus was on the ionosphere, we look here at precipitation from the perspective of the magnetosphere and unambiguously tie the precipitation characteristics to the self-consistent simulation results. In particular, following the study by Juusola et al. (2018a) investigating flow bursts inside of a BBF in the same Vlasiator run, we examine how proton precipitation can be related to dipolarising flux bundles. Section 2 describes the Vlasiator model as well as the methods developed to estimate proton precipitation from its outputs. Section 3 presents the results of the study, i.e. the features of nightside proton precipitation in the simulation under a southward IMF. Section 4 discusses those results, and Sect. 5 summarises the main conclusions.
2.1 Vlasiator
This study relies on numerical simulations using Vlasiator, a global hybrid-Vlasov model of the near-Earth plasma environment (von Alfthan et al., 2014; Palmroth et al., 2018). In the hybrid-Vlasov approach, protons are described as velocity distribution functions (VDFs) in a grid of the phase space (ordinary space and velocity space), whereas electrons are treated as a massless, charge-neutralising fluid. The time evolution of the VDFs is obtained by solving the Vlasov equation and closure of the system is achieved with Ohm's law including the Hall term (Palmroth et al., 2018).
The simulation run used in this study is a 2D–3V (two-dimensional in ordinary space and three-dimensional in velocity space) simulation in the noon–midnight meridional plane of the magnetosphere, i.e. xz in the geocentric solar magnetospheric (GSM) coordinate system. The origin of the simulation domain is set in the Earth's centre. The simulation box in ordinary space spans from (Earth radii; 1RE=6371 km) on the nightside to on the dayside and is comprised between boundaries at in the north–south direction, with a grid resolution of 300 km. The inner boundary of the magnetospheric domain lies at ∼4.7RE from the centre of the Earth. In each cell of the ordinary space, a velocity grid extends between −4020 km s−1 and 4020 km s−1 with a resolution of 30 km s−1 in Vx, Vy and Vz. A sparsity threshold is implemented in Vlasiator, below which phase-space density values are discarded to limit the computational load of the simulation. In the run used in this study, the sparsity threshold is set to 10−15 m−6 s3.
The near-Earth environment is driven by incoming solar wind from the +x wall of the simulation domain. The solar wind population consists of protons characterised by Maxwellian VDFs with a number density of 1 cm−3, a temperature of 500 kK, a bulk velocity of −750 km s−1 along the x axis and a dynamic pressure of about 0.9 nPa, carrying a purely southward IMF with a magnitude of 5 nT. Other boundary conditions are as follows: the von Neumann condition for the −x and ±z walls and periodic conditions in the out-of-plane direction (±y), and the inner boundary is a perfectly conducting cylinder with a static Maxwellian VDF for protons. Finally, the geomagnetic field is given by a 2-D line dipole along the z axis, centred at the origin and scaled to obtain a realistic magnetopause stand-off distance (Daldorff et al., 2014).
In the solar wind, the ion inertial length is λp=228 km, and the proton Larmor radius is rL=214 km. A dedicated study by Pfau-Kempf et al. (2018) showed that the ordinary space resolution of 300 km is enough to resolve most of the proton kinetics in such conditions. Besides this, the Alfvén speed is VA=109 km s−1, which is significantly greater than the velocity space resolution of 30 km s−1. Similarly, the ordinary space and velocity space resolutions are enough to resolve the ion kinetics in the transition region between stretched and dipole-like magnetic field lines in the magnetotail, where λp=906 km, rL=681 km and VA=1596 km s−1.
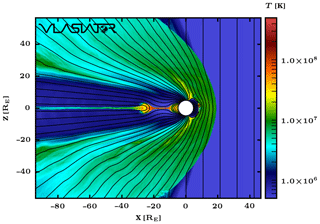
Figure 1Simulated plasma temperature in the entire simulation domain at t=1800 s. The white area corresponds to near-Earth space located inside the inner boundary at 4.7 RE. Black lines represent magnetic field lines.
Figure 1 gives an overview of the simulated area at a time step (t=1800 s) when nightside reconnection takes place. The plotted parameter is the plasma temperature, and the black lines correspond to magnetic field lines. The incoming solar wind at 500 kK with a southward IMF can be seen on the right-hand side of the figure, and the major geospace regions (bow shock, magnetosheath, dayside magnetopause, polar cusps, magnetotail lobes and plasma sheet) can be identified. A plasmoid is forming in the nightside magnetosphere (Palmroth et al., 2017), whose signature is visible between and . Juusola et al. (2018b) studied the plasma sheet during this same run and evaluated its thickness to lie essentially within 0.1–0.2 RE (i.e. just a few simulation cells) in the region of interest for our study ().
This simulation run was previously used in several studies focusing on various phenomena and regions in the near-Earth space, such as dayside magnetopause reconnection (Hoilijoki et al., 2017), ion acceleration in the magnetosheath (Jarvinen et al., 2018), magnetotail reconnection (Palmroth et al., 2017; Juusola et al., 2018a) and magnetotail current-sheet flapping (Juusola et al., 2018b). In each of these studies, the presented results showed good correspondence with earlier findings. Here, this run will be used to characterise nightside auroral proton precipitation in the simulation by making use of the VDF description of the proton population.
2.2 Precipitation spectra calculation
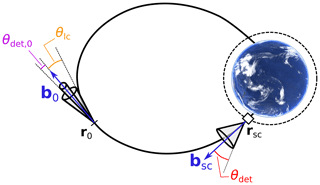
Figure 2 illustrates the definitions of angles and vectors used in this section. The configuration is shown for particles precipitating in the Southern Hemisphere to be consistent with the results shown in the rest of the paper. For particles precipitating in the Northern Hemisphere, the configuration is symmetrical.
At a given three-dimensional location r of the ordinary space, the differential intensity 𝒥 (more generally called directional differential flux) of protons at energy E for the direction along unit vector u is related to the velocity distribution function f by (Eq. 6.47 in Baumjohann and Treumann, 1997)
where mp is the proton mass and is the velocity magnitude. 𝒥, when expressed in SI units, is given in particles per square metre per second per steradian per joule.
Particle detectors aboard spacecraft estimate 𝒥 by taking the average of the incoming particle flux in a given energy channel over the detector's surface Sdet and viewing angle Ωdet, which can be written as
where u′ is the unit vector of a given velocity direction inside Ωdet, ndet is the unit vector normal to the detector's surface and rsc is the location of the spacecraft, for instance near the top of the ionosphere. Strictly speaking, is a differential intensity measured within a fixed solid angle and detector area. In practice, telescopes aboard spacecraft generally collect particles within a cone with an opening angle θdet of the order of 15∘ (e.g. Rodger et al., 2010). Assuming that the directional differential flux is uniform over the detector's surface and that ndet is aligned with the local geomagnetic field direction bsc (i.e. the telescope measures precipitating particles), and expressing the velocity distribution function in spherical coordinates in the local magnetic frame, one gets
or, by defining μ=cos θ,
with μdet=cos θdet. In the symmetrical configuration where the spacecraft observes precipitating particles in the Northern Hemisphere, ndet is aligned with −bsc, but angle definitions remain the same.
As a first-order approximation, protons remain attached to a given magnetic flux tube; one can hence trace particles backwards in time out to the magnetosphere, following magnetic field lines. Assuming smooth quasi-linear propagation, for a given particle of pitch angle θ, the quantity sin 2θ∕B is conserved along the trajectory. Let r0 be a location in the magnetosphere mapping to the spacecraft in terms of magnetic field topology. For particles travelling between r0 and rsc, we have
where B0 and θ0 correspond to the magnetic field magnitude and the particle pitch angle at r0, respectively, and Bsc and θ correspond to the same parameters at rsc. This can also be written as
with μ0=cos θ0. By differentiating Eq. (6), one gets
According to Liouville's theorem, is conserved along the trajectories of the system, i.e. in the absence of potential fields:
Using Eq. (8), and then Eqs. (6) and (7), yields, from Eq. (4),
where b0 is the unit vector with the direction of the local magnetic field at r0, and
In other words, the directional differential particle flux observed by the telescope aboard the spacecraft can be estimated by averaging the relevant subset of the particle VDF at a chosen conjugate location in the magnetosphere. The angular boundaries of the averaged phase-space domain are obtained by scaling the viewing angle of the detector to based on the ratio of magnetic field magnitudes at the spacecraft and at the conjugate location in the magnetosphere where the VDF is analysed (see Eq. 10).
For particles located at r0 to reach a spacecraft at the top of the ionosphere at ∼800 km altitude, their pitch angles must be within the bounce loss cone, whose opening angle is determined by
In the undisturbed nightside equatorial plane, θlc takes values of a few degrees at most and is smaller than 1∘ beyond 10 RE (see, e.g. Sergeev and Tsyganenko, 1982). In the presence of a rather large dipolarisation front with, for example, nT, assuming a mapping to auroral latitudes (Bsc∼53 000 nT), as in Eq. (11), gives . In Vlasiator, knowing the VDF at a given location in the magnetosphere, one can calculate the bounce loss-cone angle value and, at a given velocity magnitude v (i.e. at a given energy), average the phase-space density inside the loss cone to evaluate . It should be noted that, with this approach, the obtained directional differential precipitating flux corresponds to the differential flux which would be measured by a telescope aboard a spacecraft at the topside ionosphere with a viewing angle Ωdet=2π sr (see Eq. 2).
In practice, the methodology to estimate differential precipitating proton fluxes at r0 is as follows. First, the loss-cone angle θlc is calculated. This is achieved by following the magnetic field line from r0 to the inner boundary of the simulation domain, at about 4.7 RE, and then extrapolating the magnetic field to the top of the ionosphere using the line dipole approximation. The ratio of the magnetic field magnitudes at r0 and at the mapped region in the topside ionosphere enables the calculation of the bounce loss-cone angle using Eq. (11). Second, we estimate the differential precipitating flux by calculating
where is the average value of the phase-space density at speed v inside the bounce loss cone. This approximation of Eq. (9) is reasonable, since θ0 is very small, and hence we have inside the integral.
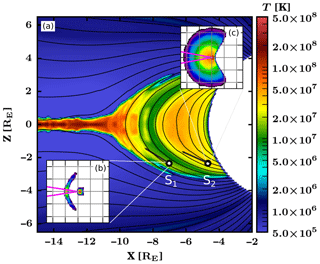
Figure 3(a) Simulated plasma temperature in the nightside magnetosphere at t=1800 s. The Sun is located beyond the right boundary of the figure. The two black circles filled with white are virtual spacecraft S1 and S2. The arrows indicate the magnetic field directions at S1 and S2. (b) Velocity distribution function of protons at S1 in the (vB, vB×V) plane. The grid spacing is 1000 km s−1. The magenta lines indicate the boundaries of the bounce loss cone. (c) Same for protons at S2.
2.3 Examples of differential precipitating proton fluxes with Vlasiator
In the simulation used in this study, full velocity distributions of protons are saved every 50 simulation cells in the x and z directions due to limitations in the file sizes. Therefore, the estimation of the differential precipitating proton flux based on Eq. (12) can be applied only in a few selected locations in the nightside magnetosphere. Figure 3 shows examples of velocity distributions observed at two virtual spacecraft S1 and S2 that are used in this study. Figure 3a shows the proton temperature in the nightside part of the noon–midnight plane at time step t=1800 s, with magnetic field lines drawn in black. It should be stressed that this temperature is that of the isotropic plasma which would have the same total pressure as the simulated distribution; thus it does not represent the temperature of the bulk plasma but rather the measured effect of combined bulk plasma and potential fast additional flows. The effect of such a combination can be seen near S1, as a stream of hot (T≈20 MK) plasma coming from the transition region reaches the virtual spacecraft, leading to a local enhancement of the proton temperature compared to its background value at S1. The white area corresponds to the region of the geospace located earthwards from the inner boundary at ∼4.7RE. Black arrows indicate the magnetic field direction at the virtual spacecraft. Figure 3b and c show slices of the velocity distributions at S1 and S2, respectively, in the plane defined by the local magnetic field direction vB and the local electric field direction vB×V (approximately aligned with the y direction, i.e. into the simulation plane). The grid spacing is 1000 km s−1. The velocity distribution at S1 consists of a core population centred near the origin and a crescent-shaped beam at about 1000 km s−1. It corresponds to the superposition of cold plasma with a low bulk velocity in the magnetic field direction with a more energetic population travelling earthwards. The velocity distribution at S2 is nearly Maxwellian, with a broad loss cone in the magnetic field direction (this loss cone will be discussed below). The width of the distribution, centred near the origin, indicates that it corresponds to hotter plasma (in comparison with the one at S1) nearly at rest in the local magnetic frame, with protons having velocities up to about 2000 km s−1. The imposed static Maxwellian VDF at the inner boundary can affect the neighbouring cells through the calculation of translation and acceleration terms in the Vlasov equation, but such effects vanish rapidly with distance to the boundary, and the plasma at S2 is unlikely to be affected by the boundary condition.
The contrast between the velocity distributions at S1 and S2 is reflected in the plasma temperature, which is 15 MK at S1 and 32 MK at S2. In Fig. 3b and c, the bounce loss cone is indicated with pink lines. As can be seen in the two examples, the loss cone is not empty, and hence a directional differential flux of precipitating protons can be derived using Eq. (12). We note that the empty part of the phase space in Fig. 3c is due to the presence of the inner boundary. Indeed, the inner boundary absorbs incoming protons, and particles bouncing back from a mirror point earthwards from the inner boundary in the Southern Hemisphere are therefore absent at virtual spacecraft S2 in the simulation. This feature does not have consequences in our study, since the relevant part of the velocity distribution function is the one located inside the bounce loss cone.
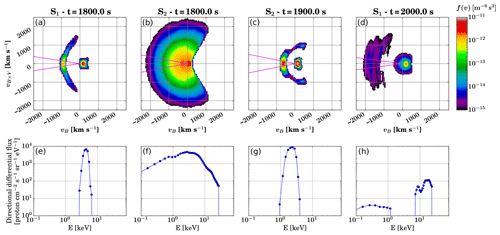
Figure 4(a, b, c, d) Examples of proton velocity distribution slices in the local magnetic frame at virtual spacecraft S1 and S2 at various time steps of the simulation. The bounce loss cone is shown with magenta lines. (e, f, g, h) Corresponding directional differential precipitating fluxes obtained with the presented method.
Figure 4 shows four examples of velocity distributions at virtual spacecraft S1 and S2 during the simulation run (Fig. 4a–d) and the associated precipitating proton differential fluxes obtained using the method described in Sect. 2.2 (Fig. 4e–h). The velocity distributions are slices in the plane defined by the magnetic field direction, vB, and the electric field direction, vB×V. Figure 4a and b are the distributions at t=1800.0 s at virtual spacecraft S1 and S2, respectively, shown in Fig. 3. The crescent-shaped beam partly in the bounce loss cone shown in Fig. 4a is associated with a precipitating differential flux narrow in energies (Fig. 4e), peaking at around 4–5 keV with values close to 104 proton cm−2 s−1 sr−1 eV−1. Although this distribution is intrinsically unstable, the development of instabilities (magnetosonic, ion–ion left-hand and firehose) requires the conditions that the field-aligned drift velocity V0 of the protons be greater than the Alfvén speed VA and that the ratio between beam (nb) and core (nc) densities be “very small” (Gary, 1991). While the distribution shown in Fig. 4a has , it exhibits V0∼1000 and VA=4379 km s−1. Since the criterion on velocities is not verified, we do not expect that the instabilities listed above can grow fast enough to significantly affect the ion distributions on the timescale needed for precipitating protons (i.e. essentially the field-aligned beam) to reach the inner boundary or even the ionosphere.
In contrast with the distribution with a crescent-shaped beam shown in Fig. 4a, the hot, nearly Maxwellian velocity distribution inside the loss cone at S2 (Fig. 4b) is associated to a broad precipitation spectrum (Fig. 4f), with energies of precipitating protons ranging from below 100 eV to nearly 30 keV. The peak differential flux values are of the order of 4000 proton cm−2 s−1 sr−1 eV−1, at energies of 2–5 keV. The sharp cut-off taking place at ∼25 keV in Fig. 4f is due to the sparsity threshold, set to 10−15 m−6 s3 in this run, hence corresponding to the lower limit of the colour axis in Fig. 4a–d. Figure 4c shows a velocity distribution relatively similar to Fig. 4a but was obtained at virtual spacecraft S2 with a delay of 100 s, indicating that the region with narrow-beam precipitation moved earthwards. The corresponding differential flux in Fig. 4g is centred around 2–3 keV, i.e. slightly lower than in Fig. 4e, while peak flux values are almost the same, with nearly 104 proton cm−2 s−1 sr−1 eV−1. The last velocity distribution, in Fig. 4d, was taken at S1 200 s after the one from Fig. 4a. The core population is broader and is partly inside the bounce loss cone, leading to a low flux of low-energy (0.1–1 keV) proton precipitation, as can be seen in Fig. 4h. A beam of low phase-space density with a complex structure partly fills the loss cone at velocities of 1300–2100 km s−1, which is shown in the precipitating spectrum as two peaks, at about 8 and 15 keV, with flux values 2 orders of magnitude lower than in Fig. 4a. These four selected examples suggest that at virtual spacecraft S1 and S2, one can observe a variety of precipitating fluxes during the Vlasiator simulation. If compared to observations, these differential fluxes are within the same order of magnitude as the NOAA 6 proton energy spectra shown in Basu et al. (2001) in terms of peak energy (1–10 keV) and slightly higher in terms of flux values (102–103 cm−2 s−1 sr−1 eV−1). Observations from the DMSP 12 spacecraft reported in Lummerzheim et al. (2001) indicate mean precipitating energy of the order of 10 keV and flux values around 103 cm−2 s−1 sr−1 eV−1. These values were, however, obtained in the evening MLT sector, where proton precipitation exhibits statistically harder energy spectra than in the midnight sector (Galand et al., 2001).
One assumption which is made during the derivation of the precipitating fluxes is that there are no field-aligned electric fields in the system (see Eq. 8). Figure S1 in the Supplement shows the parallel component of the electric field at the same time step and with a similar format to Fig. 3. This parallel component was averaged over 120 s, which corresponds roughly to one bounce period for 10 keV protons at L=9 (virtual spacecraft S1). It can be seen that the parallel electric field between S1 or S2 and the inner boundary is of the order of 0.01 to 0.1 mV m−1. When integrated along the field line between S1 and the inner boundary, this corresponds to a potential difference of the order of 1 kV. In their discussion of the effect of potential drops in the auroral acceleration region on precipitating protons, Liang et al. (2013) estimate that for ions with energies ≫1 keV the acceleration resulting from typical potential drops in the auroral acceleration region (∼1 kV up to ∼4 kV occasionally) can be neglected, which enables a reasonable mapping of auroral latitudes to the central plasma sheet. It therefore seems acceptable to neglect the effect of parallel electric fields when deriving the precipitating proton fluxes with the method described in Sect. 2.2. Furthermore, given the location of S1 and S2 on closed field lines which are being convected earthwards, there is no risk that the precipitating protons observed at S1 (or S2) are affected by processes such as magnetic reconnection before they reach the ionosphere.
3.1 Nightside proton precipitation
An overview of the dynamics of the nightside magnetosphere from t=1000 s until the end of the simulation at t=2150 s is provided with Animation S1 in the Supplement. Figure 5 shows the time evolution of the proton precipitation at virtual spacecraft S1 and S2 during this time interval. Figure 5a and b show the precipitating proton differential flux (colour scale) as well as the mean precipitating energy (black line) as a function of time, while Fig. 5c and d show the integral energy flux. It can be seen that, at virtual spacecraft S1, broad-energy proton precipitation above 1 keV starts at around t=1360 s, as the magnetic field line observed by S1 becomes slightly stretched. The energetic tail of the proton precipitation spectrum reaches up to 20 keV, and the mean precipitating energy fluctuates between 2 and 5 keV until t≈1750 s, i.e. about 90 s after the global magnetotail reconfiguration is initiated by the dominant X line near . At around t=1750 s, the precipitation becomes narrower in energy, and after t=1850 s, the mean precipitating energy increases from 4 to 20 keV, while fluxes decrease by almost 2 orders of magnitude. This corresponds to the times during which the nightside reconnection speeds up and S1 observes magnetic field lines becoming more dipolar. Between t=1900 and t=1925 s, S1 does not observe any precipitation, as the virtual spacecraft is momentarily observing lobe-type plasma and the local loss cone is empty, but precipitation resumes with high energy (10–20 keV) and relatively low differential flux values (∼102 cm−2 s−1 sr−1 eV−1) after t=1925 s, as S1 is magnetically connected to the transition region. A low-energy (<1 keV) precipitating population appears between t=1990 and t=2040 s, presumably associated with heating of the core plasma. At the end of the simulation, the precipitating mean energy decreases while differential flux values are enhanced to ∼103 cm−2 s−1 sr−1 eV−1. The integral energy flux remains within 1–6×107 keV cm−2 s−1 sr−1 during the broad-energy precipitation phase but then drops between 106 and 107 keV cm−2 s−1 sr−1 during the phase when field lines passing by S1 become dipolar (t=1800–1900 s). When precipitation observations from S1 resume (t≈1930 s), the integral energy flux remains close to 107 keV cm−2 s−1 sr−1 before briefly increasing to reach 108 keV cm−2 s−1 sr−1 and abruptly decreasing around 106 keV cm−2 s−1 sr−1 until the end of the simulation. Those integral energy flux values are in agreement with the Hardy model, according to which the nightside maximum total energy flux ranges between about 4×107 and 2×108 keV cm−2 s−1 sr−1, depending on the Kp index value (Hardy et al., 1989).
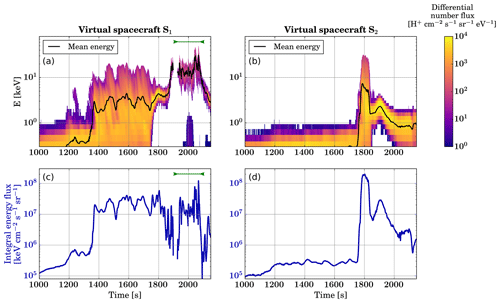
Figure 5(a) Differential number flux of precipitating protons observed at virtual spacecraft S1 as a function of time during the simulation. The black line indicates the mean precipitating energy as a function of time. (b) Same but at virtual spacecraft S2. (c) Integral energy flux associated with proton precipitation as a function of time at virtual spacecraft S1.(d) Same but at virtual spacecraft S2. The green segments in panels (a) and (c) indicate the time interval with precipitation associated with dipolarising flux bundles presented later.
At virtual spacecraft S2 (Fig. 5b and d), proton precipitation above 1 keV appears at around t=1760 s in the simulation, corresponding roughly to the time when the broad-energy precipitation at S1 becomes narrower in energy. For about 1 min, broad-energy precipitation with up to 30 keV protons and with a mean energy of 6–7 keV is observed, leading to integral flux values reaching 2×108 keV cm−2 s−1 sr−1. The precipitating energy spectrum then becomes narrower and centred around 2 keV (during t=1850–1900 s) and gradually broadens again until the end of the simulation, when the mean precipitating energy decreases below 1 keV.
While the 2-D simulation set-up with a scaled line dipole does not enable a direct mapping of the virtual spacecraft locations in terms of geomagnetic latitudes or even L values, it appears clearly that the properties and the dynamics of proton precipitation are very different at S1 and S2. From the geometry, S1 maps to higher geomagnetic latitudes than S2, and the analysis of Fig. 5 suggests that S1 represents geomagnetic latitudes which usually map to the auroral oval well, while S2 would correspond to slightly lower latitudes where the proton auroral arc can be observed around the onset of ionospheric substorms after drifting equatorwards during the growth phase (Liu et al., 2007). Indeed, precipitation is observed at S1 before the global magnetotail reconfiguration due to reconnection is initiated (around t=1660 s; Palmroth et al., 2017), which suggests that S1 maps to geomagnetic latitudes where the aurora is visible during the growth phase of substorms. On the other hand, proton precipitation is only observed at S2 around the time when the first particles that were accelerated earthwards following the global magnetotail reconfiguration reach the inner magnetosphere.
3.2 Flow bursts and precipitation
In what follows, we will focus on the proton precipitation associated with dipolarising flux bundles by considering virtual spacecraft S1 between t=1920 and t=2080 s. During this time span, S1 is on magnetic field lines mapping to the transition region near , as can be seen in Animation S2 in the Supplement. Juusola et al. (2018a) showed that, during this time period, sustained tail reconnection takes place at a dominant X line drifting from to and is associated with fast earthward flows on the earthward side of the X line.
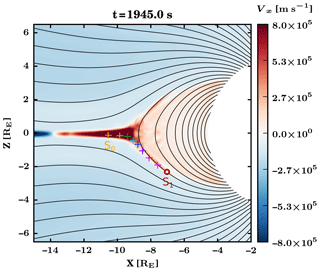
Figure 6x component of the plasma bulk velocity in the nightside part of the simulation plane at t=1945.0 s. The red circle indicates the location of virtual spacecraft S1, and the eight coloured plus signs show additional virtual spacecraft for which the parallel velocity components are shown in Fig. 7. Black lines represent magnetic field lines.
Figure 6 is a snapshot of Animation S2 at t=1945 s. The colour-coded parameter is the x component of the plasma bulk velocity, Vx. The location of virtual spacecraft S1 is indicated with a red and white circle. Eight plus signs of various colours indicate locations of additional virtual spacecraft which will be used in the following to track the field-aligned component of the plasma bulk velocity. These virtual spacecraft are arranged in such a way that one can follow the bulk properties of the plasma between S1 and the current sheet through the transition region. As can be seen in the figure, they are not located on a same field line but rather along the region of positive Vx, which corresponds to the path followed by precipitating protons as field lines are being convected earthwards. Full velocity distributions are not available at those points due to limitations in the file sizes. The spacecraft indicated with an orange plus sign, which is the furthest in the current sheet, will be called S0.
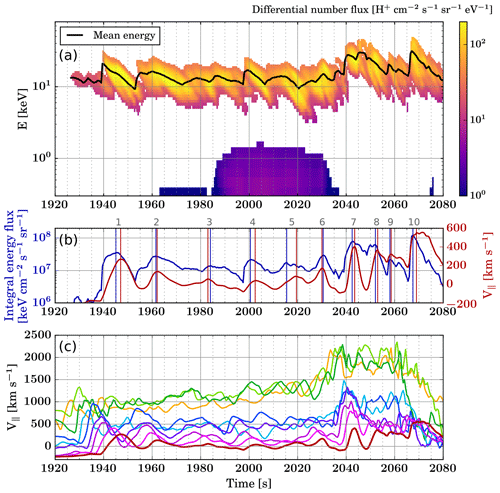
Figure 7(a) Differential number flux of precipitating protons observed at virtual spacecraft S1 between t=1920 and t=2080 s. The black line indicates the mean precipitating energy as a function of time. (b) Blue line: integral energy flux associated with proton precipitation as a function of time at virtual spacecraft S1. Red line: parallel component of the plasma bulk velocity at S1. The vertical lines indicate the times associated with peak values for these two parameters, and the numbers in grey above the panel identify the precipitation bursts discussed in the text. (c) Parallel component of the plasma bulk velocity at S1 and at the virtual spacecraft indicated with plus signs in Fig. 6, with a consistent colour code.
Figure 7 shows the precipitation flux observed at S1 between t=1920 and t=2080 s, corresponding to the time interval marked with a green line in Fig. 5a and c. Figure 7a shows the differential number flux of precipitating protons (colour scale) and the mean precipitating energy (black line). One can visually identify successive bursts of precipitating protons at energies ranging between about 5 and 50 keV. The energy dispersion of precipitating protons is visible, as within a given precipitation burst the highest energies are observed first and the lowest energies are observed last. This is also visible in the time variations of the mean precipitating energy. Between t=1985 and t=2035 s, a low-energy (<1 keV) population of precipitating protons is observed in addition to the ∼10 keV precipitation, but with fluxes lower than the main precipitating population around 10 keV by almost 2 orders of magnitude. The differential flux of the main precipitating proton population at 5–50 keV has values around 102 cm−2 s−1 sr−1 eV−1, which is relatively low compared to flux values at other times in the simulation that can reach 104 cm−2 s−1 sr−1 eV−1 (see Fig. 5a). Figure 7b shows the integral energy flux (blue line) alongside the component of the plasma bulk velocity at S1, parallel to the magnetic field (red line), V∥. Signatures of the precipitation bursts seen in Fig. 7a can be identified in both the integral energy flux and the plasma parallel bulk velocity. This suggests that the parallel bulk velocity can be used as a proxy for precipitating protons in this context.
In Fig. 7c, the time series of the plasma parallel bulk velocity at the virtual spacecraft shown in Fig. 6 are indicated with a colour code consistent with that of the symbols indicating virtual spacecraft locations. The thick red line corresponds to the parallel velocity at S1; i.e. it shows the same data as the red line in Fig. 7b. A given fluctuation in the parallel velocity at S1 can be traced back in time and tailwards by visually identifying its corresponding signature at successive tailward virtual spacecraft. For instance, the parallel velocity enhancement peaking at S1 around t=1947 s is consistent with parallel velocity enhancements visible at each of the virtual spacecraft, from the magenta one which is the closest to S1 until the orange one (S0), which is the deepest in the current sheet, peaking around t=1927 s. This suggests that some dipolarising flux bundles, which are identified through short-lived enhancements in in the current sheet, directly lead to proton precipitation into the ionosphere in the regions mapped to the current sheet. However, not all the V∥ enhancements at S1 can be related to Vx enhancements in the current sheet. For instance, the V∥ peak at S1 around t=2030 s cannot be traced back to a specific V∥ peak at S0.
Table 1Times of peak integral energy flux and plasma bulk parallel velocities at S1 and S0 for the main bursts of proton precipitation. In the last column, an en dash indicates whenever a given precipitation burst observed at S1 could not be traced back to S0.
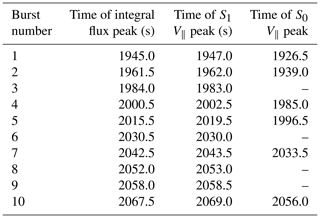
Table 1 gives the peak times of the integral energy flux, plasma bulk parallel velocity at S1 and plasma bulk parallel velocity at S0 for the 10 main precipitating flux enhancements between t=1920 and t=2080 s. These times correspond to those of local maxima of each parameter, as indicated with vertical lines in Fig. 7b for the integral energy flux and the parallel velocity at S1. For the four precipitation bursts observed at S1 which could not be traced back to S0 in the current sheet, the time of the S0 V∥ peak is replaced with an en dash in the last column. In all cases but one, the peak times for the integral energy flux and V∥ at S1 are the same within 2 s; the exception is burst number 5, for which the triple peak in flux is associated with a single broad peak in V∥, with a 4 s difference in the times of local maxima.
In the four cases where a precipitation burst cannot be directly linked to a DFB passing by S0, the signatures are lost between the cyan and blue spacecraft (burst number 3), between the blue and indigo spacecraft (burst number 6), between the indigo and purple spacecraft (burst number 8), and between the light and dark green spacecraft (burst number 9). These virtual spacecraft are located in the transition region, which suggests that the transition region can act like a buffer for DFBs, either directly transmitting them and leading to bursts of precipitating protons or releasing precipitating particles with no direct correlation with an incoming DFB from the tail.
This paper presents the first unambiguous investigations of the global terrestrial magnetic field dynamics and its effects on proton precipitation in the midnight sector using a global hybrid-Vlasov model of the near-Earth environment, Vlasiator. Mende et al. (2002) listed four possible causes for particles to precipitate: (i) injection of particles on closed geomagnetic field lines, (ii) interaction of particles with electric fields, in particular waves, (iii) compression of the magnetic flux tube and (iv) scattering on stretched magnetic field lines. All these causes can be studied using Vlasiator, except for some of the wave–particle interactions, as waves may not all be resolved by the model. It is known that proton precipitation can result from interactions with EMIC waves (Erlandson and Ukhorskiy, 2001; Sakaguchi et al., 2008; Popova et al., 2018) as well as magnetosonic waves (Xiao et al., 2014). While magnetosonic waves are well resolved in Vlasiator, it is unclear whether this is also the case for EMIC waves, as their expected spatial scale is close to the ordinary-space grid resolution in the current runs. Wave–particle interactions are expected to be particularly important in the case of loss-cone scattering of trapped particles, i.e. ring current protons in the case of auroral proton precipitation. In this study, however, the analysis of Fig. 7 suggests that the precipitating protons essentially come from the magnetotail and hence precipitate due to pitch-angle scattering resulting from the small curvature radius of the magnetic field near the neutral sheet (Sergeev and Tsyganenko, 1982). This is confirmed in Fig. S2 provided in Supplement, which shows the value of the κ parameter (see Introduction) along the x axis between −25RE and −6RE as a function of time from t=1000 s until the end of the simulation, as in Fig. 5. At the time of highest precipitating proton fluxes (i.e. after t=1800 s) beyond in the plasma sheet, κ exhibits mostly values below , hence fulfilling the Sergeev et al. (1983) criterion according to which protons get scattered into the loss cone on stretched field lines. While, on the other hand, it would prove interesting to estimate whether there is a non-negligible contribution to this precipitation from wave–particle interactions, this has to be left for a future study.
One limitation coming from the simulation set-up is related to the fact that the simulation run used in this study is two-dimensional in ordinary space, which besides preventing a 3-D description of the tail plasma requires using a line dipole instead of a point dipole for the geomagnetic field. The line dipole is scaled to reproduce a realistic dayside magnetopause stand-off distance, but it implies that geomagnetic field line equations have the form r(θ)=Ccos θ in polar coordinates, with C a constant and θ the latitude, instead of r(θ)=Ccos 2θ, in the case of a point dipole. This means that it is not possible to map L values with geomagnetic latitudes at ionospheric altitudes in this run; hence, we cannot assess how virtual spacecraft S1 and S2 are mapped to the ionosphere in terms of geomagnetic latitude. Such a discussion will be possible once 3D–3V (three-dimensional in ordinary space and three-dimensional in velocity space) Vlasiator runs are available. However, this 2-D set-up still allows us to investigate the connection between tail dynamics, such as dipolarisation fronts, and precipitation.
Despite those limitations, the precipitating proton fluxes (differential number flux and integral energy flux) observed at the two selected locations (virtual spacecraft S1 and S2) are in agreement with predictions from the Hardy model (Hardy et al., 1989, 1991) in the midnight MLT sector and for active geomagnetic conditions (Kp>3). While direct comparison with particle data from spacecraft would be desirable, the fact that DMSP satellites, which are currently the main source of direct precipitating proton observations, are on Sun-synchronous orbits essentially near the dawn–dusk plane does not allow midnight-sector observations. In the nightside magnetosphere, comparison with data from the NASA Magnetospheric Multiscale (MMS) mission would prove interesting, but it is beyond the scope of the present study.
While velocity distributions are not saved in every simulation cell in Vlasiator runs, results suggest that the parallel component of the plasma bulk velocity can be used to at least qualitatively describe the integral energy flux of precipitating protons (see Fig. 7b). The idea that a beam superimposed to the core plasma population could lead to observable effects in the VDF first and second moments (bulk velocity and temperature) was brought forward by Parks et al. (2013), who showed that the apparent slowing down and temperature increase in the solar wind associated with non-linear structures are due to the presence of a beam of particles propagating in opposite direction and with greater energy than the core solar wind population. In our case, precipitating proton beams along the magnetic field direction affect the parallel component of the plasma bulk velocity in an analogous manner. Future work could therefore include deriving a proxy for proton precipitation relying on plasma bulk parameters, which are saved in every simulation cell, to quantitatively estimate the precipitation parameters such as the integral energy flux or mean energy.
In their study of BBF-associated proton precipitation with an MHD model, Ge et al. (2012) found that dipolarisation fronts led to precipitating proton enhancements into the ionosphere, with integral energy fluxes of the order of 0.1 µW m−2. This corresponds to 6×104 keV cm−2 s−1. Assuming a uniform flux along all downwards directions as a rough approximation (2π solid angle), this gives a directional integral energy flux of the order of 104 keV cm−2 s−1 sr−1, which is roughly 3 orders of magnitude below values obtained with Vlasiator when the global magnetotail reconfiguration is taking place (see Fig. 7b). A likely explanation is that the MHD simulation has low ion temperature Ti values compared to our kinetic approach, leading to lower precipitation energy fluxes, as these are proportional to in their approach (see Eq. 1 in Ge et al., 2012). We note that the Vlasiator integral flux values are, on the other hand, in agreement with the test-particle simulation results presented in their companion paper (Zhou et al., 2012b), with integral energy fluxes of 0.2–1 mW m−2 (equivalent to 2×107–108 keV cm−2 s−1 sr−1 with the same reasoning as above) and with statistical patterns shown in Galand et al. (2001) (∼0.1 mW m−2). One strength of evaluating the proton precipitation parameters using a kinetic model is that not only integral energy fluxes but also differential fluxes can be calculated, which may enable more detailed future studies of proton precipitation and its link to global magnetospheric dynamics. Further, a test-particle approach is not fully self-consistent in the sense that the electromagnetic fields affect the particle distributions but not vice versa. Therefore the test-particle approach does not fully describe, for example, dynamics of reconnection-related precipitation.
The examination of precipitation bursts passing by virtual spacecraft S1 between t=1920 and t=2080 s suggests that these bursts are that are associated with dipolarising flux bundles originating from the vicinity of the stable X line in the current sheet. Field-aligned beams of plasma propagating earthwards associated to dipolarisation fronts have been observed and simulated not only in the central plasma sheet but also in the plasma sheet boundary layer (PSBL; Zhou et al., 2012a). In this Vlasiator run, there is unfortunately no cell located in the PSBL where the full VDF is saved at each time step to make a comparison with results from Zhou et al. (2012a); hence we focus on proton precipitation originating from the central plasma sheet. Dipolarisation front signatures in the Bz component of the current-sheet plasma can be identified in Fig. 6 of Juusola et al. (2018a) during the studied time interval (written as t=32:00–34:40 in their figure). While there are not enough precipitation bursts at S1 in the studied time period to carry out a statistical analysis of their properties (integral flux enhancement and parallel velocity enhancement at S1; Vx enhancement at S0), it can be noted that there does not seem to be a one-to-one correlation between the magnitude of the V∥ enhancement at S1 and the possibility to trace it back to S0. This suggests that the transition region, corresponding to the location in the magnetotail where tail-like geomagnetic field lines become more dipolar (near in Fig. 3), plays a role in regulating these bursts. It is known that fast flows associated with BBFs can bounce when reaching the inner magnetosphere (e.g. Ohtani et al., 2009; Juusola et al., 2013; Nakamura et al., 2013) and may even exhibit multiple overshoots and oscillations around their equilibrium position (Panov et al., 2010). Our results further indicate that, contrary to a frequent assumption, the transition region may be more than just a passive mediator between the plasma sheet and the ionosphere. DFBs could perhaps themselves experience some form of bouncing near the transition region, which could explain the regulation of the studied proton precipitation bursts.
Auroral activations concurrent with BBFs have been widely studied (e.g. Nakamura et al., 2001a; Sergeev et al., 2004; Gallardo-Lacourt et al., 2014). However, the timescales that are involved in such processes are of the order of up to 10 min, in contrast to the short-lived DFBs and associated proton precipitation bursts (<1 min duration) studied here. In terms of auroral emissions observed from the ground, it must be noted that the precipitation bursts observed at S1 might actually lead to more weakly modulated emissions than can be inferred from the integral energy flux variations at the virtual spacecraft, as the energy dispersion of precipitating protons tends to smooth the integral energy flux as particles get closer to Earth. This warrants future studies involving ground-based optical observations of the proton aurora at a high enough cadence (a few seconds at most) to investigate whether DFB-related proton aurora signatures can be seen from the ground. If not, this would imply that global ion-kinetic magnetospheric simulations, supplemented by data from spacecraft orbiting in the magnetosphere, might be the only tool to investigate the active role played by the transition region in regulating the precipitation of auroral protons to the nightside ionosphere.
This paper presents the first evaluations of auroral (∼1–30 keV) proton precipitation from a global hybrid-Vlasov magnetospheric model, Vlasiator. The simulation run considered here corresponds to relatively fast solar wind (750 km s−1) with a purely southward IMF of moderate magnitude ( nT).
The evaluation of the differential number flux of precipitating protons at a given location in the nightside magnetosphere is achieved by averaging the velocity distribution function inside the bounce loss cone within energy bins. The integral energy flux of precipitation as well as the mean precipitating energy are also calculated from the differential number flux. The main results of this study can be summarised as follows:
-
From this first case study, we find that Vlasiator reproduces auroral proton precipitation with realistic differential number fluxes and energies when compared to the Hardy model.
-
During a selected time interval when a single X line dominates the tail reconnection in the simulation, proton precipitation observed at a virtual spacecraft in the inner magnetosphere occurs in a bursty manner. In this situation, the integral precipitating energy flux exhibits variations that are mostly similar to the parallel component of the plasma bulk velocity at the virtual spacecraft. This suggests that the integral energy flux can qualitatively be described with the local parallel velocity at locations for which full velocity distributions are not saved in the Vlasiator run.
-
Finally, it is found that proton precipitation bursts can in some cases be traced back to the current sheet and are associated with dipolarising flux bundles. However, not all precipitation bursts correspond to a definite DFB, which suggests that the transition region plays a role in regulating auroral proton precipitation associated with DFBs during BBFs.
Vlasiator (http://www.physics.helsinki.fi/vlasiator/, Palmroth, 2008) is distributed under the GPL-2 open-source license at https://github.com/fmihpc/vlasiator/ (Palmroth and the Vlasiator team, 2019). Vlasiator uses a data structure developed in-house (https://github.com/fmihpc/vlsv/, Sandroos, 2019), which is compatible with the VisIt visualisation software (Childs et al., 2012) using a plugin available at the VLSV repository. The Analysator software, available at https://github.com/fmihpc/analysator/ (Hannuksela and the Vlasiator team, 2019), was used to produce the presented figures. The run described here takes several terabytes of disk space and is kept in storage maintained within the CSC – IT Center for Science. Data presented in this paper can be accessed by following the data policy on the Vlasiator website.
The supplement related to this article is available online at: https://doi.org/10.5194/angeo-37-791-2019-supplement.
MG carried out most of the analysis and prepared the paper. YPK participated in running the simulation and development of the analysis methods. UG and MB participated in the development of the analysis methods. All co-authors helped in the interpretation of the results, read the paper and commented on it.
The authors declare that they have no conflict of interest.
The work of Lucile Turc was supported by a Marie Skłodowska-Curie Individual Fellowship (no. 704681). Maxime Grandin thanks Rami Vainio for useful discussions on the mathematical formulation of the directional differential flux estimation.
This research has been supported by the European Research Council (Starting grant no. 200141-QUESPACE and Consolidator grant no. 682068-PRESTISSIMO), the Academy of Finland, Luonnontieteiden ja Tekniikan Tutkimuksen Toimikunta (grant nos. 267144, 312351 and 309937) and PRACE (grant no. 2014112573 for Tier-0 computing time in HLRS Stuttgart).
Open access funding provided by the Helsinki University Library.
This paper was edited by Anna Milillo and reviewed by Anton Artemyev and one anonymous referee.
Amm, O. and Kauristie, K.: Ionospheric Signatures Of Bursty Bulk Flows, Surv. Geophys., 23, 1–32, https://doi.org/10.1023/A:1014871323023, 2002. a
Angelopoulos, V., Baumjohann, W., Kennel, C. F., Coronti, F. V., Kivelson, M. G., Pellat, R., Walker, R. J., Luehr, H., and Paschmann, G.: Bursty Bulk Flows in the Inner Central Plasma Sheet, J. Geophys. Res., 97, 4027–4039, https://doi.org/10.1029/91JA02701, 1992. a
Angelopoulos, V., Kennel, C. F., Coroniti, F. V., Pellat, R., Kivelson, M. G., Walker, R. J., Russell, C. T., Baumjohann, W., Feldman, W. C., and Gosling, J. T.: Statistical characteristics of bursty bulk flow events, J. Geophys. Res., 99, 21257–21280, https://doi.org/10.1029/94JA01263, 1994. a
Basu, B., Decker, D. T., and Jasperse, J. R.: Proton transport model: A review, J. Geophys. Res., 106, 93–106, https://doi.org/10.1029/2000JA002004, 2001. a, b
Baumjohann, W. and Treumann, R. A.: Basic Space Plasma Physics, World Scientific, Imperial College Press, London, 1997. a
Blelly, P.-L., Lathuillère, C., Emery, B., Lilensten, J., Fontanari, J., and Alcaydé, D.: An extended TRANSCAR model including ionospheric convection: simulation of EISCAT observations using inputs from AMIE, Ann. Geophys., 23, 419–431, https://doi.org/10.5194/angeo-23-419-2005, 2005. a
Childs, H., Brugger, E., Whitlock, B., Meredith, J., Ahern, S., Pugmire, D., Biagas, K., Miller, M., Harrison, C., Weber, G. H., Krishnan, H., Fogal, T., Sanderson, A., Garth, C., Bethel, E. W., Camp, D., Rübel, O., Durant, M., Favre, J. M., and Navrátil, P.: VisIt: An End-User Tool For Visualizing and Analyzing Very Large Data, in: High Performance Visualization-Enabling Extreme-Scale Scientific Insight, Chapman & Hall/CRC, 357–372, 2012.
Daldorff, L. K. S., Tóth, G., Gombosi, T. I., Lapenta, G., Amaya, J., Markidis, S., and Brackbill, J. U.: Two-way coupling of a global Hall magnetohydrodynamics model with a local implicit particle-in-cell model, J. Comput. Phys., 268, 236–254, https://doi.org/10.1016/j.jcp.2014.03.009, 2014. a
Donovan, E., Liu, W., Liang, J., Spanswick, E., Voronkov, I., Connors, M., Syrjäsuo, M., Baker, G., Jackel, B., Trondsen, T., Greffen, M., Angelopoulos, V., Russell, C. T., Mende, S. B., Frey, H. U., Keiling, A., Carlson, C. W., McFadden, J. P., Glassmeier, K. H., Auster, U., Hayashi, K., Sakaguchi, K., Shiokawa, K., Wild, J. A., and Rae, I. J.: Simultaneous THEMIS in situ and auroral observations of a small substorm, Geophys. Res. Lett., 35, L17S18, https://doi.org/10.1029/2008GL033794, 2008. a
Eather, R. H.: Auroral Proton Precipitation and Hydrogen Emissions, Rev. Geophys. Space Phys., 5, 207–285, https://doi.org/10.1029/RG005i003p00207, 1967. a
Erlandson, R. E. and Ukhorskiy, A. J.: Observations of electromagnetic ion cyclotron waves during geomagnetic storms: Wave occurrence and pitch angle scattering, J. Geophys. Res., 106, 3883–3896, https://doi.org/10.1029/2000JA000083, 2001. a
Fairfield, D. H., Mukai, T., Brittnacher, M., Reeves, G. D., Kokubun, S., Parks, G. K., Nagai, T., Matsumoto, H., Hashimoto, K., Gurnett, D. A., and Yamamoto, T.: Earthward flow bursts in the inner magnetotail and their relation to auroral brightenings, AKR intensifications, geosynchronous particle injections and magnetic activity, J. Geophys. Res., 104, 355–370, https://doi.org/10.1029/98JA02661, 1999. a
Frey, H. U., Mende, S. B., Immel, T. J., Fuselier, S. A., Claflin, E. S., Gérard, J. C., and Hubert, B.: Proton aurora in the cusp, J. Geophys. Res.-Space, 107, 1091, https://doi.org/10.1029/2001JA900161, 2002. a
Frey, H. U., Phan, T. D., Fuselier, S. A., and Mende, S. B.: Continuous magnetic reconnection at Earth's magnetopause, Nature, 426, 533–537, https://doi.org/10.1038/nature02084, 2003. a
Galand, M.: Introduction to special section: Proton precipitation into the atmosphere, J. Geophys. Res., 106, 1–6, https://doi.org/10.1029/2000JA002015, 2001. a
Galand, M., Fuller-Rowell, T. J., and Codrescu, M. V.: Response of the upper atmosphere to auroral protons, J. Geophys. Res., 106, 127–140, https://doi.org/10.1029/2000JA002009, 2001. a, b, c
Gallardo-Lacourt, B., Nishimura, Y., Lyons, L. R., Zou, S., Angelopoulos, V., Donovan, E., McWilliams, K. A., Ruohoniemi, J. M., and Nishitani, N.: Coordinated SuperDARN THEMIS ASI observations of mesoscale flow bursts associated with auroral streamers, J. Geophys. Res.-Space, 119, 142–150, https://doi.org/10.1002/2013JA019245, 2014. a, b
Gary, S. P.: Electromagnetic ion/ion instabilities and their consequences in space plasmas: A review, Space Sci. Rev., 56, 373–415, https://doi.org/10.1007/BF00196632, 1991. a
Ge, Y. S., Zhou, X. Z., Liang, J., Raeder, J., Gilson, M. L., Donovan, E., Angelopoulos, V., and Runov, A.: Dipolarization fronts and associated auroral activities: 1. Conjugate observations and perspectives from global MHD simulations, J. Geophys. Res.-Space, 117, A10226, https://doi.org/10.1029/2012JA017676, 2012. a, b, c, d
Gilson, M. L., Raeder, J., Donovan, E., Ge, Y. S., and Kepko, L.: Global simulation of proton precipitation due to field line curvature during substorms, J. Geophys. Res.-Space, 117, A05216, https://doi.org/10.1029/2012JA017562, 2012. a, b
Hannuksela, O. and the Vlasiator team: Analysator: python analysis toolkit, available at: https://github.com/fmihpc/analysator/, last access: 5 September 2019.
Hardy, D. A., Gussenhoven, M. S., and Brautigam, D.: A statistical model of auroral ion precipitation, J. Geophys. Res., 94, 370–392, https://doi.org/10.1029/JA094iA01p00370, 1989. a, b, c, d, e
Hardy, D. A., McNeil, W., Gussenhoven, M. S., and Brautigam, D.: A statistical model of auroral ion precipitation, 2. Functional representation of the average patterns, J. Geophys. Res., 96, 5539–5547, https://doi.org/10.1029/90JA02451, 1991. a, b
Hoilijoki, S., Ganse, U., Pfau-Kempf, Y., Cassak, P. A., Walsh, B. M., Hietala, H., von Alfthan, S., and Palmroth, M.: Reconnection rates and X line motion at the magnetopause: Global 2D-3V hybrid-Vlasov simulation results, J. Geophys. Res.-Space), 122, 2877–2888, https://doi.org/10.1002/2016JA023709, 2017. a
Hubert, B., Gérard, J. C., Fuselier, S. A., and Mende, S. B.: Observation of dayside subauroral proton flashes with the IMAGE-FUV imagers, Geophys. Res. Lett., 30, 1145, https://doi.org/10.1029/2002GL016464, 2003. a
Jarvinen, R., Vainio, R., Palmroth, M., Juusola, L., Hoilijoki, S., Pfau-Kempf, Y., Ganse, U., Turc, L., and von Alfthan, S.: Ion Acceleration by Flux Transfer Events in the Terrestrial Magnetosheath, Geophys. Res. Lett., 45, 1723–1731, https://doi.org/10.1002/2017GL076192, 2018. a
Juusola, L., Kubyshkina, M., Nakamura, R., PitkäNen, T., Amm, O., Kauristie, K., Partamies, N., RèMe, H., Snekvik, K., and Whiter, D.: Ionospheric signatures of a plasma sheet rebound flow during a substorm onset, J. Geophys. Res.-Space, 118, 350–363, https://doi.org/10.1029/2012JA018132, 2013. a
Juusola, L., Hoilijoki, S., Pfau-Kempf, Y., Ganse, U., Jarvinen, R., Battarbee, M., Kilpua, E., Turc, L., and Palmroth, M.: Fast plasma sheet flows and X line motion in the Earth's magnetotail: results from a global hybrid-Vlasov simulation, Ann. Geophys., 36, 1183–1199, https://doi.org/10.5194/angeo-36-1183-2018, 2018a. a, b, c, d
Juusola, L., Pfau-Kempf, Y., Ganse, U., Battarbee, M., Brito, T., Grandin, M., Turc, L., and Palmroth, M.: A possible source mechanism for magnetotail current sheet flapping, Ann. Geophys., 36, 1027–1035, https://doi.org/10.5194/angeo-36-1027-2018, 2018b. a, b
Liang, J., Donovan, E., Spanswick, E., and Angelopoulos, V.: Multiprobe estimation of field line curvature radius in the equatorial magnetosphere and the use of proton precipitations in magnetosphere-ionosphere mapping, J. Geophys. Res.-Space, 118, 4924–4945, https://doi.org/10.1002/jgra.50454, 2013. a, b
Lin, C. S. and Hoffman, R. A.: Observation of inverted-V electron precipitation, Space Sci. Rev., 33, 415–457, https://doi.org/10.1007/BF00212420, 1982. a
Liu, J., Angelopoulos, V., Runov, A., and Zhou, X. Z.: On the current sheets surrounding dipolarizing flux bundles in the magnetotail: The case for wedgelets, J. Geophys. Res.-Space, 118, 2000–2020, https://doi.org/10.1002/jgra.50092, 2013. a
Liu, W. W., Donovan, E. F., Liang, J., Voronkov, I., Spanswick, E., Jayachandran, P. T., Jackel, B., and Meurant, M.: On the equatorward motion and fading of proton aurora during substorm growth phase, J. Geophys. Res.-Space, 112, A10217, https://doi.org/10.1029/2007JA012495, 2007. a
Lummerzheim, D., Galand, M., Semeter, J., Mendillo, M. J., Rees, M. H., and Rich, F. J.: Emission of O I(630 nm) in proton aurora, J. Geophys. Res., 106, 141–148, https://doi.org/10.1029/2000JA002005, 2001. a, b
Lyons, L. R., Nishimura, Y., Shi, Y., Zou, S., Kim, H. J., Angelopoulos, V., Heinselman, C., Nicolls, M. J., and Fornacon, K. H.: Substorm triggering by new plasma intrusion: Incoherent-scatter radar observations, J. Geophys. Res.-Space, 115, A07223, https://doi.org/10.1029/2009JA015168, 2010. a
Marchaudon, A. and Blelly, P.-L.: A new interhemispheric 16-moment model of the plasmasphere-ionosphere system: IPIM, J. Geophys. Res.-Space, 120, 5728–5745, https://doi.org/10.1002/2015JA021193, 2015. a
Mende, S. B., Frey, H. U., Immel, T. J., Mitchell, D. G., son Brandt, P. C., and Gérard, J.-C.: Global comparison of magnetospheric ion fluxes and auroral precipitation during a substorm, Geophys. Res. Lett., 29, 1609, https://doi.org/10.1029/2001GL014143, 2002. a, b
Nakamura, R., Baumjohann, W., Brittnacher, M., Sergeev, V. A., Kubyshkina, M., Mukai, T., and Liou, K.: Flow bursts and auroral activations: Onset timing and foot point location, J. Geophys. Res., 106, 10777–10790, https://doi.org/10.1029/2000JA000249, 2001a. a, b
Nakamura, R., Baumjohann, W., Schödel, R., Brittnacher, M., Sergeev, V. A., Kubyshkina, M., Mukai, T., and Liou, K.: Earthward flow bursts, auroral streamers, and small expansions, J. Geophys. Res., 106, 10791–10802, https://doi.org/10.1029/2000JA000306, 2001b. a
Nakamura, R., Baumjohann, W., Panov, E., Volwerk, M., Birn, J., Artemyev, A., Petrukovich, A. A., Amm, O., Juusola, L., Kubyshkina, M. V., Apatenkov, S., Kronberg, E. A., Daly, P. W., Fillingim, M., Weygand , J. M., Fazakerley, A., and Khotyaintsev, Y.: Flow bouncing and electron injection observed by Cluster, J. Geophys. Res.-Space, 118, 2055–2072, https://doi.org/10.1002/jgra.50134, 2013. a
Newell, P. T., Liou, K., Zhang, Y., Sotirelis, T., Paxton, L. J., and Mitchell, E. J.: OVATION Prime-2013: Extension of auroral precipitation model to higher disturbance levels, Space Weather, 12, 368–379, https://doi.org/10.1002/2014SW001056, 2014. a
Nishimura, Y., Lyons, L. R., Angelopoulos, V., Kikuchi, T., Zou, S., and Mende, S. B.: Relations between multiple auroral streamers, pre-onset thin arc formation, and substorm auroral onset, J. Geophys. Res.-Space, 116, A09214, https://doi.org/10.1029/2011JA016768, 2011. a
Nomura, R., Shiokawa, K., Omura, Y., Ebihara, Y., Miyoshi, Y., Sakaguchi, K., Otsuka, Y., and Connors, M.: Pulsating proton aurora caused by rising tone Pc1 waves, J. Geophys. Res.-Space, 121, 1608–1618, https://doi.org/10.1002/2015JA021681, 2016. a
Ohtani, S., Miyashita, Y., Singer, H., and Mukai, T.: Tailward flows with positive BZ in the near-Earth plasma sheet, J. Geophys. Res.-Space, 114, A06218, https://doi.org/10.1029/2009JA014159, 2009. a
Ohtani, S.-I., Shay, M. A., and Mukai, T.: Temporal structure of the fast convective flow in the plasma sheet: Comparison between observations and two-fluid simulations, J. Geophys. Res.-Space, 109, A03210, https://doi.org/10.1029/2003JA010002, 2004. a
Ozaki, M., Shiokawa, K., Miyoshi, Y., Kataoka, R., Yagitani, S., Inoue, T., Ebihara, Y., Jun, C. W., Nomura, R., Sakaguchi, K., Otsuka, Y., Shoji, M., Schofield, I., Connors, M., and Jordanova, V. K.: Fast modulations of pulsating proton aurora related to subpacket structures of Pc1 geomagnetic pulsations at subauroral latitudes, Geophys. Res. Lett., 43, 7859–7866, https://doi.org/10.1002/2016GL070008, 2016. a
Palmroth, M., Janhunen, P., Germany, G., Lummerzheim, D., Liou, K., Baker, D. N., Barth, C., Weatherwax, A. T., and Watermann, J.: Precipitation and total power consumption in the ionosphere: Global MHD simulation results compared with Polar and SNOE observations, Ann. Geophys., 24, 861–872, https://doi.org/10.5194/angeo-24-861-2006, 2006. a
Palmroth, M.: Vlasiator, available at: http://www.physics.helsinki.fi/vlasiator/ (last access: 5 September 2019), 2008.
Palmroth, M., Hoilijoki, S., Juusola, L., Pulkkinen, T. I., Hietala, H., Pfau-Kempf, Y., Ganse, U., von Alfthan, S., Vainio, R., and Hesse, M.: Tail reconnection in the global magnetospheric context: Vlasiator first results, Ann. Geophys., 35, 1269–1274, https://doi.org/10.5194/angeo-35-1269-2017, 2017. a, b, c
Palmroth, M., Ganse, U., Pfau-Kempf, Y., Battarbee, M., Turc, L., Brito, T., Grandin, M., Hoilijoki, S., Sandroos, A., and von Alfthan, S.: Vlasov methods in space physics and astrophysics, Living Reviews in Computational Astrophysics, 4, 1, https://doi.org/10.1007/s41115-018-0003-2, 2018. a, b, c
Palmroth, M. and the Vlasiator team: Vlasiator: hybrid-Vlasov simulation code, Github repository, available at: https://github.com/fmihpc/vlasiator/, last access: 5 September 2019.
Panov, E. V., Nakamura, R., Baumjohann, W., Angelopoulos, V., Petrukovich, A. A., Retinò, A., Volwerk, M., Takada, T., Glassmeier, K. H., McFadden, J. P., and Larson, D.: Multiple overshoot and rebound of a bursty bulk flow, Geophys. Res. Lett., 37, L08103, https://doi.org/10.1029/2009GL041971, 2010. a
Parks, G. K., Lee, E., Lin, N., Fu, S. Y., McCarthy, M., Cao, J. B., Hong, J., Liu, Y., Shi, J. K., Goldstein, M. L., Canu, P., Dandouras, I., and Rème, H.: Reinterpretation of Slowdown of Solar Wind Mean Velocity in Nonlinear Structures Observed Upstream of Earth's Bow Shock, Astrophys. J. Lett., 771, L39, https://doi.org/10.1088/2041-8205/771/2/L39, 2013. a
Pfau-Kempf, Y., Battarbee, M., Ganse, U., Hoilijoki, S., Turc, L., von Alfthan, S., Vainio, R., and Palmroth, M.: On the importance of spatial and velocity resolution in the hybrid-Vlasov modeling of collisionless shocks, Front. Phys., 6, 44, https://doi.org/10.3389/fphy.2018.00044, 2018. a
Popova, T. A., Yahnin, A. G., Demekhov, A. G., and Chernyaeva, S. A.: Generation of EMIC Waves in the Magnetosphere and Precipitation of Energetic Protons: Comparison of the Data from THEMIS High Earth Orbiting Satellites and POES Low Earth Orbiting Satellites, Geomagn. Aeronomy, 58, 469–482, https://doi.org/10.1134/S0016793218040114, 2018. a
Raeder, J., Larson, D., Li, W., Kepko, E. L., and Fuller-Rowell, T.: OpenGGCM Simulations for the THEMIS Mission, Space Sci. Rev., 141, 535–555, https://doi.org/10.1007/s11214-008-9421-5, 2008. a
Rodger, C. J., Clilverd, M. A., Green, J. C., and Lam, M. M.: Use of POES SEM-2 observations to examine radiation belt dynamics and energetic electron precipitation into the atmosphere, J. Geophys. Res.-Space, 115, A04202, https://doi.org/10.1029/2008JA014023, 2010. a
Runov, A., Angelopoulos, V., Artemyev, A., Birn, J., Pritchett, P. L., and Zhou, X. Z.: Characteristics of ion distribution functions in dipolarizing flux bundles: Event studies, J. Geophys. Res.-Space, 122, 5965–5978, https://doi.org/10.1002/2017JA024010, 2017. a
Sakaguchi, K., Shiokawa, K., Miyoshi, Y., Otsuka, Y., Ogawa, T., Asamura, K., and Connors, M.: Simultaneous appearance of isolated auroral arcs and Pc 1 geomagnetic pulsations at subauroral latitudes, J. Geophys. Res.-Space, 113, A05201, https://doi.org/10.1029/2007JA012888, 2008. a
Sandroos, A.: VLSV: file format and tools, Github repository, available at: https://github.com/fmihpc/vlsv/, last access: 5 September 2019.
Sergeev, V. A., Liou, K., Newell, P. T., Ohtani, S.-I., Hairston, M. R., and Rich, F.: Auroral streamers: characteristics of associated precipitation,convection and field-aligned currents, Ann. Geophys., 22, 537–548, https://doi.org/10.5194/angeo-22-537-2004, 2004. a, b
Sergeev, V. A. and Tsyganenko, N. A.: Energetic particle losses and trapping boundaries as deduced from calculations with a realistic magnetic field model, Planet. Space Sci., 30, 999–1006, https://doi.org/10.1016/0032-0633(82)90149-0, 1982. a, b, c
Sergeev, V. A., Sazhina, E. M., Tsyganenko, N. A., Lundblad, J. A., and Soraas, F.: Pitch-angle scattering of energetic protons in the magnetotail current sheet as the dominant source of their isotropic precipitation into the nightside ionosphere, Planet. Space Sci., 31, 1147–1155, https://doi.org/10.1016/0032-0633(83)90103-4, 1983. a, b
Spanswick, E., Donovan, E., Kepko, L., and Angelopoulos, V.: The Magnetospheric Source Region of the Bright Proton Aurora, Geophys. Res. Lett., 44, 10094–10099, https://doi.org/10.1002/2017GL074956, 2017. a
Tsyganenko, N. A.: Pitch-angle scattering of energetic particles in the current sheet of the magnetospheric tail and stationary distribution functions, Planet. Space Sci., 30, 433–437, https://doi.org/10.1016/0032-0633(82)90052-6, 1982. a
Unick, C. W., Donovan, E., Connors, M., and Jackel, B.: A dedicated H-beta meridian scanning photometer for proton aurora measurement, J. Geophys. Res.-Space Phys., 122, 753–764, https://doi.org/10.1002/2016JA022630, 2017. a
von Alfthan, S., Pokhotelov, D., Kempf, Y., Hoilijoki, S., Honkonen, I., Sandroos, A., and Palmroth, M.: Vlasiator: First global hybrid-Vlasov simulations of Earth's foreshock and magnetosheath, J. Atmos. Sol.-Terr. Phys., 120, 24–35, https://doi.org/10.1016/j.jastp.2014.08.012, 2014. a, b
Xiao, F., Zong, Q., Wang, Y., He, Z., Su, Z., Yang, C., and Zhou, Q.: Generation of proton aurora by magnetosonic waves, Sci. Rep., 4, 5190, https://doi.org/10.1038/srep05190, 2014. a, b
Yahnin, A. G., Yahnina, T. A., Semenova, N. V., Popova, T. A., and Demekhov, A. G.: Proton Auroras Equatorward of the Oval as a Manifestation of the Ion-Cyclotron Instability in the Earth's Magnetosphere (Brief Review), Geomagn. Aeronomy, 58, 577–585, https://doi.org/10.1134/S001679321805016X, 2018. a
Yahnina, T. A., Frey, H. U., Bösinger, T., and Yahnin, A. G.: Evidence for subauroral proton flashes on the dayside as the result of the ion cyclotron interaction, J. Geophys. Res.-Space, 113, A07209, https://doi.org/10.1029/2008JA013099, 2008. a
Zhang, Y., Paxton, L. J., Morrison, D., Lui, A. T. Y., Kil, H., Wolven, B., Meng, C. I., and Christensen, A. B.: Undulations on the equatorward edge of the diffuse proton aurora: TIMED/GUVI observations, J. Geophys. Res.-Space, 110, A08211, https://doi.org/10.1029/2004JA010668, 2005. a
Zhou, X.-Z., Angelopoulos, V., Runov, A., Liu, J., and Ge, Y. S.: Emergence of the active magnetotail plasma sheet boundary from transient, localized ion acceleration, J. Geophys. Res.-Space, 117, A10216, https://doi.org/10.1029/2012JA018171, 2012a. a, b
Zhou, X.-Z., Ge, Y. S., Angelopoulos, V., Runov, A., Liang, J., Xing, X., Raeder, J., and Zong, Q.-G.: Dipolarization fronts and associated auroral activities: 2. Acceleration of ions and their subsequent behavior, J. Geophys. Res.-Space, 117, A10227, https://doi.org/10.1029/2012JA017677, 2012b. a