Mercury's subsolar sodium exosphere: an ab initio calculation to interpret MASCS/UVVS observations from MESSENGER

The optical spectroscopy measurements of sodium in Mercury's exosphere near the subsolar point by MESSENGER Mercury Atmospheric and Surface Composition Spectrometer Ultraviolet and Visible Spectrometer (MASCS/UVVS) have been interpreted before with a model employing two exospheric components of different temperatures. Here we use an updated version of the Monte Carlo (MC) exosphere model developed by Wurz and Lammer (2003) to calculate the Na content of the exosphere for the observation conditions ab initio. In addition, we compare our results to the ones according to Chamberlain theory. Studying several release mechanisms, we find that close to the surface, thermal desorption dominates driven by a surface temperature of 594 K, whereas at higher altitudes micro-meteorite impact vaporization prevails with a characteristic energy of 0.34 eV. From the surface up to 500 km the MC model results agree with the Chamberlain model, and both agree well with the observations. At higher altitudes, the MC model using micro-meteorite impact vaporization explains the observation well. We find that the combination of thermal desorption and micro-meteorite impact vaporization reproduces the observation of the selected day quantitatively over the entire observed altitude range, with the calculations performed based on the prevailing environment and orbit parameters. These findings help in improving our understanding of the physical conditions at Mercury's exosphere as well as in better interpreting mass-spectrometry data obtained to date and in future missions such as BepiColombo.

1 Introduction

The Hermean particle environment is a complex system consisting of a surface-bounded exosphere (i.e., a collisionless atmosphere down to the planet's surface) and a magnetosphere that contains volatile and refractory species from the regolith as well as backscattered solar wind and interplanetary dust (Killen et al., 2007). By the end of the 1970s Mariner 10 made the first observations of the composition of the exosphere around Mercury and found hydrogen and helium (Broadfoot et al., 1976). It was only during the year 1985, and further on, that many ground-based observations identified the presence of sodium in the Hermean exosphere and found that Na emissions are temporally and spatially variable (e.g., Potter et al., 2007; Leblanc and Johnson, 2010), often enhanced near north and south poles, have a moderate north–south asymmetry (e.g., Potter and Morgan, 1985; Sprague et al., 1998; Schleicher et al., 2004), are concentrated on the dayside (Killen et al., 2007; Mouawad et al., 2011), and are correlated with in situ magnetic field observations (Mangano et al., 2015). Subsequent in situ observations made by MESSENGER provided a close-up look at the Hermean exosphere for over 10 Mercury years, including observations of the sodium exosphere. These in situ observations show, in contrast with some ground-based observations, that sodium has little or no year-to-year variation (Cassidy et al., 2015) and separately show a dawn–dusk asymmetry (Cassidy et al., 2016). Due to the significant solar radiation pressure on the Na atoms in the exosphere, which can be up to half of Mercury's surface gravitational acceleration (Smyth, 1986; Ip, 1986), the sodium exosphere exhibits many interesting effects, including the formation of an extended Na corona and a Na tail-like structure (Potter et al., 2007; Wang and Ip, 2011; Schmidt, 2013), observed also by MESSENGER (McClintock et al., 2008).

Hitherto several processes have been suggested to contribute to the sodium exosphere: thermal desorption–evaporation (TD), photon-stimulated desorption (PSD), solar wind sputtering (SP), and micro-meteorite impact vaporization (MIV; e.g., McGrath et al., 1986; Hunten et al., 1988; Potter and Morgan, 1997; Madey et al., 1998; Yakshinskiy and Madey, 1999; Leblanc et al., 2003; Wurz and Lammer, 2003; Killen et al., 2007). For several decades the community has been debating on the relative contribution of these mechanisms into the Hermean exosphere, and some modeling suggests that no single-source mechanism dominates during the entire Mercury year (Sarantos et al., 2009; Leblanc and Johnson, 2010) and release mechanisms can influence each other (Mura et al., 2009). Laboratory experiments on lunar silicate simulants indicate that, under conditions such that thermal desorption is negligible (e.g., at high latitudes or at the lunar surface, where temperatures are below the sublimation point of sodium), much of the ambient sodium population on the surface is efficiently desorbed via PSD (Yakshinskiy and Madey, 2000).

An extensive study of a subset of observations made by MASCS/UVVS, on MESSENGER, was reported by Cassidy et al. (2015). From the measured Na emission in the exosphere, they derived the transversal column density (TCD) profiles, which we use in this paper's analysis. Using the Chamberlain model they interpreted the observed TCDs with two thermal components: at low altitudes, a thermal component of 1200 K – which they suggest is due to PSD, and a hotter component at 5000 K – which they associate to MIV.

In contrast, we investigate all possible explanations using a different method. We use a Monte Carlo (MC) model in which we use different energy distributions for the particles released from the surface according to their release mechanism. Then we calculate the exospheric particle population by describing the motion of particles under the effect of a gravitational potential and the radiation pressure from the Sun. We find that the Na observation can be explained by two combined processes: a low-energy process, TD, that dominates at low altitudes and is driven by the high surface temperature and a comparably high-energy process, MIV, that is responsible for the Na observed at high altitudes.

We also implemented the Chamberlain model to compare directly to the Cassidy et al. (2015) results as well as to compare them with our MC results. The main purpose of this comparison is to examine the implications and limits of the different models in interpreting observations.

This paper is structured as follows: in Sect. 2 we briefly describe the previously published MASCS/UVVS observations of Na TCD that we use in this work. In Sect. 3 we describe the Chamberlain model, our MC model, and the modeled release processes. The resulting density profiles and a discussion of the limitations of the models are presented in Sect. 5, followed by a summary and conclusions in Sect. 6.

2 Observations

In this work we use the derived data reported by Cassidy et al. (2015), specifically the line-of-sight column density shown in Fig. 7 in their work. They derived these data from MESSENGER Mercury Atmospheric and Surface Composition Spectrometer Ultraviolet and Visible Spectrometer (MASCS/UVVS) observations of the Na D1 and D2 lines taken above the subsolar point on 23 April 2012. They do so by converting the UVVS emission radiance to line-of-sight column density N (cm⁻²) using the approximation $N={\mathrm{10}}^{\mathrm{9}}\mathrm{4}\mathit{\pi }I/g$, where 4πI is the radiance in kiloröntgen and g is the rate at which sodium atoms scatter solar photons in the D1 and D2 lines.

Cassidy et al. (2015) analyzed the UVVS limb scan data by fitting the Chamberlain model (Chamberlain, 1963) to estimate the temperature and density of the near-surface exosphere, including the effects of radiation acceleration and photon scattering. The authors concluded that none or little evidence of thermal desorption of sodium was found. This finding was surprising and was attributed to a higher binding energy of the weathered surface that would suppress thermal desorption. They also reported that observations show spatial and temporal variation but almost no year-to-year variation, and they do not observe the episodic variability reported by ground-based observers (e.g., Massetti et al., 2017).

We chose these data because the observation geometry of MESSENGER MASCS/UVVS during that day, as illustrated in Fig. 2, is easy to understand and to reproduce by our model. The goal of this work is to show an interpretation from first principles of the observed line-of-sight column density of a simple case observation with a model that accounts for several release processes rather than rely solely on the Chamberlain model that accounts only for thermal release.

3 Monte Carlo model description

We use an updated version of the MC model developed by Wurz and Lammer (2003). This model represents the exosphere by a large number of model particles, typically of the order of 10⁶. We calculate the orbits of each model particle given an initial energy and angle selected randomly from a previously specified Maxwellian velocity distribution function for model particles released via TD and MIV and non-Maxwellian ones for model particles released via PSD and SP (Gamborino and Wurz, 2018; Wurz and Lammer, 2003; Vorburger et al., 2015). Because the gas is in a non-collisional regime we can simulate each release mechanism independently. Then we calculate each model particle trajectory under the effect of a gravitational potential, the effect of radiation pressure from the Sun, and using the local physical conditions. In this sense, our calculation is ab initio because all the model parameters are derived from the observation conditions or physical principles.

The particle trajectory is determined for discrete altitude steps with start point at the surface until the particle falls back to the surface, gets ionized somewhere on its path and thus is lost from the neutral exosphere, or leaves Mercury's gravity field, thus leaving calculation domain (which is given by the Hill radius). After simulating all model particles' trajectories, we compute the species' density and column density profiles as a function of altitude and tangent altitude by applying the boundary conditions given from the particle release mechanism. For the calculation of the tangent altitude integration we assume a radially symmetric exosphere (see Fig. 2). We also calculate the flux of particles released from the surface for each release process from the physical conditions of the release processes.

The number density of Na at the surface, or the surface atomic fraction, is only used for simulating the source population produced by the high-energy processes, which are MIV and SP. To simulate the ambient Na population, which is produced by TD and PSD, we use the number density resulting from the returning flux by MIV and SP.

We include the latest value for the atomic fraction of sodium in the surface derived from MESSENGER observations (Peplowski et al., 2015) as well as the effect of radiation pressure on Na atoms the same way as implemented by Bishop and Chamberlain (1989).

In the following we briefly describe the release and loss mechanisms, we explain the different assumptions concerning the Na on the surface that are important for the simulation, and we provide information about the model implementation.

3.1 Overview of release and loss processes

Up to now, various mechanisms have been proposed as being responsible for the input and loss of atomic species to and from planetary exospheres (Wurz and Lammer, 2003; Killen et al., 2007; Wurz et al., 2007). Here we describe TD, solar SP, PSD, and MIV.

Each release mechanism is described by a probability energy and angle distribution function that defines an ensemble of particles with a characteristic energy from which we determine the released flux from the surface. Here we provide a brief description of the release and loss mechanisms, the mathematical expressions for the different probability distribution functions we assume, characteristic energy, and release flux to be used in following sections.

3.1.1 Thermal desorption

To simulate TD we consider a Maxwellian distribution function with a characteristic energy given by the thermal energy, E=k_BT_S, where k_B is the Boltzmann constant and T_S is the temperature of the surface. The thermal speed of particles with mass m released via TD is given by the mean speed of the ensemble: $v_{\mathrm{the}}=\langle v\rangle =\sqrt{\frac{\mathrm{8}{k}_B{T}_{\mathrm{S}}}{\mathit{\pi }m}}$.

In theory, the released flux, Φ_TD, is proportional to the integral in the speed domain of the Maxwell–Boltzmann distribution. In this work, however, we consider that the released Na flux by TD is originated from a separate population. This flux is calculated as a contribution from the returning flux computed for MIV and SP mechanisms after running the simulation and from the diffusion-limited exospheric flux calculated by Killen et al. (2004). This is further explained in detail in Sects. 3.3 and 5.1.

3.1.2 Micro-meteorite impact vaporization

We determine the contribution to the exosphere by MIV in the same fashion as done by Wurz et al. (2010). First, we assume that Mercury's mass accretion rate for its apocenter and pericenter is 10.7–23.0 t d⁻¹ (Müller et al., 2002). Similarly, Cintala (1992) reported that the meteoritic infall on Mercury is $\mathrm{1.402}\times {\mathrm{10}}^{-\mathrm{16}}$ g cm⁻² s⁻¹ for meteorites with mass of <0.1 g, which corresponds to a particle radius of <0.02 m. This corresponds to a flux of 0.221 kg s⁻¹ or 18.2 t d⁻¹ integrated over Mercury's surface. In contrast, Borin et al. (2009) reported an infall of $\mathrm{2.382}\times {\mathrm{10}}^{-\mathrm{14}}$ g cm⁻² s⁻¹, i.e., corresponding to 1540 t d⁻¹, which is a factor 80 times higher compared to the value by Müller et al. (2002). Later on and using a different model, Borin et al. (2010) reported an infall of $\mathrm{8.982}\times {\mathrm{10}}^{-\mathrm{15}}$ g cm⁻² s⁻¹, which is roughly 2.6 times smaller than their previous value.

To calculate the exospheric densities and height profiles we derive the volatilization of surface material from the mass influx calculated before. For our simulation of particles released via MIV we considered an average temperature of 4000 K of the impact plume (value obtained from the range given by Eichhorn, 1978a). For the total number of released sodium atoms, we find, accordingly, a mean MIV-released flux of 2.45×10¹¹ m⁻² s⁻¹ for R_orb=0.458 au, which corresponds to the observation day. We consider a uniform MIV flux over the whole planet.

3.1.3 Sputtering

This process refers to the impact of solar wind ions onto the surface, causing the release of volatiles and refractory elements mostly near the cusp regions. The predicted value of solar wind flux to the surface near the southern cusp is 4 times larger than in the north because of the offset of Mercury's magnetic dipole of 0.2 R_M (∼400 km) northward from the planetary center (Anderson et al., 2011). The plasma pressures in the cusp are 40 % higher when the interplanetary magnetic field (IMF) is anti-sunward than when it is sunward (Winslow et al., 2012), indicating that the effect of the IMF B_x direction is present. At the subsolar point, the surface is shielded from the solar wind by Mercury's magnetosphere (see review by Raines et al., 2014). However, there is a small neutral component of the solar wind (NSW) of about 10⁻⁵–10⁻³ particles at 1 au (Collier et al., 2003), which is not deflected by the Hermean magnetic field, thus permanently contributing to sputtering on the entire dayside of the planet. The energy distribution adapted with an energy cut-off (Wurz and Lammer, 2003) given by the binary collision limit of particles sputtered from a solid, f(E_e), with energy E_e of the sputtered particle, has been given as

$$\begin{array}{}\text{(1)}& f\left(E_{\mathrm{e}}\right)=C{\displaystyle \frac{E_{\mathrm{e}}}{(E_{\mathrm{e}}+E_{\mathrm{b}}{)}^{\mathrm{3}}}}\left\{\mathrm{1}-{\left[{\displaystyle \frac{(E_{\mathrm{e}}+E_{\mathrm{b}})}{E_{\max }}}\right]}^{\mathrm{1}/\mathrm{2}}\right\},\end{array}$$

where C is the constant of normalization, E_b is the surface binding energy of the sputtered particle which we consider to be equal to 2.0 eV for Na, taken from Stopping Range of Ions in Matter (SRIM) software (Ziegler et al., 2010), and where E_max is the maximal energy that can be transferred in a binary collision. The maximum of the energy distribution is at $E_{\max }=E_{\mathrm{b}}/\mathrm{2}$. This mechanism will release all species from the surface into space, reproducing more or less the local surface composition on an atomic level. The total sputtered flux from the surface, Φ_i, of species i is

$$\begin{array}{}\text{(2)}& {\mathrm{\Phi }}_i={\mathrm{\Phi }}_{\mathrm{SW}}\cdot Y_i=n_{\mathrm{0}}^i\langle v_i\rangle ,\end{array}$$

where Φ_SW is the solar wind flux impinging on the surface, and Y_i is the total sputter yield for species i. From Eq. (2) we get $n_{\mathrm{0}}^i$, the exospheric density at the surface, with 〈v_i〉 being the mean speed of sputtered particles. For the simulation we considered the mean values of particle flux and solar wind speed at Mercury for a solar wind dynamic pressure P_dyn=20 nPa determined by Massetti et al. (2003): ${\mathrm{\Phi }}_{\mathrm{sw}}=\mathrm{4.1}\times {\mathrm{10}}^{\mathrm{12}}$ m⁻² s⁻¹ and v_sw=440 km s⁻¹.

3.1.4 Photon-stimulated desorption (PSD)

When a surface is bombarded by photons of sufficient energy it can lead to the desorption of neutral atoms or ions. Solar photons with energy ≥5 eV ($\le \mathit{\lambda }=\mathrm{2500}$ Å) have enough energy to release atomic sodium from the surface of regolith grains (Yakshinskiy and Madey, 1999). In particular, the experimental results by Yakshinskiy and Madey (2000, 2004) on lunar samples show that released neutral Na atoms by electron-stimulated desorption (ESD) and PSD have suprathermal speeds. Since then, several energy and velocity distributions have been used to describe particles released via PSD, varying between Maxwellian (e.g., Leblanc et al., 2003) and non-Maxwellian distributions (e.g., Schmidt, 2013). However, the use of a non-Maxwellian distribution, in particular the Weibull distribution, has recently proven to be most suitable for describing this release mechanism (Gamborino and Wurz, 2018). The normalized Weibull distribution allows for a wide range of shapes using only two parameters for its definition. For PSD, this function is expressed as follows:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }f(v,v_{\mathrm{0}},\mathit{\kappa })=\mathit{\kappa }\mathrm{\Gamma }\left(\mathrm{1}+{\displaystyle \frac{\mathrm{1}}{\mathit{\kappa }}}\right){\left({\displaystyle \frac{m}{\mathrm{3}{k}_{\mathrm{B}}{T}_{\mathrm{s}}}}\right)}^{\mathrm{1}/\mathrm{2}}\\ {\displaystyle }& {\displaystyle }{\left[(v-v_{\mathrm{0}})\sqrt{{\displaystyle \frac{m}{\mathrm{3}{k}_{\mathrm{B}}{T}_{\mathrm{s}}}}}\mathrm{\Gamma }\left(\mathrm{1}+{\displaystyle \frac{\mathrm{1}}{\mathit{\kappa }}}\right)\right]}^{\mathit{\kappa }-\mathrm{1}}\\ \text{(3)}& {\displaystyle }& {\displaystyle }\times \exp \left[-{\left((v-v_{\mathrm{0}})\sqrt{{\displaystyle \frac{m}{\mathrm{3}{k}_{\mathrm{B}}{T}_{\mathrm{s}}}}}\mathrm{\Gamma }\left(\mathrm{1}+{\displaystyle \frac{\mathrm{1}}{\mathit{\kappa }}}\right)\right)}^{\mathit{\kappa }}\right],\end{array}$$

where k_B is the Boltzmann constant, m is the mass of the species, T_s is the surface temperature, Γ is the Gamma function, v₀ is the offset speed, and κ is the shape parameter of the distribution. The parameters have been derived as κ=1.7 and a speed offset of v₀=575 m s⁻¹ by Gamborino and Wurz (2018).

3.2 Loss processes

We include the following exospheric loss processes: (1) gravitational escape, (2) surface adsorption, and (3) ionization. The escape speed from Mercury's surface is v_esc=4.3  km s⁻¹, which is small enough to allow the escape of many exospheric particles, particularly the light ones. We compute the fraction of atoms lost by photoionization at each time step in the trajectory calculation, and we use the typical photoionization rates of Na at Mercury, which are $\mathrm{3.46}\times {\mathrm{10}}^{-\mathrm{5}}$ and $\mathrm{3.77}\times {\mathrm{10}}^{-\mathrm{5}}$ s⁻¹ during low and high solar activity, respectively (scaled from values at 1 au from http://phidrates.space.swri.edu/, last access: 19 June 2019). On average, it takes a few hours until a sodium atom is ionized, which gives enough time to complete an exospheric trajectory for most released particles. Sodium atoms will go back to Mercury's surface and be adsorbed, unless they are lost due to ionization or escape Mercury's gravity.

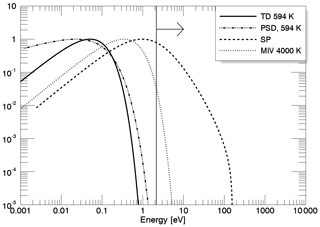
In Fig. 1 we show the different energy spectra for Na from the probability distribution functions, each normalized to a maximum of 1, for the four release mechanisms. Atoms released via TD have an energy distribution dependent on the local surface temperature, which is represented by the solid black curve, corresponding to a characteristic energy of 0.06 eV and a temperature of 594 K. Atoms released via this process have a relatively low characteristic energy compared to the escape energy of sodium atoms from Mercury's surface, which is 2.07 eV for Na atoms. Thus, TD leads to a near-surface Na exosphere that does not contribute to the planetary loss. On the other hand, atoms released via SP (dashed curve) have significantly higher characteristic energy (1 eV) and a distribution skewed to higher energies (see Eq. 1), thus reaching higher altitudes and contributing to the planetary loss. At the subsolar point, ion fluxes onto the surface and consequently the sputter yields are low compared to the pole regions (where the magnetic field cusps are located); therefore sputtered atoms can only form a low-density exosphere (Wurz et al., 2010). A long-tailed positively skewed distribution also describes the energy distribution for PSD release (see Eq. 3) shown as the dashed–dotted curve in Fig. 1, which has a characteristic energy of ∼0.1 eV; thus particles can reach higher altitudes compared to those released via TD. As can be seen in the plot, the energies are mostly below escape. Finally, atoms released via MIV (dotted curve) are modeled by a thermal distribution with temperatures of 4000 K, thus having higher characteristic energy (0.34 eV) compared to the regular TD. MIV contributes to the exosphere in a comparable amount like SP (Wurz et al., 2010) if solar wind sputtering is active. Unfortunately, the micro-meteorite influx onto Mercury's surface is not known very accurately, as discussed above.

Figure 1 Normalized energy distribution functions for several release mechanisms active on Mercury's surface to produce the sodium exosphere. The vertical solid line marks the value at which sodium atoms have enough energy to escape the gravitational field of Mercury.

3.3 Sodium in and at the surface

Smyth and Marconi (1995) introduced a qualitative description of the fate of sodium atoms ejected in Mercury's environment using two populations, the “source” and the “ambient” atoms. A few years later, Morgan and Killen (1997) expanded the description to include the diffusion of sodium from inside the regolith to the surface and the description of the expanding vapor cloud after the impact of micro-meteorites. Here we consider these two populations; the first population is the so-called source atoms, which are atoms chemically bonded in the minerals on the surface and are released by high-energy processes, either by MIV or SP. The source atoms are predominantly ionically bonded to the oxygen in a bulk silicate (Madey et al., 1998) with binding energy larger than 0.5 eV.

The released Na atoms may either escape or fall back on the surface and become ambient particles after few impacts on the surface (measured in experiments by Yakshinskiy and Madey, 1999, 2000, 2004). These particles are thermally accommodated to the local surface temperature and have counterparts absorbed in the regolith with a binding energy less than 0.5 eV, according to Hunten et al. (1988). We model this population by low-energy processes such as TD and PSD. An illustration depicting the different release, returning, and loss fluxes is shown and explained in Sect. 5.1.

Table 1 Parameters for simulation.

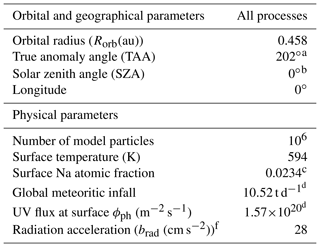
^a Taken from the Jet Propulsion Laboratory's (JPL's) HORIZONS Ephemeris (https://ssd.jpl.nasa.gov/horizons.cgi, last access: 19 June 2019). ^b Latitude = 0^∘. ^c Intermediate Composition (Peplowski et al., 2015). ^d Calculated for the specific R_orb=0.458 au and TAA = 20^∘ from the range given by Müller et al. (2002) which depends on the orbital distance. ^e For PSD. ^f Smyth and Marconi (1995).

4 Model implementation

The MC model, as described above, and the Chamberlain model (as described in the Appendix A) are evaluated for the parameters of the MESSENGER observation conditions as listed in Table 1. In this section we describe in detail how we obtained these parameters.

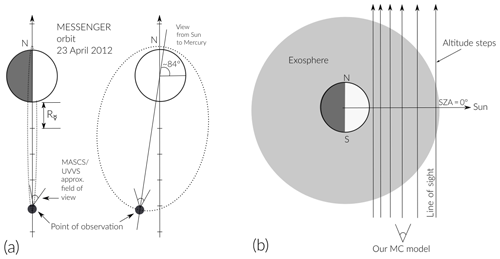
Figure 2 textbf(a) Representation to scale of MESSENGER's orbit around Mercury during the time of observations (orbit parameters taken from https://www.nasa.gov). (b) Scheme of the line of sight used in the simulations (distance between altitude steps is not to scale). Solid black lines in (b) represent the altitude steps for integration of the column density when SZA = 0^∘.

4.1 Simulation parameters and geometry

To reproduce the measured TCD profile reported by Cassidy et al. (2015), we have to know some input values for the simulation parameters. Using SPICE and Mercury's ephemeris data we find the corresponding parameters for the time of the MESSENGER observations (listed in Table 1). The dayside limb scans were taken when Mercury had a true anomaly angle (TAA) of 202^∘, MESSENGER was near the apogee, and the UVVS line of sight was pointing approximately northward – as shown in the illustration in Fig. 2 (see also top of Fig. 2 in Cassidy et al., 2015). During the day of the observation MESSENGER made three orbits around Mercury with an orientation such that its orbit plane was almost perpendicular with respect to the light rays coming from the Sun, as represented in the illustration in Fig. 2 (keeping in mind that this is just a simplified representation of the real situation). Each altitude profile extends from just above the surface, as low as 10 km, to several thousand kilometers above the surface.

Given the position of the spacecraft with respect to Mercury and the direction of the UVVS line of sight during the time of observation, we simulate particles ejected at a latitude of 0^∘ and a solar zenith angle (SZA) of 0^∘ and calculated the contribution to the TCD from this position. This is the closest to the real observation geometry that our model can compute.

In Fig. 2a we illustrate the orbit geometry and position of the MESSENGER spacecraft during the time of observation. In Fig. 2b we also illustrate the orientation of the tangent (to the surface) altitude steps we used in our model for the integration of the column density. The dawn–dusk asymmetry is not considered because the time of the observation does not include these regions.

The sodium surface atomic fraction, indicated in Table 1, is used to calculate the surface number density and release flux, and it is used only for calculating the source population produced by the high-energy processes, which are MIV and SP. To simulate the ambient sodium population, which is produced by TD and PSD, we use the surface number density resulting from the returning flux to the surface by MIV and SP.

On the other hand, the radiation pressure depends on the true anomaly angle and the solar zenith angle, and we use the value for radiation acceleration taken from Smyth and Marconi (1995) for the given TAA during the time of observations. We assume the same orbital and physical parameters for our implementation of the Chamberlain model modified by adding radiation pressure.

After computing the density profiles we integrate along the line of sight for different altitude steps and for SZA = 0^∘ to obtain the limb scans as a function of tangent altitude.

4.1.1 Temperature model

According to the infrared measurements made on Mariner 10 (Chase et al., 1976), which only include observations from the nightside up to 08:00 LT on the dayside, and considering Mercury as a blackbody emission radiator, the extrapolated dayside surface temperature as a function of latitude ϕ and longitude θ must follow a “one-fourth” law with an illumination angle and decrease like “1∕r²”, where r is the distance of Mercury to the Sun. Neglecting the thermal inertia of Mercury's lithosphere, the local dayside surface temperature for $\mathrm{0}<\left|\mathit{\theta }\right|<\mathit{\pi }/\mathrm{2}$ can be written as

$$T_{\mathrm{s}}(\mathit{\varphi },\mathit{\theta })=T_{\min }+(T_{\max }-T_{\min })(\cos \mathit{\varphi }\cos \mathit{\theta }{)}^{\mathrm{1}/\mathrm{4}},$$

where T_max is the effective temperature at the subsolar point, T_min is the nightside temperature, the longitude θ is measured from the planet-Sun axis, and the latitude ϕ is measured from the planetary Equator. To determine the effective temperature at the subsolar point we used the blackbody Stefan–Boltzmann law to obtain

$$\begin{array}{}\text{(4)}& T_{\mathrm{eff}}\approx T_{\mathrm{Sun}}{\left[{\left({\displaystyle \frac{R_{\mathrm{Sun}}}{R_{\mathrm{orb}}}}\right)}^{\mathrm{2}}{\displaystyle \frac{\mathrm{1}-\mathit{\alpha }}{\mathit{ϵ}}}\right]}^{\mathrm{1}/\mathrm{4}},\end{array}$$

where T_eff is the effective temperature of the surface, R_orb is the distance to the Sun, R_Sun is the solar radius, T_Sun=5778 K is the effective solar temperature, α=0.07 is the albedo (Mallama et al., 2002), and ϵ=0.9 is the emissivity (Murcray et al., 1970; Saari and Shorthill, 1972; Hale and Hapke, 2002). During the day of observations Mercury was at a distance of R_orb=0.458 au to the Sun. Using this value and Eq. (4), we calculated a surface temperature of $T_{\mathrm{eff}}=T_{\mathrm{S}}=\mathrm{594}$ K at the subsolar point. This is the temperature we used for the TD and PSD calculations.

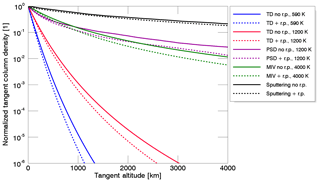
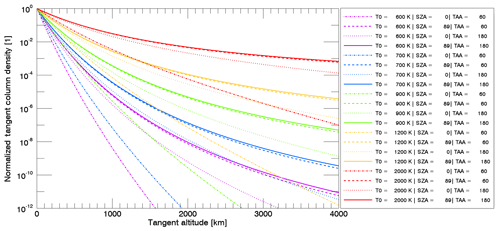
Figure 3 Column density profiles as a function of tangent altitude for Na where the column density at the surface is normalized to 1 and for the different release mechanisms: TD, PSD, MIV, and SP with and without radiation pressure (r.p.) centered at subsolar point and for different surface temperature values. The simulation was done with an ensemble of 10⁶ particles and Mercury at TAA = 0202^∘ and R_orb=0.458 au.

In Fig. 3 we show an example of the tangent column density profiles computed for the different release mechanisms and with different characteristic temperatures. All processes were simulated with and without radiation pressure to compare them. We fixed all profiles at altitude zero and a tangent column density normalized to 1 to show the different shapes and slopes for the different mechanisms and different physical parameters specified in the legend.

5 Results and discussion

Using the parameters listed in Table 1, we simulate sodium atoms released via TD, PSD, MIV, and SP and calculated the exospheric density profiles up to 10⁵ km. The integral along the line of sight gives us the column density, and if we choose the tangent altitude, we also obtain the TCD as a function of altitude. The surface TCD and released flux obtained from the simulation for each mechanism are listed in Table 2. Independently, we also implemented the Chamberlain model in the same fashion as Cassidy et al. (2015) did to compare it to our results (see description in Appendix A).

Figure 4 includes two plots where we show the derived MESSENGER observations (black cross marks) together with the results from our MC simulations and the results using the Chamberlain model. In Fig. 4a, we plot the sodium TCD as a function of altitude for TD (dashed black curve), MIV (dashed grey curves), SP (dashed–dotted grey curve), and PSD (vertical-dash black curve). The results using the Chamberlain model with the modification for radiation pressure are also plotted: the curve with square symbols corresponds to a surface temperature of 594 K, and the curve with circle symbols corresponds to an assumed temperature of 2500 K, with the TCD at the surface of this component adjusted to match the observations. The sum of the two Chamberlain profiles is represented by the solid light-grey curve. In Fig. 4b, we only plot our MC results for TD with T=594 K, and MIV (multiplied by a factor of 0.5) for $T=[\mathrm{3000},\mathrm{4000},\mathrm{5000}]$ K, together with the derived MESSENGER observations. We would like to point out again that no fitting to any surface density was applied in our model. Rather, the surface density is a result from the model itself.

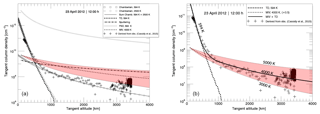
Figure 4 (a) Plots of the derived TCD from observations (black crosses), of the results from our calculations with no correction factors, and of the results using the Chamberlain model. The resulting TCD profiles from our MC model are plotted as follows: TD is the dashed black curve, MIV between 3000 and 5000 K is the shaded red area, the dashed-grey curve is MIV with a mean temperature of 4000 K, SP is the dashed–dotted grey curve, and PSD is the vertical-dash curve. The resulting profiles using the Chamberlain model are represented as the square- and circle-symbol curves. The sum of the two Chamberlain profiles represented by the solid light-grey curve. (b) Plots of the derived TCD from observations (black crosses) and of the results from our calculations: the dashed black curve is for TD, the results for MIV between 3000 and 5000 K are the shaded red area, the dashed grey curve is MIV with a mean temperature of 4000 K. MIV curves were multiplied by one-half. The sum of TD and MIV profiles is shown as the solid black curve.

At low altitudes the Chamberlain model and the TD simulation for the surface temperature agree very well, and both also agree reasonably well with the observations, which is expected from a Maxwellian population thermalized with the surface. Note that the calculated thermal profiles, both with the Chamberlain model and with our MC model, are based on the surface temperature, which was derived separately from the orbit position of Mercury, and they were not fitted to the data. The release fluxes for TD and PSD are both calculated from the ambient sodium population atoms, which we derived in the next section. The fall-off above 1000 km of the TD 594 K curve is a result of the loss of neutral sodium atoms due to ionization. Compared to any other mechanism modeled here, TD is the best match for the observations at low altitudes.

At altitudes above ∼600 km the Chamberlain model for 594 K shows densities that are too low, and only a high-temperature component of 2500 K fits the data, similar to Cassidy et al. (2015). The SP curve is too flat and does not match the observations at any given altitude. As described further on, and as shown in Fig. 6, the sputtered component of the tangent column density is expected to be substantial mainly at high latitudes, but the observation geometry gives preference to mechanisms happening at low latitudes, around the subsolar point.

The limitation of Chamberlain theory (Chamberlain, 1963) in this context is that it was originally developed for Earth's exosphere where the only controlling factors considered are the gravitational attraction and the “thermal energy conducted from below” (also known as exobase). For the case of Mercury, the only layer below the exosphere is the surface. Meaning that, the only source mechanism of exospheric particles considered in Chamberlain model is what we consider in our MC model to be thermal desorption.

Using the Chamberlain theory implies that the only way to increase the particles' characteristic energy (and thus able to reach high altitudes) is by increasing the surface temperature. One way to do this is by micro-meteorite impacts, which can lead to a Maxwellian exospheric population with a temperature of the order of a few thousand kelvins, which can explain the high-energy component in the observations. Another way to increase the temperature is by heating the surface with solar radiation. But as calculated, the surface temperature of Mercury at the subsolar point and at TAA = 202^∘ is 594 K. This temperature is not enough to let particles reach high altitudes; much higher temperatures are needed, as shown in Fig. 4. Consequently, the Chamberlain model works fine only for an exospheric population that is in thermal equilibrium with the surface temperature. For other non-Maxwellian and more energetic populations, the Chamberlain model is inadequate.

Hence, it is inevitable to consider other non-thermal and more energetic release processes to explain the Na exosphere at higher altitudes. Our results show that PSD and MIV are two possible non-thermal and high-energy mechanisms that can explain the observations at high altitudes, as shown in Fig. 4. Our MC model of the MIV TCD profile gives a good match with the observed data at high altitudes with a temperature of 4000±1000 K, a temperature range that is consistent with Eichhorn (1978a) laboratory data. An even better match is reached by adjusting the surface column density by only a factor of 0.5. Moreover, provided that the high-altitude data above 3000 km shown in Fig. 4 could be removed due to, for instance, stray-light contamination, instrumental effects, or the light coming from a background star, an MIV profile using a temperature between 3000–4000 K would better agree with the data.

On the other hand, the PSD TCD profile does not fit quite as well to the observations, and it has to be multiplied by a factor of $\mathrm{4}\times {\mathrm{10}}^{-\mathrm{4}}$ to match part of the tail, which will be addressed below. Since TD is competing with PSD for the ambient Na atoms on the surface, the Na available for PSD is much less or not available at all in the extreme case (as explained below). Therefore, the plotted curve of PSD is just an upper limit. The TCD profile for SP is also plotted in Fig. 4 for precipitating ion fluxes of the cusp region. Since the observations are at the subsolar point, the surface is shielded from precipitating ions (Kallio and Janhunen, 2003), and the SP contribution to the exosphere for these observations has to be considered to be an upper limit as well. Moreover, the TCD from SP falls off much less with altitude than the observations.

5.1 Source and loss fluxes

The sodium loss from the exosphere has to be supplied by Na from the surface to sustain a stable exosphere over several Mercury years as it was observed (Cassidy et al., 2015). As mentioned in Sect. 3.3, the source population of Na to the exosphere is considered to come mainly from the release via SP and MIV. The fraction of this population that comes back to the surface will become the ambient population and be available for TD and PSD. The conservation of mass allows us to quantify the amount of Na in the ambient population at the subsolar point, which is available for TD, by considering that the sum of the Na diffused from regolith to the surface plus the return fluxes from MIV and SP has to be equal the loss due to TD. Mathematically, the latter is expressed as

$$\begin{array}{}\text{(5)}& {\displaystyle }{\mathrm{\Phi }}_{\mathrm{source}}^{\mathrm{Ambient}}={\mathrm{\Phi }}_{\mathrm{Diff}.}+{\mathrm{\Phi }}_{\mathrm{return}}^{\mathrm{MIV}}+{\mathrm{\Phi }}_{\mathrm{return}}^{\mathrm{SP}},\text{(6)}& {\displaystyle }{\mathrm{\Phi }}_{\mathrm{loss}}^{\mathrm{Ambient}}={\mathrm{\Phi }}_{\mathrm{release}}^{\mathrm{TD}}\cdot {\mathit{\chi }}_{\mathrm{Tot}}^{\mathrm{TD}},\end{array}$$

where χ is the total fraction of Na loss, which includes the losses by ionization and gravitational escape. Φ_Diff. is the diffusion-limited exospheric flux calculated by Killen et al. (2004) to be <10⁷ cm⁻² s⁻¹. Note that the fluxes' subscript source and loss are calculated just for the ambient population and do not represent the global flux. For a steady-state system,

$$\begin{array}{}\text{(7)}& {\mathrm{\Phi }}_{\mathrm{source}}^{\mathrm{Ambient}}-{\mathrm{\Phi }}_{\mathrm{loss}}^{\mathrm{Ambient}}=\mathrm{0}.\end{array}$$

Combining Eqs. (5), (6), and (7), we derive ${\mathrm{\Phi }}_{\mathrm{release}}^{\mathrm{TD}}$ as follows:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathrm{\Phi }}_{\mathrm{release}}^{\mathrm{TD}}={\displaystyle \frac{{\mathrm{\Phi }}_{\mathrm{Diff}.}+{\mathrm{\Phi }}_{\mathrm{return}}^{\mathrm{MIV}}+{\mathrm{\Phi }}_{\mathrm{return}}^{\mathrm{SP}}}{{\mathit{\chi }}_{\mathrm{Tot}}^{\mathrm{TD}}}}\\ {\displaystyle }& {\displaystyle }={\displaystyle \frac{\mathrm{1.0}\times {\mathrm{10}}^{\mathrm{7}}{\mathrm{cm}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}+(\mathrm{5.4}\times {\mathrm{10}}^{\mathrm{5}}+\mathrm{3.28}\times {\mathrm{10}}^{\mathrm{5}}){\mathrm{cm}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}}{\mathrm{0.0102}}}\\ \text{(8)}& {\displaystyle }& {\displaystyle }=\mathrm{1.06}\times {\mathrm{10}}^{\mathrm{9}}{\mathrm{cm}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}.\end{array}$$

From Eq. (8) we can derive the surface density as $n_{\mathrm{0}}=\frac{{\mathrm{\Phi }}_{\mathrm{release}}^{\mathrm{TD}}}{v_{\mathrm{th}}}=\mathrm{1.44}\times {\mathrm{10}}^{\mathrm{10}}$ m⁻³, where $v_{\mathrm{the}}=\sqrt{\mathrm{8}{k}_{B}T/\mathit{\pi }m}=\mathrm{739}$ m s⁻¹. The radial column density, NC, can be approximated as NC $\approx n_{\mathrm{0}}\cdot H=\mathrm{8.21}\times {\mathrm{10}}^{\mathrm{14}}$ m${}^{-\mathrm{2}}=\mathrm{8.21}\times {\mathrm{10}}^{\mathrm{10}}$ cm⁻². The rest of the results of our simulations, together with the derived quantities for the ambient population, are shown in Table 2.

Table 2 Results from the MC simulation.

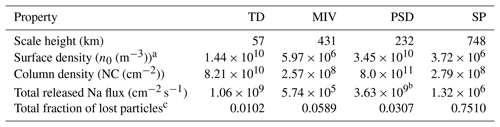
^a Based on Na surface fraction from intermediate composition (Peplowski et al., 2015) and used for MIV, PSD, and SP. ^b Adjusted to observations by a multiplication factor of $\mathrm{4}\times {\mathrm{10}}^{-\mathrm{4}}$ and considered an upper limit. ^c Including the losses by gravitational escape and ionization.

Figure 5 is a scheme illustrating the Na release processes and fate due to the different release mechanisms. For the given observations, we calculated the Na release flux from the surface and determined the losses for each process. The fraction of Na that is not lost returns to the surface and becomes part of the ambient population available for TD and PSD.

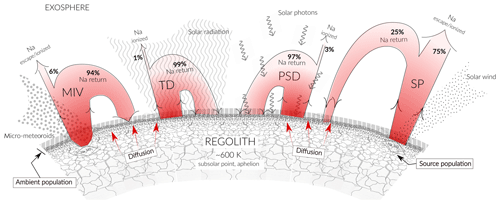
Figure 5 Scheme illustrating the different released fluxes of Na due to the different release mechanisms from the mineral compound (the source population) and from surface (the ambient population). The illustration is not to scale.

Figure 6 is an illustration of the spatial distribution of the derived released Na fluxes as a function of solar zenith angle. The radial scale represents the magnitude difference of the release flux “intensity”, I(α), for the different release mechanisms (the units are arbitrary). Note that this diagram does not represent the spatial distribution of Na depending on the mechanism but just the magnitude of the release flux for each mechanism. At the subsolar point, the main contribution of Na to the exosphere is TD, with a release flux of 2 orders of magnitude higher compared to the other release processes and with an exponential decay towards the poles because of the strong temperature dependence of sublimation. The solar wind sputtering on the surface acts mainly at high latitudes ($\mathit{\alpha }\approx \pm \mathit{\pi }/\mathrm{2}$) and is also a strong function of latitude decay. We consider that MIV acts uniformly on the entire planet, thus the release flux is not angle dependent. PSD has a cosine dependence with SZA, but since it competes with TD it is most important at mid-latitudes to high latitudes.

This illustration shows the main release mechanisms given a certain line-of-sight observation geometry. For instance, the ground-based observations done by Schleicher et al. (2004) during Mercury's transit had a limb line of sight similar to the horizontal line shown in Fig. 6. The main contribution for those limb observations when $\mathit{\alpha }\approx \pm \mathit{\pi }/\mathrm{2}$ includes a sum of SP and PSD, which provides a sputter high-energy Na exosphere and a low-energy photo-desorbed ambient Na population, which was already discussed by Mura et al. (2009). On the other hand, the vertical line of sight path crossing TD and MIV represents the line of sight of the approximate direction of MESSENGER's field of view during observations on 23 April 2012 (Cassidy et al., 2015) and discussed here. If observations are made with a line of sight corresponding to $\mathit{\alpha }\approx \pm \mathit{\pi }/\mathrm{4}$ for instance, the analysis of the source mechanisms becomes complicated because all release mechanisms will be active in some extent, and thus it will be difficult to differentiate them.

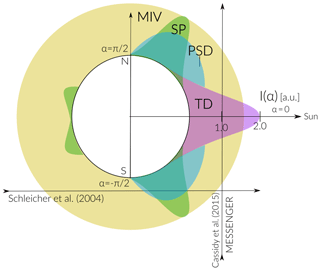
Figure 6 Scheme of the intensity distributions for the different release mechanisms as a function of solar zenith angle. The units are arbitrary, but orders of magnitude are taken from the results of our model. The horizontal arrow is an example of the line of sight of the ground-based observations by Schleicher et al. (2004). Vertical arrow represents the approximate direction of MESSENGER's field of view during observations on 23 April 2012 (Cassidy et al., 2015).

5.2 Is there a permanent Na atom layer on the surface?

Reviewed earlier reports (e.g. Leblanc et al., 2003) conclude there is a non-uniform spatially distributed but permanent “reservoir” of atomic Na available on the surface, forming part of the ambient population. This reservoir is not strongly chemically bounded to the mineral grains, but it is physisorbed on the surface, and being on the surface, it is also not part of the exosphere. Let us consider sodium adsorbed in an atomic state on the surface rather than chemically bounded to the crystal structure in the regolith (consistent with laboratory experiments by Yakshinskiy and Madey, 2000, 2004). We can calculate the theoretical Na gas density above the surface and the evaporated flux by using the empirical equation for the Na vapor pressure (Lide, 2003), and considering a surface temperature of T=594 K at the subsolar point, this gives a sodium vapor pressure of P₀=7.44 Pa.

The corresponding theoretical evaporated flux of sodium atoms from this surface reservoir would be 6.71×10²¹ atoms cm⁻² s⁻¹. This value is 14 orders of magnitude higher than the thermal Na release flux we derived from measurements, which is 4.34×10⁸ atoms cm⁻² s⁻¹. Even if the atomic Na is bound to the surface with a higher binding energy, the sublimation flux will still be enormous at this temperature. Thus, it is clear that the TD flux is limited by the availability of ambient Na on the surface, and given the large difference in theoretical and derived release fluxes, all the ambient Na is in the exosphere and not on the surface near the subsolar point. This implies that all the ambient sodium released from the bulk or that has fallen back onto the surface near the subsolar point will be immediately evaporated to the exosphere, leaving no atomic Na left in areas near the subsolar point. Therefore, based on these considerations, PSD can not compete to desorb sodium because there is no Na left available on the surface.

These interpretations follow the line of what was previously deduced from experiments by Madey et al. (1998) carried out with various oxide surfaces that resembled the Hermean and lunar regolith. The authors found that at temperatures in the range of ∼400–800 K, TD of fractional Na monolayers occurs even for low alkali coverages, with the desorption barrier (and surface lifetimes) increasing on a radiation damaged surface. Specially, their measurements indicate that at equatorial regions TD rapidly depletes the alkali atoms from the surface reservoir, whereas it is less efficient at high latitudes. This is consistent with our finding that at low altitudes and at the subsolar point, TD is the dominant process and is responsible for the exospheric Na at low altitudes up to about 600 km. On the other hand, MIV is a very plausible mechanism for explaining the high-energy component, since it releases Na present in the bulk and thus is not limited by the availability of Na on the surface.

6 Conclusions

We present the results of our Monte Carlo model of the Hermean sodium exosphere and compare them with the sodium tangent column density profile derived from MASCS/UVVS measurements during the day on 23 April 2012 (Cassidy et al., 2015). Using the correct parameters for TAA and T_S for the day of the observations, we calculate the density profiles of sodium atoms ejected from Mercury's surface through TD, PSD, MIV, and SP as release mechanisms.

We reproduce the derived sodium TCD profile as a function of altitude: below 500 km, the dominant release mechanism of Na is TD with a surface temperature of 594 K, corresponding to a characteristic energy of 0.06 eV. Because of the very high release fluxes, the Na in the exosphere near the surface is due to TD, limited by the supply of available Na atoms on the surface. Only at higher altitudes does the contribution by MIV prevail up to the observed 4000 km with a characteristic energy of 0.34 eV.

For the first 500 km with the MC model TD results agree well with the Chamberlain model using a local surface temperature of 594 K, and both agree with the measurements. As we go farther away from Mercury's surface, though, there is a more energetic component of Na atoms in the exosphere, which we find to be the result of MIV.

We have also shown that if there would be an ambient sodium layer available on the surface at the subsolar point, this would have to be immediately evaporated due to the high volatility of Na at such a high surface temperature at the given observation time. The Na release by TD is strongly limited by the supply of free Na to the surface at the local surface temperature. Moreover, release by PSD can only be responsible for the Na exosphere population at higher altitudes because of the higher energies of the released Na atoms. However, we find that we can only give an upper limit for the release of Na via PSD for the investigated observations.

Our results diverge substantially from the results by Cassidy et al. (2015). While their work is explanatory and suggests the derived observations in terms of two thermal release populations using the Chamberlain model, it seems like they arrive at a confounding near-to-the-surface sodium temperature of 1200 K. Using their assumptions and the Chamberlain model we get good agreement of our model (MC and Chamberlain) for the calculated surface temperature, which is half their value, and the results using our MC model confirm the same number.

As mentioned before, our results apply to the specific observation conditions we discussed. As shown in our diagram in Fig. 6, for other observation geometries, i.e., a different line of sight and TAA, other surface release mechanisms might be active and can dominate over others. Future work will include a larger data set with different observation conditions to test our model and determine the influence of other release processes.

The use of mass spectrometers is crucial for studying the surface composition of Mercury and ultimately understanding the origin of species found in the exosphere, since they come from the regolith and crust (except for the noble gases, hydrogen, and a few volatile species such as sulfur, which are abundant in the micro-meteorite population). To prepare for the SERENA investigation (Orsini et al., 2010), to be performed aboard the ESA's BepiColombo planetary orbiter (Milillo et al., 2010), we have updated and extended our MC model, originally developed by Wurz and Lammer (2003), which is a tool to quantitatively predict exospheric densities for several release processes using the actual physical parameters of the release process.

Appendix A: Chamberlain model implementation

Chamberlain's model (Chamberlain, 1963) is based on Liouville's theorem applied to a collisionless exosphere where the gravitational attraction and the thermal energy conducted from below are the controlling factors. The Liouville equation is solved using a Maxwellian distribution as the boundary condition at the exobase. The velocity distribution is then integrated in the region allowed by the trajectory in a gravitational field and over the velocity space, which can be divided into different populations that represent different types of particle orbits: ballistic (captive particles whose orbits intersect the critical level, i.e., surface in Mercury's case), satellite (captive particles orbiting above the critical level), and escaping (particle's velocity is larger than the escape velocity). This leads to analytic expressions for the density distributions and the loss flux. The number density at a given altitude r is given by

$$\begin{array}{}\text{(A1)}& n\left(r\right)=n\left(r_{\mathrm{c}}\right)\exp \left[-({\mathit{\lambda }}_{\mathrm{c}}-\mathit{\lambda })\right]\mathit{\zeta }\left(\mathit{\lambda }\right),\end{array}$$

where the parameter λ represents the absolute value of the potential energy expressed in units of $k_{{\mathrm{BT}}_{\mathrm{c}}}$ as follows:

$$\begin{array}{}\text{(A2)}& {\mathit{\lambda }}_{\mathrm{c}}\left(r\right)={\displaystyle \frac{GMm}{k_{{\mathrm{BT}}_{\mathrm{cr}}}}}={\displaystyle \frac{v_{\mathrm{esc}}^{\mathrm{2}}}{V^{\mathrm{2}}}},\end{array}$$

where $v_{\mathrm{esc}}=(\mathrm{2}GM/r_{\mathrm{c}}{)}^{\mathrm{1}/\mathrm{2}}$ is the escape velocity and $V=(\mathrm{2}{k}_{{\mathrm{BT}}_{\mathrm{c}}}/m{)}^{\mathrm{1}/\mathrm{2}}$ is the most probable Maxwellian velocity (thermal velocity), G is the gravitational constant, M is the mass of the planet, m is the mass of the species, k_B the Boltzmann constant, T_c is the exobase temperature, and r is the radial distance from the center of the planet. The subscript “c” stands for critical level that corresponds to the exobase, which corresponds to Mercury's surface in this case.

Equation (A1) is a combination of the barometric density equation with a partition function ζ(λ), where n(r_c) is the density at the critical level. The factor ζ may be regarded as the fraction of the isotropic Maxwellian distribution that is present at a given altitude, subject to conservation of energy and angular momentum. For no dynamical restrictions to the orbit, ζ=1, which leads to the generalized form of the (isothermal) barometric law. However, at substantial distances above the critical level the barometric law breaks down because the pressure at large distances is decidedly directional and the mean kinetic energy per atom decreases. The atmosphere is not strictly in hydrostatic equilibrium, moreover it is expanding slightly; i.e., some matter is being lost, which in the kinetic theory corresponds to evaporative loss. To treat the density distribution accurately it is necessary to examine the individual particle orbits, which is the case when ζ≠0. The analytical expressions of ζ for each class of particle orbits can be found in Chamberlain (1963). The effect of radiation pressure on sodium atoms was also incorporated following Bishop and Chamberlain (1989). Examples of sodium column density profiles for the different types of trajectories are displayed in Fig. A1, considering a surface temperature of T_c=594 K.

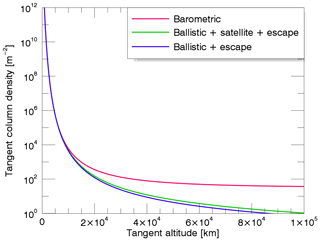
Figure A1 Examples of the TCD profiles for sodium for an exobase temperature of 594 K using the Chamberlain model. The pink curve represents the density profile for the barometric law; the green curve represents a combination of ballistic, satellite, and escape orbits; and the blue curve represents density profiles including ballistic and escaping particles.

On the other hand, sodium atoms in the atmosphere of Mercury can be accelerated by solar radiation pressure resulting from resonant scattering of solar photons. In earlier works was suggested that radiation pressure could sweep sodium off the planet, provided that the sodium is non-thermal (e.g., Ip, 1986; Bishop and Chamberlain, 1989; Wang and Ip, 2011). Under the influence of radiation pressure, particles' trajectories can depart significantly from Keplerian counterparts, thus modifying the exosphere structure. As a consequence, the sodium atoms might be expected to be pushed away from the Sun towards the nightside of Mercury as the radiation pressure increases. It has been shown that for sodium atoms, radiation acceleration can be up to 54 % of the surface gravity (Smyth and Marconi, 1995). We follow Bishop and Chamberlain (1989) by modifying the potential energy function, $\left|\mathit{\lambda }\right(r\left)\right|$, and we implement the solar radiation acceleration expression as used by Wang and Ip (2011). Equation (A3) is the new expression for the potential energy in units of k_BT and is a combination of the acceleration by gravity and radiation forces:

$$\begin{array}{}\text{(A3)}& \mathit{\lambda }\left(r\right)={\displaystyle \frac{GMm}{k_{\mathrm{BT}r}}}-{\displaystyle \frac{m{b}_{\mathrm{rp}}r\cos \left(\mathit{\theta }\right)}{k_{B}T}},\end{array}$$

where b_rp is the radiation acceleration and is a function of TAA. We used the value of b_rp from Smyth and Marconi (1995) for TAA = 202^∘. θ is the solar zenith angle. Figure A2 is another example of sodium column density profiles considering different values of surface temperature, TAA, and SZA. The variation with TAA modifies substantially the density profiles. When the radiation pressure is maximal, i.e., TAA ≈ 65, 280, and SZA = 0^∘ (subsolar point), the density profiles have a steeper slope, which means that exospheric particles are pushed back towards the surface. On the other hand, when the radiation pressure is minimal but not zero (that is when SZA = 90^∘), i.e., TAA = 180, 180, and SZA = 89^∘, the density profiles have a flatter slope, which means that exospheric particles are able to reach higher altitudes.

Figure A2 Examples of the TCD profiles for sodium using Chamberlain model for different values of temperature, T₀ = [600, 700, 900, 1200, 2000] K, and fixing parameters for maximum and close to minimum radiation pressure (max: TAA = 65 and SZA = 0^∘; ∼ min: TAA ≈ 180 and SZA = 89^∘).