Sensitivity of GNSS tropospheric gradients to processing options

An analysis of processing settings impacts on estimated tropospheric gradients is presented. The study is based on the benchmark data set collected within the COST GNSS4SWEC action with observations from 430 Global Navigation Satellite Systems (GNSS) reference stations in central Europe for May and June 2013. Tropospheric gradients were estimated in eight different variants of GNSS data processing using precise point positioning (PPP) with the G-Nut/Tefnut software. The impacts of the gradient mapping function, elevation cut-off angle, GNSS constellation, observation elevation-dependent weighting and real-time versus post-processing mode were assessed by comparing the variants by each to other and by evaluating them with respect to tropospheric gradients derived from two numerical weather models (NWMs). Tropospheric gradients estimated in post-processing GNSS solutions using final products were in good agreement with NWM outputs. The quality of high-resolution gradients estimated in (near-)real-time PPP analysis still remains a challenging task due to the quality of the real-time orbit and clock corrections. Comparisons of GNSS and NWM gradients suggest the 3^∘ elevation angle cut-off and GPS+GLONASS constellation for obtaining optimal gradient estimates provided precise models for antenna-phase centre offsets and variations, and tropospheric mapping functions are applied for low-elevation observations. Finally, systematic errors can affect the gradient components solely due to the use of different gradient mapping functions, and still depending on observation elevation-dependent weighting. A latitudinal tilting of the troposphere in a global scale causes a systematic difference of up to 0.3 mm in the north-gradient component, while large local gradients, usually pointing in a direction of increasing humidity, can cause differences of up to 1.0 mm (or even more in extreme cases) in any component depending on the actual direction of the gradient. Although the Bar-Sever gradient mapping function provided slightly better results in some aspects, it is not possible to give any strong recommendation on the gradient mapping function selection.

1 Introduction

When processing data from Global Navigation Satellite Systems (GNSS), a total signal delay due to the troposphere is modelled by epoch- and station-wise zenith total delay (ZTD) parameters, and, optimally, together with tropospheric gradients representing the first-order asymmetry of the total delay. ZTDs, which are closely related to integrated water vapour (IWV), are operationally assimilated into numerical weather models (NWMs) and have been proven to improve precipitation forecasts (Vedel and Huang, 2004; Guerova et al., 2006; Shoji et al., 2009). Previous studies demonstrated that the estimation of tropospheric gradients improves GNSS data processing mainly in terms of receiver position and ZTDs (Chen and Herring, 1997; Bar-Sever et al., 1998; Rothacher and Beutler, 1998; Iwabuchi et al., 2003; Meindl et al., 2004). Nowadays, tropospheric gradients are not assimilated into NWMs; however, they could be assimilated in future (see Zus et al., 2019) and they are essential for reconstructing slant total delays (STDs). The STDs represent the signal travel time delay between the satellite and the station due to neutral atmosphere and they are considered useful in numerical weather prediction (Järvinen et al., 2007; Kawabata et al., 2013; Bender et al., 2016) and reconstruction of 3-D water vapour fields using the GNSS tomography method (Flores et al., 2000; Bender et al., 2011).

Brenot et al. (2013) showed a significant improvement in IWV-interpolated 2-D fields when tropospheric gradients are taken into account. With the improved IWV fields, the authors studied small-scale tropospheric features related to thunderstorms. Douša et al. (2018a) demonstrated the advantage of using tropospheric gradients in the two-stage troposphere model combining NWM and GNSS data. Morel et al. (2015) presented a comparison study on zenith delays and tropospheric gradients from 13 stations at Corsica in the year 2011. Despite good agreement in the ZTD, they found notable discrepancies in tropospheric gradients when estimated by using two different GNSS processing software packages, two different gradient mapping functions, and two different processing methods: (1) double-differenced network solution, and (2) precise point positioning, PPP (Zumberge et al., 1997), solution. Douša et al. (2017) indicated a problem with systematic errors in tropospheric gradients due to absorbing instrumentation errors. Few attempts were made to compare the tropospheric gradients with independent estimates, i.e. those derived from water vapour radiometer (WVR) or NWM data. For a selected number of stations such a comparison was made in Walpersdorf et al. (2001), where ZTDs and tropospheric gradients from GPS were compared with those derived from a high-resolution NWM, ALADIN. A good correlation between GPS and NWM gradients was found for inland stations but not for coastal ones. More recently Li et al. (2015) and Lu et al. (2016) showed that with the upcoming finalization of new systems such as Galileo and BeiDou the improved observation geometry yields more robust tropospheric gradient estimates. Li et al. (2015) found an improvement of about 20 %–35 % for the multi-GNSS processing when compared with NWMs and 21 %–28 % when compared to WVR. Another multi-GNSS study on tropospheric gradients (Zhou et al., 2017) used data from a global network of 134 GNSS stations processed in six different constellation combinations in July 2016. An impact of the gradients' estimation interval (from 1 to 24 h) and cut-off elevation angle (between 3 and 20^∘) on a repeatability of receiver coordinates was examined. Better results were found for solutions where a shorter time interval of tropospheric gradient estimation was used and where the elevation cut-off angle of 7 or 10^∘ was applied. However, strategies were not compared from the point of view of actually obtained gradient values. Finally, systematic differences and impacts of a gradient mapping function or observation elevation weighting on estimated gradients have not been studied yet.

In this work, we systematically evaluate the quality of tropospheric gradients estimated from a regional GNSS dense network under different atmospheric conditions. Using a unique data set, we study the impact of several approaches. ZTDs and tropospheric gradients are then compared with the ones estimated from two NWMs – ERA5, which is a global atmospheric reanalysis, and a limited-area short-range forecast utilizing the Weather Research and Forecasting (WRF) model. Finally, we quantified systematic differences in tropospheric gradients coming from the gradient mapping function and the method of observation weighting during a local event with strong wet gradients.

2 Data and methods

2.1 Benchmark data set

The benchmark campaign was realized within the European COST Action ES1206 GNSS4SWEC to support development and validation of a variety of GNSS tropospheric products. An area in central Europe covering Germany, the Czech Republic and part of Poland and Austria was selected as a domain and May and June 2013 as a suitable time period due to the occurrence of severe weather events including extensive floods. Data from 430 GNSS stations were collected together with meteorological observations from various instruments (synoptic, radiosonde, WVR, meteorological radar, etc.). In addition, tropospheric parameters from two global and one regional NWMs were generated. Detailed information about the benchmark campaign can be found in Douša et al. (2016). Although the presented study is based on the GNSS data collected within the benchmark campaign, all the presented GNSS and NWM solutions were newly prepared for this study.

2.2 Estimation of tropospheric gradients from GNSS

The STD as a function of the azimuth (a) and elevation (e) angle can be written as follows:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}\mathrm{STD}\left(ae\right)& =\mathrm{mfh}\left(e\right)\cdot \mathrm{ZHD}+\mathrm{mfw}\left(e\right)\cdot \mathrm{ZWD}\\ & +\mathrm{mfg}\left(e\right)\cdot (\mathrm{Gn}\cdot \cos (a)+\mathrm{Ge}\cdot \sin (a\left)\right),\end{array}\end{array}$$

where ZHD denotes the zenith hydrostatic delay and ZWD denotes the zenith wet delay. The elevation angle dependency is given by mapping functions, which are different for the hydrostatic (mfh), wet (mfw) and gradient (mfg) parts. The tropospheric horizontal gradient vector is defined in the local horizontal plane with two components, one for the north–south direction (Gn) and one for the east–west direction (Ge). The GNSS gradient modelled by Eq. (1) represents a total gradient (the hydrostatic and wet components are not explicit in this formulation).

During GNSS data processing, the ZHD is commonly taken from an a priori model, e.g. Saastamoinen (1972) or Global Pressure and Temperature (GPT, Boehm et al., 2007) based on climatological data, or it can be derived from NWM data. The ZWD, or a correction to the modelled ZHD, and tropospheric gradients are estimated as unknown parameters using a deterministic or stochastic model.

Current mapping functions for hydrostatic (mfh) and wet (mfw) delay components are based either on climatological data, e.g. the Global Mapping Function, GMF (Boehm et al., 2006a), or NWM data, e.g. the Vienna Mapping Function, VMF (Boehm et al., 2006b). An advantage of the first approach is its independence of external data. Several mapping functions for tropospheric gradients have also been developed in the past, e.g. by Bar-Sever et al. (1998), by Chen and Herring (1997), or the tilting mapping function introduced by Meindl et al. (2004). The gradient mapping function (mfg) by Bar-Sever (BS) is given as

$$\begin{array}{}\text{(2)}& \mathrm{mfg}=\mathrm{mfw}\cdot \cot \left(e\right),\end{array}$$

and from the formula it is apparent that it depends on the selected mfw. The Chen and Herring (CH) mfg reads as

$$\begin{array}{}\text{(3)}& \mathrm{mfg}=\mathrm{1}/\left(\sin \right(e)\cdot \tan (e)+c),\end{array}$$

where c=0.0032. Since c is related to the scale height, it experiences spatio-temporal variations. Nevertheless, based on Balidakis et al. (2018), a variable c does not yield a statistically significant improvement in describing the atmospheric state over a constant c. Finally, the tilting mapping function is defined in a generic way as a derivative of the mfw with respect to the elevation angle:

$$\begin{array}{}\text{(4)}& \mathrm{mfg}=-\partial \left(\mathrm{mfw}\right)/\partial e.\end{array}$$

Figure 1 illustrates the variability of the gradient contribution term $(\mathrm{Gn}\cdot \cos (a)+\mathrm{Ge}\cdot \sin (a\left)\right)$ in Eq. (1) and the size of the mapping factors represented by actual values of the three mfg. We included gradient contributions corresponding to all GNSS observations in the benchmark campaign during a single day (31 May 2013). Obviously, an actual magnitude of the gradient depends on the mapping factor. While the BS mfg generates higher mapping factors and thus smaller gradient contribution terms (scatters in the y axis), the CH mfg provides lower mapping factors and thus higher gradient contribution terms. The tilting mfg then gives factors in between BS and CH mfg and results in gradient contributions in between the two. In the following we focus on BS and CH mfg only, as these can be considered two extreme cases.

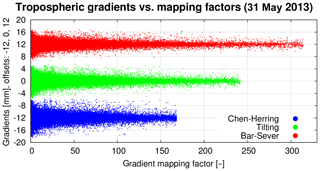
Figure 1 Variability of gradient mapping factors and tropospheric gradient contributions expressed in azimuths of individual satellites. Three mfg were studied on 31 May 2013: Chen and Herring mfg (blue), Bar-Sever mfg (red) and tilting mfg (green).

We use the G-Nut/Tefnut software (Václavovic et al., 2014) for GNSS data processing of the benchmark campaign. This software utilizes the PPP method and is capable of multi-GNSS processing in real-time (RT), near-real-time (NRT) and post-processing (PP) modes with a focus on all the tropospheric parameters' estimation: ZTDs, tropospheric gradients and slant delays (Douša et al., 2018b). Stochastic modelling of the troposphere allows an epoch-wise parameter estimation by extended Kalman filter in RT solutions (FLT) or its combination with a backward smoother which is used for NRT and post-processing solutions (FLT+SMT); see Václavovic and Douša (2015).

Table 1 describes all eight variants of solutions for the benchmark campaign produced using the G-Nut/Tefnut which differ in (a) elevation cut-off angle (3 or 7^∘), (b) gradient mapping function (Chen and Herring: CH or Bar-Sever: BS), (c) constellations (GPS only: Gx or GPS+GLONASS: GR) and (d) processing mode (post-processing using the FLT+SMT processing or simulated real time using the FLT processing only). Five variants based on the post-processing mode used the backward smoother and the ESA final orbit and clock products (http://navigation-office.esa.int/GNSS_based_products.html, last access: 14 June 2019). Three variants, abbreviated as RT1GxCH3, RT3GxCH3 and RTEGxCH3, were used to test the performance of the Kalman filter and RT orbit and clock corrections using the IGS01 (RT1GxCH3) and IGS03 (RT3GxCH3) corrections from the IGS Real-Time Service (RTS, http://rts.igs.org, last access: 14 June 2019). The IGS01 RTS product is a GPS-only single-epoch solution produced using software developed by ESA/ESOC. The IGS03 product is a GPS+GLONASS solution based on the Kalman filter and the BKG's BNC software. The last solution, RTEGxCH3, applying the ESA final product is used to test a benefit of the backward smoothing on the one hand and an impact of the quality of RT corrections on the other hand. Unfortunately, the solution based on the processing of GPS+GLONASS data in the simulated RT mode had to be rejected due to a highly variable quality of RT corrections in 2013 affecting mainly the GLONASS contribution (and we noted temporal problems in GPS solutions too; see Fig. 4).

The GPT model was used for calculating a priori ZHDs and the GMF was used for mapping hydrostatic and wet delays to the zenith. Estimated tropospheric parameters are thus independent of any meteorological information. GNSS observations were processed using 30 h data batches when starting 6 h before the midnight of a given day in order to eliminate the PPP convergence. In all variants, the observation sampling of 300 s was used with ZTDs and tropospheric gradients estimated for every epoch. The station coordinates were estimated on a daily basis. The random walk of 6 mm/sqrt(h) was applied for the ZTD and 1.5 mm/sqrt(h) for the gradients. Absolute IGS model IGS08.ATX was used for the antenna-phase centre offsets and variations. All variants used the elevation observation weighting of 1∕sin ²(e).

Table 1 Processing parameters of individual variants from the G-Nut/Tefnut software. Mode FLT denotes a simulated real-time solution using a Kalman filter only and FLT+SMT a post-processing solution using the Kalman filter and the backward smoother.

2.3 Estimation of tropospheric gradients from NWM

Tropospheric gradients and zenith delays were derived from the output of two different numerical weather models: the ERA5 (https://www.ecmwf.int/en/forecasts/datasets/archive-datasets/reanalysis-datasets/era5, last access: 14 June 2019) and a simulation utilizing the Weather Research and Forecasting (WRF) model (Skamarock et al., 2008). The ERA5 is a reanalysis produced at the European Centre for Medium-Range Weather Forecasts (ECMWF). The pressure, temperature and specific humidity fields are provided with a horizontal resolution of approximately 31 km (T639 spectral triangular truncation) on 137 vertical model levels (up to 0.01 hPa) every hour. The WRF simulations are performed at GFZ Potsdam. The initial and boundary conditions for the limited-area 24 h free forecasts (starting every day at 00:00 UTC) stem from the analysis of the Global Forecast System (GFS) of the National Centers for Environmental Prediction (NCEP). The pressure, temperature and specific humidity fields are available every hour with a horizontal resolution of 10 km on 49 vertical model levels (up to 50 hPa).

The ray-trace algorithm by Zus et al. (2012) is used to compute STDs. The tropospheric gradients are derived from STDs as follows. At first, 120 STDs are computed at elevation angles 3, 5, 7, 10, 15, 20, 30, 50, 70, and 90^∘ and all azimuths between 0 and 360^∘ with an interval of 30^∘. Second, we compute azimuth-independent STDs from the local vertical refractivity profile. Third, the differences between the azimuth-dependent STDs and the azimuth-independent STDs are computed. Finally, the gradient components are determined by a least-square fitting. For details the reader is referred to the Appendix in Zus et al. (2015).

Using 10 years of ERA5 global data, we tested different observation elevation-weighting schemes (equal versus the elevation-dependent weighting of 1∕sin ²(e)) and two mfg (BS and CH) in the least-square parameter fitting. While using different observation elevation-weighting schemes led to negligible differences in the tropospheric gradients, we found a significant systematic difference in the north-gradient component between tropospheric gradients derived with BS and CH mfg (see Appendix A). In this regard it is important to note that NWM-derived tropospheric gradients presented in this study were computed using CH mfg.

We note that tropospheric gradients can be computed with the closed-form expression depending on the north–south and east–west horizontal gradients of refractivity (Davis et al., 1993). We compared the ERA5 tropospheric gradients derived with our method and the closed-form method with GNSS tropospheric gradients from the GRCH3 solution. We find that for the considered stations (over the entire benchmark period), the root-mean-square deviation between NWM and GNSS tropospheric gradients is 10 % smaller if we apply our method instead of the closed-form method. This can be explained by the fact that our method is closer to the method actually applied in the GNSS analysis (parameter estimation).

We also compared our NWM tropospheric gradients with NWM tropospheric gradients provided by the TU Vienna (see Appendix B). We found good agreement between the estimates, in particular between our tropospheric gradients and the so-called refined horizontal gradients (Landskron and Boehm, 2018).

2.4 Comparison of gradient estimates

Absolute values of tropospheric-gradient components stay typically below 1–2 mm under standard atmospheric conditions and can reach 4–6 mm during severe weather conditions. The gradient of 1 (6) mm corresponds to about 55 (330) mm slant delay correction when projected to 7^∘ elevation angle. For an illustration, an example time series of tropospheric gradients at station LDB2 (Brandenburg, Germany) for a period between 15 May and 15 June 2013 is given in Fig. 2.

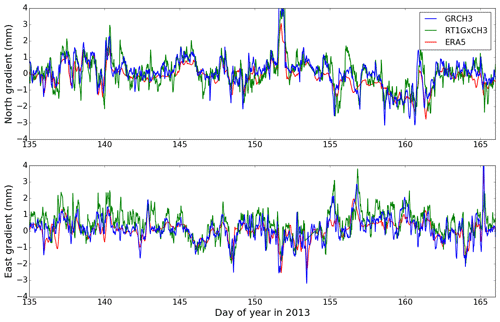
Figure 2 Tropospheric gradients retrieved from GNSS data processing (GRCH3, RT1GxCH3) and from NWM ERA5 at station LDB2 (52.209^∘ N, 14.121^∘ E, Germany) for a period from 15 May till 15 June 2013.

In the presented study, ZTDs and tropospheric gradients from all eight GNSS variants were compared to each other and also to the tropospheric parameters from ERA5 and WRF to evaluate the impact of various settings in GNSS data processing. Although about 430 GNSS stations are available in the benchmark data set, statistical results given in Sect. 3 are based on a subset of 243 stations. Firstly, 84 stations without the capability of receiving GLONASS signals were excluded. Secondly, stations which did not have at least 5 % of all the observations in the range of elevation angles between 3 and 7^∘ were excluded as well. This rule was applied to allow a systematic evaluation of elevation cut-off angle impact on tropospheric parameters. The majority of the stations (103) had to be excluded because of an inability to provide a sufficient number of observations at very low-elevation angles.

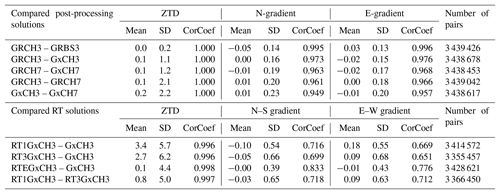
Statistics presented in Tables 3, 4 and 5 were computed directly from ZTD and tropospheric gradient differences from 243 GNSS stations over 55 d with 288 estimates per day, i.e. a total of ∼3.4 million differences. During their computation a standard data screening was applied to exclude outlier values identified as differences exceeding a given threshold value. Moreover, epochs were RT GNSS variant of solution RT3GxCH3 provided unrealistic tropospheric gradients (see Sect. 3.3) were also excluded from all the statistics computations for all compared GNSS (NWM) solutions except from the coordinates' repeatability evaluation. Identification of these unrealistic epochs was realized by a visual inspection of gradient maps (see Sect. 3.3). Actual numbers of differences used for computation of presented statistics for the two compared GNSS (NWM) solutions are provided in Tables 4 and 5.

Tropospheric parameters from the G-Nut/Tefnut software were provided every 5 min, while the output from both NWM models was available every hour. Therefore, comparisons between GNSS solutions (Sect. 3.2) are based on a 5 min interval, while comparisons between GNSS and NWM solutions (Sect. 3.3) are based on a 1 h interval.

3 Impact of applied processing settings on GNSS tropospheric gradient estimation

The section starts with an introductory evaluation of mean tropospheric gradients and formal errors of their estimates. This is followed by comparisons between individual GNSS solutions and comparisons between GNSS and NWM solutions.

3.1 Comparison of mean tropospheric gradients and formal errors of their estimates

Mean gradient magnitudes and azimuth angles (direction of gradient) over the whole benchmark period were computed for 243 GNSS stations and are presented in Table 2. Mean magnitudes of tropospheric gradients from all post-processing GNSS variants oscillated around 0.85 and 0.67 mm when using the CH mfg and the BS mfg, respectively. The latter shows about 17 % smaller gradients compared to the former if all the processing aspects remained identical. Both RT solutions also resulted with higher gradient magnitudes, namely +14 % for RT1GxCH3 and +42 % for RT3GxCH3 when compared to the corresponding GxCH3 post-processing variant. A mean gradient magnitude of about 0.7 mm was found for both NWM solutions, i.e. of about 0.1 mm smaller than for the GRCH3 solution. This can be mainly explained by the limited horizontal resolution of the NWMs.

Table 2 Mean magnitudes and azimuth angles of tropospheric gradients from all individual GNSS variants of processing and NWMs ERA5 and WRF.

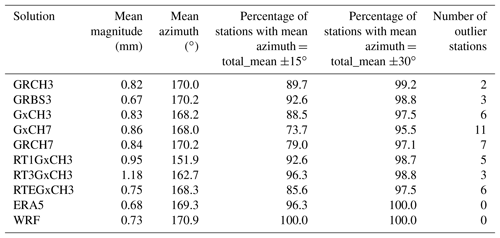
Table 2 shows that mean tropospheric gradients point towards the Equator, which is in agreement with Meindl et al. (2004). Such a mean gradient direction does not depend on the gradient mapping function. By adding GLONASS observations the mean gradient direction was changed by +2^∘; however, actual effects were found to be highly station-dependent with a typical range of ±5^∘ for individual stations. The direction of the mean gradient in both NWM solutions was in very good agreement with all GNSS post-processing variants.

Directions of the mean gradient over individual stations were mostly within ±15^∘ when compared to the total mean gradient estimated for the stations and the solution variant. On the other hand, the performance was not identical for the individual solutions. A change in cut-off elevation angle from 7 to 3^∘ led to an increased number of stations with the mean gradient direction within ±15^∘ of the total mean direction and to a decreased number of stations with a mean gradient direction differing for more than 30^∘ (regarded as outlier stations in Table 2). Two GNSS stations were marked as outliers by all processed variants, with their mean gradient direction differing by more than 50^∘ from the total variant mean. Both of them are located in an urban area in south-western Germany and use the same receiver and antenna type from Leica, which is however used by many other stations in the same region where no issues with gradient mean angle were identified. Still, the reason for their different behaviour can be of instrumental or environmental origin.

Table 3 Mean position repeatability and formal errors and their standard deviation for tropospheric parameters from individual GNSS processing variants.

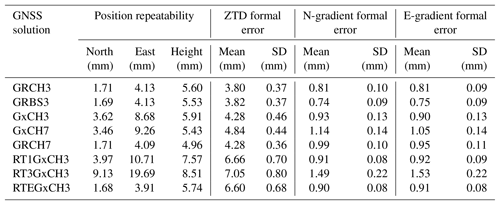
Table 3 summarizes mean repeatability of daily coordinates as well as statistical comparison of formal errors of estimated ZTDs and tropospheric gradients from different GNSS-processing variants. The station coordinates' repeatability is improved when using combined GPS+GLONASS solutions compared to GPS-only solutions, namely by factors of 2 and 1.2 in horizontal components and the height, respectively. The number of available satellites and their geometry play a significant role in this context. An increase in the elevation angle cut-off (from 3 to 7^∘) resulted in improved height repeatability, which is consistent with the results of Zhou et al. (2017) suggesting an optimal 7^∘ cut-off for the height repeatability when comparing results of a different elevation angle cut-off (3–15^∘). However, it should be noted that GPT+GMF models and the PPP method were used in both cases. In contrast, Douša et al. (2017) observed an improvement in the height repeatability even when using the elevation angle cut-off 3^∘ (compared to 7 and 10^∘) when exploiting double-difference observations, the VMF1 mapping function (Boehm et al., 2006b) and the Bernese GNSS software (Dach et al., 2015). Douša et al. (2017) also indicated worse results when using GPT+GMF compared to VMF1, which can be attributed to modelling errors in the former, particularly when applied in PPP (Kouba, 2009). We also notice a slightly better performance in the case of the BS mfg when compared to the CH mfg, while this difference was found to be statistically significant in the north and up component by the Wilcoxon signed-rank test at the 5 % significance level. The results of the forward filter processing did not show any degradation when using the ESA final products (RTEGxCH3). When using the IGS real-time product, the repeatability of all coordinates became worse by factors of 2–3 and 4–5 for the RT1GxCH3 and RT3GxCH3 variants, respectively. The latter is attributed to a lower quality of the IGS03 RT product during some periods; see Fig. 4.

Formal error of the parameter can be generally regarded as an estimation uncertainty. Formal errors increase when the number of observations and/or the geometry decrease. This can be observed in Table 3 when the elevation cut-off is increased. Formal errors are about 17 % and 11 % smaller when using the 3^∘ cut-off (GRCH3) compared to the 7^∘ cut-off (GRCH7) for horizontal gradients and ZTDs, respectively, thus indicating a higher impact on the former. A decrease in formal errors of tropospheric gradients estimated with a 3^∘ cut-off compared to a 10^∘ cut-off was previously reported also by Meindl et al. (2004). Interestingly, using the BS mfg resulted in smaller formal errors of tropospheric gradients, but we have not observed any change in formal errors of other estimated parameters. The smaller formal errors may suggest an improvement in estimated parameters using BS mfg, as also found from the coordinates' repeatability.

3.2 Comparison of individual GNSS variants with each other

Results for individual GNSS variant comparison are presented in Table 4. We notice good agreement among all the post-processing variants (top part of Table 4). The mean differences stayed below 0.2 mm for ZTD and ±0.02 mm for tropospheric gradients with one exception for the latter parameter. This was a comparison between results provided by CH and BS mfg where the mean differences reached −0.05 and 0.03 mm for the north- and east-gradient components, respectively. These small systematic effects can be attributed to the average difference between tropospheric gradients computed with BS mfg compared to CH mfg. The standard deviation (SD) indicates the smallest impact due to the change in mfg for both ZTD estimates (0.2 mm) and tropospheric gradients (∼0.14 mm). The impact increases then for both ZTD and gradients when comparing results of single and dual constellations (1.2 mm for ZTD, ∼0.17 mm for gradients). It should be noted that GLONASS observations were down-weighted by a factor of 1.5 in dual-constellation variants of the solution to reflect both a lower quality of precise products and observations. The gradients estimated with improved geometry and using more observations are expected to be more accurate and reliable. It is notable in the comparisons of single or dual constellations at different elevation cut-off angles (the impact is larger for a higher cut-off). The largest impact is eventually observed due to the elevation cut-off angle, i.e. 2.2 and ∼0.20 mm for ZTD and tropospheric gradients, respectively. Linear correlation coefficients (CorCoef) reach a value of ∼1 in all cases for the ZTD comparisons. The ZTDs were thus practically unaffected by different gradient models. For the gradient comparisons, the correlation coefficients are progressively decreasing from 0.99 to 0.95, while values of SD are increasing.

An increased scatter of RT processing is visible in significant mean differences and in the standard deviation values of ZTD and tropospheric gradients increased by a factor of 3. These are also emphasized by the reduction of correlation coefficients mainly for tropospheric gradients. The two RT solutions can still be considered of good quality if we take into consideration results found in Ahmed et al. (2016) or Kačmařík (2018), where mean biases and SD values of up to 12 mm were reported for comparisons between RT ZTD solutions based on IGS01 and IGS03 streams and post-processing solutions based on final products. Since virtually zero mean differences for both ZTD and tropospheric gradients are found in the RTEGxCH3 variant, when using the Kalman filter too, the degraded quality of RT tropospheric parameters is mainly a consequence of the poorer quality of the IGS01 and IGS03 RT products (Douša et al., 2018b).

The differences of ZTDs and tropospheric gradients from all compared variants of solutions were also statistically tested. And in all cases, the differences were found to be statistically significant at the 5 % significance level while using the Wilcoxon signed-rank test (https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.wilcoxon.html, last access: 14 June 2019). This non-parametric test was used since none of the processed variants of solutions evinced a normal distribution of their ZTDs and tropospheric gradients.

Table 4 Comparison of individual variants of the GNSS data processing run in post-processing mode (top) and in simulated real-time mode (bottom). Units: mean and SD in millimetres; CorCoef represents a linear correlation coefficient.

3.3 Comparison of individual GNSS variants with NWM

The statistics for the GNSS and NWM comparisons are summarized in Table 5. For ZTDs a mean difference of about 1 (4) mm is visible between GNSS and ERA5 with standard deviations around 9 (10) mm and correlation coefficients around 0.99 (0.99) for individual post-processing (RT) GNSS solutions. The negative mean difference of −3 mm in ZTD between GNSS and WRF might be due to the global NCEP GFS analysis which is used for the initial and boundary conditions for the WRF solution. A negative mean difference of −5 mm in ZTD between two GNSS reference solutions and a solution based on the NCEP GFS was already reported in the past (Douša et al., 2016). The standard deviations of differences are about 2 mm larger when GNSS and WRF are compared. This is probably due to the fact that the solution from WRF is based on a 24 h forecast (errors are supposed to grow with increasing forecast length), whereas the solution from ERA5 is based on a reanalysis.

Table 5 Comparison of individual variants of the GNSS data processing run in post-processing mode (top) and in simulated real-time mode (bottom) with NWM solutions. Units: mean and SD in millimetres; CorCoef represents a linear correlation coefficient.

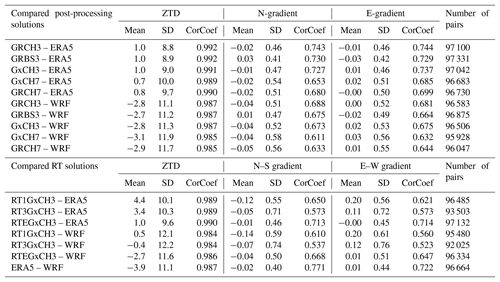
With regards to the tropospheric gradients, the mean differences between post-processed GNSS and NWM stayed within a range from −0.05 to 0.03 mm. The existing differences between two GNSS variants of solutions based on different mfg can be attributed to usage of CH mfg for derivation of NWM tropospheric gradients and to the existing systematic difference between tropospheric gradients estimated using these two mfg (see Sect. 2.2). The standard deviations between GNSS and NWM were approximately doubled or tripled when compared to standard deviations between individual variants of GNSS solutions (Table 4). They were also found to be higher for the WRF than for ERA5. Again, this can be probably explained by the fact that the solution from WRF is based on a 24 h free forecast, whereas ERA5 is based on a reanalysis.

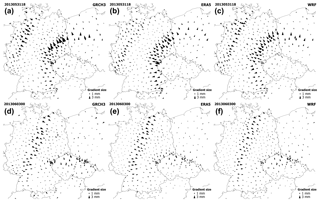
Figure 3 Tropospheric gradient maps from the GNSS GRCH3 solution (a, d), NWM ERA5 solution (b, e) and NWM WRF solution (c, f) on 31 May 2013, 18:00 UTC (a, b, c) and on 3 June 2013 00:00 UTC (d, e, f).

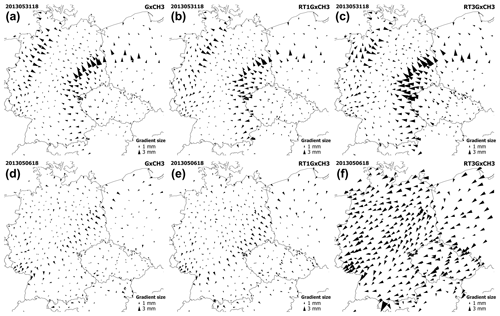
Figure 4 Tropospheric gradient maps from the GNSS GxCH3 solution (a, d), GNSS RT1GxCH3 solution (b, e) and GNSS RT3GxCH3 solution (c, f) on 31 May 2013, 18:00 UTC (a, b, c) and on 6 May 2013, 18:00 UTC (d, e, f).

Both NWMs lead to consistent results: standard deviations are smaller and correlation coefficients higher for GNSS solutions using a lower cut-off elevation angle (3^∘ instead of 7^∘) and/or more observations (GPS+GLONASS). For example, the SD for the north-gradient component between GNSS and ERA5 is 0.54 mm for the GxCH7 variant and 0.46 mm for the GRCH3 variant. This represents a decrease of 15 %. In this regard we also derived tropospheric parameters from both NWMs using a 7^∘ cut-off elevation angle and repeated the comparisons to test whether GNSS variants of a solution with a 7^∘ cut-off would be closer to NWM solutions based also on the 7^∘ cut-off angle. And we always found better agreement between any evaluated GNSS variant of the solution and the NWM solution based on the 3^∘ cut-off angle – in terms of mean difference, standard deviation and correlation coefficient. From two GNSS variants differing only in the mfg, the solution applying the BS mapping function is closer to the NWMs in terms of standard deviation. Since the CH mfg was used to derive tropospheric gradients from NWMs, the opposite situation could be expected, and we generally note that presented results of comparisons between tropospheric gradients from the GNSS GRBS3 solution and NWMs should be taken only as informative. The lower values of standard deviation can be partly understood as the magnitudes computed as $\sqrt{{\mathrm{Gn}}^{\mathrm{2}}+{\mathrm{Ge}}^{\mathrm{2}}}$ of GNSS tropospheric gradients using the BS mfg are smaller compared to the CH mfg (see Sect. 2.2), and the magnitudes of NWM tropospheric gradients are more smoothed compared to the GNSS tropospheric gradients.

In order to evaluate the statistical significance of differences of ZTDs and tropospheric gradients from all variants of GNSS solution and both NWMs, we again applied the Wilcoxon signed-rank test. Again, the differences were found to be statistically significant at the 5 % significance level in all cases.

Maps showing tropospheric gradients were generated for all the variants of GNSS solutions and both NWM solutions and were visually evaluated for the whole benchmark period. For better visualization we included all the GNSS stations of the benchmark campaign, i.e. not just the subset of 243 stations used for the presented statistics. Generally, GNSS provided homogenous fields of tropospheric gradients without noisy behaviour at the level of individual stations, and very good agreement in gradient directions and usually also in gradient magnitudes was found between GNSS and NWM gradient maps. In Fig. 3, two examples are shown for different events when weather fronts were passing over the studied area. For a description of meteorological conditions prevailing during these events the reader is referred to Douša et al. (2016). Tropospheric gradients derived from NWM provided more smoothed gradient fields, but were somehow limited to render local structures mainly due to the spatial resolutions of both NWMs. As the ERA5 model has coarser spatial resolution than the WRF model, such behaviour was a little bit more apparent in its results. On the other hand, when compared to results of the 1^∘ × 1^∘ resolution global models ERA-Interim and NCEP GFS (Douša et al., 2016), the presented NWM tropospheric gradients have larger magnitudes.

Comparing GNSS to NWM products in Table 5 indicated that the RTEGxCH3 solution driven by the Kalman filter and the ESA final product shows a comparable performance to the GxCH3 solution driven by the Kalman filter and the backward smoother. An increase in mean difference and standard deviation values for other solutions based on RT mode indicates that the quality of the RT tropospheric solution is dominated by an actual quality of RT orbit and clock corrections. In this regard, we examined systematically all tropospheric gradient maps and found that gradients from the RTEGxCH3 solution are always in very good agreement with post-processing solutions. Although there were imperfections in matching RT1GxCH3 gradients and post-processing solutions, the performance can still be considered generally good and stable. This was however not the case of the RT3GxCH3 solution, where we observed a varying quality of estimated tropospheric gradients. For the majority of epochs, in particular during the periods with strong gradients, the tropospheric gradients could be evaluated as acceptable. However, situations when gradients from all the stations point to the same direction occurred from time to time, obviously without a physical relation to the actual weather situation. An example of this behaviour is presented in Fig. 4, where tropospheric gradients from the RT3GxCH3 solution behave normally on 31 May 2013, 18:00 UTC, and became unrealistic on 6 May 2013, 18:00 UTC, where all the stations point to the south-westerly direction and reveal high-gradient magnitudes. Such issues occurred occasionally for a limited period of time in the RT3GxCH3 solution only. The reason is an instability of the RT3 stream during the initial period (the first half of 2013) affected by many interruptions, and data gaps thus caused frequent parameter re-initialization in PPP.

4 Impact of different gradient mapping functions and elevation-dependent weighting

Impacts of mapping functions on estimated ZHD (ZWD) and gradient parameters are different, though both represent something of an elevation-dependent parameter scaling. The latter is more sensitive to the mapping function compared to the former, additionally considering their relative magnitudes. The gradient mapping function is strongly driven by the cot(e) approximation (Eq. 2), which is growing quickly for low-elevation angles. Because gradients represent the second-order effect of the tropospheric delay, quickly growing with the distance from the station, they are practically estimated using low-elevation observations and, consequently, the impact of mfg becomes significant.

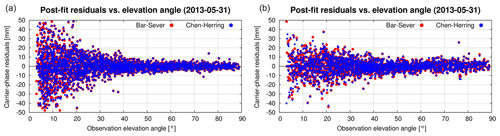
Figure 5 Post-fit-phase residuals' distribution when using different gradient mapping functions, Bar-Sever (red) and Chen and Herring (blue), and observation weighting: SINEL2 (a) and EQUAL (b).

In this section, we focus on studying systematic differences induced purely by different mfg and observation elevation-dependent weighting (OEW) during 8 days from 25 May to 1 June 2013. For two solutions defined in Sect. 2.2 and utilizing CH mfg (GRCH3) and BS mfg (GRBS3), we additionally generated four variants using various OEW schemes: (1) EQUAL, equal weighting, (2) SINEL1, 1∕sin (e) , (3) SINEL2, 1∕sin ²(e), and (4) SINEL4, 1∕sin ⁴(e). Generally, in the SINEL OEW schemes, the contribution of low-elevation observations to all estimated parameters decreases with increasing power y in 1∕sin ^y(e).

Figure 5 displays example distributions of carrier-phase post-fit residuals with respect to the elevation for the SINEL2 observation weighting (panel a), and without any weighting, i.e. EQUAL (panel b). While the residuals from the former are affected by the mfg only below 15^∘ elevation, the residuals in the latter are affected at any elevation angles even close to the zenith direction. Above a 30^∘ elevation angle, the distribution of residuals is smoother for the SINEL2 compared to the EQUAL and more stable according to our experience with many other stations. This is particularly visible when comparing the distribution of residuals at the lowest and highest elevation angles between variants, though both generally follow the expected behaviour when considering errors in GNSS observations and models. These errors include contributions from the atmosphere, multipath, uncertainty of receiver antenna-phase centre variations, a lower signal-to-noise ratio, and cycle slips, all usually increasing with the decrease in the observation elevation angle and with the smallest errors in the zenith direction. Using a weak or no elevation-dependent weighting, the hydrostatic/wet delay mapping separation errors can introduce significant errors in both ZTD and the height coordinate component (Kouba, 2009). Though we generally recommend the use of SINEL2 elevation weighting, we also show below the impact of other weighting schemes on estimated gradients.

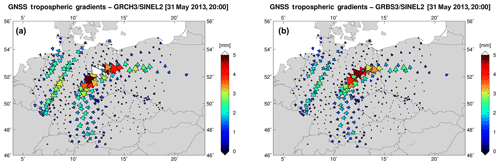
Figure 6 Tropospheric gradient maps on 31 May 2013 (18:00 UTC) from GNSS solutions using the SINEL2 observation weighting scheme: Chen and Herring mfg (a); Bar-Sever mfg (b).

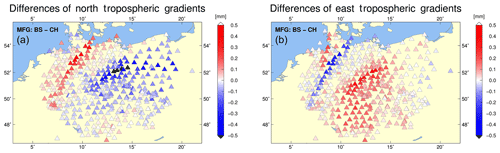
Figure 7 Mean differences (calculated over the full day of 31 May 2013) of the tropospheric north-gradient component (a) and east-gradient component (b) due to different mfg: Chen and Herring (CH) and Bar-Sever (BS) when using the SINEL2 observation weighting schemes.

Figure 6 displays maps of situations with large tropospheric gradients observed on 31 May 2013 at 18:00 UTC when using GRCH3 (panel a) and GRBS3 (panel b) solutions and applying the SINEL2 OEW scheme. The day is interesting due to the presence of an occlusion front over Germany clearly captured by strong tropospheric gradients achievable from both GNSS and NWM analyses. Such events with significant gradients captured in a dense network can help to evaluate differences between mfg and other processing parameters, while they could easily remain hidden in most of the other cases. The impact of mfg on estimated gradients shows systematic changes in gradient magnitudes – the gradients estimated with CH mfg (panel a) are always larger than with BS mfg (panel b), independent of the OEW scheme (not shown). It should be also noticed here that the magnitudes of gradients estimated using the SINEL4 scheme were significantly reduced compared to any other OEW scheme.

Figure 7 shows mean differences, calculated over all epochs on 31 May 2013, in the (panel a) north- and (panel b) east-gradient components between the two mfg (BS minus CH) when using the SINEL2 scheme. Although the magnitudes of CH gradients are always larger compared to BS gradients, the sign of the component differences depends on the gradient direction (north–south for Gn and east–west for Ge). Positive differences in the north- and east-gradient components appear when the estimated gradients point south and west, respectively, and negative differences occur when the gradients point in opposite directions.

Figure 8 Differences in tropospheric gradients between Chen and Herring and Bar-Sever mfg for four observation weighting schemes: EQUAL (EQ), SINEL (S1), SINEL2 (S2), and SINEL4 (S4).

Figure 8 shows histograms of tropospheric gradient differences of all the stations in the network when using different mfg and OEW schemes on 31 May 2013. Obviously, the impact of the mfg on estimated gradients is significantly reduced for SINEL4 (well below 0.2 mm), while it is higher for all the other schemes. This corresponds to the fact that large gradients are related to a horizontal anisotropy of the troposphere affecting more significantly low-elevation observations. The strongest effect can be observed for the EQUAL scheme, reaching systematic differences of 1.0 mm or even higher. Such systematic differences reached 2-fold values of the SD obtained from comparisons of gradients using independent sources such as GNSS and NWM; see Sect. 3.3 or Douša et al. (2017).

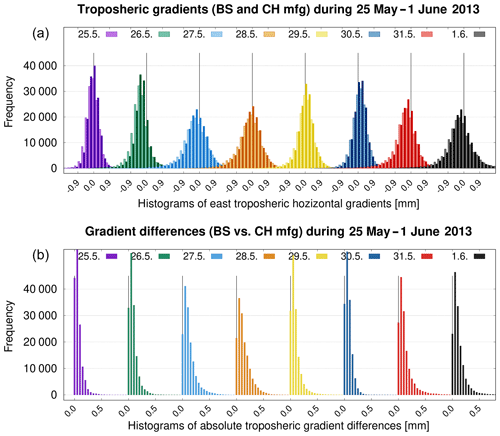
Figure 9 Eastern tropospheric horizontal gradients (a) estimated using Chen and Herring (light columns) and Bar-Sever (dark columns) mfg and the differences (b) in gradient magnitudes between them. The SINEL2 OEW scheme was applied over 8 days in May/June 2013.

Figure 9 compares magnitudes of estimated gradients (east component only) and corresponding histograms of total gradient differences over all stations in the network on 8 consecutive days (25 May–1 June 2013) when using CH and BS mfg and the SINEL2 OEW scheme. We can notice the days with a stronger tropospheric anisotropy (27–28 May, 31 May, 1 June), identifiable by the presence of gradients larger than 1.0 mm. The histograms systematically deviate from the zero on some days; prevailing negative and positive east components indicate that gradients in the network point westwards and eastwards, respectively. Differences in gradient magnitudes are then shown in panel b. The impact due to utilizing different mfg clearly corresponds to the original gradient magnitudes. Both are high during the days with a strong tropospheric anisotropy, while differences due to the mfg choice demonstrate systematic effects of up to 1 mm or more in such extreme cases.

5 Conclusions

We presented an impact assessment of selected GNSS processing settings on estimated tropospheric gradients together with an evaluation of differences resulting from the gradient mapping function and observation elevation weighting. We exploited the GNSS4SWEC benchmark campaign covering May and June in 2013 with prevailing wet weather. Although the time period covered some severe weather events, it also contained a lot of days with standard weather conditions with tropospheric gradients close to zero. Presented results could therefore be considered representative of European conditions during the warmer part of the year.

ZTD values and tropospheric gradients were estimated in eight variants of GNSS data processing and derived from two NWMs (a global reanalysis and a limited-area short-range forecast). All solutions gave tropospheric parameters in high temporal resolution (5 min). Since no meteorological data providing any information about prevailing atmospheric conditions during the evaluated time period entered the GNSS data processing (because we used empirical mapping functions and a priori tropospheric delays), estimated tropospheric gradients can be regarded as fully independent and therefore can provide additional interesting information, along with the ZTD, in support of NWMs (see Douša et al., 2016; Guerova et al., 2016).

When lowering elevation angle cut-off (from 7 to 3^∘), more accurate tropospheric gradient estimates were obtained. The standard deviations of differences of GNSS gradients to NWM gradients were reduced by 10 %, formal errors of tropospheric gradients were reduced, and station-wise mean gradient directions were also more stable. On the other hand, the usage of a lower cut-off angle led to a slightly worse station height repeatability (10 %), which is partly in contradiction with the results of Douša et al. (2017) but in agreement with Zhou et al. (2017). The discrepancy is attributed to the use of the PPP method with simplified modelling (GPT+GMF) for low-elevation observations. The 3^∘ elevation angle cut-off can nevertheless be recommended for an optimal gradient estimation from GNSS data.

A small decrease in the standard deviation of the estimated gradients (2 %) was observed when using GPS+GLONASS instead of GPS only and compared to NWM gradients. This indicates that the post-processing tropospheric gradients can be reliably estimated solely with a GPS constellation. However, it may still depend on applied software, strategy, products and processing, e.g. (near) real time. In this regard, Li et al. (2015) and Lu et al. (2016) demonstrated that tropospheric gradients from multi-GNSS PPP processing improved their agreement with those estimated from NWM and WVR when compared to stand-alone GPS processing.

Using a simulated real-time processing mode, the agreement of GNSS versus NWM tropospheric gradients revealed an increase in standard deviation of about 19 % (53 %) for IGS01 (IGS03) RT products when compared to the corresponding GNSS post-processing gradients. We also show that the quality of real-time tropospheric parameters is dominated by the quality of real-time orbit and clock corrections and to a much lesser extent by the processing mode, i.e. a Kalman filter without backward smoothing. Tropospheric gradients from the RT solution using the IGS03 RT product showed occasionally a large misbehaviour of tropospheric gradients at all GNSS stations obviously not related to weather conditions. This was caused by frequent PPP re-initializations due to interruptions and worse quality of the IGS03 RT product, while normal results were achieved by using the IGS01 RT product. Thus, providing high-resolution gradients in a (near-)real-time solution still remains challenging, which would require optimally a multi-GNSS constellation and high-accuracy RT products.

We studied systematic differences in estimated tropospheric gradients. Unlike for ZTDs, average systematic differences of up to 0.5 mm over a day, and of up to 1.0 mm or even more for individual gradient components during extreme cases, can affect the magnitude of estimated tropospheric gradients solely due to utilizing different gradient mapping functions or observation elevation-dependent weightings. While the mfg choice affects the magnitude of the estimated gradient, it does not affect the direction of the gradient. However, any difference in the magnitude causes systematic errors in gradient components which depend on the gradient direction too. At a global scale, the long-term mean gradient pointing to the Equator causes systematic differences of up to 0.3 mm in the north-gradient component between Bar-Sever and Chen and Herring mfg (see Appendix A).

Both smaller gradient formal errors and slightly improved height repeatability, which was found to be statistically significant, suggest more accurate modelling when using the Bar-Sever mfg. Without an accurate and independent gradient product, it is still difficult to make a strong recommendation among different mfg, i.e. resulting in different absolute gradient values. More work therefore needs to be done in order to find an optimal gradient mapping function, and it will require high-resolution and highly accurate NWM data sets. In any case, we could strongly recommend using the same mfg implemented in the same form whenever comparing or combining tropospheric gradients derived from different sources (GNSS, WVR or NWM). On the other hand, if tropospheric gradients are used solely for reconstructing slant total delays, different mfg should provide very similar results.

Appendix A

In Fig. 10a and b the systematic difference in the derived tropospheric gradients based on ERA5 data (average over 10 years) is shown for any point on Earth's surface between tropospheric gradients estimated utilizing the BS mfg and tropospheric gradients estimated utilizing the CH mfg, whereas there is no considerable systematic difference in the east-gradient component: it reaches up to 0.3 mm in the north-gradient component (positive in the Northern Hemisphere and negative in the Southern Hemisphere). If we exclude oceans, the maximum values can be found in north-eastern America and north-eastern Asia. In the region of the benchmark campaign, the difference is around 0.15 mm. We note that the mean tropospheric gradients point to the Equator, i.e. the north-gradient component is negative in the Northern Hemisphere and positive in the Southern Hemisphere. This can be seen in Fig. 10c and d, showing the mean north- and east-gradient components utilizing the CH mfg, and can be explained by the fact that the mean zenith delays increase towards the Equator. The systematic difference between these two mfg is due to the fact that for the same slant total delays the magnitudes of tropospheric gradients which are estimated utilizing a smaller mfg are larger than the magnitudes of tropospheric gradients which are estimated utilizing a larger mfg. The product of the mfg and the tropospheric gradients, i.e. the azimuth-dependent part of the tropospheric delay, remains approximately the same.

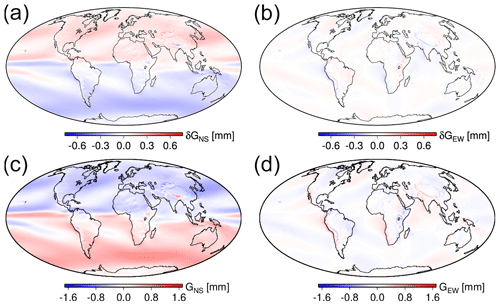
Figure A1 (a, b) Systematic difference (average over 10 years) for any point on Earth's surface between tropospheric gradients estimated utilizing the gradient mapping function of Bar-Sever and tropospheric gradients estimated utilizing the gradient mapping function of Chen and Herring. (c, d) Mean north- and east-gradient components (average over 10 years) for any point on Earth's surface utilizing the mapping function of Chen and Herring. Panels (a) and (c) show the north-gradient component, (b) and (d) the east-gradient component. The results are based on ERA5 data.

Appendix B

NWM tropospheric gradients presented in this paper were also compared with NWM tropospheric gradients provided by the TU Vienna (see http://vmf.geo.tuwien.ac.at/, last access: 14 June 2019). Specifically, we compared the NWM tropospheric gradients based on ERA5 with the so-called linearized horizontal gradients (LHGs) (Boehm and Schuh, 2007). We note that the LHGs are based on the closed-form expression depending on the north–south and east–west horizontal gradients of refractivity (Davis et al., 1993). The LHGs are solely available for several stations, and they are no longer supported (their provision ended in 2017). Recently, Landskron and Boehm (2018) provided refined horizontal gradients based on a least-square adjustment which are currently recommended for use. We decided to look at three stations available in all data sets, ONSA, POTS and WTZR, and we provide the comparisons in Fig. 11. As expected, we find better agreement between ERA5 tropospheric gradients and the refined horizontal gradients. We also find that the magnitude of the ERA5 tropospheric gradients is larger than the magnitude of the refined horizontal gradients. This is not surprising since the NWM that is used in the generation of the refined horizontal gradients has a horizontal resolution of 1^∘ only (ERA-Interim provided by the ECMWF). For example, Zus et al. (2016) showed how an increased horizontal resolution of the NWM amplifies the tropospheric gradient components under severe weather conditions.

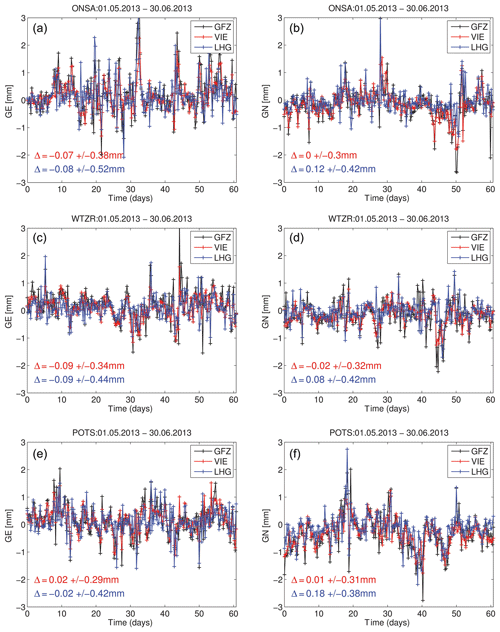
Figure B1 Panels (a), (c) and (e) show the time series (1 May–30 June 2013) of the east-gradient component for stations ONSA, WTZR and POTS, respectively. Panels (b), (d) and (f) show the time series of the north-gradient component for the same stations. The black line corresponds to the ERA5 tropospheric gradients (GFZ, regarded in the paper as NWM ERA5), the red line corresponds to the refined horizontal gradients provided by the TU Vienna (VIE) and the blue line corresponds to the so-called linearized horizontal gradients provided by the TU Vienna (LHGs). The red numbers represent the mean and standard deviation between VIE and GFZ. The blue numbers are the mean and standard deviation between LHG and GFZ.