Neutralized solar wind ahead of the Earth's magnetopause as contribution to non-thermal exospheric hydrogen

In a most recent paper by Qin and Waldrop (2016), it had been found that the scale height of hydrogen in the upper exosphere of the Earth, especially during solar minimum conditions, appears to be surprisingly large. This indicates that during minimum conditions when exobasic temperatures should be small, large exospheric H-scale heights predominate. They thus seem to indicate the presence of a non-thermal hydrogen component in the upper exosphere. In the following parts of the paper we shall investigate what fraction of such expected hot hydrogen atoms could have their origin from protons of the shocked solar wind ahead of the magnetopause converted into energetic neutral atoms (ENAs) via charge-exchange processes with normal atmospheric, i.e., exospheric hydrogen atoms that in the first step evaporate from the exobase into the magnetosheath plasma region. We shall show that, dependent on the sunward location of the magnetopause, the density of these types of non-thermal hydrogen atoms (H-ENAs) becomes progressively comparable with the density of exobasic hydrogen with increasing altitude. At low exobasic heights, however, their contribution is negligible. At the end of this paper, we finally study the question of whether the H-ENA population could even be understood as a self-consistency phenomenon of the H-ENA population, especially during solar activity minimum conditions, i.e., H-ENAs leaving the exosphere being replaced by H-ENAs injected into the exosphere.

Keywords. Magnetospheric physics (plasmasphere; solar wind-magnetosphere interactions) – solar physics, astrophysics, and astronomy (energetic particles)

1 Introduction

The density and temperature structure of the Earth's exosphere is a long-standing research subject, which in the past, due to missing observations, was mainly accessible by theoretical studies which considered the particular motions of collision-less or collision-poor atoms in the region above the exobase. In these nearly collision-free exospheric regions, ballistic particles, satellite particles and escaping particles have to be treated differently, and their different height-dependent contributions to the total local exospheric density is a complicated matter of theoretical calculations (see early work by Opik and Singer, 1961; Chamberlain, 1963; Brinkmann, 1970, or later work by Chamberlain, 1978, 1979; Fahr, 1970, 1976; Fahr and Nass, 1978; Fahr and Weidner, 1977, or Fahr and Shizgal, 1983). The general assumption in all of these studies is that from the collision-dominated region below the exobase, atoms are emitted upwards into the exosphere by Maxwellian velocity distribution functions associated with the local gas temperature at the exobase T=T_ex.

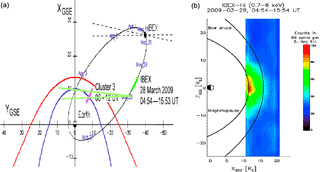
Figure 1 From its orbit, IBEX-Hi has the chance to image the solar part of the magnetosheath as source of H-ENAs in the range of 0.7–6 keV (a); (b) shows in terms of H-ENA fluxes what is seen from this region (from Fuselier et al., 2010).

This, however, is a critical and unsafe assumption, because in the transition region between collision-dominated and collision-free domains, thermodynamic equilibrium conditions are perturbed, i.e., temperatures of the different exobasic gas constituents due to the weak thermodynamic coupling deviate from each other. Especially for hydrogen, due to the strongly pronounced escape flux of these light atoms (see Jeans, 1923, or e.g., later work by Fahr and Weidner, 1977), the downward branch of the velocity distribution at the branch of super escape velocities is unpopulated if external sources of H atoms are neglected. This, in fact, has the effect to reduce the effective exobasic hydrogen temperature with respect to the exobasic oxygen temperature and thus reduces the effective H-atom escape flux (see Fahr, 1976).

Nevertheless, these reasons for H-atom deviations from local exobasic thermodynamic equilibrium conditions do not explain what surprisingly and most recently has been observed by Qin and Waldrop (2016). These authors find that the upper exospheric hydrogen density distribution, especially during solar minimum conditions, is substantially higher than can be understood as a result of a terrestrial H–exosphere connected with exobasic oxygen temperatures (see Hodges, 1994). Their exciting result is inferred from radiative transfer modeling of Lyman-alpha resonance glow measurements made with the satellite TIMED/GUVI. To best fit these results with their Lyman-alpha multiple scattering code, the authors apply two independent Maxwellian distributions for two separate exobasic hydrogen populations, one with the usual exobasic temperature according to the NRLMSISE-00 model (Picone et al., 2002) and the other with a much higher temperature with no clear origin, which thus needs to be fitted from Lyman-alpha glow data. It then, as a surprise, turns out that the presence of the hotter H component is especially pronounced under solar minimum conditions, just at times when normal exobasic temperatures should be the lowest.

In the following paper, we are going to show that this interesting finding can at least at larger exospheric heights partly be ascribed to energetic hydrogen atoms (H-ENAs) impinging onto the lower exosphere and originating from beyond the Earth's magnetopause via charge-exchange processes on the solar side of the subsonic solar magnetosheath plasma region. That the Earth's magnetopause is in fact an actively emitting H-ENA site has already directly been proven by IBEX-H-ENA measurements under suitable observational conditions from regions far above the exobase (Goldstein and McComas, 2013; also see our Fig. 1 from Fuselier et al., 2010). In the following part of the paper we shall develop a simplified description of this hot exospheric H component in order to elaborate a qualitative picture of the relevance of this H-ENA component for the upper exosphere.

2 The magnetosheath plasma and a simplified theoretical approach to sheath ENAs

Outside of the magnetopause and inside of the Earth's magneto bow shock, the shocked solar wind, the so-called “magnetosheath plasma”, is deflected from its original antisolar direction and its flow is forced to become tangential to the outer magnetopause surface. The resulting global plasma flow, in reality, is rather complicated in its geometric structure, its asymmetries and its time dependencies. With all of these complications concerning time-dependent and space-dependent specialities in densities, bulk velocities and temperatures, this global plasma system does not allow for an easy theoretical representation.

First predictions for this plasma flow were made on the basis of gasdynamic models by Spreiter and Stahara (1980). In these models, it is assumed that the bulk properties of the shocked solar wind flow can be described by a monofluid hydrodynamic approach with frozen-in magnetic fields only included by a kinematic approximation. To better understand the influence of the self-consistent magnetic fields involved, Zwan and Wolf (1976) proposed a plasma depletion model including the effect of magnetic fields on the magnetosheath flow, which, however, was later criticized by Southwood and Kivelson (1995) since it did not allow for the needed forces to drive the sheath flow. Furthermore, the effect of magnetic field reconnection in the magnetosheath was considered by Cowley and Owen (1989) and Cooling et al. (2001). Then Song et al. (1992a, b) and Fuselier et al. (2002) have compared model predictions with data from the Active Magnetospheric Particle Tracer Explorers/Ion Release Modul (AMPTE/IRM) and found that while gasdynamic models predict too high bulk velocities, magneto-hydrodynamic (MHD) models including reconnection propose just the opposite, in both cases strongly deviating from measurements. In a more recent study by Cooling (2003), based on data from the satellites GEOTAIL and WIND, it was found that remarkable asymmetries in the dawn and dusk values of plasma density and velocity are pronounced, which in addition are subject to time-dependent variations. In a recent paper by Parks et al. (2016), even more complications in the features of the plasma flow downstream of the Earth's magneto bow shock were pointed out based on data from the CLUSTER II space mission. It is shown there that dependent on the upstream solar wind data, the downstream bulk velocities sometimes remain super-Alfvénic and ion distribution functions, though most often nearly isotropic, can sometimes be very complex showing multiple beams of reflected, gyrating or shock-escaping ions. These very complicating facts are even more stressed by Longmore et al. (2005) in view of more recent CLUSTER in situ data. These latter data show that the magnetosheath plasma does not at all have an axisymmetrical shape concerning flow and density structures, in contrast significant asymmetries exist between dawn and dusk sectors and between northern and southern hemispheres. The magnetosheath flow close to the magnetopause at highest and lowest latitudes are found to be sub-Alfvénic, while at mid-latitudes and at the flanks of the magnetopause they tend to be super-Alfvénic. In addition, everything seems to be strongly subject to time-variations and does not have a clear trigger in the solar wind magnetic field direction.

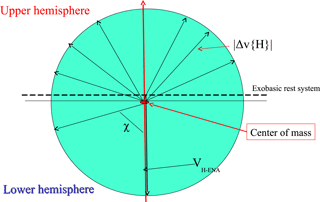
Figure 2 Illustration of H-ENA reflections at the O-exobase: The elastic H–O–atom collision in a velocity reference frame at rest with respect to the exobase is shown; the initial H-ENA velocity is turned around the center-of-mass velocity vector and becomes the final H-ENA velocity. For more information see Appendix A.

This all taken together shows clearly that there does not exist an easy way towards an appropriate 3-D representation of the global structure of the magnetosheath plasma, and hence for the ongoing considerations in this paper we therefore have to make essential simplifications guided by modern MHD simulations of multi-component interactions in case of the heliospheric plasma interface (see, for example, the review by Izmodenov and Baranov, 2006).

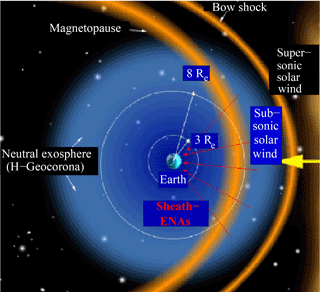
As at least evident, neutral exospheric hydrogen atoms originating at and ascending from the exobase, as shown in the analysis presented by Zoennchen et al. (2013), propagate to large geocentric distances. In fact, their density extends to beyond the magnetopause region (i.e., to beyond 8 up to 10 Earth radii, r_E, depending on solar wind conditions, e.g., see Shue et al., 1998). In this outer region of shocked, subsonic solar wind plasma, these atoms undergo resonant charge-exchange reactions with the ambient protons of the shocked solar wind and, as newly appearing energetic neutral H atoms (H-ENAs), they thereafter partly impinge on the Earth's exobase if their inherited velocity direction is within the appropriate space angle $\mathrm{d}\mathrm{\Omega }=\mathit{\pi }\left(r_{\mathrm{ex}}^{\mathrm{2}}/r_{\mathrm{mp}}^{\mathrm{2}}\right)$. Assuming for the solar side of the bow shock a strong perpendicular MHD shock (compression ratio s≃4), then according to Rankine–Hugoniot standards the shocked solar wind plasma should be highly subsonic there (M_s≤0.1). This implies that the energetic magnetosheath protons (keV) in this subsolar region are practically represented by an isotropic suprathermal Maxwellian distribution in velocity space. Hence via resonant H–H⁺ charge exchange, these protons colliding with low-energy exobasic H atoms effectively produce isotropically distributed high-energy (keV) neutral atoms (H-ENAs), which are decoupled from the plasma flow and from magnetosheath magnetic fields and thus are partly and directly shot downwards onto the Earth's exobase.

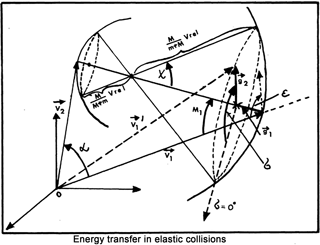
When impinging onto the exobase, these H-ENAs are elastically colliding with the most abundant atomic species of this region, which is the mono-atomic oxygen atom, i.e., 16-times more massive than H atoms. In a velocity space diagram showing the O- and the H-atom velocities before and after the elastic collision (see Fig. 2), one can see that the center of mass velocity of this system is close to the O-atom velocity and the H-atom velocity after the collision is found by turning the relative velocity vector by an angle χ around the “center of mass” velocity vector. For hard-sphere collisions, modeling elastic O–H collisions reasonably well, it is known that all turning angles χ are equally probable. Therefore it can be found that with a high probability of $\mathrm{\Pi }\left(\mathrm{up}\right)\simeq {\sum }_{\mathrm{1}}^j(\mathrm{1}/\mathrm{2}{)}^i$ (i.e., for j≃4, cut-down because of successive energy losses, thus with a probability of 93 %), H-ENAs impinging on the exobase are finally, after consecutive collisions, reflected back into the upward hemisphere through the upper exosphere back to space (see also the collision geometry illustrated in Fig. 2).

The whole global 3-D charge-exchange scenario, in reality and in a rigorous treatment, is highly asymmetric both in configuration- and velocity-space (see Fig. 3) and it would be hard to describe it in an adequately detailed 6-D manner.

Figure 3 Sketch of the scenario.

Figure 4 H-ENA production between the magnetopause (MP) and the bow shock (BS).

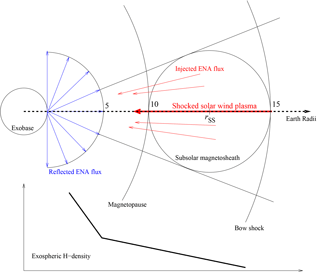
One can, however, dare to simplify and symmetrize the problem for the sake of calculating the main features of this physical context of hot hydrogen atoms (H-ENAs) reflected upwards from the exobase back to space in order to investigate qualitatively their role for the exosphere. Thus, for simplification reasons, we approximate things here only considering the H-ENA irradiation of the solar side of the spherical exobase surface with radius r_ex. This part is essentially irradiated by H-ENAs originating in the subsolar sphere of the magnetosheath, as is indicated in Fig. 4. As supported by CLUSTER measurements, the magnetosheath plasma in the subsolar region is characterized by a strongly shocked solar wind plasma with a subsonic signature approaching the nose of the magnetopause with decreasing bulk velocity. Here, we consider only the solar exobase irradiation by those H-ENAs originating in this subsolar magnetosheath region (Fig. 4), though H-ENA fluxes from magnetosheath regions at high latitudes or from the flanks do certainly also contribute, but as minor contributions they are not considered here. This is because in these regions the plasma bulk velocities are growing again and are oriented away from the exobase, so that the proton distribution function contains less and less velocity vectors directed towards the exobase.

For the purpose of the following estimation, the following assumptions might appear acceptable: the density of the supersonic solar wind upstream of the Earth's bow shock at about 1 AU is adopted with n_p1=5 cm⁻³. Downstream of the subsolar part of the Earth's bow shock, assumed to act as a strong perpendicular shock with a compression ratio of s≃4, the shocked solar wind then, according to a monofluidal gasdynamic Rankine–Hugoniot approach, becomes compressed by a factor of 4 and the downstream plasma becomes strongly subsonic with Mach numbers of the order of M_s≤0.1 (see e.g., Serrin, 1959; Gombosi, 1998; Erkaev et al., 2000). As a consequence of that low Mach number flow (see Fahr and Siewert, 2015; Fahr et al., 2015), one can expect, as is also in the case of the heliosheath plasma, a nearly incompressible magnetosheath plasma density with $n_{\mathrm{p}\mathrm{2}}=s\cdot n_{\mathrm{p}\mathrm{1}}=\mathrm{20}$cm⁻³ (indices “1” and “2” characterize solar wind quantities upstream and downstream of the bow shock, respectively). The shocked solar wind has an energy of the order of $k{T}_{\mathrm{p}\mathrm{2}}\simeq (\mathrm{3}/\mathrm{8})\cdot (m{U}_{\mathrm{1}}^{\mathrm{2}}/\mathrm{2})\simeq \mathrm{1}$ keV (i.e., thermalized solar wind; U₁≃400 km s⁻¹; T_p2≃10⁶ K) with a velocity distribution function, which due to the very low Mach number M_s≃0.1 can be considered as quasi-isotropic Maxwellian with a nearly negligible bulk velocity shift, in view of the small bulk velocity U₂ associated with the high thermal proton velocities of the order of $\sqrt{\mathrm{8}k{T}_{\mathrm{p}\mathrm{2}}/\mathit{\pi }m}$.

On the basis of that, we shall now calculate the flux of H-ENAs produced by means of the charge-exchange reactions of the shocked solar wind protons with cold exobasic hydrogen atoms in the subsolar region of the magnetosheath. These latter exospheric hydrogen density distributions have been found and published by several authors like Rairden et al. (1986), Hodges (1994), Ostgaard et al. (2003), Bailey and Gruntman (2011) or Zoennchen et al. (2011, 2013). Here we start with the result derived from TWINS-LAD data by Zoennchen et al. (2013) for summer solstice conditions yielding at larger radial distances r≥r₀ an asymptotic radial density profile of exobasic H atoms in the form

$$\begin{array}{}\text{(1)}& n_{\mathrm{H}}=n_{\mathrm{H}\mathrm{0}}\cdot {\left({\displaystyle \frac{r}{r_{\mathrm{0}}}}\right)}^{-\mathrm{2.7}},\end{array}$$

with a reference density n_H0=50 cm⁻³ at a reference height r₀=8 r_E.

Hence along a radial line of sight cutting through the subsolar magnetosheath (see Fig. 4), the following total production rate Γ_ENA(v) of H-ENAs with a velocity v hitting the exobase can be calculated:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathrm{\Gamma }}_{\mathrm{ENA}}\left(v\right){\mathrm{d}}^{\mathrm{3}}v=\\ \text{(2)}& {\displaystyle }& {\displaystyle }\underset{r_{\mathrm{MP}}}{\overset{r_{\mathrm{BS}}}{\int }}\stackrel{v_{\mathrm{H}}}{\int }{f}_{\mathrm{p}}^{\mathrm{ss}}\left(v_{\mathrm{p}}\right)f_{\mathrm{H}}\left(v_{\mathrm{H}}\right)\mathit{\sigma }\left(v_{\mathrm{rel}}\right)v_{\mathrm{rel}}{\mathrm{d}}^{\mathrm{3}}{v}_{\mathrm{p}}{\mathrm{d}}^{\mathrm{3}}{v}_{\mathrm{H}}\mathrm{d}r,\end{array}$$

where $f_{\mathrm{p}}^{\mathrm{ss}}$ and f_H denote the local distribution functions of solar wind magnetosheath protons in the subsolar region and the exobasic H atoms, respectively; σ is the charge-exchange cross section for proton–H-atom collisions; $v_{\mathrm{rel}}=\left|{\mathit{v}}_{\mathrm{p}}-{\mathit{v}}_{\mathrm{H}}\right|$ is the relative velocity between these collision partners; d³v_p and d³v_H denote the differential 3-D velocity space volumes of protons and H atoms, respectively; and dr is the increment along the radial line of sight from the magnetopause r_MP up to the bow shock r_BS. The above expression Γ_ENA(v)d³v due to the conditions mentioned above (i.e., suprathermal protons, cold exospheric H atoms; i.e., v_H≪v_p) can then be sufficiently well approximated by the following expression:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathrm{\Gamma }}_{\mathrm{ENA}}\left(v\right){\mathrm{d}}^{\mathrm{3}}v\simeq n_{\mathrm{p}\mathrm{2}}\cdot n_{\mathrm{H}\mathrm{0}}\cdot \mathit{\sigma }\left(v\right)\cdot v\\ \text{(3)}& {\displaystyle }& {\displaystyle }\cdot \left[A_{\mathrm{2}}\exp \left[-{\displaystyle \frac{m{v}^{\mathrm{2}}}{\mathrm{2}k{T}_{\mathrm{p}\mathrm{2}}}}\right]v^{\mathrm{2}}\mathrm{d}v\right]\cdot \underset{r_{\mathrm{MP}}}{\overset{r_{\mathrm{BS}}}{\int }}{\displaystyle \frac{{\mathrm{d}}^{\mathrm{2}}\mathrm{\Omega }}{\mathrm{4}\mathit{\pi }}}{\left({\displaystyle \frac{r}{r_{\mathrm{0}}}}\right)}^{-\mathrm{2.7}}\mathrm{d}r,\end{array}$$

where ${\mathrm{d}}^{\mathrm{2}}\mathrm{\Omega }=\mathit{\pi }(r_{\mathrm{ex}}/r{)}^{\mathrm{2}}$ denotes the space angle under which the exobase appears from a space point at distance r and the quantity A₂ is the Maxwell normalization factor defined by $A_{\mathrm{2}}=(m/\mathrm{2}\mathit{\pi }k{T}_{\mathrm{p}\mathrm{2}}{)}^{\mathrm{3}/\mathrm{2}}$. Hence one obtains

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathrm{\Gamma }}_{\mathrm{ENA}}\left(v\right){\mathrm{d}}^{\mathrm{3}}v\simeq n_{\mathrm{p}\mathrm{2}}\cdot n_{\mathrm{H}\mathrm{0}}\cdot \mathit{\sigma }\left(v\right)\cdot v\\ \text{(4)}& {\displaystyle }& {\displaystyle }\cdot \left[A_{\mathrm{2}}\exp \left[-{\displaystyle \frac{m{v}^{\mathrm{2}}}{\mathrm{2}k{T}_{\mathrm{p}\mathrm{2}}}}\right]v^{\mathrm{2}}\mathrm{d}v\right]\cdot \underset{r_{\mathrm{MP}}}{\overset{r_{\mathrm{BS}}}{\int }}{\displaystyle \frac{r_{\mathrm{ex}}^{\mathrm{2}}}{\mathrm{4}{r}^{\mathrm{2}}}}{\left({\displaystyle \frac{r}{r_{\mathrm{0}}}}\right)}^{-\mathrm{2.7}}\mathrm{d}r,\end{array}$$

yielding

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathrm{\Gamma }}_{\mathrm{ENA}}\left(v\right){\mathrm{d}}^{\mathrm{3}}v\simeq {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{n}_{\mathrm{p}\mathrm{2}}\cdot n_{\mathrm{H}\mathrm{0}}\cdot \mathit{\sigma }\left(v\right)\cdot v\\ {\displaystyle }& {\displaystyle }\cdot \left[A_{\mathrm{2}}\exp \left[-{\displaystyle \frac{m{v}^{\mathrm{2}}}{\mathrm{2}k{T}_{\mathrm{p}\mathrm{2}}}}\right]v^{\mathrm{2}}\mathrm{d}v\right]{\displaystyle \frac{r_{\mathrm{ex}}^{\mathrm{2}}}{r_{\mathrm{0}}^{\mathrm{2}}}}\\ \text{(5)}& {\displaystyle }& {\displaystyle }\cdot \underset{r_{\mathrm{MP}}}{\overset{r_{\mathrm{BS}}}{\int }}{\left({\displaystyle \frac{r}{r_{\mathrm{0}}}}\right)}^{-\mathrm{4.7}}\mathrm{d}r,\end{array}$$

or with ${\mathit{\psi }}_{\mathrm{0}}=\frac{\mathrm{1}}{\mathrm{2}}{n}_{\mathrm{p}\mathrm{2}}\cdot n_{\mathrm{H}\mathrm{0}}\cdot r_{\mathrm{0}}\cdot x_{\mathrm{ex}}^{\mathrm{2}}$ reads

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathrm{\Gamma }}_{\mathrm{ENA}}\left(v\right){\mathrm{d}}^{\mathrm{3}}v\simeq {\mathit{\psi }}_{\mathrm{0}}\mathit{\sigma }\left(v\right)\cdot v\\ {\displaystyle }& {\displaystyle }\cdot \left[A_{\mathrm{2}}\exp \left[-{\displaystyle \frac{m{v}^{\mathrm{2}}}{\mathrm{2}k{T}_{\mathrm{p}\mathrm{2}}}}\right]v^{\mathrm{2}}\mathrm{d}v\right]\underset{x_{\mathrm{MP}}}{\overset{x_{\mathrm{BS}}}{\int }}{x}^{-\mathrm{4.7}}\mathrm{d}x\\ {\displaystyle }& {\displaystyle }={\mathit{\psi }}_{\mathrm{0}}\mathit{\sigma }\left(v\right)\cdot v\cdot \left[A_{\mathrm{2}}\exp \left[-{\displaystyle \frac{m{v}^{\mathrm{2}}}{\mathrm{2}k{T}_{\mathrm{p}\mathrm{2}}}}\right]v^{\mathrm{2}}\mathrm{d}v\right]\\ \text{(6)}& {\displaystyle }& {\displaystyle }\cdot {\displaystyle \frac{\mathrm{1}}{\mathrm{3.7}}}\left[x_{\mathrm{MP}}^{-\mathrm{3.7}}-x_{\mathrm{BS}}^{-\mathrm{3.7}}\right],\end{array}$$

where the normalized radial distance is given by $x=r/r_{\mathrm{0}}$, and the reader may be reminded that rough values give $x_{\mathrm{MP}}\simeq \mathrm{10}/\mathrm{8}$ and $x_{\mathrm{BS}}\simeq \mathrm{15}/\mathrm{8}$.

Let us assume now that this flux is more or less homogeneously hitting the exobase from an extended area of the subsolar magnetosheath region, i.e., from an associated space angle d²Ω_in which we can calculate with the help of Fig. 4. The center of the H-ENA emitting subsolar region may have a radial distance of $r_{\mathrm{ss}}=r_{\mathrm{MP}}+(\mathrm{1}/\mathrm{2})(r_{\mathrm{BS}}-r_{\mathrm{MP}})=(\mathrm{1}/\mathrm{2})(r_{\mathrm{MP}}+r_{\mathrm{BS}})$. Then the space angle for the H-ENA input is given by

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathrm{d}}^{\mathrm{2}}{\mathrm{\Omega }}_{\mathrm{in}}={\displaystyle \frac{\mathit{\pi }\mathrm{\Delta }{r}_{\mathrm{ss}}^{\mathrm{2}}}{r_{\mathrm{ss}}^{\mathrm{2}}}}\\ {\displaystyle }& {\displaystyle }=\mathit{\pi }{\displaystyle \frac{(\mathrm{1}/\mathrm{4})(r_{\mathrm{BS}}-r_{\mathrm{MP}}{)}^{\mathrm{2}}}{(\mathrm{1}/\mathrm{4})(r_{\mathrm{BS}}+r_{\mathrm{MP}}{)}^{\mathrm{2}}}}\\ {\displaystyle }& {\displaystyle }=\mathit{\pi }{\displaystyle \frac{(r_{\mathrm{BS}}-r_{\mathrm{MP}}{)}^{\mathrm{2}}}{(r_{\mathrm{BS}}+r_{\mathrm{MP}}{)}^{\mathrm{2}}}}\\ {\displaystyle }& {\displaystyle }=\mathit{\pi }{\left({\displaystyle \frac{\mathrm{5}}{\mathrm{15}}}\right)}^{\mathrm{2}}\\ \text{(7)}& {\displaystyle }& {\displaystyle }={\displaystyle \frac{\mathit{\pi }}{\mathrm{9}}}.\end{array}$$

Since this H-ENA injection rate, as we shall show below, induces a hemispherical symmetric, isotropic ENA outflux Φ_ENA(v_out) from the exobase, each subsolar exobase point consequently has to balance inflows and outflows by the relation

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathrm{2}\mathit{\pi }{\mathrm{\Phi }}_{\mathrm{ENA}}\left(v_{\mathrm{out}}\right)\left(\mathit{\pi }{r}_{\mathrm{ex}}\right){\mathrm{d}}^{\mathrm{3}}{v}_{\mathrm{out}}\\ \text{(8)}& {\displaystyle }& {\displaystyle }={\mathrm{\Gamma }}_{\mathrm{ENA}}\left(v_{\mathrm{in}}\right){\mathrm{d}}^{\mathrm{3}}{v}_{\mathrm{in}}\left(\mathit{\pi }{\mathrm{\Delta }}^{\mathrm{2}}{r}_{\mathrm{ss}}\right)\cdot {\mathrm{d}}^{\mathrm{2}}{\mathrm{\Omega }}_{\mathrm{in}},\end{array}$$

where we have distinguished between incoming and associated outgoing velocities v_in and v_out, as we shall also explain further below. Due to the typical energies of the incoming H-ENAs (∼ 1 keV) compared to the H-atom escape energy $E_{\mathrm{esc}}\simeq \mathrm{7}\cdot {\mathrm{10}}^{-\mathrm{4}}$ keV, the influence of the Earth's gravitational field on these H-ENA trajectories can be completely neglected (i.e., straight trajectories). This is also true for the outgoing H-ENAs as we shall also show next.

When an incoming energetic H-ENA approaches the exobase, it most probably will undergo an elastic collision with the most abundant atomic atmospheric species there, i.e., with the mono-atomic oxygen atoms (NB m_O=16m_H). During such elastic collisions, the colliding ENA experiences a deflection of its initial relative velocity by an angle χ with a probability $\mathit{\delta }\left(\mathit{\chi }\right)=(\mathrm{d}\mathit{\chi }/\mathrm{d}p)\mathit{\delta }p$ around the center of mass of the colliding atoms (p being the collisional impact parameter; for a sketch of the collision geometry in velocity space see the sketch given as Fig. 12 in Fahr, 1978, or its reproduction given in Appendix A). While the velocity of the center of mass v_M is conserved during the collision process, the relative velocity Δv_H of the H atom with respect to v_M is turned around this conserved center-of-mass velocity by the angle χ (see Fig. 2 in this paper and Figs. 11 and 12 in Fahr, 1978). The two relative velocities of the O and the H atom with respect to the center-of-mass velocity are thus given by

$$\begin{array}{}\text{(9)}& \left|\mathrm{\Delta }{\mathit{v}}_{\mathrm{H}}\right|={\displaystyle \frac{m_{\mathrm{O}}}{m_{\mathrm{H}}+m_{\mathrm{O}}}}{v}_{\mathrm{H}}={\displaystyle \frac{\mathrm{16}}{\mathrm{17}}}{v}_{\mathrm{H}}\end{array}$$

and

$$\begin{array}{}\text{(10)}& \left|\mathrm{\Delta }{\mathit{v}}_{\mathrm{O}}\right|={\displaystyle \frac{m_{\mathrm{H}}}{m_{\mathrm{H}}+m_{\mathrm{O}}}}{v}_{\mathrm{H}}={\displaystyle \frac{\mathrm{1}}{\mathrm{17}}}{v}_{\mathrm{H}},\end{array}$$

where $v_{\mathrm{H}}\simeq \sqrt{\mathrm{3}k{T}_{\mathrm{p}\mathrm{2}}/m}\gg v_{\mathrm{esc}}$ is the mean thermal proton velocity in the subsonic solar wind inherited via charge transfer by the H-ENA. With the above result, one can conclude that the distribution function of the reflected H-ENAs being emitted from the exobase to outer space is also a Maxwellian; however, with income velocities v_in converted into reduced outcome velocities $v_{\mathrm{out}}=(\mathrm{16}/\mathrm{17})v_{\mathrm{in}}$ and with a space angle d²Ω_out=2π instead of an income space angle ${\mathrm{d}}^{\mathrm{2}}{\mathrm{\Omega }}_{\mathrm{in}}=\mathit{\pi }/\mathrm{9}$. The resulting exobasic density n_ex,ENA is then obtained from the following ENA balance request for the local vertical fluxes

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{n}_{\mathrm{ex},\mathrm{ENA}}{r}_{\mathrm{ex}}^{\mathrm{2}}\cdot \int {\left[v\cdot A_{\mathrm{2}}\exp \left[-{\displaystyle \frac{m{v}^{\mathrm{2}}}{\mathrm{2}k{T}_{\mathrm{p}\mathrm{2}}}}\right]v^{\mathrm{2}}\mathrm{d}v\right]}_{\mathrm{out}}\\ {\displaystyle }& {\displaystyle }\cdot \underset{\mathrm{0}}{\overset{{\mathit{\vartheta }}_{\mathrm{out}}}{\int }}{\cos }^{\mathrm{2}}\mathit{\vartheta }\mathrm{d}\mathit{\vartheta }\\ {\displaystyle }& {\displaystyle }={\mathit{\psi }}_{\mathrm{0}}\mathrm{\Delta }{r}_{\mathrm{ss}}^{\mathrm{2}}\int \mathit{\sigma }\left(v\right)\cdot {\left[v\cdot A_{\mathrm{2}}\exp \left[-{\displaystyle \frac{m{v}^{\mathrm{2}}}{\mathrm{2}k{T}_{\mathrm{p}\mathrm{2}}}}\right]v^{\mathrm{2}}\mathrm{d}v\right]}_{\mathrm{in}}\\ \text{(11)}& {\displaystyle }& {\displaystyle }\cdot {\displaystyle \frac{\mathrm{1}}{\mathrm{3.7}}}\left[x_{\mathrm{MP}}^{-\mathrm{3.7}}-x_{\mathrm{BS}}^{-\mathrm{3.7}}\right]\underset{\mathrm{0}}{\overset{{\mathit{\vartheta }}_{\mathrm{in}}}{\int }}{\cos }^{\mathrm{2}}\mathit{\vartheta }\mathrm{d}\mathit{\vartheta },\end{array}$$

yielding

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{n}_{\mathrm{ex},\mathrm{ENA}}={\mathit{\psi }}_{\mathrm{0}}{\mathit{\sigma }}_{\mathrm{0}}\left(v_{\mathrm{0}}\right){\displaystyle \frac{\mathrm{1}}{\mathrm{3.7}}}\left[x_{\mathrm{MP}}^{-\mathrm{3.7}}-x_{\mathrm{BS}}^{-\mathrm{3.7}}\right]\\ \text{(12)}& {\displaystyle }& {\displaystyle }\cdot {\displaystyle \frac{\mathrm{\Delta }{r}_{\mathrm{ss}}^{\mathrm{2}}}{r_{\mathrm{ex}}^{\mathrm{2}}}}{\displaystyle \frac{\int {\left[v\cdot A_{\mathrm{2}}\exp \left[-\frac{m{v}^{\mathrm{2}}}{\mathrm{2}k{T}_{\mathrm{p}\mathrm{2}}}\right]v^{\mathrm{2}}\mathrm{d}v\right]}_{\mathrm{in}}}{\int {\left[v\cdot A_{\mathrm{2}}\exp \left[-\frac{m{v}^{\mathrm{2}}}{\mathrm{2}k{T}_{\mathrm{p}\mathrm{2}}}\right]v^{\mathrm{2}}\mathrm{d}v\right]}_{\mathrm{out}}}}{\displaystyle \frac{\mathrm{1}+\cos {\mathit{\vartheta }}_{\mathrm{in}}}{\mathrm{1}+\cos {\mathit{\vartheta }}_{\mathrm{out}}}},\end{array}$$

where the quantity ψ₀ has already been defined by ${\mathit{\psi }}_{\mathrm{0}}=\frac{\mathrm{1}}{\mathrm{2}}{n}_{\mathrm{p}\mathrm{2}}\cdot n_{\mathrm{H}\mathrm{0}}\cdot r_{\mathrm{0}}\cdot x_{\mathrm{ex}}^{\mathrm{2}}$, and the reference value ${\mathit{\sigma }}_{\mathrm{0}}\left(v_{\mathrm{0}}\right)={\mathrm{10}}^{-\mathrm{15}}$ cm² (relying on its very small variability in the covered velocity range) has been introduced as the charge-exchange cross section at the reference velocity $v_{\mathrm{0}}=\sqrt{\mathrm{3}k{T}_{\mathrm{p}\mathrm{2}}/m}$. Furthermore, ϑ_in and ϑ_out denote the border angle limitations of the input cone and the output cone, respectively. Due to the hemispherical ENA emission from the exobase, one evidently has ${\mathit{\vartheta }}_{\mathrm{out}}=\mathit{\pi }/\mathrm{2}$. For the limiting input angle ϑ_in, we obtain from the following definition

$$\begin{array}{}\text{(13)}& {\mathrm{d}}^{\mathrm{2}}{\mathrm{\Omega }}_{\mathrm{in}}={\displaystyle \frac{\mathit{\pi }}{\mathrm{9}}}=\mathrm{2}\mathit{\pi }\underset{\mathrm{0}}{\overset{{\mathit{\vartheta }}_{\mathrm{in}}}{\int }}\sin \mathit{\vartheta }\mathrm{d}\mathit{\vartheta }=\mathrm{2}\mathit{\pi }\left(\mathrm{1}-\cos {\mathit{\vartheta }}_{\mathrm{in}}\right),\end{array}$$

leading to $\cos {\mathit{\vartheta }}_{\mathrm{in}}=\mathrm{17}/\mathrm{18}$. That then leads to the following expression:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{n}_{\mathrm{ex},\mathrm{ENA}}\simeq \mathrm{2}{\mathit{\psi }}_{\mathrm{0}}{\mathit{\sigma }}_{\mathrm{0}}\left(v_{\mathrm{0}}\right){\displaystyle \frac{\mathrm{1}}{\mathrm{3.7}}}\left[x_{\mathrm{MP}}^{-\mathrm{3.7}}-x_{\mathrm{BS}}^{-\mathrm{3.7}}\right]\\ \text{(14)}& {\displaystyle }& {\displaystyle }\cdot {\displaystyle \frac{\mathrm{\Delta }{r}_{\mathrm{ss}}^{\mathrm{2}}}{r_{\mathrm{ex}}^{\mathrm{2}}}}{\displaystyle \frac{\int {\left[v\cdot A_{\mathrm{2}}\exp \left[-\frac{m{v}^{\mathrm{2}}}{\mathrm{2}k{T}_{\mathrm{p}\mathrm{2}}}\right]v^{\mathrm{2}}\mathrm{d}v\right]}_{\mathrm{in}}}{\int {\left[v\cdot A_{\mathrm{2}}\exp \left[-\frac{m{v}^{\mathrm{2}}}{\mathrm{2}k{T}_{\mathrm{p}\mathrm{2}}}\right]v^{\mathrm{2}}\mathrm{d}v\right]}_{\mathrm{out}}}}.\end{array}$$

Reminding ourselves that both of the above requested integrals as Maxwellian moments represent the mean thermal velocity of the associated distribution functions, one thus simply finds

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{n}_{\mathrm{ex},\mathrm{ENA}}\simeq \mathrm{2}{\mathit{\psi }}_{\mathrm{0}}{\mathit{\sigma }}_{\mathrm{0}}\left(v_{\mathrm{0}}\right){\displaystyle \frac{\mathrm{1}}{\mathrm{3.7}}}\left[x_{\mathrm{MP}}^{-\mathrm{3.7}}-x_{\mathrm{BS}}^{-\mathrm{3.7}}\right]\\ {\displaystyle }& {\displaystyle }\cdot {\displaystyle \frac{\mathrm{\Delta }{r}_{\mathrm{ss}}^{\mathrm{2}}}{r_{\mathrm{ex}}^{\mathrm{2}}}}{\displaystyle \frac{{\sqrt{\mathrm{3}k{T}_{\mathrm{p}\mathrm{2}}/m}}_{\mathrm{in}}}{{\sqrt{\mathrm{3}k{T}_{\mathrm{p}\mathrm{2}}/m}}_{\mathrm{out}}}}\\ \text{(15)}& {\displaystyle }& {\displaystyle }=\mathrm{0.6}\cdot {\mathit{\psi }}_{\mathrm{0}}{\mathit{\sigma }}_{\mathrm{0}}\left(v_{\mathrm{0}}\right){\displaystyle \frac{\mathrm{\Delta }{r}_{\mathrm{ss}}^{\mathrm{2}}}{r_{\mathrm{ex}}^{\mathrm{2}}}}\left[x_{\mathrm{MP}}^{-\mathrm{3.7}}-x_{\mathrm{BS}}^{-\mathrm{3.7}}\right].\end{array}$$

Putting in numbers for ψ₀ and σ₀(v₀), one obtains

$$\begin{array}{}\text{(16)}& n_{\mathrm{ex},\mathrm{ENA}}\simeq \mathrm{4.3}\cdot {\mathrm{10}}^{-\mathrm{3}}{\mathrm{cm}}^{-\mathrm{3}}.\end{array}$$

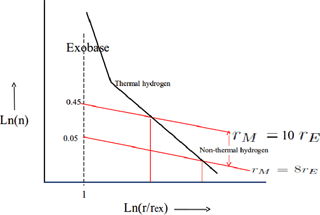
While the exobasic H-atom density is falling off like r^−2.7, the H-ENAs being reflected from the exobase in view of their high velocities do not care for the Earth's gravitational field and hence their density falls off like r⁻². In principle, this should lead to a cross-over point of the two H-density profiles as indicated in Fig. 5.

Figure 5 Qualitative view of competing H densities.

Looking at the numbers given, however, this cross-over point would be far beyond the magnetopause.

3 Shrinking of the escape cone

As a small refinement, another geometrical consideration may be carried out for the case of the H-ENAs evaporating from the exobase and arriving at distances r>r_ex, namely that the widespread velocity cone of H-ENAs being hemispherically reflected from the exobase, with an initial cone angle of ${\mathit{\beta }}_{\mathrm{c},\mathrm{ex}}=\mathit{\pi }/\mathrm{2}$, will systematically be reduced with increasing height to an increasingly narrower velocity cone in velocity space, the larger the radial distance r from the exobase becomes (see Fig. 6).

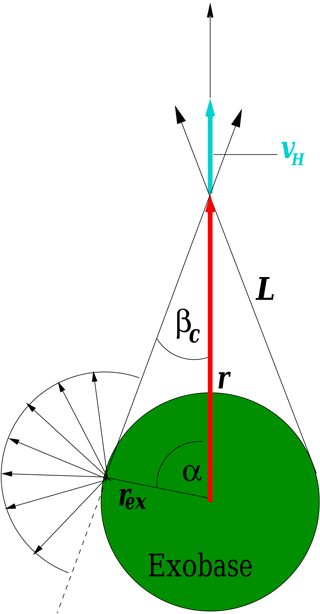
Figure 6 Shrinking of the velocity cone of H-ENAs escaping from the exobase to space: Close to the exobase, velocity vectors are distributed over a full hemisphere, at large distance only over a much reduced cone, which increases the effective radial bulk velocity.

This shrinking of the velocity cone of the H-ENA velocities increases the cone-averaged upward bulk velocity. This evident increase in the effective radial H-ENA bulk velocity 〈v_ENA,z〉 can be calculated with the following expression:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }〈v_{\mathrm{ENA},\mathrm{z}}〉=v_{\mathrm{H}}{\displaystyle \frac{\frac{\mathrm{1}}{\mathrm{4}\mathit{\pi }}{\iint }_{\mathrm{0}}^{{\mathit{\beta }}_{\mathrm{c}}}\cos \mathit{\beta }\sin \mathit{\beta }\mathrm{d}\mathit{\beta }\mathrm{d}\mathit{\varphi }}{\frac{\mathrm{1}}{\mathrm{4}\mathit{\pi }}{\iint }_{\mathrm{0}}^{{\mathit{\beta }}_{\mathrm{c}}}\sin \mathit{\beta }\mathrm{d}\mathit{\beta }\mathrm{d}\mathit{\varphi }}}\\ {\displaystyle }& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{v}_{\mathrm{H}}{\displaystyle \frac{\mathrm{1}-{\cos }^{\mathrm{2}}{\mathit{\beta }}_{\mathrm{c}}}{\mathrm{1}-\cos {\mathit{\beta }}_{\mathrm{c}}}}\\ \text{(17)}& {\displaystyle }& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{v}_{\mathrm{H}}\left(\mathrm{1}+\cos {\mathit{\beta }}_{\mathrm{c}}\right),\end{array}$$

where β_c is the critical, local cone angle of the H-ENA velocity distribution function at r. For H-ENAs escaping from the exobase r_ex, it can be calculated by the expression

$$\begin{array}{}\text{(18)}& \cos {\mathit{\beta }}_{\mathrm{c}}={\displaystyle \frac{L}{r}}={\displaystyle \frac{\sqrt{r^{\mathrm{2}}-r_{\mathrm{ex}}^{\mathrm{2}}}}{r}}=\sqrt{\mathrm{1}-{\displaystyle \frac{r_{\mathrm{ex}}^{\mathrm{2}}}{r^{\mathrm{2}}}}},\end{array}$$

(for L see Fig. 6) meaning that with the shrinkage of this cone, the radial ENA bulk velocity is growing with radial distance by

$$\begin{array}{}\text{(19)}& 〈v_{\mathrm{ENA},\mathrm{z}}〉={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{v}_{\mathrm{H}}\left(\mathrm{1}+\sqrt{\mathrm{1}-{\displaystyle \frac{r_{\mathrm{ex}}^{\mathrm{2}}}{r^{\mathrm{2}}}}}\right).\end{array}$$

This expression for large distances asymptotically yields the result $〈v_{\mathrm{ENA},\mathrm{z}}(r\to \mathrm{\infty })〉=v_{\mathrm{H}}$. This finally shows that the ENA density at radial distances r≫r_ex, instead by (1∕r²), rather falls off like

$$\begin{array}{}\text{(20)}& n_{\mathrm{ENA}}\left(r\right)=n_{\mathrm{ex},\mathrm{ENA}}\cdot {\displaystyle \frac{r_{\mathrm{ex}}^{\mathrm{2}}}{r^{\mathrm{2}}}}{\displaystyle \frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\sqrt{\mathrm{1}-\frac{r_{\mathrm{ex}}^{\mathrm{2}}}{r^{\mathrm{2}}}}\right)}},\end{array}$$

which, however, is only a small correction with respect to the (1∕r²) drop-off used in our calculations above.

4 The Lyman-alpha glow contribution by H-ENAs and a look into self-consistency in H-ENA production

Thinking of H-ENA densities perhaps growing over the exobasic H densities beyond some critical radial distance r_c, one could be seduced to ask whether or not the escaping H-ENAs in fact do partly reproduce themselves by a second-generation charge exchange in the magnetosheath and thus contribute to the H-ENA production in the trans-magnetopause region. This idea is especially interesting, because it is not a priori clear what sort of H atoms, i.e., exobasic H atoms or H-ENAs, are in fact responsible for the Lyman-alpha signal registered at the largest exospheric heights. For the exospheric H densities inferred from TWINS-LAD Lyman-alpha measurements, it can not be excluded that H densities derived from such Lyman-alpha measurements at heights around 8 r_E (see Zoennchen et al., 2013) are partly or even fully due to H-ENAs themselves. In that case of being fully due to H-ENAs, the presence of these H-ENAs originating from charge-exchange processes in the magnetosheath should in fact be self-replacing, i.e., these H-ENAs could be a phenomenon of a self-consistency. For that purpose we are carrying out the following study of the specific contribution of H-ENAs to the Lyman-alpha glow emission at the largest exospheric heights with $r\ge r_{\mathrm{0}}\simeq \mathrm{8}{r}_{\mathrm{E}}$.

Their relative contribution to the full ENA production is the ratio ${\mathit{\xi }}_{\mathrm{ENA}}={\mathit{\beta }}_{\mathrm{ENA}}^{\ast }/{\mathit{\beta }}_{\mathrm{ENA}}$ of the two production rates due to H-ENAs and due to normal exospheric H atoms, given by

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathit{\beta }}_{\mathrm{ENA}}^{\ast }\simeq n_{\mathrm{p}\mathrm{2}}\cdot n_{\mathrm{ENA},\mathrm{0}}\cdot {〈\mathit{\sigma }{v}_{\mathrm{rel}}〉}^{\ast }\cdot \underset{r_{\mathrm{MP}}}{\overset{\mathrm{\infty }}{\int }}{\left({\displaystyle \frac{r}{r_{\mathrm{0}}}}\right)}^{-\mathrm{2}}\mathrm{d}r\\ \text{(21)}& {\displaystyle }& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{n}_{\mathrm{p}\mathrm{2}}\cdot n_{\mathrm{ENA},\mathrm{0}}\cdot {〈\mathit{\sigma }{v}_{\mathrm{rel}}〉}^{\ast }\cdot r_{\mathrm{0}}{\left({\displaystyle \frac{r_{\mathrm{MP}}}{r_{\mathrm{0}}}}\right)}^{-\mathrm{1}}\end{array}$$

and

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathit{\beta }}_{\mathrm{ENA}}\simeq n_{\mathrm{p}\mathrm{2}}\cdot n_{\mathrm{H}\mathrm{0}}〈\mathit{\sigma }{v}_{\mathrm{rel}}〉\cdot \underset{r_{\mathrm{MP}}}{\overset{\mathrm{\infty }}{\int }}{\left({\displaystyle \frac{r}{r_{\mathrm{0}}}}\right)}^{-\mathrm{2.7}}\mathrm{d}r\\ \text{(22)}& {\displaystyle }& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{1.7}}}\cdot n_{\mathrm{p}\mathrm{2}}\cdot n_{\mathrm{H}\mathrm{0}}\cdot 〈\mathit{\sigma }{v}_{\mathrm{rel}}〉\cdot r_{\mathrm{0}}{\left({\displaystyle \frac{r_{\mathrm{MP}}}{r_{\mathrm{0}}}}\right)}^{-\mathrm{1.7}},\end{array}$$

where ${〈\mathit{\sigma }{v}_{\mathrm{rel}}〉}^{\ast }$ and 〈σv_rel〉 are average charge-exchange frequencies between hot H-ENAs or cold exobasic H atoms, respectively, and the subsonic hot magnetosheath protons. This then consequently means

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathit{\xi }}_{\mathrm{ENA}}={\displaystyle \frac{{\mathit{\beta }}_{\mathrm{ENA}}^{\ast }}{{\mathit{\beta }}_{\mathrm{ENA}}}}\\ {\displaystyle }& {\displaystyle }={\displaystyle \frac{\frac{\mathrm{1}}{\mathrm{2}}{n}_{\mathrm{p}\mathrm{2}}{n}_{\mathrm{ENA},\mathrm{0}}{〈\mathit{\sigma }{v}_{\mathrm{rel}}〉}^{\ast }{r}_{\mathrm{0}}{\left(\frac{r_{\mathrm{MP}}}{r_{\mathrm{0}}}\right)}^{-\mathrm{1}}}{\frac{\mathrm{1}}{\mathrm{1.7}}{n}_{\mathrm{p}\mathrm{2}}{n}_{\mathrm{H}\mathrm{0}}〈\mathit{\sigma }{v}_{\mathrm{rel}}〉r_{\mathrm{0}}{\left(\frac{r_{\mathrm{MP}}}{r_{\mathrm{0}}}\right)}^{-\mathrm{1.7}}}}\\ \text{(23)}& {\displaystyle }& {\displaystyle }={\displaystyle \frac{\mathrm{1.7}}{\mathrm{2}}}({\displaystyle \frac{r_{\mathrm{MP}}}{r_{\mathrm{0}}}}{)}^{\mathrm{0.7}}\cdot {\displaystyle \frac{n_{\mathrm{ENA},\mathrm{0}}{〈\mathit{\sigma }{v}_{\mathrm{rel}}〉}^{\ast }}{n_{\mathrm{H}\mathrm{0}}〈\mathit{\sigma }{v}_{\mathrm{rel}}〉}}\end{array}$$

and thus leads to the expression

$$\begin{array}{}\text{(24)}& {\mathit{\xi }}_{\mathrm{ENA}}=\mathrm{0.85}\cdot ({\displaystyle \frac{r_{\mathrm{MP}}}{r_{\mathrm{0}}}}{)}^{\mathrm{0.7}}\cdot {\displaystyle \frac{n_{\mathrm{ENA},\mathrm{0}}{〈\mathit{\sigma }{v}_{\mathrm{rel}}〉}^{\ast }}{n_{\mathrm{H}\mathrm{0}}〈\mathit{\sigma }{v}_{\mathrm{rel}}〉}}.\end{array}$$

Now one can make use of the fact that the charge-exchange cross section at energies of $E_{\mathrm{rel},\mathrm{0}}=(m/\mathrm{2})\cdot v_{\mathrm{rel},\mathrm{0}}^{\mathrm{2}}$ is varying only very mildly with E_rel or v_rel and hence one can use a Taylor series expansion of the cross section with respect to the deviation Δv_rel from v_rel,0 in the form developed by Fahr (2003) and with the charge-exchange cross section given by Maher and Tinsley (1977), which then leads to

$$\begin{array}{ll}{\displaystyle }& {\displaystyle \frac{〈\mathit{\sigma }{v}_{\mathrm{rel}}^{\ast }〉}{〈\mathit{\sigma }{v}_{\mathrm{rel}}〉}}={\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{0}}\left[\mathrm{1}+\frac{\mathrm{2}B}{\sqrt{{\mathit{\sigma }}_{\mathrm{0}}}}\left(\mathrm{1}-\frac{x_{\mathrm{rel}}}{X_{\mathrm{rel}}}\right)\right]\left(v_{\mathrm{rel},\mathrm{0}}+\mathrm{\Delta }{v}_{\mathrm{rel}}\right)}{{\mathit{\sigma }}_{\mathrm{0}}\cdot v_{\mathrm{rel},\mathrm{0}}}}\\ \text{(25)}& {\displaystyle }& {\displaystyle }=\left[\mathrm{1}+{\displaystyle \frac{\mathrm{2}B}{\sqrt{{\mathit{\sigma }}_{\mathrm{0}}}}}\left(\mathrm{1}-{\displaystyle \frac{x_{\mathrm{rel}}}{X_{\mathrm{rel}}}}\right)\right]\left(\mathrm{1}+{\displaystyle \frac{\mathrm{\Delta }{v}_{\mathrm{rel},\mathrm{0}}}{v_{\mathrm{rel},\mathrm{0}}}}\right),\end{array}$$

where the quantities x_rel and X_rel are defined by

$$\begin{array}{}\text{(26)}& x_{\mathrm{rel}}={\displaystyle \frac{v_{\mathrm{rel},\mathrm{0}}}{\sqrt{\frac{\mathrm{2}k{T}_{p,\mathrm{2}}}{m}}}}\simeq \mathrm{1}\end{array}$$

and

$$\begin{array}{}\text{(27)}& X_{\mathrm{rel}}=\sqrt{{\displaystyle \frac{\mathrm{64}}{\mathrm{9}\mathit{\pi }}}\left(\mathrm{1}+{\displaystyle \frac{T_{\mathrm{H}}}{T_{\mathrm{p},\mathrm{2}}}}\right)+M_{\mathrm{s}}^{\mathrm{2}}},\end{array}$$

with T_H≃10³ K; $T_{p,\mathrm{2}}\simeq {\mathrm{10}}^{\mathrm{6}}$ K; and M_s≃0.1. The above expression thus leads to

$$\begin{array}{ll}{\displaystyle \frac{〈\mathit{\sigma }{v}_{\mathrm{rel}}^{\ast }〉}{〈\mathit{\sigma }{v}_{\mathrm{rel}}〉}}& {\displaystyle }=\left[\mathrm{1}+{\displaystyle \frac{\mathrm{2}B}{\sqrt{{\mathit{\sigma }}_{\mathrm{0}}}}}\left(\mathrm{1}-{\displaystyle \frac{\mathrm{1}}{\sqrt{\frac{\mathrm{64}}{\mathrm{9}\mathit{\pi }}}}}\right)\right]\left(\mathrm{1}+{\displaystyle \frac{\mathrm{\Delta }{v}_{\mathrm{rel},\mathrm{0}}}{v_{\mathrm{rel},\mathrm{0}}}}\right)\\ \text{(28)}& {\displaystyle }& {\displaystyle }=\left[\mathrm{1}+{\displaystyle \frac{\mathrm{2}B}{\sqrt{{\mathit{\sigma }}_{\mathrm{0}}}}}(\mathrm{1}-\mathrm{0.66})\right]\left(\mathrm{1}+{\displaystyle \frac{\mathrm{\Delta }{v}_{\mathrm{rel},\mathrm{0}}}{v_{\mathrm{rel},\mathrm{0}}}}\right),\end{array}$$

and hence one obtains with 2B $/\sqrt{{\mathit{\sigma }}_{\mathrm{0}}}=\left(\mathrm{2}\cdot \mathrm{6.8}/\sqrt{\mathrm{20}}\right)\cdot {\mathrm{10}}^{-\mathrm{2}}=\mathrm{0.14}$ (see Maher and Tinsley, 1977)

$$\begin{array}{ll}{\displaystyle \frac{〈\mathit{\sigma }{v}_{\mathrm{rel}}^{\ast }〉}{〈\mathit{\sigma }{v}_{\mathrm{rel}}〉}}& {\displaystyle }=[\mathrm{1}+\mathrm{0.34}\cdot \mathrm{0.14}]\left(\mathrm{1}+{\displaystyle \frac{\mathrm{\Delta }{v}_{\mathrm{rel},\mathrm{0}}}{v_{\mathrm{rel},\mathrm{0}}}}\right)\\ \text{(29)}& {\displaystyle }& {\displaystyle }=\mathrm{1.048}\cdot \left(\mathrm{1}-\sqrt{{\displaystyle \frac{\mathrm{64}}{\mathrm{9}\mathit{\pi }}}}\right)\simeq \mathrm{1.6}.\end{array}$$

This means that the average ENA charge-exchange production per atom is higher by a factor of 1.6 for hot H-ENAs as collision partners compared to cold exobasic H atoms. Thus, we finally come to the result

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathit{\xi }}_{\mathrm{ENA}}=\mathrm{0.85}\cdot {\left({\displaystyle \frac{r_{\mathrm{MP}}}{r_{\mathrm{0}}}}\right)}^{\mathrm{0.7}}\cdot {\displaystyle \frac{n_{\mathrm{ENA},\mathrm{0}}{〈\mathit{\sigma }{v}_{\mathrm{rel}}〉}^{\ast }}{n_{\mathrm{H}\mathrm{0}}〈\mathit{\sigma }{v}_{\mathrm{rel}}〉}}\\ \text{(30)}& {\displaystyle }& {\displaystyle }=\mathrm{1.33}\cdot {\left({\displaystyle \frac{r_{\mathrm{MP}}}{r_{\mathrm{0}}}}\right)}^{\mathrm{0.7}}\cdot {\displaystyle \frac{n_{\mathrm{ENA},\mathrm{0}}}{n_{\mathrm{H}\mathrm{0}}}}.\end{array}$$

When reminding ourselves of the density representations found in this article, namely Eq. (1) and

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{n}_{\mathrm{ENA}}=n_{\mathrm{ex},\mathrm{ENA}}\cdot {\left({\displaystyle \frac{r}{r_{\mathrm{ex}}}}\right)}^{-\mathrm{2}}\\ \text{(31)}& {\displaystyle }& {\displaystyle }\ge \mathrm{0.048}\cdot n_{\mathrm{H},\mathrm{ex}}\cdot {\left({\displaystyle \frac{r}{r_{\mathrm{ex}}}}\right)}^{-\mathrm{2}},\end{array}$$

this will then tell us that

$$\begin{array}{}\text{(32)}& {\mathit{\xi }}_{\mathrm{ENA}}\ge \mathrm{0.048}\cdot {\left({\displaystyle \frac{r_{\mathrm{MP}}}{r_{\mathrm{0}}}}\right)}^{\mathrm{0.7}}=\mathrm{0.048}\cdot {\mathrm{\Psi }}^{\mathrm{0.7}}.\end{array}$$

So, even under extremely unlikely magnetopause locations of $(r_{\mathrm{MP}}/r_{\mathrm{0}})\simeq \mathrm{2}$, the above result would still mean that ξ_ENA≃0.08, i.e., H-ENAs can only reproduce themselves by less than 10 %. Hence one can conclude that the H-ENA component discussed in this article can not be a self-consistent phenomenon, i.e., the Lyman-alpha glow observed by TWINS-LAD (Zoennchen et al., 2013) is due to exobasic H atoms only. To say it in other words, the self-consistency of magnetosheath ENAs could only then be expected under conditions of a magnetosheath plasma that is “optically thick” with respect to charge-exchange collisions of H-ENAs with magnetosheath protons, i.e., τ_sheath≃1. It turns out, however, that this “optical thickness” τ_sheath of the magnetosheath plasma with its extension $D=r_{\mathrm{BS}}-r_{\mathrm{MP}}$ has a value of only

$$\begin{array}{ll}{\displaystyle }{\mathit{\tau }}_{\mathrm{sheath}}& {\displaystyle }\simeq n_{\mathrm{sheath}}〈{\mathit{\sigma }}_{\mathrm{ex}}{v}_{\mathrm{rel}}〉{\displaystyle \frac{D}{v_{\mathrm{H}-\mathrm{ENA}}}}\\ {\displaystyle }& {\displaystyle }\simeq n_{\mathrm{sheath}}〈{\mathit{\sigma }}_{\mathrm{ex}}〉\left(r_{\mathrm{BS}}-r_{\mathrm{MP}}\right)\\ \text{(33)}& {\displaystyle }& {\displaystyle }=\mathrm{4.5}\cdot {\mathrm{10}}^{-\mathrm{4}}.\end{array}$$

5 The Lyman-alpha glow emission of terrestrial H-ENAs

Finally, it may be interesting to study how much the above discussed H-ENAs in the upper exosphere contribute to the terrestrial Lyman-alpha glow emission that, for example, is measured with a broad-band Lyman-alpha photometer by the satellite package TWINS-LAD (see Zoennchen et al., 2011, 2013; Bailey and Gruntman, 2013). For that purpose, one has to look at the spectral profile of the solar Lyman-alpha line emission that enters the Earth's exosphere from the solar direction. This profile of the full disk solar Lyman-alpha emission is a strongly inverted Gaussian with a strong spectral depletion near the center of the line (see observations from the Orbiting Solar Observatory, OSO, shown by Bonnet et al., 1978). As a reasonable approach to these OSO observations the following functional form of the solar line can be used (see Scherer et al., 2000):

$$\begin{array}{l}{\displaystyle \frac{I\left(\mathit{\lambda }\right)}{I_{\mathrm{0}}}}=I_{\mathrm{norm}}\left\{a\exp \left[-{\left({\displaystyle \frac{\mathit{\lambda }-{\mathit{\lambda }}_{\mathrm{0}}}{\mathrm{\Delta }a}}\right)}^{\mathrm{2}}\right]\right.\\ \text{(34)}& {\displaystyle }\left.-b\exp \left[-{\left({\displaystyle \frac{\mathit{\lambda }-{\mathit{\lambda }}_{\mathrm{0}}}{\mathrm{\Delta }b}}\right)}^{\mathrm{2}}\right]\right\},\end{array}$$

where the following numbers are used:

$$\begin{array}{ll}{\displaystyle }a& {\displaystyle }=\mathrm{7.9589}\\ {\displaystyle }b& {\displaystyle }=\mathrm{5.6930}\\ {\displaystyle }\mathrm{\Delta }a& {\displaystyle }=\mathrm{0.351}\mathit{\AA }\\ {\displaystyle }\mathrm{\Delta }b& {\displaystyle }=\mathrm{0.2}\mathit{\AA }.\end{array}$$

The quantity I_norm normalizes the area below the spectral curve to unity by

$$\begin{array}{}\text{(35)}& I_{\mathrm{norm}}={\left(\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\displaystyle \frac{I\left(\mathit{\lambda }\right)}{I_{\mathrm{0}}}}\mathrm{d}\mathit{\lambda }\right)}^{-\mathrm{1}}={\displaystyle \frac{\mathrm{1}}{\sqrt{\mathit{\pi }}\left(a\mathrm{\Delta }a-b\mathrm{\Delta }b\right)}}\end{array}$$

and I₀ denotes the full-disk average of the solar Lyman-alpha flux at 1 AU.

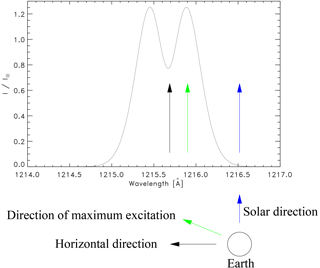
Now we look at those H-ENAs bouncing off the dayside exobase with a thermally broad distribution around the bulk velocity U_ENA of roughly 300 km s⁻¹ and moving off in zenith direction into the solar direction. These H atoms are resonantly absorbing from the blueshifted wing of the solar profile with a mean blueshift of $\mathrm{\Delta }{\mathit{\lambda }}^z={\mathit{\lambda }}_{\mathrm{0}}(U_{\mathrm{ENA}}/c)\simeq$ (1216∕1000) Å = 1.2 Å and with an equal spread around this absorption peak due to the thermally broad H-ENA distribution. Thus, the resonant excitation of these H-ENAs would be centered around the spectral place ${\mathit{\lambda }}_{\mathrm{ENA}}^z={\mathit{\lambda }}_{\mathrm{0}}+\mathrm{\Delta }\mathit{\lambda }$, where the spectral intensity of the incoming solar line is larger than at line center. On the other hand, when looking into the dawn–dusk regions of the geocorona, the H-ENA Lyman-alpha resonance glow would be connected with H-ENAs moving off the exobase into the direction perpendicular to the solar line. This is why for these ENAs the spectral Doppler shift vanishes, as it does for the exobasic H atoms, and these H atoms are thus excited mainly in the line center where the spectral solar intensity is smaller by a factor of about 1∕2 compared to the spectral intensity maxima. For an illustrative view, see Fig. 7.

Figure 7 Resonant excitation of H-ENAs parallel and perpendicular to the solar line.

At this moment it is, however, hard to make clear predictions on the anisotropy of the H-ENA radiation glow without more exact resonant scattering calculations on the basis of exact H-ENA distribution functions. It may, nevertheless, be already predictable now that the sun-dusk H-ENA glow anisotropy could come up to a factor of 2, also meaning that the density of H-ENAs concerning their glow contribution in the solar direction would also be weighted by such a factor of 2 with respect to the corresponding contribution from exobasic H atoms.

6 Conclusions

At the end of this article, we once again want to refer back to the beginning where we looked at the problem raised by Qin and Waldrop (2016) who had found indications for the existence of a non-thermal exospheric hydrogen component in their Lyman-alpha glow observations with the satellite TIMED/GUVI, a component for which no explanation as yet is available. In this article, we have discussed a non-thermal hydrogen component originating from charge-exchange interactions of exobasic terrestrial hydrogen atoms with protons of the shocked solar wind plasma ahead of the magnetopause. Though this H component definitely represents a contribution to non-thermal hydrogen in the terrestrial exosphere with a relative relevance increasing with height, it has also become clear from the calculations presented in this article that this contribution cannot explain the observations made by Qin and Waldrop (2016). Concerning the Lyman-alpha resonance glow, the trans-magnetopause contribution discussed in this article due to its rather low relative density in heights below three Earth radii can only become recognizable at large heights of about five to eight Earth radii, while Qin and Waldrop (2016) claim to clearly identify the influence of a non-thermal H component from their glow measurements already at heights of 3000 km. Thus, an idea, alternative to ours presented here and bringing in suprathermal H atoms at lower heights, might be to study whether the observationally indicated non-thermal H component could perhaps be due to a non-thermalized form of H atoms originating in the upper thermosphere via photo-dissociation of H₂O through OH producing photo-dissociative H atoms with velocities of about 8 km s⁻¹ (e.g., see Keller, 1990), which as non-thermalized H products represent a hydrogen component with an effective temperature of about 4000 K.

Appendix A

This figure, reproduced from the paper by Fahr (1978), is provided to illustrate the process of an elastic collision of two particles with different masses m and M and velocities v₁ and v₂ before the collision. At the course of the collision, the magnitude of the relative velocity $v_{\mathrm{rel}}=[{\mathit{v}}_{\mathrm{1}}-{\mathit{v}}_{\mathrm{2}}]$ between the two particles is conserved, as is the center-of-mass velocity. The newly originating velocities ${\mathit{v}}_{\mathrm{1}}^{\prime }$ and ${\mathit{v}}_{\mathrm{2}}^{\prime }$, resulting after the collision has occurred, are connected with a turn of the relative velocity vector around the center-of-mass velocity. Thus, the resulting velocities are found to be placed on the two shells around the center-of-mass velocity, the smaller for the heavier mass, the larger for the smaller mass, all in connection with the resulting turning angle χ.

Figure A1 Schematic representation of a collision between particles of unequal masses in the local velocity space for the calculation of elastic energy transfers.