Solar wind and kinetic heliophysics

This paper reviews recent aspects of solar wind physics and elucidates the role Alfvén waves play in solar wind acceleration and turbulence, which prevail in the low corona and inner heliosphere. Our understanding of the solar wind has made considerable progress based on remote sensing, in situ measurements, kinetic simulation and fluid modeling. Further insights are expected from such missions as the Parker Solar Probe and Solar Orbiter.

The sources of the solar wind have been identified in the chromospheric network, transition region and corona of the Sun. Alfvén waves excited by reconnection in the network contribute to the driving of turbulence and plasma flows in funnels and coronal holes. The dynamic solar magnetic field causes solar wind variations over the solar cycle. Fast and slow solar wind streams, as well as transient coronal mass ejections, are generated by the Sun's magnetic activity.

Magnetohydrodynamic turbulence originates at the Sun and evolves into interplanetary space. The major Alfvén waves and minor magnetosonic waves, with an admixture of pressure-balanced structures at various scales, constitute heliophysical turbulence. Its spectra evolve radially and develop anisotropies. Numerical simulations of turbulence spectra have reproduced key observational features. Collisionless dissipation of fluctuations remains a subject of intense research.

Detailed measurements of particle velocity distributions have revealed non-Maxwellian electrons, strongly anisotropic protons and heavy ion beams. Besides macroscopic forces in the heliosphere, local wave–particle interactions shape the distribution functions. They can be described by the Boltzmann–Vlasov equation including collisions and waves. Kinetic simulations permit us to better understand the combined evolution of particles and waves in the heliosphere.

1 Introduction

1.1 Hannes Alfvén and his wave

The European Geosciences Union (EGU) has awarded the Hannes Alfvén Medal to me for the year 2018. Receiving this important award gives me great enjoyment, and I also feel deeply honored. My warm and sincere thanks go to the EGU and the medal committee for choosing me as this year's awardee. As we all know, Alfvén received the 1970 Nobel Prize in physics for his work in magnetohydrodynamics and plasma physics. As a young researcher in the field of space science I first came across Alfvén's eminent work mostly through his combined electromagnetic–hydrodynamic waves (Alfvén, 1942), which have become famous and are now named after him. Alfvén waves are ubiquitous in the universe. They occur in the solar wind, in stellar coronas and winds, in planetary magnetospheres and in many other astrophysical plasmas.

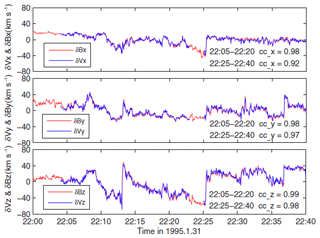
Figure 1 Alfvén waves (Wang et al., 2012) with very high correlations between the fluctuations of the Cartesian components of the magnetic field vector and flow velocity vector evaluated in the de Hoffmann–Teller frame. The respective correlation coefficients (cc's) are also indicated.

To give at least one example of Alfvén waves, I show in Fig. 1 a nice case stemming from measurements of the WIND spacecraft made at 1 AU in 1995 (Wang et al., 2012). These large-amplitude Alfvénic fluctuations (shown here component-wise for a 40 min period with a time resolution of 3 s) reveal a very high correlation between the variations of the magnetic field vector and flow velocity vector, which was evaluated in the de Hoffmann–Teller frame in which the convective electric field of the solar wind is transformed away. The time variations of the magnetic and flow fields appear erratic, reveal large abrupt excursions and occur on all scales, indicating that we are dealing not with a simple wave but with a kind of Alfvénic turbulence covering a wide range of frequencies or wave numbers. Similar fluctuations are observed everywhere in the inner heliosphere (Tu and Marsch, 1995), in particular in fast solar wind streams originating from coronal holes. A recent detailed review of the properties of Alfvénic turbulence in high-speed solar wind streams (with hints from cometary plasma turbulence) was published by Tsurutani et al. (2018).

Returning to Alfvén's achievements, I would like to mention that later in my career I also learned about the Alfvén critical point in the outer solar corona, i.e., the location (Marsch and Richter, 1984) around which the rotation (forced by the solar magnetic field) of the Sun's coronal plasma maximizes and then ceases again, and where the plasma thus detaches from the corona to transform into the solar wind plasma. Some of Alfvén's pioneering work in magnetohydrodynamics and space plasma physics, in particular on the Earth's ionosphere and magnetosphere, was concisely described by the last year's awardee (Priest, 2017) in his medal lecture and shall not be repeated here. Alfvén (1950) himself recapitulated and summarized most of his novel ideas and deep insights in his book entitled Cosmical Electrodynamics, which contains the main fundamentals and many applications of the – at that time still young – field of space plasma physics.

About 70 years later, this field has enormously expanded. Given that the ordinary hadronic and leptonic matter (albeit representing merely 5 % of the total energy density) in the universe is mostly in the plasma state, the physics branches of electrodynamics, magnetohydrodynamics and plasma kinetics have indeed become of cosmical importance and today exert a dominating influence on many research areas of modern astrophysics. One such field is the solar wind and the Sun's astrosphere, which we call the heliosphere. In this paper I will not be able to give adequate credit to all that has been done and published in heliophysics, but I will cite some noteworthy reviews and specific papers below which will give the reader a taste of the wider literature.

1.2 The solar wind and Eugene Parker

The solar wind emanating from our nearby star, the Sun, is for us the most relevant example of a stellar wind, because it is even amenable to in situ measurements within the entire heliosphere, which is the plasma cavity carved out of the local interstellar medium by the solar wind flow and its associated magnetic field. The solar wind is inextricably linked with another great scientist in space physics, Eugene Parker, who in 1958 wrote his seminal paper (Parker, 1958) on the “Dynamics of the Interplanetary Gas and Magnetic Fields”, and somewhat later reviewed (Parker, 1965) the early theoretical work in this – then still new – field. Today, the experimental and theoretical literature on the solar wind abounds and is unmanageable, given the results obtained by so many spacecraft that have been sent to space for investigation of the near-Earth and planetary plasma environments, and the Sun and its extended heliosphere that reaches out to more than 100 AU.

In Parker's early model of the solar wind outflow from the corona with a temperature constant with height, a simple formula can be obtained for the sonic Mach number $M=V\left(r\right)/c_{\mathrm{0}}$ (with flow speed V and constant sound speed c₀) as a function of the distance from the Sun r in units of the critical radius r_c, where by definition M_c=1 and the flow becomes supersonic. This formula reads

$$\begin{array}{}\text{(1)}& M^{\mathrm{2}}-\ln \left(M^{\mathrm{2}}\right)=\mathrm{4}\left(\ln \left({\displaystyle \frac{r}{r_{\mathrm{c}}}}\right)+{\displaystyle \frac{r_{\mathrm{c}}}{r}}\right)+C,\end{array}$$

with C being an integration constant. At large distances, M>1 and $n\approx (r^{\mathrm{2}}V{)}^{-\mathrm{1}}$, and the supersonic solar wind results. As we shall see later, the solar wind as we know it today, after decades of remote-sensing observations of the Sun and of comprehensive in situ plasma measurements, appears rather complex and quite variable. In particular the magnetically highly structured and non-uniformly expanding solar corona creates a similarly structured flow pattern of the solar wind. We will discuss the solar corona and the solar wind sources in detail after this Introduction, then address the topic of magnetohydrodynamic (MHD) turbulence and subsequently elaborate some key point of kinetic heliophysics. The paper then ends with brief prospects of the future and provides some final conclusions.

1.3 A little more history: the Helios mission

My personal career has largely been shaped by the Helios mission, which was an American–German twin-space-probe mission to investigate the innermost part of interplanetary space (the inner heliosphere within Earth's orbit) and the solar influences on the interplanetary medium (today we speak of space weather). Two nearly identical, but oppositely spinning (spin of Helios 1 pointing north and of Helios 2 south), spacecraft were launched (H1: 10 December 1974; H2: 15 January 1976) into highly elliptical orbits with low perihelia, for Helios 1 at 0.31 AU and Helios 2 at 0.29 AU. These orbits were designed to provide the opportunity to separate spatial and temporal effects, to cover ±7.5^∘ of solar latitude, and to study radial gradients (0.3–1 AU) and phenomena (particles and fields) traveling outward from the Sun. The Helios mission characteristics and its first scientific results were described in a special issue of the old Journal of Geophysics, and results from the plasma instrument in particular were described by Rosenbauer et al. (1977).

When Helios was conceived and planned, ESA did not even exist, and the mission was the first great space endeavor of the former West Germany. Incidentally, the old Greek word Helios means the Sun and is the name of its god. After completing my PhD in 1976 at Kiel University, I started working at the Max Planck Institute (MPI) for Extraterrestrial Physics in Garching near Munich; the Helios probes had already been launched and were delivering novel particle and field data. I was lucky then in getting the chance to work on the proton data obtained by the excellent plasma experiment that Helmut Rosenbauer and Rainer Schwenn had built, my dear colleagues with whom I collaborated later for a major period of my career in Lindau at the MPI for Aeronomy. I would like to take this opportunity to thank them for this successful collaboration and their continuous support. Both passed away much too early. The ample results of the Helios mission were made public in a two-volume book which contains extensive scientific review articles and was co-edited by Rainer and myself (Marsch and Schwenn, 1990).

1.4 Kinetic heliophysics

The Helios instruments delivered unprecedented particle and field data, and especially data on the three-dimensional distribution function of protons in velocity space measured at locations in real space between 0.3 and 1 AU (Marsch, 1991a, b). Their physical interpretation required going way beyond fluid theory and employing the powerful tools of kinetic plasma physics. Thus kinetic heliophysics largely emerged from such a comprehensive approach. Heliophysics in a broad sense is the physics of the Sun, in analogy to astrophysics. In particular, it encompasses the physics of the solar wind and the heliosphere. The heliosphere was found to range from the solar corona far out to the heliopause at about 124 AU, which was finally revealed by the plasma wave instrument on the Voyager 1 spacecraft (Gurnett et al., 2013). As the Sun varies over its activity cycle, so does the related heliosphere. Its variations during the solar cycle are reviewed in the book edited by Balogh et al. (2008).

Table 1 Theoretical description of the solar wind in terms of particle distribution functions or their velocity moments.

Figure 2 Composite SOHO image taken in 1996: innermost region showing in the iron line Fe XV 28.4 nm the corona above the disk at a temperature of about 2 MK, middle region showing the Sun's outer atmosphere as it appears in ultraviolet light in the line O VI 103.2 nm of oxygen ions flowing away from the Sun to form the solar wind and outer region showing the extended structured corona as recorded by the white-light coronagraph measuring the light scattered by free coronal electrons. A Sun-grazing comet is also visible as a bent trace on the left.

Usually, most heliospheric plasma phenomena are described merely by magnetohydrodynamics. Yet under the low-density and high-temperature conditions typical of the weakly collisional heliospheric plasma the solar wind particles and fields are strongly affected by kinetic plasma processes. The plasma instrumentation of future missions to be described below will in the near future provide novel high-resolution in situ measurements of particle velocity distributions and wave-field spectra. Thus to analyze and interpret these data, a multi-scale systems approach to heliophysical macroscopic and microscopic phenomena will be required, supported by numerical simulations. An interesting prospective on the future of kinetic heliophysics was recently given by Howes (2017).

The fundamental theoretical description of any plasma is given by the Maxwell equations together with the Boltzmann–Vlasov equations, which represent on a kinetic level all particles involved in terms of their phase-space densities. In the solar wind case, this means that electrons, protons and alpha particles (about 4 %), as well as many minor heavy ions, have to be considered separately. Their physical description is achieved in two ways; one may either stay with the full Boltzmann equation or reduce information by taking its velocity moments from which the single/multi-fluid or magnetohydrodynamic fields can then be derived. In Table 1 I compose some of the key elements of such theoretical descriptions of the solar wind plasma. For detailed information see the modern textbooks that give an exhaustive introduction into (Baumjohann and Treumann, 1996) and an advanced treatment of (Treumann and Baumjohann, 1997) space plasma physics.

After all these preparatory remarks and introductory discussion I now turn to the main subjects. Before doing so, I would like to emphasize that this paper is not supposed to be a balanced and comprehensive review of these subjects, which are much too broad anyway, but rather gives a selective and personal perspective on the many topics discussed. I apologize to the reader for this limitation and for not being able to give adequate credit here to the wider research community. But several recent and older review papers mentioned later will provide that service.

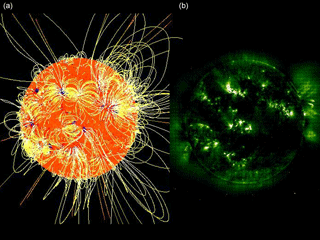
Figure 3 (a) Solar magnetic field constructed from potential-field extrapolation of the surface magnetic field after Wiegelmann and Solanki (2004); (b) image of the corona taken by the SOHO extreme ultraviolet imaging telescope in the emission line Fe XII 19.5 nm of iron. Note the coincidence of bright regions with closed magnetic field loops and dark areas with open magnetic field lines. Magnetically active regions mainly consist of closed loops in which plasma can be confined and cause bright emission. Yet the large-scale magnetic field is open in coronal holes, from which plasma can escape on open field lines as solar wind, and where the electron density, and thus the emission, is strongly reduced.

2 Solar corona and solar wind sources

2.1 The Sun's magnetic field and corona

The solar corona emerges naturally and becomes visible for the human naked eye during solar eclipses, beautiful spectacles that have been experienced by mankind since its cultural beginnings. In the modern space age, we have routinely observed the corona for decades by means of spaceborne coronagraphs. Subsequently, I mostly refer to the SOHO (Solar and Heliospheric Observatory) mission, in which I myself was deeply involved. For a description of this outstanding mission and its first results see the books edited by Fleck et al. (1995) and Fleck and Svestka (1997). This is not the place to appreciate the enormous progress made by the results that were obtained from the SOHO payload and the many instruments flown on more recent spacecraft and space probes with the aim of studying the Sun, its corona and the solar wind. I just illustrate the corona in Fig. 2, which shows the corona as imaged at three wavelengths against the stars in the night sky. One can note the dark areas above the northern and southern pole, associated with dilute coronal holes in the emission, and the three bright extended streamers originating from the dense equatorial lower corona. Fast wind is known to emanate mostly from the poles, and slow wind from the equator, during this near-minimum period of the solar cycle. For a comprehensive observational review of coronal holes see the article by Cranmer (2009). Semi-empirical models of the slow and fast solar wind have been discussed by Wang (2012).

Obviously, the type of ambient solar wind (either fast or slow) is closely connected with the structure and topology of the Sun's magnetic field. On open field lines the coronal plasma cannot be confined but is free to expand, cools off and transforms into the solar wind. In contrast on closed field lines, coming in the shape of multi-scale loops as shown in Fig. 3 after Wiegelmann and Solanki (2004) in the left frame, the plasma can be magnetically confined, apparently heating up and then cooling by strong emission of ultraviolet light (as shown in the right frame) yet without solar wind particle emission. Thus the coronal magnetic structure determines on a large scale (fraction of a solar radius or tens of degrees as seen from the Sun's center) the spatial distribution of the solar wind plasma streams emanating from the Sun. For a more detailed discussion on the association of coronal holes with the high-speed solar wind see the review by Cranmer (2002). A modern review of coronal magnetic field models was written by Wiegelmann et al. (2017).

The solar corona is commonly referred to as being at a temperature of 1 MK. This statement needs to be better specified if we consider the multi-species nature of the coronal plasma. In addition to the major species protons and electrons, we have a varying amount of alpha particles (with typically 5 % in fractional number density in the solar wind) and all kinds of heavy ions coming in different ionization stages, in particular iron ions that dominate the coronal ultraviolet emission. All these particles are not in thermal equilibrium with each other, and therefore there is nothing like the coronal temperature. Wilhelm (2012) has reviewed the coronal-hole temperature observations. The electrons seem to be the coolest component, hardly reaching 1 MK. In contrast, the heavy ions tend to have higher temperatures than the protons in proportion to their masses, so that all ions in coronal holes and the associated high-speed streams are found to have about the same thermal speed, $v_{\mathrm{i}}=\sqrt{\frac{k_{\mathrm{B}}{T}_{\mathrm{i}}}{m_{\mathrm{i}}}}$ (T_i is the ion temperature and m_i its mass, and k_B is the Boltzmann constant). There is still no agreement on the physical reason for this kinetic behavior, yet a wave origin appears most likely. An up-to-date discussion of this issue and a review of the ample observational evidence obtained by in situ and remote-optical measurements are contained in the recent article by Cranmer et al. (2017), reviewing the origins of the ambient solar wind and implications for space weather.

2.2 Magnetic network and transition region funnels

Figure 4 This SOHO image taken on 18 March 2003 shows, in the helium line He II 30.4 nm emitted at a temperature of about 60–80 kK, the chromospheric network on the solar disk and two huge prominences off the solar limb. Prominences often are at the origin of the solar eruptions that drive coronal mass ejections (CMEs). The magnetic network has typical cell sizes of 20–30 Mm, with strong magnetic fields of about 100 G concentrated in the network lanes, and spreads rather uniformly over the entire solar disk (surface).

As we have learned in the previous sections, fast solar wind streams appear to originate in coronal holes. The sources of the fast solar wind in polar coronal holes can generally be seen in the chromospheric He I 584 nm line and in the Ne VIII 770 nm line of the low corona, either as dark polar caps in radiance diagrams or as regions of predominant blue shift (Wilhelm et al., 2000). Prior to that, Hassler et al. (1999) showed that a relationship exists between the outflow velocity and the chromospheric magnetic network structure shown in Fig. 4, suggesting that the solar wind is connected to the network and emanates from localized regions along the boundaries of the network cells. The magnetic structure of the solar transition region in a polar coronal hole as observed in various ultraviolet lines that are emitted at different temperatures was analyzed by Marsch et al. (2006a).

Yet, the detailed origin of the solar wind within the network structure remained less clear. Then Tu et al. (2005) could establish that the wind seems to start flowing at about 10 km s⁻¹ out of the low corona at heights above the photosphere between 5 and 20 Mm in the so-called magnetic funnels of the chromospheric network. This result was obtained by a correlation of the maps of Doppler velocity and radiance in spectral lines emitted by various ions with the force-free magnetic field as extrapolated from photospheric magnetograms to different altitudes. This finding is illustrated in Fig. 5, which shows the solar disk (left) together with a segment of the coronal magnetic field at the pole (top) and a further blow-up of part of that field (right), which reveals its form as an expanding coronal funnel.

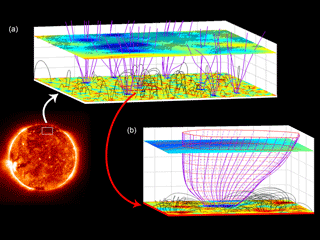
Figure 5 Illustration after Tu et al. (2005) of the solar magnetic transition region, showing the solar disk (left) together with a segment of the coronal magnetic field at the pole (a) and a further blow-up of part of that field (b), which attains the shape of a rapidly expanding coronal funnel. The open magnetic field lines are drawn in magenta, and the field strength is indicated in blue on the top plane at a height of 20 Mm, where the outflow speed of 10 km s⁻¹ is indicated by hatched areas.

These observations motivated Hackenberg et al. (2000) to model the nascent solar wind flow in a coronal funnel within a fluid model, whereby the funnel magnetic field was prescribed by a simple potential field. The heating of the corona was achieved by wave energy absorption via the sweeping mechanism. Thus rather steep temperature gradients could be obtained, which lead to rapid acceleration and the critical point of the flow being located close to the Sun at about one solar radius. Such plasma outflow was indeed observed (Wiegelmann et al., 2005) via the associated Doppler shift of ultraviolet spectral lines in close connection with the inferred coronal magnetic field modeled as a potential field. Later, He et al. (2008) also modeled the outflow in a coronal funnel with additional mass and energy supplied at a height of 5 Mm above the photosphere.

The work of Hackenberg et al. (2000) and He et al. (2008) followed the earlier model set up by Marsch and Tu (1997) on the connection between the solar wind and the chromospheric network (see again Fig. 4), which again followed in its reasoning the work by Tu and Marsch (1997) on the fast solar wind. They assumed in their two-fluid model calculations that the outflowing coronal-hole plasma could be heated and accelerated by absorption of high-frequency Alfvén/ion-cyclotron waves. The existence of these waves in the lower corona was an ad hoc assumption which still needs to be validated. In the distant solar wind they have indeed been frequently observed as I will discuss in subsequent sections. I finally point the reader's attention to more recent work by Cranmer et al. (2013) on the problem of how to connect magnetic activity of the Sun's high-resolution magnetic carpet or chromospheric network to the turbulent inner heliosphere.

2.3 Coronal Alfvén waves excited by magnetic reconnection

“Can the solar wind be driven by magnetic reconnection in the Sun's magnetic carpet [or network]?” was the question investigated by Cranmer and van Ballegooijen (2010). What is the mechanism exciting Alfvén waves in the solar corona? Various scenarios have been discussed in the literature. For example, Axford and McKenzie (1992) and Axford et al. (1999) suggested that frequent reconnection in the chromospheric magnetic network could lead to many large-amplitude Alfvén waves, whereby a small closed loop may reconnect with a field line in a unipolar magnetic region. A similar mechanism at supergranular scale was proposed by Fisk et al. (1999), who suggested that Alfvén waves may be generated by reconnection between open fields or funnels and solar magnetic flux freshly emerging within a supergranule. This process should define the Poynting vector and mass flux into the corona required to drive fast outflow. The solar wind energy equation can then simply be written as an equation for the squared final solar wind speed, u_f, in the form

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{u}_{\mathrm{f}}^{\mathrm{2}}={\displaystyle \frac{{\int }_{S_{\mathrm{i}}}〈\frac{c}{\mathrm{4}\mathit{\pi }}(\mathit{E}\times \mathit{B})〉\cdot \mathrm{d}\mathit{s}}{{\int }_{S_{\mathrm{i}}}〈\mathit{\rho }\mathit{u}〉\cdot \mathrm{d}\mathit{s}}}-{\displaystyle \frac{G{M}_{\mathrm{s}}}{r_{\mathrm{i}}}}=V_{\mathrm{A}}^{\mathrm{2}}\left(r_{\mathrm{i}}\right)-{\displaystyle \frac{G{M}_{\mathrm{s}}}{r_{\mathrm{i}}}},\end{array}$$

whereby the index i refers to the inner surface S_i (located at the height r_i) through which the wave Poynting flux escapes. The brackets indicate some average as obtained by integration over that reference surface. Here the other symbols have their standard meaning: G is the gravitational constant, c the speed of light, M_s the mass of the Sun, ρ the mass density, u the coronal flow velocity, E the electric and B the magnetic field, and V_A(r_i) the equivalent Alfvén speed at height r_i. To drive fast streams, this has to clearly exceed the solar escape velocity from the reconnection surface, which is v_∞=618 km s⁻¹.

More recently, De Pontieu et al. (2007) reported that Alfvén waves with sufficient strength to drive coronal flows had unambiguously been observed in the solar atmosphere. They used images of high temporal and spatial resolution obtained with the Solar Optical Telescope (SOT) on board the Japanese Hinode satellite. These observations revealed that the chromosphere, the thin layer located between the solar surface and corona, is permeated by Alfvén waves of strong amplitudes on the order of 10 to 25 km s⁻¹ and periods of 100 to 500 s. Their estimated energy flux (and comparisons with simulations) indicates that these Alfvén waves can in fact accelerate fast solar wind streams. The required energy flux amounts to several hundreds watt per square meter. Also, Tomczyk et al. (2007) clearly identified Alfvén waves from SOHO observations of the lower corona. The observational evidence for Alfvénic wave energy injection at the base of the fast solar wind has been reviewed by McIntosh (2012).

2.4 On modern solar wind fluid models

Modeling of the solar wind has a long history. For a modern treatment of the basics of the solar wind see the book by Meyer-Vernet (2007). In the Introduction I mentioned Parker's classical 1958 paper which initiated single-fluid models. Here I cannot review all the modeling efforts made ever since and the vast amount of subsequent papers addressing this topic on the basis of single-, two- or multi-fluid equations, which in modern times are also solved in three dimensions by means of numerical codes or even replaced by fully kinetic simulations. For a comprehensive recent review of the models from the chromosphere to 1 AU I refer the reader to the paper of Hansteen and Velli (2012), who stress the consideration of solar corona and wind as a unified system. Some of the empirical constraints placed on the models by in situ and remote-sensing measurements have been discussed by Marsch (1999). The emphasis here is on kinetic heliophysics and Alfvén waves, and thus the work by Cranmer and van Ballegooijen (2005) “On the generation, propagation, and reflection of Alfvén waves from the solar photosphere to the distant heliosphere” will be discussed. They scrutinized the ample empirical material on this subject and tried to reproduce in particular the radial evolution of the wave amplitude.

It should be pointed out, however, that their perturbation technique is not at all a consistent turbulence theory, and it was not made clear in their paper if the iterative scheme used converges. In the work by Velli (1993) and Velli et al. (1992) this crucial theme of linear versus nonlinear cascade is discussed extensively, and the linear theory is re-derived carefully. Concerning this issue see also the papers of Verdini et al. (2005, 2010), who attempted to derive a rigorously self-consistent theory, and of Verdini and Velli (2007) on Alfvén waves and turbulence in the solar atmosphere and solar wind.

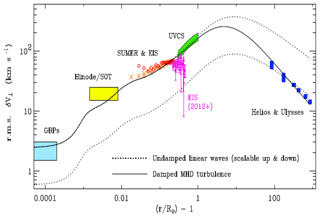
Figure 6 Dependence on radial solar distance of the transverse velocity amplitudes of MHD fluctuations in coronal holes and fast solar wind. The model curves and photospheric G-band bright-point data are taken from Cranmer and van Ballegooijen (2005). Other data are from type II spicule motions observed by Hinode/SOT, nonthermal line broadenings from SOHO, and direct in situ measurement from the Helios and Ulysses missions and composed by Cranmer et al. (2017). A note of caution is appropriate for this integrated overview plot. The shown velocity fluctuations have been inferred from very different empirical data sets and relate to completely different frequency regimes of measurements made at various radial distances from the Sun.

Fig. 6 shows the height dependence of transverse velocities in the coronal hole and fast wind, as obtained from remote-sensing and in situ measurements. The root-mean-square transverse wave amplitude (interpreted as being due to Alfvén waves) is displayed versus radial distance from the Sun. This picture was put together by Cranmer et al. (2017) from various optical and plasma data sources. The dotted line indicates the run of the amplitude as achieved from their model calculations for undamped waves, whereas the continuous line includes wave damping, which apparently only sets in at interplanetary distances. For further spectroscopic evidence for coronal waves as inferred by observations of the wave-induced broadenings of ultraviolet emission lines measured on SOHO see in particular the review by Wilhelm et al. (2007).

In order to describe wave damping, a kinetic approach for the damping rate and a wave spectral transfer equation are required (Cranmer and van Ballegooijen, 2005), properties which complicate the fluid models considerably. Therefore many modelers preferred to consider simpler wave energy functions, which mimic the plasma heating and acceleration by terms declining exponentially with a certain damping length that needs to be adjusted to obtain the desired energy and momentum deposition into the particles. For example, in the work of Suess et al. (1999), the authors used a time-dependent, two-fluid (2-D in spherical polar coordinates) MHD model, but with separate thermal T_e and T_p equations. Thus they obtained after 1 day steady ambient outflow, slow and dense at the equator and fast and dilute at the poles. The heating functions for electrons Q_e and protons Q_p were assumed to depend on solar co-latitude θ and distance r from the Sun (solar radius R_s) in the simple exponential form

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{Q}_{\mathrm{e},\mathrm{p}}=Q_{\mathrm{0}}{f}_{\mathrm{e},\mathrm{p}}(r,\mathit{\theta })\exp (-\mathrm{0.1}(r-R_{\mathrm{s}})/R_{\mathrm{s}}),\\ \text{(3)}& {\displaystyle }& {\displaystyle }\mathrm{with}{Q}_{\mathrm{0}}=\mathrm{5}\times {\mathrm{10}}^{-\mathrm{8}}\mathrm{erg}{\mathrm{cm}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}},\end{array}$$

where $f_{\mathrm{e},\mathrm{p}}(r,\mathit{\theta })$ describes the co-latitude dependence, essentially of the normalized particle density, and Q₀ is the basic surface volumetric heating rate that is sufficient to drive the solar wind.

In this model they achieved a satisfactory agreement of their results with the Ulysses measurements of the solar wind during the first perihelion passage, whereby the spacecraft rapidly scanned the solar latitude between 0 and 80 ^∘ (McComas et al., 1998). Clearly, the temperature equations for electron and protons must be considered separately to obtain these results and to be consistent with the observational constraints on the coronal and solar wind temperatures discussed before. Furthermore, the energy deposition for heating should comply with available energy from Alfvén-wave damping, as shown in the Fig. 6 above, where the little blue boxes indicate the in situ measured values of the wave amplitudes. In the next section I am going to discuss the waves and MHD turbulence in detail. Concerning solar wind modeling, Cranmer et al. (2007) developed a self-consistent complex model for coronal heating and solar-wind acceleration from anisotropic magnetohydrodynamic turbulence, an issue which I touch upon briefly below.

3 Selected results on magnetohydrodynamic turbulence

In Fig. 6 the radial evolution of the mean turbulence amplitude δv_⟂ of the transverse fluctuations is presented, which reaches its maximum of up to 200 km s⁻¹ near 10 R_s and subsequently declines to the in situ measured values ranging from about 100 km s⁻¹ (at 0.3 AU) down to 20 km s⁻¹ (at 1 AU). According to the Helios observations in fast solar wind streams, most of the turbulence power resides in Alfvén waves originating from coronal holes. These Alfvénic fluctuations near 0.3 AU and their subsequent radial evolution and statistical properties were first described in detail by Denskat and Neubauer (1982, 1983).

Later Marsch and Tu (1990a) did a comprehensive study of these fluctuations based on the combined plasma and magnetic field data, so that they could make use of the so-called Elsässer variables (Grappin et al., 1990; Tu et al., 1989). Some of their results are composed in Fig. 7, which shows turbulence spectra as a function of the radial distance from the Sun as measured by Helios in slow (left) and fast (right) solar wind. Note the distinct steepening of the spectra in fast wind, indicating the radial evolution towards the celebrated Kolmogorov $-\mathrm{5}/\mathrm{3}$ spectrum, and also the predominance of outward-propagating Alfvén waves. Turbulence in slow wind appears to be much less Alfvénic but is already more developed near the Sun at 0.31 AU and more so further out.

Bourouaine et al. (2012) again analyzed the radial variation of the power spectra of the magnetic field from 0.3 to about 0.9 AU, using Helios 2 spacecraft measurements in fast solar wind, and determined the breakpoints in those spectra. The time resolution of the magnetic field data allowed them to analyze the spectra up to 2 Hz. They inferred that the spatial scale corresponding to the breakpoint follows the proton inertial but not gyroradius scale. All the Helios observations were made in the ecliptic plane.

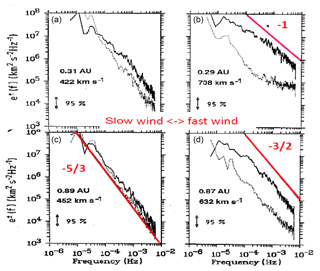
Figure 7 Dependence on radial solar distance (Marsch and Tu, 1990a) of the energy spectra of outward- (e⁺, continuous curves) and inward-propagating (e⁻, dotted curves) Alfvén waves as measured by Helios in slow (a, c) and fast (b, d) solar wind. The frequency axis of panels (a) and (b) is the same as for panels (c) and (d). The theoretical spectral slopes and indices are given in red for comparison with the measured spectra. Note the distinct steepening of the e⁺ spectrum in fast wind, indicating the radial evolution towards the Kolmogorov $-\mathrm{5}/\mathrm{3}$ spectrum, and the predominance of outward-propagating Alfvén waves, i.e., $e^{+}\gg e^{-}$. Turbulence in slow wind appears to be more developed near the Sun even at 0.31 AU, and it is less Alfvénic.

With the Ulysses mission higher heliospheric latitudes became accessible up to 80 ^∘, and thus power spectra of Alfvén waves could be measured in situ there as well. The power spectrum indices for the magnetic field components and magnitude have been published, for example by Horbury et al. (1996), and indicated that the spectral evolution over the solar poles is retarded and that the Alfvén waves keep their high correlation to larger distances from the Sun.

Besides the dominant Alfvén waves, there exist magnetoacoustic fluctuations in the solar wind as well, although their relative amplitudes are much smaller (at the level of a few percent only), and they seem to be mainly of slow-mode type (Bavassano et al., 2004; Marsch and Tu, 1990b) and rarely of fast-mode nature. MHD slow-mode waves are characterized by the typical anti-correlation between their magnetic and thermal pressure (or plasma density), a signature which can easily be tested by measured data. Recently, Yao et al. (2011) demonstrated with WIND data obtained at 1 AU that multi-scale pressure-balanced structures (i.e., non-propagating slow-mode-type fluctuations convected by the flow) exist ubiquitously in solar wind. Howes et al. (2012) also showed that the compressible fluctuations are mostly slow-mode waves. A modern comprehensive general review of MHD turbulence, including a section on intermittency not dealt with here, was provided by Bruno and Carbone (2013).

Given all these observations, a two-component turbulence model (Tu and Marsch, 1993) with Alfvén waves parallel to the mean field and two-dimensional perpendicular turbulence superposed on magnetic flux tubes was suggested and discussed by several authors (Bavassano et al., 2004; Tu and Marsch, 1995). Convected structures (McComas et al., 1995) and shocks (discontinuities) are embedded in or propagating on this ambient solar wind. The flux-tube angular scale was inferred by Thieme et al. (1990) to be of the angular size of 2⁰–4⁰ as seen from Sun center, corresponding to the supergranules (20–30 Mm in size) that make up the chromospheric magnetic network shown in Fig. 4. Obviously, imprints from the network survive the solar wind acceleration (Borovsky, 2008; Bruno et al., 2001; Marsch and Tu, 1997) and subsequent outflow and are still detectable near Helios' perihelion. Even over the solar poles this seems to be the case, because one may interpret the micro-streams detected by Ulysses (McComas et al., 1995; Neugebauer et al., 1995) as remnants of the magnetic network.

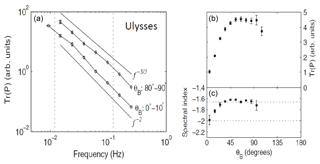
Figure 8 Anisotropy of turbulence spectra from Ulysses (Horbury et al., 2008) as a function of the angle θ_B of the sampling direction with respect to the local mean magnetic field. (a) Spectra derived from the trace of the correlation matrix. (b) Mean amplitude and (c) spectral index as a function of the angle θ_B. Note the the maximal power is observed for perpendicular (corresponding to k_⟂) sampling and the steepest spectrum for parallel (corresponding to k_∥) sampling.

A key issue of modern studies of solar wind turbulence is spectral anisotropy. Using Ulysses magnetic field data, Horbury et al. (2008) analyzed the anisotropy of magnetic turbulence spectra as a function of the sampling direction of the instrument (flow direction of the wind) with respect to the local mean magnetic field. These power spectra shown in Fig. 8 were based on the trace of the two-point correlation matrix of the magnetic field vector components. Apparently, the maximal power was observed for perpendicular (corresponding to k_⟂, with spectral index $-\mathrm{5}/\mathrm{3}$) sampling and the steepest spectrum for parallel (corresponding to k_∥, with index −2) sampling. Power and spectral index anisotropy of the entire inertial range of turbulence in the fast solar wind were provided by Wicks et al. (2010).

Obviously, the observed fluctuations are fairly anisotropic with respect to their mean amplitudes as well as the scale-dependent distribution of turbulent energy, important quantities which depend on both wave vector components. Revisiting the old Helios data, He et al. (2013) studied the radial evolution of the wave vector anisotropy of turbulence spectra in the solar wind between 0.3 and 1.0 AU. Many more studies have been done since then in this active research field. The review by Horbury et al. (2012) provides a concise overview. Another review that is highly focused on the space-time structure and wave vector anisotropy in space plasma turbulence was recently published by Narita (2018).

4 Kinetic heliophysics

One of the very hard questions in the theory of MHD and plasma turbulence concerns the dissipation of turbulent fluctuation. This subject is still under heavy investigation (Howes et al., 2008; Schekochihin et al., 2009), involving analytical studies (Howes et al., 2006; Schekochihin et al., 2008) as well as increasingly numerical simulations (Groŝelj et al., 2017) in addition to direct observations. In space plasmas Coulomb collisions are usually rare, and thus the free path of a particle can vary enormously and be rather long in terms of the size of the system under consideration. For example, see Table 2 for some relevant electron parameters. Thus fluid concepts need to be well justified or may become obsolete. In addition to Maxwell's equations for electromagnetism, one is then forced to consider, for the particle species involved, the complexity of phase space (in time, and in coordinate and velocity space) and must be concerned with the velocity distribution (instead of its mean value). This is the genuine domain of kinetic heliophysics (Howes, 2017; Marsch, 2006).

4.1 Microstate of the solar wind

The solar wind is a multi-component and non-uniform plasma, has multiple physical scales and empirically reveals a complex magnetic field topology. The solar wind plasma is tenuous and thus weakly collisional; it is permeated by random fluctuations and thus turbulent as discussed in the previous section. Therefore, one is confronted with the following phenomena:

• free energy for plasma micro-instabilities,

• wave–particle interactions (quasi-linear diffusion),

• strong deviations from local collisional equilibrium,

• remote processes being reflected locally,

• accelerated suprathermal particle populations.

Consequently one has to deal with non-equilibrium thermodynamics and complicated transport (with non-classical transport coefficients, e.g., for heat conduction). For that purpose one is forced to employ the full Vlasov–Boltzmann equation (Baumjohann and Treumann, 1996; Treumann and Baumjohann, 1997) including wave–particle interactions (Gary, 1991) and binary Coulomb collisions (Helander and Sigmar, 2002). Here I consider this equation in the frame moving with the plasma mean flow velocity, according to the form given in the concise review by Dum (1990). This approach has the advantage that by taking velocity moments one readily retains the fluid equations. The description of the particle velocity distribution function f in phase space (with the coordinates t,x and v) is governed by the kinetic equation

Table 2 Collisionality of the solar atmosphere and wind.

$$\begin{array}{ll}{\displaystyle \frac{\mathrm{d}f}{\mathrm{d}t}}& {\displaystyle }+\mathrm{w}\cdot {\displaystyle \frac{\partial f}{\partial \mathit{x}}}+(\mathit{w}\times \mathbf{\Omega })\cdot {\displaystyle \frac{\partial f}{\partial \mathit{w}}}-\mathit{w}{\displaystyle \frac{\partial f}{\partial \mathit{w}}}:{\displaystyle \frac{\partial \mathit{u}}{\partial \mathit{x}}}\\ \text{(4)}& {\displaystyle }& {\displaystyle }+\left(-{\displaystyle \frac{\mathrm{d}\mathit{u}}{\mathrm{d}t}}+{\displaystyle \frac{e}{m}}{\mathit{E}}^{\prime }\right)\cdot {\displaystyle \frac{\partial f}{\partial \mathit{w}}}={\displaystyle \frac{\mathit{\delta }f}{\mathit{\delta }t}},\end{array}$$

where the convective derivative with the mean flow velocity is

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{\mathrm{d}f}{\mathrm{d}t}}={\displaystyle \frac{\partial f}{\partial t}}+\mathit{u}\cdot {\displaystyle \frac{\partial }{\partial \mathit{x}}}.\end{array}$$

The random or relative velocity is defined as $\mathit{w}=\mathit{v}-\mathit{u}$. The average <w>=0 by definition, whereby the brackets mean velocity-space integration. The particle mass is m and charge e. Further, $\mathrm{\Omega }=eB/\left(mc\right)$ is the gyrofrequency, and the electric field in the moving frame is ${\mathit{E}}^{\prime }=\mathit{E}+\frac{\mathrm{1}}{c}\mathit{u}\times \mathit{B}$, with electric field E and magnetic field B in the inertial frame. The relevant fluid moments are the mean or drift velocity u, the pressure or stress tensor 𝒫, and the heat flux vector Q. I have for the pressure tensor (scalar pressure is p) in dyadic notation the expressions

$$\begin{array}{}\text{(6)}& \mathcal{P}=<\mathit{w}\mathit{w}>,\mathrm{with}p=n{k}_{\mathrm{B}}T={\displaystyle \frac{\mathrm{1}}{\mathrm{3}}}\mathrm{Trace}\left(\mathcal{P}\right),\end{array}$$

with the temperature T and density n. Finally, the heat flux vector is $\mathit{Q}=<\mathit{w}(\mathit{w}\cdot \mathit{w})/\mathrm{2}>$. The right-hand side of Eq. (4) is the collision or wave–particle interaction term, a second-order partial differential operator which may be written in conservation form in terms of the acceleration (or friction force) A(v) and the diffusion tensor 𝒟(v) as follows:

$$\begin{array}{}\text{(7)}& {\displaystyle \frac{\mathit{\delta }f}{\mathit{\delta }t}}={\displaystyle \frac{\partial }{\partial \mathit{v}}}\cdot \left(-\mathit{A}\left(\mathit{v}\right)f+\mathcal{D}\left(\mathit{v}\right)\cdot {\displaystyle \frac{\partial f}{\partial \mathit{v}}}\right).\end{array}$$

I recall that the dot in the above equations just means the scalar product of two vectors. Concerning the analytical and numerical mathematics of collisions, I recommend the textbook of Helander and Sigmar (2002) on collisional transport in magnetized plasmas for further reading. Equations (4)–(7) form, together with the Maxwell equations, the theoretical basis of kinetic heliophysics.

As the solar wind plasma consists of electrons, protons and alpha particles as major and many heavy ions as minor (very low relative number density) species, one has to write down for each of them a Vlasov-Boltzmann equation including mutual coupling terms in order to describe the solar wind completely. Whereas the kinetics are theoretically well defined, the difficulties come with the boundary conditions in the solar corona. As I discussed above, they may be very complex, as the solar magnetic field is highly structured and varies temporally. Due to gravity the lower solar atmosphere is strongly barometrically stratified, and thus the densities vary strongly with height along any given magnetic field line, and so do the collision rates of the particles. Therefore, it is an enormous step going from the simple Parker model to a kinetic description of the solar wind. For the electrons alone this step has been taken by several authors as discussed in the subsequent section.

4.2 Electron velocity distribution and the strahl

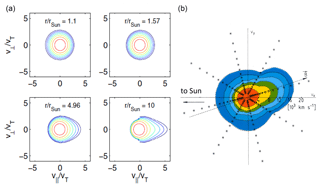
Figure 9 (a) Four numerically calculated electron velocity distribution functions (Smith et al., 2012) for different distances from the solar surface. (b) Typical measured (by Helios beyond 0.3 AU) electron distribution function (Pillip et al., 1987a) revealing a strong field-aligned distortion of its shape, the so-called strahl. Colored isocontours are spaced at levels that differ by a factor of $\sqrt{\mathrm{10}}$ (left) and 10 (right) between them, with a reference level of unity at the maximum. Asterisks in the right frame indicate the measurement channels.

What do the electrons contribute to the solar wind? They are practically massless as compared to the ions, and thus they do not contribute much to the mass flux but do contribute substantially to the specific (per mass density) energy in the wind. In the single-fluid description it is just their pressure, the gradient of which corresponds to the lowest-order electric field in the wind frame. The electron pressure matters in the ion dynamics and gives in the Parker model a total pressure of just twice the proton pressure, for equal proton and electron temperatures, as the densities are equal by the quasi-neutrality condition. As the collisional coupling to the ions is weak, one may then consider the electrons separately and try to solve their kinetic equation with reasonable boundary conditions.

Such model calculations have been done by various authors (e.g., Lie-Svendsen et al., 1997; Pierrard et al., 1999, and references therein) and were reviewed by Pierrard (2012) with emphasis on the interplanetary electric field and electron heat conduction. Smith et al. (2012) studied specifically the electron transport in fast solar wind emanating from a coronal hole. The electron velocity distribution function (VDF) was calculated from the highly collisional lower corona close to the Sun to the weakly collisional regions farther out to 10 R_s. The electron kinetic equation was solved with a finite-element method in velocity space using a linearized Fokker–Planck collision operator deriving from Eq. (7). The ion density and temperature profiles were assumed to be known, but the electric field and electron temperature were determined self-consistently. The sensitivity of the heat flux to the assumed ion temperature profile and the applied boundary condition far from the Sun was also investigated in detail.

The results for the electron VDFs are shown in Fig. 9 and demonstrate quantitatively how much the electrons and their heat flux differ from the predictions made by assuming a high number of collisions, in which case the VDF should remain isotropic and stay Maxwellian. Obviously, substantial distortions occur in the model calculations which reflect the non-uniformity of the coronal magnetic field and stratification of the plasma density. Note in particular the emergence of an electron strahl (German for “beam”) in Fig. 9 in the left frames due to the weakly collisional expansion of the electrons in the magnetic mirror of the coronal hole. This strahl (see the right frame) was previously detected in situ by Helios (Rosenbauer et al., 1977) and found to be most pronounced near its perihelion at 0.3 AU. The typical characteristics of the electron VDF and their radial variations in the solar wind as measured by the Helios plasma experiment can be found in the twin publications by Pillip et al. (1987a, b).

These authors studied especially the variations in the pitch-angle distributions and the focusing/broadening of the strahl with radial distance from the Sun and as a function of the stream structure of the solar wind. Concerning kinetic modeling of the electron pitch-angle distributions, it turned out that Coulomb collisions are not efficient enough at strahl energies, and therefore electron scattering by whistler waves had to be invoked to explain the observations. I refer the reader to the review by Vocks (2012) for further information and specific references.

4.3 Proton velocity distributions

Proton velocity distributions have been measured in considerable detail for decades by various spacecraft. An early comprehensive review on ion-kinetic phenomena was published by Feldman and Marsch (1997). Here I will restrict myself to a discussion of the Helios results, because the proton measurements of Helios still remain unique, owing to the high quality of the plasma experiment (Rosenbauer et al., 1977) and the novelty of the measurements (Marsch et al., 1982a, b) enabled then by the close approach of the Helios twin probes to the Sun. The future Solar Orbiter and Parker Solar Probe missions with their improved instrumentation are certainly going to improve on the Helios results and promise surprises, and they are expected to yield new insights into the particle kinetics in the innermost heliosphere.

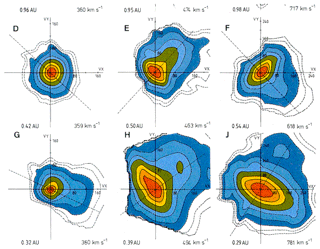
Figure 10 Proton velocity distributions (VDFs) in the solar wind near Helios' perihelion and farther out after Marsch et al. (1982a). The colored isocontours are spaced at a factor of $\sqrt{\mathrm{10}}$, with unity referring to the maximum of the distribution. The VDFs come in a variety of shapes ranging from isotropy to being anisotropic in perpendicular temperature and showing a field-aligned beam or tail. The plots are cuts through the VDFs in the ecliptic plane, with the dashed line giving the magnetic field projection.

Inspection of Fig. 10 shows that the prominent kinetic features are the proton beam and the core temperature anisotropy, with $T_{⟂}>T_{\parallel }$. These features are striking evidence for wave–particle interactions occurring in the solar wind, which may lead to irreversible perpendicular heating of the protons. But Verscharen and Marsch (2011) also discussed the possibility of apparent temperature anisotropies due to wave activity in the solar wind. Moreover, Tu et al. (2002) studied with Helios data the formation of the proton beam distribution in high-speed solar wind, and Tu et al. (2004) analyzed the dependence of the proton beam drift velocity on the proton core plasma beta. More recent studies on ion-driven instabilities in the solar wind were carried out by Gary et al. (2015) on the basis of WIND plasma data. First direct evidence for solar wind proton pitch-angle scattering by waves causing quasi-linear diffusion was established by Marsch and Tu (2001a). Using Helios measurements, Tu and Marsch (2002) further investigated the anisotropy regulation and plateau formation through pitch-angle diffusion of solar wind protons in resonance with cyclotron waves. Then Heuer and Marsch (2007) analyzed in detail and on a large statistical basis the diffusion plateaus appearing in the VDFs of fast-solar-wind protons.

4.3.1 Ion-cyclotron waves and pitch-angle scattering

The idea that the resonant interaction of the solar wind ions with ion-cyclotron waves could be the mechanism heating the ions and accelerating them to generate high-speed streams has been around in the literature for a long time. More recently Marsch and Tu (2001b) revisited theoretically within quasi-linear theory (giving the details of A and 𝒟 in Eq. 7) the heating and acceleration of coronal ions interacting with plasma waves through cyclotron and Landau resonance. Only rather recently (Narita et al., 2016b) have the wave–particle resonance conditions actually been tested empirically for ion-kinetic waves in the solar wind. The comprehensive review by Hollweg and Isenberg (2002) is concerned with the relevant observational and theoretical knowledge (as of 2002) with emphasis on the cyclotron resonance kinematics. More recently, Chandran et al. (2010) considered the interactions between protons and oblique Alfvén/ion-cyclotron waves in collisionless low-β plasmas in which the proton distribution function is strongly modified by wave pitch-angle scattering.

On the basis of Helios plasma data Marsch and Bourouaine (2011) again studied the pitch-angle diffusion of the protons by waves, and Bourouaine et al. (2010) had previously found that the observed proton anisotropy and Alfvén/ion-cyclotron-wave intensity were closely correlated. As shown in Marsch and Bourouaine (2011), it is obvious from the detailed structure of the diffusion operator (Eq. 7), which involves the pitch-angle-gradient derivation, that any VDF that is a function of the quantity (the energy per unit mass)

$$\begin{array}{}\text{(8)}& E(w_{\parallel },w_{⟂})={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(w_{⟂}^{\mathrm{2}}+(w_{\parallel }-V_{\mathrm{A}}{)}^{\mathrm{2}})\end{array}$$

is conserved along the characteristics of the diffusion operator, which here I shall consider only for non-dispersive Alfvén waves (V_A is the Alfvén speed). The protons diffuse, while fulfilling the cyclotron resonance condition, on circles centered at V_A. The two VDFs displayed in Fig. 11 reveal the striking characteristics of diffusion. It forces the contours to follow concentric circles as prescribed by proton pitch-angle scattering in weakly dispersive waves, which propagate along the mean field with a parallel phase speed of V_A. In particular, the core parts of the VDFs are not elliptically shaped but bent, such that the contours are nested to the diffusion circles. Particle-in-cell simulations by Gary and Saito (2003) of Alfvén-cyclotron wave scattering theoretically confirmed the effects observed in proton velocity distributions. Clear observational signatures of Alfvén-cyclotron wave–ion scattering were also reported from the Advanced Composition Explorer (ACE) solar wind observations by Gary et al. (2005).

In the work by Heuer and Marsch (2007) dispersive Alfvén/ion-cyclotron waves were also considered, which lead to more complex diffusion plateaus, a process they accounted for numerically in their analysis of about 10 000 individual VDFs measured between 0.3 and 1 AU in the ecliptic plane. They concluded that outward-propagating ion-cyclotron waves, which are resonant with the protons in the anti-beamward half of the core, dissipate by resonant interaction with the core protons and form the observed, almost complete diffusion plateaus in the anti-beamward half of the core. To my knowledge, this was the first study that successfully attempted to put the idea of quasi-linear diffusion on a broad empirical basis.

Further evidence was provided by He et al. (2015) for the continuous occurrence (in the WIND spacecraft plasma and field data) of cyclotron resonance causing pitch-angle scattering in the observed core proton VDF together with quasi-parallel left-hand Alfvén/ion-cyclotron waves. Signatures of Landau and right-hand cyclotron resonances were also persistently inferred for the drifting proton beam, existing together with simultaneous quasi-perpendicular right-hand kinetic Alfvén waves. Convincing statistical evidence (in the angle distribution of magnetic helicity of solar wind turbulence) of Alfvén/ion-cyclotron waves had previously been provided by He et al. (2011). For short time periods, direct observations of individual ion-cyclotron wave trains propagating nearly parallel to the local magnetic field were reported at 1 AU by Jian et al. (2009) and 0.3 AU by Jian et al. (2010). Corresponding solar wind turbulence spectra extending over a wide range of scales, and their association with ion instabilities was reviewed by Alexandrova et al. (2014).

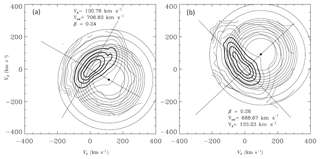
Figure 11 Two proton velocity distribution functions in fast solar wind after Marsch and Bourouaine (2011). The black dot indicates the location of the Alfvén speed in the wind frame. Close inspection shows the strongly deformed cores (continuous dark contours) and their bent edges, which are nestled to the circular diffusion lines and even reach out to the positive half of velocity space. These measurements were made on 14 April 1976 at (a) 21:59:53 and (b) 22:24:14 (hours:minutes:seconds), and at a heliocentric distance of 0.3 AU.

4.3.2 Collisional effects on proton distributions

Only rarely do Coulomb collisions matter, yet sometimes they are strong enough to even enforce a local Maxwellian VDF (see the upper left example in Fig. 10). However, the effective collision rates can become substantially enhanced (up to a factor of about 10) if the observed deviations from a Maxwellian are accounted for in the collision rates, and if they are calculated with the full operator (Eq. 7), in which for example the nonthermal (e.g., beam) distribution is inserted. This was shown by Marsch and Livi (1985) and Livi and Marsch (1986), who studied in detail the collisional relaxation of solar wind proton velocity distributions with beams and temperature anisotropies. These collisional effects far from thermodynamic equilibrium have not yet fully been appreciated in kinetic heliophysics and have not been considered in any kinetic model of the solar wind. On the other hand, simple kinetic calculations (Livi and Marsch, 1987) have indicated that insufficient friction for protons propagating in a magnetic mirror can even lead to the generation of tails and double beams by ion collisional runaway. The recent work on the effects of collisions on solar wind protons and heavy ions is reviewed by Matteini et al. (2012).

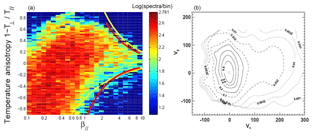
Figure 12 (a) Temperature anisotropy, $A=\mathrm{1}-T_{⟂}/T_{\parallel }$, versus proton plasma beta β as derived from measured VDFs for the radial distance range R≤0.4 AU. The color bar indicates the logarithmically spaced bins of the number of occurrence. The yellow lines refer to the fire hose (with A>0) and mirror/ion-cyclotron (with A<0) instability. The red lines indicate the boundaries of the color-bin cloud. (b) A typical proton distribution function with anisotropic core and extended tail along the magnetic field. The anisotropy is $A=-\mathrm{0.4}$; the plasma beta is very high, β=24; and the solar distance is 0.35 AU. The figures were taken from Marsch et al. (2006b).

4.3.3 Kinetic plasma wave instabilities

The topic of plasma waves and associated micro-instabilities is rather broad. For the solar wind context I refer the reader to the general textbook of Gary (1993). Given the measured proton distributions shown in Fig. 10, one can broadly state that most VDFs are found to be stable or merely marginally unstable in the solar wind. The old review by Marsch (1991a) of the Helios results gives typical examples for instabilities as inferred, or directly derived (Dum et al., 1980), from measured VDFs. Comparatively many proton VDFs seem to be prone to the instability that is driven by the prominent core temperature anisotropy. Several constraints for this instability have been derived by Gary et al. (2001) (see also references therein) using model VDFs adjusted to the measured parameters.

A comprehensive review of kinetic heliophysics was written about a decade ago by Marsch (2006). I cite his evaluation of the situation here again, concerning unstable waves:

The four salient wave modes (and free energy sources) are: (1) ion acoustic wave (ion beam, electron heat flux); (2) electromagnetic ion Alfvén-cyclotron wave (proton beam and core temperature anisotropy); (3) magnetosonic wave (proton beam, ion differential streaming); (4) whistler-mode and lower-hybrid wave (core-halo drift, electron heat flux). The quasi-linear evolution of these waves and instabilities, let alone their nonlinear evolution or possible saturation, and the associated spatial evolution of the VDFs in the non-uniform corona and interplanetary medium have not yet been explored.

This statement remains partly valid even a solar cycle later, but the older literature mostly considered local plasma processes.

However, in the past decade serious attempts have been made to explain the radial evolution of the VDFs and to understand the complex ion–wave interactions involved. The review of Matteini et al. (2012) entitled Ion Kinetics in the Solar Wind: Coupling Global Expansion to Local Microphysics addresses, according to its abstract, the following issues:

We discuss selected ion-kinetic processes relevant in the context of the expanding solar wind. We focus on the role of wave–wave and wave–particle interactions, plasma instabilities and Coulomb collisions on the overall kinetic evolution of ions. We review recent results from the hybrid expanding box model, which enables the coupling of the large scale effects of the solar wind expansion to the microscale kinetics of ions. We discuss how different plasma processes develop and influence each other during the expansion, as well their role in the shaping of ion distribution functions, and we compare the simulation results with the observed trends in the solar wind.

I recommend this modern review to the reader of the present paper.

In the remainder of this subsection I will focus on the instabilities associated with the distinct temperature anisotropy of the protons. The old Helios review (Marsch, 1991a) already dealt with this topic. More recently, Kasper et al. (2002) analyzed on the basis of WIND observations the fire hose stability constraint on the solar wind proton temperature anisotropy. In an influential letter Hellinger et al. (2006) then analyzed the data again and found that the observed proton temperature anisotropy seems to be constrained by oblique instabilities (mirror and fire hose), contrary to the prediction of linear theory that yields a dominance of the proton cyclotron instability. Moreover, Bale et al. (2009) showed for the first time that the magnetic fluctuations in the solar wind are enhanced along the temperature anisotropy thresholds.

Following Hellinger's analysis scheme Marsch et al. (2006b) also studied with Helios data the limits on the core temperature anisotropy of solar wind protons. Some of their results (for the distance range, R≤0.4 AU) are presented in Fig. 12, which shows on the left side an occurrence rate diagram of the anisotropy A versus parallel proton plasma β_∥, and on the right side a typical VDF with strongly anisotropic core and rather extended tail along the local field direction. This distribution illustrates that the overall temperature anisotropy A does not adequately reflect the detailed shape of the VDF, and so using it in a bi-Maxwellian-based wave kinetic stability analysis may be misleading. The reason is that the important pitch-angle diffusion discussed previously is very sensitive to the curvature of the distribution in velocity space but not simply to A and β_∥. The left frame of the figure shows that indeed the majority of the measured parameters lie on a diagonal ridge between and far from the two yellow stability threshold lines.

Apparently, linear stability analysis based on moments of the VDF does not provide the right answer to the question of why the VDFs are as complex as observed and why their nonthermal traits seem to last that long, although linear theory would predict anisotropy relaxation on the gyrokinetic time scale of several seconds. Already in the early days of the Helios mission, Dum et al. (1980) emphasized the subtleties and pitfalls of stability analysis when being based on dispersion relations using model VDFs instead of the measured ones with all their detailed characteristics. These caveats remain valid still today. Direct nonlinear simulation in phase space will help us in finding the correct answers beyond linear stability analysis. A variety of numerical schemes (Groŝelj et al., 2017) have been developed for fusion plasmas. The adaption of these codes and their application to space plasmas and heliophysics appears promising, given that there exists so much empirical knowledge about the ion and electron VDFs as well as the wave and turbulence spectra, against which the simulation results can be tested.

4.3.4 On kinetic Alfvén and slow waves

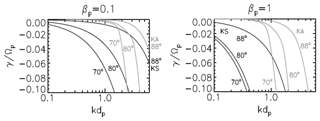
Figure 13 Damping rates (γ) of very obliquely propagating kinetic wave modes, the kinetic Alfvén wave (KAW) and kinetic slow magnetoacoustic wave (KSW) after Narita and Marsch (2015). Both are shown versus wave number (k) for various propagation angles with respect to the mean magnetic field. The units are the proton gyrofrequency Ω_p and inertial length $d_{\mathrm{p}}=V_{\mathrm{A}}/\mathrm{\Omega }$. Left panel is for β_p=0.1 and right for β_p=1.0. Note that substantial damping sets in at longer wavelength for the KSW than KAW. Thus the kinetic slow wave is more prone to Landau damping for a wider angular range.

In the previous sections we have seen that beams and temperature anisotropies usually occur in solar wind proton VDFs. They are manifestations of ubiquitous kinetic wave–ion interactions, which involve cyclotron and Landau resonances with plasma waves. Kinetic instabilities and resonant ion diffusion are believed to play key roles in the dissipation of MHD turbulence and interplanetary ion heating and differential acceleration.

In recent years, the so-called kinetic Alfvén wave (KAW) has received considerable attention and was argued to provide a major channel for MHD turbulence dissipation. The review by Hollweg (1999) revisits its main characteristics and the older literature. According to the recent review by Podesta (2013), it is reasonable to conclude from the existing in situ observations that KAWs (in the form of kinetic Alfvén turbulence) are almost always present in the solar wind near 1 AU. Howes et al. (2008) developed a model of turbulence in magnetized plasmas and discussed its implications for the dissipation range. Hughes et al. (2018) further studied by means of simulations the role of kinetic Alfvén waves in the dissipation of solar wind turbulence.

Narita and Marsch (2015) proposed as another possible dissipation mechanism the proton Landau damping of the perpendicular kinetic slow mode, following Howes et al. (2012), who showed that the compressible component of inertial range solar wind turbulence is primarily in the kinetic slow mode. It is linked to the oblique MHD slow mode (Verscharen et al., 2017) yet has shorter wavelengths going down to the proton inertial length. I recall here the properties of small-scale pressure-balanced structures (Yao et al., 2011), which essentially are the non-propagating slow-mode waves. Numerical simulations (Verscharen et al., 2012a, b) and in situ observations by Horbury et al. (2008) indicate that the MHD turbulent cascade preferably transfers energy in the direction perpendicular to the background magnetic field. If the kinetic slow mode is also replenished by this cascade, the damping of this wave can lead to both perpendicular and parallel heating of the protons.

The Fig. 13 shows the damping rates of very obliquely propagating kinetic wave modes, the KAW and kinetic slow magnetoacoustic wave (KSW) for a Maxwellian proton VDF. Both damping rates are shown versus wave number for various propagation angles with respect to the mean magnetic field. Note that substantial damping sets in at longer wavelengths for the KSW than KAW. Thus the kinetic slow wave is more prone to Landau damping for a wider angular range, in particular for higher plasma beta. This conclusion will change considerably if the real measured VDFs (see previous figures) were implemented in a stability analysis according to Dum et al. (1980) and Marsch (1991a). Such an analysis has not yet been done but should be carried out in the future, given the possible relevance of these modes for turbulence dissipation.

4.3.5 Parametric decay of the Alfvén wave

It has been known for a long time that the large-amplitude Alfvén waves (see the wave example in Fig. 1 again) are prone to parametric decay and damping (consult the paper of Araneda et al. (2007) or Malara and Velli (1996) and the many older references therein), as the product of which ion-cyclotron and slow-mode/ion-acoustic daughter waves can be generated. Modern computers permit simulation of this process kinetically and thus make it possible to follow the ion kinetics in phase space, instead of just calculating the pump wave decay products within the MHD paradigm. Araneda et al. (2008) used linear Vlasov theory and 1-D hybrid simulations to study the parametric instabilities of a circularly polarized parallel-propagating Alfvén wave. Linear and weakly nonlinear instabilities of the Alfvén wave were found to drive ion-acoustic-like and cyclotron waves, leading to the formation of a proton beam and anisotropic core, similar to the ones presented in Fig. 10.

Some of the results obtained by Araneda et al. (2008) are shown here in Fig. 14. Initially, a distinct temperature anisotropy occurs due to the particle transverse sloshing motion imposed by the slowly decreasing pump wave. Later on, a field-aligned isolated proton beam gradually emerges, then a flattening of the VDF becomes visible near the resonance velocity and finally the anisotropic core reshapes. This is caused through proton pitch-angle scattering by the growing daughter waves, leading to parabolic shell-like trajectories for protons with negative v_z in velocity space. Such effects are also observed in the measured VDFs as shown in Fig. 11. The reshaping of the VDF takes place within about 2000 gyroperiods, which may be several minutes in the solar wind. The kinetics of parametric instabilities of Alfvén waves and associated evolution of ion distribution functions have been studied by Matteini et al. (2010a), and the parametric decay of linearly polarized shear-Alfvén waves in oblique propagation was investigated by means of one- and two-dimensional hybrid simulations by Matteini et al. (2010b).

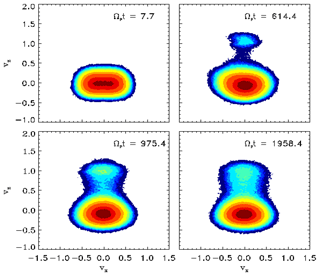
Figure 14 Contour plots of proton VDFs in the (v_x,v_z) velocity plane after Araneda et al. (2008). These VDFs originated in a simulation run for a dispersive Alfvén pump wave and refer to four instants of time. The color coding of the contours corresponds to 75 % (dark red), 50 % (red) and 10 % (yellow) of the maximum of the VDF, with a final proton beam density of about 7 %.

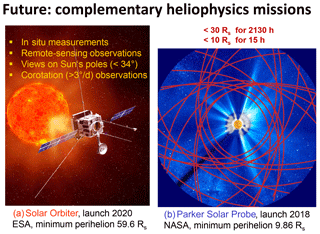
Figure 15 Illustration of the future complementary heliophysics missions, Solar Orbiter of ESA (a) and Parker Solar Probe of NASA (b). Some key parameters of the missions are given together with characteristics of their orbits.

These numerical simulations clearly demonstrate that kinetic effects must be accounted for when studying parametric instabilities of Alfvén/ion-cyclotron waves in the solar wind. Moreover, the nonlinear development of these waves can lead to the formation of an anisotropic core and beam in the proton VDF resembling the observed ones. Kinetic wave–ion interactions in the solar wind are therefore rather relevant to understanding the measured proton VDFs, which seem to be in dynamic equilibrium with the Alfénic turbulence. Turbulence dissipation is largely caused by absorption of wave energy via inelastic proton scattering at the sunward side of the VDF. In addition turbulence is dissipated by means of Landau damping the KAW component propagating almost perpendicularly to the local magnetic field. The weak compressive (oblique slow-mode and ion-acoustic) component of the turbulence is further dissipated by Landau damping on the slope of the proton beam.

All these processes also occur in the interaction of alpha particles and other heavy ions with the waves, as was shown by means of simulations by Araneda et al. (2009). The turbulent heating and acceleration of ${\mathrm{He}}^{++}$ ions by spectra of Alfvén-cyclotron waves in the expanding solar wind was studied through 1.5-D hybrid simulations by Maneva et al. (2013). Moreover, Maneva et al. (2014) discussed the regulation of ion drifts and anisotropies by parametrically unstable finite-amplitude Alfvén-cyclotron waves in the fast solar wind. Just recently, Shoda et al. (2018) investigated again the frequency-dependent Alfvén-wave propagation in the solar wind and specified the conditions for onset and suppression of the parametric decay instability. Their results suggest that density fluctuations are possibly generated by the evolution of that instability driven by high-frequency ($f>{\mathrm{10}}^{-\mathrm{3}}$ Hz) Alfvén waves. For the detailed wave spectra observed in that domain see, for example, the review of Alexandrova et al. (2014).

Kinetic Alfvén turbulence will heat electrons and ions as shown by recent numerical particle-in-cell simulations (see, e.g., the paper of Hughes et al. (2018), in which further references concerning previous simulations can be found). The turbulence energy trickling through the proton inertial scale to the electrons then cascades (mainly mediated by whistler waves) down to the electron inertial scale, where it is finally transferred through thermalization to solar wind electrons. According to recent in situ observations and their analysis using the modern four-point magnetometer (Narita et al., 2016a), the small-scale turbulence (with wavelength shorter than the ion inertial length) in the solar wind is primarily composed of highly obliquely propagating whistler waves. In contrast, fully kinetic numerical plasma simulations by Groŝelj et al. (2017) seem to indicate that three-dimensional kinetic Alfvén-wave turbulence, as it is expected from a critically balanced cascade, prevails over a limited range of sub-ion scales. Future work is required to clarify this controversial issue.

5 Conclusions and prospects

In this paper I have addressed selected scientific topics of the solar wind and kinetic heliophysics, which encompass many special fields of space plasma physics. Naturally, a multitude of issues remain unresolved and under debate. Yet some important conclusions can be drawn:

• Fast solar wind is essentially driven by Alfvén waves.

• Wave–particle interactions mainly with kinetic Alfvén/ion-cyclotron and slow-magnetosonic/ion-acoustic waves affect and shape ion distributions.

• Electron kinetics is largely determined by Coulomb collisions and whistler turbulence.

• Mass and energy are supplied to the open corona by magnetic activity in funnels and loops in the network.

I did not address solar transients and coronal mass ejections, which appear to be driven by large-scale Lorentz forces, arising from magnetic flux emergence (Priest, 2017) and plasma eruption. The general structure and dynamics of the corona–heliosphere connection has been reviewed by Antiochos et al. (2012). Here I have put my emphasis on the fast solar wind, because it seems to be the easiest type of wind to understand and to explain theoretically. But many open questions remain, and there are plenty of subjects for future research. Some key topics are addressed by the following questions:

• Where and how does the coronal plasma originate?

• What is the role of magnetic reconnection in mass and energy supply to the corona and wind?

• How is the nascent solar wind accelerated in coronal funnels in the transition region?

• Does the slow solar wind also originate from opening coronal loops of various scales?

• How are Alfvén waves excited, propagating and dissipating in the lower corona?

• What are the coronal sources of solar wind turbulence, and how is turbulence ultimately dissipated?

We hope to get answers by continuous scrutinizing of data archives from previous missions, from numerical simulations and new modeling, and most importantly from the results of novel upcoming missions like the Parker Solar Probe (Fox et al., 2016) and Solar Orbiter (Marsch et al., 2001; Müller et al., 2013) (see also the study report SRE-2009-5 Solar-Orbiter4.pdf located on the ESA mission website). Figure 15 illustrates some general features of these two key heliophysics missions.

The complementary missions Solar Orbiter and Parker Solar Probe will lead the space-plasma and solar-physics community into an exciting new era of heliospheric physics, which will offer unprecedented possibilities to study the Sun, its corona and the solar wind. Two of the main science goals of Solar Orbiter are to answer the following questions:

• What drives the solar wind and where does the coronal magnetic field originate from?

• How do solar transients drive heliospheric variability?

Two of the key science goals of the Parker Solar Probe are to

• determine the structure and dynamics of the magnetic fields at the sources of solar wind,

• trace the flow of energy that heats the corona and accelerates the solar wind.

If we can answer these questions and reach these goals, with the help of the powerful scientific payloads of these two missions and by a creative analysis of the data they will provide, we can expect breakthroughs in kinetic heliophysics and major advances in solar physics as well.

I may close by reminding the reader of the starting point of this paper, which was the Alfvén wave. It appears to be running like a golden thread through all the themes discussed here. In particular the acceleration of the fast solar wind nowadays is largely modeled in the spirit of Hannes Alfvén. The pressure gradient (the Poynting flux) of his wave turns out to be the main agent driving fast solar wind streams, and the Alfvén-wave energy dissipation seems to heat coronal ions way beyond 1 MK.