A new method to identify flux ropes in space plasmas

Flux ropes are frequently observed in the space plasmas, such as solar wind, planetary magnetosphere and magnetosheath etc., and play an important role in the reconnection process and mass and flux transportation. One usually uses bipolar signature and strong core field to identify the flux ropes. We propose here one new method to identify flux ropes based on the correlations between the variables of the data from in situ spacecraft observations and the “target function to be correlated” (TFC) from the ideal flux rope model. Through comparing the correlation coefficients of different variables at different times and scales, and performing weighted-average techniques, this method can derive the scales and locations of the flux ropes. We compare it with other methods and also discuss the limitation of our method.

1 Introduction

Magnetic flux ropes, as one universal structure in the space plasma, are formed as a helical magnetic structure with magnetic field lines wrapping and rotating around a central axis (e.g., Hughes and Sibeck, 1987; Slavin et al., 2003; Zong et al., 2004; Zhang et al., 2010). It is generally believed that flux ropes can be generated by magnetic reconnection in the eruptive energy processes, such as rapid variations of the reconnection rate at a single X line (e.g., Nakamura and Scholer, 2000; Wang et al., 2010; Fu et al., 2013) or multiple X-line reconnections (e.g., Lee et al., 1985; Deng et al., 2004). Flux ropes play important roles in dissipating magnetic energy and controlling the microscale dynamics of magnetic reconnection (e.g., Drake et al., 2006; Daughton et al., 2007; Wang et al., 2016; Fu et al., 2017). These structures have been frequently observed and widely studied recently in the magnetosphere, magnetosheath and solar wind (e.g., Hu and Sonnerup, 2001; Slavin et al., 2003; Zong et al., 2004; Zhang et al., 2010; Huang et al., 2012, 2014a, b, 2015, 2016a, b; Rong et al., 2013). Many works have tried to model flux rope from in situ measurements based on the force-free constant-alpha flux rope (e.g., Lepping et al., 1990), the non-force-free model (e.g., Hidalgo et al., 2002), or the Grad–Shafranov equilibrium (e.g., Hu and Sonnerup, 2002).

Flux ropes embedded in current sheet are characterized by the bipolar signature of the normal component of a magnetic field, strong core field in the axis direction and enhancement in magnetic field strength. Therefore, one uses negative–positive (positive–negative) bipolar signatures of the south–north magnetic field component in the earthward (tailward) flow with an enhancement in the cross-tail component and strength of magnetic field to identify flux ropes in the magnetotail (e.g., Slavin et al., 2003; Huang et al., 2012). At the magnetopause, the bipolar variation is usually along the Sun–Earth direction, and the core field is typically along the dawn–dusk direction (e.g., Zhang et al., 2010). However, flux ropes in the magnetosheath, which has been reported recently by MMS (Magnetospheric Multiscale mission; Huang et al., 2016b), can move in any direction due to the large fluctuations of the shocked solar wind. This leads to difficultly in identifying the flux ropes there.

Several attempts are made to survey flux ropes in the Earth's magnetotail by eyes based on their signatures, such as bipolar variation of the north–south magnetic field (e.g., Richardson et al., 1987; Slavin et al., 2003). Also, some methods are proposed to automatically, in some degrees, survey flux ropes or flux transfer events (FTEs) via bipolar field deflections (e.g., Kawano and Russell, 1996; Vogt et al., 2010; Jackman et al., 2014; Smith et al., 2016). Karimabadi et al. (2009) have applied a data mining technique (MineTool) to search FTEs using magnetic field and plasma data. Recently, Smith et al. (2017) developed a method to automatically detect cylindrically symmetric force-free flux ropes in the magnetotail only using magnetic field data. That method first locates the significant deflections in the north–south magnetic field component with peaks in the dawn–dusk component or total field. Then, the candidates use minimum variance analysis (MVA) to determine a local coordinate system. Finally, the candidates are fitted by a force-free model to determine whether they belong to flux ropes or not.

For some flux ropes with short duration, the plasma data do not have enough high time resolution or, even worse, are not available. Thus, the identification of flux ropes relies heavily on the magnetic field data. All aforementioned automatic methods are a bit complex, or require plasma data. Therefore, to identify flux rope only using the magnetic field data from a single spacecraft, we propose a new and simple method based on the correlation coefficients between the signal and the ideal model of flux rope to identify flux ropes in space plasmas. The paper will be presented as follows: an introduction of the method in Sect. 2, the test of the method on artificial data from the model in Sect. 3, the applications of the method on the Cluster and MMS data in Sect. 4, and the summary given in Sect. 5.

2 Approach

In this section, we simply introduce our method.

Firstly, we derive the “target function to be correlated” (TFC) from the ideal model of flux rope. Considering the variable and complicated observed flux ropes, we use the ideal non-force-free model of flux rope proposed by Elphic and Russell (1983), named the Elphic and Russell (E–R) model because most of flux ropes with nonnegligible perpendicular currents are not consistent with the force-free model (e.g., Hidalgo et al., 2002; Zong et al., 2004; Zhang et al., 2010; Borg et al., 2012; Huang et al., 2012, 2016b). This model is constructed with an intense core field inside of flux rope, which is shown in Fig. 1. The equation of this model in the cylindrical coordinate (Y is defined as the axis orientation of flux rope) can be modified as below:

$$\begin{array}{}\text{(1)}& \left\{\begin{array}{l}{B}_y=B\left(r\right)\cos \left(\mathit{\alpha }\right(r\left)\right),\\ B_{\mathit{\phi }}=B\left(r\right)\sin \left(\mathit{\alpha }\right(r\left)\right),\\ B\left(r\right)=B_{\mathrm{0}}\exp (-r^{\mathrm{2}}/b^{\mathrm{2}}),\end{array}\right.\end{array}$$

where $\mathit{\alpha }\left(r\right)=\mathit{\pi }/\mathrm{2}(\mathrm{1}-\exp (-r^{\mathrm{2}}/a^{\mathrm{2}})$); B_y is the core field component; B₀, a, and b are the constants; and r is the radial distance to the flux rope center.

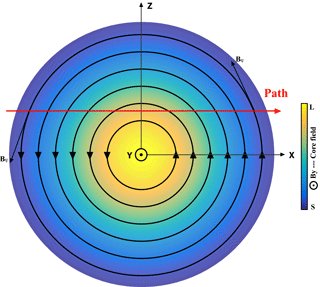
Figure 1 Sketched diagram of the cylindrical flux rope. The flux rope has a right-handed structure. The black circled lines are the magnetic field lines. The red arrow is the projection of spacecraft path. The rectangular coordinate is used in our analyses. Y is the axis orientation of the flux rope, and the X–Z plane is the cross section perpendicular to the axis orientation. The core field is out of plane, and the color represents the relative strength of core field (yellow: large, blue: small).

Figure 1 shows a sketched diagram of the cylindrical flux rope from the E–R model. For convenience, the rectangular coordinate is used in our analyses (shown in Fig. 1). Y is the axis orientation of the flux rope, and the X–Z plane is the cross section perpendicular to the axis orientation. X can be treated as Sun–Earth orientation, Y is the dawn–dusk orientation, and Z is similar to the south–north orientation in the magnetotail. If one spacecraft crosses the flux rope following the red path in Fig. 1, the B_z component will be characterized as bipolar signature, and the B_y component and total magnetic field B_t have strong peaks.

Figure 2 shows the observations when one virtual spacecraft crosses the ideal flux rope (see spacecraft path in Fig. 1). Here we assume the scale of flux rope as one unit, and 1 unit s⁻¹ of moving speed of the spacecraft, thus set a=0.735 units and b=0.735 units, B₀=10 nT, and use the B_z as the bipolar variation component, B_y as the core field component, B_t as the total magnetic field. The center of the flux rope is located at 2.5 s. One can see the B_z bipolar signature, and the peaks of core field and total magnetic field inside the flux rope.

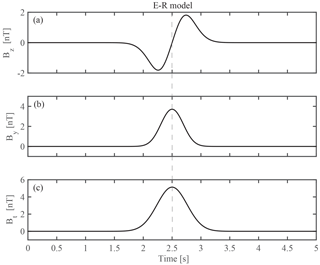
Figure 2 The three variables B_z (a), B_y (b) and B_t (c) of the ideal cylindrical flux rope described by the E–R model.

Considering the previous observations, in which the B_z component during the crossing of the flux rope usually does not reach zero like that shown in Fig. 2a, we select one part of the ideal flux rope as the TFC which is shown in Fig. 3. The TFC is similar to the sinusoidal function when one performs fast Fourier transform (FFT) analysis. We only used two components (B_y and B_z) and magnetic strength (B_t) as the TFC since only B_z and B_y components and B_t have very obvious typical features usually from in situ measurements (i.e., B_z has bipolar signature, B_y is strong core field, and B_t has peak inside flux ropes), and B_x component does not have common features from observation viewpoint (e.g., Slavin et al., 2003; Huang et al., 2014a).

Secondly, we calculate the Pearson correlation coefficients between the signal and the TFC at different times and different scales (Hotelling, 1953). Before calculating the correlation coefficients, the amplitude of the TFC will be estimated from the signal. For example, the maximum value of B_t during the time interval is used as the amplitude of B_t in the TFC. The sliding time window is used in the calculation of the correlation coefficients. The calculated results of correlation coefficients are similar to the power spectral densities by FFT that display the power spectral density at different times and different frequencies. The higher the values of the correlation coefficients, the more suitable for the description of the model on the signal.

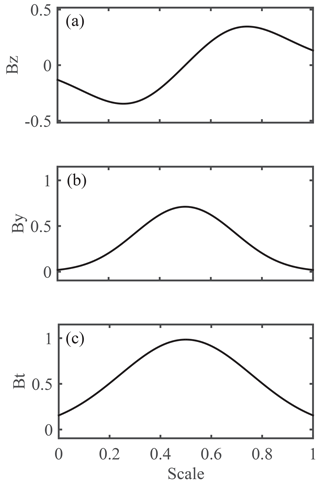
Figure 3 The target-function-to-be-correlated (TFC) derived from E–R model. The amplitudes and scale are dimensionless.

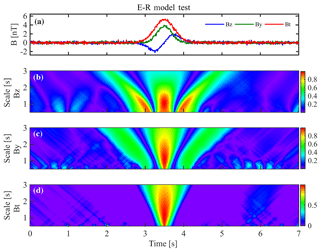
Figure 4 The test results on the E–R model. (a) Three variables B_z, B_y and B_t from E–R model with 10 % random noise; (b–d) the correlation coefficients between the variables of B_z, B_y and B_t and the TFC shown in Fig. 3, respectively. The scale on the vertical axes of (b–d) is τ, as mentioned in the text, which can also be seen as a unit.

Thirdly, we compare the correlation coefficients of the bipolar variation component B_z, core field component B_y and total magnetic field B_t, and find out the high correlations (larger than the given threshold) at the same time and the same scale. This is due to the fact that the bipolar signature in B_z, enhancements of core field B_y and magnetic strength B_t should appear simultaneously with the same duration when one spacecraft crosses the flux ropes.

Fourthly, we infer the location and the scale of the flux ropes based on the weighted average (it will be shown later), and the amplitude from minimum to maximum values of the bipolar variation.

3 Model test

One test is performed on the artificial data from E–R model with the random noise. Figure 4 presents the test results. The test artificial data are shown in Fig. 4a where the noise is 10 % of the amplitude of the flux rope. A series of the calculations are carried on B_z, B_y and B_t to obtain the correlation coefficients. One should point out that the absolute values of the correlation coefficients of B_z and B_y are given in Fig. 4b and c respectively, because the bipolar structure can be positive–negative or negative–positive variation and the core field can be positive or negative. It can be seen that the correlation coefficients are largest at the scale τ of 0.6–1.5 units during the crossing of the flux rope (around time ∼ 3.5 s).

We set the threshold as 0.9 to represent the results in Fig. 5 where only the correlation coefficients with > 0.9 are displayed with black shadows. All correlation coefficients of the three variables have peaks at the time ∼ 3.5 s with the scale τ∼1 units. We use the weighted-average technique (shown below) to identify the flux rope and estimate its scale τ.

$$\begin{array}{}\text{(2)}& \mathit{\tau }=\sum {\mathrm{coef}}_i\times {\mathit{\tau }}_i/\sum {\mathrm{coef}}_i,\end{array}$$

where coef_i is the correlation coefficient at scale τ_i.

Figure 5e shows the estimated results. The crossing of the flux rope is marked with “1” and the duration is its scale, and the center of the flux rope is at the center of the line. In this test, the scale is estimated as 1.039 units, and the location is 3.496 s. The amplitude is estimated to be 4.43 nT from minimum to maximum values of the bipolar variation. Aforementioned sets, one can estimate the error of the scale as 3.9 %, i.e., (1.039–$\mathrm{1.0})/\mathrm{1.0}=\mathrm{3.9}$ %. Therefore, our method can successfully identify the flux rope and estimate its scale, location and amplitude.

4 Application

In this section, we apply our new method to the spacecraft measurements in the magnetosheath and the magnetotail.

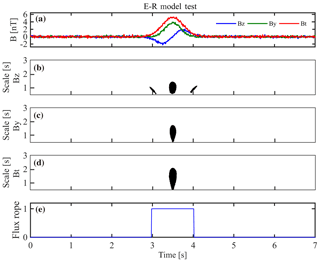
Figure 5 The test results on E–R model with a threshold of 0.9. (a) Three variables B_z, B_y and B_t from E–R model with 10 % random noise; (b–d) the correlation coefficients (≥0.9) between the variables of B_z, B_y and B_t and the TFC, respectively; (e) the index when the virtual spacecraft cross the flux rope (if the spacecraft cross the flux rope, the index is 1; if not, the index is 0). The duration of the index presents the timescale of the flux rope. The scale on the vertical axes of (b–d) is the same as in Fig. 4.

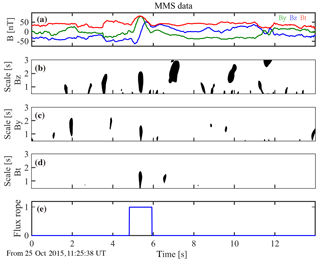
Figure 6 Testing the method on MMS data in the magnetosheath. The same format as in Fig. 5. The scale on the vertical axes of (b–d) uses seconds as the unit.

4.1 Flux rope in the magnetosheath

Flux ropes are successfully identified in the magnetosheath using the unprecedented high-resolution data from the MMS (Burch et al., 2015) mission (Huang et al., 2016b). Their observations have demonstrated that highly dynamical strong-wave activities and electron-scale physics occur in the magnetosheath ion-scale flux ropes. Figure 6 gives the observations of ∼14 s from MMS2 on 25 October 2015 and the test results of our method. The unit length of the TFC uses the same unit as the real observations, i.e., seconds (“s”). The amplitude (B₀) of the TFC is determined by the maximum value of B_t during the interval when calculating correlation coefficients. Similar to the model test, we use the same variables to present the components of the bipolar variation, core field and total magnetic field after transformed to MVA (Huang et al., 2016b). The threshold of the correlation coefficients is also set as 0.9 in Fig. 6. We can see that the correlation coefficients of the three variables (Fig. 6b–d) only have high values at the same time around time = 5.5 s, implying that one flux rope is identified by this method. Based on the weighted-average method in Eq. (2), the timescale of the flux rope is 1.11 s, and its central location is at 5.38 s. The amplitude is estimated as 115 nT. All these results are consistent with previous findings from multispacecraft data in Huang et al. (2016b).

Figure 7 Testing the method on Cluster data in the magnetotail. The same format as in Fig. 6.

4.2 Flux rope in the magnetotail

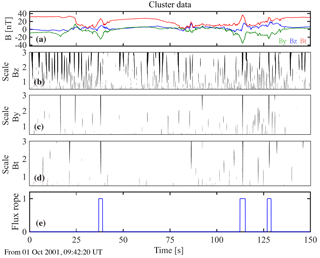
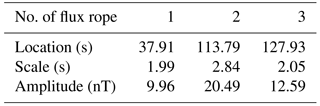
Flux ropes are frequently observed in the magnetotail and play an important role during magnetic reconnection and magnetotail dynamics (e.g., Slavin et al., 2003; Zong et al., 2004; Chen et al., 2007; Huang et al., 2012, 2016a; Fu et al., 2015, 2016). Chen et al. (2008) have identified several flux ropes filled with energetic electrons during magnetic reconnection on 1 October 2001 by using the Cluster data. Figure 7 shows the magnetic field in GSM coordinates from the Cluster mission (Escoubet et al., 1997) in the magnetotail and the application results of our method. There are several bipolar variations in B_z during this time interval (Fig. 7a). Figure 7b–d present the correlation coefficients (larger than 0.9 of the threshold) of the three variables. Here we try to identify small-scale flux ropes, so that we perform the method only at short timescales. These are full of high correlation coefficients (grey shadows in Fig. 7b–d). After compare with the correlation coefficients at the same time and same scale, our method resolves three possible flux ropes in Fig. 7e. The results are summarized in Table 1. The three structures are close to the ideal flux rope with bipolar signature in B_z, and peaks in core field B_y and total magnetic field B_t. All three flux ropes identified by our method have been reported in Chen et al. (2007).

Table 1 The location, scale and amplitude of the flux ropes identified by the method. The amplitude is defined as the values of the bipolar variation from minimum to maximum.

We should point out that our method can only identify the flux rope and derive its duration. If the plasma velocity data are available, then we can estimate the actual spatial scale of the flux ropes. If multispacecraft data are available for the time interval of interest, one can derive the size, the orientation and the motion of the flux rope using the multispacecraft methods such as those of Sonnerup et al. (2004), Shi et al. (2005, 2006) and Zhou et al. (2006a, b). However, the separation of the Cluster was much larger than the size of the flux ropes on 1 October 2001, implying that one cannot use the multispacecraft method here.

5 Summary and discussion

In summary, we developed a new method to identify flux ropes in the space plasmas. This method is based on the correlation coefficients between the signal and the TFC from the non-force-free E–R model. If the correlation coefficients of three variables (B_z, B_y and B_t) of the signal have high values of correlation coefficients at the same time and same scale, one can deduce the existence of one flux rope and estimate its location and its timescale (i.e., the duration). The tests on the artificial data and the in situ realistic spacecraft data show that our method can successfully search out the flux ropes and obtain their locations and timescales.

Bipolar variation in the B_z component and the enhancement in core field and magnetic field strength are the typical signatures for most flux ropes. But it does not mean that all observations from any crossing of the spacecraft would have those signatures, which depends on the spacecraft trajectory (especially for bipolar components). However, one only can select or identify the flux rope showing the typical signatures and miss other flux rope that do not have the typical signatures. Some special field structures may induce similar signatures along some special trajectories. But this opportunity does not often occur in the magnetotail. Moreover, one can use the plasma measurements to rule out this possibility.

The aforementioned attempts are made to identify flux ropes in the Earth's magnetotail by eyes or half-automatically based on the bipolar variation of B_z (e.g., Richardson et al., 1987; Slavin et al., 2003; Kawano and Russell, 1996; Vogt et al., 2010; Jackman et al., 2014; Smith et al., 2016). The identifications by eyes would miss a lots of flux ropes and take too much time. Karimabadi et al. (2009) used a data mining technique (MineTool) to search flux ropes using both magnetic field and plasma data. That method is too complex to apply in the data analysis. Smith et al. (2017) proposed one method to automatically detect force-free flux ropes based on magnetic field data from a single spacecraft. In the present study, we used the TFC derived from non-force-free flux rope model to calculate the correlation coefficients with the signal, and then compare the large correlation coefficients of different variables to identify the flux rope. Our method is flexible, reliable and easy to apply with the in situ spacecraft data compared with other methods. We will quantitatively model the flux ropes identified by our method and derive more information on the flux ropes. For example, we can statistically survey and investigate the locations, scales and global distributions of flux ropes in the magnetosheath using MMS data.

We should point out that there are several limitations in our method:

1. Our method can only detect the nearly ideal cylindrical flux rope since we used non-force-free E–R model to describe the TFC, which limits the application of this method. The non-force-free model proposed by E–R is just one possible solution of all the flux rope that satisfies $J\times B\ne \mathrm{0}$. Actually, one can use other flux rope models to replace E–R model and extend our method to identify the flux ropes.

2. If the flux ropes are not regular, there are large time deviations among B_z, B_y and B_t that will lead to some flux ropes being missed when we apply the method.

3. The threshold value of correlation coefficients can affect the results, such as when the threshold value is so small that the method detects some possible structures that do not belong to flux ropes, or so large that the method will miss some flux ropes.

4. The correlation coefficients at small scales (especially in B_y and B_t) could be very large, which may affect our results. The method may find some possible structures related to such fluctuations. We will improve this method and apply it to detect the flux ropes in the turbulent magnetosheath in the future.