the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Data mining for vortices on the Earth's magnetosphere – algorithm application for detection and analysis
Yaireska M. Collado-Vega
Virginia L. Kalb
David G. Sibeck
Kyoung-Joo Hwang
Lutz Rastätter
Unsteady processes in the solar wind–magnetosphere interaction, such as vortices developed at the magnetopause boundary by the Kelvin–Helmholtz instability, may contribute to the process of mass, momentum and energy transfer into the Earth's magnetosphere. The research described in this paper validates an algorithm to automatically detect and characterize vortices based on velocity data from simulations. The vortex identification algorithm (VIA) systematically searches the 3-D velocity fields to identify critical points where the magnitude of the velocity vector vanishes. The velocity gradient tensor is computed and its invariants are used to assess vortex structure in the flow field. We use the Community Coordinated Modeling Center (CCMC) Runs on Request capability to create a series of model runs initialized from the conditions observed by the Cluster mission in the Hwang et al. (2011) analysis of Kelvin–Helmholtz vortices observed during southward interplanetary magnetic field (IMF) conditions. We analyze further the properties of the vortices found in the runs, including the velocity changes within their motion across the magnetosheath. We also demonstrate the potential of our tool to identify and characterize other transient features (e.g., flux transfer events, FTEs) with vortical internal structures. We find that the vortices are associated with flows on the magnetosheath side of the magnetopause that reach speeds greater than the solar wind speed at the bow shock.
Keywords. Magnetospheric physics (MHD waves and instabilities; solar wind–magnetosphere interactions) – space plasma physics (numerical simulation studies)
- Article
(11048 KB) - Full-text XML
-
Supplement
(7616 KB) - BibTeX
- EndNote
Large eddy structures or vortices can mark regions of intense flow activity and are important in understanding physical transport processes. Coherent vortical structures are often the most important physical mechanisms for generating and sustaining turbulent motion. One important mechanism of vortex generation is the Kelvin–Helmholtz instability. When the different layers of a stratified fluid are in relative motion, the shear causes a wrinkling of their interface, which is amplified by nonlinearities to produce vortical motion. Such a situation exists when the solar wind passes the Earth's magnetopause. Finding and studying these vortices is important for understanding the Sun–Earth connection. Even in the initial stages, these vortices can transfer momentum, energy and mass from the solar wind to the Earth's magnetosphere (Miura, 1984; Nykyri and Otto, 2001; Hasegawa et al., 2004a).
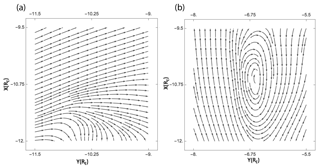
Figure 1Streamlines are mapped to show an example of the method used to identify vortices in the data. If the norm of R is greater than the norm of S, we consider this point to lie at the center of a possible vortex. In (a) we have the case where and in (b) where the location of a vortex is then considered.
Recently Hwang et al. (2011) reported in situ observations of nonlinearly developed Kelvin–Helmholtz vortices during southward interplanetary magnetic field (IMF) conditions using Cluster data. The nonlinearity can facilitate mass transfer by initiating reconnection within the vortices (Hasegawa et al., 2006; Takagi et al., 2006; Nakamura and Fujimoto, 2006). Hwang et al. (2012) also described the first in situ observations of Kelvin–Helmholtz waves at high latitudes using Cluster data under dawnward IMF, which demonstrates another means by which solar wind plasma can enter the magnetosphere. Kavosi and Raeder (2015) showed that Kelvin–Helmholtz waves are much more ubiquitous than previously thought, and they can occur under most solar wind and IMF conditions. These cases also demonstrate that the KH instability appears under varying orientations of the IMF, even though the past reports suggested KH events occur preferentially during northward IMF (Kivelson and Chen, 1995; Fujimoto et al., 2003; Hasegawa et al., 2004a).
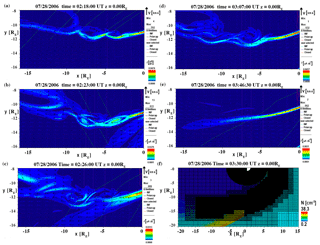
Figure 2Figure from Hwang et al. (2011) where vortices were found using the BATS-R-US simulation. The region of the dawnside flank magnetopause is blown up ( and ), the current density is color-coded, and flow velocities are denoted by arrows (a–e). The grid in the X–Y plane used for the simulation is shown in panel (f) where density is color-coded here.
Collado-Vega et al. (2007) used the results of a 3-D magnetohydrodynamics (MHD) simulation driven by real solar wind conditions to investigate vortices generated mostly under northward IMF. They presented statistics for a total of 304 vortices found near the ecliptic plane on the magnetopause flanks. Large-scale vortices of up to 10 RE were found, with 273 of the vortices generated under northward IMF, and 31 generated under southward IMF. The vortices generated under northward IMF were more prevalent on the dawnside than on the duskside and were substantially less ordered on the dawnside than on the duskside. The investigation relied on a manual search of the data, facilitated by the visualization tool MHD Explorer, implemented in Interactive Data Language (IDL). Since then, we have developed methods to automate this process by the use of data-mining techniques. A second study, Collado-Vega et al. (2013), used the first stages of the automated approach to analyze vortex development when the IMF abruptly switched from southward to northward with other solar wind conditions fixed. This was the first time that vortices formed during high-latitude reconnection were visualized. Even though the vortex detection algorithm was successfully implemented, the visualization code was embedded in another software tool maintained by others, and both were dependent on the IDL platform proprietary software. As such, the code was not available for experimentation and development, nor easily shared. We are now using a “C” language implementation of the algorithm as well as a stand-alone visualization code and have made steps in the direction of an open software tool. We have also made improvements to the algorithm based upon the results of the current work. This work also extends previous analyses by including the visualization of the magnetic field.
The vortices found in the second study were not linked to specific observed vortices in satellite data. The present paper goes a step further, and it validates the algorithm by a direct comparison of VIA-found vortices with independently vetted vortices. Using the CCMC's Runs on Request capability, we used the model runs initialized from the same conditions observed by the Cluster mission in the Hwang et al. (2011) analysis of Kelvin Helmholtz vortices observed during southward IMF. We wanted to have an initial platform where we could cross-check our findings with vortices already observed at the magnetosphere. The fast data characterization and vortex detection made possible with this algorithm will permit the researcher to identify magnetosphere locations for further investigation in large simulation output data sets. This not only saves time, but also diminishes the potential for missing features of interest.
Taking advantage of this capability, we analyze further the properties of the identified vortices, including speed and extent. We also analyze the velocity changes within their motion across the magnetosheath, and we establish the potential of our tool to characterize other transient features that have vortical internal structures like some flux transfer events (FTEs). Section 2 describes the methodology and how the algorithm works. Section 3 describes the data analysis of the features found and the comparison with those from Hwang et al. (2011). Section 4 further analyzes the vortices structures, and Sect. 5 includes a summary and concluding remarks.
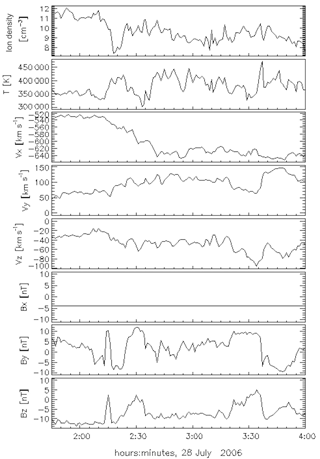
Figure 3Solar wind conditions used for the MHD simulation used by Hwang et al. (2011). It shows the ion density, temperature, vx, vy, vz, Bx, By and Bz.
In this paper, we focus our attention on the simulation run employed by Hwang et al. (2011) to study Kelvin Helmholtz vortices during southward IMF. We acquired the 3-dimensional BATS-R-US model (Powell et al., 1999; Gombosi et al., 2004; Tóth et al., 2012) runs from the CCMC database (cdf files), interpolated to a uniform grid with custom Python code using CCMC's Kameleon library, and extracted the velocity components to ingest into the custom analytics for vortex identification in our VIA. The code has runtime options for a search region bounding box, and a preferential vorticity direction. We limited the region to that referenced in Hwang's study (, ), and vorticity axis within 45∘ of the Z axis. The algorithm then computes the velocity gradient tensor for each point in the flow field, ∇v, which can be written as the sum of a symmetric part and an antisymmetric part . S corresponds to the strain field in the three dimensions of its eigenvectors. R corresponds to the rotation. If the norm of R is greater than the norm of S, we consider this point to lie at the center of a possible vortex, since the rotational strength magnitude exceeds the shear strain rate (Hunt et al., 1988).
For these points, we transform the velocity field to a coordinate system with Z axis defined by the vorticity vector at that point (∇×v). The velocity field is then projected onto the new X–Y plane where local streamlines are computed. A point is a possible vortex if its neighborhood exhibits both closed streamlines and a velocity magnitude minimum at the projected point. Figure 1 show the streamlines computed for a data set where and where , respectively. A major update to the algorithm is the addition of the Lambda 2 criterion, a Galilean invariant method that can adequately identify vortices from a 3-D velocity field (Jeong and Hussain, 1995), and it is useful to fine-tune the vortex classification. This new addition has been shown to help identify false positives, which is a capability that we did not have before. This method requires that at least 2 eigenvalues of S2+R2 are negative. This algorithm is successful at finding the vortex center, but it is not immune to false hits. We can try to screen for these false hits by grouping the vortices into classes by spatial proximity. The class size can be used as a filter to eliminate isolated points that are more likely to be numerical artifacts. The vortex algorithm provides the location from which to begin, so the locations of interest are identified faster, and they can be visualized using any available and compatible tool.
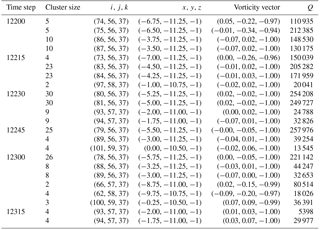
Table 1Properties of the vortices found with our algorithm separated into time step, cluster size, transformed coordinate system, vortex coordinates, vorticity vector and Q value.
2.1 Analysis
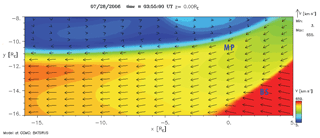
We used MHD model runs available at the CCMC website, specifically the run for 28 July 2006 used by Hwang et al. (2011). This is a BATS-R-US model run with a very high spatial resolution of 0.125 Earth Radii on the dayside (subsolar) region and the flank magnetopause. Figure 2 shows the MHD simulation results using the BATS-R-US code presented in Hwang et al. (2011). The figure shows the dawnside region of the magnetosphere (, ) and how the instability grows from the first panel (a) to the last one (e). Panel (f) shows the grid on the X–Y plane used for the simulation. The colors represent the current density, except in panel (f) where it represents the density, and the arrows represent the flow direction. Some vortices can be seen starting to develop in diagram (a) around , and , .
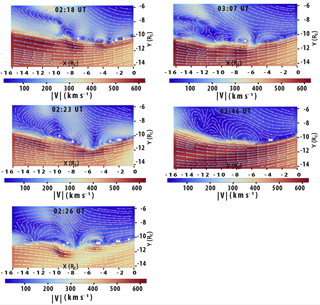
Figure 4The white dots mark where the vortex centers were found using our VIA and they are visualized using Mathematica software for the same time steps as shown in Fig. 2. The colors represent velocity magnitude and the arrows indicate the flow direction.
Figure 53-D representation of the vorticity vectors from the structure found on the Z=0 cut plane around and (shown at the left). The tool can give more information on the extent of the vorticity vectors (shown in black screwlike symbols – center) and where they are located in the magnetosphere domain, with the x, y and z axes represented in red, green and blue colors, respectively (shown at the right).
For several boundary crossing observations by Cluster, Hwang et al. (2011) tested the Kelvin–Helmholtz instability criteria for incompressible plasma conditions (Hasegawa, 1975) using the plasma and field parameters (Eq. 1). In this equation, v1,2 represent flow velocity, ρ1,2 the plasma mass density, and B1,2 magnetic field on sides 1 and 2, respectively. This equation indicates whether or not the interface is unstable to the instability, but not whether the instability develops nonlinearly. The results showed that the wave fronts observed during the different tested crossings were unstable to the Kelvin–Helmholtz instability and could grow nonlinearly.
Having already noted the location of the vortices determined by Hwang et al. (2011), we used the same simulation results to test the data mining capability of our tool. Figure 3 shows the solar wind conditions used as input for the MHD simulation. It shows the ion density, temperature, vx, vy, vz, Bx, By and Bz. For most of the time interval, the IMF is southward.
Table 1 displays in order the time step, the cluster size (group of vortices by spatial proximity), the local transformed coordinate system of the vorticity vector, the vortex coordinates in the geocentric solar magnetosphere (GSM), the vorticity vector and the value Q, the second invariant of the velocity gradient tensor which is used to identify points where the rotational strength exceeds the strain rate. A total of 86 179 vortex structures were detected (clusters, classes) with a mean of 345 for each time step for the data of 28 July 2006 from 02:15 to 03:55 UT. This covers the entire simulation space and includes vorticity vectors in all directions (not preferentially in the Z direction). Figure 4 shows the vortices found using our data mining tool for the same time steps as those in Fig. 2. Looking at both figures, we can conclude that all vortices found by Hwang et al. (2011) are found by our data mining tool. The figure shows the vortex centers by a white dot and the velocity streamlines surround them with the colors corresponding to the velocity magnitude. At 03:46 UT two rotations are visible with the streamline at around , and , . These are vortices with centers near but not at the Z=0 cut plane shown in the figure.
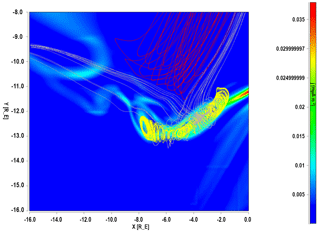
Figure 6Close-up view of a flux transfer event in the MHD simulation at 02:23 UTC (centered at and ) seen in Fig. 2b. The color lines represent the magnetic field lines, with red being closed magnetic field lines, gray being “open” field lines (which are magnetic field lines connected on one side to Earth and on the other side to the solar wind), and yellow lines being those magnetic field lines of the IMF in the solar wind. This 2-D display shows the connectivity of the magnetic field lines of the flux transfer event.
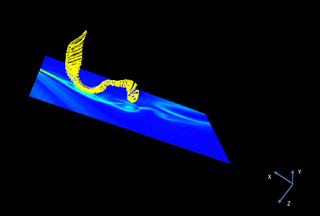
Figure 73-D display of the FTE shown in Fig. 6. The solar magnetic field lines of the flux transfer event on the X–Y plane are shown in the yellow color.
Our tool also yields more information concerning the 3-D extent and duration of the vortices. Our algorithm identified a coherent structure at the Z=0 plane around and that extends from to Z=1RE that Hwang et al. (2011) described as a fully developed Kelvin–Helmholtz vortex. Figure 5 shows the 3-D representation of this coherent structure with the vorticity vectors shown in black (middle figure) and where they are located in the magnetosphere, with the X, Y and Z axes represented in red, green and blue colors respectively. This shows that our findings are consistent with the assessment done by Hwang et al. (2011).
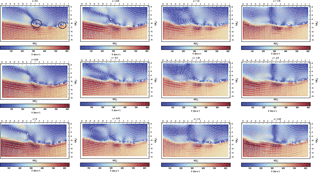
Figure 8The extension along the Z axis of the vortices and FTE presented in the time step of 02:18 UTC. The velocity magnitude is represented by the background color and streamlines are represented by arrows (left to right). The Kelvin–Helmholtz vortex and FTE are emphasized in the first panel by black circles. The white dots represent the center of the vortices as found by our algorithm. The FTE is still visible at , whereas the Kelvin–Helmholtz vortex center is last seen at .
Hwang et al. (2011) described some of the vortical structures seen in Fig. 2b as flux transfer events, which are transient flux tubes that occur after magnetic reconnection on the dayside magnetopause. Any spacecraft encountering this flux tube would see a change in the magnetic field characteristics of the magnetopause boundary. These signatures are best described in boundary normal coordinates (LMN) to the magnetopause, which were first described by Russell and Elphic (1978). The flux tube exhibits bipolar signatures in the normal component of the magnetic field when these magnetosheath field lines not connected to the magnetosphere drape over the connected flux tube (Le et al., 1993). The bipolar signatures normal to the magnetopause appear in both magnetosheath and magnetospheric magnetic field lines draped over and under the FTE, because it bulges outward in both directions. They may also appear within the FTE itself, if there is a field-aligned current along the axis of the event. Saunders et al. (1984) showed evidence of such plasma vorticity within FTEs, which was attributed to an Alfvén wave propagating along the axis.
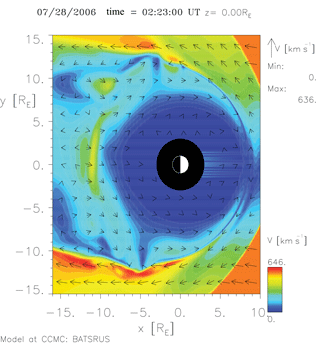
Figure 9X–Y cut at 02:23 UTC showing velocity vectors superposed on the velocity magnitude. It is observed that on the dawnflank region nearby the observed vortices, the magnetosheath velocity magnitude is higher than that observed in the solar wind outside the bow shock, higher than 600 km s−1. This diagram was made using the visualization tool available online through the CCMC website.
We found that our tool could also identify such features of FTEs due to their vortical structure in the simulation. Using the Space Weather Explorer visualization tool available at the CCMC, we analyzed information about the topology of the first vortical structure (center at and ) seen in Fig. 2b. Figure 6 shows the 2-D visualization of the tool for the same coordinates and time step of Fig. 2b. The color lines represent the magnetic field lines, with red being closed magnetic field lines, gray being “open” field lines (which are magnetic field lines connected on one side to Earth and on the other side to the solar wind), and yellow lines being those magnetic field lines of the IMF in the solar wind. The figure shows that the vortical structure contains a mix of “open” magnetic field lines and magnetic field lines from the solar wind, so we infer that this structure is indeed a flux transfer event. Figure 7 shows the 3-D window display using the same visualization tool of the same structure shown in Fig. 6, which shows the 3-D structure of the flux transfer event with the solar wind magnetic field lines shown in yellow color. This suggests that our tool can identify not only vortices created by the Kelvin–Helmholtz instability but also FTEs, as long as they exhibit an internal vortical structure (Saunders et al., 1984).
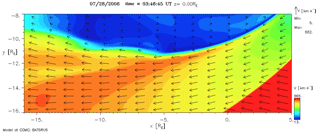
Figure 10Close-up of the X–Y cut at 03:46 UT time step of the simulation where it appears that there no vortices are formed at the boundary. The quantities represented are the same as in Fig. 9. The flow speeds along the boundary are still elevated compared to the flow speed of the solar wind.
To study the vortex properties in more depth, we visualized how the structure of the vortices changed in the Z direction, which is the axis of rotation for the targeted vortices. Figure 7 shows the extent of the FTE and vortices at the time step of 02:18 UTC from Hwang et al. (2011). The figure shows the 2-D image for the vortex structures found with the velocity magnitude represented in color. It covers from Z=0.5RE to , showing the evolution of these vortical structures along their axis of rotation. The Kelvin–Helmholtz vortex and FTE are emphasized on the first diagram by black circles. It can be seen that the Kelvin–Helmholtz vortex is less extended than the FTE in this case. The FTE is still visible at , whereas the Kelvin–Helmholtz vortex center is last seen at . This type of analysis measures how large the vortices are, how they change temporally, and also how elongated they can be.
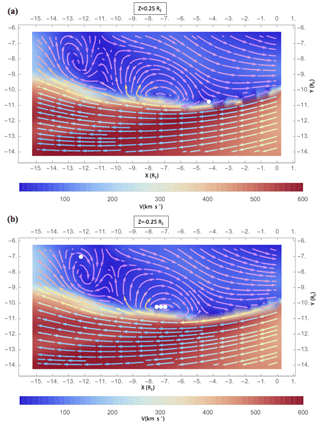
Figure 11With our algorithm we find that there are vortices present at the Z=0.25RE (a) and the coordinate (b) at 03:46 UTC. The center of the vortices is represented by the white dots.
These figures verify that our VIA is able to locate vortices created by the Kelvin–Helmholtz instability and vortical structures formed by bursty magnetic reconnection in the form of flux transfer events. This actually demonstrates that at least some FTEs have vortical velocity structures. Our tool can be used to find how common these vortical FTE structures are. Scientific modeling of the magnetosphere is of special importance since observational data are sparse and relegated to point observations. However, as numerical models increase in spatial resolution, analysis of their results becomes more difficult and time consuming, and it requires an automated search mechanism to focus on important transient features for model validation and inter-comparison. This is a great data mining tool for research purposes since it minimizes the time spent searching for such signatures, in this case on the Earth's magnetosphere.
2.2 Flow acceleration associated with vortices
Figure 9 shows flow velocity magnitudes at 02:23 UTC, when the vortex at and was identified. Magnetosheath velocities reach values higher than 600 km s−1 near the vortex location, which is greater than the solar wind speed outside of the bow shock. Two questions arise: (1) is the Kelvin–Helmholtz vortex structure causing this kind of localized acceleration on the magnetosheath, or (2) is magnetic reconnection on the dayside causing these localized flow accelerations? Past studies have found magnetosheath flow accelerating near the magnetopause when the IMF was northward. Phan et al. (1997) attributed this acceleration to the magnetic forces associated with draping of the field lines around the magnetopause. Chen et al. (1993) also proposed draping to be the source of the magnetosheath flow acceleration. On the other hand, Saunders et al. (1984) suggested that the presence of Kelvin–Helmholtz waves was made unstable due to the super-Alfvénic velocity shear occurring in reconnection accelerated flows under southward IMF. Our case is for southward IMF, and we see the accelerated flows close to the magnetosheath side of the vortices found.
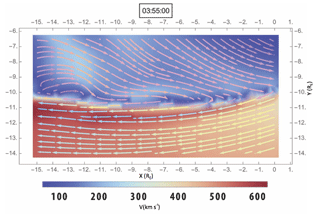
Figure 13Output from our code that shows the velocity magnitude as the background color with no vortices detected at 03:55 UTC on the X–Y plane or close by.
To determine whether the accelerated flows are only seen when the vortices are present, we need to compare times where vortices are found near the boundary with times when they are not. No vortex is visible in the diagram shown in Fig. 10 at the Z=0 cut plane using the visualization tool available through the CCMC website. However, speeds around the magnetosheath reach values similar to those in the solar wind speed, around 500–600 km s−1. The time step was run through our algorithm and some vortices were present nearby to the equatorial plane like the ones shown in Fig. 11 at Z=0.25RE (a) and at (b). Consequently, the high-speed flows at the magnetopause are found to be associated with the presence of vortices.
Figure 12 shows the flows at 03:55 UT (close to the end of the simulation run), when no vortex is visible on the boundary. This plot was made using the visualization tools available online through the CCMC. Flow speeds are definitely high at the magnetopause as represented by the background color, but do not reach solar wind values as seen by the bow shock separation. This time step was searched by the double scrutiny test of the Lambda 2 method. No vortex was found in the vicinity of the Z=0 cut plane for this time step. Figure 13 shows the output from our VIA where no vortex was found at the Z=0 cut plane.
These results could indicate that vortices could contribute to such localized acceleration as they convect antisunward. By contrast, Saunders et al. (1984) argued that the Kelvin–Helmholtz waves were driven by the super-Alfvénic shear created by the accelerated reconnected flows. In our case, flow is accelerated to speeds equal to or higher than the solar wind speed when vortices are present at the boundary. Presumably, this type of plasma acceleration could be a combination of the Alfvénic outflow created by magnetic reconnection and the presence of the Kelvin–Helmholtz vortices at the boundary. In Fig. 13 it is noticeable that the speed at the magnetosheath close to the boundary is not of the order of the solar wind speed, which in this case is around 650 km s−1, but slightly slower (about 480 to 500 km s−1). At the flank, the speeds are considered high for the magnetosheath flow. Thus, the reconnection process could be accelerating the flow through the draping of the reconnected magnetic field lines, making the boundary unstable to the Kelvin–Helmholtz instability. The vortices can then develop and increase the acceleration even further. Inspection shows that the J×B force and the pressure gradient are higher when vortices are present. The pressure gradient forces are greater than the J×B forces, and consequently the acceleration seen in the magnetosheath is the fluid dynamic effect of enhanced flow velocities over ridges in the magnetopause surface. An animation with all the frames in the simulation referring to the same coordinates (, ) and background as Fig. 4 is included as Supplement. The animation shows the evolution of the vortices as also the increase in speed near the boundary that happens when the vortices are present.
The large data sets that are now available through magnetospheric simulations and also spacecraft missions require an automated search algorithm to focus on specific areas or features such as transients on the magnetopause boundary. It is really difficult to visually identify small-scale features in a 3-D vector field, both from the aspect of visualization and sheer data volume, without an automatic search algorithm like the one described in this paper.
We have leveraged a technique used in fluid dynamics to automatically detect vortical structure and elucidate its properties. The algorithm provides information on the 3-D properties and extent of the identified vortical structures. We have identified vortical structures not only attributed to the Kelvin–Helmholtz instability, but to flux transfer events. The magnetic topology seen in this vortical structures confirms this.
Our data demonstrate that the algorithm can identify vortical structures in a simulation based on solar wind conditions where Kelvin–Helmholtz vortices were found in observations by the Cluster mission for southward IMF (Hwang et al., 2011). This is valuable feedback to the theory and scientific understanding of the phenomena, with the huge advantage that the simulation data offer a high temporal- and spatial-resolution view. Our technique thus provides a means to exploit the high temporal and spatial resolution of simulation data and derive feature-specific information to feed back into the science discovery process.
We have also demonstrated that the Kelvin–Helmholtz vortices, analyzed and formed under southward IMF for the case shown, are associated with the accelerated flows observed on the magnetosheath side, with speeds higher than the solar wind speed observed at the bow shock. No such accelerated flows were visible when no vortices were present at the boundary. These accelerated flows can be attributed to the draping of the magnetic field lines in conjunction with the super-Alfvénic shear occurring at the boundary due to the Kelvin–Helmholtz vortices. Inspection shows that the J×B force and the pressure gradient are higher when the vortices are present.
In the near future, we plan to leverage this capability to include the magnetic field topology and delve into the specific vortex characteristics to increase the science return from the data. We also want to compare the simulation results with in situ observations by different spacecraft data for algorithm validation. One promising application of our VIA is the possibility to search vortical structures in data from missions like the Magnetospheric Multiscale Mission (MMS), in which four satellites fly in a tetrahedral formation with a small separation.
Simulation results were provided by the Community Coordinated Modeling Center at Goddard Space Flight Center through their public Runs on Request system (http://ccmc.gsfc.nasa.gov). The Block-Adaptive-Tree-Solarwind-Roe-Upwind-Scheme (BATS-R-US; ID KyoungJoo_Hwang_101309_1a) Model was developed by Tamas Gombosi et al. at the Center for Space Environment Modeling, University of Michigan.
The supplement related to this article is available online at: https://doi.org/10.5194/angeo-36-1117-2018-supplement.
YMCV wrote the manuscript, helped with the algorithm development and analyzed the algorithm output data. VLK developed the algorithm, processed the simulation data, created custom visualizations for the algorithm results, and helped with the editing of the manuscript. DGS helped with the analysis and editing of the manuscript. KJH is the author of a previous analysis used in the paper. LR helped with the simulations used.
The authors declare that they have no conflict of interest.
This work was supported by the FY2015 Science Innovation Fund from NASA
Headquarters. The authors would like to thank Jay Friedlander for his amazing help with the manuscript figures.
The topical editor, Elias Roussos, thanks two anonymous
referees for help in evaluating this paper.
Chen, S.-H., Kivelson, M. G., Gosling, J. T., Walker, R. J., and Lazarus, A. J.: Anomalous aspects of magnetosheath flow and of the shape and oscillations of the magnetopause during an interval of strongly northward interplanetary magnetic field, J. Geophys. Res., 98, 5727–5742, 1993. a
Collado-Vega, Y. M., Kessel, R. L., Shao, X., and Boller, R. A.: MHD flow visualization of magnetopause boundary region vortices observed during high-speed streams, J. Geophys. Res., 112, A06213, https://doi.org/10.1029/2006JA012104, 2007. a
Collado-Vega, Y. M., Kessel, R. L., Sibeck, D. G., Kalb, V. L., Boller, R. A., and Rastaetter, L.: Comparison between vortices created and evolving during fixed and dynamic solar wind conditions, Ann. Geophys., 31, 1463–1483, https://doi.org/10.5194/angeo-31-1463-2013, 2013. a
Fujimoto, M., Tonooka, T., and Mukai, T.: Vortex-Like Fluctuations in the Magnetotail Flanks and their Possible Roles in Plasma Transport, in Earth's Low-Latitude Boundary Layer, American Geophysical Union, 2003. a
Gombosi, T. I., Powell, K. G., De Zeeuw, D. L., Clauer, C. R., Hansen, K. C., Manchester, W. B., Ridley, A. J., Roussev, I. I., Sokolov, I. V., Stout, Q. F., and Toth, G.: Solution-adaptive magnetohydrodynamics for space plasmas: Sun-to-Earth simulations, Comput. Sci. Eng., 6, 14–35, 2004. a
Hasegawa, A.: Plasma Instabilities and Nonlinear Effects, Springer, Verlag, 1975. a
Hasegawa, H., Fujimoto, M., Phan, T.-D., Rème, H., Balogh, A., Dunlop, M. W., Hashimoto, C., and TanDokoro, R.: Transport of solar wind into Earth's magnetosphere through rolled-up Kelvin-Helmholtz vortices, Nature, 430, 755–758, 2004a. a, b
Hasegawa, H., Fujimoto, M., Takagi, K., Saito, Y., Mukai, T., and Rème, H.: Single-spacecraft detection of rolled-up Kelvin-Helmholtz vortices at the flank magnetopause, J. Geophys. Res., 111, A09203, https://doi.org/10.1029/2006JA011728, 2006. a
Hunt, J., Wiley, A., and Moin, P.: Eddies, Stream, and Convergence Zones in Turbulent Flows, Studying Turbulence Using Numerical Simulation Databases, 1, 193–208, 1988. a
Hwang, K.-J., Kuznetsova, M. M., Sahraoui, F., Goldstein, M. L., Lee, E., and Parks, G. K.: Kelvin-Helmholtz waves under southward interplanetary magnetic field, J. Geophys. Res., 116, A08210, https://doi.org/10.1029/2011JA016596, 2011. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p
Hwang, K.-J., Goldstein, M. L., Kuznetsova, M. M., Wang, Y., Viñas, A. F., and Sibeck, D. G.: The first in situ observation of Kelvin-Helmholtz waves at high-latitude magnetopause during strongly dawnward interplanetary magnetic field conditions, J. Geophys. Res., 117, A08233, https://doi.org/10.1029/2011JA017256, 2012. a
Jeong, J. and Hussain, F.: On the Identification of a Vortex, J. Fluid Mech., 285, 69–94, 1995. a
Kavosi, S. and Raeder, J.: Ubiquity of Kelvin–Helmholtz waves at Earth's magnetopause, Nat. Commun., 6, 7019, https://doi.org/10.1038/ncomms8019, 2015. a
Kivelson, M. G. and Chen, S. H.: The Magnetopause: Surface waves and instabilities and their possible dynamical consequences, vol. 90 of Geophys. Monogr. Ser., chap. Physics of the Magnetopause, American Geophysical Union, 257–268, 1995. a
Le, G., Russell, C. T., and Kuo, H.: Flux transfer events: spontaneous or driven?, Geophys. Res. Lett., 20, 791–794, 1993. a
Miura, A.: Anomalous transport by magnetohydrodynamic Kelvin-Helmholtz instabilities in the solar wind-magnetosphere interaction, J. Geophys. Res., 89, 801–818, 1984. a
Nakamura, T. and Fujimoto, M.: Magnetic reconnection within MHD-scale Kelvin-Helmholtz vortices triggered by electron inertial effects, Elsevier, 37, 522–526, 2006. a
Nykyri, K. and Otto, A.: Plasma transport at the magnetospheric boundary due to reconnection in Kelvin-Helmholtz vortices, Geophys. Res. Lett., 28, 3565–3568, 2001. a
Phan, T. D., Larson, D., McFadden, J., Lin, R. P., Carlson, C., Moyer, M., and Paularena, K. I.: Low-latitude dusk flank magnetosheath, magnetopause, and boundary layer for low magnetic shear: Wind observations, J. Geophys. Res., 102, 19883–19895, 1997. a
Powell, K., Roe, P., Linde, T., Gombosi, T. I., and Zeeuw, D. L. D.: A solution-adaptive upwind scheme for ideal magnetohydrodynamics, J. Comp. Phys., 154, 284–309, 1999. a
Russell, C. T. and Elphic, R. C.: Initial ISEE magnetometer results: Magnetopause observations, Space Sci. Rev., 22, 681–715, 1978. a
Saunders, M. A., Russell, C. T., and Sckopke, N.: Flux transfer events: Scale size and interior structure, Geophys. Res. Lett., 11, 131–134, 1984. a, b, c, d
Takagi, K., Hashimoto, C., Hasegawa, H., Fujimoto, M., and TanDokoro, R.: Kelvin-Helmholtz instability in a magnetotail flank-like geometry: Three dimensional MHD simulations, J. Geophys. Res., 111, A08202, https://doi.org/10.1029/2006JA011631, 2006. a
Tóth, G., Van der Holst, B., Sokolov, I. V., De Zeeuw, D. L., Gombosi, T. I., Fang, F., Manchester, W. B., Meng, X., Najib, D., Powell, K. G., Stout, Q. F., Glocer, A., Ma, Y.-J., and Opher, M.: Adaptive Numerical Algorithms in Space Weather Modeling, J. Comput. Phys., 231, 870–903, 2012. a