the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A Nonlinear Generalized Boussinesq Equation ((2+1)-D) for Rossby-Khantadze Waves
Laila Zafar Kahlon
Tamaz David Kaladze
Hassan Amir Shah
Taimoor Zaka
Syed Assad Ul Azeem Bukhari
In the following paper, we investigate nonlinear Rossby-Khantadze waves, by taking into account inhomogeneity in the geomagnetic field and angular velocity – due to Earth's differential rotation. Considering the system to be weakly nonlinear, we make use of perturbation theory to derive a new (2+1)-D generalized form of Boussineq equation. We evaluate the obtained equation by using the qualitative theory of ordinary differential equations (ODEs), and bifurcation theory of dynamical systems. The obtained numerical results show that the aforementioned solutions of the traveling waves correspond to Rossby-Khantadze solitons.
- Article
(763 KB) - Full-text XML
- BibTeX
- EndNote
Numerous investigations conducted by ground-based and satellite observations gives proof of the presence of zonal flows in various regions of the terrestrial atmosphere (Pedlosky, 1987). This is based on the fact of the non-uniform heating caused by the sun in the Earth's atmospheric regions. These ultra-low frequency (ULF) perturbations in ionosphere E and F regions occur due to the sheared flow with nonhomogeneous velocities along the meridians (Shukla and Stenflo, 2003; Onishchenko et al., 2004; Satoh, 2004; Kaladze et al., 2007; Kaladze et al., 2008). The effects of sheared flow on the properties of linear and non-linear waves in the ionosphere and under suitable conditions they give rise various nonlinear structures like zonal flows (ZFs), vortices, and solitons etc.
Sheared Rossby waves have gained much attention due to their prominent role in the global atmospheric circulation. Such slow long-period planetary waves have phase velocities ∼ 1–100 m s−1, which is around the velocity of the ionospheric (local) winds. Their frequency is in the order of 10−4–10−6 s−1 at middle latitudes, whereas the period is at 2 h to 14 d. Besides the slow Rossby waves, fast perturbations also exist in the moderate-latitude ionosphere, which are created by the latitudinal inhomogeneity of the Earth'magnetic field and the Hall effect. The first theoretical evidence of such large-scale EM perturbations in the ionospheric E- and F-regions was made by Khantadze (1986, 1999, 2001), and in this work, he differentiated between fast and slow large-scale EM planetary waves. Consequently, fast EM planetary waves were named Khantadze modes, and these waves were observed by Soyuz and Proton rockets (Burmaka et al., 2006) at the middle latitude and by the world network of ionospheric and magnetic observations (Sharadze et al., 1988; Sharadze, 1991; Alperovich and Fedorov, 2007). Detailed analysis of such planetary EM waves was carried out by Kaladze (2003), Kaladze et al. (2004) and Khantadze et al. (2010).
The spatial inhomogeneity along the meridians, of both the ambient magnetic field and the Coriolis force parameter generates coupled modes called the Rossby-Khantadze (RK) waves (see e.g., Kaladze et al., 2011). The existence of sheared RK electromagnetic vortices in the E region of Earth's ionosphere is studied thoroughly by Kaladze et al. (2011, 2012, 2013a, b, 2014). In those works, the authors have not only shown the self-organization of coupled RK waves into dipolar solitary vortices, but also predicted the generation of magnetic field in the system due to the aforementioned waves. More recently, different nonlinear processes having relevance to the generation of zonal flows (sheared) by Rossby waves are considered. The key factor for the generation of zonal flows in short-wavelength Rossby waves is Reynold's stress (Shukla et al., 2003; Onishchenko et al., 2004). Rossby waves causes the generation of zonal flows in E layer of ionosphere (Kaladze et al., 2007). Such nonlinear Rossby wave structures splits into various parts, and this splitting is dependent on zonal flow's energy (Kaladze et al., 2008). Along with the analytical side, numerical work on RK waves with sheared zonal flows in the E layer of the ionosphere is worked out as well (Futatani et al., 2013, 2015). In these works, breaking of vortices is studied, where the energy is transferred from sheared flow into these multiple pieces (daughter waves). It is worth noting that equatorially propagating Rossby solitary waves by sheared flows have been predicted and discussed (Qiang et al., 2001) and their presence was confirmed through observations by Freja and Viking satellites (Bostrom, 1992; Lindqvist et al., 1994; Dovner et al., 1994; Qiang et al., 2001). In Jian et al. (2009)'s work, the authors studied the nonlinear propagation of sheared Rossby waves in stratified neutral fluids and obtained modified Korteweg-de Vries (MKdV) equation, which is characterised by a cubic nonlinearity. Kahlon et al. (2024), investigated the MKdV equation with cubic nonlinearity for Rossby-Khantadze nonlinear waves.
Zonal flow's generation in the ionosphere's E region by Rossby-Khantadze waves having magnetic field is also shown (Kaladze et al., 2012; Kahlon and Kaladze, 2015), where it has been predicted that there exists a possibility of the magnetic field generation, at the strength of 103 nT. Kaladze et al. (2019) studied the nonlinear interaction of magnetized Rossby waves with inclusion of zonal flows in the Earth's ionospheric E-layer, in which MKdV solitons were obtained. The possibility of planetary Rossby wave's existence in the dynamo E-area of weakly ionised ionosphere was predicted by Forbes (1996). It was also shown that the theoretical work corresponds with the experimental interpretations. Much later, Vukcevic and Popovic (2020) investigated the possibility of soliton formation at different latitudes in ionosphere. Direct observed data of satellites of such soliton structures from Earth's surface are discussed.
In the context of shallow water waves and in plasmas, several researchers have extended the KdV and MKdV equations to higher dimensions, in order to obtain realistically accurate results. Kadomstev-Petviashvilli (KP) equation and Zakharov-Kuznetsov (ZK) equation have gained much attention over the years (Vukcevic and Popovic, 2020; Kadomtsev and Petviashvili, 1970; Groves and Sun, 2008; Infeld and Rowland, 2000; Zakharov and Kuznetsov, 1974). Both of these equations are (2+1) – dimensional in nature and are very useful in plasma models (as one can get almost complete information by taking parallel and perpendicular dimension into account). While modelling shallow water waves, Johnson (1996) investigated a (2+1) – dimensional Boussinesq equation for gravitational surface waves. Making use of the surface wave theory, Mitsotakis (2009) investigated the Boussinesq equation and simulated the propagation of such waves. In the context of geophysics, many authors (Gottwald, 2003; Yang et al., 2016, 2018; Zhang et al., 2017a, b) have investigated ZK equation by considering nonlinear Rossby waves from the quasi-geostropic potential vorticity equation. Although, the Boussinesq equation in the study of the nonlinear Rossby-Khantadze waves is not reported so far.
It is very useful to find exact solutions of nonlinear partial differential equations. Several techniques have recently been used to find such solutions, including but not limited to the method of trigonometric series (Ma and Fuchssteiner, 1996), the method of tan()-expansion (Manafian and Aghdaei, 2016), sine-cosine method (Wazwaz, 2005), Wronskian method (Ma and You, 2005), separation of variables approach (Lin and Zhang, 2007), Septic B-spline method (El-Danaf, 2008), the transformative functional rational method (Ma and Lee, 2009), the symmetry algebric method (Ma and Chen, 2009), the homotopy perturbation method (Ganji et al., 2009), the modified method of mapping and the extended mapping method (Zhang et al., 2010), qualitative theory of the bifurcation method and dynamical systems (Zhang et al., 2011), the multiple exp-function method (Ma and Zhu, 2012), the modified ()- method of expansion (Miao and Zhang, 2011), the modified trigonometric function series method (Zhang et al., 2011) infinite series method and Jacobi elliptic functional method (Zhang et al., 2012; Tasbozan et al., 2016), RBF approximation method (Uddin, 2014) ()-expansion method (Zhang et al., 2014), Hirota bilinear method (Lü et al., 2016; Ma and Fuchssteiner, 1996; Lü and Ma, 2016), lattice Boltzmann method (Wang and Yan, 2016) to name a few.
In the present work, for the partially ionized and conducting ionospheric E plasma we consider the stream-function and evolution of geomagnetic field for electromagnetic Rossby-Khantadze (RK) waves, which provides novelty to this work. In Sect. 2, we set the system of initial equations. In Sect. 3, by using the reductive perturbation technique we obtain the linear dispersion equation from the lowest order of ε. In Sect. 4, we derive the Boussinesq equation for Rossby-Khantadze nonlinear waves from our considered set of equations. In Sect. 5, we study the dynamical analysis of the Boussinesq equation and get its exact traveling solitary solutions. In second last section, discussions are presented in Sect. 6. The summary and conclusion are made in Sect. 7.
We start by considering a weakly ionised system, as is characteristic to ionospheric plasmas. Here ions, electrons and neutral particles are embedded in a nonhomogeneous geomagnetic field, , and the angular velocity is taken into consideration as, . We consider the 2D incompressible motion i.e., , which represents the velocity of the neutral gas where , and is the stream function.
We make use of a slab geometry with zonally x, latitudinally y, and locally vertical direction along z axis. Furthermore, the behavior of the nonlinear Rossby-Khantadze sheared electromagnetic waves is expressed by the 2D system of equations (e.g., Kaladze et al., 2011, 2014; Song and Yang, 2009; Liu et al., 2019) as given below:
Here in the Eq. (1a) we consider vorticity as, , from momentum equation of single fluid where is the latitudinally inhomogenous angular velocity with . Here, . While the parameter with , being the nonhomogeneity in the geo-magnetic field, n is charged particles's number density, is the Jacobian. Equation (1b) shows the z-component of perturbed magnetic field. Note that lesser contribution of charged particles (in comparison of neutrals) plays their role (Kaladze et al., 2013a, b) in the inductive current.
To solve the set of Eq. (1), we use the boundary condition
representing the flow along the meridional directions, as explained by Pedlosky (1987) and Satoh (2004).
By introducing the following dimensionless parameters, we can express Eq. (1) in dimensionless form
Here asterisk denotes the dimensional variables, which are further dropped in the equation below. Here L0 is the zonally length; H is a vertically length and U0 is the velocity. Finally, Eq. (1) takes the form
with the following boundary conditions
In this section, to investigate the non-linear Boussinesq equation describing the solitary Rossby-Khantadze waves. Here we make use of multiple scale and asymptotic expansion approach.
The expression
describes the stream function with representing the background stream function where c0 is a constant, refers to background flow, and ψ′ is the disturbance in stream function. While the perturbed magnetic field is:
Thus, the set of Eq. (4) can be expressed as
where
By applying the multiple scale approach we find the following stretched coordinates,
in the comoving frame of reference the differential operator can be expressed in the following manner
The perturbed stream function and perturbed magnetic fields are expanded as
Using Eqs. (9), (10) and (11) into Eq. (7) we get from the lowest order i.e. :
Next order O(ε2) gives
From the second set of Eq. (13), we get
Next order gives
Equation (15b) gives
Assume that Eq. (12) has the solution
Thus, from Eqs. (12) and (20) we get the following linear dispersion relation
and from the boundary condition given by Eq. (5) we get
The obtained Eq. (18) is the Rayleigh-Kuo equation describing the Rossby-Khantadze waves. By solving Eq. (12) simultaneously and the coefficients are locally constant and , we get the following dispersion equation
where and . Equation (20) describes the dispersion equation of sheared Rossby-Khantadze waves. In the absence of α we get two solutions, one independent solution of Rossby waves and the second one for Khantadze waves.
By introducing the dimensionless variables and (with , a = and ) then we rewrite the dispersion relation (20)
Here . For the E-ionosphere layer, the parameters have the following , 2, , kg m−3, the parameter α0= () (Kaladze et al., 2011).
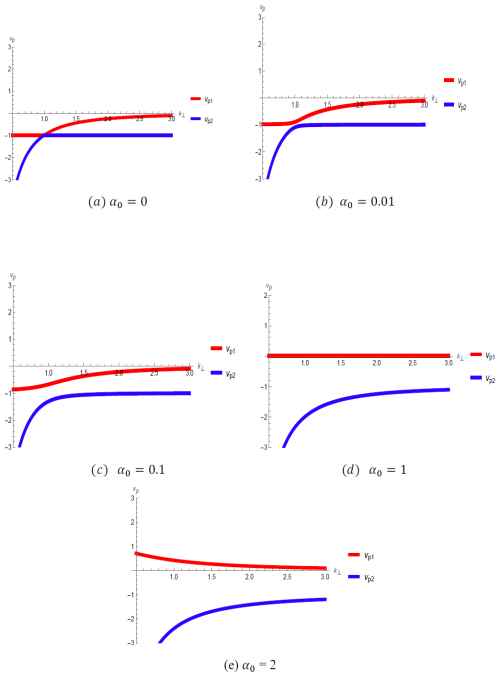
Figure 1 represents the phase velocity vp of the obtained coupled Rossby-Khantadze waves is plotted with wave number k⟂ by varying α0. Red curve vp1 is for “+” and blue vp2 is for “–” signs before the radicand in Eq. (21).
In this section, by taking into account the separation of variables techniques we will derive the nonlinear Boussinesq Equation describing the solitary nonlinear structures.
Further, we assume that Eq. (13) has the solution
with
By using the separation of variables approach and using Eqs. (22) and (23) in Eq. (13) we obtain
Put
From Eq. (24) we get
with q(y) and γ are given by .
And
The boundary conditions are given by
From Eqs. (26) and (28) we have
In order to arrive at the evolution equation, we use Eqs. (20), (25) and (26) and substitute into Eq. (15)
where
Equation (31) is the evolution equation for Ψ3 and we obtain its solution by multiplying by φ1(y) and then integrating over y to get
where the coefficients are:
Noting that
By using Eq. (36) in Eq. (34) we obtain
Rewriting Eq. (37) as
where
This equation describes the evolution of spatial-temporal amplitude of Rossby-Khantadze waves. When gives a1=0, our Eq. (38) reduces to the standard Boussinesq equation ((2+1) – dimensional). Otherwise, Eq. (38) is the general form of Boussinesq equation (i.e. a1= 0).
In order to solve the generalized Boussinesq equation, we follow the methodology developed by Kaladze et al. (2013b) and later make use of methods of dynamical analysis to get extended information about the solution of the equation, and to obtain its trajectories and fixed points in phase space.
We use the following co-moving frame A=∅(ξ) with to turn Eq. (39) into an ordinary differential equation. Then after integrating it once over ξ gives us,
with g as the constant of integration.
We can now express Eq. (40) as a set of two first order autonomous equations as
From Eq. (40) we express the Hamiltonian of the system as
where h is a constant value.
In order to get the fixed points of our system, we suppose where ∅1 is the fixed point. Such that,
Equation (43) is a quadratic equation and has two roots, which are given below
and
where
Let , then g0 is the extremum values of f(ϕ)+g.
Suppose (ϕi,0) (where i=1, 2) be one of the singular points of the system of equation, then from our system, the characteristic values
Based on the qualitative theory for the dynamical system we know that Eq. (44)
- i.
If then (ϕi, o) is a center point
- ii.
If then (ϕi, o) is a saddle point
- iii.
If then (ϕi,0) is degenerate saddle point
Thus, above analysis provides the bifurcations phase portraits of Eq. (42).
In this part, based on this dynamical theory, we will deduce the traveling wave solution to Eq. (42) by considering g=0.
The Eq. (41) reduce to the system as follows
It is expected that Eq. (41) has a homoclinic orbits Γ1 (which corresponds to a solitary wave profile).
In ϕ−y plane, Γ1 is given as
with .
Equations (47) and (48) give
Here we suppose that ϕ(0)=ϕo and integrate Eq. (49) along homoclinic orbits Γ1, we get
and
Equations (50) and (51) give
where .
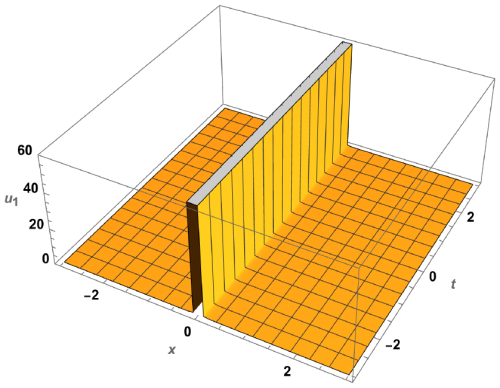
From Eqs. (52) and (53) along with transformation A=ϕ(ξ), we get the solution of solitary wave,
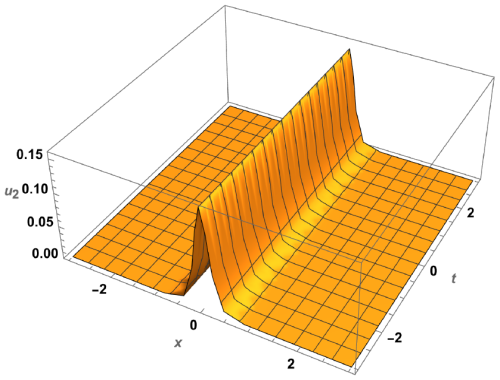
and
It is shown from the obtained solutions that the considered Rossby-Khantadze waves are solitary in nature.
In this paper, investigation of large-scale Rossby-Khantadze nonlinear waves by incorporating sheared zonal flows in the ionospheric plasma found in the E-layer, is presented. The spatially nonhomogeneous Earth's angular velocity with the background magnetic field are taken. The spatial inhomogeneity in the magnetic field allows the coupling of Rossby and Khantadze waves named Rossby-Khantadze waves.
In this work, we considered a system of equations for Boussinesq model equation from the initial set of equations namely, momentum equation, continuity equation and Maxwell equation. This provides the nonlinear interaction of considered Rossby-Khantadze waves. By taking the curl of momentum equation, we obtain the vorticity equation which is the first system of equation. We obtain the equation of magnetic induction by using the Maxwell's equation, by taking the parameters of the E layer of ionosphere into account. The system of equations explains how Rossby-Khantadze nonlinear waves propagate in considered sheared zonal flow ionospheric E region. In earlier work, the authors take into account Rossby waves while here we take coupled Rossby and Khantadze waves. For the linear consideration, the linear dispersion relation of the fast (Khantadze) and slow (Rossby) electromagnetic (EM) wave in the ionospheric E-region is analyzed with two modes of frequency ω1 and ω2. The numerical work of obtained frequencies is shown. The phase velocities depending on wave number is shown in Fig. 1 (with red color describes ω1 while blue ones to ω2). For small wave vector, ω1 approaches to the finite value, while for the ω2 becomes −∞. For small α0, strong coupling is shown between two modes. With increasing α0 the Rossby modes approaches to the positive values, ergo at α0=1, it approaches to zero and for the values α0>1, its phase velocity approaches to positive value, while the waves with ω2 are always propagating along the latitudinally westward direction. For large wave vector, both modes lose their dispersing property.
In order to investigate the nonlinear behavior of coupled RKWs we use multiple scale analysis and asymptotic expansion, to derive nonlinear Boussinesq equation with spatially dependent coefficients. By using the method of multiple scale and hence considering finite amplitude perturbations, we obtain a new Boussinesq ((2+1) dimensional) equation. We have also presented the qualitative description of dynamical systems. Thus, based on the ideas of this work, we cannot only obtain the exact traveling wave solutions in the future research, but can also do the stability analysis, and determine the parameters at which the onset of chaos takes place. Furthermore, this can help us to understand not only the solitary profiles, but also the nonlinear periodic wave solutions associated to the Boussinesq equation.
By taking lowest order O() of Eq. (7) we get an eigen-value Eq. (21). This order, however, does not bring information about the amplitude of the Rossby-Khantadze waves. Thenceforth we use the next order, O(ε2) of Eq. (7) and obtain non-singular solutions. The obtained equation still doesn't provide information about the wave amplitude. Therefore, we need to go to the next order.
The next order of Eq. (7) provides a longitudinal dispersion effect, which competes with a weak nonlinear effect. This explains that if the perturbation problem has an effective solution, then the secular term F must be satisfied from Eq. (34), otherwise the wave's amplitude would be infinite and have no significance in practice. By doing some mathematical steps, from next order we get the nonlinear Boussinesq Eq. (41). By considering g=0, we also investigate the dynamical analysis and have done a fixed points analysis analytically. We also obtain the travelling solitary structures shown in Figs. 2–3. The obtained results might be helpful for understanding the data which is obtained by satellites orbiting the earth's ionosphere region.
The considered sheared RK waves give insights on large-scale processes and are observed mainly during magnetic storms as well as sub-storms, artificial explosions, earthquakes, etc. Hence, for the future experimental work, the theoretical findings of Rossby-Khantadze electromagnetic type oscillations will provide valuable information.
This study has explored the nonlinear dynamics of Rossby-Khantadze waves in weakly ionized ionospheric plasma, particularly emphasizing the presence of sheared zonal flows. By deriving the boussinesq equation, which incorporates nonlinearity, we have established a robust framework for analyzing the propagation characteristics of Rossby-Khantadze waves across the E-layer of the ionosphere.
The use of the multiple scale analysis and asymptotic expansion has led to the identification of solitary wave solutions that exhibit significant variations influenced by different parameter values. Overall, the findings of this research not only enhance our understanding of wave phenomena in the ionosphere but also have broader implications for various plasma environments, including those found in space and laboratory settings.
No data sets were used in this article.
LZK: conceptualization (equal); formal analysis (equal); investigation (equal); methodology (equal); writing; original draft (equal); supervision (equal); writing – review and editing (equal). TDK: conceptualization (equal); investigation (equal); methodology (equal); writing – review and editing (equal). HAS: methodology (equal); investigation (equal); supervision (equal); writing - review and editing (equal). TZ: formal analysis (equal); methodology (equal); writing; – original draft (equal). SAB: investigation (equal); writing – review and editing (equal).
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors. Also, please note that this paper has not received English language copy-editing. Views expressed in the text are those of the authors and do not necessarily reflect the views of the publisher.
This paper was edited by Claudia Borries and reviewed by two anonymous referees.
Alperovich, L. S. and Fedorov, E. N.: Hydromagnetic Waves in the Magnetosphere and the Ionosphere, Springer, https://link.springer.com/book/10.1007/978-1-4020-6637-5 (last access: 17 September 2025), 2007.
Bostrom, R.: Observations of weak double layers on auroral field lines, IEEE T. Plasma Sci., 20, 756–763, https://doi.org/10.1109/27.199524, 1992.
Burmaka, V. P., Lysenko, V. N., Chernogor, L. F., and Chernyak, Y. V.: Wave-like processes in the ionospheric F region that accompanied rocket launches from the Baikonur site, Geomagn. Aeronomy, 46, 742–759, https://link.springer.com/article/10.1134/S0016793206060107a, 2006.
Dovner, P. O., Eriksson, A. I., Bostrom, R., and Holback, B.: Freja multiprobe observations of electrostatic solitary structures, Geophys. Res. Lett., 21, 1827–1830, https://doi.org/10.1029/94GL00886, 1994.
El-Danaf, T. S. A.: Septic B-spline method of the Korteweg-de Vries–Burger's equation, Communications in Nonlinear Science and Numerical Simulation, 13, 554–566, https://doi.org/10.1016/j.cnsns.2006.05.010, 2008.
Forbes, J. M.: Planetary waves in the thermosphere-ionosphere system, J. Geomagn. Geoelectr., 48, 91–98, https://www.jstage.jst.go.jp/article/jgg1949/48/1/48_1_91 (last access: 17 September 2025), 1996.
Futatani, S., Horton, W., and Kaladze, T. D.: Nonlinear propagation of Rossby-Khantadze electromagnetic planetary waves in the ionospheric E-layer, Phys. Plasmas, 20, 102903, https://doi.org/10.1063/1.4826592, 2013.
Futatani, S., Horton, W., Kahlon, L. Z., and Kaladze, T. D.: Rossby-Khantadze electromagnetic planetary waves driven by sheared zonal winds in the E-layer ionosphere, Phys. Plasmas, 22, 012906, https://doi.org/10.1063/1.4906362, 2015.
Ganji, Z. Z., Ganji, D. D., and Rostamiyan, Y.: Solitary wave solutions for a time-fraction generalized Hirota–Satsuma coupled KdV equation by an analytical technique, Appl. Mathemat. Modell., 33, 3107–3113, https://doi.org/10.1016/j.apm.2008.10.034, 2009.
Gottwald, G. A.: The Zakharov-Kuznetsov equation as a two-dimensional model for nonlinear Rossby waves, arXiv preprint nlin/0312009, https://doi.org/10.48550/arXiv.nlin/0312009, 2003.
Groves, M. D. and Sun, S. M.: Fully localised solitary-wave solutions of the three-dimensional gravity–capillary water-wave problem, Archive for rational mechanics and analysis, 188, 1–91, https://doi.org/10.1007/s00205-007-0085-1, 2008.
Infeld, E. and Rowlands, G.: Nonlinear waves, solitons and chaos, Cambridge University Press, https://doi.org/10.1017/CBO9781139171281, 2000.
Jian, S., Lian-Gui, Y., Chao-Jiu, D. A., and Hui-Qin, Z.: mKdV equation for the amplitude of solitary Rossby waves in stratified shear flows with a zonal shear flow, Atmos. Ocean. Sci. Lett., 2, 18–23, https://doi.org/10.1080/16742834.2009.11446771, 2009.
Johnson, R. S.: A two-dimensional Boussinesq equation for water waves and some of its solutions, J. Fluid Mech., 323, 65–78, 1996.
Kadomtsev, B. B. and Petviashvili, V. I.: On the stability of solitary waves in weakly dispersing media, in: Doklady Akademii Nauk, Russian Academy of Sciences, 192, 753–756, 1970.
Kahlon, L. Z. and Kaladze, T. D.: Generation of zonal flow and magnetic field in the ionospheric E-layer, J. Plasma Phys., 81, 905810512, https://doi.org/10.1017/S002237781500080X, 2015.
Kahlon, L. Z., Shah H. A., Kaladze, T. D., Ain, Q. T., and Bukhari, S. A.: Brief Communication: A modified Korteweg–de Vries equation for Rossby–Khantadze waves in a sheared zonal flow of the ionospheric E layer, Nonlin. Process. Geophys., 31, 1–6, https://doi.org/10.5194/npg-31-1-2024, 2024.
Kaladze, T. D.: Planetary electromagnetic waves in the ionospheric E-layer, in: Proc. First Cairo Conf. Plasma Physics and Applications (CCPPA '03), Cairo, Egypt, 11–15 October 2003, edited by: Kunze, H.-J., El-Khalafawy, T., and Hegazy, H., German-Egyptian Cooperation, Shriften des Forschungszentrums Jülich, Bilateral seminars of the International Bureau, 34, 68, https://juser.fz-juelich.de/record/892417 (last access: 17 September 2025), 2004.
Kaladze, T. D., Aburjania, G. D., Kharshiladze, O. A, Horton, W., and Kim, Y.-H: Theory of magnetized Rossby waves in the ionospheric E layer, J. Geophys. Res., 109, A05302, https://doi.org/10.1029/2003JA010049, 2004.
Kaladze, T. D., Tsamalashvili, L. V., Wu, D. J., Pokhotelov, O. A., Sagdeev, R. Z., Stenflo, L., and Shukla, P. K.: Rossby-wave driven zonal flows in the ionospheric E-layer, J. Plasma Phys., 73, 131–140, https://doi.org/10.1017/S0022377806004351, 2007.
Kaladze, T. D., Pokhotelov, O. A., Stenflo, L., Rogava, J., Tsamalashvili, L. V., and Tsik-Lauri, M.: Zonal flow interaction with Rossby waves in the Earth's atmosphere: a numerical simulation, Phys. Lett. A, 372, 5177–5180, https://doi.org/10.1016/j.physleta.2008.06.008, 2008.
Kaladze, T. D., Tsamalashvili, L. V., and Kahlon, L. Z.: Rossby-Khantadze electromagnetic planetary vortical motions in the ionospheric E-layer, J. Plasma Phys., 77, 813–828, https://doi.org/10.1017/S0022377811000237, 2011.
Kaladze, T., Kahlon, L., Horton, W., Pokhotelov, O., and Onishchenko, O.: Shear flow driven Rossby-Khantadze electromagnetic planetary vortices in the ionospheric E-layer, Europhys. Lett., 106, 29001, https://doi.org/10.1209/0295-5075/106/29001, 2014.
Kaladze, T. D., Kahlon, L. Z., and Tsamalashvili, L. V.: Excitation of zonal flow and magnetic field by Rossby-Khantadze electromagnetic planetary waves in the ionospheric E-layer, Phys. Plasmas, 19, 022902, https://doi.org/10.1063/1.3681370, 2012.
Kaladze, T., Tsamalashvili, L., Kaladze, D., Ozcan, O., Yesil, A., and Inc, M.: Modified KdV equation for magnetized Rossby waves in a zonal flow of the ionospheric E-layer, Phys. Lett. A, 383, 125888, https://doi.org/10.1016/j.physleta.2019.125888, 2019.
Kaladze, T. D., Horton, W., Kahlon, L. Z., Pokhotelov, O., and Onishchenko, O.: Zonal flows and magnetic fields driven by large-amplitude Rossby-Alfvén-Khantadze waves in the E layer ionosphere, J. Geophys. Res.-Space, 118, 7822–7833, https://doi.org/10.1002/2013JA019415, 2013a.
Kaladze, T. D., Horton, W., Kahlon, L. Z., Pokhotelov, O., and Onishchenko, O.: Generation of zonal flow and magnetic field by coupled Rossby-Alfvén-Khantadze waves in the Earth's ionospheric E-layer, Phys. Scripta, 88, 065501, https://doi.org/10.1088/0031-8949/88/06/065501, 2013b.
Khantadze, A. G.: Hydromagnetic gradient waves in dynamo region of the ionosphere, Bull. Acad. Sci. Georgian SSR 123, 69, ISSN 0132-1447, 1986 (in Russian).
Khantadze, A. G.: On the electromagnetic planetary waves in the Earth's ionosphere, J. Georgian Geophys. Soc. B, Phys. Atmos. Ocean and Cosmic Rays 4, 125, ISSN 1512-1127, 1999 (in Russian).
Khantadze, A. G.: A new type of natural oscillations in conducting atmosphere, Dokl. Earth Sci., 376, 93, ISSN: 1531-8354, ISSN: 1028-334X, 2001.
Khantadze, A. G., Jandieri, G. V., Ishimaru, A., Kaladze, T. D., and Diasamidze, Zh. M.: Electromagnetic oscillations of the Earth's upper atmosphere (review), Ann. Geophys., 28, 1387–1399, https://doi.org/10.5194/angeo-28-1387-2010, 2010.
Lin, C. and Zhang, X. L.: The formally variable separation approach for the modified Zakharov–Kuznetsov equation, Communications in Nonlinear Science and Numerical Simulation, 12, 636–642, https://doi.org/10.1016/j.cnsns.2005.06.004, 2007.
Lindqvist, P. A., Marklud, G. T., and Blomberg, L. G.: Plasma characteristics determined by the Freja electric field instrument, Space Sci. Rev., 70, 593–602, https://doi.org/10.1007/BF00756888, 1994.
Liu, Q.-S., Zhang, Z.-Y., Zhang,R.-G., and Huang, C.-X.: Dynamical Analysis and Exact Solutions of a New (2+1)-Dimensional Generalized Boussinesq Model Equation for Nonlinear Rossby Waves, Communication Theoretical Physics, 71, 1054–1062, https://ctp.itp.ac.cn/EN/abstract/abstract17542.shtml (last access: 17 September 2025), 2019.
Lü, X. and Ma, W. X. : Study of lump dynamics based on a dimensionally reduced Hirota bilinear equation, Nonlinear Dynamics, 85, 1217–1222, https://doi.org/10.1007/s11071-016-2755-8, 2016.
Lü, X., Chen, S. T., and Ma, W. X.: Constructing lump solutions to a generalized Kadomtsev–Petviashvili–Boussinesq equation, Nonlinear Dynamics, 86, 523–534, https://doi.org/10.1007/s11071-016-2905-z, 2016.
Ma, W. X. and Chen, M.: Direct search for exact solutions to the nonlinear Schrödinger equation, Applied Mathematics and Computation, 215, 2835–2842, https://doi.org/10.1016/j.amc.2009.09.024, 2009.
Ma, W. X. and Fuchssteiner, B.: Explicit and exact solutions to a Kolmogorov-Petrovskii-Piskunov equation, International Journal of Non-Linear Mechanics, 31, 329–338, https://doi.org/10.1016/0020-7462(95)00064-X, 1996.
Ma, W. X. and Lee, J. H.: A transformed rational function method and exact solutions to the 3+1 dimensional Jimbo–Miwa equation. Chaos, Solitons and Fractals, 42, 1356–1363, https://doi.org/10.1016/j.chaos.2009.03.043, 2009.
Ma, W. X. and You, Y.: Solving the Korteweg-de Vries equation by its bilinear form: Wronskian solutions, Transactions of the American mathematical society, 357, 1753–1778, https://doi.org/10.1090/S0002-9947-04-03726-2, 2005.
Ma, W. X. and Zhu, Z.: Solving the (3+1)-dimensional generalized KP and BKP equations by the multiple exp-function algorithm, Applied Mathematics and Computation, 218, 11871–11879, https://doi.org/10.1016/j.amc.2012.05.049, 2012.
Manafian, J. and Aghdaei, M. F.: Abundant soliton solutions for the coupled Schrödinger-Boussinesq system via an analytical method, The European Physical Journal Plus, 131, 97, https://doi.org/10.1140/epjp/i2016-16097-3, 2016.
Miao, X. J. and Zhang, Z. Y.: The modified G′G-expansion method and traveling wave solutions of nonlinear the perturbed nonlinear Schrödinger's equation with Kerr law nonlinearity, Communications in Nonlinear Science and Numerical Simulation, 16, 4259–4267, https://doi.org/10.1016/j.cnsns.2011.03.032, 2011.
Mitsotakis, D. E.: Boussinesq systems in two space dimensions over a variable bottom for the generation and propagation of tsunami waves, Mathematics and Computers in Simulation, 80, 860–873, https://doi.org/10.1016/j.matcom.2009.08.029, 2009.
Onishchenko, O. G., Pokhotelov, O. A., Sagdeev, R. Z., Shukla, P. K., and Stenflo, L.: Generation of zonal flows by Rossby waves in the atmosphere, Nonlin. Process. Geophys., 11, 241–244, https://doi.org/10.5194/npg-11-241-2004, 2004.
Pedlosky, J.: Geophysical fluid dynamics, Vol. 710, New York, Springer, https://doi.org/10.1007/978-1-4612-4650-3, 1987.
Qiang, Z., Zuntao, F., and Shikuo, L.: Equatorial envelope Rossby solitons in a shear flow, Adv. Atmos. Sci., 18, 418–428, https://doi.org/10.1007/BF02919321, 2001.
Satoh, M.: Atmospheric Circulation Dynamics and General Circulation Models, Springer, New York, https://doi.org/10.1007/978-3-642-13574-3, 2004.
Sharadze, Z. S.: Phenomena in the middle-latitude ionosphere, PhD Thesis, Moscow, 1991.
Sharadze, Z. S., Japaridze, G. A., Kikvilashvili, G. B., and Liadze, Z. L.: Wave disturbances of non-acoustical nature in the middle-latitude ionosphere, Geomagn. Aeronomy, 28, 446–451, 1988 (in Russian).
Shukla, P. K. and Stenflo, L.: Generation of zonal flows by Rossby waves, Phys. Lett. A, 307, 154–157, https://doi.org/10.1016/S0375-9601(02)01675-4, 2003.
Song, J. and Yang, L. G.: Classical Areas of Phenomenology: Modified KdV equation for solitary Rossby waves with β effect in barotropic fluids, Chinese Physics B, 18, 2873–2877, https://doi.org/10.1088/1674-1056/18/7/042, 2009.
Tasbozan, O., Çenesiz, Y., and Kurt, A.: New solutions for conformable fractional Boussinesq and combined KdV-mKdV equations using Jacobi elliptic function expansion method, The European Physical Journal Plus, 131, 1–14, https://doi.org/10.1140/epjp/i2016-16244-x, 2016.
Uddin, M.: On the selection of a good value of shape parameter in solving time-dependent partial differential equations using RBF approximation method, Applied Mathematical Modelling, 38, 135–144, https://doi.org/10.1016/j.apm.2013.05.060, 2014.
Vukcevic, M. and Popovic, L. Č.: Solitons in the ionosphere- Advantages and perspectives, Proceedings of the XII Serbian-Bulgarian Astronomical Conference, (XII SBAC) Sokobanja, Serbia, 25–29 September 2020, edited by: Popović, L. Č., Srećković, V. A., Dimitrijević, M. S., and Kovačević, A., Publ. Astron. Soc. “Rudjer Bošković”, 20, 85–91, https://doi.org/10.3390/app11167194, 2020.
Wang, H. and Yan, G.: Lattice Boltzmann model for the interaction of (2+1)-dimensional solitons in generalized Gross–Pitaevskii equation, Applied Mathematical Modelling, 40, 5139–5152, https://doi.org/10.1016/j.apm.2015.12.035, 2016.
Wazwaz, A. M.: Exact solutions with solitons and periodic structures for the Zakharov–Kuznetsov (ZK) equation and its modified form, Communications in Nonlinear Science and Numerical Simulation, 10, 597–606, https://doi.org/10.1016/j.cnsns.2004.03.001, 2005.
Yang, H. W., Xu, Z. H., Yang, D. Z., Feng, X. R., Yin, B. S., and Dong, H. H.: ZK-Burgers equation for three-dimensional Rossby solitary waves and its solutions as well as chirp effect, Advances in Difference Equations, 1–22, https://doi.org/10.1186/s13662-016-0901-8, 2016.
Yang, H. W., Chen, X., Guo, M., and Chen, Y. D.: A new ZK–BO equation for three-dimensional algebraic Rossby solitary waves and its solution as well as fission property, Nonlinear Dynamics, 91, 2019–2032, https://doi.org/10.1007/s11071-017-4000-5, 2018.
Zakharov, V. E. and Kuznetsov, E. A.: On three dimensional solitons, Zhurnal Eksp. Teoret. Fiz, 66, 594–597, 1974.
Zhang, R., Yang, L., Song, J., and Liu, Q.: (2+1)-Dimensional nonlinear Rossby solitary waves under the effects of generalized beta and slowly varying topography, Nonlinear Dynamics, 90, 815–822, https://doi.org/10.1007/s11071-017-3694-8, 2017a.
Zhang, R., Yang, L., Song, J., and Yang, H.: (2+1) dimensional Rossby waves with complete Coriolis force and its solution by homotopy perturbation method, Computers and Mathematics with Applications, 73, 1996–2003, https://doi.org/10.1016/j.camwa.2017.02.036, 2017b.
Zhang, Z. Y., Liu, Z. H., Miao, X. J., and Chen, Y. Z.: New exact solutions to the perturbed nonlinear Schrödinger's equation with Kerr law nonlinearity, Applied Mathematics and Computation, 216, 3064–3072, https://doi.org/10.1016/j.amc.2010.04.026, 2010.
Zhang, Z. Y., Li, Y. X., Liu, Z. H., and Miao, X. J.: New exact solutions to the perturbed nonlinear Schrödinger's equation with Kerr law nonlinearity via modified trigonometric function series method, Communications in Nonlinear Science and Numerical Simulation, 16, 3097–3106, https://doi.org/10.1016/j.cnsns.2010.12.010, 2011.
Zhang, Z. Y., Gan, X. Y., Yu, D. M., Zhang, Y. H., and Li, X. P.: A note on exact traveling wave solutions of the perturbed nonlinear Schrödinger's equation with Kerr law nonlinearity, Communications in Theoretical Physics, 57, 764, https://doi.org/10.1088/0253-6102/57/5/05, 2012.
Zhang, Z., Huang, J., Zhong, J., Dou, S. S., Liu, J., Peng, D., and Gao, T.: The extended ()-expansion method and travelling wave solutions for the perturbed nonlinear Schrödinger's equation with Kerr law nonlinearity, Pramana, 82, 1011–1029, https://doi.org/10.1007/s12043-014-0747-0, 2014.
- Abstract
- Introduction
- Mathematical Preliminaries
- Perturbation and weakly nonlinear approach
- Derivation for the nonlinear Boussinesq Equation
- Dynamical Analysis for the New Boussinesq equation
- Solution for the Boussinesq equation
- Discussion
- Summary and conclusion
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Review statement
- References
- Abstract
- Introduction
- Mathematical Preliminaries
- Perturbation and weakly nonlinear approach
- Derivation for the nonlinear Boussinesq Equation
- Dynamical Analysis for the New Boussinesq equation
- Solution for the Boussinesq equation
- Discussion
- Summary and conclusion
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Review statement
- References