Study of temperature anisotropy and kappa distribution impacts on EMIC waves in multi-species magnetized plasma

This research investigates the impact of temperature anisotropy on electromagnetic ion cyclotron (EMIC) waves in a multi-ion magneto-plasma environment composed of H⁺, He⁺, and O⁺ ions, with a particular emphasis on the role of the kappa distribution function. The study delves into how variations in temperature anisotropy influence the behavior and properties of EMIC wave propagation, considering the complex interplay between anisotropic thermal effects and the non-Maxwellian kappa distribution. Through a comprehensive analysis involving theoretical modeling and numerical simulations, the research elucidates how these factors alter wave dispersion relations, growth rates, and spatial structures of EMIC waves. The results reveal significant deviations from classical Maxwellian predictions, highlighting the necessity of incorporating kappa distributions for accurate descriptions of wave behavior in realistic plasma conditions. This enhanced understanding has broader implications for space physics, astrophysical phenomena, and laboratory plasma experiments, where non-equilibrium conditions and multiple ion species are prevalent. The results are analyzed in the context of the space-plasma-parameter-relevant region within Earth's magnetosphere.

1 Introduction

Electromagnetic ion cyclotron (EMIC) waves are transverse, low-frequency (below the proton cyclotron frequency) waves typically in the range of 0.1–5 Hz, which manifest as Pc1–Pc2 pulsations on the ground. These waves are primarily generated in the equatorial region of Earth's magnetosphere and propagate along magnetic field lines as left-handed, circularly polarized waves, guided toward the ionosphere (Sugiyama et al., 2015). Their oblique propagation characteristics and interactions with anisotropic plasma distributions have been extensively studied (Cattaert et al., 2007). Experimental evidence for naturally occurring ion cyclotron instabilities has been comprehensively summarized by Cornwall (1965).

In the auroral acceleration region, located at magnetic latitudes of approximately ±70° and altitudes above 4000 km, large-amplitude electric field structures have been observed. The parallel electric fields in this region, concentrated around 6000 km altitude, are strongly associated with field-aligned currents (Yan et al., 2008). This region is characterized by low plasma beta (β) and cold plasma environments, making it a critical zone for understanding wave–particle interactions. EMIC waves play a vital role in space plasma physics, particularly in the Earth's magnetosphere, where they influence particle dynamics, energy transfer, and plasma stability (Gary and Lee, 1994). These waves interact with energetic particles, drive pitch-angle scattering, and facilitate the heating of ion populations, making them a cornerstone of magnetospheric studies (Kennel and Petschek, 1966; Chen and Hasegawa, 1974). The triggered emissions associated with EMIC waves have been observed in satellite data and analyzed in theoretical studies (Omura et al., 2010).

The propagation of EMIC waves at frequencies near the ion cyclotron frequency has been extensively studied under the assumption of Maxwellian velocity distributions, which describe thermal plasmas. However, real plasma environments, especially in the magnetosphere, often deviate from thermal equilibrium due to the presence of suprathermal particles (Sugiyama et al., 2015). The kappa distribution function (Vasyliunas, 1968) is widely used to describe such non-thermal plasma environments. It is characterized by the parameter which governs the extent of high-energy tails in the particle velocity distribution. Lower kappa values correspond to stronger deviations from thermal equilibrium, making the kappa distribution particularly relevant for modeling space plasmas where suprathermal particles dominate (Pierrard and Lazar, 2010). A generalized plasma dispersion function for kappa-Maxwellian velocity distributions has been formulated to describe the wave behavior in these conditions (Hellberg and Mace, 2002).

Temperature anisotropy, where the temperature differs along directions parallel and perpendicular to the magnetic field, further adds complexity to the plasma environment. This anisotropy significantly influences wave growth, dispersion characteristics, and stability. In anisotropic magneto-plasma, enhanced perpendicular temperatures relative to the parallel component can amplify EMIC wave growth and alter dispersion relations compared to isotropic conditions (Hellinger and Matsumoto, 2000). When coupled with the kappa distribution, temperature anisotropy introduces novel wave behaviors and complexities that deviate significantly from Maxwellian models (Lazar et al., 2006). The effects of temperature anisotropy on wave growth have been observed in bi-kappa-distributed plasmas, where deviations from Maxwellian distributions further modify wave dispersion (Lazar, 2012). The influence of suprathermal protons on EMIC wave instability thresholds has also been examined in kappa-distributed plasmas (Xiao et al., 2007).

Despite extensive research on plasma instabilities, a significant gap remains in understanding how temperature anisotropy and kappa distributions simultaneously affect EMIC wave dynamics. The novelty of this study lies in addressing this critical gap by examining how temperature anisotropy influences the dispersion relations, growth rates, and spatial structures of EMIC waves in a multi-ion magneto-plasma under the influence of the kappa distribution. Unlike earlier works that focused predominantly on single-ion plasmas or isotropic temperature assumptions, this research emphasizes the role of multi-ion plasma composition (e.g., H⁺, He⁺, O⁺) and varying kappa values, which are particularly relevant for understanding wave–particle interactions near the plasmapause and auroral acceleration regions. Previous studies have demonstrated how EMIC waves grow and dampen under different conditions, including oblique propagation and multi-ion species effects (Xue et al., 1996a, b).

This study investigates the combined effects of temperature anisotropy and the kappa distribution on EMIC wave dynamics, focusing on perpendicular and parallel resonant energies, growth rate, and growth length in a multi-ion plasma environment. By incorporating these complex plasma conditions, we aim to advance the accuracy of space plasma models, particularly within the magnetosphere, where these factors are paramount. The findings hold significant implications for space weather forecasting and the mitigation of associated disturbances, given the influence of EMIC waves on particle precipitation, ion heating, and geomagnetic activity. By quantifying the individual and combined impact of the kappa distribution and temperature anisotropy, this research provides deeper insights into EMIC wave behavior, enhancing our understanding of wave–particle interactions in space plasmas and thereby improving the interpretation of satellite data.

2 Basic trajectories

Considering the trajectory of a charged particle in the presence of EMIC waves, various properties have been derived for different kappa distribution indices (Meda and Ahirwar, 2021). Given that the wave propagates along the z axis in the direction of the background magnetic field, the left-handed circularly polarized EMIC wave in a cold magnetized plasma with angular frequency ω can be expressed as follows:

$$\begin{array}{}\text{(1)}& {\displaystyle }{B}_x=\cos (k_{\mathrm{\Pi }l}z-\mathit{\omega }t),\text{(2)}& {\displaystyle }{B}_y=\sin (k_{\mathrm{\Pi }l}z-\mathit{\omega }t).\end{array}$$

When the system moves with the wave, the electric field reduces to zero. The total wave magnetic field is

$$\begin{array}{}\text{(3)}& B=B_x\cos \left(k_{\mathrm{\Pi }l}\mathrm{z}\right)x+B_y\sin \left(k_{\mathrm{\Pi }l}\mathrm{z}\right)y,\end{array}$$

where B is the wave magnetic field amplitude, k_Πl is the wave number along the z axis, and ω is angular frequency.

In the wave frame, moving with phase velocity, the position and velocity transformations are (Meda and Ahirwar, 2021)

$$\begin{array}{}\text{(4)}& {\displaystyle }{Z}^{\mathrm{wave}}=Z^{\mathrm{lab}}-\left({\displaystyle \frac{\mathit{\omega }}{k_{\mathrm{\Pi }l}}}\right)t,\text{(5)}& {\displaystyle }{V}^{\mathrm{wave}}=V^{\mathrm{lab}}-\left({\displaystyle \frac{\mathit{\omega }}{k}}\right)t.\end{array}$$

As $\frac{ck}{\mathit{\omega }}\gg \mathrm{1},$ the magnetic field amplitude is assumed to be identical in both the laboratory and wave frames. Z^wave is the position of the particle in the wave frame of reference. V^wave is the position of the particle in the laboratory frame of reference.

Thus, the equation of motion for an ion in the presence of the wave is given by

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{d{v}_l}{dt}}={\displaystyle \frac{q_{\mathrm{l}}}{m_{\mathrm{l}}c}}\left[\left(V_l\times B_O\right)+\left(V_l\times B\right)\right],\end{array}$$

where q_l is the ion charge, m_l is the ion mass, c is the speed of light, B_O is the background magnetic field, and B is the wave magnetic field.

We use cylindrical coordinates in velocity space as follows:

$$\begin{array}{}\text{(7)}& {\displaystyle }{v}_{lx}=V_{\perp l}\cos \mathit{\varphi },\text{(8)}& {\displaystyle }{v}_{ly}=V_{\perp l}\sin \mathit{\varphi },\text{(9)}& {\displaystyle }{v}_{\perp lz}=V_{\mathrm{\Pi }l},\end{array}$$

where V_⊥l is the perpendicular velocity magnitude, V_Πl is the parallel velocity, ϕ is the gyrophase angle, and Π means parallel to the magnetic field; it refers to the component of velocity along the background magnetic field direction. The perpendicular component of the equation of motion is

$$\begin{array}{}\text{(10)}& {\displaystyle \frac{\mathrm{d}{V}_{\perp l}}{\mathrm{d}t}}=-V_{\mathrm{\Pi }l}{\mathrm{\Omega }}_l\sin (k_{\mathrm{\Pi }}z-\mathit{\varphi }),\text{(11)}& {\displaystyle }{V}_{\perp l}=V_{\mathrm{\Pi }lo}+V_l,\text{(12)}& {\displaystyle }{V}_{\mathrm{\Pi }l}=V_{lo}+\mathit{\delta }{V}_{\mathrm{\Pi }l},\end{array}$$

where V_Πi represents initial values at t=0. Substituting Eqs. (1) to (5) in Eqs. (11) and (12) we find the following perturbations in perpendicular and parallel velocities due to the EMIC wave (Meda and Ahirwar, 2021).

$$\begin{array}{}\text{(13)}& {\displaystyle }\begin{array}{rl}\mathit{\delta }{V}_{\perp l}& ={\displaystyle \frac{\left[h{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}\right(V_{\mathrm{\Pi }{\mathrm{H}}^{+}}-\frac{\mathit{\omega }}{\mathrm{\Pi }K}\left)\right]}{[k_{\mathrm{\Pi }}{V}_{\mathrm{\Pi }{\mathrm{H}}^{+}o}-(\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}\left)\right]}}\\ & \times \left[\cos \right(k_{\mathrm{\Pi }l}z-\mathit{\omega }t-\mathrm{\Psi })-\mathit{\epsilon }\cos (k_{\mathrm{\Pi }l}z-\mathit{\omega }t-\mathrm{\Psi }-\\ & (k_{\mathrm{\Pi }l}{V}_{\mathrm{\Pi }{\mathrm{H}}^{+}o}-(\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}\left)\right)t]+{\displaystyle \frac{\left[h{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}\right(V_{\mathrm{\Pi }{\mathrm{He}}^{+}}-\frac{\mathit{\omega }}{K_{\mathrm{\Pi }}}\left)\right]}{[k_{\mathrm{\Pi }}{V}_{\mathrm{\Pi }{\mathrm{He}}^{+}o}-(\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}\left)\right]}}\\ & \times \left[\cos \right(k_{\mathrm{\Pi }l}z-\mathit{\omega }t-\mathrm{\Psi })-\mathit{\epsilon }\cos (k_{\mathrm{\Pi }l}z-\mathit{\omega }t-\mathrm{\Psi }-\\ & (k_{\mathrm{\Pi }l}{V}_{\mathrm{\Pi }{\mathrm{He}}^{+}o}-(\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}\left)\right)t]+{\displaystyle \frac{\left[h{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}\right(V_{\mathrm{\Pi }{\mathrm{O}}^{+}}-\frac{\mathit{\omega }}{K}\left)\right]}{[k_{\mathrm{\Pi }}{V}_{\mathrm{\Pi }{\mathrm{O}}^{+}o}-(\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}\left)\right]}}\\ & \times \left[\cos \right(k_{\mathrm{\Pi }l}z-\mathit{\omega }t-\mathrm{\Psi })-\mathit{\epsilon }\cos (k_{\mathrm{\Pi }l}z-\mathit{\omega }t\\ & -\mathrm{\Psi }-(k_{\mathrm{\Pi }l}{V}_{{\mathrm{O}}^{+}o}-(\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}\left)\right)t]\end{array}\text{(14)}& {\displaystyle }\begin{array}{rl}\mathit{\delta }{V}_{\mathrm{\Pi }l}& ={\displaystyle \frac{-h{V}_{\perp o}{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}}{[k_{\mathrm{\Pi }}{V}_{\mathrm{\Pi }{\mathrm{H}}^{+}o}-(\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}\left)\right]}}\times \left[\cos \right(k_{\mathrm{\Pi }}z-\mathit{\omega }t-\mathrm{\Psi })\\ & -\mathit{\epsilon }\cos (k_{\mathrm{\Pi }}z-\mathit{\omega }t-\mathrm{\Psi }-(k_{\mathrm{\Pi }}{V}_{\mathrm{\Pi }{\mathrm{H}}^{+}o}-(\mathit{\omega }-{\mathrm{\Omega }}_l)\left)t\right]\\ & +{\displaystyle \frac{-h{V}_{\perp o}{\mathrm{\Omega }}_v{\mathrm{H}}^{+}}{[k_{\mathrm{\Pi }}{V}_{\mathrm{\Pi }{\mathrm{He}}^{+}o}-(\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}\left)\right]}}\times \left[\cos \right(k_{\mathrm{\Pi }}z-\mathit{\omega }t-\mathrm{\Psi })\\ & -\mathit{\epsilon }\cos (k_{\mathrm{\Pi }}z-\mathit{\omega }t-\mathrm{\Psi }-(k_{\mathrm{\Pi }}{V}_{\mathrm{\Pi }{\mathrm{He}}^{+}o}-(\mathit{\omega }-{\mathrm{\Omega }}_l)\left)t\right]\\ & +{\displaystyle \frac{-h{V}_{\perp o}{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}}{[k_{\mathrm{\Pi }}{V}_{\mathrm{\Pi }{\mathrm{O}}^{+}o}-(\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}\left)\right]}}\times \left[\cos \right(k_{\mathrm{\Pi }}z-\mathit{\omega }t-\mathrm{\Psi })\\ & -\mathit{\epsilon }\cos (k_{\mathrm{\Pi }}z-\mathit{\omega }t-\mathrm{\Psi }-(k_{\mathrm{\Pi }}{V}_{{\mathrm{O}}^{+}o}-(\mathit{\omega }-{\mathrm{\Omega }}_l)\left)t\right]\end{array}\end{array}$$

Here, $z=z_{\mathrm{0}}+V_{\mathrm{\Pi }}t$ and $\mathit{\psi }={\mathit{\psi }}_{\mathrm{0}}-\mathit{\omega }t$, where ε= 0 for non-resonant particles and ε= 1 for resonant particles, and $h=\frac{B}{B_{\mathrm{0}}}$, where $l={\mathrm{H}}^{+}/{\mathrm{He}}^{+}/{\mathrm{O}}^{+}$.

3 Distribution function

To examine resonant and non-resonant energies, growth rates, and growth lengths, we apply a kappa distribution function as an extension within a multi-ion magneto-plasma environment of previous work (Meda and Ahirwar, 2021; Livadiotis, 2017; Summers and Thorne, 1991).

$$\begin{array}{}\text{(15)}& \begin{array}{rl}{F}_k\left(V_l\right)& ={\displaystyle \frac{\mathrm{1}}{{\mathit{\pi }}^{\mathrm{3}/\mathrm{2}}{V}_{\perp {\mathrm{H}}^{+}}^{\mathrm{2}}{V}_{\mathrm{\Pi }{\mathrm{H}}^{+}}^{\mathrm{2}}}}{\displaystyle \frac{\mathrm{\Gamma }\left(k_{\mathrm{p}}+\mathrm{1}\right)}{k_{\mathrm{p}}^{\mathrm{3}/\mathrm{2}}\mathrm{\Gamma }\left(k_{\mathrm{p}}-\mathrm{1}/\mathrm{2}\right)}}\\ & \times {\left\{\mathrm{1}+{\displaystyle \frac{V_{\mathrm{\Pi }{\mathrm{H}}^{+}}^{\mathrm{2}}}{k_{\mathrm{p}}{V}_{\perp {\mathrm{H}}^{+}}^{\mathrm{2}}}}+{\displaystyle \frac{V_{\perp {\mathrm{H}}^{+}}^{\mathrm{2}}}{k_{\mathrm{p}}{V}_{T\perp {\mathrm{H}}^{+}}^{\mathrm{2}}}}\right\}}^{-k_{\mathrm{p}}-\mathrm{1}}\\ & +{\displaystyle \frac{\mathrm{1}}{{\mathit{\pi }}^{\mathrm{3}/\mathrm{2}}{V}_{\perp {\mathrm{He}}^{+}}^{\mathrm{2}}{V}_{\mathrm{\Pi }{\mathrm{He}}^{+}}^{\mathrm{2}}}}{\displaystyle \frac{\mathrm{\Gamma }\left(k_{\mathrm{p}}+\mathrm{1}\right)}{k_{\mathrm{p}}^{\mathrm{3}/\mathrm{2}}\mathrm{\Gamma }\left(k_{\mathrm{p}}-\mathrm{1}/\mathrm{2}\right)}}\\ & \times {\left\{\mathrm{1}+{\displaystyle \frac{V_{\mathrm{\Pi }{\mathrm{He}}^{+}}^{\mathrm{2}}}{k_{\mathrm{p}}{V}_{\perp {\mathrm{He}}^{+}}^{\mathrm{2}}}}+{\displaystyle \frac{V_{\perp {\mathrm{He}}^{+}}^{\mathrm{2}}}{k_{\mathrm{p}}{V}_{T\perp {\mathrm{He}}^{+}}^{\mathrm{2}}}}\right\}}^{-k_{\mathrm{p}}-\mathrm{1}}\\ & +{\displaystyle \frac{\mathrm{1}}{{\mathit{\pi }}^{\mathrm{3}/\mathrm{2}}{V}_{\perp {\mathrm{O}}^{+}}^{\mathrm{2}}{V}_{\mathrm{\Pi }{\mathrm{O}}^{+}}^{\mathrm{2}}}}{\displaystyle \frac{\mathrm{\Gamma }\left(k_{\mathrm{p}}+\mathrm{1}\right)}{k_{\mathrm{p}}^{\mathrm{3}/\mathrm{2}}\mathrm{\Gamma }\left(k_{\mathrm{p}}-\mathrm{1}/\mathrm{2}\right)}}\\ & \times {\left\{\mathrm{1}+{\displaystyle \frac{V_{\mathrm{\Pi }{\mathrm{O}}^{+}}^{\mathrm{2}}}{k_{\mathrm{p}}{V}_{\perp {\mathrm{O}}^{+}}^{\mathrm{2}}}}+{\displaystyle \frac{V_{\perp {\mathrm{O}}^{+}}^{\mathrm{2}}}{k_{\mathrm{p}}{V}_{T\perp {\mathrm{O}}^{+}}^{\mathrm{2}}}}\right\}}^{-k_{\mathrm{p}}-\mathrm{1}}\end{array}\end{array}$$

$$l={\mathrm{H}}^{+}/{\mathrm{He}}^{+}/{\mathrm{O}}^{+}.$$

k_p is the kappa distribution index.

The bi-kappa distribution at resonance velocity is implemented as follows (Meda and Ahirwar, 2021; Livadiotis, 2017; Summers and Thorne, 1991).

$$\begin{array}{}\text{(16)}& \begin{array}{rl}{F}_k\left(V_{\mathrm{\Pi }l}\right)& ={\displaystyle \frac{\mathrm{1}}{{\mathit{\pi }}^{\mathrm{1}/\mathrm{2}}{V}_{T\mathrm{\Pi }{\mathrm{H}}^{+}}^{\mathrm{2}}}}{\displaystyle \frac{\mathrm{\Gamma }\left(k_{\mathrm{p}}+\mathrm{1}\right)}{k_{\mathrm{p}}^{\mathrm{3}/\mathrm{2}}\mathrm{\Gamma }\left(k_{\mathrm{p}}-\mathrm{1}/\mathrm{2}\right)}}\\ & {\left\{\mathrm{1}+{\displaystyle \frac{V_{\mathrm{\Pi }{\mathrm{H}}^{+}}^{\mathrm{2}}(\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}{)}^{\mathrm{2}}}{K_{\mathrm{\Pi }}{V}_{T\mathrm{\Pi }{\mathrm{H}}^{+}}^{\mathrm{2}}}}\right\}}^{-k_{\mathrm{p}}-\mathrm{1}}\\ & +{\displaystyle \frac{\mathrm{1}}{{\mathit{\pi }}^{\mathrm{1}/\mathrm{2}}{V}_{T\mathrm{\Pi }{\mathrm{He}}^{+}}^{\mathrm{2}}}}{\displaystyle \frac{\mathrm{\Gamma }(k_{\mathrm{p}}+\mathrm{1})}{k_{\mathrm{p}}^{\mathrm{3}/\mathrm{2}}\mathrm{\Gamma }(k_{\mathrm{p}}-\mathrm{1}/\mathrm{2})}}\\ & \times {\left\{\mathrm{1}+{\displaystyle \frac{V_{\mathrm{\Pi }{\mathrm{He}}^{+}}^{\mathrm{2}}(\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}{)}^{\mathrm{2}}}{K_{\mathrm{\Pi }}{V}_{T\mathrm{\Pi }{\mathrm{He}}^{+}}^{\mathrm{2}}}}\right\}}^{-k_{\mathrm{p}}-\mathrm{1}}\\ & +{\displaystyle \frac{\mathrm{1}}{{\mathit{\pi }}^{\mathrm{1}/\mathrm{2}}{V}_{T\mathrm{\Pi }{\mathrm{O}}^{+}}^{\mathrm{2}}}}{\displaystyle \frac{\mathrm{\Gamma }(k_{\mathrm{p}}+\mathrm{1})}{k_{\mathrm{p}}^{\mathrm{3}/\mathrm{2}}\mathrm{\Gamma }(k_{\mathrm{p}}-\mathrm{1}/\mathrm{2})}}\\ & \times {\left\{\mathrm{1}+{\displaystyle \frac{V_{\mathrm{\Pi }{\mathrm{O}}^{+}}^{\mathrm{2}}(\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}{)}^{\mathrm{2}}}{K_{\mathrm{\Pi }}{V}_{T\mathrm{\Pi }{\mathrm{O}}^{+}}^{\mathrm{2}}}}\right\}}^{-k_{\mathrm{p}}-\mathrm{1}}\end{array}\end{array}$$

In the above equation $V_{T\perp l}^{\mathrm{2}}$ and $V_{T\mathrm{\Pi }l}^{\mathrm{2}}$ are thermal velocity.

$$\begin{array}{}\text{(17)}& {\displaystyle }\begin{array}{rl}{V}_{T\perp l}^{\mathrm{2}}& =\left[{\displaystyle \frac{k_{\mathrm{p}}-\mathrm{3}/\mathrm{2}}{k}}{\displaystyle \frac{\mathrm{2}{k}_{\mathrm{p}}{T}_{\perp {\mathrm{H}}^{+}}}{m_{{\mathrm{H}}^{+}}}}\right]+\left[{\displaystyle \frac{k_{\mathrm{p}}-\mathrm{3}/\mathrm{2}}{k}}{\displaystyle \frac{\mathrm{2}{k}_{\mathrm{p}}{T}_{\perp {\mathrm{He}}^{+}}}{m_{{\mathrm{He}}^{+}}}}\right]\\ & +\left[{\displaystyle \frac{k_{\mathrm{p}}-\mathrm{3}/\mathrm{2}}{k}}{\displaystyle \frac{\mathrm{2}{k}_{\mathrm{p}}{T}_{\perp {\mathrm{O}}^{+}}}{m_{{\mathrm{O}}^{+}}}}\right]\end{array}\text{(18)}& {\displaystyle }\begin{array}{rl}{V}_{T\mathrm{\Pi }l}^{\mathrm{2}}& =\left[{\displaystyle \frac{k_{\mathrm{p}}-\mathrm{3}/\mathrm{2}}{k_{\mathrm{p}}}}{\displaystyle \frac{\mathrm{2}{k}_{\mathrm{p}}{T}_{\mathrm{\Pi }{\mathrm{H}}^{+}}}{m_{{\mathrm{H}}^{+}}}}\right]+\left[{\displaystyle \frac{k_{\mathrm{p}}-\mathrm{3}/\mathrm{2}}{k_{\mathrm{p}}}}{\displaystyle \frac{\mathrm{2}{k}_{\mathrm{p}}{T}_{\mathrm{\Pi }{\mathrm{He}}^{+}}}{m_{{\mathrm{He}}^{+}}}}\right]\\ & +\left[{\displaystyle \frac{k_{\mathrm{p}}-\mathrm{3}/\mathrm{2}}{k_{\mathrm{p}}}}{\displaystyle \frac{\mathrm{2}{k}_{\mathrm{p}}{T}_{\mathrm{\Pi }{\mathrm{O}}^{+}}}{m_{{\mathrm{O}}^{+}}}}\right]\end{array}\end{array}$$

The kappa distribution function is represented as follows (Summers and Thorne, 1991).

$$\begin{array}{}\text{(19)}& Z_k\left(\mathit{\xi }\right)={\displaystyle \frac{\mathrm{1}}{{\mathit{\pi }}^{\mathrm{1}/\mathrm{2}}{k}_{\mathrm{p}}^{\mathrm{1}/\mathrm{2}}}}{\displaystyle \frac{\mathrm{\Gamma }\left(k_{\mathrm{p}}+\mathrm{1}\right)}{\mathrm{\Gamma }\left(k_{\mathrm{p}}-\mathrm{1}/\mathrm{2}\right)}}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\displaystyle \frac{{\left(\mathrm{1}+\frac{x^{\mathrm{2}}}{k_{\mathrm{p}}}\right)}^{-k_{\mathrm{p}}}\mathrm{d}x}{\left(x-\mathit{\xi }\right)}}\end{array}$$

$$\mathit{\xi }={\displaystyle \frac{\left(\mathit{\omega }-{\mathrm{\Omega }}_l\right)}{K_{\mathrm{\Pi }}{V}_{T\mathrm{\Pi }l}}}$$

In cases where the perpendicular temperature exceeds the parallel temperature, free energy stored in this anisotropy can drive wave instabilities, leading to the amplification of EMIC waves. The condition for instability is typically expressed as

$${\displaystyle \frac{T_{\perp }}{T_{\parallel }}}=\mathrm{1}+{\displaystyle \frac{\mathit{\omega }}{{\mathrm{\Omega }}_i}}.$$

As reported in the study by Gary and Wang (1996), temperature anisotropy significantly impacts the growth rate and modifies the dispersion properties of EMIC waves. The difference between perpendicular and parallel temperatures in the plasma introduces a source of free energy, which can either enhance or suppress wave propagation. When the anisotropy is sufficiently large, it can destabilize certain wave modes, causing them to grow under specific conditions.

4 Dispersion relation

Consider the cold plasma dispersion relation for EMIC waves (Ahirwar et al., 2006):

$$\begin{array}{}\text{(20)}& \begin{array}{rl}{\displaystyle \frac{c^{\mathrm{2}}{k}_{\mathrm{\Pi }}^{\mathrm{2}}}{{\mathit{\omega }}^{\mathrm{2}}}}& =\left({\displaystyle \frac{{\mathit{\omega }}_{{\mathrm{pH}}^{+}}^{\mathrm{2}}}{{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}^{\mathrm{2}}}}\right){\left(\mathrm{1}-{\displaystyle \frac{\mathit{\omega }}{{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}}}\right)}^{-\mathrm{1}}\\ & +\left({\displaystyle \frac{{\mathit{\omega }}_{p{\mathrm{He}}^{+}}^{\mathrm{2}}}{{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}^{\mathrm{2}}}}\right){\left(\mathrm{1}-{\displaystyle \frac{\mathit{\omega }}{{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}}}\right)}^{-\mathrm{1}}\\ & +\left({\displaystyle \frac{{\mathit{\omega }}_{p{\mathrm{O}}^{+}}^{\mathrm{2}}}{{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}^{\mathrm{2}}}}\right){\left(\mathrm{1}-{\displaystyle \frac{\mathit{\omega }}{{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}}}\right)}^{-\mathrm{1}},\end{array}\end{array}$$

where ${\mathit{\omega }}_{\mathrm{pl}}^{\mathrm{2}}=\frac{\mathrm{4}\mathit{\pi }{N}_l{e}^{\mathrm{2}}}{m_l}$.

This establishes the squared plasma frequency for the ions, while Ω_l represents the cyclotron frequency of the respective multi-ion species.

The dispersion relation for an ion electromagnetic cyclotron wave propagating along the direction of an external magnetic field in a system consisting of ions, electrons, and non-ionized particles including both resonant and non-resonant particles involved in electrical and wave transmission is described by the dispersion relation of cold plasma and is also close to the dispersion relation of hot plasma provided that plasma ck/ω≫1.

5 Wave energy for EMIC by kappa distribution function for multi-ion magneto-plasma

The perpendicular and parallel resonant energy for ions H⁺, He⁺ and O⁺ can be derived from the fundamental equation of wave energy per unit wavelength for a single ion species. Based on the study by Meda and Ahirwar (2021) (Kennel and Petschek, 1966), the expression for the perpendicular resonant energy for different ion species in a multi-ion plasma with a kappa distribution function is given as follows.

$$\begin{array}{}\text{(21)}& \begin{array}{rl}{W}_{r\perp l}& ={\displaystyle \frac{{\mathit{\pi }}^{\frac{\mathrm{3}}{\mathrm{2}}}{B}^{\mathrm{2}}}{C^{\mathrm{2}}{K}_{\mathrm{\Pi }}^{\mathrm{2}}\mathit{\omega }}}\left[{\displaystyle \frac{\mathrm{\Gamma }\left(k_{\mathrm{p}}+\mathrm{1}\right)}{k_{\mathrm{p}}^{\frac{\mathrm{3}}{\mathrm{2}}}\mathrm{\Gamma }\left(k_{\mathrm{p}}-\frac{\mathrm{1}}{\mathrm{2}}\right)V_{T\mathrm{\Pi }{\mathrm{H}}^{+}}^{\mathrm{2}}}}{\mathit{\omega }}_{{\mathrm{pH}}^{+}}^{\mathrm{2}}{\displaystyle \frac{T_{\perp }}{T_{\mathrm{\Pi }}}}\left({\displaystyle \frac{\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}}{{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}}}\right)+\mathrm{1}\right]\\ & {\left[\mathrm{1}+{\displaystyle \frac{{\left(\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}\right)}^{\mathrm{2}}}{K_{\mathrm{\Pi }}^{\mathrm{2}}{V}_{T\mathrm{\Pi }{\mathrm{H}}^{+}}^{\mathrm{2}}}}\right]}^{-k_{\mathrm{p}}-\mathrm{1}}+{\displaystyle \frac{{\mathit{\pi }}^{\mathrm{3}/\mathrm{2}}{B}^{\mathrm{2}}}{C^{\mathrm{2}}{K}_{\mathrm{\Pi }}^{\mathrm{2}}\mathit{\omega }}}\\ & \left[{\displaystyle \frac{\mathrm{\Gamma }\left(k_{\mathrm{p}}+\mathrm{1}\right)}{k_{\mathrm{p}}^{\mathrm{3}/\mathrm{2}}\mathrm{\Gamma }\left(k_{\mathrm{p}}-\mathrm{1}/\mathrm{2}\right)V_{T\mathrm{\Pi }{\mathrm{He}}^{+}}^{\mathrm{2}}}}{\mathit{\omega }}_{p{\mathrm{He}}^{+}}^{\mathrm{2}}{\displaystyle \frac{T_{\perp }}{T_{\mathrm{\Pi }}}}\left({\displaystyle \frac{\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}}{{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}}}\right)+\mathrm{1}\right]\\ & {\left[\mathrm{1}+{\displaystyle \frac{{\left(\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}\right)}^{\mathrm{2}}}{K_{\mathrm{\Pi }}^{\mathrm{2}}{V}_{T\mathrm{\Pi }{\mathrm{He}}^{+}}^{\mathrm{2}}}}\right]}^{-k_{\mathrm{p}}-\mathrm{1}}+{\displaystyle \frac{{\mathit{\pi }}^{\mathrm{3}/\mathrm{2}}{B}^{\mathrm{2}}}{C^{\mathrm{2}}{K}_{\mathrm{\Pi }}^{\mathrm{2}}\mathit{\omega }}}\\ & \left[{\displaystyle \frac{\mathrm{\Gamma }\left(k_{\mathrm{p}}+\mathrm{1}\right)}{k_{\mathrm{p}}^{\mathrm{3}/\mathrm{2}}\mathrm{\Gamma }\left(k_{\mathrm{p}}-\mathrm{1}/\mathrm{2}\right)V_{T\mathrm{\Pi }{\mathrm{O}}^{+}}^{\mathrm{2}}}}{\mathit{\omega }}_{p{\mathrm{O}}^{+}}^{\mathrm{2}}{\displaystyle \frac{T_{\perp }}{T_{\mathrm{\Pi }}}}\left({\displaystyle \frac{\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}}{{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}}}\right)+\mathrm{1}\right]\\ & {\left[\mathrm{1}+{\displaystyle \frac{{\left(\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}\right)}^{\mathrm{2}}}{K_{\mathrm{\Pi }}^{\mathrm{2}}{V}_{T\mathrm{\Pi }{O}^{+}}^{\mathrm{2}}}}\right]}^{-k_{\mathrm{p}}-\mathrm{1}}\end{array}\end{array}$$

Parallel resonant energy is as follows.

$$\begin{array}{}\text{(22)}& \begin{array}{rl}{W}_{r\mathrm{\Pi }l}& ={\displaystyle \frac{{\mathit{\pi }}^{\mathrm{3}/\mathrm{2}}{B}^{\mathrm{2}}}{C^{\mathrm{2}}{K}_{\mathrm{\Pi }}^{\mathrm{2}}\mathit{\omega }}}[{\displaystyle \frac{\mathrm{\Gamma }(k_{\mathrm{p}}+\mathrm{1})}{k_{\mathrm{p}}^{\mathrm{3}/\mathrm{2}}\mathrm{\Gamma }(k_{\mathrm{p}}-\mathrm{1}/\mathrm{2})V_{T\mathrm{\Pi }{\mathrm{H}}^{+}}^{\mathrm{2}}}}{\mathit{\omega }}_{{\mathrm{pH}}^{+}}^{\mathrm{2}}\\ & {\displaystyle \frac{T_{\perp l}}{T_{\mathrm{\Pi }l}}}\left({\displaystyle \frac{\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}}{{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}}}{)}^{\mathrm{2}}\right][\mathrm{1}+{\displaystyle \frac{(\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}{)}^{\mathrm{2}}}{K^{{\mathrm{2}}_{\mathrm{\Pi }}}{V}_{T\mathrm{\Pi }{\mathrm{H}}^{+}}^{\mathrm{2}}}}{]}^{-k_{\mathrm{p}}-\mathrm{1}}+{\displaystyle \frac{{\mathit{\pi }}^{\mathrm{3}/\mathrm{2}}{B}^{\mathrm{2}}}{C^{\mathrm{2}}{K}_{\mathrm{\Pi }}^{\mathrm{2}}\mathit{\omega }}}\\ & \left[{\displaystyle \frac{\mathrm{\Gamma }(k_{\mathrm{p}}+\mathrm{1})}{k_{\mathrm{p}}^{\mathrm{3}/\mathrm{2}}\mathrm{\Gamma }(k_{\mathrm{p}}-\mathrm{1}/\mathrm{2})V_{T\mathrm{\Pi }{\mathrm{He}}^{+}}^{\mathrm{2}}}}{\mathit{\omega }}_{p{\mathrm{He}}^{+}}^{\mathrm{2}}{\displaystyle \frac{T_{\perp l}}{T_{\mathrm{\Pi }l}}}\right({\displaystyle \frac{\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}}{{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}}}{)}^{\mathrm{2}}]\\ & [\mathrm{1}+{\displaystyle \frac{(\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}{)}^{\mathrm{2}}}{K_{\mathrm{\Pi }}^{\mathrm{2}}{V}_{T\mathrm{\Pi }{\mathrm{He}}^{+}}^{\mathrm{2}}}}{]}^{-k_{\mathrm{p}}-\mathrm{1}}+{\displaystyle \frac{{\mathit{\pi }}^{\mathrm{3}/\mathrm{2}}{B}^{\mathrm{2}}}{C^{\mathrm{2}}{K}_{\mathrm{\Pi }}^{\mathrm{2}}\mathit{\omega }}}\\ & \left[{\displaystyle \frac{\mathrm{\Gamma }(k_{\mathrm{p}}+\mathrm{1})}{k_{\mathrm{p}}^{\mathrm{3}/\mathrm{2}}\mathrm{\Gamma }(k_{\mathrm{p}}-\mathrm{1}/\mathrm{2})V_{T\mathrm{\Pi }{\mathrm{O}}^{+}}^{\mathrm{2}}}}{\mathit{\omega }}_{p{\mathrm{O}}^{+}}^{\mathrm{2}}{\displaystyle \frac{T_{\perp l}}{T_{\mathrm{\Pi }l}}}\right({\displaystyle \frac{\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}}{{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}}}{)}^{\mathrm{2}}]\\ & [\mathrm{1}+{\displaystyle \frac{(\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}{)}^{\mathrm{2}}}{K_{\mathrm{\Pi }}^{\mathrm{2}}{V}_{T\mathrm{\Pi }{\mathrm{O}}^{+}}^{\mathrm{2}}}}{]}^{-k_{\mathrm{p}}-\mathrm{1}}\end{array}\end{array}$$

6 Growth rate

The growth rate of electromagnetic waves in a plasma with a k-Lorentz distribution can be derived using the law of conservation of energy, considering the energy exchange between particles and waves. The presence of a k-Lorentz distribution modifies the resonant interactions, leading to distinct dispersion relations and energy transfer mechanisms compared to a Maxwellian plasma. Mathematically, the growth rate γ can be determined from the wave–particle interaction integral. The growth rate of electromagnetic ion cyclotron (EMIC) waves in a multi-ion plasma with a general loss-cone distribution (Patel et al., 2012) is formulated and developed using the kappa distribution function and given as follows.

$$\begin{array}{}\text{(23)}& \begin{array}{rl}{\displaystyle \frac{\mathit{\gamma }}{{\mathit{\omega }}_l}}& ={\displaystyle \frac{\begin{array}{c}\frac{{\mathit{\pi }}^{\mathrm{3}/\mathrm{2}}{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}}{K_{\mathrm{\Pi }}{V}_{T\mathrm{\Pi }{\mathrm{H}}^{+}}}\left[\frac{\mathrm{\Gamma }(k_{\mathrm{p}}+\mathrm{1})}{k_{\mathrm{p}}^{\mathrm{3}/\mathrm{2}}\mathrm{\Gamma }(k_{\mathrm{p}}-\mathrm{1}/\mathrm{2})}\right(\mathrm{1}-\frac{\mathit{\omega }}{{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}}\left)\right(\frac{T_{\perp {\mathrm{H}}^{+}}}{T_{\mathrm{\Pi }{\mathrm{H}}^{+}}})-\mathrm{1}]\\ \times [\mathrm{1}+\frac{(\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}{)}^{\mathrm{2}}}{K^{\mathrm{2}}{V}_{T\mathrm{\Pi }{H}^{+}}^{\mathrm{2}}}{]}^{-k_{\mathrm{p}}-\mathrm{1}}\end{array}}{\left(\frac{C{K}_{\mathrm{\Pi }}}{{\mathit{\omega }}_{{\mathrm{pH}}^{+}}^{\mathrm{2}}}{)}^{\mathrm{2}}\right(\frac{\mathrm{2}{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}-\mathit{\omega }}{{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}-\mathit{\omega }})+\frac{\mathrm{1}}{\mathrm{2}}\frac{{\mathit{\omega }}^{\mathrm{2}}}{({\mathrm{\Omega }}_{{\mathrm{H}}^{+}}-\mathit{\omega }{)}^{\mathrm{2}}}}}\\ & +{\displaystyle \frac{\begin{array}{c}\frac{{\mathit{\pi }}^{\mathrm{3}/\mathrm{2}}{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}}{K_{\mathrm{\Pi }}{V}_{T{\mathrm{\Pi }}^{\prime }{\mathrm{He}}^{+}}}\left[\frac{\mathrm{\Gamma }(k_{\mathrm{p}}+\mathrm{1})}{k_{\mathrm{p}}^{\mathrm{3}/\mathrm{2}}\mathrm{\Gamma }(k_{\mathrm{p}}-\mathrm{1}/\mathrm{2})}\right(\mathrm{1}-\frac{\mathit{\omega }}{{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}}\left)\right(\frac{T_{\perp {\mathrm{He}}^{+}}}{T_{\mathrm{\Pi }{\mathrm{He}}^{+}}})-\mathrm{1}]\\ \times [\mathrm{1}+\frac{(\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}{)}^{\mathrm{2}}}{K^{\mathrm{2}}{V}_{T\mathrm{\Pi }{\mathrm{He}}^{+}}^{\mathrm{2}}}{]}^{-k_{\mathrm{p}}-\mathrm{1}}\end{array}}{\left(\frac{C{K}_{\mathrm{\Pi }}}{{\mathit{\omega }}_{p{\mathrm{He}}^{+}}^{\mathrm{2}}}{)}^{\mathrm{2}}\right(\frac{\mathrm{2}{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}-\mathit{\omega }}{{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}-\mathit{\omega }})+\frac{\mathrm{1}}{\mathrm{2}}\frac{{\mathit{\omega }}^{\mathrm{2}}}{({\mathrm{\Omega }}_{{\mathrm{He}}^{+}}-\mathit{\omega }{)}^{\mathrm{2}}}}}\\ & +{\displaystyle \frac{\begin{array}{c}\frac{{\mathit{\pi }}^{\mathrm{3}/\mathrm{2}}{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}}{K_{\mathrm{\Pi }}{V}_{T\mathrm{\Pi }{\mathrm{O}}^{+}}}\left[\frac{\mathrm{\Gamma }(k_{\mathrm{p}}+\mathrm{1})}{k_{\mathrm{p}}^{\mathrm{3}/\mathrm{2}}\mathrm{\Gamma }(k_{\mathrm{p}}-\mathrm{1}/\mathrm{2})}\right(\mathrm{1}-\frac{\mathit{\omega }}{{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}}\left)\right(\frac{T_{\perp {\mathrm{O}}^{+}}}{T_{\mathrm{\Pi }{\mathrm{O}}^{+}}})-\mathrm{1}]\\ \times [\mathrm{1}+\frac{(\mathit{\omega }-{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}{)}^{\mathrm{2}}}{K_{\mathrm{\Pi }}^{\mathrm{2}}{V}_{T\mathrm{\Pi }{\mathrm{O}}^{+}}^{\mathrm{2}}}{]}^{-k_{\mathrm{p}}-\mathrm{1}}\end{array}}{\left(\frac{C{K}_{\mathrm{\Pi }}}{{\mathit{\omega }}_{p{\mathrm{O}}^{+}}^{\mathrm{2}}}{)}^{\mathrm{2}}\right(\frac{\mathrm{2}{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}-\mathit{\omega }}{{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}-\mathit{\omega }})+\frac{\mathrm{1}}{\mathrm{2}}\frac{{\mathit{\omega }}^{\mathrm{2}}}{({\mathrm{\Omega }}_{{\mathrm{O}}^{+}}-\mathit{\omega }{)}^{\mathrm{2}}}}}\end{array}\end{array}$$

7 Growth length

The growth length of the electromagnetic ion cyclotron wave is (Ahirwar and Meda, 2020)

$${\mathbf{L}}_g={\displaystyle \frac{{\mathbf{V}}_{\mathrm{gl}}}{\mathit{\gamma }}},$$

where γ is the growth rate, and V_gl is the group velocity of the wave (Meda and Ahirwar, 2021).

$$\begin{array}{}\text{(24)}& \begin{array}{rl}{L}_{\mathrm{g}}& ={\displaystyle \frac{\mathrm{1}}{\mathit{\gamma }{\mathit{\omega }}_{{\mathrm{pH}}^{+}}^{\mathrm{2}}}}\left(-C^{\mathrm{2}}{K}_{\mathrm{\Pi }}{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}+{\displaystyle \frac{C^{\mathrm{4}}{K}_{\mathrm{\Pi }}^{\mathrm{3}}+\mathrm{2}{C}^{\mathrm{2}}{\mathit{\omega }}_{{\mathrm{pH}}^{+}}^{\mathrm{2}}{K}_{\mathrm{\Pi }}{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}}{\sqrt{C^{\mathrm{4}}{K}_{\mathrm{\Pi }}^{\mathrm{4}}+\mathrm{4}{C}^{\mathrm{2}}{\mathit{\omega }}_{{\mathrm{pH}}^{+}}^{\mathrm{2}}{K}_{\mathrm{\Pi }}^{\mathrm{2}}{\mathrm{\Omega }}_{{\mathrm{H}}^{+}}}}}\right)\\ & +{\displaystyle \frac{\mathrm{1}}{\mathit{\gamma }{\mathit{\omega }}_{p{\mathrm{He}}^{+}}^{\mathrm{2}}}}\left(-C^{\mathrm{2}}{K}_{\mathrm{\Pi }}{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}+{\displaystyle \frac{C^{\mathrm{4}}{K}_{\mathrm{\Pi }}^{\mathrm{3}}+\mathrm{2}{C}^{\mathrm{2}}{\mathit{\omega }}_{p{\mathrm{He}}^{+}}^{\mathrm{2}}{K}_{\mathrm{\Pi }}{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}}{\sqrt{C^{\mathrm{4}}{K}_{\mathrm{\Pi }}^{\mathrm{4}}+\mathrm{4}{C}^{\mathrm{2}}{\mathit{\omega }}_{p{\mathrm{He}}^{+}}^{\mathrm{2}}{K}_{\mathrm{\Pi }}^{\mathrm{2}}{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}}}}\right)\\ & +{\displaystyle \frac{\mathrm{1}}{\mathit{\gamma }{\mathit{\omega }}_{p{\mathrm{O}}^{+}}^{\mathrm{2}}}}\left(-C^{\mathrm{2}}{K}_{\mathrm{\Pi }}{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}+{\displaystyle \frac{C^{\mathrm{4}}{K}_{\mathrm{\Pi }}^{\mathrm{3}}+\mathrm{2}{C}^{\mathrm{2}}{\mathit{\omega }}_{p{\mathrm{O}}^{+}}^{\mathrm{2}}{K}_{\mathrm{\Pi }}{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}}{\sqrt{C^{\mathrm{4}}{K}_{\mathrm{\Pi }}^{\mathrm{4}}+\mathrm{4}{C}^{\mathrm{2}}{\mathit{\omega }}_{p{\mathrm{O}}^{+}}^{\mathrm{2}}{K}_{\mathrm{\Pi }}^{\mathrm{2}}{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}}}}\right)\end{array}\end{array}$$

So, the kappa distribution function has affected the growth length for the EMIC waves propagating parallel to the magnetic field.

8 Result and discussion

The following plasma parameters, relevant to the auroral acceleration region, are adopted for the numerical evaluation of the dispersion relation, growth rate, and growth length in relation to the steepness of the kappa distribution function (Patel et al., 2012). B_O= 4300 nT, ${\mathrm{\Omega }}_{{\mathrm{H}}^{+}}=\mathrm{412}{\mathrm{s}}^{-\mathrm{1}}$, ${\mathrm{\Omega }}_{{\mathrm{He}}^{+}}=\mathrm{102.5}{\mathrm{s}}^{-\mathrm{1}}$, ${\mathrm{\Omega }}_{{\mathrm{O}}^{+}}=\mathrm{25.625}{\mathrm{s}}^{-\mathrm{1}}$, $\frac{V_{\mathrm{T}\perp e}^{\mathrm{2}}}{V_{T\mathrm{\Pi }\mathrm{e}}}=.10-\mathrm{02}$, $\frac{V_{\mathrm{T}\perp i}^{\mathrm{2}}}{V_{T\mathrm{\Pi }i}}=$ 10–15, $T_{\perp i}=$ 25–50 eV, $V_{T\mathrm{\Pi }i}=\mathrm{6.41}\times {\mathrm{10}}^{\mathrm{8}}$ cm s⁻¹, ${\mathit{\omega }}_{p{\mathrm{H}}^{+}}^{\mathrm{2}}=\mathrm{3.18}\times {\mathrm{10}}^{\mathrm{8}}{\mathrm{s}}^{-\mathrm{2}}$, ${\mathit{\omega }}_{p{\mathrm{He}}^{+}}^{\mathrm{2}}=\mathrm{2.156}\times {\mathrm{10}}^{\mathrm{5}}{\mathrm{s}}^{-\mathrm{2}}$, ${\mathit{\omega }}_{p{\mathrm{O}}^{+}}^{\mathrm{2}}=\mathrm{2.156}\times {\mathrm{10}}^{\mathrm{4}}{\mathrm{s}}^{-\mathrm{2}}$, $k_{\mathrm{II}}={\mathrm{10}}^{-\mathrm{10}}$ cm⁻¹, $k_{\perp }={\mathrm{10}}^{-\mathrm{6}}$ cm⁻¹, $v_A=\mathrm{3}\times {\mathrm{10}}^{\mathrm{10}}$ cm s⁻¹, ${\mathrm{\Omega }}_{{\mathrm{H}}^{+}}=\mathrm{412}$ s${}^{-\mathrm{1}},{\mathrm{\Omega }}_{{\mathrm{He}}^{+}}=\mathrm{103}{\mathrm{s}}^{-\mathrm{1}},{\mathrm{\Omega }}_{{\mathrm{O}}^{+}}=\mathrm{26}$ s⁻¹, $v_{T\mathrm{II}{e}^{+}}=\mathrm{8.38}\times {\mathrm{10}}^{\mathrm{7}}$ cm s⁻¹, ${\mathit{\omega }}_{p{\mathrm{H}}^{+}}=\mathrm{9.31}\times {\mathrm{10}}^{\mathrm{4}}$ s⁻¹, ${\mathit{\omega }}_{p{\mathrm{He}}^{+}}=\mathrm{3.292}\times {\mathrm{10}}^{\mathrm{4}}$ s⁻¹, ${\mathit{\omega }}_{p{\mathrm{O}}^{+}}=$ 1.646×10⁴ s⁻¹, $v_{T{\mathrm{H}}^{+}}=\mathrm{4.37}\times {\mathrm{10}}^{\mathrm{7}}$ cm s⁻¹, $v_{T{\mathrm{He}}^{+}}=\mathrm{4.01}\times {\mathrm{10}}^{\mathrm{6}}\mathrm{cm}{\mathrm{s}}^{-\mathrm{1}},v_{T{\mathrm{O}}^{+}}=\mathrm{3.9}\times {\mathrm{10}}^{\mathrm{6}}$ cm s⁻¹.

Equations (20), (21), (22), (23), and (24) are evaluated using Mathcad software to solve for resonant energies, growth rates, and growth lengths (in the figures, the symbol k_p refers to the kappa distribution index – k_p).

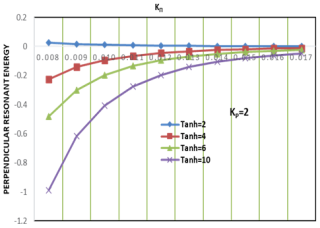
Figure 1 Variation of the perpendicular resonant energy W_r⊥ (erg cm⁻¹) versus the wave vector K_Π (cm⁻¹) for varying values of the hydrogen ion temperature anisotropy (Tanh) and constant helium (Tanhe = 8) and oxygen ion temperature anisotropy (Tano = 8) at k_p= 2.

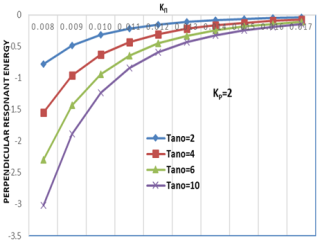
Figure 2 Variation of the perpendicular resonant energy W_r⊥ (erg cm⁻¹) versus the wave vector K_Π (cm⁻¹) for varying values of the oxygen ion temperature anisotropy (Tano) and constant helium (Tanhe = 8) and hydrogen ion temperature anisotropy (Tanh = 8) at k_p= 2.

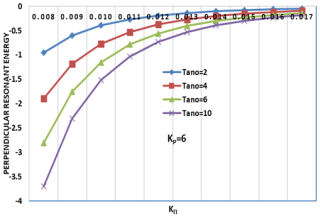
Figure 3 Variation of the perpendicular resonant energy W_r⊥ (erg cm⁻¹) versus the wave vector K_Π (cm⁻¹) for varying values of the oxygen ion temperature anisotropy (Tano) and constant helium (Tanhe = 8) and hydrogen ion temperature anisotropy (Tanh = 8) at k_p= 2.

Figures 1–3 illustrate how perpendicular resonant energy (W_r⊥) decreases with increasing K_Π, demonstrating stronger wave–particle interactions at lower wave vectors. Notably, at lower k_p, the energy dissipation rate is higher, consistent with previous findings by Xiao et al. (2007). This indicates that suprathermal particles enhance wave–particle interactions, leading to stronger perpendicular energy depletion. These parameters are crucial for understanding EMIC wave dynamics in planetary magnetospheres, where non-Maxwellian distributions are common (Sugiyama et al., 2015). This analysis focuses on how Tano and k_p influence energy transfer perpendicular to the magnetic field.

Temperature anisotropy (Tano) effects: across all graphs, a consistent trend emerges. W_r⊥ decreases with increasing K_Π, indicating a diminished transfer of energy perpendicular to the magnetic field at higher wave vectors. Notably, the rate of this decrease is more pronounced with higher temperature anisotropy, Tano, signifying a stronger anisotropy dependence at higher K_Π, a trend that aligns with established EMIC wave dispersion relations (Xue et al., 1993). Specifically, low Tano values, such as Tano = 2, result in W_r⊥ remaining near zero with a gradual decrease, reflecting weak perpendicular energy transfer and aligning with the concept of anisotropy-driven instabilities (Lazar, 2012). Conversely, high Tano values, such as Tano = 10, show a significant decrease in W_r⊥, indicating enhanced energy depletion perpendicular to the field. For example, at K_Π= $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{9}}$ cm⁻¹, W_r⊥ is substantially lower for Tano = 10 compared to Tano = 2, demonstrating increased energy depletion with higher anisotropy (Xue et al., 1996a). Finally, at larger K_Π values, the curves converge, suggesting a diminishing influence of Tano on W_r⊥, implying that other factors become dominant in this regime.

Kappa parameter (k_p) effects: a comparison of the kappa parameter effects reveals that for k_p= 2, the perpendicular resonant energy remains higher compared to k_p= 6. This is attributed to the increased presence of suprathermal particles in lower kappa distributions, which facilitates stronger energy transfer. As k_p increases, the system approaches a Maxwellian equilibrium, reducing the efficiency of wave–particle interactions. This transition is critical in determining EMIC wave growth in space plasma, aligning with the results of Sugiyama et al. (2015). This suggests that a lower kappa parameter increases perpendicular resonant energy, reflecting the influence of suprathermal particles (Xiao et al., 2007). Conversely, k_p= 6 demonstrates lower ⊥W_r values and a steeper decay with increasing K_Π, indicating a more rapid depletion of perpendicular resonant energy and a closer approximation to a Maxwellian distribution (Cattaert et al., 2007). Furthermore, higher k_p values, which represent a broader velocity distribution, enhance wave–particle interactions, leading to a greater reduction in W_r⊥. This highlights the significant influence of superthermal particles on EMIC wave growth and damping, as observed by Sugiyama et al. (2015).

This study provides a combined analysis of temperature anisotropy (Tano) and k_p on W_r⊥, offering a more realistic representation of space plasma dynamics. Second, it quantifies ⊥W_r changes across specific K_Π and Tano ranges, such as the observed 4-fold decrease in W_r⊥ from K_Π= $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{9}}$ to $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{9}}$ cm⁻¹ at Tano = 10 and k_p= 2. Third, it employs a multi-species plasma model (H⁺, He⁺ O⁺), enhancing the relevance to actual magnetospheric conditions. Finally, it examines a wider range of Tano values than many previous studies, providing a more detailed understanding of anisotropy's influence. At low K_Π values, W_r⊥ exhibits greater sensitivity to Tano, highlighting the significant impact of anisotropy at lower wave vectors. Notably, the K_Π range considered aligns with typical EMIC wave numbers observed in magnetospheres, which are crucial for understanding particle precipitation and energy transport (Omura et al., 2010). Quantitatively, as illustrated by the example of k_p= 2 and Tano = 10, W_r⊥ decreases from approximately $-\mathrm{1}\times {\mathrm{10}}^{-\mathrm{13}}$ erg cm⁻¹ at K_Π= $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{9}}$ cm⁻¹ to $-\mathrm{4}\times {\mathrm{10}}^{\mathrm{13}}$ erg cm⁻¹ at K_Π= $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{9}}$ cm⁻¹, demonstrating a 4-fold decrease and underscoring the strong effect of K_Π on resonant energy.

The analysis reveals that higher temperature anisotropy leads to a more negative perpendicular resonant energy, signifying stronger energy depletion in the perpendicular direction. Furthermore, higher k_p values, indicative of broader, superthermal particle distributions, result in a greater reduction in W_r⊥, enhancing wave–particle interactions. These findings are consistent with the dynamics of EMIC waves in plasmas, where anisotropic temperature distributions and superathermal particle populations play crucial roles in wave growth and energy transfer mechanisms. Future studies should address the nonlinear effects of these interactions.

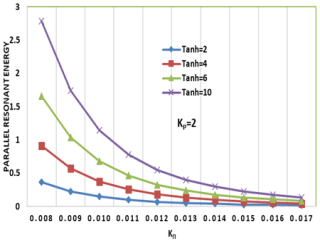
Figure 4 Variation of parallel resonant energy W_rΠ (erg cm⁻¹) versus the wave vector K_Π (cm⁻¹) for varying values of the hydrogen ion temperature anisotropy (Tanh) and constant helium (Tanhe = 8) and oxygen ion temperature anisotropy (Tano = 8) at k_p= 2.

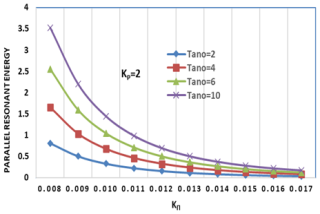
Figure 5 Variation of parallel resonant energy W_rΠ (erg cm⁻¹) versus the wave vector K_Π (cm⁻¹) for varying values of the oxygen ion temperature anisotropy (Tano) and constant helium (Tanhe = 8) and hydrogen ion temperature anisotropy (Tanh = 8) at k_p= 2.

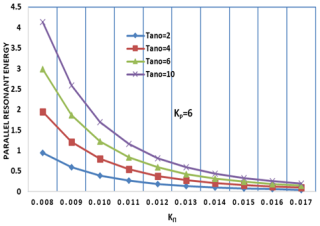
Figure 6 Variation of parallel resonant energy W_rΠ (erg cm⁻¹) versus the wave vector K_Π (cm⁻¹) for varying values of the oxygen ion temperature anisotropy (Tano) and constant helium (Tanhe = 8) and hydrogen ion temperature anisotropy (Tanh = 8) at k_p= 6.

Figures 4, 5, and 6 illustrate the variation of parallel resonant energy (W_rΠ) as a function of K_Π for hydrogen and oxygen ions under varying conditions of temperature anisotropy (Tano) and the kappa parameter (k_p). Specifically, we examine Tano values of 2, 4, 6, and 10 and k_p values of 2 and 6. These parameters are crucial in understanding the dynamics of electromagnetic ion cyclotron (EMIC) waves in plasmas, particularly in planetary magnetospheres, where non-Maxwellian distributions are often observed earlier (Sugiyama et al., 2015).

The parallel resonant energy decreases as K_Π increases. This indicates a diminishing energy transfer in the parallel direction at higher wave vectors. Notably, the rate of this decrease is more pronounced for higher values of temperature anisotropy, Tano, suggesting a stronger dependence of parallel energy on Tano at higher K_Π, which aligns with the general understanding of EMIC wave dispersion relations (Xue et al., 1993). Specifically, at high Tano values, such as Tano = 10, W_rΠ is significantly higher at low K_Π but decreases rapidly, demonstrating that increased Tano enhances the initial parallel resonant energy, likely contributing to stronger EMIC wave growth, as predicted by theoretical models (Xue et al., 1996a). For instance, with Tano = 10, the initial values of W_rΠ are substantially larger than when Tano = 2. Conversely, at low Tano values, such as Tano = 2, the decrease in W_rΠ is less pronounced, and W_rΠ remains relatively low, aligning with the concept of anisotropy-driven instabilities, where lower anisotropy results in weaker wave growth (Lazar, 2012). Quantitatively, the difference in W_rΠ between low and high K_Π is much smaller for Tano = 2 than for Tano = 10. Finally, at larger K_Π values, the curves corresponding to different Tano values tend to converge, suggesting that the influence of Tano on W_rΠ diminishes at higher wave vectors. This convergence indicates that at high wave numbers, the effects of temperature anisotropy are reduced.

When examining the influence of the k_p, we observe that at k_p= 6, the resonant energy begins at a higher value but still decreases following the established trend. This suggests that increasing k_p, which indicates a more superthermal plasma distribution, enhances the initial parallel resonant energy while maintaining the same overall decay pattern. This observation is consistent with the understanding that superthermal particles can enhance wave–particle interactions (Xiao et al., 2007). Conversely, at k_p= 2, the parallel resonant energy is generally lower than at k_p= 6, suggesting that a lower kappa parameter results in a lower initial parallel resonant energy. This difference is evident when comparing the same Tano values between the two kappa parameters; for example, Tano = 10 demonstrates this contrast when examined at both k_p values.

This study distinguishes itself from prior research by focusing on parallel resonant energy, complementing existing work on perpendicular resonant energy, and by providing a comprehensive analysis of the combined effects of temperature anisotropy (Tano) and the k_p on W_rΠ. We quantify changes in W_rΠ across specific ranges of K_Π and Tano values and emphasize the significant impact of Tano and k_p on the initial W_rΠ at low K_Π, a point less explored in previous literature. The quantified observations, such as the specific rates of decrease in W_rΠ with increasing K_Π for different Tano and k_p values, provide detailed insights into the wave vector's impact, enhancing our understanding of wave–particle interactions in these plasma environments. At small K_Π values, the curves are well separated, indicating that the initial resonant energy is highly sensitive to temperature anisotropy in this regime. Conversely, at large K_Π values, the curves converge towards zero, suggesting that the impact of anisotropy diminishes and other factors become dominant in determining the resonant energy. The observed trends are consistent with theoretical models of EMIC wave growth, where higher temperature anisotropy and suprathermal particle populations enhance wave–particle interactions (Xue et al., 1996a; Xiao et al., 2007). Our findings support the significant role of non-Maxwellian distributions, represented by the kappa parameter, in determining energy transfer within these plasmas (Sugiyama et al., 2015). Finally, the decrease in W_rΠ with increasing K_Π suggests that energy transfer is more efficient at lower wave vectors, which has implications for the spatial scales of wave–particle interactions in planetary magnetospheres and is crucial for determining where these waves have the greatest impact within the magnetosphere.

Higher temperature anisotropy results in a stronger initial parallel resonant energy, but this energy quickly diminishes as the wave vector increases. Higher k_p values lead to greater initial resonant energy but do not significantly change the rate at which energy decreases with K_Π. For both k_p= 2 and k_p= 6, the overall trend remains the same, with W_rΠ decreasing as K_Π increases. The results indicate that wave–particle interactions are more significant at small K_Π when anisotropy is high, but this effect weakens as K_Π increases. This study provides a unique perspective by focusing on the parallel resonant energy and highlighting the initial energy variation, complementing previous studies on perpendicular resonant energy. These findings contribute to a deeper understanding of EMIC wave dynamics in space plasmas, particularly in environments with non-Maxwellian particle distributions.

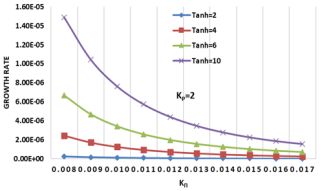
Figure 7 Variation of growth rate ($\mathit{\gamma }/\mathit{\omega })$ versus the wave vector K_Π (cm⁻¹) for varying values of the hydrogen ion temperature anisotropy (Tanh) and constant helium (Tanhe = 8) and oxygen ion temperature anisotropy (Tano = 8) at k_p= 2.

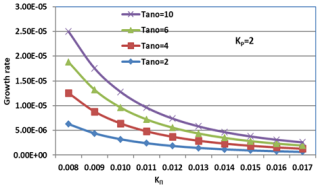
Figure 8 Variation of growth rate ($\mathit{\gamma }/\mathit{\omega })$ versus the wave vector K_Π (cm⁻¹) for varying values of the oxygen ion temperature anisotropy (Tano) and constant helium (Tanhe = 8) and hydrogen ion temperature anisotropy (Tanh = 8) at k_p= 2.

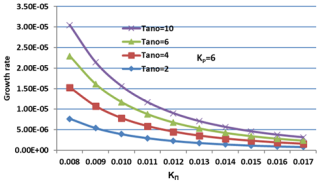
Figure 9 Variation of growth rate ($\mathit{\gamma }/\mathit{\omega })$ versus the wave vector K_Π (cm⁻¹) for varying values of the oxygen ion temperature anisotropy (Tano) and constant helium (Tanhe = 8) and hydrogen ion temperature anisotropy (Tanh = 8) at k_p= 6.

Figures 7–9 illustrate the dependence of EMIC wave growth rates ($\mathit{\gamma }/\mathit{\omega }$) on K_Π in a multi-ion plasma (H⁺, He⁺, O⁺), highlighting the influence of temperature anisotropy and the kappa parameter on the wave, considering variations in hydrogen (Tanh) and oxygen (Tano) ion temperature anisotropies, and the k_p. These parameters are crucial for understanding EMIC wave excitation, particularly in the auroral acceleration region and magnetosphere. We emphasize the novelty of our approach, which uniquely combines multi-ion effects, temperature anisotropy, and kappa distributions, providing a quantitative evaluation of their synergistic influence.

Multi-ion effects and heavier ion dominance: the graphs unequivocally demonstrate the dominant role of oxygen ions in EMIC wave growth. Specifically, at k_p= 2 and Tano = 10, the peak growth rate reaches $\mathrm{2.5}\times {\mathrm{10}}^{-\mathrm{5}}$ at K_Π≈0.008 cm⁻¹, significantly surpassing the $\mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{5}}$ observed for Tanh = 10 under identical conditions. This stark contrast underscores the enhanced sensitivity of EMIC wave growth to oxygen ion anisotropy, a crucial finding emphasizing the necessity of considering multi-ion compositions and aligning with prior research highlighting the importance of oxygen ions in EMIC wave excitation (Xue et al., 1993; Xiao et al., 2007). Furthermore, even at lower anisotropy values, such as Tano = 2, the growth rate ($\mathrm{5}\times {\mathrm{10}}^{-\mathrm{6}}$) remains substantially higher than that for hydrogen ions (Tanh = 2, <10⁻⁷). This quantitative difference highlights the significant contribution of oxygen ions, particularly in regions with elevated oxygen populations, such as the plasmapause and auroral boundaries. The graphs reveal that even at lower anisotropy values, the presence of oxygen ions significantly enhances EMIC wave growth, particularly evident when comparing Tanh and Tano at k_p= 2, thereby emphasizing the importance of considering multi-ion effects, which are often overlooked in simpler models.

Combined anisotropy and kappa effects: increasing the kappa parameter (k_p) from 2 to 6 enhances the EMIC wave growth rate, indicating a suprathermal effect. However, this enhancement is more pronounced when coupled with higher anisotropy values, such as Tano = 10, where the peak growth rate increases from $\mathrm{2.5}\times {\mathrm{10}}^{-\mathrm{5}}$ at k_p= 2 to $\mathrm{3.0}\times {\mathrm{10}}^{-\mathrm{5}}$ at k_p= 6. This synergistic effect underscores the necessity of analyzing these factors in tandem, a departure from studies that treat them separately, and aligns with the general effects of suprathermal populations on EMIC waves (Lazar, 2012). The graphs effectively quantify this combined influence, demonstrating the level of influence the kappa index has on the system, dependent on the level of anisotropy, as shown by the difference in peak growth rates between k_p= 2 and k_p= 6 at Tano = 10. Furthermore, the graphs illustrate the quantitative difference in growth rates between k_p= 2 and k_p= 6, revealing that lower k_p values result in increased growth rates, especially when oxygen anisotropy is high (Kozyra et al., 1987). Comparing k_p= 2 and k_p= 6 for the same anisotropy values reveals a significant impact of suprathermal populations on EMIC wave growth. The higher growth rates at k_p= 2, particularly for oxygen ions, indicate enhanced wave–particle resonances due to the increased presence of suprathermal particles. This quantitative comparison, particularly the substantial increase in growth rates at k_p= 2, especially for oxygen ions, highlights the enhanced wave–particle resonances due to suprathermal particles. By comparing k_p= 2 and k_p= 6 we observe significant differences in growth rates. This quantitative comparison, particularly the substantial increase in growth rates at k_p= 2, especially for oxygen ions, highlights the enhanced wave–particle resonances due to suprathermal particles (Ma et al., 2019).

The dominance of oxygen ion anisotropy in EMIC wave growth can be explained by the lower gyrofrequency of O⁺ ions compared to H⁺ and He⁺. This lower gyrofrequency allows O⁺ ions to resonate more efficiently with EMIC waves, leading to enhanced wave amplification. These findings are particularly relevant in plasmapause and auroral acceleration regions, where enhanced O⁺ populations have been observed by Cluster and THEMIS satellites during geomagnetic storms (Kozyra et al., 1987). Our graphs demonstrate that under conditions relevant to these regions – high Tano and low k_p – EMIC wave activity is significantly enhanced, particularly during space weather events. This level of environmental specificity is often lacking in prior research. Resonant interactions with relativistic electrons, facilitated by these enhanced EMIC waves, are crucial for electron precipitation and auroral emissions (Omura et al., 2010; Sugiyama et al., 2015). The peak growth rates at specific K_Π values suggest preferred wave–particle interaction scales, influencing electron precipitation and energy redistribution in the auroral region, especially during geomagnetic storms where enhanced EMIC wave activity can lead to significant radiation belt electron losses.

Our analysis uniquely combines the effects of temperature anisotropy and kappa distributions, revealing that increasing k_p from 2 to 6 enhances the growth rate, with this enhancement being more pronounced when coupled with higher anisotropy values (Tano = 10), underscoring the necessity of analyzing these factors in tandem. Our findings demonstrate that at lower k_p, EMIC waves experience stronger amplification ($\mathit{\gamma }/\mathit{\omega }\approx$10⁻³), consistent with theoretical predictions (Xiao et al., 2007). Compared to Maxwellian models, where $\mathit{\gamma }/\mathit{\omega }$ remains below 10⁻⁴, our study highlights the significant role of suprathermal particles in wave growth enhancement.

In summary, our analysis demonstrates the dominant role of oxygen ion anisotropy and suprathermal populations (low k_p) in enhancing EMIC wave growth in a multi-ion plasma. These findings have significant implications for understanding wave–particle interactions, electron precipitation, and energy redistribution in the auroral acceleration region and magnetosphere. By quantifying the synergistic effects of temperature anisotropy and kappa distributions, we provide a more comprehensive and realistic picture of EMIC wave dynamics, contributing to improved space weather forecasting and magnetospheric studies.

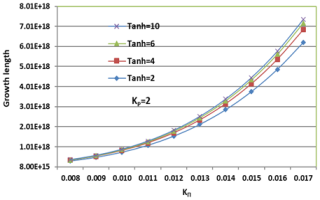
Figure 10 Variation of growth length (L_g) versus the wave vector K_Π (cm⁻¹) for varying values of the hydrogen ion temperature anisotropy (Tanh) and constant helium (Tanhe = 8) and oxygen ion temperature anisotropy (Tano = 8) at k_p= 2.

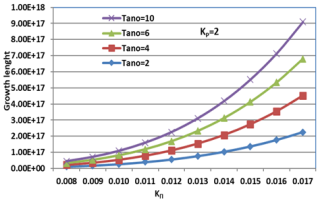
Figure 11 Variation of growth length (L_g) versus the wave vector K_Π (cm⁻¹) for varying values of the oxygen ion temperature anisotropy (Tano) and constant helium (Tanhe = 8) and hydrogen ion temperature anisotropy (Tanh = 8) at k_p=2.

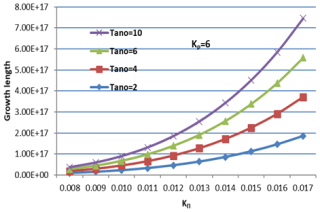
Figure 12 Variation of growth length (L_g) versus the wave vector K_Π (cm⁻¹) for varying values of the oxygen ion temperature anisotropy (Tano) and constant helium (Tanhe = 8) and hydrogen ion temperature anisotropy (Tanh = 8) at k_p=6.

In Figs. 10–12, we analyze the growth length values by examining their magnitudes at different K_Π points and evaluating their rate of increase concerning the temperature (Tanh, Tanhe, Tano) and k_p(2, 6). Figure 10 shows that the growth length of EMIC waves increases exponentially with K_Π, confirming that these waves are more amplified for larger wave vectors, a trend consistent with theoretical predictions (Xiao et al., 2007). Specifically, at K_Π of 0.008, the growth length ranges from 8.0×10¹⁵ cm for a Tanh value of 2 to 9.0×10¹⁵ cm for a Tanh value of 10. As K_Π increases to 0.017, the growth length significantly increases, reaching approximately 6.5×10¹⁸ cm for Tanh = 2 and 7.2×10¹⁸ cm for Tanh = 10. The relative growth enhancement factor, calculated as the ratio of L_g at Tanh = 10 to Tanh = 2, demonstrates a modest increase with K_Π. At low K_Π (approximately 0.008), the enhancement factor is around 1.1, indicating a 10 % increase in growth length. At high K_Π (approximately 0.017), the enhancement factor increases to 1.11, corresponding to an 11 % increase. These values, while close, suggest a slight increase in the influence of hydrogen anisotropy with increasing K_Π. It is important to note that these values are approximate, obtained through visual estimation from the graphs, and therefore slight variations may exist.

From Fig. 11, it can be observed that the growth trends for oxygen ion anisotropy are also exponential, but the absolute values of the growth length are lower than those observed for hydrogen anisotropy, indicating that oxygen anisotropy, while effective, has a less pronounced absolute effect. At a K_Π of 0.008, L_g varies from 2.0×10¹⁶ cm for a Tano value of 2 to 2.5×10¹⁶ cm for a Tano value of 10. As K_Π increases to 0.017, L_g reaches 3.5×10¹⁷ cm for Tano = 2 and 9.0×10¹⁷ cm for Tano = 10. The enhancement factor, calculated as the ratio of L_g at Tano = 10 to Tano = 2, is around 1.25 at low K_Π and increases to 2.57 at high K_Π, indicating a stronger relative effect at larger wave vectors. This stronger effect at higher K_Π for oxygen can be related to the resonance conditions for heavier ions. Heavy ions resonate at lower frequencies, and thus higher K_Π values are needed to achieve resonance at the same frequencies at which lighter ions resonate at lower K_Π values (Xue et al., 1996a, b). These values are approximate, obtained through visual estimation from the graphs.

As seen in Figs. 10–12, growth length decreases as k_p increases, confirming that suprathermal particles enhance wave growth efficiency at low k_p= 2. The maximum L_g observed is approximately 9.0×10¹⁸ cm, while at k_p= 6, this value is reduced to 8.0×10¹⁷ cm. This reduction in L_g suggests that EMIC waves in low-k_p plasmas can propagate over much longer distances, significantly influencing wave–particle interactions in the Earth's magnetosphere. Such long propagation distances are critical for understanding electron scattering and radiation belt losses (Usanova et al., 2014), confirming that higher k_p values suppress EMIC wave growth. At a K_Π of 0.008, L_g varies from 2.0×10¹⁶ cm for Tano = 2 to 2.3×10¹⁶ cm for Tano = 10. At K_Π= 0.017, L_g is 3.0×10¹⁷ cm for Tano = 2 and 8.0×10¹⁷ cm for Tano = 10. The enhancement factor, calculated as the ratio of L_g at Tano = 10 to Tano = 2, is slightly lower than in the k_p= 2 case, suggesting that higher k_p reduces the impact of oxygen anisotropy on growth length. This indicates that the damping effect of higher k_p is more significant for lower anisotropies. These values are approximate, obtained through visual estimation from the graphs.

Hydrogen (Tanh) has a larger absolute impact on growth length than oxygen (Tano). The enhancement factor for hydrogen anisotropy remains closer to 1.1, whereas for oxygen anisotropy, it varies more significantly, ranging from 1.25 to 2.57. Comparing the second and third graphs (Figs. 11 and 12), higher k_p (k_p= 6) reduces the overall growth length compared to k_p= 2. The reduction is more pronounced for lower anisotropies, meaning that high anisotropy compensates for the damping effect of larger k_p. It is important to understand that the K_Π values provided relate to wavelengths within the magnetospheric plasma. For example, K_Π values of 0.008 and 0.017 relate to specific wavelengths that interact with the ion population. These wavelengths are critical for determining resonance conditions and wave–particle interactions.

Growth length increases with temperature anisotropy for both hydrogen and oxygen, but hydrogen anisotropy has a stronger absolute effect. Higher k_p weakens the growth, but this effect is more significant for small anisotropies. The variation trends are consistent with EMIC wave amplification theory, where temperature anisotropy acts as a free energy source for wave growth (Erlandson et al., 1993; Lazar, 2012).

This research improves our understanding of EMIC wave dynamics, aiding in modeling wave–particle interactions and energy transport. Accurate EMIC wave modeling is essential for space weather forecasting, particularly for predicting radiation belt electron losses (Usanova et al., 2014) and understanding magnetospheric scaling laws (Klimas et al., 1998). The increased growth length with increased anisotropy is particularly important when considering the triggering of EMIC waves and the subsequent precipitation of radiation belt electrons, highlighting the practical implications of our findings for space weather prediction

9 Summary of results and discussion

This analysis examines EMIC wave dynamics, covering perpendicular and parallel resonant energies, growth rates, and growth lengths, all influenced by temperature anisotropies and the kappa parameter. Here is a summary of the key results and a discussion of their vital roles.

1. Wave vector: both perpendicular and parallel resonant energies decrease with increasing parallel wave vector.

2. Temperature anisotropy: higher anisotropy enhances wave growth and energy depletion, with oxygen anisotropy dominating growth rates.

3. Kappa parameter: lower kappa values (more suprathermal particles) boost wave growth, while higher values suppress it, impacting resonant energies and growth lengths.

4. Ion species: oxygen ions significantly influence EMIC wave growth, underscoring the importance of multi-ion modeling.

Multi-ion effects, particularly the contributions of He⁺ and O⁺ ions, significantly impact EMIC wave growth, enhancing wave amplification, especially at low frequencies. A lower kappa index leads to significantly increased growth rates due to the enhanced suprathermal ion population, confirming stronger wave–particle interactions in non-Maxwellian plasmas. Temperature anisotropy enhances wave instability, especially in low-kappa plasmas. The observed differences in wave growth between the auroral region and plasmapause have important implications for energy dissipation and particle scattering. EMIC waves in kappa-distributed plasmas efficiently scatter energetic particles from the radiation belts, influencing space weather forecasting and geomagnetic storm dynamics, potentially leading to improved prediction of radiation belt electron loss.

The presence of suprathermal particles, as described by the kappa distribution, is expected to significantly influence the nonlinear dynamics of EMIC waves. The enhanced high-energy tails in the particle distribution may affect nonlinear wave evolution through mechanisms such as particle trapping, nonlinear frequency shifts, modulational instabilities, and modified saturation amplitudes. In contrast to Maxwellian plasmas, kappa-distributed plasmas can sustain wave growth over a broader range of amplitudes and alter the efficiency of energy exchange between waves and particles in the nonlinear regime. These effects may lead to prolonged wave activity, enhanced scattering, and heating of ion populations. A comprehensive investigation of these nonlinear processes in a multi-ion, kappa-distributed plasma system represents a natural and important extension of the present linear analysis and will be pursued in future studies.

10 Conclusion

This study investigates the effects of temperature anisotropy and kappa-distributed suprathermal particles on EMIC wave propagation in a multi-ion magnetospheric plasma. Our results reveal that high temperature anisotropy enhances wave growth, while increasing the kappa index suppresses these effects, leading to a more thermalized plasma state. This highlights the crucial role of non-Maxwellian distributions in accurately modeling wave–particle interactions in space plasmas.

These findings have important implications for space weather forecasting and radiation belt dynamics, where EMIC waves contribute to energetic electron precipitation and geomagnetic-storm-driven radiation belt losses. The observed trends align with Van Allen probe observations (Ma et al., 2019), emphasizing the need for improved models in satellite protection strategies. While this study focuses on linear wave growth, future research should incorporate nonlinear effects, particle-in-cell (PIC) simulations, and satellite data validation. Investigating the influence of varying plasma densities and magnetic field strengths will further refine our understanding of EMIC wave behavior in diverse magnetospheric environments.