Magnetospheric response to solar wind forcing: ultra-low-frequency wave–particle interaction perspective

Solar wind forcing, e.g., interplanetary shock and/or solar wind dynamic pressure pulses impacting Earth's magnetosphere, manifests many fundamental important space physics phenomena, including producing electromagnetic waves, plasma heating, and energetic particle acceleration. This paper summarizes our present understanding of the magnetospheric response to solar wind forcing in the aspects of radiation belt electrons, ring current ions and plasmaspheric plasma physics based on in situ spacecraft measurements, ground-based magnetometer data, magnetohydrodynamics (MHD) and kinetic simulations.

Magnetosphere response to solar wind forcing is not just a “one-kick” scenario. It is found that after the impact of solar wind forcing on Earth's magnetosphere, plasma heating and energetic particle acceleration started nearly immediately and could last for a few hours. Even a small dynamic pressure change in interplanetary shock or solar wind pressure pulse can play a non-negligible role in magnetospheric physics. The impact leads to generation of a series of waves, including poloidal-mode ultra-low-frequency (ULF) waves. The fast acceleration of energetic electrons in the radiation belt and energetic ions in the ring current region response to the impact usually contains two contributing steps: (1) the initial adiabatic acceleration due to the magnetospheric compression, (2) followed by the wave–particle resonant acceleration dominated by global or localized poloidal ULF waves excited at various L-shells.

Generalized theory of drift and drift–bounce resonance with growth- or decay-localized ULF waves has been developed to explain in situ spacecraft observations. The wave-related observational features like distorted energy spectrum, “boomerang” and “fishbone” pitch angle distributions of radiation belt electrons, ring current ions and plasmaspheric plasma can be explained in the framework of this generalized theory. It is worth pointing out here that poloidal ULF waves are much more efficient at accelerating and modulating electrons (fundamental mode) in the radiation belt and charged ions (second harmonic) in the ring current region. The results presented in this paper can be widely used in solar wind interacting with other planets such as Mercury, Jupiter, Saturn, Uranus and Neptune and other astrophysical objects with magnetic fields.

1 Introduction

“We have to learn again that science without contact with experiments is an enterprise which is likely to go completely astray into imaginary conjecture” (Alfvén and Arrhenius, 1976).

The paper is based on my Hannes Alfvén Medal lecture at the European Geosciences Union (EGU) General Assembly 2020 and organized as follows with emphasis on Sects. 2, 3, 4 and 5.

1. Introduction

2. Magnetospheric response to solar wind forcing

3. Generalized drift resonance

4. Generalized drift–bounce resonance

5. Nonlinear and multiple drift or drift–bounce resonance

6. Outstanding questions and concluding remarks

1.1 Hannes Alfvén and China

The EGU awarded the Hannes Alfvén Medal to me for the year 2020. I feel deeply honored and very happy to obtain so much recognition for my work, because Hannes Alfvén was one of the giants in space physics and astrophysics and also one of my heroes.

As we all know, Alfvén received the 1970 Nobel Prize in Physics for his work in magnetohydrodynamics (MHD) and plasma physics, while few people know that he could speak some Chinese (Fig. 1) besides Swedish and English as indicated by Wikipedia (https://en.wikipedia.org/wiki/Hannes_Alfv%C3%A9n; last access: 1 October 2021). In fact, he visited China twice, his first visit being on invitation by Jeoujang Jaw, who was the founder of the Chinese space program (Zhang and Yin, 2018). During his total of 50 d visiting in China, Hannes Alfvén gave a number of lectures and promoted China's space physics. Also, in the early 1990s, the first textbook I took to learn space physics – Cosmical Electrodynamics (the second edition, 1963) – was in fact a gift from Hannes Alfvén during his first Chinese visit. Alfvén's Cosmical Electrodynamics contains the main fundamentals of space plasma physics.

Figure 1 Hannes Alfvén's handwritten signature in Chinese (top) and his name seal in traditional Chinese characters.

As a student who majored in space science, I first studied Alfvén's eminent works – the motion of charged particles (Alfvén and Fälthammar, 1963) and “Existence of Electromagnetic–Hydrodynamic Waves” (Alfvén, 1942). The latter one is now named after him as Alfvén waves. Seventy-eight years after the publication of the paper “Existence of Electromagnetic–Hydrodynamic Waves”, Alfvén waves have “propagated” to plenty of regimes of cosmic plasmas. Now, it is understood that Alfvén waves are ubiquitous and of fundamental importance in plasma physics, space physics and astrophysics, and they occur in planetary magnetospheres, in laboratory plasma, in stellar coronas and winds, and in many other astrophysical plasmas in the universe.

1.2 ULF waves and solar wind forcing

Ultra-low-frequency (ULF) waves are electromagnetic waves originating in Earth's magnetosphere with a frequency range from about 1 mHz to 10 Hz. Usually, ULF waves containing larger power are the lower-frequency ones, and the intensity of the wave power in general has an inverse relation with respect to its frequency (e.g., Lanzerotti and Southwood, 1979; Zong et al., 2017).

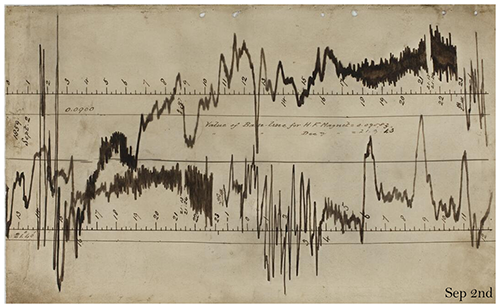
Figure 2 The “Carrington event” of 2 September 1859 recorded at Greenwich Observatory, London (51.4769° N, 0.0005° W): https://geomag.bgs.ac.uk/education/carrington.html, last access: 1 October 2021. Greenwich Observatory magnetometer traces (horizontal force (H) on top and declination (D) on the bottom; the two traces are offset by 12 h) during the time of the solar flare on 1 September 1859.

ULF waves are first observed on the ground and are also known as geomagnetic pulsations. The solar storm of 1859 (Carrington, 1860, also known as the Carrington event) was probably associated with a huge solar coronal mass ejection (CME) hitting Earth's magnetosphere and induced arguably the largest geomagnetic storm on record on 1–2 September 1859 (Stewart, 1861). As we can see from Fig. 2, the first geomagnetic pulsation has been recorded as quasi-sinusoidal magnetic field variations during the great magnetic storm that occurred in 1859 (Stewart, 1861). Geomagnetic pulsations (Fig. 2) are ULF plasma waves that originated in Earth's magnetosphere.

The magnetic field perturbation of the toroidal-mode ULF waves is in the azimuth direction, and the electric field is radial perturbation usually associated with a small wave number, whereas the poloidal-mode ULF waves are often associated with a larger wave number, and the magnetic field of the poloidal mode is radially perturbed.

Oscillations of magnetic field lines can be sustained through the collisionless plasma interaction in the magnetosphere, whereas the ULF waves can also be diminished when they pass through Earth's atmosphere and ionosphere due to the ionospheric conductivity (Southwood and Hughes, 1983). In Earth's ionosphere, due to the presence of collisional plasma and a neutral atmospheric population, the oscillated magnetic field in the ULF range would be exponentially decayed by generating an additional Hall current and Pedersen current, and the direction of the magnetic field oscillation will be rotated through 90°. Thus, the decayed ULF waves can eventually propagate to the ground in the form of electromagnetic waves. Having considered the direction rotation due to the ionosphere, the D component of the ground magnetic field on the bottom trace of Fig. 2 mainly represents the poloidal-mode ULF waves (Wang et al., 2010; Zong et al., 2017).

The relationship between ULF waves in the magnetosphere and the magnetic field dissonances on the ground is as follows (Southwood and Hughes, 1983):

$$\begin{array}{}\text{(1)}& b_{\mathrm{g}}/b_{\mathrm{m}}\sim \left({\mathrm{\Sigma }}_{\mathrm{H}}/{\mathrm{\Sigma }}_{\mathrm{P}}\right)e^{-kh},\end{array}$$

where Σ_P and Σ_H are the height-integrated Pedersen and Hall conductivity, respectively, b_g is the magnetic field on the ground and b_m is the ULF field just above the ionosphere, and h is the thickness of the ionosphere. As we can see from the formula, Earth's ionosphere prefers to shield ULF waves with a large wave number k since the thickness of the ionosphere h is insensitive in time. Thus, the poloidal-mode ULF waves of large wave numbers will decay significantly when they pass through Earth's ionosphere, and this is hard to observe on the ground. However, the toroidal-mode ULF waves usually have a small wave number, and it will be easier to pass through the ionosphere and be identified from ground magnetometer records.

ULF waves can act as important media of the magnetospheric dynamics for the mass, momentum and energy transport processes. Therefore, it is important to understand the global properties and how the energy is transported from the solar wind to the magnetosphere, ionosphere and finally the ground through ULF wave–charged particle interactions.

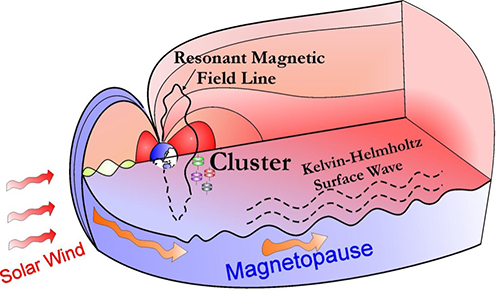
Figure 3 Illustration showing how the solar wind disturbances and Kelvin–Helmholtz surface waves excite the ULF waves and field line resonances (FLRs) in Earth's magnetosphere.

Earth's magnetospheric activity is mainly controlled by the solar wind plasma and the accompanying interplanetary magnetic field (IMF) (e.g., Yue et al., 2009, 2010, 2011; Yue and Zong, 2011). The energy coupling between the solar wind and Earth's magnetosphere can take various forms and most often would excite different plasma waves inside the magnetosphere, one of which is the ULF wave. In the 1940s, the geomagnetic signals related to the interplanetary shock impact were identified through the ground-based magnetometer observations and named a “Storm Sudden Commencement” (SSC) (Chapman and Bartels, 1940). Now, it is well known as the impact of dynamic pressure impulses associated with the interplanetary shocks driven by coronal mass ejections (CMEs) or corotating interaction regions (CIRs).

It is now known after extensive studies that the solar wind dynamic pressure pulses (including negative and positive types) as well as the interplanetary shock can have profound effects on the magnetosphere system (Zhang et al., 2010; Zong et al., 2017). The positive or negative pressure pulses correspond to the sudden enhancements or drops of the solar wind dynamic pressures, respectively, and are often caused by the abrupt changes in solar wind density and/or solar wind speed. One of the typical representatives is the interplanetary shock.

When solar wind dynamic pressure pulses impinge on the magnetosphere, the sudden rise or drop in dynamic pressure will first compress or inflate the magnetosphere. In the meantime, the fast magnetosonic waves will be launched inside the magnetosphere, and then standing ULF waves usually will be formed subsequently in the magnetosphere, occasionally even inside the plasmasphere (e.g., Zong et al., 2009; Zhang et al., 2010; Liu et al., 2010), thus transporting the energy of solar wind into the magnetosphere. The generation mechanisms of different dayside ULF waves can be distinguished by their preferable occurring region. The K–H instability mechanism needs a shear flow to meet the instability threshold condition, and therefore the main occurring regions are the dawn and dusk flank sides of the magnetopause. The dynamic pressure pulses by contrast are responsible for the dayside local noon region (Fig. 3).

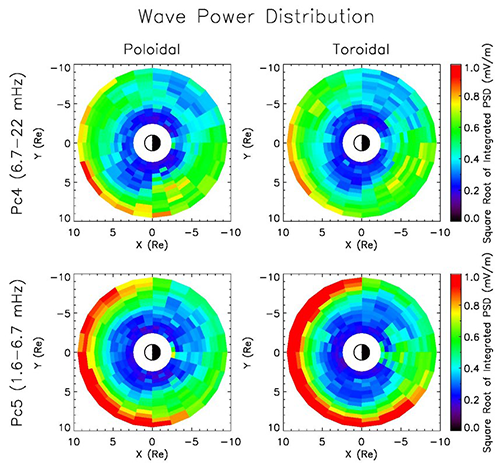
Figure 4 The equatorial distribution of ULF wave power investigated based on electric field measurements of 12 years (1 January 2008–31 December 2019) from THEMIS (Liu et al., 2009). The square roots of the integrated power spectral density of the azimuthal electric field (Ea, poloidal mode) and radial electric field (Er, toroidal mode) in the Pc4 and Pc5 frequency ranges are averaged in each bin.

Figure 4 shows the responses of both poloidal-mode and toroidal-mode ULF waves to the solar wind forcing at different magnetic local time sectors. It is suggested that Pc4 and Pc5 ULF wave power is mainly supplied from external solar wind sources, i.e., solar wind forcing (Liu et al., 2009, 2010). As is shown in Fig. 4, the distributions of the wave power (square root of integrated power spectral density) of the azimuthal electric field (Ea, poloidal-mode) component are averaged from 12-year THEMIS data sets. The wave power is found to be stronger in the dayside magnetosphere compared to that in the nightside. Also, the wave power in the pre-midnight region is larger than that in the post-midnight region. The wave power is observed dominantly at higher L-shells, which show the consistency with the scenario that the poloidal-mode Pc4 and Pc5 ULF waves generally have external sources – solar wind forcing including interplanetary shocks and solar wind positive and negative dynamic pressure pulses (e.g., Zong et al., 2009; Zhang et al., 2010; Liu et al., 2010).

The study of magnetospheric response to solar wind forcing related to a sudden change in solar wind dynamic pressure has at least two obvious advantages: the magnetospheric response to sudden change in the solar wind dynamic pressure will generate significant and easily identified electromagnetic signals, and the energy source for excited ULF waves is rather clear and without temporal ambiguity. Thus, in the present paper, based on the ULF wave–charged particle interactions, I will focus on how the magnetosphere response to solar wind forcing – the solar wind dynamic pressure pulses, including positive and negative ones.

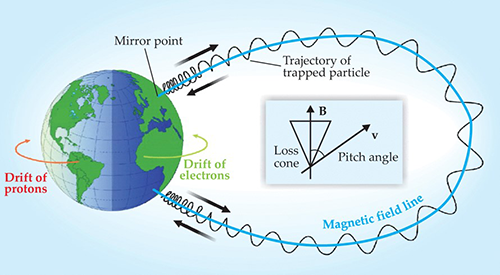
Figure 5 A schematic view of the charged-particle motion in Earth's inner magnetosphere. Particle gyro motion around field lines, “bounce” back-and-forth motion and drift motion due to the gradient and curvature of the magnetic field. Ions drift towards west and electrons drift east and thus generate the ring current, an electric current circulating around Earth. Adopted from Fig. 2 in Day (2008).

1.3 Charged particles in the inner magnetosphere

The inner magnetosphere includes the radiation belt, ring current and plasmasphere, which are three overlapping regions with energy of their particle population quite different (Yue et al., 2017a, b). The Van Allen radiation belt is composed of energetic particles with energy greater than 100 keV, whereas the ring current contains mainly energetic ion species (hydrogen, helium, and oxygen) of tens of keV to about 400 keV. The ring current and Van Allen radiation belt are overlapped in space with a cold plasmaspheric population (typically a few eV).

The plasma density in the magnetosphere controls the timescale in response to the solar wind forcing. The mass density is one of the key parameters for the Alfvén speed which determines the magnetospheric response to the low-frequency ion variation in the ULF wave range, whereas the background electron density dominates the electrons oscillating in the very-low-frequency (VLF) and radio wave range. Thus, the mass density is one of the controlling factors for the radiation belt and ring current dynamic process.

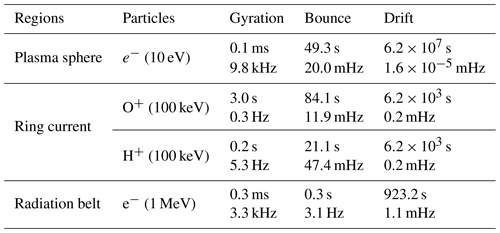
Charged particles in Earth's magnetosphere will experience three kinds of periodical motions corresponding to three different invariants: gyrating around magnetic field lines, bouncing back and forth along the field line between “mirror points” located at lower altitude, and drifting across the field lines due to the electric field as well as the gradient and curvature of the magnetic field lines; see Fig. 5. When the charged particles move in the inner magnetosphere, the timescales for the three kinds of motion can be estimated with the dipole magnetic field:

$$\begin{array}{}\text{(2)}& \begin{array}{r}{T}_c=\left(\mathrm{0.66}\mathrm{s}\right){\displaystyle \frac{\mathrm{100}\mathrm{nT}}{B}}A,\\ T_{\mathrm{b}}=\left(\mathrm{5}\min \right)\left({\displaystyle \frac{l_{\mathrm{0}}}{\mathrm{10}{R}_{\mathrm{E}}}}\right)\left({\displaystyle \frac{\mathrm{keV}}{W_{\parallel }}}\right)A^{\frac{\mathrm{1}}{\mathrm{2}}},\\ T_D=\left(\mathrm{56}\mathrm{h}\right){\left({\displaystyle \frac{r}{\mathrm{5}{R}_E}}\right)}^{\mathrm{2}}\left({\displaystyle \frac{B}{\mathrm{100}\mathrm{nT}}}\right)\left({\displaystyle \frac{\mathrm{keV}}{W}}\right),\end{array}\end{array}$$

where A is the mass ratio of the particle to the proton, W is the particle's kinetic energy, l₀ is the length along the magnetic field line between two mirror points in the Northern Hemisphere and Southern Hemisphere, r is the distance to Earth's center from the Equator and B is the magnitude of the magnetic field. The representative values are given in Table 1.

The dynamics of radiation belt and ring current are strongly governed by the interactions between differently charged-particle populations that are coupled through the variation of all kinds of electromagnetic waves and wave–particle interactions. The mentioned three invariants do not always remain constant. The violations of these invariants may result from interactions with variations of the magnetic field and electric field when the timescale of the electromagnetic field disturbances is comparable to the three kinds of periodical motions – drift, bounce or gyration frequency of the particles.

Table 1 Timescales of motion of charged particles in the magnetosphere (L=4.5, α_eq=60°, B=350 nT).

Besides the magnetic reconnection, the solar wind energy can also be transported into the magnetosphere, the ionosphere and finally the ground through ULF waves. The mechanisms concerning how ULF waves interact with charged particles in the magnetosphere and their involvement in energy-transporting process would be addressed by spacecraft constellation observations and particle simulations. It will help us understand the complex but fundamental problems of mass, energy and momentum transport processes in the magnetosphere and have a wide range of applications in space weather (e.g., Friedel et al., 2002; Shprits et al., 2008; Elkington et al., 2016).

2 Magnetospheric response to solar wind forcing

2.1 “One-kick” scenario

Charged particles in Earth's magnetosphere can be significantly affected by the impact of the passage of an interplanetary shock (Matsushita et al., 1961; Brown et al., 1961; Ullaland et al., 1970). Enhanced precipitation of ∼ 10s keV electrons into Earth's atmosphere has been observed immediately and lasts up to ∼ 10 min when an interplanetary shock impacts the geospace system (Su et al., 2011; Yue et al., 2013).

The sudden changes in charged-particle fluxes in the inner magnetosphere, including both relativistic electrons in the radiation belt (Arnoldy, 1982; Blake et al., 1992; Li et al., 1993; Hudson et al., 1994; Tan et al., 2004; Zong et al., 2009; Hao et al., 2019) and energetic ions (Zong et al., 2012, 2017; Ren et al., 2016, 2017a) in the ring current region, are noted to be closely related to a SSC caused by the interplanetary shock impacting Earth's magnetosphere. These results suggest that a significant portion of energetic charged particles in the ring current and radiation belt and region could be produced even before the build-up of the enhanced ring current which produces the magnetic storm.

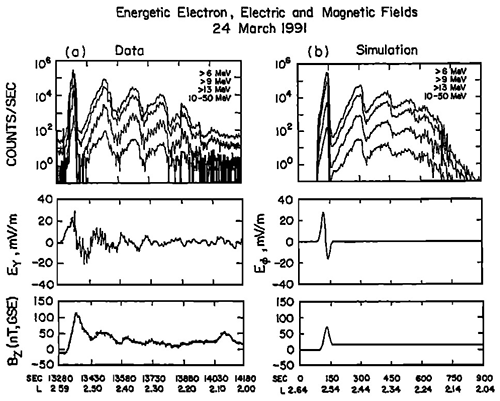
Figure 6 Satellite observation and simulation comparisons at the time of the 24 March 1991 SSC. Panels show four energetic electron channel measurements over 10–50 MeV, the measured electric field, the Bz magnetic field component and the simulated results in the same format at a spatial location corresponding to the trajectory of the CRRES satellite (Li et al., 1993).

Energetic particles of both electrons and ions up to 15 MeV have been observed in the radiation belt due to the impact of a strong interplanetary shock on Earth's magnetosphere on 24 March 1991 (Blake et al., 1992). It is believed that both relativistic ions and electrons are accelerated quickly by an induced electric field pulse generated by the passage of the interplanetary shock (Li et al., 1993; Hudson et al., 1994). A rapid (a few minutes) formation of a new electron radiation belt at L≃2.5 was observed in the slot region besides the inner and outer radiation belts, which lasted for a few years (Blake et al., 1994).

Let us assume that a running pulse with a bipolar electric field has been generated inside the magnetosphere by the compression and relaxation of Earth's magnetosphere caused by the interplanetary shock impinging on Earth's magnetosphere. As shown in Fig. 6, test particles interacting with this assumed asymmetric bipolar electric field pulse (“one kick”) caused by the passage of the interplanetary shock have been proposed to explain the newly formed electron radiation belt at L≃2.5 (Li et al., 1993; Hudson et al., 1994). This simulation has shown that a few MeV energetic electrons at L>6 could be energized up to 40 MeV and be radially transported to L≃2.5 during a fraction of their azimuthal drift period. The simulation results can reproduce the observed very energetic electron injection and their drift echoes. The acceleration process can be understood as the first adiabatic invariant being conserved (adiabatic acceleration) and the electrons being accelerated by the assumed single bipolar electric field pulse. The timescale of acceleration processes is about 1 min since the electromagnetic pulse would be running away in that time period. This is the so-called “one-kick” scenario of an interplanetary shock interacting with Earth's magnetosphere.

Since then, extensive test particle and MHD simulations have been carried out to study the particle acceleration related to the interplanetary shock impact (e.g., Hudson et al., 1995; Kress et al., 2007). It has been pointed out (Friedel et al., 2002) that the one-kick model was capable of reproducing some observational features for the event on 24 March 1991. However, it seems that the model can explain only this sole shock event and is not applicable for other interplanetary shock events in the magnetosphere. Thus, it remains unsettled how shock-related energetic particles are created and accelerated in the magnetosphere (Friedel et al., 2002; Baker et al., 2004).

2.2 Poloidal ULF wave–charged particle interaction scenario

In the magnetosphere, the energetic charged particles are mainly drifting in the azimuthal direction, with electrons drifting eastward and ions drifting westward. The electric field of poloidal-mode ULF waves also lies in the azimuthal direction. When both the drift direction of charged particles and the propagating direction of ULF waves are the same, the electric field carried by poloidal ULF waves would accelerate/decelerate the drifting charged particles. However, it should be noted that only those resonant electrons with a drift speed of approximately the wave propagation speed of the poloidal-mode ULF wave could gain energy constantly. Charged particles bearing both the acceleration and deceleration processes would cancel out, with a relatively small energy gain during one wave period.

As we have already shown in the introduction, ULF waves in Earth's magnetosphere could be excited by the impinging of positive or negative solar wind dynamic pressure pulses. Energetic charged-particle fluxes modulated by ULF waves in the Pc5 band were first found by Brown et al. (1961). A close correlation between the charged-particle flux variations and the intensity of ULF waves has been found for both case studies (e.g., Tan et al., 2004; Zong et al., 2007) and statistical surveys (e.g., Rostoker et al., 1998; Mathie and Mann, 2001; O'Brion et al., 2003).

Due to the comparable periods between the drift and bounce motions of the charged particles and the ULF waves in the inner magnetosphere, drift resonance or drift–bounce resonance may be satisfied. One-to-one correlation between ULF wave cycles and fluctuations of charged-particle fluxes have been found, which indicates ongoing wave–particle interactions, and the interactions would accelerate the magnetospheric particles significantly (Zong et al., 2007, 2009, 2017).

Now, tremendous efforts have been made to understand how the interplanetary shocks affect the charged particles in radiation belt and ring current region. By using observations from the Cluster and Double Star constellation, it has been found that, after solar wind dynamic pressure pulses impinging upon the magnetosphere, the acceleration of radiation belt energetic electrons could start immediately and can last for up to a few hours (Zong et al., 2009, 2012, 2017). The prime acceleration mechanisms are drift resonance or drift–bounce resonance, with ULF waves excited by the interplanetary shock impacting the magnetosphere.

A direct observation of such a ULF wave–charged particle interaction scenario is shown in Fig. 7. The onset of strong ULF waves is associated closely with a strong interplanetary shock impact on the magnetosphere on 7 November 2004. At the same time, the energetic electrons are accelerated quickly and are directly one-to-one correlated with the shock-induced ULF waves. As shown in Fig. 7, at 18:27 UT on 7 November 2004, an interplanetary shock with a maximum dynamic pressure of ∼ 70 nPa hit the magnetosphere. At the same time, large-amplitude ULF waves with electric fields of ∼ 40 mV m⁻¹ were observed when a Cluster spacecraft fleet moved on the morning side of the plasmasphere. The ULF waves are excited by the IP shock impinging on the magnetosphere. The one-to-one correlations between the flux variations of energetic electrons and the ULF wave oscillations suggest that the shock-induced ULF waves cause the observed charged-particle acceleration.

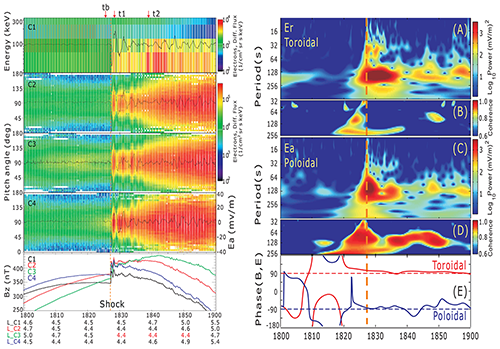
Figure 7 Left: from top to bottom, (a) the energetic electron spectrum, the pitch angle distributions overplotted with azimuthal electric field Ea (black line) in the mean-field-aligned (MFA) coordinate system, and (e) the magnetic field Bz components. The dashed vertical line shows the interplanetary shock arrival time. Right: measurements from Cluster C3. (a) Continuous wavelet power spectrum of the radial electric field, (b) the squared wavelet coherence between the radial electric field and the integrated energetic electron flux, and (c–d) the same for the azimuthal electric field. (e) Phase difference between electric fields and magnetic fields for the toroidal mode (red) and poloidal mode (blue), indicating that both the poloidal and toroidal modes are standing waves (Zong et al., 2009).

With an amplitude as high as 40 mV m⁻¹, the electric field of poloidal ULF waves on the charged-particle drift path can double the energy of electrons by a few hundred keV in only several wave periods. This is much faster than other acceleration processes, e.g., gyro resonances via VLF waves, suggesting that the observed ULF waves are sufficient to explain the observed electron acceleration through drift resonance.

The toroidal and poloidal modes have similar wave powers; however, coherences between the electric fields for both poloidal- and toroidal-mode ULF waves and the integrated energetic electron flux are rather different based on the wavelet technique (Grinsted et al., 2004). The high coherences of above 0.9 appear continuously and only with the poloidal-mode ULF waves. This confirms that the energetic electrons are accelerated predominantly by the poloidal wave-carried electric field.

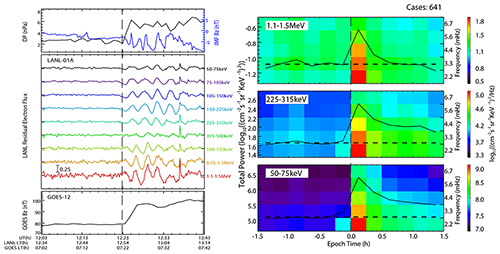
Figure 8 Left: the response of the magnetic field and electron fluxes at geosynchronous orbit to an IP shock on 29 May 2003. Left: shifted interplanetary magnetic field (IMF) and solar wind dynamic pressure observed by ACE. The vertical dashed line indicates the shock arrival time at geosynchronous orbit. Energetic electron fluxes measured by LANL satellite (LANL-01A); the response of the geosynchronous magnetic field observed by GOES 12. Right: superposed epoch analysis of 641 dynamic power spectra of the electron fluxes at geosynchronous orbit related to IP shocks. Bottom to top: median value of the dynamic power spectrum of the electron fluxes for nine channels (50–75 keV, 225–315 keV, and 1.1–1.5 MeV). Epoch time zero is denoted by the black vertical dashed line (after Liu and Zong, 2015).

This scenario has been further examined by systematic statistical study based on geosynchronous energetic particle observations for 215 interplanetary shock events during 1998–2007 (Liu and Zong, 2015). It is shown that electron fluxes with an energy of less than ∼ 300 keV increase after the shock impact, whereas electron fluxes with an energy of higher than ∼ 300 keV show smaller increases, become unchanged or even decrease eventually at geosynchronous orbit (Fig. 8). The electron flux oscillations following the shock arrival have also been investigated. Statistical analyses revealed a frequency preference for energetic electron flux oscillations of 2.2 and 3.3 mHz (Liu and Zong, 2015). The compressional effect of IP shocks can cause acceleration due to both magnetic field magnitude enhancement and the related azimuthal electric field. The electron fluxes increasing or decreasing are dependent on the pre-conditional phase-space density profile. The energy change in electrons is attributed to the compressional effect of interplanetary shocks and the interaction with shock-induced ULF waves.

It is also indicated that energetic electrons with low energy (high energy) will resonate with high-m (low-m) ULF waves and have different modulation features. The results show the magnetospheric response to ULF waves excited by the interplanetary shock impact from the energetic particle point of view.

In brief, the interplanetary shock related to energetic electron acceleration in the radiation belt starts almost immediately following the shock arrival. The acceleration process includes two contributing steps: the first acceleration is related to the initial magnetospheric compression by the interplanetary shock impact and then immediately followed by drift-resonant or drift–bounce-resonant acceleration by poloidal ULF waves excited by the passage of the interplanetary shock (Zong et al., 2009, 2012, 2017). This is the shock-induced ULF wave–particle interaction scenario. Such a scenario in shock-induced ULF waves' interaction with charged particles has been further confirmed by many other satellite observations (Clauderpierre et al., 2013; Foster et al., 2015; Korotova et al., 2018).

3 Generalized theory on the drift resonance

In this section, the traditional drift resonance theory will be introduced first, and then the generalized drift resonance theory on charged particles resonating with growth and damping ULF waves and charged particles resonating with azimuthally localized ULF waves will be described. Finally, I will show how radiation belt relativistic electrons resonate with localized growth and damping ULF waves in detail.

In the magnetosphere, the frequencies of ULF waves are comparable to the frequency of a charged particle's drift or bounce motion. Analogous to gyro resonance, it was suggested in the 1960s that charged particles trapped by Earth's magnetic field could resonantly interact with ULF waves standing on a field line through the particles' bounce and drift motions (Dungey, 1964; Southwood, 1969).

The drift–bounce resonance condition is written as

$$\begin{array}{}\text{(3)}& \mathit{\omega }-m\cdot {\mathit{\omega }}_{\mathrm{d}}=N\cdot {\mathit{\omega }}_{\mathrm{b}},\end{array}$$

where N is an integer (normally 0, ±1, and ±2), m represents the azimuthal wave number, and ω, ω_d and ω_b are wave frequency, particle drift and bounce frequencies, respectively. Since ω_d and ω_b depend on the charged particle's energy, for a given location, the resonance energy can be determined in theory if the ULF wave's frequency is known. To meet the resonance condition, the wave azimuthal propagation direction needs to be the same with the particle gradient and curvature drift direction, i.e., eastward propagation wave (positive m) for electrons and westward propagation wave (negative m) for ions.

The charged particles are moving in the electric field carried by the ULF waves during their drift–bounce motions, and thus their energy can be accordingly changed. The energy change rate of a charged particle interacting with poloidal-mode ULF waves can be written as in Southwood and Kivelson (1981, 1982):

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{\mathrm{d}W}{\mathrm{d}t}}=\mathit{\mu }{\displaystyle \frac{\partial B_{\mathrm{P}}}{\partial t}}+qE\cdot V_{\mathrm{d}},\end{array}$$

where $\frac{\mathrm{d}W}{\mathrm{d}t}$, E, V_d, and μ are the change rate of the particle energy, the wave electric field, the particle drift velocity and the particle magnetic moment, respectively. The subscript p denotes the component parallel to the background magnetic field.

For energetic electrons resonant with ULF waves, the bounce frequency is usually much higher than the wave frequency and the particle's drift frequency (Zong et al., 2009). Therefore, charged particles' interaction with ULF waves via the drift–bounce resonance can only be excited at N=0 (fundamental mode), as shown in Fig. 9. In this way, the drift–bounce resonance degenerates to the drift resonance; the bounce motion has no relationship with the ULF wave–particle interaction.

$$\begin{array}{}\text{(5)}& \mathit{\omega }=m\cdot {\mathit{\omega }}_{\mathrm{d}}\end{array}$$

Once the drift resonance condition is satisfied, the resonant electrons with fundamental-mode ULF waves seem to be stagnant azimuthally in the ULF wave moving frame. Thus, the resonant electrons can be accelerated very quickly since only a one-directional electric field can be experienced by the resonant electrons. Resonating with the fundamental poloidal ULF waves is a very efficient way to accelerate electrons in the radiation belt region since the electric field of poloidal ULF waves is the same as the charged-particle drift direction (Zong et al., 2009, 2017; Hao et al., 2019).

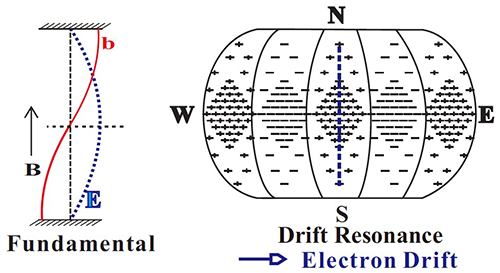
Figure 9 Fast acceleration of electrons by resonating with poloidal ULF waves. A schematic of N=0 drift resonance in a fundamental-mode standing wave. The eastward and westward electric fields are indicated by plus and minus, respectively, and their magnitudes correspond to the density of the symbols.

3.1 Generalized drift resonance with growth and damping ULF waves

In the traditional drift resonance theory, the ULF wave growth rate is assumed to be time-independent and positive, and the amplitude of the ULF wave is extremely small. This is not in agreement with satellite observations in the magnetosphere, and the interplanetary-shock-induced ULF waves usually have huge amplitudes and experience growth (a positive growth rate) and damping (a negative growth rate) stages (Zong et al., 2009; Zhang et al., 2010; Liu et al., 2010). Thus, a more generalized theory dealing with the interaction between ULF waves and charged particles in the magnetosphere for a time-dependent ULF wave evolution is required.

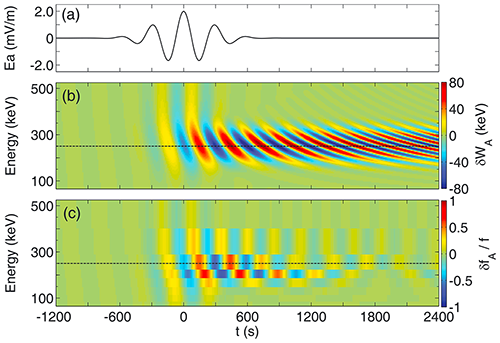
Figure 10 Energetic electrons' interaction with a ULF wave during its growth and damping stages. (a) ULF wave-associated electric field in the azimuthal direction, (b) electron energy gain from the ULF wave as a function of time and energy, with the resonant energy of 250 keV represented by the dashed line, and (c) predicted spectrum of electron residual phase-space densities observed by a magnetic electron ion spectrometer (MagEIS)-like particle detector with finite time and energy resolution (Zhou et al., 2016).

A drift resonance theory with growth and damping ULF waves has been developed (Zhou et al., 2016; Zong et al., 2017). In there, a time-dependent imaginary wave frequency has been adopted to describe the growth and damping of the waves in the generalized drift resonance theory; therefore, the interactions between charged particles and growth and damping ULF waves can be studied (Zhou et al., 2016; Zong et al., 2017).

The generalized drift resonance theory with growth and damping ULF waves allows a time-dependent ULF wave growth rate, which is large and positive in the wave's leading growth phase and decreases to negative values gradually in the damping phase. This assumption is based on ULF waves excited by the interplanetary shock impact on the magnetosphere (Tan et al., 2004; Zong et al., 2009; Zhang et al., 2010; Clauderpierre et al., 2013; Foster et al., 2015; Korotova et al., 2018; Hao et al., 2019).

The wave-associated electric field can be given by

$$\begin{array}{}\text{(6)}& E=E_{\mathit{\varphi }}{e}^{-\frac{t^{\mathrm{2}}}{{\mathit{\tau }}^{\mathrm{2}}}}{e}^{i\left(m\mathit{\varphi }-{\mathit{\omega }}_{\mathrm{r}}t\right)}{e}_{\mathit{\varphi }},\end{array}$$

where τ is the timescale of wave growth and decay, ϕ is the magnetic longitude (increasing eastward), ω_r is the real part of the wave angular frequency, and m is the wave azimuthal wave number. Equation (6) describes a Gaussian amplitude envelope of the electric field oscillation.

The change rate of a particle's kinetic energy within the waves is given by

$$\begin{array}{}\text{(7)}& {\displaystyle \frac{\mathrm{d}W}{\mathrm{d}t}}=qE\cdot v_{\mathrm{d}},\end{array}$$

where W is a particle's kinetic energy, q is a particle's charge, and v_d is the magnetic gradient and curvature drift velocity. In the terrestrial dipole field, it is approximated by

$$\begin{array}{}\text{(8)}& v_{\mathrm{d}}=-{\displaystyle \frac{\mathit{\gamma }+\mathrm{1}}{\mathrm{2}\mathit{\gamma }}}{\displaystyle \frac{\mathrm{6}{L}^{\mathrm{2}}W}{q{B}_{\mathrm{E}}{R}_{\mathrm{E}}}}\left(\mathrm{0.35}+\mathrm{0.15}\sin {\mathit{\alpha }}_{\mathrm{eq}}\right)e_{\mathit{\varphi }},\end{array}$$

where R_E is Earth's radius, B_E is the equatorial magnetic field on Earth's surface, L is the L-shell parameter, and γ is the relativistic Lorentz factor. For a nonrelativistic, equatorially mirroring particle, v_dv_d can be rewritten as

$$\begin{array}{}\text{(9)}& v_{\mathrm{d}}=-{\displaystyle \frac{\mathrm{3}{L}^{\mathrm{2}}W}{q{B}_{\mathrm{E}}{R}_{\mathrm{E}}}}{e}_{\mathit{\varphi }}.\end{array}$$

Therefore, the change rate of kinetic energy can be rewritten as

$$\begin{array}{}\text{(10)}& {\displaystyle \frac{\mathrm{d}W}{\mathrm{d}t}}=-{\displaystyle \frac{\mathrm{3}{L}^{\mathrm{2}}W}{B_{\mathrm{E}}{R}_{\mathrm{E}}}}{E}_{\mathit{\varphi }}{e}^{\frac{t^{\mathrm{2}}}{{\mathit{\tau }}^{\mathrm{2}}}}{e}^{i\left(m\mathit{\varphi }-{\mathit{\omega }}_{\mathrm{r}}t\right)},\text{(11)}& {\displaystyle }\mathit{\delta }W=-{\displaystyle \frac{\sqrt{\mathit{\pi }}}{\mathrm{2}}}{\displaystyle \frac{\mathrm{3}{L}^{\mathrm{2}}W}{B_{\mathrm{E}}{R}_{\mathrm{E}}}}\cdot E_{\mathit{\varphi }}k\left(\mathit{\tau }\right)g\left(t,\mathit{\tau }\right)\exp i\left(m\mathit{\varphi }-m{\mathit{\omega }}_{\mathrm{d}}t\right),\end{array}$$

which indicates that the frequency of δW is mω_d rather than ω_r. Here k(τ) and g(t,τ) are defined by

$$\begin{array}{}\text{(12)}& {\displaystyle }k\left(\mathit{\tau }\right)=\mathit{\tau }\exp \left[{\displaystyle \frac{-{\left(m{\mathit{\omega }}_{\mathrm{d}}-{\mathit{\omega }}_{\mathrm{r}}\right)}^{\mathrm{2}}{\mathit{\tau }}^{\mathrm{2}}}{\mathrm{4}}}\right],\text{(13)}& {\displaystyle }g\left(t,\mathit{\tau }\right)=\mathrm{erf}\left({\displaystyle \frac{t}{\mathit{\tau }}}-i{\displaystyle \frac{m{\mathit{\omega }}_{\mathrm{d}}\mathit{\tau }-{\mathit{\omega }}_{\mathrm{r}}\mathit{\tau }}{\mathrm{2}}}\right)+\mathrm{1}.\end{array}$$

As we can see from Fig. 10, with the wave amplitude increasing, the electron flux phase-space density (PSD) oscillates with a gradual enhancement, and the phase difference between electrons with a lower and higher energy changes from a small value to ∼ 180° when the amplitude of the ULF wave stops growing, whereas, in the ULF wave damping stage, both the variations of energetic electron PSD and the phase shift between electron fluxes with different energies continue to increase till the phase-mixing effect attenuates the particle PSD oscillations. A distorted energy spectrum can be expected as the results of energetic electrons resonating with a growth and damping ULF wave.

Resonant charged-particle signatures can be explained by the generalized theory, whereas equations in the traditional drift resonance theory are invalid. It is found that the distorted energy spectrum predicted from the generalized theory for the interactions between charged particles and growth and damping ULF waves is in very good agreement with observations from Van Allen Probes. Thus, the generalized theory for drift resonance with growth and damping ULF waves can provide new insights into the interactions between ULF waves and charged particles in the magnetosphere.

3.2 Generalized drift resonance with localized ULF waves: “boomerang” pitch angle distribution

ULF waves in the traditional drift resonance theory are considered to be globally distributed, and the amplitude of ULF waves is azimuthally uniform, i.e., independent of magnetic longitude (magnetic local time). However, the observations have suggested that there may be localized ULF waves. Pitch angle distribution of boomerang stripes is found to be the result of drift dispersion among resonant charged particles interacting with localized ULF waves in an azimuthally distant region of the magnetosphere (Hao et al., 2017; Zong et al., 2017). Therefore, we have introduced a magnetic longitude dependence of the ULF wave amplitude into generalized drift resonance with localized ULF waves.

As shown in Li et al. (2017), the von Mises function is adopted to study the effect of a localized ULF wave (magnetic longitude dependence) in the ULF wave–charged particle interaction. The spatial localized ULF waves described here are transverse, poloidal ULF waves with azimuthal electric field oscillations, whereas the temporal evolution of these ULF waves is the same as the traditional one (e.g., Southwood and Kivelson, 1981), i.e., the wave is time-independent and very small in terms of the wave magnitude.

The electric field of the localized ULF waves is given by

$$\begin{array}{}\text{(14)}& \begin{array}{rl}E\left(t,\mathit{\varphi }\right)& ={\displaystyle \frac{E_{\mathit{\varphi }\mathrm{0}}}{\mathrm{2}\mathit{\pi }{I}_{\mathrm{0}}\left(\mathit{\xi }\right)}}\exp \left[\mathit{\xi }\cos \left(\mathit{\varphi }-{\mathit{\varphi }}_{\mathrm{0}}\right)\right]\\ & \cdot \exp i\left(m\mathit{\varphi }-\mathit{\omega }t\right){\widehat{e}}_{\mathit{\varphi }},\end{array}\end{array}$$

where m is the ULF wave number, ϕ is the magnetic longitude (increasing eastward), and ω is the ULF wave angular frequency.

Thus, the average rate of the particle energy gain from the transverse ULF waves is (Northrop, 1963)

$$\begin{array}{}\text{(15)}& {\displaystyle \frac{\mathrm{d}{W}_A}{\mathrm{d}t}}={\displaystyle \frac{q{v}_{\mathrm{d}\mathit{\varphi }}{E}_{\mathit{\varphi }\mathrm{0}}}{\mathrm{2}\mathit{\pi }{I}_{\mathrm{0}}\left(\mathit{\xi }\right)}}\exp \left[\mathit{\xi }\cos \left(\mathit{\varphi }-{\mathit{\varphi }}_{\mathrm{0}}\right)\right]\cdot \exp i\left(m\mathit{\varphi }-\mathit{\omega }t\right),\end{array}$$

where the subscript A denotes the average over many gyration periods, q is the particle's charge, and V_dϕ is the azimuthal component of the particle's drift speed.

The azimuthal drift speed V_dϕ of the particle can be obtained from the following equation if an equatorially mirroring particle is considered in the dipole field

$$\begin{array}{}\text{(16)}& V_{\mathrm{d}\mathit{\varphi }}=-\mathrm{3}{L}^{\mathrm{2}}W/\left(q{B}_{\mathrm{E}}{R}_{\mathrm{E}}\right),\end{array}$$

where L is the L-shell number, R_E is Earth's radius, and B_E is the magnitude of the equatorial magnetic field.

Then, the energy gain δW_A from the ULF waves can be obtained if we integrate dW_A $/$ dt along the particle's unperturbed drift orbit.

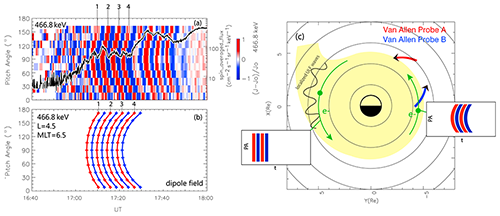
Figure 11 Comparison between observed boomerang stripes and pitch angle dispersion by the time-of-flight backward-tracing method. (a) Pitch angle evolution of 466.8 keV electrons. (b) Arrival time estimation for peaks and valleys of 466.8 keV electrons with pitch angle varying from 5 to 175°. Electron drift velocity is calculated in the terrestrial dipole field with the relativistic effect included. (c) A diagram for the pitch angle evolution of electrons interacting with localized ULF waves. The plasmasphere is indicated in yellow.

Keeping this in mind, the generalized drift resonance theory of particles' interaction with localized ULF waves is applicable for the event mentioned in Li et al. (2017) and for the pitch angle evolution of “Boomerang-shaped” by Hao et al. (2017), which used Chinese navigation satellite and Van Allen Probe data. The boomerang-shaped pitch angle evolutions of relativistic electrons appear immediately after an interplanetary shock impinges on the magnetosphere on 7 June 2014 as shown in Fig. 11. The observed electron flux at different pitch angles is strongly modulated by ULF waves excited by the interplanetary shock impact.

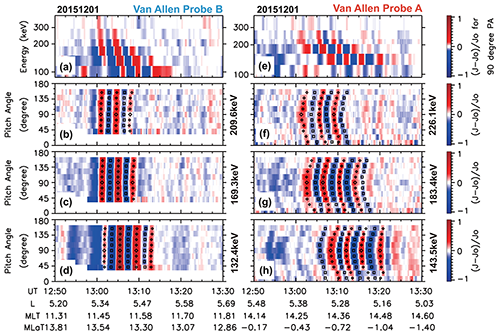
Figure 12 Observed data of electrons from MagEIS-A and MagEIS-B on 1 December 2015. (a) Residual flux profile in the energy-versus-time plot from MagEIS-B. (b–d) Residual flux profile in the pitch-angle-versus-time plot of energies 209.6, 169.3 and 132.4 keV. Rhombuses and squares are maximum and minimum points on the residual flux of stripes. (e) The same as (a) but from MagEIS-A in the same time interval. (f–h) The same as (b) but for 226.1, 183.4 and 143.5 keV measured from MagEIS-A (Zhao et al., 2020).

As demonstrated in Fig. 11, shock-induced ULF waves are suggested to be confined in a limited azimuthal region (possibly the plasmaspheric plume), which is westward of the Van Allen Probe spacecraft. Then, ULF wave-modulated energetic electrons drift out of the ULF wave–charged particle interaction region before they are observed by the distant spacecraft. The drift speed of the modulated energetic particle depends on its energy and pitch angle. The difference in energy and pitch angle of the energetic electrons would produce a drift dispersion; i.e., equatorially mirroring 90° pitch angle electrons would drift more quickly and be observed first. This effect will lead to distorted particle pitch angle stripes to form boomerang-shaped evolutions in pitch angle spectra for each electron energy band. The observed boomerang stripes as well as modulations in the electron energy spectrogram can be reproduced by using the time-of-flight backward-tracing method (Hao et al., 2017; Zong et al., 2017).

Furthermore, ULF wave–radiation belt electron drift resonance can be depicted by quasi-periodic stripes, either straight or boomerang-shaped, in the pitch angle spectrum of electron fluxes as shown in Figs. 12 and 13. Boomerang-shaped stripes on pitch angle distribution are evolved from straight ones after resonant electrons drift away from the azimuthally localized ULF wave–particle interaction region. Also, it provides a new method based on the time-of-flight tracing technique to identify the region of ULF waves interacting with particles. Thus, it is crucial to take both the spatial distribution and temporal evolution of ULF waves into consideration for both drift resonance and drift–bounce resonance (Zhao et al., 2020).

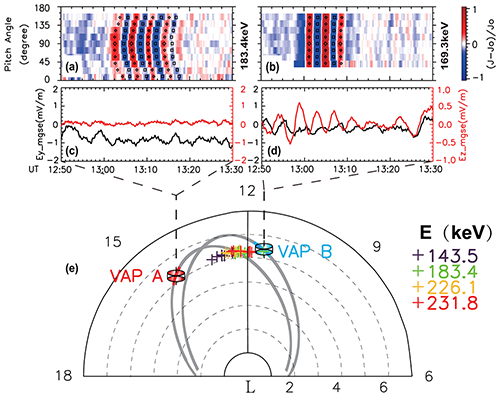
Figure 13 Pitch angle distribution observed by Van Allen Probe A and Van Allen Probe B. (c) The source places and Van Allen Probe orbits in the equatorial plane. These cross-shaped symbols represent the results from the time-of-flight backward-tracing method from Van Allen Probe A. The local time labeled is magnetic local time, while numbers on the x axis are L-shells (Zhao et al., 2020).

The study of boomerang-shaped evolutions in pitch angle spectra would tell us not only where the drift resonance is taking place, but also the possible scale size of the ULF wave–particle interaction at a location distant from the spacecraft. These results add new understanding to the radiation belt dynamics.

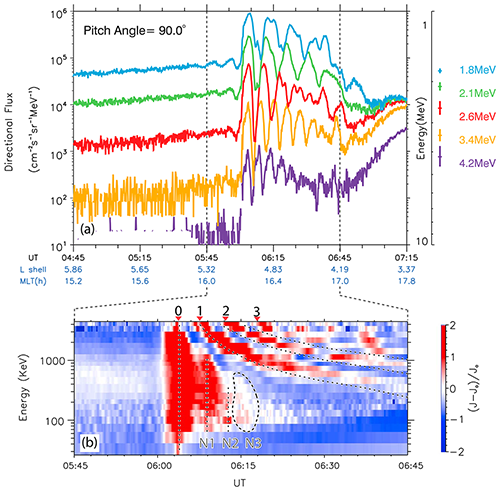
Figure 14 The response of electrons to the storm sudden commencement. (a) 90° relativistic and ultra-relativistic electron fluxes measured. The width of each energy channel is plotted on the right of the panel. (b) Residual flux ($J-J_{\mathrm{0}}/J_{\mathrm{0}}$) of 90° electrons in the energy-versus-time plot. Dashed lines with numbers 1, 2, and 3 give the predicted energy-dependent arrival times of the first, second, and third drift echoes of the initial flux enhancement (as marked with the vertical dashed line 0). N1, N2, and N3 indicate series of ultra-low-frequency modulation to the population not in resonance with the m = 1 mode ultra-low-frequency wave, of which the arrival time does not match the prediction of drift echoes. MLT: magnetic local time (Hao et al., 2019).

3.3 Radiation belt “relativistic electron” acceleration by drift resonance

What will happen if charged particles are in drift resonance with both growth and damping ULF waves and localized ULF waves? An excellent example is given in Fig. 14, and relativistic energetic electrons resonating with localized growth and damping ULF waves can lead to very rapid ultra-relativistic electron acceleration in the radiation belt region.

As shown in Fig. 14, strong intensifications of relativistic and ultra-relativistic electron fluxes have been observed by Van Allen Probe B following an interplanetary shock impact on Earth's magnetosphere during the 16 July 2017 SSC. This is the result of ultra-relativistic electrons in the outer radiation belts interacting with the interplanetary-shock-excited ULF waves.

The relativistic and ultra-relativistic electron fluxes oscillate strongly in the ULF Pc5 frequency range (Fig. 14). For a relativistic electron with an energy above ∼ 1 MeV, the oscillation periods modulated by the ULF waves are close to its drift period in the magnetosphere. Thus, the evolution of the energy spectrogram modulated by ULF waves resembles energetic electron injection with its drift echoes. At lower energy, nevertheless, the electron oscillation period is controlled predominantly by ULF waves, which is almost independent of its energy.

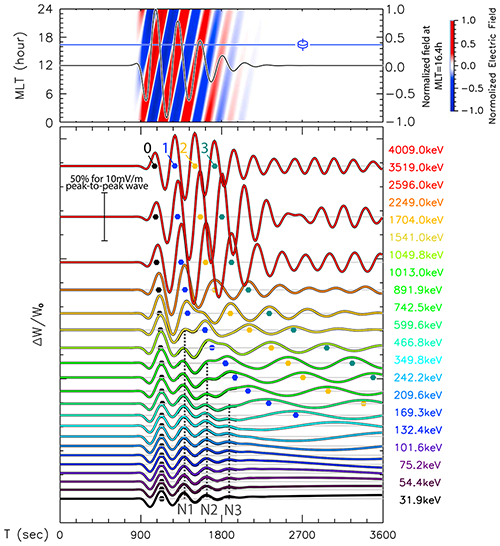
Figure 15 Simulated electron responses in comparison with observations shown in Fig. 14. The normalized electric field is a function of magnetic local time and time. The imaginary probe is placed at MLT = 16.4 h, as marked with the blue line. The electric field near the imaginary probe has been overplotted with the black line. Bottom: predicted net energy gain of electrons in the electric field of the m = 1 poloidal wave with a sudden onset and a fast-damping stage in their undisturbed drifting motions. The peaks of energy gain in the time sequence of the near-resonant channels marked with colored dots 0, 1, 2, and 3 correspond to the first (dispersionless) and following (dispersive) stripes 0, 1, 2, and 3 in Fig. 14. The vertical dashed lines N1, N2, and N3 refer to the simulated energy dispersionless modulations in the energy channels far from resonance.

According to the generalized drift resonance theory on charged particles resonating with growth and damping ULF waves (Zhou et al., 2016; Zong et al., 2017), the frequency of charged-particle flux modulations will shift from the wave frequency to mω_d if the ULF waves have decayed, and tilted stripes would be formed in the energy spectrum. When ULF waves disappeared, the formed acceleration and deceleration of charged-particle stripes will keep drifting with their respective speeds. Energy-dependent drift motion along the drift orbit between the interaction region and the spacecraft causes the charged-particle flux oscillation (Fig. 15).

As indicated in Fig. 15, the spacecraft observations and numerical simulations based on the generalized charged-particle drift resonance theory with both growth and damping ULF waves and localized ULF waves agree with each other extremely well.

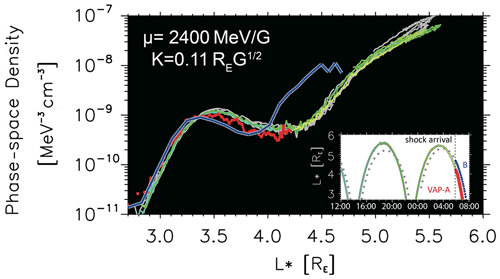
Figure 16 Radial profile of electron phase-space density (PSD) at μ=2400 MeV G⁻¹, $K=\mathrm{0.11}{R}_{\mathrm{E}}\cdot G\sim \mathrm{1}/\mathrm{2}$ measured by the Relativistic Electron–Proton Telescope (REPT) on board Van Allen Probes. Red (blue) curve presents the PSD measurement from Probe A (Probe B) after the shock arrival. Blue-to-green (gray) curve presents the PSD measured by Probe A (Probe B) before the shock arrival. Inset: the L^* value as a function of universal time of Van Allen Probes from 12:00 15 July to 08:00 16 July 2017. Vertical dashed line denotes the shock arrival.

Figure 16 presents the phase-space density of ultra-relativistic electrons during the 16 July 2017 interplanetary shock. Before the shock arrival, the PSD distribution $f\left(L^{*}\right)|\mathit{\mu }$, K remained almost unchanged. After the shock arrival, the electron distribution was significantly modified by the interplanetary shock impact within 2 h, and the PSD enhancement of over an order of magnitude is found at 4<L^*<4.5 (Hao et al., 2019).

It has been found that the shock-induced ULF waves with an azimuthal wave number of 1 were the dominant component. Within an hour, the relativistic electron can be accelerated by as much as more than 10 times in terms of electron flux (Fig. 16) by observed ULF waves (Hao et al., 2019). Therefore, ULF waves are very powerful for accelerating ultra-relativistic electrons in the radiation belt. The energy spectrum of relativistic electrons has confirmed that ULF waves triggered by the interplanetary shock impact can accelerate outer radiation belt ultra-relativistic electrons up to 3.4 MeV very efficiently in less than an hour (Fig. 16). Also, when an interplanetary shock impinges on the magnetosphere, besides the initial adiabatic acceleration, the spectrum of magnetospheric electrons will be rotated first (Wilken et al., 1986). Further, additional acceleration can happen via drift resonance with ULF waves (Zong et al., 2009, 2017).

In brief, the radiation belt ultra-relativistic electrons can be effectively accelerated by interplanetary-shock-induced ULF waves within an hour. It has been shown that these observed complex and mixed signatures are consistent with the generalized drift resonance between relativistic electrons and localized ULF waves with both growth and damping features. The observed main features of ultra-relativistic electrons can be reproduced well by numerical results based on the generalized ULF wave–particle drift resonance scenario. This suggests that the generalized drift resonance theory with both growth and damping ULF waves and localized ULF waves is valid and needs to be taken into account for the radiation belt dynamics.

4 Generalized theory on the drift–bounce resonance

In this section, the classical drift–bounce resonance concept will be introduced first. Then, a more generalized theory will be described on charged particles' drift–bounce resonance with growth and damping ULF waves. Finally, I will show how poloidal ULF waves interact with a cold plasmaspheric population and the ionospheric outflow.

As mentioned in the above section, the classical drift–bounce resonance condition can be expressed as $\mathit{\omega }-m\cdot {\mathit{\omega }}_{\mathrm{d}}=N\cdot {\mathit{\omega }}_{\mathrm{b}}$, where N is an integer (normally 0, ±1, ±2), m represents the azimuthal wave number, and ω,ω_d and ω_b are the ULF wave frequency and the drift and bounce frequencies of the charged particles in the magnetosphere, respectively. In Earth's magnetosphere, the bounce frequency of an ion (especially heavy ions, e.g., oxygen ions) is close enough to its drift as well as ULF wave frequencies. Thus, the bounce motion must be considered for charged particle–ULF wave interactions. Charged particles' drift and bounce frequencies (ω_d and ω_b) are dependent on their kinetic energy; thus, the energy of resonant particles can be decided if the ULF wave frequency and azimuthal wave number m are already known.

Since the gradient and curvature drifts of charged particles are in the azimuthal direction in Earth's magnetosphere, the energies of charged particles can be affected significantly by azimuthal electric field oscillations of poloidal ULF waves. This drift–bounce resonance occurs when particles with a certain energy match the local drift–bounce resonance condition. If the ULF waves are the second harmonic, these resonant charged particles could experience a one-directional electric field, as shown in Fig. 17. This will lead to fast acceleration of charged particles.

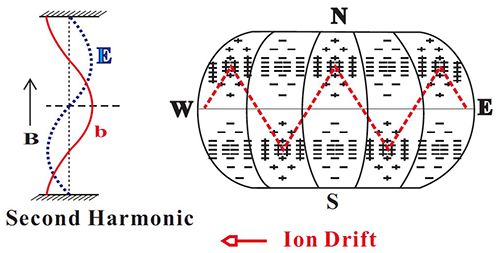
Figure 17 Fast acceleration of charged particles by the second-harmonic poloidal ULF wave. A schematic of resonant charged particles satisfying the N=1 drift–bounce resonance condition in a second-harmonic standing wave. The westward electric fields are indicated by plus and minus, and their magnitudes correspond to the density of the symbols.

Figure 17 shows the ions satisfying the N=1 drift–bounce resonance condition in a second-harmonic ULF wave (Zong et al., 2017). The particle behavior is examined in a stretched string model in the wave frame. The westward electric fields are indicated by plus and minus, with their magnitudes corresponding to the density of the symbols. The red dashed lines show the guiding center orbits of the resonant particles in a second-harmonic poloidal ULF wave.

It appears that the resonant ions always stay in the westward wave electric field within each bounce period and will gain a net energy continuously. However, if ions that satisfy the drift–bounce resonance condition in the fundamental mode are considered, these charged particles would experience an accelerating phase (westward electric field) and a decelerating phase (eastward electric field) within a single bounce period, and therefore its energy gain can be very small.

Also, if energetic electrons are considered, their guiding center motion will appear as a vertical line in the second-harmonic ULF wave. The acceleration and deceleration of the electron will cancel out completely over each bounce period. Thus, only in the fundamental-mode wave could the electron experience a fast acceleration over a wave cycle as shown in the previous section.

Thus, in principle, energetic ions in the second-harmonic poloidal standing waves will be accelerated much more efficiently compared to those in the fundamental-mode ULF waves. Furthermore, it has been pointed out that the charged particles in the ring current energy range, e.g., oxygen ions, could satisfy all $n=\pm \mathrm{1}$, ±2 drift–bounce resonance conditions easily. This implies that the drift–bounce resonance is preferred for oxygen ions and is potentially an important mechanism for the ring current oxygen acceleration (Zong et al., 2010, 2012, 2017; Ren et al., 2016, 2017a).

4.1 Drift–bounce resonance with growth and damping ULF waves: “fishbone” pitch angle distribution

In the classical drift–bounce resonance theory, the ULF wave growth rate is assumed to be time-independent and positive, and the amplitude of the ULF wave is extremely small. This does not agree with satellite observations in the magnetosphere, and the interplanetary-shock-induced ULF waves usually have huge amplitudes and experience growth (a positive growth rate) and damping (a negative growth rate) stages (Tan et al., 2004; Zong et al., 2009; Zhang et al., 2010; Liu et al., 2010). Thus, a more generalized theory dealing with time-dependent ULF waves' interaction with charged particles is required.

The change rate of the particle's kinetic energy within the growth and damping stages of the waves is given by Zhu et al. (2020) and Ren et al. (2019a):

$$\begin{array}{}\text{(17)}& {\displaystyle \frac{\mathrm{d}W}{\mathrm{d}t}}={\mathrm{\Sigma }}_{N=-\mathrm{\infty }}^{\mathrm{\infty }}\dot{W_N}{e}^{iN\mathit{\theta }}g\left(t\right)e^{i\left(m{\mathit{\omega }}_{\mathrm{d}}+m{\mathit{\varphi }}_{\mathrm{0}}-{\mathit{\omega }}_{\mathrm{r}}\right)t}.\end{array}$$

Here conventional notations are used. g(t) describes the growth and damping of the waves:

$$\begin{array}{}\text{(18)}& g\left(t\right)=\left\{\begin{array}{l}{e}^{{\mathit{\gamma }}_{\mathrm{1}}(t-t_{\mathrm{0}})},t<t_{\mathrm{0}},\\ e^{-{\mathit{\gamma }}_{\mathrm{2}}(t-t_{\mathrm{0}})},t>t_{\mathrm{0}}.\end{array}\right.\end{array}$$

For odd harmonic waves,

$$\begin{array}{}\text{(19)}& \begin{array}{rl}\mathit{\delta }W& \approx {\sum }_{l=\mathrm{0}}^{\mathrm{\infty }}\dot{a_{\mathrm{2}l}}\times \left(-i\right)\times {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}({\displaystyle \frac{\cos \mathrm{2}l\mathit{\theta }+i\sin \mathrm{2}l\mathit{\theta }}{\mathrm{2}l{\mathit{\omega }}_{\mathrm{b}}+m{\mathit{\omega }}_{\mathrm{d}}-{\mathit{\omega }}_{\mathrm{r}}}}\\ & +{\displaystyle \frac{\cos \mathrm{2}l\mathit{\theta }-i\sin \mathrm{2}l\mathit{\theta }}{-\mathrm{2}l{\mathit{\omega }}_{\mathrm{b}}+m{\mathit{\omega }}_{\mathrm{d}}-{\mathit{\omega }}_{\mathrm{r}}}})e^{i\left(m\mathit{\varphi }-{\mathit{\omega }}_{\mathrm{r}}t\right)}\\ & ={\sum }_{l=\mathrm{0}}^{\mathrm{\infty }}\dot{a_{\mathrm{2}l}}\times {\displaystyle \frac{i\left(\mathit{\omega }-m{\mathit{\omega }}_{\mathrm{d}}\right)\cos \mathrm{2}l\mathit{\theta }-\left(\mathrm{2}l{\mathit{\omega }}_{\mathrm{b}}\right)\sin \mathrm{2}l\mathit{\theta }}{{\left(m{\mathit{\omega }}_{\mathrm{d}}-\mathit{\omega }\right)}^{\mathrm{2}}-{\left(\mathrm{2}l{\mathit{\omega }}_{\mathrm{b}}\right)}^{\mathrm{2}}}}\\ & \times e^{i\left(m\mathit{\varphi }-{\mathit{\omega }}_{\mathrm{r}}t\right)}.\end{array}\end{array}$$

For even harmonic waves,

$$\begin{array}{}\text{(20)}& \begin{array}{rl}\mathit{\delta }W& \approx {\sum }_{l=\mathrm{0}}^{\mathrm{\infty }}{\dot{b}}_n\times {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}({\displaystyle \frac{\cos \left(\mathrm{2}l+\mathrm{1}\right)\mathit{\theta }+i\sin \left(\mathrm{2}l+\mathrm{1}\right)\mathit{\theta }}{\left(\mathrm{2}l+\mathrm{1}\right){\mathit{\omega }}_{\mathrm{b}}+m{\mathit{\omega }}_{\mathrm{d}}-{\mathit{\omega }}_{\mathrm{r}}}}\\ & -{\displaystyle \frac{\cos \left(\mathrm{2}l+\mathrm{1}\right)\mathit{\theta }-i\sin \left(\mathrm{2}l+\mathrm{1}\right)\mathit{\theta }}{-\left(\mathrm{2}l+\mathrm{1}\right){\mathit{\omega }}_{\mathrm{b}}+m{\mathit{\omega }}_{\mathrm{d}}-{\mathit{\omega }}_{\mathrm{r}}}})e^{i\left(m\mathit{\varphi }-{\mathit{\omega }}_{\mathrm{r}}t\right)}\\ & ={\sum }_{l=\mathrm{0}}^{\mathrm{\infty }}{\dot{b}}_n{\displaystyle \frac{\begin{array}{c}-i\left(\mathit{\omega }-m{\mathit{\omega }}_{\mathrm{d}}\right)\sin \left(\mathrm{2}l+\mathrm{1}\right)\mathit{\theta }\\ -\left(\mathrm{2}l+\mathrm{1}\right){\mathit{\omega }}_{\mathrm{b}}\cos \left(\mathrm{2}l+\mathrm{1}\right)\mathit{\theta }\end{array}}{{\left(\mathit{\omega }-m{\mathit{\omega }}_{\mathrm{d}}\right)}^{\mathrm{2}}-{\left(\mathrm{2}l+\mathrm{1}\right)}^{\mathrm{2}}{\mathit{\omega }}_{\mathrm{b}}^{\mathrm{2}}}}{e}^{i\left(m\mathit{\varphi }-{\mathit{\omega }}_{\mathrm{r}}t\right)}.\end{array}\end{array}$$

The simulation based on the generalized theory of drift–bounce resonance (Zhu et al., 2020) is employed to reproduce the time evolution of the pitch angle distributions of energetic protons observed by Van Allen Probe A on 28 January 2014 (Fig. 18). This event was first reported by Yamamoto et al. (2019); however, the temporal variations of inclination angles of each fishbone are not addressed.

As illustrated in Fig. 18, the inclination of pitch angle stripes increases, and fishbone-like structures appear in the proton pitch angle distribution when the waves are growing (Liu et al., 2020). According to the generalized drift–bounce resonance theory (Zhu et al., 2020; Liu et al., 2020; Ren et al., 2019a), the increasingly inclined stripes are the manifestation of increasing phase shift across resonant pitch angles. These observational features can be well predicted by the generalized drift–bounce resonance theory. The right column of Fig. 18 shows the simulation result. A notable feature is the time change in pitch angles at which flux oscillation is strongest. In other words, the resonant pitch angle changes with time. The black dashed lines illustrate this tendency. At the beginning, protons resonate at middle pitch angles, e.g., ∼ 60 and ∼ 120°, whereas, at the end, the resonance pitch angle of hydrogen ions is slightly moving away from middle pitch angles.

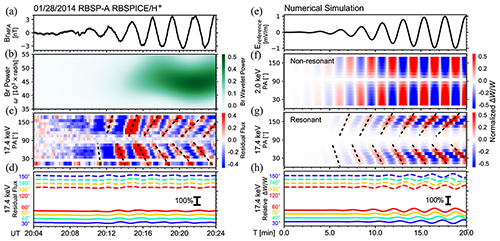
Figure 18 The pitch angle distribution of protons. (a–d) Van Allen Probe A observations. During the shown time interval, the waves grow. (a) Radial component (Br) of the magnetic field. (b) Dynamic power spectrum of Br. (c) Pitch angle distribution of 17.4 keV protons. The color code shows residual flux. As illustrated by the black dashed lines, the pitch angle stripes become more and more inclined. (d) Line version of (c). (e–h) Numerical simulation. (e) Electric field in the simulation observed by a virtual off-equatorial spacecraft. (f) Pitch angle distribution of 2.0 keV protons, which are far away from resonance. The color code shows normalized $\mathrm{\Delta }W/W$, which can be directly compared to residual flux. (g) Pitch angle distribution of resonant, 17.4 keV protons. The color code shows normalized $\mathrm{\Delta }W/W$ (Liu et al., 2020).

Drift–bounce resonance with growth and damping ULF waves can result in the increasingly inclined pitch angle stripes. When the amplitude of the ULF wave is growing, the stripes of the hydrogen ion pitch angle become more and more inclined. It is shown in Fig. 18 that the ULF waves resonate with 17.4 keV hydrogen ions at pitch angles around ∼ 40 and 140°.

At the beginning of the wave growth stage, the wave growth rate is large enough to “hide” the phase shift, causing relatively vertical stripes. Then, as the wave grows and its growth rate decreases to zero, the “hidden” phase shift gradually appears, causing the stripes to become more and more inclined. Fishbone-like pitch angle structures, thus, are formed by interaction with growth and damping ULF waves (Liu et al., 2020).

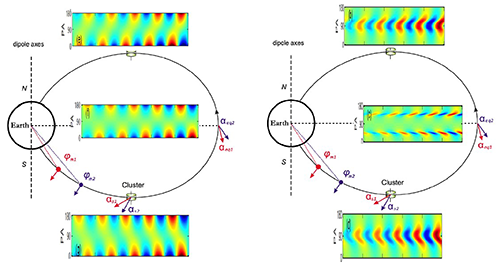
Figure 19 Generalized drift–bounce theory prediction on resonant ions with the second-harmonic ULF waves in the Southern Hemisphere, magnetic equator, and Northern Hemisphere. Left and right: non-resonant and resonant particles. A schematic of the time-of-flight effect as ions bounce along a magnetic field line. The red and blue ions have the same energy but different equatorial pitch angles. The symbols a_eq and a_s denote the equatorial pitch angle and the local pitch angle detected by the virtual satellite, respectively. Pitch angle distributions at different latitudes are shown qualitatively (after Zhu et al., 2020).

Figure 19 summarizes how non-resonant and resonant energetic ions respond to the second-harmonic growth and damping ULF waves as observed in the Southern Hemisphere, magnetic equator, and Northern Hemisphere. By analyzing spacecraft observations and reproducing them via the generalized drift–bounce resonance theory, it is found that time-varying phase shift across resonant pitch angles can indeed occur, and the effect caused by growth or damping of ULF waves is significant. As a result, the inclination of pitch angle stripes would increase or decrease with time, causing fishbone-like pitch angle structures.

It is important to note here that fishbone-like structures in ion pitch angle distribution observed by Van Allen Probes and THEMIS spacecraft can be well reproduced by the generalized drift–bounce resonance theory and therefore provide a more realistic picture of drift–bounce resonance in Earth's magnetosphere. Therefore, it is important to investigate the influence of the temporal variations of the wave growth rate on the flux oscillations and their phase shift. The generalized drift–bounce resonance theory sheds light on the wave–particle interaction between charged particles and ULF waves.

4.2 ULF waves' interaction with cold plasmaspheric charged particles

How do plasmaspheric charged particles of a very low energy (∼ eV) respond to ULF waves? For a plasmaspheric charged particle with an energy of a few eV, its drift frequency is much smaller than the bounce frequency: ω_d≪ω_b. Therefore, the drift–bounce resonance between the plasmaspheric charged particles and the ULF waves should be dominated by the bounce resonance: $\mathrm{\Omega }=N\cdot {\mathit{\omega }}_{\mathrm{b}}$.

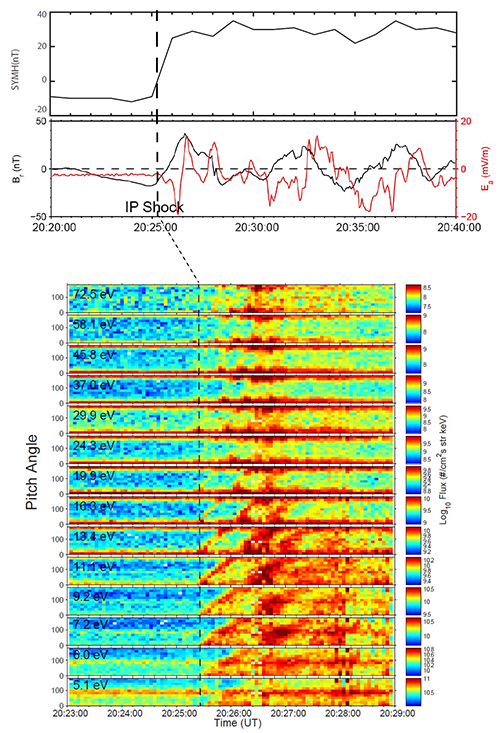
Figure 20 Top panel shows the SYM-H index, the poloidal (Br, Ea) wave magnetic and electric fields and pitch angle distributions of plasmaspheric electron response to the interplanetary shock impact. Representative electrons with pitch angle distributions for 14 energy channels ranging between 5 and 72.5 eV. The vertical dashed line marks the arrival time of the interplanetary shock at 20:25:10 UT (Zong et al., 2017).

However, once the drift–bounce resonance condition is satisfied, cold plasmaspheric electrons can still be affected by the poloidal-mode ULF waves (e.g., Pc5 band). Cold plasmaspheric electrons experience acceleration by the azimuthal electric field of poloidal-mode ULF waves, which is similar to drift–bounce resonance of oxygen or hydrogen ions (Zong et al., 2017; Ren et al., 2017a).

For the plasmaspheric population, the cold electron drift frequency (ω_d) would include both the gradient and curvature drift term (ω_d.gc), the convection E×B drift term (${\mathit{\omega }}_{\mathrm{d}.\mathrm{Econ}\times B}$) and the plasmaspheric corotation electric field term (${\mathit{\omega }}_{\mathrm{d}.\mathrm{Ecor}\times B}$) (Ren et al., 2017b):

$$\begin{array}{}\text{(21)}& {\mathit{\omega }}_{\mathrm{d}}=-{\displaystyle \frac{\mathrm{6}WLP\left(\mathit{\alpha }\right)}{q{B}_{\mathrm{E}}{R}_{\mathrm{E}}^{\mathrm{2}}}}+{\displaystyle \frac{\mathrm{2}{\mathrm{\Psi }}_{\mathrm{0}}{L}^{\mathrm{3}}\sin \mathrm{\Phi }}{B_{\mathrm{E}}{R}_{\mathrm{E}}^{\mathrm{2}}}}+{\mathrm{\Omega }}_{\mathrm{E}},\end{array}$$

where $P\left(\mathit{\alpha }\right)=\mathrm{0.35}+\mathrm{0.15}\sin \mathit{\alpha }$ (Hamlin et al., 1961), α is the charged-particle equatorial pitch angle, W is the particle energy, L is the McIlwain L-shell value, B_E is the magnitude of Earth's magnetic field at the Equator on Earth's surface, R_E is Earth's radius, Ψ₀ is the electric potential causing the plasma convection in the magnetosphere, Φ is the azimuthal angle and Ω_E is the angular frequency of Earth's rotation.

For a given plasma electron with energy between 1 and 1 keV, the drift–bounce resonant conditions for N=1 and N=2 can be satisfied with a ULF wave number $\left|m\right|\mathit{<}\mathrm{100}$ (Ren et al., 2017b, 2018, 2019b). As we can see from Fig. 20, a sharp enhancement of the SYM-H index has been observed, indicating the interplanetary shock arrival. ULF waves with a large amplitude oscillation (∼ 15 mV m⁻¹) have been observed immediately after the interplanetary shock impinges on the magnetosphere.

Outstanding and surprising features are that both energy and pitch angle dispersion signatures of plasmaspheric electrons with an energy of 6 to 19.9 eV have been observed clearly. In the dispersion, the electron with a small pitch angle (almost the field-aligned (0°)) has been observed first, whereas the anti-field-aligned (180°) electrons are observed at last. Different from the lower-energy plasmaspheric electrons, one can see that the pitch angle of a higher energy (above 19.9 eV) electron oscillates between 0 and 180°, and the pitch angle dispersion signature cannot be seen clearly. The period of these successive dispersion signatures is found to be ∼ 40 s, the same as the observed ULF wave period (third harmonic). Therefore, these multi-dispersions are the results of electron bounce resonance with the interplanetary-shock-induced ULF waves.

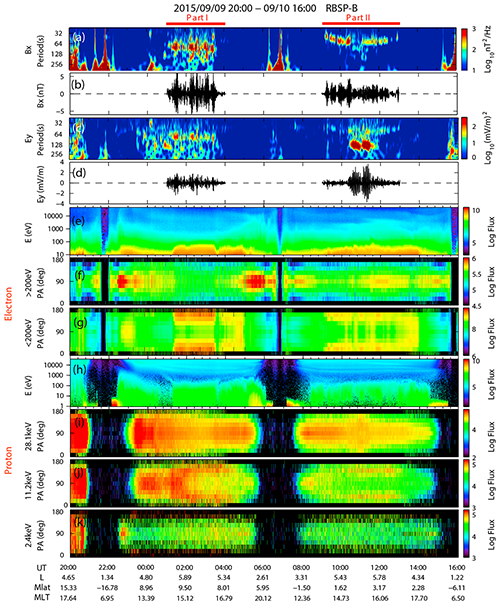
Figure 21 Overview of Van Allen Probe B observations of ULF wave power spectra, energy spectra, and pitch angle distributions from 20:00 UT on 9 September 2015 to 16:00 UT on 10 September 2015: (a) wavelet power spectrum of original B_x; (b) B_x component; (c) wavelet power spectrum of original E_y; (d) E_y component; (e–g) electron energy spectrum and pitch angle distributions; (h–k) hydrogen ion energy spectrum and pitch angle distributions (Ren et al., 2017b).

It is worth pointing out that the ULF wave–particle interaction or plasmaspheric charged-particle acceleration region can be determined by backward-tracing dispersion signatures of both the energy and the pitch angle. Then, the region of electron acceleration is found to be inside the plasmasphere: it is located off the Equator at around −32° in the Southern Hemisphere.

These can be explained by plasmaspheric electrons interacting with the third-harmonic ULF waves with large-amplitude electric fields at the off-equatorial plasmasphere. The pitch angle dispersion signatures are due to the flux oscillation of “local” non-resonant and resonant plasmaspheric electrons but not electrons injected from Earth's ionosphere.

Furthermore, the energy gain of resonant plasmaspheric electrons can be about 20 % in one wave cycle from the observed interplanetary-shock-induced large-amplitude ULF wave electric field (Zong et al., 2017). In general, these results agree with the framework predicted by the generalized drift–bounce resonance theory (Fig. 18).

Figure 21 presents further evidences of both plasmaspheric electrons (<200 eV) and ring current ions (10–20 keV) in response to ULF waves simultaneously. ULF waves with a period of ∼ 1 min, which have been observed in two consecutive orbits, lasted several hours. The ULF waves are the second harmonic; thus, the drift–bounce resonance condition can be satisfied with N=1 for both plasmaspheric electrons and ring current energetic hydrogen ions.

Bidirectional pitch angle distributions for both plasmaspheric electrons and ring current hydrogen ions (10–20 keV) are observed simultaneously when ULF waves have been observed, and plasmaspheric electron fluxes have been enhanced several times. These observational facts agree with the expectations of the drift–bounce resonance scenario, indicating the importance of ULF waves in the dynamics of plasmaspheric electrons.

4.3 ULF waves' interaction with ionospheric outflow: mass spectrometer

Ionospheric outflow is one of the predominant plasma sources of Earth's magnetosphere. It has been shown that the dayside ionospheric outflow ions can interact with ULF waves (Liu et al., 2019; Ren et al., 2015). It is evident that polarization drift caused by large-amplitude electric fields associated with ULF waves may play a significant role in the modulation of singly charged oxygen ions, which may lead to an additional acceleration of oxygen ions (Yue et al., 2016). This process can be non-adiabatic if the ULF wave-borne electric field is large enough. It is revealed that the interaction between ULF waves and ionospheric outflow ions occurs predominantly in the perpendicular direction to the ambient magnetic field. The cold ionospheric ions are not only added an energy of $W_{E\times B}=\frac{\mathrm{1}}{\mathrm{2}}{m}_i{\left(\frac{\left|E\times B\right|}{B^{\mathrm{2}}}\right)}^{\mathrm{2}}$ by ULF waves to make them clearly “visible”, but are also separated into ion species according to different masses. The ULF wave modulation on the ionospheric outflow is mass-dependent, and this indicates that the ULF wave–charged particle interaction can serve as a mass spectrometer to distinguish ion species.

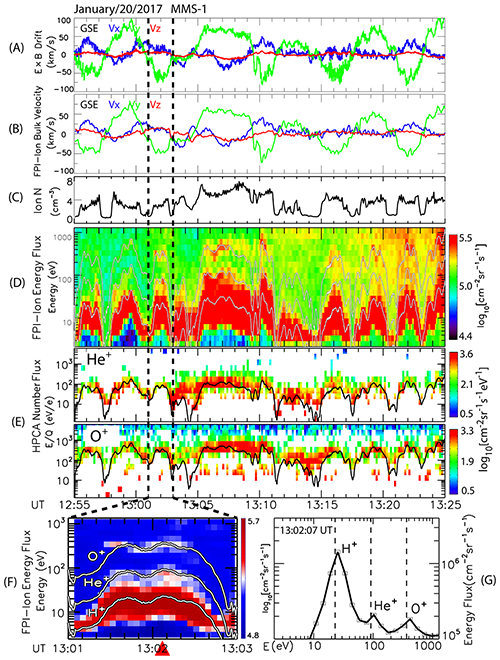
Figure 22 The responses of cold ions to ultra-low-frequency waves. (a) E×B drift velocity, derived from magnetic and electric field measurements. (b) Ion bulk velocity. (c) Ion number density. (d) The energy–time spectrogram. The three white curves correspond to, from bottom to top, the E×B drift energy of H+, He+, and O+, respectively. (e) The energy–time spectrogram of He+ and O+ number fluxes. The black curves correspond to E×B drift energy. (f) Ion energy spectrogram taken between 13:01 and 13:03 UT. (g) Ion energy spectrogram at 13:02:07 UT. The white curves in (f) and the black dashed lines in (g) correspond to E×B drift energy (Liu et al., 2019).

As clearly shown in Fig. 22, ionospheric outflow ions can be modulated by ULF wave-driven E×B drift. As a result, the charged particle's energy rises and falls periodically in coincidence with the ULF oscillation. The energy of H⁺, He⁺, and O⁺ ions of ionospheric origin can be as high as ∼ 75, 300, and 1200 eV, respectively.

It is worth pointing out that the effect of polarization drift should be taken into account due to the large-amplitude electric field of the ULF waves. The particle's energy (W_total), including both E×B drift and polarization drift, can be expressed as

$$\begin{array}{}\text{(22)}& W_{\mathrm{total}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{m}_i{\left(\left|{\displaystyle \frac{E\times B}{B^{\mathrm{2}}}}+{\displaystyle \frac{m_i}{e{B}^{\mathrm{2}}}}{\displaystyle \frac{\mathrm{d}E}{\mathrm{d}t}}\right|\right)}^{\mathrm{2}}.\end{array}$$

The last term in Eq. (20) represents the effect of polarization drift, which is proportional to the ion mass. Therefore, the polarization drift effect is more profound for heavier ions (oxygen ions) than lighter ions (hydrogen ions).

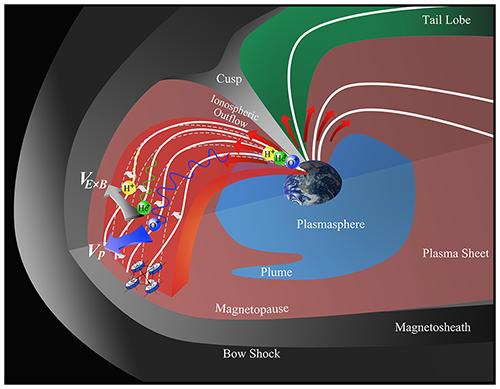
Figure 23 A schematic of the interaction between ULF waves and ionospheric outflow ions, including H⁺, He⁺, and O⁺ (white curves). They are modulated by ULF waves that stand along background magnetic field lines, via ULF wave-induced E×B drift and polarization drift. The E×B drift energy is proportional to ion mass, suggesting that ULF waves can act as mass spectrometers. Polarization drift also plays a non-negligible role in the O⁺ modulation (Liu et al., 2019).

The observations suggest that the ionospheric heavier ions (oxygen) are modulated significantly by ULF wave-induced E×B drift and polarization drift (Fig. 23). It is shown that the polarization drift is contributed mainly from ULF oscillations whose period is less than 1 min, whereas only ∼ 20 % was contributed from oscillations with a period greater than 1 min. It is suggested that O⁺ can be accelerated significantly by both ULF wave-induced E×B drift and polarization drift. This acceleration process is non-adiabatic, which agrees with previous theoretical studies (e.g., Cole, 1976; White et al., 2002; Bellan, 2008).

The polarization drift of ionospheric singly charged oxygen ions (O⁺) induced by ULF wave fields is particularly interesting for magnetospheric physics, since O⁺ ions can become the dominant ion species (up to 60 %–80 %) in terms of ring current energy density (Daglis et al., 1999; Zong et al., 2001; Fu et al., 2001; Yue et al., 2019) during magnetic storm time periods. O⁺ ions in the magnetosphere originate from Earth's ionosphere. Therefore, it is fundamentally important to know how ionospheric singly charged oxygen ions with a few electron Volt are accelerated to tens of kilo-electron Volt and become one of the most important magnetospheric components.

4.4 Off-equatorial minima effects on ULF wave–particle interaction in the dayside outer magnetosphere

In the inner magnetosphere dominated by the dipole field, the bounce and drift frequencies of charged particles are unimodal functions of pitch angle from 0 to 180° (Hamlin et al., 1961). However, in the dayside outer magnetosphere, there exist off-equatorial magnetic field minima due to solar wind compression, which can change the trajectories of particles, forcing the orbits of particles with pitch angles near 90° to bifurcate and form the so-called Shabansky orbits (Shabansky, 1971). Figure 24 shows the trajectory of a Shabansky particle and the magnetic field profiles. Running in an image-dipole magnetic field model, the trajectory of the test particle with pitch angle near 90° bifurcates in the dayside magnetosphere, as shown in panels a and b. Since the magnetic field strength along one field line gets its minima off the Equator on the dayside (red line in panel c), particles with pitch angles near 90° will bounce between two mirror points in the high-latitude minima. By affecting the bounce and drift motions of particles, off-equatorial minima also modify corresponding frequency–pitch angle relations and change the conventional ULF wave–particle interaction pattern in the inner magnetosphere.

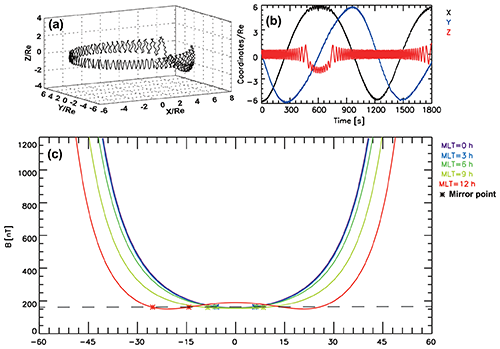
Figure 24 The trajectory projections and magnetic field profiles of a Shabansky particle running in an image-dipole magnetic field. (a–b) The trajectory of a Shabansky particle in geocentric solar ecliptic (GSE) coordinates and its time-varying locations. (c) The magnetic field strength on the drifting shell of a Shabansky particle at different MLTs, with asterisk points referring to corresponding mirror points.

Figure 25 shows the pitch angle distributions of a fundamental-mode ULF wave–ion interaction event observed by the Magnetospheric Multiscale (MMS) on 20 January 2017 (Li et al., 2021). The MMS was located near the subsolar magnetopause for this event. The cold (<1 keV) ion responses in this event have been studied by Liu et al. (2019), which was mentioned in Sect. 4.3. This work focuses on the energetic (>1 keV) ion responses. The spectrograms show series of quasi-periodical twisted pairs, forming “paw-track-like” pitch angle structures. The arrival of 90–180° pitch angle ions precedes that of 0–90° pitch angle ions, agreeing with the results of Yang et al. (2011). The conventional pattern of drift–bounce resonance manifests as two ∼ 180° phase shifts across resonant pitch angles (Zhu et al., 2020). However, the spectrogram shows more than two ∼ 180° phase shifts, indicating more than two resonant pitch angles for a given energy.

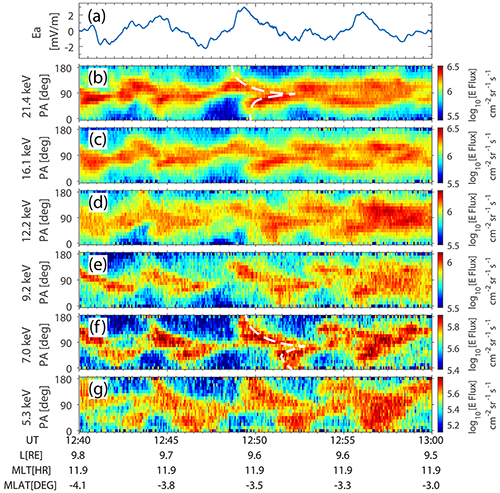
Figure 25 MMS observations on the ULF wave electric field poloidal component and pitch angle distributions of 5.3–21.4 keV ions between 12:40 and 13:00 UT on 20 January 2017. (a) The azimuthal electric field Ea in MFA coordinates. (b–g) The pitch angle–time spectrograms of 5.3–21.4 keV ions (adapted from Li et al., 2021).

Figure 26 illustrates the scenario of how off-equatorial minima affect drift–bounce resonance. Due to the compression of the solar wind, the equatorial magnetic field minimum of the dipole field bifurcates in the dayside outer magnetosphere, forming two off-equatorial minima. The presence of off-equatorial minima changes particles' trajectories and forms two kinds of particles: those with pitch angle close to 90° are trapped in the high-latitude minima and execute Shabansky orbits, while others with larger field-aligned velocity bounce across the Equator. Besides, off-equatorial minima modified the frequencies of particle bounce and drift motions. In the inner magnetosphere, the bounce and drift frequencies of particles are unimodal functions of pitch angle. Consequently, there are at most two resonant pitch angles at fixed energy. In the 20 January 2017 event, off-equatorial minima change the bounce (drift) frequency–pitch angle relation from a unimodal function to a trimodal function (Fig. 26c–d), making it possible to form more than two resonant pitch angles at fixed energy. Because of the trimodal shape of the bounce (drift) frequency, each of the 0–75, 75–105, and 105–180° parts of the pitch angle structure corresponds to a group of the conventional drift–bounce resonance pattern, which forms the paw-track-like pitch angle distribution.

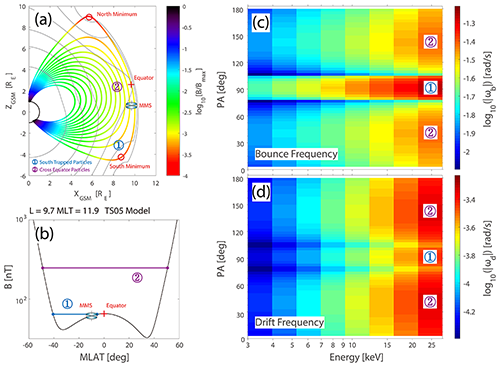
Figure 26 The schematic of off-equatorial magnetic field minima effects on particles' bounce and drift motions. (a) Dayside magnetic field lines and magnetic field strength contours, modeled with the TS05 and IGRF models. The color codes represent the normalized magnetic field strength ${\log }_{\mathrm{10}}[B/B_{\max }]$. (b) The modeled magnetic field strength along the magnetic field line where the MMS was located (L-shell = 9.7, MLT = 11.9). (c–d) The calculated proton bounce and drift frequencies at the magnetic field line where the MMS was located, using the guiding center method described in Roederer and Zhang (2014). Blue (1) and purple (2) represent particles trapped in the southern high-latitude minima and particles across the Equator, respectively (adapted from Li et al., 2021).

In addition, off-equatorial minima can also affect the trajectories of energetic electrons, leading to abnormal electron drift features in pitch angle–time spectrograms in the dayside magnetosphere. Figure 27 shows the solar wind conditions and pitch angle distributions of energetic electrons observed by the Van Allen Probes on 11 March 2016 (Zhao et al., 2021). During the time interval 12:51–14:51 UT, both reverse- and normal-boomerang stripes (mentioned in Sect. 3.2) are observed by two probes, with corresponding solar wind dynamic pressure over 10 nPa. Normal-boomerang stripes indicate that energetic electrons with 90° pitch angle drift more quickly at fixed energy, which agrees with the charged-particle drift motion pattern in the dipole field (e.g., Hao et al., 2017; Zhao et al., 2020). By contrast, reverse-boomerang stripes indicate a slower abnormal drift velocity–pitch angle relation to particles with 90° pitch angle drift, which is contrary to the pattern of particle drift motion in the dipole field. Test-particle simulations in an image-dipole magnetic field reproduced the observed reverse-boomerang feature at larger L-shells, suggesting that the reverse-boomerang stripes result from off-equatorial minima due to the compression of the magnetopause. In this event, the solar wind dynamic pressure is so large (>10 nPa) that the off-equatorial minima effects can be observed in the inner magnetosphere (at L-shell ∼ 5.9). Meanwhile, normal-boomerang stripes can be observed in the inner region (like L-shell ∼ 4.0), where the magnetic field is less affected by the solar wind dynamic pressure (the magnetic field is expected to be more dipole-like).

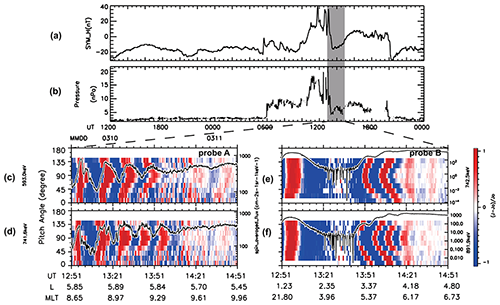
Figure 27 Reverse- and normal-boomerang stripes observed by Van Allen Probes, respectively, with the solar wind conditions from the OMNI data set. (a) SYM-H index. (b) The dynamic pressure, with the gray region referring to the corresponding time interval (the time shift has been considered) of the event below. (c–d) Electron residual fluxes $(J-J_{\mathrm{0}})/J_{\mathrm{0}}$, J and J₀ refer to electron origin flux and its 20 min running average of 593.0, 741.6 keV on the pitch angle–time spectrogram. (e–f) Similar to panels (c)–(d) but for an electron residual flux of 742.5 and 891.9 keV measured by MagEIS-B (adapted from Zhao et al., 2021).

However, the electron reverse-boomerang stripes are not as common as the normal-boomerang stripes from the observations of Van Allen Probes (Zhao et al., 2021), since the orbits of Van Allen Probes are mainly located in the inner magnetosphere. Therefore, reverse-boomerang stripes on electron pitch angle distributions can be observed by Van Allen Probes only when large compression on the magnetopause forms off-equatorial minima even in the inner magnetosphere. In addition, particles with pitch angles near 90° will bounce between high-latitude mirror points if off-equatorial minima exist in the dayside magnetosphere (Fig. 24a). Consequently, localized second-harmonic ULF waves could interact with these Shabansky electrons by drift resonance, which have not been reported before.

In conclusion, off-equatorial minima can affect the bounce and drift motions of both ions and electrons, changing the conventional ULF wave–particle interaction pattern. These results reveal new kinds of ULF wave–particle interaction, which potentially affect the efficiency of particle energization for magnetospheric activities relevant to particle energization.

5 Nonlinear and multiple drift or drift–bounce resonances

In the traditional drift or drift–bounce resonance theory, the weak ULF wave–particle interaction is assumed and charged-particle trajectories are unperturbed; thus, a linearization theory can be applied. However, the observed ULF waves in the magnetosphere usually have a larger magnitude; therefore, the traditional theory needs to be extended to a nonlinear regime since charged-particle trajectories are strongly disturbed (Li et al., 2018; Degeling et al., 2019). In this section, the concepts of the nonlinear and multiple drift or drift–bounce resonances will be presented.

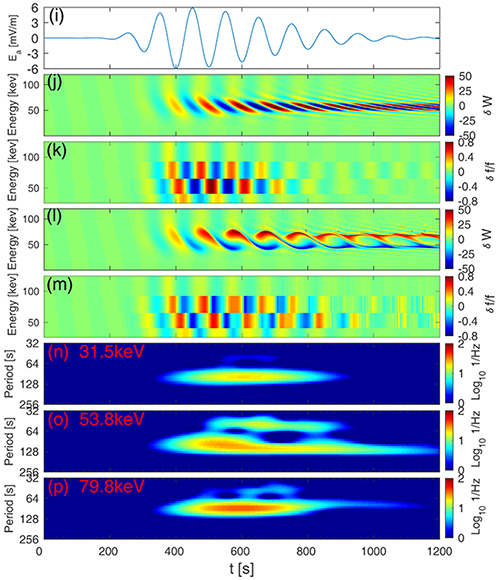
Figure 28 Comparison of predicted signatures for both linear (traditional theory) and nonlinear theory. (i) The panel corresponds to ULF waves with increasing and decreasing amplitudes; (j, l) the energy spectrum of the electron energy gain/loss from ULF waves, obtained from the linear (j) and nonlinear (l) theories; (k, m) the energy spectrum of the electron-residual PSD at each energy channel, obtained from the linear (k) and nonlinear (m) theories; (n–p) wavelet power spectrum of the electron-residual PSD obtained from the nonlinear theory in the 31.5, 53.8 and 79.8 keV energy channels (Li et al., 2018).

5.1 Nonlinear drift and drift–bounce resonance

A nonlinear theory of drift resonance has been developed to formulate the charged-particle motion due to the ULF wave of a large amplitude (Li et al., 2018, 2020; Degeling et al., 2019). Observable signatures such as rolled-up structures in the energy spectrum are predicted. As shown in Fig. 28l, the δW oscillations are strongest at the resonant energy of 54 keV, and there appears a sharp, 180° phase shift across the resonant energy. A rolled-up structure eventually appears at around the resonant energy; this feature could not be predicted by the linear theory.

Such a rolled-up structure has been observed in the energy spectrum by the Van Allen Probes (Li et al., 2018). This provides solid evidence of the nonlinear drift resonance. The nonlinear drift resonance can be very important in ULF wave–charged particle interactions in the radiation belts (Li et al., 2018; Degeling et al., 2019).

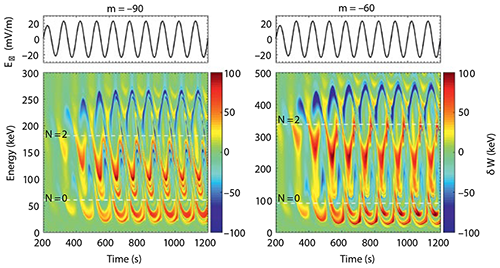
Figure 29 The interactions between ULF waves and energetic oxygen ions at two different energies. The top-left and top-right panels show the electric field profile as a function of time. The bottom panels show the corresponding energy changes, W, experienced by O⁺ ions as a function of their energy and time at the Equator at L=5.7. The wave frequency and azimuthal wave number correspond to f∼ 10 mHz $m=-\mathrm{90}$ in the left column, $m=-\mathrm{60}$ in the right column, and the maximum electric field amplitude is 23.8 mV m⁻¹ at the Equator (Rankin et al., 2020).

5.2 Multiple drift and/or drift–bounce resonances

Multiple drift and/or drift–bounce resonances can occur with different plasma species or the same species at different energies simultaneously. As shown in Fig. 29, it is probable that ULF waves can interact with the energetic oxygen ions at two different energies via both drift resonance (N=0) and drift–bounce resonance (N=2) simultaneously (Rankin et al., 2020).

It is found that the oxygen ion differential flux strongly peaks at the Equator. Oxygen flux for drift–bounce resonance peaks at much higher latitudes than that for drift resonance; this can be understood as pitch angle dependence of the resonance energy.

More observations are needed to verify the features of flux modulations resulting from simultaneous multiple resonances of drift and drift bounce in more detail and the resulting ring current dynamics caused by poloidal-mode ULF waves in Earth's magnetosphere. Singly charged oxygen ions undergoing drift resonance and drift–bounce resonance can yield new insight into the ring current dynamics of heavy ions that interact with ULF waves.

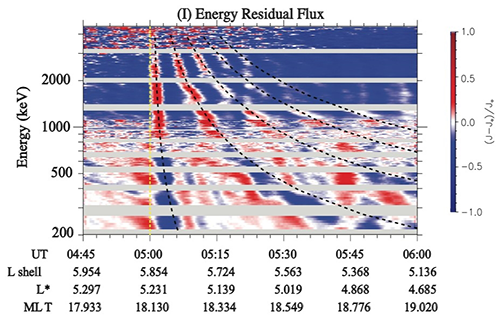
Figure 30 The residual flux profile of 90° pitch angle electrons of 200–4000 keV based on the high-resolution data of MagEIS-B from 04:45 to 06:00 UT on 11 May 2017. The color indicates the value of the residual flux. Red means positive, blue means negative and white means nearly zero. The results of estimated electron drift are overplotted by the black dashed curves. The sudden drop in solar wind dynamic pressure at 05:00 UT is marked by the yellow dashed line (Ma et al., 2021).

Another aspect is that multiple ULF waves with different m can interact with a single plasma population simultaneously. Ultra-high-energy-resolution data from MagEIS on board Van Allen Probes (Ma et al., 2021) in Fig. 30 are used to show how magnetospheric charged particles respond to a negative solar wind dynamic pressure pulse. As shown in Fig. 30, the residual fluxes for electrons with an energy less than 800 keV are decreasing or dropouts, whereas ones with an energy larger than 800 keV are increasing following the arrival of the negative dynamic pressure pulse. The estimated arrival times of electron drift are overplotted by the black dashed curves.

The electron flux oscillations are consistent with the scenario described in Sect. 3.3. For the energetic electron with an energy above ∼ 800 keV, the modulated periods by the ULF waves (low m) are close to its drift periods. However, for energetic electrons with an energy less than ∼ 800 keV, the oscillation is controlled by ULF waves (high m). These mixture signatures are consistent with energetic electrons at different energies resonating with ULF waves of different azimuthal wave numbers.

Also, it has been shown that ULF waves can interact with relativistic electrons by drift resonance and ions by drift–bounce resonance at the same time (Yang et al., 2010; Ren et al., 2016). Thus, multiple drift and/or drift–bounce resonances can occur simultaneously. These provide a basis for further understanding the dynamic coupling between the radiation belt electrons and the ring current populations in the magnetospheric response to solar wind forcing.

6 Outstanding questions and concluding remarks

Magnetospheric physics is now in an extremely vibrant phase, with several ongoing and highly successful missions, e.g., Cluster, THEMIS, Van Allen Probes, and the MMS spacecraft, providing amazing observations and data sets. Since there are many unsolved fundamental problems, in this paper I have addressed selected topics of ULF wave–charged particle interactions, which encompass many special fields of radiation belt, ring current and plasmaspheric physics. Although great progress has been made in recent decades, clear answers have not been found yet as to the following.

• Do ULF waves mediate coupling between plasmaspheric and ring current ion species and radiation belt energetic electrons? If so, do the ring current ion-excited second-harmonic poloidal ULF waves of moderate m number cause the energization of radiation belt electrons?

• What role do the high-m poloidal-mode ULF waves play in the energization of storm-time ring current ions? Is this a prerequisite for a super magnetospheric storm or not?

• How commonly do the high-m poloidal-mode waves occur at the plasmapause, and can they be seen as the signature of existence of the plasmapause? What is the role of the plasmaspheric ion constituency in this? Are high-m poloidal-mode ULF waves generated mainly by an exterior solar wind driver or excited by the ring current ions?

• What is the role of ULF waves in other planets with a magnetosphere, e.g., Saturn, Jupiter, or Mercury? What is the role of ULF waves in other planets or comets without a magnetic field, e.g., Mars, Venus, and Halley's Comet?

The response of the magnetosphere to the impact by an interplanetary shock or a solar wind dynamic-pressure impulse is not just a one-kick scenario. Instead, the impact generates a series of waves, including poloidal-mode ULF waves. A generalized theory of drift–bounce resonance with growth or decay and/or localized ULF waves has been developed to explain the observations. Energy- and pitch-angle-dependent behaviors for both resonant and non-resonant populations can be well predicted by the generalized drift resonance theory.

The studies on ULF waves' interaction with charged particles will magnificently enrich our understanding of the interactions of the solar wind and solar wind forcing with the planet's magnetosphere (often causing large geomagnetic disturbances), which is a ubiquitous phenomenon occurring throughout the plasma universe but uniquely accessible within Earth's magnetosphere. It is realized that the poloidal ULF wave is more effective at accelerating and modulating electrons (fundamental mode) in the radiation belt as well as charged ions (second harmonic) in the ring current region.

A part of ultra-high-energy-resolution data already provide us with new insight into the drift or drift–bounce resonance, especially for multiple drift and/or drift–bounce resonances. Any future magnetospheric mission plans should take into consideration the allowance for charged-particle detectors to have high energy resolution, high pitch angle resolution and the capability to separate ion mass and charge compositions.