A comparison of contact charging and impact ionization in low-velocity impacts: implications for dust detection in space

We investigate the generation of charge due to collision between projectiles with sizes below ∼1 µm and metal surfaces at speeds ∼0.1 to 10 km s⁻¹. This corresponds to speeds above the elastic limit and well below speeds where volume ionization can occur. Impact charge production at these low to intermediate speeds has traditionally been described by invoking the theory of shock wave ionization. By looking at the thermodynamics of the low-velocity solution of shock wave ionization, we find that such a mechanism alone is not sufficient to account for the recorded charge production in a number of scenarios in the laboratory and in space. We propose a model of capacitive contact charging that involves no direct ionization, in which we allow for projectile fragmentation upon impact. Furthermore, we show that this model describes measurements of metal–metal impacts in the laboratory well. We also address contact charging in the context of ice-on-metal collisions and apply our results to rocket observations of mesospheric dust. In general, we find that contact charging dominates at speeds of up to a few kilometres per second and complements shock wave ionization up to speeds where direct ionization can take place. The conditions that we consider can be applied to dust particles naturally occurring in space and in Earth's upper atmosphere and their direct impacts on rockets, spacecraft, and impacts of secondary ejecta.

1 Introduction

The variables in any experiment studying the impact of dust grains – be it of terrestrial, meteoric, interplanetary, or interstellar origin – span many orders of magnitude. By variables we mean the aggregation of ambient parameters and intrinsic parameters of the projectile dust grains and impact surfaces. The ambient parameters such as neutral and charged species densities and temperature can span several orders of magnitude. Combining this fact with the notion that the material properties of the plethora of different dust types that can produce charge in an impact process are also highly variable, there are arguably no single experiments or theoretical considerations that can give a satisfactory explanation of observed phenomena across all possible combinations of variables. In this paper, we focus on what we find is a gap in the knowledge about impact charge production at low-impact speeds, i.e. v_p≲10 km s⁻¹.

Early experimental studies of impact ionization of micrometre-sized grains on metal surfaces were applied in designing highly sensitive micrometeor detectors; see e.g. Auer and Sitte (1968) and Adams and Smith (1971). The mode of operation of such detectors is to measure the material-specific charge generation, which in general yields a semi-empirical relation of the form Q∝m^αv^β. This allowed for detection of grains down to sizes ∼100 nm at speeds between the order of 1 km s⁻¹ and some tens of km s⁻¹. The velocity range is important here, as it has been proposed to be bounded by the limit for production of ionization on impact – which we shall understand here as the release of electrons and ions according to a Saha equation. The pioneering developments in the late 60s and early 70s motivated the employment of impact particle detectors on spacecraft such as HELIOS, Galileo, and Cassini, which have all successfully detected cosmic dust (see e.g. Auer, 2012).

In a treatment of impact charging at speeds of up to some tens of km s⁻¹, Drapatz and Michel (1974) proposed a mechanism for charge generation by shock wave propagation into both projectile and impact surface. This theory is often referred to as shock wave ionization. This mechanism has been widely used in describing the charge generation in dust accelerators and spacecraft dust impacts. For typical impact speeds in many interplanetary spacecraft and laboratory experiments (≳10 km s⁻¹), the shock wave model performs very well. However, as discussed in the current work, we find that the proposed theory in its extrapolation down to lower speeds of a few km s⁻¹ does not describe the charge generation at low speeds sufficiently. In general, we find that it underestimates the amount of generated charge. There are several applications in the laboratory and in space (satellites, rockets, and even spacecraft) that encounter low-impact speeds by particles down to nanoscale size where the shock wave ionization theory thus may not be used.

Motivated by the notions above, we propose in this paper a new charging theory for impact speeds below ∼10 km s⁻¹ and projectile sizes down to nanoscale. The theory utilizes the concept of contact (capacitive) charging and furthermore includes the parameterization of fragmentation of the projectile particles on impact into a distribution of smaller grains. The resulting charge generation is then dependent on the degree of fragmentation and affinity to exchange charge capacitively; the latter is dependent on the difference in work function between projectile and impact surface. In this work, we do not address the exact material-specific speed limit at which the impact charge mechanism changes from contact charging to shock wave ionization. However, we address in depth the plausible velocity regime in which one or the other mechanism should dominate. A theoretical treatment of the “discontinuity” in charging efficiency at speeds of the order of 1 km s⁻¹ is not within the scope of the current work.

The models of charging and fragmentation that constitute our novel approach are presented in Sect. 2.1 and 2.2. The shock wave ionization theory is presented in Sect. 2.3. The results from comparisons of charging models in metal–metal and ice–metal collisions are presented in Sect. 3. The thermodynamics and limitations of the shock wave ionization model at low speeds are discussed in Sect. 4.1. In Sect. 4.2, we furthermore discuss the application areas of a contact charging model for low-velocity impacts of dust on metal surfaces in spacecraft and rockets. Lastly, a conclusion is presented in Sect. 5.

2 Charging and fragmentation models

The current paper concerns itself in essence with the competition between the charging efficiency of two mechanisms: ionization and capacitive charging. The ionization mechanism is here represented by shock wave ionization – that compressibility in solids allows for high enough energy density for charges (electrons) to separate from their respective solids (nanoscale and microscale particles) when the impact speed is high enough. For this mechanism to take place, the particles need to impact a much larger bulk solid at speeds of several km s⁻¹, typically. The capacitive charging mechanism can be explained by its name in that it does not in principle differ from the macroscopic effects observed in a regular capacitor. It states that any particle with a non-zero conductivity can set up a potential difference with a bulk material if they have different work functions. Some confusion might lie in that this mechanism is often called “contact charging”, which might indicate that the separation between the particle and impact surface is zero. This is not true, as there would be no capacitive coupling in such a case. Rather, the effective separation is around 1 nm due to quantum effects. Then, due to different affinities of the “capacitor” surfaces to keep or emit electrons, an effective potential is set up in which electrons trapped in potential wells on the surfaces of the capacitively connected bodies can jump from one to another. We must emphasize that the two mechanisms treated here are fundamentally different: no ionization or dissociation takes place in contact charging due to broken bonds. The mechanisms can, as is a key result from our efforts, contribute to charge production simultaneously in a certain impact velocity range – i.e. they compete. It is also important to underline that we allow incoming particles to shatter – or fragment – in our treatment of contact charging. Fragmentation is simply breaking a projectile particle into a distribution of particles without any ionization taking place. One implication of our application of fragmentation in connection with contact charging is that the charge production is closely bounded to the distribution of fragments. Another consequence is that the experimental setups analysed here promote unipolar charge distributions, which is exactly what has been shown from rocket probings of mesospheric ice particles and in laboratory measurements of ice-on-metal collisions, as elaborated on in Sect. 3.3.

In the sections below, we introduce the theoretical framework for our contact charging model based on fragmentation and capacitive charging as well as the theory of shock wave ionization with special emphasis on the low-velocity regime. We utilize our model on two slightly different types of projectile grains.

The motivation behind the model presented below and the approach for its utilization can be summarized as follows: at speeds comparable to or lower than the critical limit for significant deformation or cratering in a grain–surface collision – see e.g. Jones et al. (1996) – there is little to no available material or energy for impact ionization. Moreover, the incoming projectile grains will fragment, as low-energy collisions essentially can be viewed as a collision cascade as opposed to a sublimation-like destruction process. The consequence is that impact ionization models such as shock wave ionization underestimate the produced charge for dust–surface interactions at low velocities. Our solution is to invoke a model in which no direct charge (plasma) production takes place but rather takes advantage of the fact that (semi-)conducting grains can have a capacitive coupling to surfaces when there is a difference in effective work function between them. In such a scenario, the charge production is in simple terms due to electrons jumping between the surfaces of fragments and target in an effective potential.

2.1 Fragmentation model

At speeds ≳100 m s⁻¹, both metal particles (Froeschke et al., 2003) and water ice particles (Tomsic et al., 2003) of sizes r_d≳10 nm fragment to a high degree. For water ice, molecular dynamics simulations and experimental evidence show a dependence of impact angle on the degree of fragmentation (Tomsic et al., 2001). Moreover, bulk properties can be used as a good approximation for those sizes. The case for smaller particles approaching the sub-nanoscale is somewhat more complicated, as the yield stress, cohesive energy and work function can change as one approaches the atomic size limit (Qi and Wang, 2002; Rennecke and Weber, 2014). We must note that the extrapolation of both the theoretical and experimental results cited here to a wide range of velocities and other grain parameters must be done with great caution, as we try to accomplish here. In Sect. 3.1, we motivate our choice of fragment size limits in accordance with our current understanding of collisions with our initial parameters. In the current work we employ two slightly different fragmentation models for pure metal particles and ice particles with impurities of meteoric smoke. Meteoric smoke particles (MSPs) are coagulates and/or agglomerates of the remains of meteor ablations. However, it should be noted that the size distributions of fragments have the same proportionality with size in the two models, and thus the applications of our model in the two cases have a certain resemblance.

Figure 1 shows a sketch of the impact geometry. The process can be summarized as follows: an incoming grain (projectile) of size above ∼10 nm hits a surface at a speed which allows it to deform plastically. Due to internal shears, a portion of the particle can fragment into a distribution of smaller particles – which can also deform. In this work we have modelled the charge production for both a fragmenting and non-fragmenting particle. The speed at which the fragments interact with the surface is of the order of the initial speed of the main grain. The degree of fragmentation is controlled in our model by a parameter h introduced below. For the impact energies encountered in this paper, i.e. for corresponding impact velocities of a few km s⁻¹, collisions can be assumed to be fully plastic (Rennecke and Weber, 2014), and we thus can utilize Hertzian deformation theory for the main projectile (with radius r_d in Fig. 1). The contact area over which a capacitive coupling is established (as described in Sect. 2.2 below) is defined as (John et al., 1980)

$$\begin{array}{}\text{(1)}& {\displaystyle }& {\displaystyle }A=\mathit{\alpha }\mathit{\pi }{r}_{\mathrm{p}}^{\mathrm{2}},\text{(2)}& {\displaystyle }& {\displaystyle }\mathit{\alpha }={\left({\displaystyle \frac{\mathrm{5}}{\mathrm{4}}}{\mathit{\pi }}^{\mathrm{2}}{\mathit{\rho }}_p{v}_{\mathrm{p}}^{\mathrm{2}}[k_{\mathrm{t}}+k_{\mathrm{p}}]\right)}^{\frac{\mathrm{2}}{\mathrm{5}}},\end{array}$$

where r_p is the projectile radius, v_p the projectile impact velocity, ρ_p its density and k_t and k_p the target and projectile elasticities defined by Young's modulus E according to $k_i\approx \mathrm{0.89}/\mathit{\pi }{E}_i$. The deformation parameter α can be derived from Hertzian deformation theory, and we have used a result by Soo (1971). We assume that impact duration (≳ picoseconds) is long enough to establish charge equilibrium. Considering the thermal speed of electrons, their mobility is by far high enough to obtain equilibrium for temperatures during impact. We must stress that our assumption of grains obeying Hertzian deformation is only true for the lower part of the investigated velocity range and that the main point of the current work is to study the speeds at which ionization efficiency is low and capacitive charging dominates. The upper boundary of 10 km s⁻¹ is somewhat arbitrary in that it is a limit at which with certainty almost no contact charging takes place and that shock wave ionization dominates. This is elaborated upon in Sect. 2.3. Furthermore, we have defined a parameter h which gives the height of a cylinder of cross section A in which all the material is fragmented. Molecular dynamics studies (Tomsic et al., 2003) and rocket results for low-impact velocities (presented below) suggest that part of the grain material is decoupled from the rest. Thus only a small part of the projectile contributes to the capacitively generated charge. Such an understanding implies in our model, for velocities well below the volume ionization regime, that only a fraction $\mathrm{3}h\mathit{\alpha }/\mathrm{4}{r}_{\mathrm{p}}$ of the original particle is involved in charge production. The rest of the particle is shielded or decoupled from the target surface. As shown in our results below, h∼0.1r_p offers a good fit for rocket data. Note that we have disregarded polarization effects, as the characteristic polarization potential switching times for particles of sizes used here are likely much longer than the collision time (or contact time) (Havnes and Hartquist, 2016).

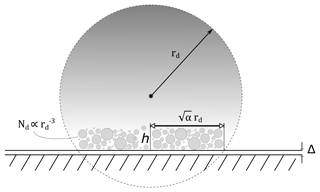
Figure 1 Contact geometry for the charging model of capacitive contact charging. An incoming grain of size above ∼10 nm can fragment into a distribution of particles (fragments) that can furthermore deform and interact with the contact surface in a similar manner to the incoming main grain. The d subscript denotes dust here.

We employ the same parameterization of fragment size distribution in both the fragmentation-at-impact model (iron particles) and fragment-in-projectile model (ice particles containing meteoric smoke particles – MSPs), namely

$$\begin{array}{}\text{(3)}& N_{\mathrm{f}}\left(r_{\mathrm{d}}\right)=N_{\mathrm{0}}{r}_{\mathrm{f}}^{-\mathrm{3}},\end{array}$$

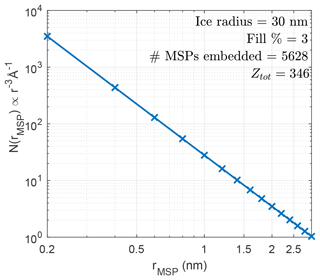
where r_d and r_f are the respective incoming dust particle and fragment radius in metres and N₀ is a constant defined by the available volume for fragmentation. The distribution gives absolute number densities (non-cumulative). The similarity between the two fragmentation models arises from the fact that grain–grain or grain–surface collisions (Evans, 1994) and condensation of dust (Antonsen, 2019) yield the same r⁻³ dependency. The grain–surface collision may be viewed as a collision cascade in free space, which typically yields similar size dependencies. It has also been confirmed that fragments of mesospheric ice containing impurities of meteoric smoke have a size distribution consistent with this model (Antonsen et al., 2017). Motivated by Antonsen and Havnes (2015), we also assume that for ice containing MSPs, the ice will evaporate quickly and moreover have a much lower affinity for charge exchange. Thus it is only the embedded MSPs that contribute to the charge production. It should be pointed out that the two fragmentation models are fundamentally different in that for iron particles the fragments are produced at impact, while for ice particles the fragments (MSPs) keep their original size distribution resulting from condensation and/or coagulation. This latter model is consistent with findings on how ice particles containing impurity fragments are detected in sounding rocket impact probes at speeds ∼1000 m s⁻¹. Throughout the discussion below, we assume that the fragments are spherical grains. We also take into account lattice sphere packing and use a value of 70 % representable for HCP (hexagonal-close-packed), FCC (face-centred cubic), CCP (cubic-close-packed), and BCC (body-centered-cubic) lattice structures. The 70 % value implies that 30 % of the grain volume is vacuum. The fragment size distributions use a default size range of 0.5 to 4 nm in our numerical simulations. For some materials, such as iron, the lower size limit must be shifted in order to disregard quantum effects, as discussed in Sect. 3. The size distribution of fragments in a complete fragmentation of a 30 nm ice particle with embedded MSPs is shown in Fig. 2. The produced charge Z_tot is the charge number bound to fragments, calculated with our capacitive contact charging model. The model does not quantize charges and only averages over the distribution of fragments, which may overpredict the contribution from the smaller fragments. The value of Z_tot is a factor ∼5–10 larger than what is usually measured with sounding rockets (Havnes et al., 2014) and is thus a confirmation that only part of the projectile particle contributes to the measured charge. We elaborate on the charge yield scaling for fragmented particles in Appendix A.

Figure 2 Size distribution of parameterized MSP particles inside an ice particle of size 30 nm. Note that Z_tot is the upper bound on charge production for the case of complete charging of fragments. Annotated values show the result of employing our charging model on such a grain.

2.2 Contact charging

The motivation for the current work is that at low-impact speeds ≲1000 m s⁻¹ the charging of dust can be dominated by a capacitive charging mechanism where the projectile particle and (metal) target surface have an effective co-capacitance dependent on the difference in work function between target and projectile. As described in Sect. 2.1 above, we take into account the incoming projectile particle fragment at the speeds investigated, and we present a theory of contact charging for the individual fragments in the current section. The tensile strength of fragments increases with decreasing radius, and we assume that a capacitive charging model utilized on fragments is valid for much higher speeds compared to when utilized on single projectiles. In the following we give a short introduction to the contact charging theory presented by John et al. (1980) and further developed by Wang and John (1988) to describe plastic projectiles, applied on our problem. It is assumed that all impacts arrive perpendicularly to the target, i.e. an impact angle $\mathit{\theta }=\mathit{\pi }/\mathrm{2}$.

The fundamental mechanism behind contact charging as investigated here is a capacitive coupling between a particle and a surface over an effective separation $\mathrm{\Delta }\sim {\mathrm{10}}^{-\mathrm{9}}$ m (Dahneke, 1972). The produced charge can be described as a function of time by

$$\begin{array}{}\text{(4)}& Q=C{V}_{\mathrm{c}}\left(\mathrm{1}-e^{-\frac{\mathit{\delta }t}{\mathit{\tau }}}\right),\end{array}$$

where V_c is the difference in work function of the contacting materials, $C=\mathit{ϵ}A/Z_e$ the capacitance, and τ the charge relaxation time. For conductors, $\mathit{\tau }\sim {\mathrm{10}}^{-\mathrm{17}}-{\mathrm{10}}^{-\mathrm{19}}$ s and $\mathrm{1}-\exp (-\mathit{\delta }t/\mathit{\tau })\approx \mathit{\delta }t/\mathit{\tau }$, and it can be shown that Eq. (4) reduces to

$$\begin{array}{}\text{(5)}& Q=\mathit{\chi }\mathit{\pi }{r}_{\mathrm{p}}^{\mathrm{2}}{v}_{\mathrm{p}}{\displaystyle \frac{\mathit{ϵ}{V}_{\mathrm{c}}}{Z_e}}{\left({\displaystyle \frac{\mathrm{4}{\mathit{\rho }}_{\mathrm{p}}}{\mathrm{3}Y}}\right)}^{\frac{\mathrm{1}}{\mathrm{2}}},\end{array}$$

where we have introduced the yield stress Y of the material that yields first and the permittivity ϵ≈ϵ₀. The parameter χ is a constant between 0 and 1 that we have introduced in our parameterization of fragment charging. It can be understood as the proportion of fragments which are charged until equilibrium or alternatively as the charging probability of a single fragment. The χ parameter is thus in essence a fitting parameter, and we note that we do not include the possibility of size dependency of it in our model. Note that it was used (set to non-unity) when producing the results in Figs. 4 and 5. In Table 1 we summarize the parameters used to produce the presented results. It must be noted that even if bulk values can be extrapolated to very small particle sizes, some of the parameters utilized in the numerical computations here vary with temperature, which we do not take into account here: the static, i.e. low-frequency equilibrium, relative permittivity of ice increases with decreasing temperature (Auty and Cole, 1952; MacDowell and Vega, 2010). The yield stress and Young's moduli for olivine and ice may also change significantly with temperature (Evans and Goetze, 1979; Nunez-Valdez et al., 2010; Nimmo, 2004). While metals are somewhat more resilient to changes in parameters related to internal stress, their work function increases with decreasing size due to a change in polarizability as particles become small (Wood, 1981).

Table 1 Material properties used in the calculation of contact charging yields for silver (Ag), iron (Fe), water ice, stainless steel (SS) and a meteoric smoke analogue (MSP).

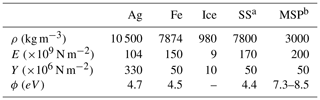
^a Stainless steel 316. ^b Meteoric smoke particles, here olivine at 300 K (Rapp et al., 2012).

2.3 Shock wave impact ionization

It is recognized that impact ionization is a combination of mechanisms, each dominating for certain parts in a wide velocity range. In this paper, we take it as fact that the impact ionization will tend towards a volume ionization mechanism – as a consequence of a Thomas–Fermi model for electronic structure – as impact speeds exceed ∼50 km s⁻¹ (see e.g. Auer, 2012). For velocities below such high speeds, the accepted and most widely used model for impact ionization is that of Drapatz and Michel (1974), which describes ionization as a result of shock waves propagating through colliding entities.

The model of shock wave ionization does not, however, describe ionization for the entire velocity range below ∼50 km s⁻¹. This was also recognized in the earliest formulations of the theory and discussions on its validity. There are in fact at least two velocity regimes – low (v_p≲5−10 km s⁻¹) and high (v_p≳10 km s⁻¹) – that display different semi-empirical charge yields. The charge production mechanism is different in the two velocity regimes, and one focus of the present work is to put the theory of shock wave ionization in the low-velocity regime under scrutiny. In Sect. 4.1 we discuss in detail the thermodynamics of the low-velocity regime shock wave ionization as it was formulated by Drapatz and Michel (1974).

For the high-velocity regime, the shock wave ionization model assumes that the ionization state freezes at some point during expansion of the impact cloud arising from impact (Raizer, 1960; Kuznetsov and Raizer, 1965). The degree of ionization can then be calculated from a Saha equation (Dresser, 1968):

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{n_{+}{n}_{-}}{n_{\mathrm{0}}}}={\displaystyle \frac{\mathrm{2}{\mathit{\psi }}_{+}}{{\mathit{\psi }}_{\mathrm{0}}}}{\left({\displaystyle \frac{\mathrm{2}\mathit{\pi }m{k}_{\mathrm{B}}T}{h^{\mathrm{2}}}}\right)}^{\frac{\mathrm{3}}{\mathrm{2}}}\exp \left[-{\displaystyle \frac{e{V}_I^{\mathrm{1}}}{k_{\mathrm{B}}T}}\right],\end{array}$$

where n₊, n₋, and n₀ are the respective number densities of ions, electrons, and neutrals; ψ are atomic weights for the ionic and atomic states; T denotes the temperature; k_B denotes Boltzmann's constant; $\left|e\right|=\mathrm{1.6}\times {\mathrm{10}}^{-\mathrm{19}}$ Coulombs; h denotes Planck's constant, and $V_I^{\mathrm{1}}$ denotes the first ionization potential of projectile atoms.

For the low-velocity regime, Drapatz and Michel (1974) pointed out that impurity ionization predominantly from alkali metals in the projectiles was responsible for the charge yield. One must then utilize the fact that electrons bound in metals follow a distribution (Copley and Phipps, 1935; for potassium on tungsten)

$$\begin{array}{}\text{(7)}& n_{-}=\mathrm{2}{\left({\displaystyle \frac{\mathrm{2}\mathit{\pi }m{k}_{\mathrm{B}}T}{h^{\mathrm{2}}}}\right)}^{\frac{\mathrm{3}}{\mathrm{2}}}\exp \left[-{\displaystyle \frac{e\mathit{\varphi }}{k_{\mathrm{B}}T}}\right],\end{array}$$

where ϕ is the work function of the projectile. This ultimately leads, after insertion into Eq. (6), to what can be recognized as the Saha–Langmuir equation:

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{n_{+}}{n_{-}}}={\displaystyle \frac{{\mathit{\psi }}_{+}}{{\mathit{\psi }}_{\mathrm{0}}}}\exp \left[-e{\displaystyle \frac{\mathit{\varphi }-V_I^{\mathrm{1}}}{k_{\mathrm{B}}T}}\right],\end{array}$$

where for the materials discussed here ${\mathit{\psi }}_{+}/{\mathit{\psi }}_{\mathrm{0}}\approx \mathrm{2}$.

In the following, we consider the situation where both target and projectile are conductive. This means, in simplified terms, that electrons can easily move between potential wells on the surface of the projectile and target and have time to equilibrate the charge within the collision time τ. Then, in all generality, the charge yield can be described by power laws in both velocity and particle size. The charge production is thus often described by the formula

$$\begin{array}{}\text{(9)}& Q\left[\mathrm{C}\right]=\mathit{\gamma }{m}_{\mathrm{p}}\left[\mathrm{kg}{]}^{\mathit{\alpha }}{v}_{\mathrm{p}}\right[{\mathrm{km}\mathrm{s}}^{-\mathrm{1}}{]}^{\mathit{\beta }},\end{array}$$

where the constants γ,α, and β are all strongly dependent on material properties and velocity regime (see e.g. Mocker et al., 2013; Collette et al., 2014; Kissel and Krueger, 1987). For the application on micrometeoroid impacts on spacecraft, the most widely cited value for velocity dependence is β≈3.5 adopted from McBride and McDonnell (1999); however, values of 2.5–6.2 have been reported for common spacecraft materials (Mann et al., 2019). The exponent α for mass dependence is usually found to be ∼0.7 for the low-velocity regime and close to unity for the high-velocity regime. It has already been pointed out, by Kissel and Krueger (1987), that for low-velocity impacts (v_p<5 km s⁻¹) α should be close to $\mathrm{2}/\mathrm{3}$. This is to say that the charge yield is proportional to the incoming projectile cross section $r_{\mathrm{p}}^{\mathrm{2}}$. The same authors also pointed out that, in both the low- and high-velocity regime, ionization at the target could also be described by the same power law stated in Eq. (9). However, the exponent for mass dependency would be one dimension in particle size lower, i.e. $Q_{\mathrm{target}}\propto r_{\mathrm{p}}^{\mathrm{2}}$ for high projectile velocities and Q_target∝r_p for low velocities. In this work, we do not discuss the additional effect of direct target ionization. In Sect. 4.1 we elaborate in that low-velocity impact charging must probably be described by a different physical mechanism than shock wave ionization as described here.

3 Results

In Sect. 3.2 and 3.3 below, we present results from calculations of contact charging for projectiles of metal and projectiles of ice on metal surfaces, respectively. The simulations employ the fragmentation and charging models described above. For calculations of ice-on-metal charge yields, we assume that the ice particles are contaminated with meteoric smoke particles. This model is descriptive for icy dust particles (or aerosols) in Earth's mesosphere, and we compare our results with in situ measurements of mesospheric ice.

3.1 A note on projectile size and fragment size sensitivity

The choice of default projectile grain size (30 nm) in the presented model results below may be motivated by it being typical for mesospheric icy dust grains usually encountered by sounding rockets. It is also among the smaller projectile sizes (see e.g. Fig. 2 in Mann et al., 2019) which can be readily generated in typical dust accelerator experiments. Moreover, the charge produced at a specific projectile size can be directly scaled to larger sizes according to the scaling relation given in Eq. (A5). Normalizing the calculated yield to the projectile mass furthermore allows for direct comparison to semi-empirical laboratory results.

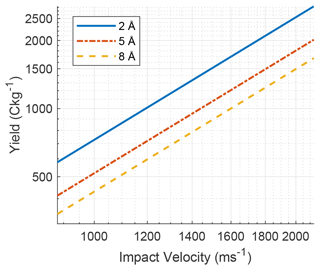
We must also address the choice of limits in fragment size distributions and sensitivity to changes in the lower cut-off limit. In their treatment of collisional charging of interstellar grains, Draine and Sutin (1987) argued on the basis of results by Omont (1986) that bulk properties would sufficiently describe grains of polycyclic aromatic hydrocarbons (PAHs) down to sizes of only 3 Å – or ≳30 molecules. That is to say that, at least for carbonaceous or PAH dust, one can model particles as conducting spheres and disregard quantum effects when calculating the equilibrium charge due to polarization (image) and capture of charged species. We use this as one reason to model fragments of impacted projectiles as conducting spheres down to sub-nanoscale. In our framework of modelling metal-on-metal interaction, we must note that the atomic interspacing is ∼2 Å in a BCC lattice structure. Thus, to obtain a grain that satisfies the constraints used in the references above, we must increase our cut-off to ∼6 Å for iron fragments. This is also in agreement with the findings of Jones et al. (1996) for minimum fragment size in low-velocity impacts. In Fig. 3 we compare the response of our contact charging model for different low-size cut-offs in the fragment size distributions. The differences are small – an increase from 2 to 8 Å in cut-off only decreases yield by around 30 %. Thus we increase the low-size cut-off of iron fragments to 7 Å in this work while still keeping the conducting sphere assumption elaborated on above.

Figure 3 Sensitivity of contact charge generation in an Fe-on-Ag collision to different values of the lowest allowed fragment sizes. Cut-off values are labelled in the legend.

3.2 Metal–metal collisions

In the following simulations, we have used iron as a projectile material and silver as a target material. This is due to experiments with this combination being done in the past both at the LASP dust accelerator (Collette et al., 2014) and at the Heidelberg dust accelerator facility (Mocker et al., 2013). The Fe–Ag combination may be applicable to dust impacts on spacecraft as iron is common in e.g. micrometeorites. It was also used as an example by Drapatz and Michel (1974) in the original formulation of the shock wave ionization theory. Thus, it is possible to compare our results with several others. It should be noted, however, that different experiments may have different complex geometry and working principles. The data produced by the different experiments may therefore have intrinsically systematic differences, and direct intercomparison must be done with care.

Figure 4 shows a comparison of our calculations of iron projectiles on a silver target to the semi-empirical results obtained by Mocker et al. (2013). It shows that our model utilized with bulk material properties and a very high degree of fragmentation (or charging probability) overpredicts the observed charge production, however, with a very similar power law exponent. Although the Mocker et al. results have not been obtained for the projectile velocities as low as the lowest velocities shown in the figure, we have utilized the semi-empirical law from their work, as their results are virtually indistinguishable from the results of Collette et al. (2014), which were obtained for velocities down to 2 km s⁻¹. We must however note that since we have extrapolated these results to lower speeds, some caution should be taken when comparing the two in this part of the velocity range. A further deeper discussion of the charge production for the lower velocities is presented in Sect. 4.2. The Mocker et al. data (blue curves) show a discontinuity – or sudden increase in yield – at ∼11 km s⁻¹. Since the thermodynamics and chemistry of the fragmentation process might not be valid at speeds much higher than this limit, we focus on comparing our curves with the experimental data at speeds below the discontinuity. The lower limit of contact charging, shown as a solid black line, is the case where we consider that the entire original projectile participates in the capacitive coupling. This assumption implies that the entire particle must be bound together, while it still allows for plastic deformation. Such a situation is not probable but provides a lower boundary on the charge production. The fragmentation model results are sketched as a dashed black line. In general, it has a slope very close to the semi-empirical model, but its values are 2 orders of magnitude higher. We note that Fig. 4 shows a default run with default parameters suitable for bulk material, and refinement of these will lead to different results, as shown below. Moreover, as shown in Appendix A, there is a strong dependency on the parameterization of the fragmentation size distribution. Refining the parameterization yields a much better similarity to the experimental results.

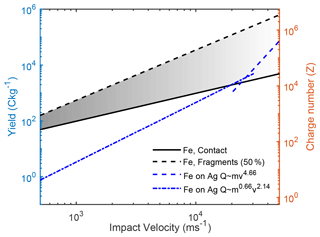
Figure 4 Simulation of contact charging of iron projectiles ($r_{\mathrm{p},\mathrm{0}}=\mathrm{30}$ nm) on a silver target with (black dashed line) and without (black solid line) a fragmentation model. The power laws plotted in blue were acquired experimentally by Mocker et al. (2013). In this calculation, the yield pressure of iron was set to Y=50 GPa, and the fragment size span was set to [0.2,3] nm. The label “50 %” indicates that in this calculation, χ=0.5; cf. Eq. (5).

Although it is not the purpose or motivation of this work to explain the entire charging mechanism at low-impact speeds with fragmentational contact charging, we nevertheless have calculated a best fit of our model to experimental data with reasonable parameters. In Fig. 5 we show the result of a simulation with a set of parameters that produces a “best fit”. The yield stress was increased by a factor 3 compared to Fig. 4. The yield stress is in any case a parameter with a significant uncertainty for nano- and micro-scale particles. Moreover, the fraction of fragments that become charged was reduced to χ=1 %. This parameter is difficult to define and has a large intrinsic uncertainty. A final adjustment was made to the size distribution, where the smallest possible fragment size was changed from the default value of 0.5 to 0.7 nm.

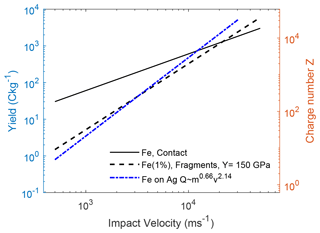
Figure 5 Simulation of contact charging of iron projectiles on a silver target. This simulation was a “best-fit” run, in which the fraction of charged fragments, yield pressure, and fragment size span was allowed to change. This shows the case for χ=0.01, cf. Eq. (5), Y =150 GPa, and fragment size span [0.7, 3] nm.

Since many of the parameters used in our charge model are valid for bulk projectiles, the validity of extrapolating the model to sizes ≲10 nm can be a topic for discussion. In a more rigorous treatment, one may have to take into account curvature and polarization effects for the smallest fragments. Nevertheless, our model shows that at low speeds, fragments can indeed produce charge in a capacitive coupling very efficiently as opposed to ionization through a Saha process. We also leave the untreated issue of how much the pre-charge, which can be very large for the large projectiles that dominate the low-velocity range, contributes to the yield.

3.3 Ice–metal collisions

It is technically challenging to set up laboratory experiments for studying low-impact velocities (≲1 km s⁻¹) and small projectiles (≲100 nm) simultaneously. Dust accelerators typically use samples of projectile particles which span several orders of magnitude, while the energy is fixed and determined by the strength of a static accelerating potential (see e.g. Thomas et al., 2017 for LASP setup). Such a configuration implies that only very large projectiles will have low-impact speeds. The pre-charges collected by the particles in such experiments are usually large – close to field emission limits.

It is however possible to use sounding rockets to obtain a point measurement in the low size and speed range: typical sounding rockets utilized in upper atmosphere research operate at low speeds ∼1 km s⁻¹, and naturally occurring dust particles in the mesosphere (∼50–100 km above sea level) typically have sizes ∼1–100 nm. Thus, in situ measurement can be compared to laboratory measurements for certain experimental setups. For the results below, we utilize the rocket-borne Faraday impact probe MUDD (MUltiple Dust Detector). Inside it, incoming projectile dust particles hit a slanted stainless steel plane on which they deposit pre-charge acquired mainly by ambient electron and ion collection and produce contact charge. Photoelectric charging can become important under certain conditions. A detailed technical description, projectile dust dynamics, and utilization of the instrument can be found in Havnes et al. (2014), Antonsen and Havnes (2015), and Antonsen et al. (2017).

As previously stated, we utilize the fact that dust grains in the mesosphere are contaminated with meteoric smoke – recondensed and agglomerated remnants of meteoric ablation. In Fig. 6 we show the result of two limiting cases of contact charging of “dirty ice”. The solid black line describes a situation where no impurities contribute to the produced contact charge (the pre-charge is assumed to be zero). This might be plausible for very low speeds, where ice particles of sizes ∼10 nm experience less fragmentation (see e.g. Tomsic et al., 2003). For projectile speeds of the order of a few hundred metres per second, the fragmentation model (dashed line) should provide a more physically sound charge yield. For a typical rocket speed of 800–1000 m s⁻¹, the fragmentation model and single projectile have roughly the same yield. We find that the predicted charge number for this velocity range is consistent with what has been measured with rocket-borne Faraday cups (Havnes and Næsheim, 2007; Havnes et al., 2014). The grey shaded area shows values of the predicted charge yield where the ice particles have a capacitive coupling but are allowed to have a non-unity dielectric constant (cf. Wang and John, 1988). This effectively means that the ice particles are insulating, which may be a better description. The true yield of a pure ice projectile should therefore probably lie below the solid black line in Fig. 6.

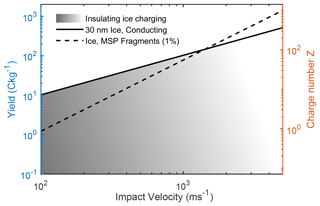
Figure 6 Contact charge yield of 30 nm ice particles with MSP impurities impacting on stainless steel. The shaded area shows possible yields for the case of a mixture of insulating and conducting particles.

In the following we attempt to simulate the current recorded by MUDD during a flight in the MAXIDUSTY campaign (Andøya Space Center, 30 June 2016). We assume the finding of Antonsen (2019) that small ice fragments thermalize and evaporate very quickly and MSP fragments dominate the produced signal. The size distribution of MSPs inside ice was previously found to be $N\propto r_{\mathrm{f}}^{-[\mathrm{2.6},\mathrm{4.4}]}$ (Antonsen et al., 2017); thus, an exponent of −3 should fit well. Consequently, we can employ the same fragmentation model as for metal–metal collisions. We use a volume content of MSPs of 1 %, which is in the middle of the range of what has been found from rocket measurements and satellite measurements (Hervig et al., 2012). Other parameters used in the calculations are listed in Table 1. We also note that the impact plane in MUDD is slanted; however, we assume that the contact time is of the same order as for head-on collisions and long enough to reach equilibrium.

The rocket traversed a dust layer situated at ∼81–87 km at a velocity ≈810 m s⁻¹. We use the accurate and high-altitude resolution number densities and sizes of ice particles as found by a combination of ALOMAR RMR lidar data, in situ photometer, and DUSTY Faraday cup data as described in Havnes et al. (2019). We have assumed, as in the cited paper, that the mesospheric ice particles are monodisperse, and we have utilized an average pre-charge on the ice particles. The electron and ion densities for this flight were done with Faraday-rotation antennae and capacitive probes, and the acquisition is explained in the same reference. We note that a more rigorous modelling of the MUDD currents could allow for size and charge distributions rather than an average of these. Figure 7 shows the comparison between measured MUDD currents and simulated MUDD currents using the described fragmentation model. The two curves display a very high similarity down to the smallest scales and only differ significantly at the upper ∼1 km of the dust layer. Combined with the fact that the fragments – i.e. the embedded MSPs – do not carry significant pre-charge, our results present a convincing case for contact charging being the dominant charging process for the speeds and particle sizes encountered when probing the dust in Earth's mesosphere. For reasons elaborated on in Sect. 4.2 below, the expected contribution from shock wave ionization as calculated with Drapatz' and Michel's low-velocity solution is negligible in comparison with contact charging and even direct pre-charge current in MUDD, at the rocket's velocity. Thus we have not included a comparison simulation for impact shock wave ionization here.

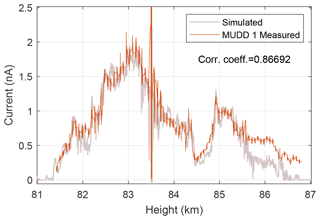
Figure 7 Measurements from the impact Faraday cup MUDD flown on the MXD-1 sounding rocket payload (red) and a best fit from simulation of contact charging (grey) using the fragmentation model described in Sect. 2.1. V_c=0.5 eV was found to be the best fit for fragments of density ρ=3000 kg m⁻³ and yield pressure 50 MPa. The minimum fragment size threshold was set to 0.3 nm.

4 Discussion

As presented in Sect. 2.3, it was pointed out by Kissel and Krueger (1987) that the Saha–Langmuir solution (SLS) from Drapatz and Michel (1974) underestimates impact charge generation for speeds ≲5 km s⁻¹. The low-velocity solution of their theory assumes that charge is generated mainly by impurity diffusion through the molten projectile material. Although Mocker et al. (2013), whose results we have used for comparison, conclude with an agreement with the SLS, it must be noted that they find that the appearance of Fe in impact time-of-flight mass spectra occurs at much lower speeds (3.6 km s⁻¹) than the SLS predicts. Hydrocode simulations aiming at predicting the threshold of impact plasma generation in iron-on-metal collisions have found a threshold of 8 km s⁻¹ (Ratcliff et al., 1997). Results from the Cassini Cosmic Dust Analyzer have confirmed occurrence of metal ions in time-of-flight mass spectra at speeds ≳10 km s⁻¹ (Hillier et al., 2007). The takeaway from these notions is that both direct impact plasma generation and the SLS probably are insufficient in explaining charge generation in low-velocity impacts.

To investigate the applicability of an SLS at speeds of the order of 1 km s⁻¹, we look closer at the thermodynamics of the process in Sect. 4.1. In Sect. 4.2 we discuss possible areas of application of our contact charging model, with emphasis on spacecraft and sounding rocket observations.

4.1 Thermodynamics of low-velocity limit of shock wave ionization

A first-order estimate of the mean diffusion distance of an impurity ion inside a cooling – i.e. solidifying – metal grain can be found by recognizing that the diffused area must be D(T)τ_s, where D(T) is the temperature-dependent diffusivity over a solidification time τ_s. We have that the one-dimensional mean diffusion distance is

$$\begin{array}{}\text{(10)}& \mathit{\delta }r=\left|{\left(D\left(T\right){\mathit{\tau }}_{\mathrm{s}}\right)}^{\frac{\mathrm{1}}{\mathrm{2}}}\right|.\end{array}$$

This can be interpreted as the thickness of a shell from which impurities can reach the surface of a cooling grain. For the purpose of comparing diffusion of alkali impurities through iron particles with the results of Drapatz and Michel (1974), we utilize the mean diffusivity $\stackrel{\mathrm{‾}}{D\left(T\right)}=\mathrm{5}\cdot {\mathrm{10}}^{-\mathrm{9}}\exp (-\mathrm{5000}/\stackrel{\mathrm{‾}}{T})$ m² s⁻¹.

We assume the particle has bulk properties, which is suitable for clusters of size of the order of 10 nm. The available volume from which ions can be released is then (denoting the grain radius r_f)

$$\begin{array}{}\text{(11)}& \mathit{\delta }V\left({\mathit{\tau }}_{\mathrm{s}}\right)={\displaystyle \frac{\mathrm{4}\mathit{\pi }}{\mathrm{3}}}\left[r_{\mathrm{f}}^{\mathrm{3}}-(r_{\mathrm{f}}-\mathit{\delta }r{)}^{\mathrm{3}}\right].\end{array}$$

Then the upper bound on the number of impurity ions released from a single grain becomes

$$\begin{array}{}\text{(12)}& N_{\mathrm{im}}=K{\displaystyle \frac{\mathrm{4}\mathit{\pi }{\mathit{\rho }}_{\mathrm{p}}\mathit{\xi }}{\mathrm{3}{M}_{\mathrm{p}}}}\left[r_{\mathrm{f}}^{\mathrm{3}}-(r_{\mathrm{f}}-\mathit{\delta }r{)}^{\mathrm{3}}\right],\end{array}$$

where ξ is the impurity content by volume and ρ_p and M_p are the mass density and molecular mass of the grain (“projectile”) material, respectively. We use here ξ∼1%, which is representable for alkali metal content in Earth's crust and in raw smelted iron and steel. K is the atomic packing factor, which is set to 0.7 in our calculations. The resulting single charge impurity ionization predicted by the Saha–Langmuir equation then becomes

$$\begin{array}{}\text{(13)}& Z_{\mathrm{im}}=N_{\mathrm{im}}{\displaystyle \frac{n_{\mathrm{im}}}{n_{\mathrm{im}}+n_{Fe}}}\approx \mathrm{2}{N}_{\mathrm{im}}{e}^{-\frac{e\mathit{\varphi }-V_I^{\mathrm{1}}}{k_{\mathrm{B}}T}},\end{array}$$

where e is the elementary charge, ϕ is the work function of the impurity material, and $V_I^{\mathrm{1}}$ is the first ionization potential. The difference between these for potassium (K), which is used in this work as a dominant impurity, is $\mathit{\varphi }-V_I^{\mathrm{1}}\approx \mathrm{1.8}$ eV. Factor 2 arises from the statistical weights in Eq. (8).

It is clear that we also require a parameterization of the temperature inside the expanding shock. For this purpose we utilize the fact that the relationship between the shock front velocity u and the projectile velocity v_p is governed to first order by the ratio of the difference in mass density between the projectile and target through energy conservation. We have for specific energy

$$\begin{array}{}\text{(14)}& \mathit{\epsilon }={\displaystyle \frac{u^{\mathrm{2}}}{\mathrm{2}}}={\displaystyle \frac{v_{\mathrm{p}}^{\mathrm{2}}}{\mathrm{2}}}/{\left({\displaystyle \frac{{\mathit{\rho }}_{\mathrm{p}}}{{\mathit{\rho }}_{\mathrm{t}}}}\right)}^{\frac{\mathrm{1}}{\mathrm{2}}}+\mathrm{1},\end{array}$$

which for our example case of iron projectiles on a silver surface yields u≈0.62v_p. This is to say that ∼40 % of the initial energy goes into expansion of the shock. It can be shown that the temperature behind the shock for monoatomic gases ($\mathit{\gamma }=\mathrm{5}/\mathrm{3}$) is (Zel'Dovich and Raizer, 1967)

$$\begin{array}{}\text{(15)}& {\displaystyle \frac{T}{T_{\mathrm{0}}}}={\displaystyle \frac{\mathrm{5}}{\mathrm{16}}}{\mathrm{Ma}}^{\mathrm{2}},\end{array}$$

where $\mathrm{Ma}=u/v_{\mathrm{th},N}$ is the shock front Mach number and T₀ is the pre-collision temperature.

In the following calculations of impurity ionization production, we have used the fact that the solidification temperature of nanoscale iron particles is 1000 K (Fedorov et al., 2017). Furthermore, we employ a cooling rate of 10¹² K s⁻¹, which has been found from molecular dynamics simulations to be representable for nanoscale metal particles (Shibuta and Suzuki, 2011). This gives typical solidification times of ${\mathit{\tau }}_{\mathrm{s}}\sim {\mathrm{10}}^{-\mathrm{9}}$ s, which is 2 orders of magnitude smaller than the cooling time used by Drapatz and Michel (1974). In the current model, we restrain the diffusivity coefficient with a hard stop at the solidification temperature and do not parameterize solidification/crystallization effects. Moreover, we do not discuss here the evaporation of impurities from the surface of the main particle; we simply assume all impurities are removed and thus present an upper bound on impurity charge production. By the set of equations above, we find that the limit for impurity production for a 3 nm iron grain is a Mach number of 3.3, corresponding to a velocity v_p∼1 km s⁻¹.

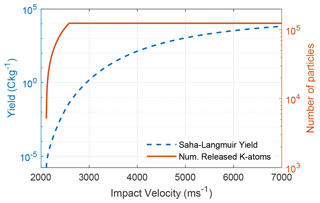
Figure 8 Results from calculation of impurity (1 % potassium) charging using the Saha–Langmuir equation (blue, dashed) and fragmentation model described in this work. The solid red line shows the number of released K atoms as a function of velocity and therefore constitutes a theoretical upper bound on the charge number (for singly charged ions).

In Fig. 8 we have not parameterized the temperature decrease in the expanding volume behind the shock. However, depending on whether or not thermodynamic equilibrium can be reached or not, this effect might be a significant inhibitor of thermal ionization described by the S–L equation. For an adiabatic expansion, we have that

$$\begin{array}{}\text{(16)}& {\displaystyle \frac{T\left({\mathit{\tau }}_{\mathrm{s}}\right)}{T_{\mathrm{0}}}}={\left({\displaystyle \frac{V_{\mathrm{0}}}{V\left({\mathit{\tau }}_{\mathrm{s}}\right)}}\right)}^{\mathit{\gamma }-\mathrm{1}}.\end{array}$$

Thus, in the case of a 30 nm projectile particle and a solidification time of ${\mathit{\tau }}_{\mathrm{s}}={\mathrm{10}}^{-\mathrm{9}}$ s, it is found that the limiting expansion velocity to accommodate diffusion should be of the order of u∼100 m s⁻¹, which is clearly never the case. In this regard, we note that the assumption of thermodynamic equilibrium may not be suitable for the set of parameters encountered in the current work. Moreover, we must note that the emissivity of nanoscale dust grains is strongly dependent on size and material properties, so the cooling time may also need refinement (Rizk et al., 1991).

We summarize our result of low-velocity impact charging in Fig. 9. The SLS vanishes below ∼2 km s⁻¹. The contact charge solution overestimates the experimentally acquired yield in the entire range. The two curves have almost the velocity and mass dependence, and possible downshifts of the contact charge solution were discussed in Sect. 3.2. Notably, we have used χ=1 here, which provides an upper boundary on the charge yield. We must note that in the mechanism proposed in the current work, we have not taken into account charge production at the surface. Such an effect may be expected to scale with the particle radius rather than cross section at low speeds, as mentioned in Sect. 2.3. To first order, one may therefore disregard such additional charging, as it introduces another layer of complexity into modelling efforts. There is also a possibility of impurities on the surface – which are arguably always present in metals – that can produce additional charging. Extending our theory to include the contributions from impurities may require a treatment of surface chemistry and evaporation microphysics which is beyond the goal of our study. Nevertheless, our results must always be read with the ulterior notion that volatile impurities such as alkali metals can introduce additional charge.

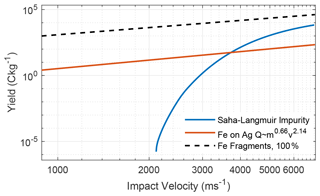
Figure 9 Comparison of specific yields from our contact charging model (dashed) to the Saha–Langmuir solution from Drapatz and Michel (1974) (solid blue) and the semi-empirical law obtained by Mocker et al. (2013) (solid red). All lines represent Fe-on-Ag impacts, and in the Saha–Langmuir solution we have used potassium as the impurity. The label “100 %” in the legend corresponds to χ=1 and indicates that all produced fragments collide with the surface.

4.2 Relevance for dust detection on spacecraft and rockets

In Sect. 3.3 we demonstrated the applicability of our model to rocket measurements of dust (or aerosols) in the upper mesosphere of Earth. Other related types of dust, namely those originating in the ablation of meteors in the altitude range ∼70 to 140 km, are candidates for comparison with a contact charging model. Free dust grains of meteoric origin have recently been observed by sounding rockets (Havnes et al., 2018), and other novel experiments have been aimed at investigating such particles (see e.g. Strelnikov et al., 2021).

The number of catalogued man-made space debris objects in the near-Earth space is already of the order of 10⁴, with the number of objects increasing inversely with size (Klinkrad, 2006). Estimates of the number of objects smaller than 100 µm have large uncertainties but have been cited as of the order of tens of billions (Schildknecht, 2007). The probability of any satellite encountering a space debris object during its lifetime is therefore non-vanishing. Besides this, typical orbital speeds of low Earth-orbiting satellites are ≲8 km s⁻¹ and decreasing with increasing orbital altitude. Thus, even without considering whether the grains of debris are prograde or retrograde, debris–satellite interactions may readily occur at speeds relevant for contact charging. Additional charging or upsets due to contact charging are arguably undesirable for e.g. satellites measuring plasma parameters.

Based on recent observations by the Parker Solar Probe (PSP), Szalay et al. (2020) concluded that β meteoroids (β describing the ratio of the radiation pressure force to gravity) dominate the recorded dust flux. They found that such grains typically have larger impact velocities than circularly bounded dust, but for β≲0.5, there may be a non-vanishing flux of β meteoroids with impact speeds in the upper limit of the velocity range investigated in the present work for contact charging. From their results of modelling the dynamics of dust in bounded circular orbits, based on a model of Pokorný and Kuchner (2019), it is clear that there may well be a smaller number of impacts on PSP that can be traced to such dust grains.

Page et al. (2020) reported that although β meteoroids can produce dust impact fluxes as measured on PSP near perihelion, some of the directionality in the dust flux data can be consistent with prograde circular orbit dust. At perihelion, the impact velocity of these is still too large to apply a contact charge model (∼20 km s⁻¹); however, there might be a possibility that one can use such a model on prograde dust further away from the Sun with lower impact velocities. In regards to further explorations of the utilization of our model on spacecraft data, dependence of impact inclination in contact charge production should also be studied.

Another possible candidate for employment of our model on spacecraft data is secondary ejecta. Secondary ejecta, which are material from craters generated by dust impacts on the spacecraft body, have energies much lower than the impacting grains. Such secondary grains have been observed as stray light in optical images from e.g. STEREO (Cyr et al., 2009). Szalay et al. (2020) also noted that such secondary particles were observed with the WISPR experiment on PSP (see e.g. Vourlidas et al., 2016) and that the ejecta correlated well with antenna measurements of dust impacts.

One impediment to utilizing our model on dust in space is that it may be difficult to determine its composition and structure. In consequence, the work function of the projectile material may be unknown and moreover size-dependent (Wood, 1981). In some cases, where the projectile grains have very low conductivity, it may be required to either (1) assign an effective work function (Matsusaka et al., 2010) or (2) extend our theory to insulating particles. The latter can in brief be described as letting the ratio $\mathrm{\Delta }t/\mathit{\tau }\to \mathrm{0}$ in Eq. (4). The result is a slightly lower velocity dependence in the charge production, $Q_{\mathrm{c}}\propto v_{\mathrm{p}}^{\mathrm{3}/\mathrm{5}}$. The charge production will also be significantly weaker than for conducting or semi-conducting grains (John et al., 1980; Wang and John, 1988).

The ESA Solar Orbiter (ESO) was launched in February 2020. Its orbit is different from PSP in that its perihelia are larger than ∼0.28 AU throughout its lifetime – versus ∼0.046 AU for PSP. In addition, ESO has a planned 25^∘ inclination in its nominal mission. The orbital parameters will ensure that ESO will encounter prospective bounded dust grains and β meteoroids with generally lower velocities than for PSP. It is not in the scope of this paper to analyse the expected dust flux of ESO, but it can be expected that a larger number of dust impacts can involve a contact charging mechanism compared to PSP.

5 Conclusions

In this work we have investigated the production of charge in impacts of projectiles of iron and agglomerates of ice and meteoric smoke on a metal surface at speeds ≲10 km s⁻¹. We introduce a novel model of contact charging due to a capacitive coupling between metal surfaces and fragments of projectile grains. Here we show that our model is consistent with laboratory measurements of Fe-on-Ag collisions as well as rocket measurements of icy dust particles on stainless steel. Our method can be utilized with a large range of projectile dust types, where the intrinsic properties of the grains are known. We also find that our theory may be used to explain certain observations of dust by the recently launched spacecraft NASA Parker Solar Probe and ESA Solar Orbiter. We moreover find that the currently accepted theory for impact charging at the speeds of interest here, namely the shock wave ionization theory of Drapatz and Michel (1974), is insufficient in explaining laboratory observations of charge generation in metal-on-metal impacts alone. Consequently, we suggest that at low speeds, there must be a significant contribution to the produced charge by contact charging – i.e. the two discussed mechanisms both contribute significantly to impact charge production at speeds from ∼3 up to the limit where direct ionization becomes important.

Appendix A: Scaling relation for charge yield of fragmented particles

In this Appendix we give a scaling relation for charge production by capacitive charging when employing a fragmentation model.

The available material from which fragments can form is given by the Hertzian deformation presented in Sect. 2.1 above and is

$$\begin{array}{}\text{(A1)}& V_{\mathrm{c}}=\mathit{\alpha }h\mathit{\pi }{r}_{\mathrm{p}}^{\mathrm{2}}\propto r_{\mathrm{p}}^{\mathrm{3}}\sim Q_{\mathrm{p}}.\end{array}$$

The largest possible spherical fragment (of volume V_s) that can be formed from this material, using V_s(r_f)=V_c(r_p), has radius

$$\begin{array}{}\text{(A2)}& r_{\max }={\left({\displaystyle \frac{\mathrm{3}h\mathit{\alpha }{r}_{\mathrm{p}}^{\mathrm{2}}}{\mathrm{4}}}\right)}^{\frac{\mathrm{1}}{\mathrm{3}}}\propto r_{\mathrm{p}}.\end{array}$$

As contact charging scales with the cross section of fragments, we calculate the total surface area of all (discretely distributed) fragments:

$$\begin{array}{}\text{(A3)}& S_{\mathrm{tot}}^{\prime }=\sum _{\forall i}\mathit{\pi }\left(N_{\mathrm{0}}{r}_{f,i}^{-\mathrm{3}}\right)r_{f,i}^{\mathrm{2}},\end{array}$$

where we have used the fact that the fragments are distributed in size according to $N_{\mathrm{f}}\propto r_{\mathrm{f}}^{-\mathrm{3}}$. If we assume that the size distribution is continuous, we can moreover find that

$$\begin{array}{}\text{(A4)}& S_{\mathrm{tot}}=\mathit{\pi }{N}_{\mathrm{0}}\underset{r_{\min }}{\overset{r_{\max }}{\int }}\mathrm{d}{r}_{\mathrm{f}}\cdot r_{\mathrm{f}}^{-\mathrm{1}}=\mathit{\pi }{N}_{\mathrm{0}}\ln \left({\displaystyle \frac{r_{\max }}{r_{\min }}}\right),\end{array}$$

where r_min is the smallest possible fragment radius.

Now we recall the scaling $Q_{\mathrm{p}}\sim r_{\mathrm{p}}^{\mathrm{3}}$ from Eq. (A1), which constrains the amount of material available for fragmentation. Inserting the result from Eq. (A2) into Eq. (A4), we finally obtain that the charge production of a fragmented projectile particle scales with size (and velocity according to its dependence in α):

$$\begin{array}{}\text{(A5)}& Q_{\mathrm{p}}\propto r_{\mathrm{p}}^{\mathrm{3}}\ln \left({\displaystyle \frac{{\left(\mathrm{3}h\mathit{\alpha }{r}_{\mathrm{p}}^{\mathrm{2}}\right)}^{\mathrm{1}/\mathrm{3}}}{{\mathrm{4}}^{\mathrm{1}/\mathrm{3}}{r}_{\min }}}\right)\propto r_{\mathrm{p}}^{\mathrm{3}}\ln \left({\displaystyle \frac{r_{\mathrm{p}}{v}_{\mathrm{p}}^{\mathrm{4}/\mathrm{15}}}{r_{\min }}}\right).\end{array}$$

This result is also intuitively reasonable, that since there are many more small particles than large ones, the surface area of the small particles contributes more to the total area and thus charge production. Moreover, we note that the sensitivity to the parameter r_min becomes even more important for size distributions with steeper inverse power laws than the one chosen here. This solution will never become unphysical (singularity as r_min→0), as r_min has a natural lower bound, in this paper its dependence on velocity, which one must assume that it has, since atoms and molecules have finite sizes. However, we assume that a feasible value would be of the order of ∼1 Å (=0.1 nm), which is the order of the length of a single atom or molecule. As seen in Sect. 3, our charge production model is relatively sensitive to this parameter.