BeiDa Imaging Electron Spectrometer observation of multi-period electron flux modulation caused by localized ultra-low-frequency waves

We present multi-period modulation of energetic electron flux observed by the BeiDa Imaging Electron Spectrometer (BD-IES) on board a Chinese navigation satellite on 13 October 2015. Electron flux oscillations were observed at a dominant period of ∼190 s in consecutive energy channels from ∼50 to ∼200 keV. Interestingly, flux modulations at a secondary period of ∼400 s were also unambiguously observed. The oscillating signals at different energy channels were observed in sequence, with a time delay of up to ∼900 s. This time delay far exceeds the oscillating periods, by which we speculate that the modulations were caused by localized ultra-low-frequency (ULF) waves. To verify the wave–particle interaction scenario, we revisit the classic drift-resonance theory. We adopt the calculation method therein to derive the electron energy change in a multi-period ULF wave field. Then, based on the modeled energy change, we construct the flux variations to be observed by a virtual spacecraft. The predicted particle signatures well agree with the BD-IES observations. We demonstrate that the particle energy change might be underestimated in the conventional theories, as the Betatron acceleration induced by the curl of the wave electric field was often omitted. In addition, we show that azimuthally localized waves would notably extend the energy width of the resonance peak, whereas the drift-resonance interaction is only efficient for particles at the resonant energy in the original theory.

1 Introduction

Magnetospheric ultra-low-frequency (ULF) waves, also known as geomagnetic pulsations, are plasma waves in the frequency range of ∼1 mHz to 1 Hz. Since the start of the space age, ULF waves have been extensively observed and widely regarded as hydromagnetic waves (e.g., Brown et al., 1961; Chen and Hasegawa, 1974; Kivelson and Southwood, 1985; Zong et al., 2017). These waves are found to play an important role in particle transport and acceleration in the solar terrestrial system (e.g., Hudson et al., 2001; Zong et al., 2009; Claudepierre et al., 2013; Foster et al., 2015). Particularly, ULF waves in the Pc 3–5 bands (Jacobs et al., 1964) can effectively interact with energetic particles via drift resonance, as the period of the waves is comparable with the drift period of the particles (e.g., Elkington et al., 1999; Dai et al., 2013; Li et al., 2017a; Hao et al., 2019). As regards the drift-resonance wave–particle interaction, the energy transfer between the ULF waves and the energetic particles is most efficient for a specific energy, called the resonance energy, at which the particles would experience a steady electric field during their drift motion, thereby resulting in a cumulative net energy change.

A theoretical framework has been developed by Southwood and Kivelson (1981) to systematically understand the drift-resonance interaction between ULF waves and energetic particles. With the assumptions of an undisturbed particle trajectory and a monochromatic wave which has an infinitely small growth rate, they analytically derived the energy gain of the particle in the ULF wave field and the corresponding signature to be observed by a particle detector. According to their theory, particle flux observed at a fixed location would oscillate with a large amplitude at the resonant energy, and the resonant particle flux would be in anti-phase with respect to the azimuthal electric field of the wave. At lower or higher energies, the amplitude of the flux oscillation would rapidly decrease, and the phase difference between the particle flux and the azimuthal electric field would be ±90^∘. In other words, the phase shift across the resonant energy would be 180^∘. The amplitude profile and phase relationship of the flux modulation have been widely used as characteristic signatures to identify the drift-resonance interaction (e.g., Claudepierre et al., 2013; Hao et al., 2014; Chen et al., 2016). This conventional drift-resonance theory has been recently adapted by Zhou et al. (2015, 2016). They introduced a finite growth rate, as well as a finite damping rate, to describe the whole lifespan of the ULF wave in a more realistic way. In the case of their modified wave field, the phase shift of the particle fluxes across the resonant energy would be in the range of 90 to 180^∘, depending on the evolution of the wave amplitude. This modified signature of drift resonance has been verified by spacecraft observations (e.g., Zhou et al., 2015; Chen et al., 2016; Li et al., 2017a). In addition, ULF waves in the magnetosphere have been found to be azimuthally localized (e.g., Takahashi et al., 1985; Liu et al., 2009; Shen et al., 2018; Barani et al., 2019), whereas a uniform ULF wave field is assumed in the conventional drift-resonance theory. Li et al. (2017b) newly introduced a von Mises function into the drift-resonance theory to describe the localized characteristics of the ULF wave. They applied the revised theory to a previously reported event (Li et al., 2017a) and found that the observed particle signatures were better reproduced with the localized ULF wave. The localized-drift-resonance scenario is also addressed by Hao et al. (2017). They reported “boomerang stripes” observed by the Van Allen Probes (Blake et al., 2013; Mauk et al., 2013) and attributed the newly discovered features in the particle flux modulation to the interaction between relativistic electrons and localized poloidal ULF waves. The azimuthally localized nature of the ULF waves implies the possibility that energetic particles may interact with different waves along their drift trajectory, though it has rarely been reported.

In this paper, we present a case study of energetic electron flux modulated by ULF waves. Multi-period oscillations are unambiguously identified in the electron fluxes observed by BD-IES (BeiDa Imaging Electron Spectrometer; Zong et al., 2018). We propose a natural and straightforward explanation that the flux variations were caused by multiple localized ULF waves at different periods. In the context of limited observations, we validate the localized wave–particle interaction scenario with a comparison between the observational signatures and the theoretical prediction of adiabatic energy change and particle flux. First, we revisit the original drift-resonance theory by Southwood and Kivelson (1981) and its recent extensions (Zhou et al., 2016; Li et al., 2017b) and fix a flaw in these prevailing drift-resonance theories. We show that the Betatron acceleration caused by the curl of the wave electric field, which is omitted in these theories, is comparable with the energy change caused by the poloidal electric field along the drift trajectory of the particle. The flawed theories, in general, can still give the correct characteristic phase relationship and amplitude profile of the particle flux modulation but overestimate the strength of the wave electric field. Then, with the corrected theory, we calculate the adiabatic energy change and the electron flux variation. It is found that the theoretically predicted signatures are in agreement with the BD-IES observations. Also, we present possible circumstantial evidence provided by ground-based magnetometers. Besides, we briefly discuss the width of the resonant amplitude peak and its relation to the azimuthal extent of the localized ULF waves.

2 Data

The electron flux data in this study are obtained by the BeiDa Imaging Electron Spectrometer (BD-IES) on board a Chinese 55^∘ inclined-geosynchronous-orbit (IGSO) spacecraft. This instrument, built by Peking University, employs a pin-hole technique (Zou et al., 2013) and an anti-proton contamination design (Luo et al., 2015) to measure the differential electron flux from ∼50 to ∼600 keV in eight energy channels (Zou et al., 2018a, b). The centroids of the channels are 59, 80.5, 111.5, 150, 205, 280, 380, and 520 keV, respectively. The temporal resolution of the flux measurement is ∼10 s. The ground-based magnetometer data are provided by NASA's Space Physics Data Facility and INTERMAGNET (International Real-time Magnetic Observatory Network) at the cadence of 1 s.

3 Observation

Figure 1 presents an overview of the electron flux obtained by BD-IES on 13 October 2015. The IGSO spacecraft with BD-IES on board passes through the radiation belt twice per orbit. Figure 1a and b show the electron flux in a full pass of the spacecraft through the radiation belt in the format of spectrogram and series plots, respectively. The multi-period modulation of the energetic electron fluxes was observed from ∼ 10:15 to ∼ 11:00 UT when the spacecraft traveled into the outer radiation belt. A zoomed-in view of the event is shown in Fig. 1c. The colored solid lines represent the omnidirectional differential electron fluxes, while the black dotted lines refer to the 190 s running-averaged fluxes. The flux modulations at the dominant period of ∼190 s, as well as the secondary oscillation at ∼400 s, are readily apparent. Figure 1d provides a zoomed-in view of Fig. 1c to have a closer look at the multi-period oscillations in the 150 keV electron flux. Note that the secondary flux oscillation was barely significant at 150 keV, while the dominant ∼190 s modulation was observed in at least four consecutive energy channels from 59 to 150 keV. This difference is discussed in Sect. 4.3 and attributed to the different azimuthal extent of the localized ULF waves.

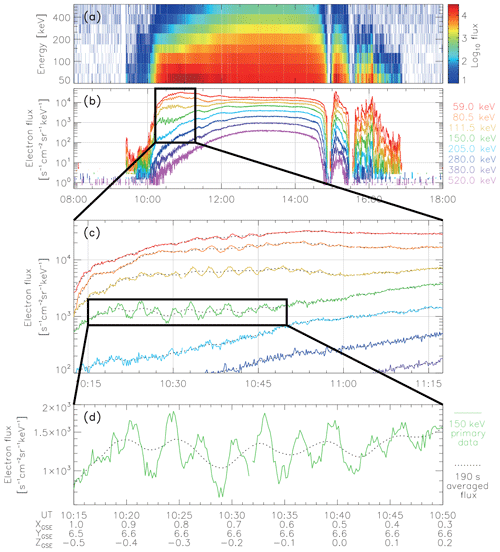
Figure 1 Overview of the electron flux observed by BD-IES. (a, b) Spectrogram and series plot of the electron flux in a full pass of the spacecraft through the radiation belt on 13 October 2015. (c) Zoomed-in view of the electron flux oscillation. (d) Zoomed-in view of the multi-period electron flux modulation. The spacecraft position in GSE (Geocentric Solar Ecliptic) coordinates in units of R_E (Earth's radius) is shown below panel (d).

Figure 2 shows the wavelet power spectrum (Grinsted et al., 2004) in order to quantitatively compare the amplitudes of the flux modulations at different periods and across the energy channels. The horizontal dashed lines in black and white mark the wave periods of 400 and 190 s, respectively. The comparison of the modulation amplitude across different energy channels is usually made by calculating the residuals of the particle fluxes (e.g., Claudepierre et al., 2013; Chen et al., 2016; Hao et al., 2017). The residual flux, defined as $\frac{J-J_{\mathrm{0}}}{J_{\mathrm{0}}}$, represents the flux variation normalized to the background flux so that the relative change of the particle flux caused by the waves can be quantitatively compared across different energy channels. Here J is the original differential flux obtained by the particle detector at a certain energy channel and J₀ is the corresponding background flux which can be represented by the running-averaged flux (e.g., Claudepierre et al., 2013; Hao et al., 2017). Unfortunately, the residual flux is hard to derive in our event. For one thing, it is difficult to choose a proper width of the averaging window to calculate the averaged flux, since multi-period oscillations were observed. For another, a sharp increase of electron flux was observed at ∼ 10:05 UT when the spacecraft traveled across the outer boundary of the radiation belt. False signatures would be included if J₀ is obtained by any running-averaging procedure. Therefore, the comparison of the modulation amplitude is alternatively achieved in our study by a careful selection of the color bars to display the wavelet power spectrum. As the wavelet power is proportional to the square of the oscillation amplitude (Torrence and Compo, 1998), the upper limit of the color bar for each energy channel is chosen to be the square of the mean value of the electron flux in the selected interval from 10:15 to 11:15 UT, and the widths of the color bars are consistently set to be 2. In this case, the same color in the wavelet power spectra refers to the same relative change of the electron flux. As shown in Fig. 2, the flux modulation at the period of ∼190 s can be clearly identified in four consecutive energy channels from 59 to 150 keV. The oscillation at ∼400 s is evidently observed at 150 keV. This secondary oscillation can still be weakly recognized at 111.5 keV but not at other energy channels. Besides, the electron flux modulation exhibits an energy-dispersive characteristic. Oscillations were first observed in the 150 keV energy channel at ∼ 10:15 UT. For lower energies from 111.5 to 59 keV, the electron flux oscillations were observed afterwards, with increasing time delays of up to ∼ 15 min.

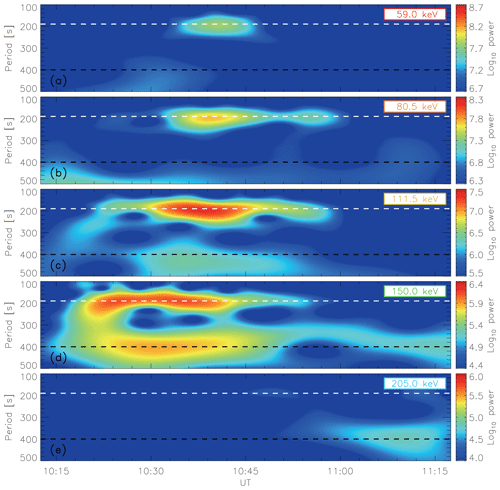
Figure 2 Wavelet analysis of the electron fluxes. (a–e) Wavelet power spectrograms of the electron fluxes from 59 to 205 keV. The white and black dashed lines mark 190 and 400 s, respectively.

In the following section, we revisit the drift-resonance theory to seek a possible explanation for these observed particle signatures.

4 Discussion

4.1 Drift-resonance theory revisited

In the original drift-resonance theory, Southwood and Kivelson (1981) proposed a path-integral approach to study the particle behavior in transverse ULF waves. The energy gain of a charged particle in the equatorial plane is calculated by integrating qE⋅v_d along the unperturbed particle drift orbit, where q and v_d denote the charge and drift velocity of the particle, respectively. The wave electric field E is described by a monochromatic plane wave $E_{\mathit{\phi }}{\mathit{e}}_{\mathit{\phi }}=E_{\mathrm{0}}\exp \left[i\left(m\mathit{\phi }-\mathit{\omega }t\right)\right]{\mathit{e}}_{\mathit{\phi }}$, where ω is the angular frequency, m is the azimuthal wave number, and E₀ is a constant that describes the amplitude of the wave. Here and throughout the paper, the equations are presented in cylindrical coordinates $\left(r,\mathit{\phi },z\right)$. For a symmetric background magnetic field, the unperturbed drift orbit of an equatorially mirroring particle can be given by r=r₀, $\mathit{\phi }={\mathit{\phi }}_{\mathrm{0}}+{\mathit{\omega }}_{\mathrm{d}}t$, and ${\mathit{\omega }}_{\mathrm{d}}=\frac{v_{\mathrm{d}}}{r}=\frac{\mathrm{1}}{r}\frac{\mathit{\mu }}{\mathit{\gamma }q}\frac{\mathrm{\nabla }B}{B}$, where μ is the first adiabatic invariant, γ is the Lorentz factor, and (r₀,φ₀) is the initial position. Note that it is impractical to postulate a constant wave amplitude, in which case any integration in time would strongly depend on the initial conditions. In practice, Southwood and Kivelson (1981) introduced a positive, infinitely small, and time-independent imaginary part of wave angular frequency by $\mathit{\omega }={\mathit{\omega }}_{\mathrm{r}}+i\mathit{\zeta }$, where $\frac{\mathit{\zeta }}{{\mathit{\omega }}_{\mathrm{r}}}\ll \mathrm{1}$. Then, the particle energy gain from the wave can be obtained by an integral along the unperturbed drift trajectory backwards until the time when the amplitude of the wave is negligible:

$$\begin{array}{}\text{(1)}& \mathit{\delta }W=\underset{L}{\int }q\mathit{E}\cdot {\mathit{v}}_{\mathrm{d}}\mathrm{d}t\propto -{\displaystyle \frac{i}{\mathit{\omega }-m{\mathit{\omega }}_{\mathrm{d}}}}{E}_{\mathit{\phi }}.\end{array}$$

For particles of a specific energy, called the resonant energy, that satisfies mω_d=ω_r, the fraction $-\frac{i}{\mathit{\omega }-m{\mathit{\omega }}_{\mathrm{d}}}$ equals $-\frac{\mathrm{1}}{\mathit{\zeta }}$, which is a large negative real number. That is to say, the energy change of the particle would oscillate at a large amplitude in anti-phase with the wave electric field. For lower or higher energies, the denominator is dominated by its real part so that the energy change is ∓90^∘ out of phase with the wave electric field. With a further assumption of constant energy and spatial gradients, the variation of particle flux is in proportion to the energy change. Therefore, particle flux modulation caused by drift resonance would present a characteristic 180^∘ phase shift across the resonant energy.

Recent adaption of the drift-resonance theory adopted the unperturbed path-integral method but introduced variations to E₀ and ζ to describe the spatial distribution and temporal evolution of the wave in a more realistic way. Zhou et al. (2015, 2016) considered a finite time-dependent ζ and showed that the phase shift of the electron flux oscillation across the resonant energy is time-dependent. The phase shift would grow from 90^∘ at the beginning and become 180^∘ when the wave amplitude reaches its maximum. Then, when the wave starts damping, the phase shift would keep growing as the drift velocities of the particles depend on their energies. This characteristic phase relationship is presented as “increasing tilted stripes” in the particle flux spectrogram. Li et al. (2017b) introduced an analog of a Gaussian envelope to E₀ in the azimuthal dimension. Because it takes different times for particles of different energies to drift from the wave-active region to the detector, a time delay between the particle fluxes observed at different channels would arise from this time-of-flight effect. In terms of phase, the time delay enlarges the initial phase shift across the resonant energy.

While the characteristic particle signatures of drift resonance predicted by these prevailing theories have been proved by recent spacecraft observations, the particle energy change therein is derived in an incomplete way. In the guiding-center approximation (Northrop, 1961), the rate of particle energy change averaged over a gyration is given by $\frac{\mathrm{d}W}{\mathrm{d}t}=q\mathit{E}\cdot \mathit{u}+\frac{\mathit{\mu }}{\mathit{\gamma }}\frac{\partial B}{\partial t}$, where u is the velocity of the guiding center (Northrop, 1963). For the unperturbed motion of an equatorially mirroring particle in a dipole-like magnetic field, u equals the drift velocity v_d. Hence, qE⋅v_d represents the rate of energy change caused by the wave electric field along the unperturbed guiding-center trajectory. The Betatron acceleration caused by the curl of the wave electric field, denoted by $\frac{\mathit{\mu }}{\mathit{\gamma }}\frac{\partial B}{\partial t}$, is wrongly omitted in those drift-resonance theories (e.g., Zhou et al., 2015, 2016; Li et al., 2017b). Note that, for poloidal waves, ∇×E is controlled by $\frac{\partial E}{\partial r}$, since E is in the azimuthal direction. Consequently, the particle energy change would be greatly influenced by the radial gradient of wave-electric-field amplitude, although the particle drifts at a constant L shell in the unperturbed-orbit approximation. Observational and modeling studies showed that the power of the ULF wave electric field generally increases with radial distance within the outer-radiation-belt region (e.g., Perry et al., 2005; Ozeke et al., 2012, 2014) and is structured by plasma density inhomogeneities (e.g., Degeling et al., 2018). In the following discussions, we amend the omissions in the previous drift-resonance theories, while retaining the unperturbed-orbit approximation for the simplicity of calculation.

We confine our discussion to the equatorial plane. The background field is given by ${\mathit{B}}_{\mathrm{0}}=B_{\mathrm{0}}{\mathit{e}}_z=\frac{B_{\mathrm{E}}}{L^{\mathrm{3}}}{\mathit{e}}_z$, where B_E is the magnitude of the equatorial magnetic field at Earth's surface. In this case, the particle drift velocity v_d equals $-\frac{\mathit{\mu }}{\mathit{\gamma }q}\frac{\mathrm{3}}{r}{\mathit{e}}_{\mathit{\phi }}$. The poloidal ULF wave fields can be given by ${\mathit{E}}_{\mathrm{1}}=-\frac{\partial A}{\partial t}{\mathit{e}}_{\mathit{\phi }}\stackrel{△}{=}{E}_{\mathit{\phi }}{\mathit{e}}_{\mathit{\phi }}$ and ${\mathit{B}}_{\mathrm{1}}=\mathrm{\nabla }\times \left(A{\mathit{e}}_{\mathit{\phi }}\right)=-\frac{\partial A}{\partial z}{\mathit{e}}_{\mathrm{r}}+\frac{\mathrm{1}}{r}\frac{\partial \left(rA\right)}{\partial r}{\mathit{e}}_z$, where A=Ae_φ is the magnetic vector potential. Then, the rate of particle energy change caused by the electric field along the unperturbed path of its guiding center is denoted by

$$\begin{array}{}\text{(2)}& q\mathit{E}\cdot {\mathit{v}}_{\mathrm{d}}={\displaystyle \frac{\mathit{\mu }}{\mathit{\gamma }}}{\displaystyle \frac{\mathrm{3}}{r}}{\displaystyle \frac{\partial A}{\partial t}}=-{\displaystyle \frac{\mathit{\mu }}{\mathit{\gamma }}}{\displaystyle \frac{\mathrm{3}}{r}}{E}_{\mathit{\phi }}.\end{array}$$

For fundamental mode waves, it is reasonable to further assume that the amplitude of the wave does not vary in the vicinity of the Equator (i.e., $\frac{\partial A}{\partial z}=\mathrm{0}$). Then, the wave magnetic field would only have a parallel component, in which case the Betatron acceleration term can be calculated by

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{\mathit{\mu }}{\mathit{\gamma }}}{\displaystyle \frac{\partial B}{\partial t}}={\displaystyle \frac{\mathit{\mu }}{\mathit{\gamma }}}{\displaystyle \frac{\partial }{\partial t}}{\displaystyle \frac{\partial \left(rA\right)}{\partial r}}=-{\displaystyle \frac{\mathit{\mu }}{\mathit{\gamma }}}\left({\displaystyle \frac{\mathrm{1}}{r}}+{\displaystyle \frac{\mathrm{1}}{E_{\mathit{\phi }}}}{\displaystyle \frac{\partial E_{\mathit{\phi }}}{\partial r}}\right)E_{\mathit{\phi }}.\end{array}$$

One may easily find that the total rate of particle energy change is in proportion to qE⋅v_d:

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}W}{\mathrm{d}t}}& =q\mathit{E}\cdot {\mathit{v}}_{\mathrm{d}}+{\displaystyle \frac{\mathit{\mu }}{\mathit{\gamma }}}{\displaystyle \frac{\partial B}{\partial t}}=-{\displaystyle \frac{\mathit{\mu }}{\mathit{\gamma }}}\left({\displaystyle \frac{\mathrm{4}}{r}}+{\displaystyle \frac{\mathrm{1}}{E_{\mathit{\phi }}}}{\displaystyle \frac{\partial E_{\mathit{\phi }}}{\partial r}}\right)E_{\mathit{\phi }}\\ & ={\displaystyle \frac{\mathrm{4}+\frac{r}{E_{\mathit{\phi }}}\frac{\partial E_{\mathit{\phi }}}{\partial r}}{\mathrm{3}}}q\mathit{E}\cdot {\mathit{v}}_{\mathrm{d}}.\end{array}\end{array}$$

In other words, the amendments do no change the characteristic phase relationship in the particle signatures but alter the ratio between the strength of the ULF wave field and particle energy modulation. Particularly, for the zeroth-order approximation that the amplitude of the wave electric field does not change with radial distance (e.g., in the vicinity of the radial amplitude peak), the fraction $\frac{\mathrm{4}+\frac{r}{E_{\mathit{\phi }}}\frac{\partial E_{\mathit{\phi }}}{\partial r}}{\mathrm{3}}$ equals 4∕3. For the empirical electric field model denoted by E_φ∝exp [σr] (e.g., Perry et al., 2005; Ozeke et al., 2014), the fraction $\frac{\mathrm{4}+\frac{r}{E_{\mathit{\phi }}}\frac{\partial E_{\mathit{\phi }}}{\partial r}}{\mathrm{3}}$ equals $\frac{\mathrm{4}+\mathit{\sigma }r}{\mathrm{3}}$, where σ is a constant factor in the order of 0.3 $R_{\mathrm{E}}^{-\mathrm{1}}$. In the outer radiation belt (e.g., r=6 R_E), $\frac{\mathrm{4}+\mathit{\sigma }r}{\mathrm{3}}$ is around 2, which means the negligence of $\frac{\mathit{\mu }}{\mathit{\gamma }}\frac{\partial B}{\partial t}$ can result in a ∼50 % underestimate of the particle energy change.

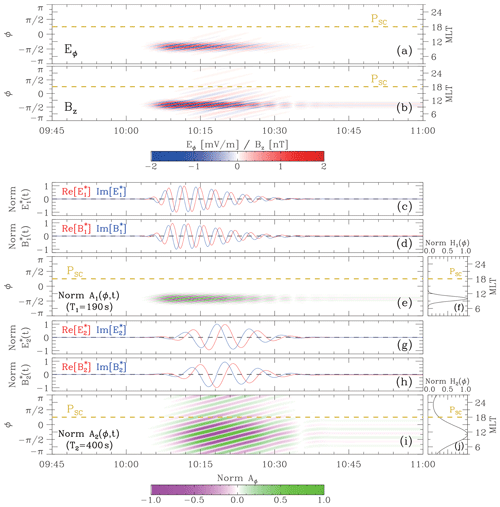
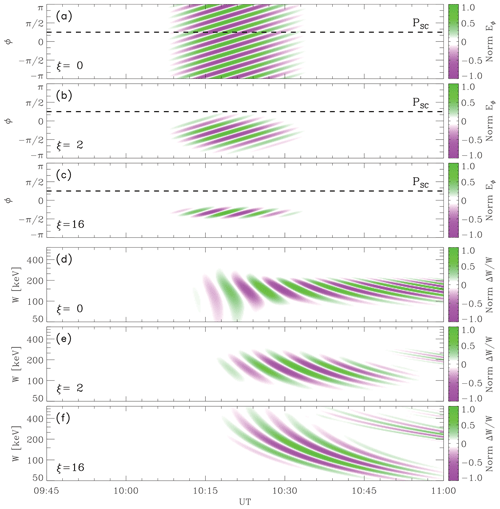
Figure 3 The modeled ULF electric field. (a, b) The modeled wave electric field and magnetic field as a function of UT (universal time) and MLT (magnetic local time). (c–j) The normalized azimuthal distribution and temporal evolution of each monochromatic wave. The real parts (Re) and the imaginary parts (Im) of the functions are shown in red and blue, respectively. φ=0 corresponds to MLT=15. The horizontal dashed lines, labeled P_SC, mark the azimuthal location of the virtual spacecraft.

4.2 The localized-drift-resonance scenario

As described in Sect. 3, the electron flux modulations were first observed in the 150 keV energy channel at ∼ 10:15 UT. The flux oscillations were observed sequentially afterwards in lower energy channels. According to Li et al. (2017b), this dispersive characteristic implies that the ULF waves were azimuthally confined and that the particle detector was located outside the region of strong wave activity. Thus, it is natural to attribute the observed multi-period modulation to multiple localized ULF waves. In consideration of the limited observations, we reproduce the particle signatures observed by BD-IES to substantiate this localized wave–particle scenario. First, we assume a modeled ULF wave field and employ the integral method described in Sect. 4.1 to calculate the changes of electron energy. Then, the energy changes are transformed into flux variations to compare with the observations. More specifically, the magnetic vector potential of the modeled ULF wave is given by

$$\begin{array}{}\text{(5)}& \begin{array}{rl}\mathit{A}& =A{\mathit{e}}_{\mathit{\phi }}=\sum _{n=\mathrm{1},\mathrm{2}}{A}_i\left(r,\mathit{\phi },t\right){\mathit{e}}_{\mathit{\phi }}\\ & =\sum _{n=\mathrm{1},\mathrm{2}}{A}_{\mathrm{0},n}{G}_n\left(r\right)H_n\left(\mathit{\phi }\right)F_n\left(\mathit{\phi },t\right){\mathit{e}}_{\mathit{\phi }},\end{array}\end{array}$$

where the subscripts 1 and 2 refer to the two modeled monochromatic ULF waves. For each of the monochromatic waves, the constant factor A_0,n denotes its amplitude. The second term, G_n(r), describes the distribution of wave amplitude in the radial direction. The third term, $H_n\left(\mathit{\phi }\right)=\frac{\exp \left[{\mathit{\xi }}_n\cos \left(\mathit{\phi }-{\mathit{\phi }}_{\mathrm{0},n}\right)\right]}{\mathrm{2}\mathit{\pi }{I}_{\mathrm{0}}\left({\mathit{\xi }}_n\right)}$, is a von Mises function, describing the azimuthal distribution of the ULF wave (Li et al., 2017b). Here φ_0,n is the central azimuth of the wave-active region, ξ_n is the concentration parameter, and I₀(ξ_n) is the zeroth-order modified Bessel function of the first kind. The von Mises distribution is an analogue of the normal distribution for a periodic variable. For a large positive ξ, the distribution is highly concentrated, whereas when ξ approaches zero, it reduces to a uniform distribution. The growth, damping, and propagation of the wave is described in the last term, F_n(φ,t), by

$$\begin{array}{}\text{(6)}& \begin{array}{rl}{F}_n\left(\mathit{\phi },t\right)& ={\displaystyle \frac{\sqrt{\mathit{\pi }}}{\mathrm{2}}}{\mathit{\tau }}_{\pm ,n}\exp \left[-{\displaystyle \frac{{\mathit{\omega }}_n^{\mathrm{2}}{\mathit{\tau }}_{\pm ,n}^{\mathrm{2}}}{\mathrm{4}}}\right]\\ & \cdot \mathrm{erf}\left[{\displaystyle \frac{t-t_{\mathrm{0},n}}{{\mathit{\tau }}_{\pm ,n}}}+{\displaystyle \frac{{\mathit{\omega }}_n{\mathit{\tau }}_{\pm ,n}}{\mathrm{2}}}i\right]\\ & \cdot \exp \left[i\left(m_n\mathit{\phi }-{\mathit{\omega }}_n{t}_{\mathrm{0},n}+{\mathit{\theta }}_{\mathrm{0},n}\right)\right]+C_n\left(\mathit{\phi }\right),\end{array}\end{array}$$

where $\mathrm{erf}\left[z\right]=\frac{\mathrm{2}}{\sqrt{\mathit{\pi }}}{\int }_{\mathrm{0}}^z\exp \left[-t^{\mathrm{2}}\right]\mathrm{d}t$ is the error function; ω_n, m_n, and θ_0,n are the frequency, azimuthal wave number, and initial phase, respectively; and t_0,n denotes the time when the wave amplitude reaches its maximum value. The wave grows or damps at the timescale of ${\mathit{\tau }}_{+,n}$/${\mathit{\tau }}_{-,n}$, synthesized as ${\mathit{\tau }}_{\pm ,n}$ in Eq. (6), before or after t_0,n. C_n(φ) is a function independent of time given by

$$\begin{array}{}\text{(7)}& \begin{array}{rl}{C}_n\left(\mathit{\phi }\right)& ={\displaystyle \frac{\sqrt{\mathit{\pi }}}{\mathrm{2}}}{\mathit{\tau }}_{+,n}\exp \left[-{\displaystyle \frac{{\mathit{\omega }}_n^{\mathrm{2}}{\mathit{\tau }}_{+,n}^{\mathrm{2}}}{\mathrm{4}}}\right]\left(\mathrm{erf}\left[{\displaystyle \frac{{\mathit{\omega }}_n{\mathit{\tau }}_{+,n}}{\mathrm{2}}}i\right]+\mathrm{1}\right)\\ & \cdot \exp \left[i\left(m_n\mathit{\phi }-{\mathit{\omega }}_n{t}_{\mathrm{0},n}+{\mathit{\theta }}_{\mathrm{0},n}\right)\right]\\ & -{\displaystyle \frac{\sqrt{\mathit{\pi }}}{\mathrm{2}}}{\mathit{\tau }}_{\pm ,n}\exp \left[-{\displaystyle \frac{{\mathit{\omega }}_n^{\mathrm{2}}{\mathit{\tau }}_{\pm ,n}^{\mathrm{2}}}{\mathrm{4}}}\right]\mathrm{erf}\left[{\displaystyle \frac{{\mathit{\omega }}_n{\mathit{\tau }}_{\pm ,n}}{\mathrm{2}}}i\right]\\ & \cdot \exp \left[i\left(m_n\mathit{\phi }-{\mathit{\omega }}_n{t}_{\mathrm{0},n}+{\mathit{\theta }}_{\mathrm{0},n}\right)\right].\end{array}\end{array}$$

Since $\underset{t\to -\mathrm{\infty }}{lim}\mathrm{erf}\left[\frac{t-t_{\mathrm{0},n}}{{\mathit{\tau }}_{\pm ,n}}+\frac{{\mathit{\omega }}_n{\mathit{\tau }}_{\pm ,n}}{\mathrm{2}}i\right]=-\mathrm{1}$, the choice of C_n(φ) ensures an infinitely small wave amplitude at $t=-\mathrm{\infty }$ for all azimuths ($\underset{t\to -\mathrm{\infty }}{lim}F\left(\mathit{\phi },t\right)=\mathrm{0}$). The wave electromagnetic fields are given by

$$\begin{array}{}\text{(8)}& \begin{array}{rl}\mathit{E}& =-{\displaystyle \frac{\partial \mathit{A}}{\partial t}}=\sum _{n=\mathrm{1},\mathrm{2}}{A}_{\mathrm{0},n}{G}_n\left(r\right)H_n\left(\mathit{\phi }\right){\displaystyle \frac{\partial F_n\left(\mathit{\phi },t\right)}{\partial t}}{\mathit{e}}_{\mathit{\phi }}\\ & =\sum _{n=\mathrm{1},\mathrm{2}}{A}_{\mathrm{0},n}{G}_n\left(r\right)H_n\left(\mathit{\phi }\right)\exp \left[-{\displaystyle \frac{{\left(t-t_{\mathrm{0},n}\right)}^{\mathrm{2}}}{{\mathit{\tau }}_{\pm ,n}^{\mathrm{2}}}}\right]\\ & \cdot \exp \left[i\left(m_n\mathit{\phi }-{\mathit{\omega }}_{n}t+{\mathit{\theta }}_{\mathrm{0},n}\right)\right]{\mathit{e}}_{\mathit{\phi }}\end{array}\end{array}$$

and

$$\begin{array}{}\text{(9)}& \begin{array}{rl}\mathit{B}& =\mathrm{\nabla }\times \mathit{A}={\displaystyle \frac{\mathrm{1}}{r}}{\displaystyle \frac{\partial \left(rA\right)}{\partial r}}{\mathit{e}}_z=\left({\displaystyle \frac{\mathrm{1}}{r}}+{\displaystyle \frac{\mathrm{1}}{A}}{\displaystyle \frac{\partial A}{\partial r}}\right)A{\mathit{e}}_z\\ & =\sum _{n=\mathrm{1},\mathrm{2}}{A}_{\mathrm{0},n}\left({\displaystyle \frac{\mathrm{1}}{r}}+{\displaystyle \frac{\mathrm{1}}{G_n}}{\displaystyle \frac{\partial G_n}{\partial r}}\right)G_n\left(r\right)H_n\left(\mathit{\phi }\right)F_n\left(\mathit{\phi },t\right){\mathit{e}}_z.\end{array}\end{array}$$

We adopt a set of parameters (somewhat arbitrarily to fit the particle signatures observed by BD-IES) as follows: $A_{\mathrm{0},\mathrm{1}}=\mathrm{1.1}$ mV m⁻¹, m₁=20, ${\mathit{\omega }}_{\mathrm{1}}=\frac{\mathrm{2}\mathit{\pi }}{\mathrm{190}}$, ξ₁=16, ${\mathit{\phi }}_{\mathrm{0},\mathrm{1}}=-\frac{\mathrm{5}\mathit{\pi }}{\mathrm{12}}$, $t_{\mathrm{0},\mathrm{1}}=\mathrm{600}$ s, ${\mathit{\theta }}_{\mathrm{0},\mathrm{1}}=-\frac{\mathrm{3}\mathit{\pi }}{\mathrm{5}}$, ${\mathit{\tau }}_{+,\mathrm{1}}=\mathrm{200}$ s and ${\mathit{\tau }}_{-,\mathrm{1}}=\mathrm{800}$ s; $A_{\mathrm{0},\mathrm{2}}=\mathrm{0.2}$ mV m⁻¹, m₂=7, ${\mathit{\omega }}_{\mathrm{2}}=\frac{\mathrm{2}\mathit{\pi }}{\mathrm{400}}$, ξ₂=1, ${\mathit{\phi }}_{\mathrm{0},\mathrm{2}}=-\frac{\mathit{\pi }}{\mathrm{3}}$, $t_{\mathrm{0},\mathrm{2}}=\mathrm{1100}$ s, ${\mathit{\theta }}_{\mathrm{0},\mathrm{2}}=\mathrm{0}$, ${\mathit{\tau }}_{+,\mathrm{2}}=\mathrm{400}$ s, and ${\mathit{\tau }}_{-,\mathrm{2}}=\mathrm{600}$ s. Here t=0 and φ=0 correspond to 10:00 UT and 15:00 MLT, respectively. Since our calculation would be confined to the unperturbed particle orbit at r₀=7 R_E (consistent with the spacecraft position), parameters describing the radial distribution of the wave amplitude are simply set as $G_{\mathrm{1},\mathrm{2}}\left(r_{\mathrm{0}}\right)=\mathrm{1}$. The modeled electromagnetic fields, which consists of two localized ULF waves, are shown in Fig. 3a and b. In view of the striking difference of the amplitude, we also show the normalized characteristics of the two monochromatic waves separately. We present the electromagnetic fields in the form of the separation of variables by $E_n=E_n^{*}\left(t\right)H_n\left(\mathit{\phi }\right)\exp \left[i{m}_n\mathit{\phi }\right]$ and $B_n=B_n^{*}\left(t\right)H_n\left(\mathit{\phi }\right)\exp \left[i{m}_n\mathit{\phi }\right]$. The temporal evolution of the waves $E_n^{*}\left(t\right)$ are shown in Fig. 3c, d, g, and h. The azimuthal distributions of wave magnitude H_n(φ) are shown in Fig. 3e and i. The different azimuthal concentrations of the two monochromatic waves (ξ₁=16 and ξ₂=1) would cause a difference in the energy width of the modulated particles. The wider azimuthal extent of the 400 s wave may explain the narrower energy range of the electron flux modulation in the particle spectrum observed by BD-IES, which will be discussed in detail in Sect. 4.3.

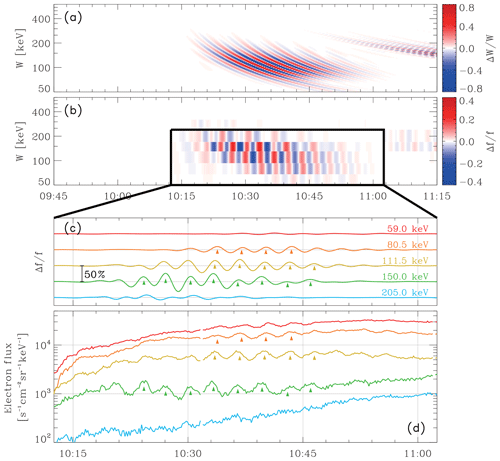
Figure 4 The modeled electron energy change and the corresponding residual flux. (a) The energy change of the electrons in the modeled ULF wave field. (b) The spectrogram of the modeled electron residual flux observed by the virtual spacecraft. (c) Zoomed-in view of the calculation result. (d) The electron flux observed by BD-IES. The triangles mark the modulation peaks.

To verify the localized-drift-resonance scenario, we numerically calculate the energy change of the electrons caused by the modeled ULF wave and predict the particle signatures to be observed by a virtual spacecraft. The orange dashed lines in Fig. 3 mark the position of the virtual spacecraft which is away from the regions of strong wave activities. Specifically, the virtual spacecraft is placed at $\mathit{\phi }=\frac{\mathit{\pi }}{\mathrm{4}}$, while the central positions of the wave-active regions are ${\mathit{\phi }}_{\mathrm{0},\mathrm{1}}=-\frac{\mathrm{5}\mathit{\pi }}{\mathrm{12}}$ and ${\mathit{\phi }}_{\mathrm{0},\mathrm{2}}=-\frac{\mathit{\pi }}{\mathrm{3}}$. The azimuthal of the virtual spacecraft corresponds to MLT=18, consistent with the position of BD-IES in our event. Figure 4a shows the relative energy change of the electrons. Multi-period patterns are readily apparent at ∼150 keV. The final step to achieve a comparison between theory and observation is transforming the calculated energy changes into particle flux variations. According to Zhou et al. (2016) and Li et al. (2017b), the transformation can be performed in two steps. First, the variation of phase space density is derived from the energy change, provided a power law spectrum of the electrons $\left(f\propto W^{-n}\right)$. Then, the change of phase space density can be further transformed into the flux variation following the standard relationship $f=\frac{j}{p^{\mathrm{2}}}$, where j is the flux and p is the particle momentum (e.g., Hilmer et al., 2000; Chen et al., 2005; Roederer and Zhang, 2014). Note that the relative changes of the phase space density $\left(\frac{\mathrm{d}f}{f}\right)$ and the particle flux $\left(\frac{\mathrm{d}j}{j}\right)$ are essentially equivalent (e.g., Zhou et al., 2016; Chen et al., 2016; Li et al., 2017b). The calculated phase space density change under the localized-drift-resonance scenario is shown in Fig. 4b. Here the power law exponent n equals 2.5 in our calculation, and the widths of the energy channels of the virtual spacecraft are identical to those of BD-IES. A comparison between the results of our numerical calculation and the BD-IES observations is presented in Fig. 4c and d. The triangles mark the modulation peaks. It is shown that the multi-period particle signatures are well reproduced by our numerical calculation.

Besides the particle signatures, ground-based magnetic field observations can provide circumstantial evidence to the localized-drift-resonance scenario, although we lack the accompanied in situ electromagnetic field observations. The spacecraft with BD-IES on board was located in the Southern Hemisphere with its footpoint mapped at ∼66^∘ S geographic latitude during the event. In the vicinity of the ∼66^∘ isopleth, we find three geomagnetic stations, tagged PG4 (Antarctica), CSY (Casey), and DRV (Dumont Durville), that provided 3-dimensional magnetic field measurements. The stations were located on Antarctica, south of the spacecraft footpoint, which means that they correspond to a slightly higher L shell than BD-IES. For the two stations in the dusk sector, CSY and DRV, closer to the footpoint of BD-IES in the longitudinal direction, no ULF perturbation in the Pc 3–5 band were observed. Meanwhile, the PG4 station located in the noon sector observed large-amplitude ULF waves. The observation of ULF waves away from the footpoint of BD-IES and the absence of wave activities in the vicinity of the footpoint support the idea that the ULF waves in our event were restricted to azimuthally limited regions. (See Figs. S1 and S2 in the Supplement for more details.)

Figure 5 The width of electron flux modulation varied with the azimuthal distribution of the modeled ULF waves. (a–c) Modeled ULF waves of different spatial extents in the azimuthal direction. (d–f) The normalized electron energy gains from the corresponding ULF waves.

4.3 The resonance width

In the drift-resonance scenario, the amplitude of the flux oscillate peaks at the resonance energy and rapidly decreases at lower or higher energies. The resonance width describes the energy extent of this amplitude peak. For a global monochromatic wave with an infinitely small growth rate, the energy change oscillation is theoretically restricted to the resonant energy with an infinitely narrow width. However, flux oscillations observed by actual particle detectors usually show finite resonance widths. As pointed out by previous studies, the resonance width depends on the widths of the energy channels (e.g., Southwood and Kivelson, 1981), particle phase space density gradient (e.g., Zhou et al., 2016; Chen et al., 2016), and growth rate of the wave (e.g., Zhou et al., 2015). We propose that the azimuthal extent of the localized ULF waves also plays an important role in the resonance width under the localized-drift-resonance scenario. Figure 5 shows an example of the particle signatures in response to the localized ULF waves of different azimuthal distributions. The only difference among the wave fields shown in Fig. 5a–c is the concentration parameter ξ, whereas all other parameters are set the same. The corresponding particle signatures observed by the virtual spacecraft are shown in Fig. 5d–f. For an increasingly concentrated wave field (demonstrated by an increasing value of ξ), the width of the resonant amplitude peak extends. In other words, particles of a wider energy range can gain nonzero net energy changes from the highly localized waves. This broadened resonance width can be explained by the incomplete cancellation of the positive and negative energy changes. For a monochromatic ULF wave of azimuthally uniform distribution, a non-resonant particle experiences alternating electric fields during its drift motion. The gain and loss of the energy cancel each other out. However, for a localized ULF wave, a non-resonant particle may leave the region of strong wave activity with uncanceled energy change as it proceeds with its azimuthal drift motion, which in turn results in a variation of the non-resonant particle flux.

4.4 Other possible scenarios and future work

Although the localized-drift-resonance scenario applies well in our event, we do not rule out other possible explanations, considering the limited observations and the simplistic numerical calculation. The particle trajectory is assumed to be unperturbed while the electron gains and loses energy in the ULF wave field. This assumption would be invalid for large-amplitude waves which could alter the particle motion significantly. Li et al. (2018) conducted a more self-consistent analysis with the perturbed particle trajectory taken into account. They employed the pendulum equation to describe the particle motion and derived the corresponding energy change. According to their theory, multi-period oscillations of particle fluxes are expected to be observed near the resonant energy, as a large-amplitude poloidal-mode ULF wave would typically produce “rolled-up” structures in the particle energy spectrum. Besides, the bounce motion of the particles is neglected in our simple calculation, though the spacecraft with BD-IES on board was located off the equatorial plane in our event. For bouncing particles, the interaction with ULF waves is more complicated even if we only consider the drift-resonance process. In this case, not only the azimuthal distribution of the ULF electric field but also its morphology along the field line plays an important role in the wave–particle interaction. In addition, the ULF magnetic field can modify the pitch angle of the particle (e.g., Chaston et al., 2017, 2018), although the Lorentz force is perpendicular to the particle velocity and causes no energy change. Unfortunately, the pitch angle distribution of the energetic electrons observed by the BD-IES instrument has not yet been resolved. Hence, we focus on equatorial mirroring electrons, since there has already been a bunch of parameters in our numerical calculation.

Additionally, multi-period signatures, especially the “frequency-doubling” feature, have been investigated and attributed to several independent mechanisms. Higuchi et al. (1986) first reported this harmonic structure in the magnetic field observed by geostationary satellites. They proposed that the multi-period structure in the compressional component of the magnetic field was formed by requiring the balance of overall pressure as there existed a modulation of the plasmas by the magnetic field. Other possible causes of the frequency-doubling signatures include the periodic motion of the field line nodes (Takahashi et al., 1987), nonlinear drift-bounce resonance (Southwood and Kivelson, 1997), ballooning-mirror mode instability (Sibeck et al., 2012), and E×B effect (Zhang et al., 2019). As the secondary period of the flux modulation observed by BD-IES in the present event happened to be nearly twice the dominant period, it could be possible that the multi-period modulations of the electron fluxes were caused by either mechanism(s) mentioned above.

5 Summary

We present BD-IES observations of multi-period electron flux modulations. Oscillations at the dominant period of ∼ 190 s were observed in four consecutive energy channels. Meanwhile, a ∼400 s secondary modulation was also unambiguously observed at 150 keV, as well as weakly identified at 111.5 keV. The observed particle signatures are attributed to the drift-resonance interaction between the energetic electrons and two localized ULF waves of different azimuthal distributions and different periods.

We revisit the theoretical scheme of drift resonance developed by Southwood and Kivelson (1981) and its recent adaptations and fix a flaw in the prevailing theories. We show that the Betatron acceleration caused by the curl of the wave electric field, often omitted in these theories, plays an non-negligible role in the modulation of particle fluxes. The amplitude of this induced modulation is comparable with the energy change caused by the electric field along the drift path of the particle. Fortunately, the flawed theories still give the correct characteristic phase relationship in the particle signatures because the two terms of energy changes, qE⋅v_d and $\frac{\mathit{\mu }}{\mathit{\gamma }}\frac{\partial B}{\partial t}$, are in phase. But the flawed theories might overestimate the strength of the wave electromagnetic fields, in the usual case that the wave amplitude increases with radial distance within the outer radiation belt.

Based on the modified drift-resonance theory, we reproduce the particle signatures observed by BD-IES with an azimuthally confined modeled ULF wave of multi-periods. The good agreement between our numerical calculation and the BD-IES observation demonstrates that multiple localized ULF waves can apply combined effects on the energetic particles, which is foreseeable by the localized-drift-resonance theory but rarely reported in observations. In addition, the relationship between the width of the resonant amplitude peak and the azimuthal extent of the wave-active region is studied. We illustrate that highly localized ULF waves can cause net energy changes of the non-resonant particles due to the incomplete cancellation of the energy gains and losses in the alternating wave fields. Hence, the azimuthal concentration of the waves extends the energy width of the resonance peak.