the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Non-locality of Earth's quasi-parallel bow shock: injection of thermal protons in a hybrid-Vlasov simulation
Markus Battarbee
Urs Ganse
Yann Pfau-Kempf
Lucile Turc
Thiago Brito
Maxime Grandin
Tuomas Koskela
Minna Palmroth
We study the interaction of solar wind protons with Earth's quasi-parallel bow shock using a hybrid-Vlasov simulation. We employ the global hybrid model Vlasiator to include effects due to bow shock curvature, tenuous upstream populations, and foreshock waves. We investigate the uncertainty of the position of the quasi-parallel bow shock as a function of several plasma properties and find that regions of non-locality or uncertainty of the shock position form and propagate away from the shock nose. Our results support the notion of upstream structures causing the patchwork reconstruction of the quasi-parallel shock front in a non-uniform manner. We propose a novel method for spacecraft data to be used to analyse this quasi-parallel reformation.
We combine our hybrid-Vlasov results with test-particle studies and show that proton energization, which is required for injection, takes place throughout a larger shock transition zone. The energization of particles is found regardless of the instantaneous non-locality of the shock front, in agreement with it taking place over a larger region. Distortion of magnetic fields in front of and at the shock is shown to have a significant effect on proton injection.
We additionally show that the density of suprathermal reflected particles upstream of the shock may not be a useful metric for the probability of injection at the shock, as foreshock dynamics and particle trapping appear to have a significant effect on energetic-particle accumulation at a given position in space. Our results have implications for statistical and spacecraft studies of the shock injection problem.
- Article
(7039 KB) - Full-text XML
- BibTeX
- EndNote
Collisionless plasma shocks are a ubiquitous source of plasma acceleration, common within stellar, planetary, and interplanetary environments. Shock dynamics have been studied in great detail at Earth's bow shock. In regions of shock geometry where the angle θBn between the shock-normal direction and the upstream interplanetary magnetic field (IMF) direction B is small (≲45∘), the shock is considered quasi-parallel (see e.g. Burgess et al., 2005). In this region, if the shock is a strong fast-mode supercritical shock, a fraction of thermal incident ions are reflected, streaming away from the shock along the magnetic field lines, forming the foreshock region (Fairfield, 1969; Eastwood et al., 2005). The streaming energized particles excite instabilities such as a right-hand ion–ion beam instability, building a wave field of ultra-low-frequency (ULF) waves (Hoppe et al., 1981) with periods around ∼30 s, which further interact with the particles themselves and are convected toward the bow shock. As the waves are convected with the supersonic solar wind flow, they appear mostly left-handed in the spacecraft frame. The incident ULF waves can experience nonlinear steepening, possibly forming shocklets (Hada et al., 1987; Wilson, 2016) or short large-amplitude magnetic structures (SLAMS; Schwartz et al., 1992; Burgess, 1995; Lucek et al., 2008), eventually causing the patchwork reformation of the bow shock (Scholer and Terasawa, 1990; Thomas and Winske, 1990; Schwartz and Burgess, 1991; Burgess, 1995) as incoming structures proceed to build a new shock front periodically (Burgess, 1989). At Mercury this reformation has been studied through mainly magnetic field measurements in Sundberg et al. (2013). The complicated structure of the shock-associated transition region was linked with local reconnection in Gingell et al. (2019). As the location of the shock front is challenging to define due to movement (i.e. the non-stationarity of a well-defined shock front, the formation and convection of a new shock front, and even the disappearance of the old front), we now discuss this uncertainty of the shock position which we designate the “non-locality” of the shock. As plasma parameters across a quasi-parallel shock can be non-monotonic, non-locality encompasses more than mere thickness of a well-defined shock front. Our definition of non-locality can also be measured using spacecraft, providing a novel metric for quantifying space plasma observations. In this study, we limit our analysis to ion scales and assume that the reformation of the quasi-parallel bow shock happens on temporal and spatial scales similar to those of steepened ULF waves and associated transient structures.
An important open question for space physics and particle acceleration is the shock injection problem (see e.g. Zank et al., 2001), which is how exactly thermal particles are reflected at a supercritical quasi-parallel shock. Injection from a thermal population is a necessary step in efficient diffusive shock acceleration (DSA; Axford et al., 1977; Blandford and Ostriker, 1978; Bell, 1978; Krymsky et al., 1979), which is a major source of energetic particles throughout the universe. The injection problem has been studied extensively during the past decades with, amongst others, observations (Sckopke et al., 1983; Thomsen et al., 1983; Gosling et al., 1989; Johlander et al., 2016), analytical work (Schwartz et al., 1983; Malkov et al., 2016), test-particle modelling (Gedalin, 2001, 2016; Battarbee et al., 2011; Johlander et al., 2016), and particle-in-cell simulations (Caprioli et al., 2015, 2017; Liseykina et al., 2015; Sundberg et al., 2016; Hao et al., 2016). Significant historical work using 1D or 2D local hybrid simulations can be found in e.g. Burgess (1989), Scholer (1990), and Kucharek and Scholer (1991). Previous studies have suggested three methods for injection: specular reflection (Gosling et al., 1982), shock drift acceleration (SDA; Giacalone, 1992; Lever et al., 2001; Burgess, 1987) and associated shock surfing (Lever et al., 2001), and thermal leakage from the downstream (Ellison, 1981; Edmiston et al., 1982; Lyu and Kan, 1990; Malkov, 1998). These three methods were derived from assumptions of macroscopic, planar, and stationary shock fronts and are thus a limited but important first step towards understanding the concept. Magnetic mirroring as described through quasi-linear theory and conservation of the first adiabatic invariant is usually excluded, as changes to magnetic fields may occur on scales much smaller and faster than those of ion gyromotion.
In this paper, we investigate the complex structure and non-locality of Earth's quasi-parallel bow shock as well as the injection problem both through hybrid-Vlasov simulations and test-particle runs. In Sect. 2 we present our hybrid-Vlasov simulations. In Sect. 3 we present results from two different hybrid-Vlasov datasets. In Sect. 4 we introduce our test-particle simulation method, and in Sect. 5 we present results of test-particle injection and energization. Section 6 presents the analysis and discussion of our findings, and we present our conclusions in Sect. 7.
Throughout this study, we use the following terminology:
-
An injected particle has interacted with the bow shock and returned to the upstream. This may also be called reflection. During this process, particles gain energy in the solar wind frame.
-
A transmitted particle has passed through the bow shock to the far downstream. The particle may or may not be energized during this process.
-
Energization is when during a single shock encounter, a particle gains energy in the solar wind frame so that it is no longer part of the incident plasma thermal distribution.
-
Acceleration is when injected particles continue to gain energy through continuous and/or repeated shock interactions, such as DSA. This takes place over longer temporal and spatial scales and is outside the scope of this study.
-
Non-locality of the quasi-parallel bow shock is a measure of the disagreement between different measurements of where the bow shock is locally estimated to be. This could also be referred to as the uncertainty of the shock position.
-
The shock-normal direction is normal to the local, reforming shock front. This direction is highly variable.
-
The bow-normal direction is the normal direction for a parabola, estimating the global shape of the shock front. This direction is very stable.
-
The shock-normal angle θBn is the angle between the upstream magnetic field and the shock-normal direction. The shock-normal direction or a vector antiparallel to it is chosen in order to constrain the value to . Due to fluctuations of both the upstream field and the local shock front, this angle is very unpredictable.
-
The bow-normal angle is the angle between the upstream magnetic field and the bow-normal direction. Like θBn, it is usually limited to , but in regions of significant magnetic field deformation, it is allowed to have values >90∘. This measure allows for the analysis of shock interaction due to upstream magnetic field fluctuations while smoothing out the local reformation effects of the quasi-parallel shock front.
In modelling Earth's bow shock, we employ Vlasiator (von Alfthan et al., 2014; Pfau-Kempf, 2016; Palmroth et al., 2018), a hybrid-Vlasov code designed to simulate Earth's magnetosphere and the surrounding space environment. Vlasiator models kinetic proton-scale plasma physics by calculating the evolution of the proton distribution function on a Cartesian 3D velocity grid within each cell of a Cartesian spatial grid. In the presented runs, the spatial simulation domain is 2D. Modelling distribution functions directly instead of using a particle-in-cell method allows for the accurate analysis of even the tenuous portions of non-thermal populations in the foreshock and gives us a realistic model of foreshock and bow shock evolution. The noise-free distribution function formalism further allows for using the magnetic field B and electric field E values as input to test-particle studies without a need for low-pass filtering.
Vlasiator models ions as distribution functions, solving the Vlasov equation for the ion (proton) distribution with electrons modelled as a cold, massless, charge-neutralizing fluid. Closure is provided via Ohm's law, including the Hall term. We assume that effects due to the electron pressure gradient can be neglected. Vlasiator is capable of modelling a number of ion kinetic effects even without resolving the ion skin depth (Pfau-Kempf et al., 2018), and Hoilijoki et al. (2017) reported how Vlasiator simulated global reconnection rates in agreement with empirical formulae. Dubart et al. (2020) shows that resolving the ion inertial length is not required for correctly resolving electromagnetic-ion-cyclotron (EMIC) waves in the magnetosheath. Vlasiator has been used for several interesting foreshock and bow shock studies (Palmroth et al., 2015; Pfau-Kempf et al., 2016; Turc et al., 2018; Blanco-Cano et al., 2018; Turc et al., 2019). Our choice of simulation parameters does not quite resolve the ion inertial length but instead ensures the correct scale separation between global and local dynamics (e.g. bow shock curvature and ULF-wave-induced shock ripples) and a noise-free representation of both thermal and non-thermal plasma. Tóth et al. (2017) have investigated how reconnection physics were affected by overresolving the inertial length (at the expense of scale separation), but they did not study the consequences of underresolving it.
In this paper, we use two datasets (simulations S1 and S2) modelling two different bow shock strengths and interplanetary magnetic field intensities. Results from these simulations have previously been published in Palmroth et al. (2015), Turc et al. (2018), and Turc et al. (2019). They are ecliptic-plane (x–y) 2D–3V simulations (2D in the spatial domain and 3D in the velocity domain) parametrized using the geocentric–solar–ecliptic (GSE) coordinate system with no tilt for Earth's dipole. The x coordinate is along the Earth–Sun axis; the z coordinate is aligned with Earth's magnetic axis; and the y coordinate completes the right-handed system. We save variables such as field values and distribution function moments every 0.5 s. The simulation extent is 2000×1750 spatial cells, covering the ranges and , where RE=6371 km is an Earth radius. The simulation domain extent in the z direction is only one cell thick with periodic boundary conditions. Each spatial cell is a cube with a length of 228 km along each edge. Our velocity domain employs a sparse representation (von Alfthan et al., 2014) and has a resolution of 30 km s−1. The simulation domain is initialized with a somewhat fast and somewhat hot solar wind inflow of m−3, T=0.5 MK, and km s−1. The magnetic field in simulation S1 is nT, whereas in simulation S2 it is nT. The quasi-radial IMF in these runs allows us to focus on the quasi-parallel bow shock. The somewhat hot solar wind ensures that the inflow Maxwellian distribution is resolved adequately. Earth's magnetic dipole is implemented at a realistic value of 8.0×1022 Am2, and the simulation domain inner boundary is a perfectly conducting sphere located at r = 31 800 km or about 5 RE. The simulation set-up results in solar wind Alfvénic Mach numbers of and and magnetosonic Mach numbers of and in front of the bow shock nose and thus, strong fast-mode supercritical shocks. The simulations were run for s and s, respectively. To facilitate a comparison with existing numerical studies, we note that for both simulation runs the solar wind ion inertial length is 125.4 km=0.020 RE. For S1, the solar wind plasma beta is β1=2.3, and for S2, it is β2=0.57
Figure 1 depicts the Vlasiator simulation domain for simulation S1. The colour map depicts proton densities, showing a dense magnetosheath between the bow shock and the magnetosphere, as well as variations in the upstream plasma density within the proton foreshock region. A fuchsia contour depicts where plasma density has increased 2-fold over solar wind values, providing a rough estimate of the bow shock position. Black lines illustrate magnetic field lines, showing how the foreshock is permeated by fluctuations, as well as visualizing the complicated nature of magnetic-flux compression and deflection at the quasi-parallel bow shock. The white circle indicates the simulation inner boundary, and two overlapping white rectangles indicate our regions of interest within the simulation. The larger white rectangle is used for visualizing test-particle studies of proton injection, whereas the smaller rectangle is used for the analysis of quasi-parallel bow shock non-locality. Plotting artefacts for magnetic field lines at x<10 RE are a result of visual post-processing and are not present in the scientific results presented.
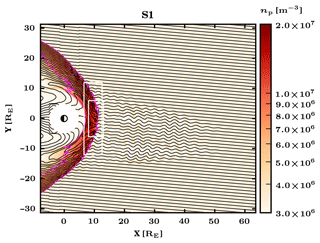
Figure 1Overview of the Vlasiator simulation S1 (BIMF=5 nT and MA=10) at time t=500 s, with proton number density (colour map) overlaid with an estimate of the bow shock position according to plasma compression (fuchsia curve, ). Also shown are magnetic field lines (black curves) and two white overlapping rectangles indicating zoomed-in regions used for the analysis of local bow shock structure (smaller rectangle) and test-particle studies (larger rectangle).
In this section, we present results of hybrid-Vlasov simulations. First, we fit the global position of the bow shock using a quartic estimation and calculate the bow-normal angle to estimate the general direction of the shock normal. As our fit is so close to a parabola, we will henceforth for simplicity refer to it as a parabola. Then, we use several local measurements of plasma properties to estimate the rapidly moving and varying local position of the shock and use their disagreement to define a non-locality of the shock.
3.1 Bow shock location and the shock-normal angle
In previous hybrid-method investigations into ion injection at kinetic plasma shocks, the shock descriptions have been usually either 1D (see e.g. Lyu and Kan, 1990; Scholer, 1990; Scholer and Terasawa, 1990; Onsager et al., 1991; Su et al., 2012), or if they were 2D or 3D, they were limited to local geometries (Guo and Giacalone, 2013; Caprioli et al., 2015, 2017; Hao et al., 2016; Sundberg et al., 2016). In a local planar shock, it is feasible to simply define the shock-normal direction from simulation box parameters and evaluate 1D cuts along this line for defining the shock shape. However, as seen in Fig. 1, in a global 2D simulation, the curved bow shock has a bow-normal direction dependent on the nose angle , which complicates evaluating the shock-normal direction (Thomas and Winske, 1990). Shock and injection investigations within global simulations have recently been published in e.g. Savoini et al. (2010, 2013), Karimabadi et al. (2014), and Savoini and Lembège (2015).
We now determine a rough estimate of the global bow shock shape. We do this by finding the contour where plasma density increases 2-fold over the solar wind value (). The value of 2np,sw was chosen based on visual inspection. We then fit the fourth-order polynomial
using the nose angle and the radial distance at each contour position. This fit is performed at times t0=438 s and tf=538 s. We found that intermediate time steps are described well by performing linear interpolation in time of the polynomial coefficients.
One of the most commonly used criteria for defining the dynamics and injection characteristics of a shock is the shock-normal angle θBn, i.e. the angle between the shock-normal direction and the upstream magnetic field. The upstream magnetic field direction in the quasi-parallel shock region varies greatly due to upstream fluctuations (Greenstadt and Mellott, 1985). Thus, even within the quasi-parallel regime, the shock may exhibit a wide variety of shock-normal angles.
As the shock front evolves, reforms, and fluctuates, the local shock-normal direction also evolves. The local instantaneous shock-normal direction can end up being perpendicular or even reversed to the mean bow shock direction and is thus challenging to evaluate in a meaningful manner. In this study, we define an alternative measure, the bow-normal direction , which is the normal direction for the parabolic fit to the mean shape of the global shape of the shock front. This is calculated as
and accordingly . We use this bow-normal direction both for defining the bow-normal plasma bulk velocity component, used for calculating the magnetosonic Mach number of the shock, and for defining a bow-normal angle , describing the angle between the local wave-distorted magnetic field and the bow-normal direction.
3.2 Shock non-locality
The locations of quasi-perpendicular and subcritical collisionless plasma shocks can, for the most part, be estimated well due to the upstream remaining undisturbed. However, at supercritical quasi-parallel shocks, the upstream is characterized by magnetic and density fluctuations and an abundance of suprathermal particles. This can make defining the exact position of the quasi-parallel shock challenging. This localization is further hindered by the fact that the position of the shock changes locally at timescales related to shock reformation. Additionally, the global position of the shock changes at larger timescales due to variations in solar wind driving conditions. This non-stationarity of the shock is observed as e.g. spacecraft encountering the shock multiple times during what is expected to be a single crossing (see e.g. Lucek et al., 2002; Sundberg et al., 2016; Gingell et al., 2017). In order to investigate the injection problem, we now attempt to define the local quasi-parallel shock position within a larger shock transition zone (Burgess, 1995) on reformation-related timescales. We also present a novel method for quantifying the uncertainty of the shock position, suitable for use in spacecraft observations and future investigations of the quasi-parallel bow shock.
We evaluate the location of the shock as a transition between the upstream and downstream conditions using three plasma properties. The first is plasma compression, using the previously introduced criterion of . The second is the heating of the solar wind core population Tcore>4Tsw similar to the method of Wilson et al. (2014b, a), with the value 4Tsw selected based on visual inspection. To achieve this, the Vlasiator distribution function is split into core and suprathermal parts (np,core and np,st). The plasma contained in each velocity space cell is evaluated as belonging to the core distribution if it is inside a sphere centred at with a radius of 690 km s−1. Cells outside this sphere are considered as belonging to the suprathermal distribution. The third criterion is when the plasma magnetosonic Mach number, calculated using the local fast magnetosonic mode speed and the bow-normal plasma bulk velocity, falls below 1. We do not include any further criteria based on the magnetic field direction or magnitude, as magnetic field compression at a quasi-parallel shock is sporadic and limited, and the transition region has a wide range of local field orientations (see e.g. Fig. 1 of Gingell et al., 2019). We emphasize that the presented methods will potentially register shocklets and SLAMS as they take part in the reformation process.
In Fig. 2 we present in panels (a) and (b) snapshots of plasma density from simulations S1 and S2, respectively, at time t=500 s, zoomed in on the nose of the quasi-parallel bow shock (indicated by the smaller white rectangle in Fig. 1). We have plotted the plasma density with overlaid contours representing the bow shock positions according to criteria for plasma density (fuchsia), solar wind core heating (green), and magnetosonic Mach number (pale blue).
The three contours are highly variable and agree on the position of the quasi-parallel shock only on the order of 50 % of the time. We have selected four positions for profile cuts, depicted by black dashed lines in panel (a), showcasing different kinds of shock crossings. These simulate what a spacecraft might observe, except that they are spatial instead of temporal profiles. Line profiles for the three plasma properties used to gauge the shock position are shown in panels (c), (d), (e), and (f). Graphed quantities are scaled so that a value of 1 is where the shock is estimated to be. The distance between the positions of bow shock parametrization closest and farthest from Earth is the disagreement between the three parametrizations and is shown as shaded grey regions. This distance estimates the uncertainty of the shock position or the extent of the shock transition region within which the three plasma properties estimate the shock to be. We designate this distance the shock non-locality. It is defined in units of Earth radii instead of e.g. upstream gyroscales in order to facilitate the comparison of bow shock structure sizes between different IMF conditions.
The cut shown in panel (c), at y=3.8 RE, shows regions of low plasma density in what would appear to be the downstream, likely a result of a new shock front forming at x≈11 RE, with the old shock position closer to x≈10.5 RE. Panel (d), at y=2.8 RE, shows the active reformation of the quasi-parallel bow shock, with the first and last estimated shock positions disagreeing by over 1.0 RE, as a new front is forming at x≈11.7 RE. The cut in panel (e), at y=1.2 RE, is an example of a well-defined shock front where all criteria agree, and panel (f) shows an intermediate case where the three criteria disagree somewhat and the shock transition seems to extend radially over a distance of several hundred kilometres. An animation depicting time evolution of Fig. 2 is available as supplementary Video A (see Sect. “Video supplement” at the end of the paper for further information).
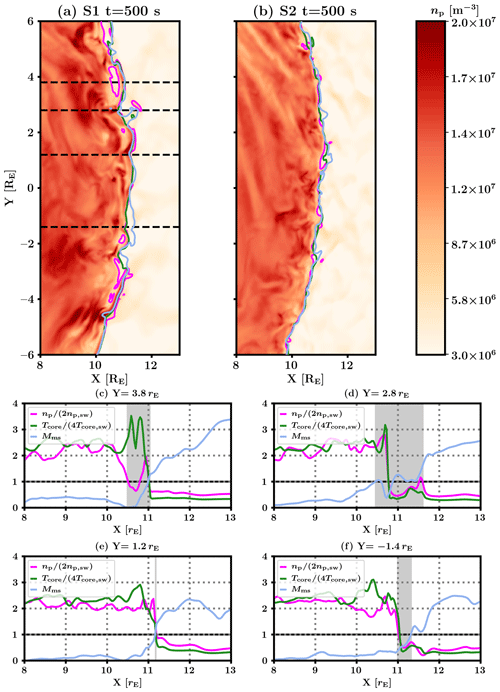
Figure 2Proton number density overlaid with bow shock positions according to criteria for plasma density (fuchsia, ), solar wind core heating (green, Tcore=4Tsw), and the magnetosonic Mach number (pale blue, Mms=1). Panel (a) is for S1 (Bsw=5 nT); panel (b) is for S2 (Bsw=10 nT). Both are at t=500 s. Panels (c)–(f) show line profiles of the three bow shock criteria along the dashed black lines shown in (a), corresponding with differing amounts of shock non-locality.
We now describe how we evaluate the non-locality of the quasi-parallel bow shock in Vlasiator simulations. At 1 ∘ nose angle intervals, we draw a profile across the shock in the bow-normal direction and measure where along the profile each of our three shock criteria (plasma density , solar wind core heating Tcore=4Tsw, and magnetosonic Mach number Mms=1) indicate the local position of the shock. Then, for each profile, we calculate the distance between the positions of bow shock parametrization closest and farthest from Earth. This distance estimates the extent of the shock transition region, i.e. the non-locality of the shock. In panels (a) and (b) of Fig. 3, we plot stacked profiles displaying the temporal evolution of shock non-locality for simulations S1 and S2, respectively. Regions of enhanced shock non-locality appear to move along the shock front away from the nose region (indicated with a dashed line), as shown by the diagonal ridges. S1 shows significantly larger and clearer non-locality structures than S2. Still, there exists a qualitative similarity to the structures seen for both simulations. We note that the motion of structures away from the nose might be due to either deflected plasma flow carrying structures along the front or due to foreshock wave fronts convecting in and interacting with a curved bow shock at increasing nose angle positions. An analysis of this interaction is postponed until a further study. In panels (c) and (d), we show that logarithmic histograms of accumulated shock non-locality measurements, showing that a well-defined shock is the most common occurrence and that enhanced values of non-locality are increasingly rare. This also confirms that S2 has, on average, lower measurements of shock non-locality than S1.
Quantifying the non-locality of the quasi-parallel bow shock using spacecraft data will be more challenging than for simulations. Simulations allow us to directly measure spatial scales, whereas spacecraft motion in relation to quasi-parallel reformation is slow, and thus, the use of a constellation of spacecraft and multipoint techniques are usually needed in order to infer spatial scales. An estimate of spatial scales and non-locality can be achieved by evaluating the solar wind flow velocity and multiplying that with the time difference between the first and last of the three presented metrics agreeing on being in the downstream. We note that this is not a perfect measure, as showcased by Fig. 2c, where all three values are in agreement at X=11 RE despite the density falling again drastically around X≈10.6 RE. Constellation spacecraft measurements can however be used to verify the propagation direction of these structures, so a rarefaction within the sheath could be distinguished from a bow shock moving inwards and outwards, increasing our understanding of shock reformation dynamics and the extent of the shock transition region.
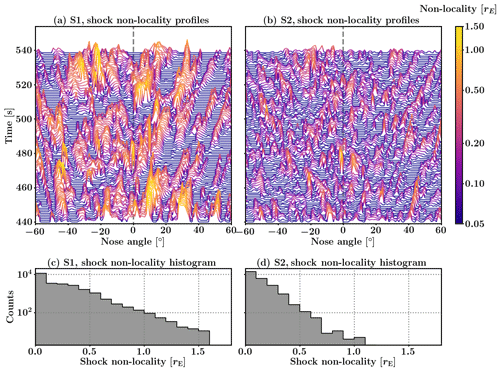
Figure 3(a, b) Profiles of measured shock non-locality as a function of nose angle for simulations S1 and S2, respectively. The y axis indicates simulation time, used as the base level corresponding with a well-defined shock with a non-locality measure of 0. Regions of enhanced non-locality are shown as coloured peaks of the curve, as presented in the colour bar. A dashed vertical line indicates a nose angle of 0∘. Both panels show chains of enhanced non-locality regions which move away from the nose region and decrease in intensity as they approach the flanks. Under each stacked profile plot we show a histogram depicting the occurrence rate of different non-locality values, with (c) depicting S1 and (d) depicting S2.
The Vlasiator model tracks the evolution of distribution functions as volume averages on a Cartesian mesh. Thus, particle trajectories are not a direct output of the code, and tracing particle histories requires the use of a post-processing tracer. In order to evaluate injection probabilities, particles need to be tracked as they meet the bow shock and interact with it, ultimately either returning to the upstream or being transmitted to the downstream. Thus, we chose to use a test-particle method to track the motion of single protons within the evolving, locally interpolated electric- and magnetic field output from the Vlasiator simulation. The particle propagation uses a Boris-push algorithm (Boris, 1970) with a conservative time step of Δt=0.005 s. This time step is not limited by particle gyrotimes but rather ensures that particles up to 105 eV travel less than 1∕10th of a simulation cell per time step. E and B field values for each particle step are acquired from the Vlasiator output files using linear interpolation in both time and space. Thus, the test particles act as tracers for an infinitesimal element of the distribution function.
Our goal is to use test-particle simulations to investigate proton injection at the quasi-parallel bow shock. For this purpose, we initialize our particles from the thermal solar wind core population, evenly distributed along a smooth curve a short distance in front of the bow shock. We follow the particles as they approach the shock region and interact with it. If a particle reaches again a boundary well in front of the shock, it is considered injected, and if it passes far into the downstream, it is considered transmitted. Once a particle has been flagged as injected or transmitted, it is no longer propagated. A significant portion of test particles spend so much time within the shock structure that they are not flagged as either injected or transmitted at the end of the run, and their fate remains inconclusive.
The particle initialization curve is placed 0.9 RE outward of the parabolic bow shock fit, extending between nose angles ±40∘. This is visible in panel (a) of Fig. 4 as the location of the first test-particles. An injection flagging boundary is placed 0.1 RE beyond the injection curve, and a transmission flagging boundary is placed 1.5 RE inward of the parabolic bow shock fit. These values were chosen so that the majority of changes to local quasi-parallel bow shock structure due to reformation fall within this region. We specifically note that the solar wind core heating criterion always triggers within this region.
Each test-particle run consists of N=105 protons, initially isotropic in the frame co-moving with the inflow plasma, which results in a mean simulation frame energy of 1.9 keV. For each test run, particle velocities were chosen as monoenergetic (10, 20, 50, 100, 200, or 500 eV) in the inflow plasma frame and randomly distributed in direction. Additionally a Maxwellian test run was performed, with particles picked randomly from a Maxwellian 0.5 MK distribution centred in the inflow plasma frame. For this distribution, the mean energy is 65 eV, and the most probable energy is 43 eV. Particles were placed into the simulation as groups of 25 000 particles every 0.5 s for 10 s, starting at t0=438 s. Particle propagation was halted at time tf=538 s.
In Fig. 4, we display snapshots of test-particle propagation for simulation S1 and an initially Maxwellian distribution of 0.5 MK in the solar wind frame. The grayscale region shows a logarithmic test-particle density, with black indicating single particles and white indicating over 100 particles per cell. We display contours parametrizing the shock position on top and also plot two black parabolas which act as the injection and transmission flagging boundaries. Animations depicting the evolution of test-particle populations for all initialization parameters and simulations S1 and S2 are available in supplementary Video B and Video C, respectively.
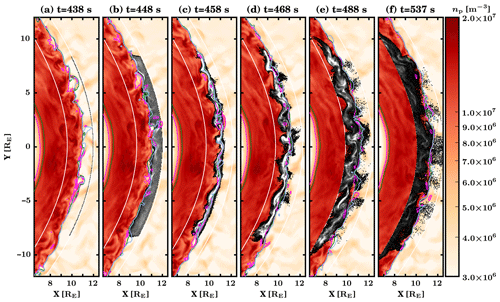
Figure 4Test-particle propagation for simulation S1 and an Maxwellian 0.5 MK initialization at six different times. Vlasiator simulation proton number density is overlaid with the logarithmic density of test-particles in greyscale, with white indicating over 100 particles in a cell. Two black parabolas are the transmission boundary (left) and the injection boundary (right). Three contours indicate estimates of the local shock position: plasma compression (fuchsia, ), solar wind core heating (green, Tcore>4Tsw), and the magnetosonic Mach number (pale blue, Mms<1).
The panels in Fig. 4 show how solar wind protons start as an even curve (panel a) and are launched into the simulation over 10 s, after which the first ones have already accumulated as white regions at the shock front (panel b). We note how the steepened structure at Y≈2 RE in panel (b) causes an accumulation of test particles at its −Y edge and that the regions of plasma depletion (fuchsia contour at e.g. Y≈6 RE, Y≈2 RE, and RE) remain void of test particles at this time. By the time of panel (c), all test-particles had reached the shock transition region; the white regions of test-particle accumulation had followed shock ripples; and many of the previously void regions had been filled with test particles. In panel (d) we see regions of efficient reflection causing particles to be returned to the upstream direction, but several regions also allow particles to move past the shock front, reminiscent of magnetosheath jets (Němeček et al., 1998; Hietala et al., 2009; Palmroth et al., 2018). By the time of panel (e), particles have spread to most of the magnetosheath all the way to the transmission boundary. Panel (f) displays how both transmission and injection can be slow processes, with 20 %–40 % of particles still within the simulation after 90–100 s of test-particle propagation, both in the upstream and in the downstream of the shock. For these particles, their ultimate fate of being injected or transmitted could not be evaluated from these simulations. Judging from panel (f) of Fig. 4, a portion of these particles would likely be injected.
Evaluation of test-particle interactions with the shock structure as seen in Fig. 4 did not provide a quantitative answer as to where within the shock transition region particles truly feel the impact of the shock. As a particle injected into the upstream necessarily will experience energization in the solar wind frame, we tracked the solar wind frame energies of transmitted and injected particles and measured the regions where particles gained or lost the most energy. In Fig. 5 we plot 2D histograms of the mean particle energy rate of change 〈ΔE∕Δt〉, which was calculated by measuring particle energy changes over 0.5 s intervals and finding the average by normalizing the result with the amount of test-particles measured at each position in parameter space. As energy gains and losses can be significant near strong electric fields (up to 1 keV per measurement interval), we use the energy preceding each interval as the y coordinate. This emphasizes energy losses at high energies and energy gains at low energies. The black contours depict logarithmic counts of measurements, starting from a single particle with the thin dotted line. The count contours in panels (c) and (g) do not have a strong peak at the 10 eV initialization energy because those particles are advected efficiently towards the downstream, whereas slightly energized particles can gyrate over a larger distance and enhance the relative counts around 100 eV.
We note that the energization colour map is a symmetric logarithmic plot, with a small linear region between ±10 eV s−1. The presented initialization energies of 10 and 100 eV correspond to 44 and 138 km s−1 plasma frame velocities, respectively. We show energization plots for only those particles which were registered as transmitted or injected by the end of the test-particle simulation. A grey band indicates the simulation frame solar wind ram energy, which is the minimum energy required for a particle to travel sunwards and thus the minimum energy for injection (1.9 keV for the solar wind speed of 600 km s−1). In the first two rows of Fig. 5, the x axis shows the distance Δx from the closest instantaneous position where the solar wind core heating shock criterion is met. The last two rows plot the instantaneous shock non-locality for the measurement, extracted from the nose angle bins calculated in Sect. 3.2.
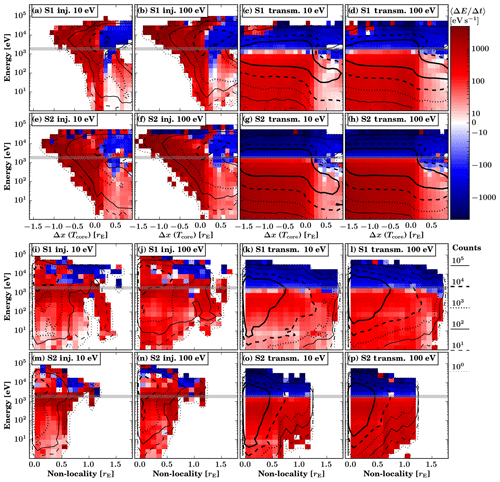
Figure 5Mean energization experienced by test particles over their shock interaction. Particle energy changes over 0.5 s intervals are integrated and averaged, recording them always at the pre-interval energy. Energization tracking is performed separately for injected (columns 1 and 2) and transmitted (columns 3 and 4) particles. The top two rows (a–h) track energization as a function of current particle solar wind frame energy and Δx from the closest position where the solar wind core heating shock criterion is met, and the bottom two rows (i–p) track energization as a function of current particle solar wind frame energy and shock non-locality. Rows 1 and 3 are from Simulation S1; rows 2 and 4 are from S2. Black logarithmic contours indicate the counts of measurements used for evaluating mean energization. A grey band indicates the minimum energy required for propagating upstream against the solar wind flow (1.9 keV for 600 km s−1). It is important to note that large values of shock non-locality can indicate signals of shock structure downstream as well as upstream of the parabolic shock fit position.
The top half of Fig. 5 clearly shows how particles start at the bottom-right corner of each panel at initialization energies and the upstream of the shock and how they on average gain energy as they approach the shock. In the downstream, the energization of injected particles is very efficient up to about 10 keV and takes place over an extended distance instead of being constrained to a thin shock front at Δx(Tcore)≈0. Injected particles continue to gain energy in the whole downstream region, but they begin to lose energy once back in the upstream. It is noteworthy that particles which end up injected can penetrate up to almost 1.5 RE into the downstream before returning upstream – but those particles are a minority and found at only high energies and thus large gyroradii. These particles could perhaps be considered to be experiencing thermal leakage. Conversely, it is also possible that at least some of these measurements are made at times when the Tcore estimate of the shock position has extended further upstream, making these particles appear to be further downstream than they actually are. The black contours depicting measurement counts show enhancement close to Δx=0 and E≳1.9 keV, consistent with those particles dwelling and being energized at the shock front. That area is also where injected particles may have their lowest simulation frame energies which would facilitate lingering at the shock front. Evaluating the particle count contours, we see that injected particles gain energy in the upstream as they approach the shock but are not energized above the solar wind ram energy. The final required energization takes place in the downstream over a distance of up to 1.5 RE.
The behaviour of transmitted particles seen in Fig. 5 is slightly different. They also start at the bottom-right corner, at low energies and upstream of the shock, and experience energization already as they approach the shock. Throughout the downstream, these particles have a wide spread in energy, and the dominant mechanism is to cool particles in the downstream rest frame, energizing (solar wind frame) low-energy particles and decreasing the energy of high-energy outliers. This is clearly visible as they split into blue (top) and red (bottom) halves of the panels. It should be noted that a small number of particles in the transmitted-particles group are actually able to enter the upstream after exceeding the solar wind kinetic energy of 1.9 keV, but the efficient deceleration there returns them to the downstream and, ultimately, the transmission boundary. Both transmitted and injected particles are able to reach energies of up to ∼50 keV.
The two bottom rows of Fig. 5 evaluate the mean energization of test-particles as a function of energy and shock non-locality. Particle count contours show that the majority of measurements are made at regions where the shock is well defined, i.e. the non-locality measure is low. However, comparing these counts with the statistics of Fig. 3 shows that there is little to no preference for particles spending time in regions of high or low shock non-locality. Although panels (i), (j), (m), and (n) do not exhibit drastic energization preference for any single non-locality value, there are a number of conclusions to draw from them. At low energies (E≲1 keV), S1 shows an energization feature at non-locality values of ∼1.2 RE, whereas S2 indicates more efficient energization at non-localities at around 0.5 RE. This would indicate a connection with the inherent size of foreshock structures in the two runs, respectively (Turc et al., 2018). The majority of the energization of injected particles happens once particles have reached energies of E≳1.9 keV, allowing them to dwell in the vicinity of the shock and sample a wider range of non-locality values. Finally, at very high energies E≳10 keV, a preference can be detected for energization at small values of non-locality and deceleration at large values of non-locality, as indicated by the predominantly red and blue regions, respectively. For transmitted particles, there appears to be no clear indication of preferential energization parameter regions, but we again detect that particles energized to 1.9 keV can sample a wider range of non-locality values.
Finally, we calculate injection probabilities for test particles in runs S1 and S2 as functions of a selection of parameters (detailed below) describing the first-detected particle–shock interaction. For each test particle, we evaluate these properties at the first moment the particle reaches a point in the simulation space that fulfils the solar wind core heating (Tcore>4Tsw) criterion for the shock. Due to the non-locality of the quasi-parallel shock front, estimating when the particle–shock interaction is most significant is challenging, but we selected the one of our three methods which we visually estimated to be most meaningful (see also panels c–f of Fig. 2).
In Fig. 6, we plot the estimated injection probabilities for test-particle runs using S1 and S2, using the previously described test-particle datasets with six different solar wind frame initialization energies and a Maxwellian initialization. The first three rows use properties of particles in the simulation frame, namely the pitch-cosine μ=cos (α) (where α is the angle between the particle velocity and the local magnetic field direction), the incidence angle (the angle between the particle direction of travel and the opposite of the bow-normal direction ), and the shock-frame kinetic energy E. The last two rows of Fig. 6 use shock properties, namely the local bow-normal angle and the locally measured shock non-locality. Again, these values were measured at the moment the particle first encountered the shock, according to the solar wind core heating criterion. Error bars are provided by the Agresti–Coull method with a 95 % confidence interval.
The first row of Fig. 6 indicates that if the particle encounters the shock with negative pitch-cosine, it is likely to be injected. In our simulation set-up, most particles travel roughly in the −vx direction, and with the IMF pointing roughly anti-sunward, most particles have pitch-cosines close to 1. A significant deviation from this suggests local magnetic field directions which have changed significantly due to foreshock wave effects. Our results indicate that these magnetic field deflections can enhance injection probabilities.
According to the second row, if the particle has a large incidence angle (the bow-normal velocity component is positive or small compared to the bow-perpendicular velocity component), injection is again likely. Incidence angles above 90∘ in fact suggest the particle was travelling away from the bow shock when it first met a shock structure. This could perhaps happen due to the particle gyrating along a deflected magnetic field line with a pitch-angle close to 0 so that its perpendicular velocity causes it to encounter a shock peninsula such as the one seen at Y=2.8 RE in Fig. 2 from behind. We note that these plots show on average larger injection probabilities for higher plasma frame particle initialization energies. This is as expected, as higher plasma frame initialization energies enable greater maximum energies when transforming into the spacecraft or simulation frame.
In the third row, we plot injection probabilities as a function of simulation frame energy, which corresponds very well to shock-frame energy due to the shock being mostly stationary on a global scale. This panel shows clearly how particles with greater initialization energies in the solar wind frame have a much larger spread in energy in the shock frame. Both very small and very large energies in the shock frame can lead to efficient injection. Small energies result in the particle spending much time at the shock, possibly then being accelerated in the shock frame with an upstream-directed velocity. Very large energies on the other hand mean that the particle does not need to be energized; it is enough to bend its path to the upstream in order to inject it. What we also see is that particles with a higher solar wind frame initialization energy tend to have a greater chance of being injected at a given shock-frame energy. These particles have a larger velocity component tangential to the shock, which suggests that being able to perform gyromotion in the fields at the shock is important for the injection and energization process.
The fourth row shows the injection probability as a function of the local bow-normal angle . For S1, we see a small bump for low initialization energies at ∼70∘ and a significant increase for all energies at ∼85∘. Considering bow-normal angles above 90∘ may seem odd, but these regions are where foreshock fluctuations and shock effects have caused the local magnetic field to twist back on itself. For simulation S2, with a lower Mach number, these situations are not detected.
The fifth row indicates the injection probability as a function of the shock non-locality measure at the moment the particle first encounters the plasma with . Both simulations S1 and S2 show a peak in the injection probability at a non-locality value of ∼0.4 RE, with even the lowest initialization energies having a ∼10 % probability in S1. For simulation S1, there is a decline in the injection probability as the non-locality value increases beyond ∼0.8 RE, with an additional peak of injection at energies >100 eV at 1.5 RE. These peak positions are in rough agreement with the results of Fig. 5, except for the ∼0.4 RE peak for S1. As that signal is very strong at all initialization energies, it is most likely the result of a singular transient effect causing a strongly deflected magnetic field. We note that it is not related to the incident particle gyroradius, as it has a theoretical maximum value (for km s−1) of 0.2 RE for S1.
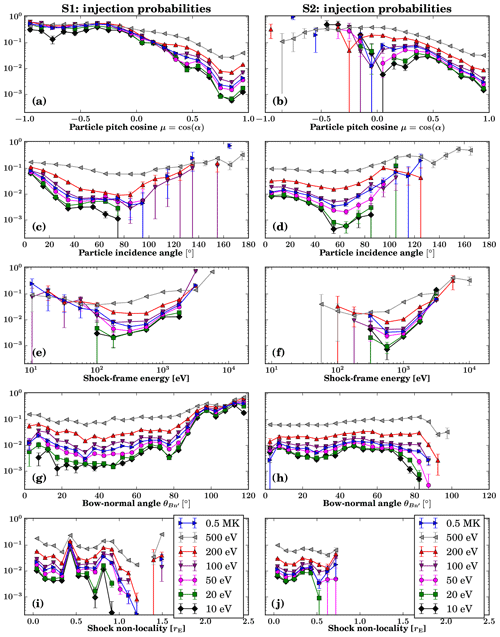
Figure 6Test-particle injection probabilities for six different solar wind frame initialization energies and a 0.5 MK Maxwellian initialization and five different parameters. Left column: S1. Right column: S2. Rows 1 through 3 (a–f) show properties of particles, namely the pitch-cosine μ=cos (α), the incidence angle, and the shock-frame energy. Rows 4 and 5 (g–j) show shock properties, namely the local bow-normal angle and the local shock non-locality. Displayed values were taken at the first encounter of each particle with the condition . Error bars are provided by the Agresti–Coull method with a 95 % confidence interval.
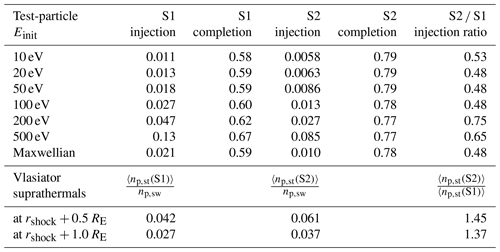
As a final step, in Table 1 we display the overall calculated injection probabilities per test-particle run for six test-particle initialization energies and a Maxwellian initialization. Due to the limited time period of test-particle propagation, at the end of the run a portion of particles were still within the shock transition zone. This is indicated by the completion ratio . We find that the completion ratio for S1 rises somewhat with increasing initialization energy, but it is very stable for S2. In agreement with expectations, the injection rate increases monotonically with greater initialization energies. The injection rates for Maxwellian distributions are located between the values for 50 and 100 eV initializations. The mean energy for 0.5 MK is approximately 65 eV. As a point of comparison, we also extracted the Vlasiator simulation suprathermal particle densities at positions 0.5 and 1.0 RE upstream of the shock, averaged over nose angles between ±45∘ and between simulation times t0=438 s and tf=538 s. To facilitate a comparison of these Vlasiator suprathermal particle densities 〈np,st〉 with test-particle injection probabilities, the values are given in units of solar wind density and included as the final two rows of Table 1. We note that although the suprathermal particle density derives from the injection probability, it measures both freshly injected protons and those protons which have spent longer in the upstream. The order of Vlasiator S1 and S2 upstream suprathermal particle densities as a function of Mach number is thus opposite to that of test-particle injection probabilities. This effect is likely not an artefact of the test-particle method but rather results from energetic particles being trapped in the upstream, interacting with the ULF waves. Although S2 is less efficient at injection, the foreshock wave–particle trapping interactions can cause reflected particles to spend extended periods of time in the upstream before returning to the shock. Supplementary Video B and Video C visualize the different dynamics between simulations S1 and S2. The suprathermal particle dynamics of S1 and S2 were investigated in Turc et al. (2018), as shown in their Fig. 2b–d.
Table 1Test-particle proton statistics using simulations S1 (MA≈10) and S2 (MA≈5) with six different solar wind frame initialization energies Einit and also a Maxwellian initialization distribution with a temperature of 0.5 MK. Columns list the estimated injection probability and the completion ratio . Also shown is the ratio of injection probabilities for S2 and S1. The final two rows show suprathermal proton density measurements 〈np,st〉 extracted from Vlasiator simulations S1 and S2 at positions 0.5 and 1.0 RE upstream of the mean bow shock position, averaged over nose angles between ±45∘ and the test-particle run time extent.
We now discuss our results presented in Sects. 3 and 5, attempting to clarify questions related to the non-locality of the quasi-parallel bow shock and thermal particle injection at Earth's quasi-parallel bow shock. We note that our approach has a number of differences compared with previous shock injection studies. We make no pre-selection that particles must encounter the shock with only a single big energization like e.g. Sundberg et al. (2016). We track particle injection based on a spatial boundary, instead of requiring the ion to achieve a given energy. In our simulation the mean solar wind energy or the shock ram energy is , and a requirement of 5–10 times this energy for particle injection (such as required by Caprioli et al., 2015) is met by approximately 40 %–50 % of our injected particles. We additionally note that the complicated global shock geometry used in our study prevents the use of simple injection measures such as a positive vx component (Sundberg et al., 2016). We note that in modelling the cross-shock potential we neglect the electron pressure gradient term. The majority of the potential difference at the shock is, however, included in the Lorentz and Hall terms (Eastwood et al., 2007; Yang et al., 2009).
Examination of Fig. 2 shows that the spatial structure of bow shock non-locality depends on the magnitude of the upstream magnetic field and thus, the spatial scale of foreshock structures. In Fig. 3, it is evident that S1 shows clearer structures and stronger peaks of non-locality. The fine structure seen in S2 is as expected due to the increased magnetic field strength, which gives rise to smaller-scale structures in the foreshock and higher frequencies for the ULF waves (Turc et al., 2018), which in turn are expected to drive shock reformation. We suggest that spacecraft measurements of bow shock crossings could be evaluated using our definition of non-locality, inferring tendencies for the non-locality of the bow shock versus e.g. IMF conditions and position nose angle. Although our method was defined as a function of radial distance, it should be applicable for spacecraft time series as well, as suggested in Sect. 3.2.
We also investigated the energization taking place during the first shock encounter of protons, before diffusive acceleration per se. We found that protons were weakly energized over a large distance as they approached the shock, that strong energization took place at the shock and over a distance of up to 1 RE in the downstream, and that those protons which returned to the upstream experienced solar wind frame energy losses over the whole upstream region. Particles did, however, dwell longer at the mean shock front position (panels a, b, e, and f of Fig. 5). We found that the majority of injected particles did not penetrate far into the downstream, but a few did. As they had achieved high energies, they might constitute injection through thermal leakage from the downstream. As we initialized our particles isotropic in the upstream plasma frame, we could see that particles which had simulation frame energies well below the solar wind energy were actually preferentially injected, similar to the SLAMS reflection test-particle studies of Johlander et al. (2016) (see panels e and f of Fig. 6). Protons with shock-frame particle energies close to the solar wind ram energy were more likely to be transmitted.
Interestingly, our result of energization taking place over a large area somewhat contradicts the results of e.g. Guo and Giacalone (2013), who in simulations of an MA=4 shock saw initial energization very close to the shock (within ∼ 10 c∕ωci of the shock, or in our nomenclature, ∼ 0.2 RE, where ωci is the ion cyclotron frequency). The difference may be caused by our integral energization tracking method differing from their method. The size of bow shock reformation in our simulation is (at ∼ 50 c∕ωpi, where ωpi is the ion plasma frequency) in agreement with the results of e.g. Omidi et al. (2013) and Caprioli and Spitkovsky (2013).
We also evaluated particle energization as a function of shock non-locality. For the most part, energization rates appear to be equal at all non-locality values, although at low energies each simulation showed increased energization at a non-locality length scale which appears related to the spatial scale of foreshock structures. This result supports the theory of protons being efficiently energized between the existing shock and incoming shocklets and SLAMS or steepened ULF waves.
Statistical analysis of correlations between shock and particle properties and the injection probability is presented in Fig. 6. The most obvious result is that there are very few injected particles at large incidence angles, especially at lower initialization energies. For S1, there appears to be a connection between the enhanced injection probability and incidence angles close to 0. A small incidence angle will likely correlate with greater-than-average simulation frame initialization energy, and higher energy is known to increase the injection probability. We also reported on an increase in the injection probability both with increasing solar wind frame energy and with shock-frame energy diverging from the solar wind ram energy.
The fourth row of Fig. 6 highlights the importance of magnetic field deflections upstream and at the shock for efficient particle injection. Simulation S1 with the higher Mach number and larger foreshock structures is much more efficient at forming strong deflections, resulting in bow-normal angles of above 80∘, whereas they are absent in S2. We emphasize that these measurements were performed within the globally quasi-parallel region of the bow shock, between nose angles ∘. We also note that in S1, there is an increase in injection at low initialization energies for bow-normal angles ≤15∘. This is likely the same effect as what Sundberg et al. (2016) described as injected ions encountering a locally quasi-perpendicular field downstream of the shock. This also warrants further investigation. The strong deformation of magnetic fields can also lead to other forms of energization such as localized reconnection found in the quasi-parallel shock transition region (Gingell et al., 2019). Resolving these effects appears to require higher-resolution simulations.
The fifth row of Fig. 6 evaluates the link between shock front non-locality and proton injection. S1 exhibits a peculiar peak in the injection probability at ∼0.4 RE, which we presume to be due to a reformation-associated transient. S2 does not exhibit large non-locality values, but for S1, the injection probability seems to fall past values of ∼0.9 RE, with another peak at ∼1.5 RE. At low initialization energies, injection probabilities appear to fall off faster with increasing non-locality of the shock. Similar to Fig. 5, slight enhancements in the injection can be seen at non-locality values which appear to be related to the size of foreshock structures in the vicinity of the shock front. We propose that the lack of a strong link between injection and non-locality shows how shock injection at a curved reforming quasi-parallel shock is a complicated process, and local 2D simulations showing clear-cut cyclical reformation and injection are capable of investigating only an idealized subset of reforming shock fronts.
We finally note that on timescales represented in our test-particle simulations, local structures of the quasi-parallel bow shock do have a significant effect on particle injection at all initialization energies. This is likely akin to what e.g. Hao et al. (2017) and Sundberg et al. (2016) reported on, with rippled shapes of the shock front and advected magnetic fluctuations resulting in regions of localized injection. At the same time, our results suggest that energization of injected particles takes place over an extended region both at the shock and especially downstream of it. Thus, the injection of ions at a quasi-parallel shock may happen via multiple different routes and phenomena.
The overall injection probabilities inferred from our test-particle studies agree with the strength of the shock (and the Alfvénic Mach number), indicating the overall injection probability of the shock. However, we note that the suprathermal particle density registered in the upstream of the shock did not agree with this result, indicating that the evolution of suprathermal particle populations throughout the foreshock is a complicated process and not a simple indicator of local shock reflectivity. One important effect to note is that of particle trapping between foreshock waves, as reported by Wu et al. (2015). We suggest that when performing studies of shock reflectivity using spacecraft measurements, extra care should be taken to differentiate freshly injected particles from an evolved foreshock population.
We have investigated the dynamics of the reforming quasi-parallel bow shock of Earth in connection with the injection of thermal solar wind protons, using both hybrid-Vlasov and test-particle studies. Our noise-free hybrid-Vlasov simulations have allowed us to probe the reforming quasi-parallel bow shock dynamics in greater detail than previously possible, accounting for correct scale separation, the global dynamics of bow shock curvature, and effects stemming from tenuous upstream particle distributions. Our results have shown that the energization and injection of solar wind ions within this region are not local effects taking place at a single shock location but rather are spread out over a larger shock transition region spanning up to 1.5 RE. We confirm enhanced particle injection with a higher shock Alfvénic Mach number and plasma frame particle energy as expected. We also find that whenever the shock-associated magnetic field is deflected a great deal, particle injection is enhanced. A weak enhancement could also be seen in one of our simulations at very small bow-normal angles , so the interaction of magnetic field directions just upstream and downstream of the shock requires further study.
In our investigation, we defined a new metric for the bow shock, indicating the magnitude of non-locality of the shock front, associated with reformation. This metric was seen to correlate with the parameters of the foreshock and associated fluctuations and also thus the shock Alfvénic Mach number. We showed how enhancements of non-locality travelled away from the shock nose and towards the flanks, indicating persistent interaction between the upstream ULF wave field and the shock front. We found that the energization of cool solar wind frame particles was not dependent on a specific value of shock non-locality, which is in agreement with our finding of particle energization within the quasi-parallel bow shock region taking place over a large extent, not only at the shock front. At very high energies E≳10 keV, some preference was seen for particle energization at small values of non-locality. Although the metric was defined as a spatial measurement, it can be applied to spacecraft measurements and used to investigate the effect of shock reformation on the energization of injected particles, particularly at high energies.
Our study concentrated on two bow shock simulations, so additional studies into the locality of the injection and the energization of solar wind particles using a more extensive simulation database are warranted.
We further note that the local density of suprathermal particles may be a poor indicator of the injection efficiency of the shock due to large-scale dynamics of the foreshock region, such as particle trapping. This is an important factor when using either simulation results or spacecraft observations for estimating injection efficiencies at the bow shock.
Vlasiator (http://www.physics.helsinki.fi/vlasiator/; Palmroth, 2020) is distributed under the GPL-2 open-source license at https://github.com/fmihpc/vlasiator/ (Palmroth and the Vlasiator team, 2020). Vlasiator uses a data structure developed in-house (https://github.com/fmihpc/vlsv/; Sandroos, 2019), which is compatible with the VisIt visualization software (Childs et al., 2012) using a plugin available at the VLSV repository. The Analysator software (https://github.com/fmihpc/analysator/; Hannuksela and the Vlasiator team, 2020) was used to produce the presented figures. The run described here takes several terabytes of disk space and is kept in storage maintained within the CSC – IT Center for Science. Data presented in this paper can be accessed by following the data policy on the Vlasiator web site.
The supplementary Video A, Video B, and Video C provide video extensions of Figs. 2 and 4, showcasing the evolution of the quasi-parallel shock front profiles and the associated non-locality (Video A) and the evolution, transmission, and injection of test-particle populations of various initialization parameters for simulations S1 (Video B) and S2 (Video C).
Video A (Battarbee et al., 2020a) is a video extension of Fig. 2. It is an animation of proton number density overlaid with bow shock positions according to criteria for plasma density (fuchsia, ), solar wind core heating (green, Tcore=4Tsw), and magnetosonic Mach number (pale blue, Mms=1). Panel (a) is for S1 (Bsw=5 nT); panel (b) is for S2 (Bsw=10 nT). Both are at t=500 s. Panels (c)–(f) show line profiles of the three bow shock criteria along the dashed black lines shown in panel (a), corresponding with differing amounts of shock non-locality.
Video B (Battarbee et al., 2020b) is a video extension of Fig. 4. It shows test-particle propagation for simulation S1 (Bsw=5 nT), with six different monoenergetic initializations as well as a Maxwellian 0.5 MK initialization. The Vlasiator simulation proton number density is overlaid with the logarithmic density of test particles in greyscale, with white indicating over 100 particles in a cell. Two black parabolas are the transmission boundary (left) and the injection boundary (right). Three contours indicate estimates of the local shock position: plasma compression (fuchsia, ), solar wind core heating (green, Tcore>4Tsw), and the magnetosonic Mach number (pale blue, Mms<1).
Video C (Battarbee et al., 2020c) is a video extension of Fig. 4. It shows test-particle propagation for simulation S2 (Bsw=10 nT), with six different monoenergetic initializations as well as a Maxwellian 0.5 MK initialization. The Vlasiator simulation proton number density is overlaid with the logarithmic density of test particles in greyscale, with white indicating over 100 particles in a cell. Two black parabolas are the transmission boundary (left) and the injection boundary (right). Three contours indicate estimates of the local shock position: plasma compression (fuchsia, ), solar wind core heating (green, Tcore>4Tsw), and the magnetosonic Mach number (pale blue, Mms<1).
MB carried out the analysis and wrote the paper. UG and YPK have made significant contributions to the simulation methods and analysis. All co-authors helped in the interpretation and visualization of the results and read and commented on the paper.
The authors declare that they have no conflict of interest.
We acknowledge the European Research Council for Starting Grant (no. 200141-QuESpace), with which Vlasiator (Palmroth, 2020) was developed. The Finnish Centre of Excellence in Research of Sustainable Space supports Vlasiator development and science as well. The CSC – IT Center for Science in Finland is acknowledged for the use of the Sisu supercomputer and Grand Challenge award leading to the results presented here. We wish to thank Lynn B. Wilson III and Andreas Johlander for fruitful commentary on this topic.
This research has been supported by the European Research Council (PRESTISSIMO; grant no. 682068), the Academy of Finland, Luonnontieteiden ja Tekniikan Tutkimuksen Toimikunta (grant nos. 312351 and 267144), and the H2020 Marie Skłodowska-Curie Actions (FRoST; grant no. 704681).
Open access funding provided by Helsinki University Library.
This paper was edited by Yoshizumi Miyoshi and reviewed by two anonymous referees.
Axford, W. I., Leer, E., and Skadron, G.: The Acceleration of Cosmic Rays by Shock Waves, in: 15th International Cosmic Ray Conference, Vol. 11, Dept. of Cosmic Rays, Central Research Institute for Physics of the Hungarian Academy of Sciences, Budapest, International Union of Pure and Applied Physics, Bulgarska akademiia na naukite, p. 132, 1977. a
Battarbee, M., Laitinen, T., and Vainio, R.: Heavy-ion acceleration and self-generated waves in coronal shocks, Astron. Astrophys., 535, A34, https://doi.org/10.1051/0004-6361/201117507, 2011. a
Battarbee, M., Ganse, U., Pfau-Kempf, Y., Turc, L., Brito, T., Grandin, M., Koskela, T., and Palmroth, M.: Supplementary Video A, TIB AV-Portal, https://doi.org/10.5446/42960, 2020a. a
Battarbee, M., Ganse, U., Pfau-Kempf, Y., Turc, L., Brito, T., Grandin, M., Koskela, T., and Palmroth, M.: Supplementary Video B, TIB AV-Portal, https://doi.org/10.5446/42961, 2020b. a
Battarbee, M., Ganse, U., Pfau-Kempf, Y., Turc, L., Brito, T., Grandin, M., Koskela, T., and Palmroth, M.: Supplementary Video C, TIB AV-Portal, https://doi.org/10.5446/42962, 2020c. a
Bell, A. R.: The acceleration of cosmic rays in shock fronts. I, Mon. Not. R. Astron. Soc., 182, 147–156, 1978. a
Blanco-Cano, X., Battarbee, M., Turc, L., Dimmock, A. P., Kilpua, E. K. J., Hoilijoki, S., Ganse, U., Sibeck, D. G., Cassak, P. A., Fear, R. C., Jarvinen, R., Juusola, L., Pfau-Kempf, Y., Vainio, R., and Palmroth, M.: Cavitons and spontaneous hot flow anomalies in a hybrid-Vlasov global magnetospheric simulation, Ann. Geophys., 36, 1081–1097, https://doi.org/10.5194/angeo-36-1081-2018, 2018. a
Blandford, R. D. and Ostriker, J. P.: Particle acceleration by astrophysical shocks, Astrophys. J., 221, L29–L32, https://doi.org/10.1086/182658, 1978. a
Boris, J.: Acceleration calculation froma a scalar potential, Tech. rep., Princeton Univ., N. J. Plasma Physics Lab., MATT-769, 1970. a
Burgess, D.: Shock drift acceleration at low energies, J. Geophys. Res., 92, 1119–1130, https://doi.org/10.1029/JA092iA02p01119, 1987. a
Burgess, D.: Cyclic behavior at quasi-parallel collisionless shocks, Geophys. Res. Lett., 16, 345–348, https://doi.org/10.1029/GL016i005p00345, 1989. a, b
Burgess, D.: Foreshock-shock interaction at collisionless quasi-parallel shocks, Adv. Space Res., 15, 159–169, https://doi.org/10.1016/0273-1177(94)00098-L, 1995. a, b, c
Burgess, D., Lucek, E. A., Scholer, M., Bale, S. D., Balikhin, M. A., Balogh, A., Horbury, T. S., Krasnoselskikh, V. V., Kucharek, H., Lembège, B., Möbius, E., Schwartz, S. J., Thomsen, M. F., and Walker, S. N.: Quasi-parallel Shock Structure and Processes, Space Sci. Rev., 118, 205–222, https://doi.org/10.1007/s11214-005-3832-3, 2005. a
Caprioli, D. and Spitkovsky, A.: Cosmic-ray-induced filamentation instability in collisionless shocks, Astrophys. J., 765, L20, https://doi.org/10.1088/2041-8205/765/1/L20, 2013. a
Caprioli, D., Pop, A.-R., and Spitkovsky, A.: Simulations and Theory of Ion Injection at Non-relativistic Collisionless Shocks, Astrophys. J., 798, L28, https://doi.org/10.1088/2041-8205/798/2/L28, 2015. a, b, c
Caprioli, D., Yi, D. T., and Spitkovsky, A.: Chemical Enhancements in Shock-Accelerated Particles: Ab initio Simulations, Phys. Rev. Lett., 119, 171101, https://doi.org/10.1103/PhysRevLett.119.171101, 2017. a, b
Childs, H., Brugger, E., Whitlock, B., Meredith, J., Ahern, S., Pugmire, D., Biagas, K., Miller, M., Harrison, C., Weber, G. H., Krishnan, H., Fogal, T., Sanderson, A., Garth, C., Bethel, E. W., Camp, D., Rübel, O., Durant, M., Favre, J. M., and Navrátil, P.: VisIt: An End-User Tool For Visualizing and Analyzing Very Large Data, in: High Performance Visualization–Enabling Extreme-Scale Scientific Insight, 357–372, Chapman & Hall/CRC Press, 2012. a
Dubart, M., Ganse, U., Osmane, A., Johlander, A., Battarbee, M., Grandin, M., Pfau-Kempf, Y., Turc, L., and Palmroth, M.: Resolution dependence of magnetosheath waves in global hybrid-Vlasov simulations, Ann. Geophys. Discuss., https://doi.org/10.5194/angeo-2020-24, in review, 2020. a
Eastwood, J. P., Lucek, E. A., Mazelle, C., Meziane, K., Narita, Y., Pickett, J., and Treumann, R. A.: The foreshock, Space Sci. Rev., 118, 41–94, https://doi.org/10.1007/s11214-005-3824-3, 2005. a
Eastwood, J. P., Bale, S. D., Mozer, F. S., and Hull, A. J.: Contributions to the cross shock electric field at a quasiperpendicular collisionless shock, Geophys. Res. Lett., 34, L17104, https://doi.org/10.1029/2007GL030610, 2007. a
Edmiston, J. P., Kennel, C. F., and Eichler, D.: Escape of heated ions upstream of quasi-parallel shocks, Geophys. Res. Lett., 9, L17104, https://doi.org/10.1029/GL009i005p00531, 1982. a
Ellison, D. C.: Monte Carlo Simulation of charged particles upstream of the Earth's bow shock, Geophys. Res. Lett., 8, 991–994, https://doi.org/10.1029/GL008i009p00991, 1981. a
Fairfield, D. H.: Bow shock associated waves observed in the far upstream interplanetary medium, J. Geophys. Res., 74, 3541–3553, https://doi.org/10.1029/JA074i014p03541, 1969. a
Gedalin, M.: Influence of the rippling on the collisionless ion and electron motion in the shock front: A model study, J. Geophys. Res.-Space, 106, 21645–21655, https://doi.org/10.1029/2000JA000185, 2001. a
Gedalin, M.: Transmitted, reflected, quasi-reflected, and multiply reflected ions in low-Mach number shocks, J. Geophys. Res.-Space, 121, 10754–10767, https://doi.org/10.1002/2016JA023395, 2016. a
Giacalone, J.: Shock drift acceleration of energetic protons at a planetary bow shock, J. Geophys. Res., 97, 8307–8318, https://doi.org/10.1029/92JA00313, 1992. a
Gingell, I., Schwartz, S. J., Burgess, D., Johlander, A., Russell, C. T., Burch, J. L., Ergun, R. E., Fuselier, S., Gershman, D. J., Giles, B. L., Goodrich, K. A., Khotyaintsev, Y. V., Lavraud, B., Lindqvist, A., Strangeway, R. J., Trattner, K., Torbert, R. B., Wei, H., and Wilder, F.: MMS Observations and Hybrid Simulations of Surface Ripples at a Marginally Quasi-Parallel Shock, J. Geophys. Res.-Space, 122, 11003–11017, https://doi.org/10.1002/2017JA024538, 2017. a
Gingell, I., Schwartz, S., Eastwood, J., Stawarz, J., Burch, J., Ergun, R., Fuselier, S., Gershman, D., Giles, B., Khotyaintsev, Y., Lavraud, B., Lindqvist, P., Paterson, W., Phan, T., Russell, C., Strangeway, R., Torbert, R., and Wilder, F.: Statistics of Reconnecting Current Sheets in the Transition Region of Earth's Bow Shock, J. Geophys. Res.-Space, 125, e2019JA027119, https://doi.org/10.1029/2019JA027119, 2019. a, b, c
Gosling, J. T., Thomsen, M. F., Bame, S. J., Feldman, W. C., Paschmann, G., and Sckopke, N.: Evidence for specularly reflected ions upstream from the quasi-parallel bow shock, Geophys. Res. Lett., 9, 1333–1336, https://doi.org/10.1029/GL009i012p01333, 1982. a
Gosling, J. T., Thomsen, M. F., Bame, S. J., and Russell, C. T.: Ion reflection and downstream thermalization at the quasi-parallel bow shock, J. Geophys. Res.-Space, 94, 10027–10037, https://doi.org/10.1029/JA094iA08p10027, 1989. a
Greenstadt, E. W. and Mellott, M. M.: Variable field-to-normal angles in the shock foreshock boundary observed by ISEE 1 and 2, Geophys. Res. Lett., 12, 129–132, https://doi.org/10.1029/GL012i003p00129, 1985. a
Guo, F. and Giacalone, J.: The acceleration of thermal protons at parallel collisionless shocks: three-dimensional hybrid simulations, Astrophys. J., 773, 158, https://doi.org/10.1088/0004-637X/773/2/158, 2013. a, b
Hada, T., Kennel, C. F., and Terasawa, T.: Excitation of compressional waves and the formation of shocklets in the Earth's foreshock, J. Geophys. Res., 92, 4423–4435, https://doi.org/10.1029/JA092iA05p04423, 1987. a
Hannuksela, O. and the Vlasiator team: Analysator: python analysis toolkit, Github repository, available at: https://github.com/fmihpc/analysator/, last access: 23 April 2020. a
Hao, Y., Lu, Q., Gao, X., and Wang, S.: Ion dynamics at a rippled quasi-parallel shock: 2D hybrid simulations, Astrophys. J., 823, 7, https://doi.org/10.3847/0004-637X/823/1/7, 2016. a, b
Hao, Y., Gao, X., Lu, Q., Huang, C., Wang, R., and Wang, S.: Reformation of rippled quasi-parallel shocks: 2-D hybrid simulations, J. Geophys. Res.-Space, 122, 6385–6396, https://doi.org/10.1002/2017JA024234, 2017. a
Hietala, H., Laitinen, T. V., Andréeová, K., Vainio, R., Vaivads, A., Palmroth, M., Pulkkinen, T. I., Koskinen, H. E. J., Lucek, E. A., and Rème, H.: Supermagnetosonic Jets behind a Collisionless Quasiparallel Shock, Phys. Rev. Lett., 103, 245001, https://doi.org/10.1103/PhysRevLett.103.245001, 2009. a
Hoilijoki, S., Ganse, U., Pfau-Kempf, Y., Cassak, P. A., Walsh, B. M., Hietala, H., von Alfthan, S., and Palmroth, M.: Reconnection rates and X line motion at the magnetopause: Global 2D-3V hybrid-Vlasov simulation results, J. Geophys. Res.-Space, 122, 2877–2888, https://doi.org/10.1002/2016JA023709, 2017. a
Hoppe, M. M., Russell, C. T., Frank, L. A., Eastman, T. E., and Greenstadt, E. W.: Upstream hydromagnetic waves and their association with backstreaming ion populations: ISEE 1 and 2 observations, J. Geophys. Res.-Space, 86, 4471–4492, https://doi.org/10.1029/JA086iA06p04471, 1981. a
Johlander, A., Vaivads, A., Khotyaintsev, Y. V., Retinò, A., and Dandouras, I.: Ion Injection at Quasi-parallel Shocks seen by the Cluster Spacecraft, Astrophys. J., 817, L4, https://doi.org/10.3847/2041-8205/817/1/L4, 2016. a, b, c
Karimabadi, H., Roytershteyn, V., Vu, H. X., Omelchenko, Y. A., Scudder, J., Daughton, W., Dimmock, A., Nykyri, K., Wan, M., Sibeck, D., Tatineni, M., Majumdar, A., Loring, B., and Geveci, B.: The link between shocks, turbulence, and magnetic reconnection in collisionless plasmas, Phys. Plasmas, 21, 062308, https://doi.org/10.1063/1.4882875, 2014. a
Krymsky, G., Kuzmin, A., Petukhov, S., and Turpanov, A.: Physical Principles of Regular Acceleration Mechanism of Charged Particles, in: Proceedings, 16th International Cosmic Ray Conference, Vol. 3, 39–43, Kyoto, 1979. a
Kucharek, H. and Scholer, M.: Origin of diffuse superthermal ions at quasi-parallel supercritical collisionless shocks, J. Geophys. Res., 96, 21195–21205, https://doi.org/10.1029/91JA02321, 1991. a
Lever, E., Quest, K., and Shapiro, V.: Shock surfing vs. shock drift acceleration, Geophys. Res. Lett., 28, 1367–1370, https://doi.org/10.1029/2000GL012516, 2001. a, b
Liseykina, T. V., Dudnikova, G. I., Vshivkov, V. A., and Malkov, M. A.: Ion-acoustic shocks with reflected ions: modelling and particle-in-cell simulations, J. Plasma Phys., 81, 495810507, https://doi.org/10.1017/S002237781500077X, 2015. a
Lucek, E. A., Horbury, T. S., Dunlop, M. W., Cargill, P. J., Schwartz, S. J., Balogh, A., Brown, P., Carr, C., Fornacon, K.-H., and Georgescu, E.: Cluster magnetic field observations at a quasi-parallel bow shock, Ann. Geophys., 20, 1699–1710, https://doi.org/10.5194/angeo-20-1699-2002, 2002. a
Lucek, E. A., Horbury, T. S., Dandouras, I., and Rème, H.: Cluster observations of the Earth's quasi-parallel bow shock, J. Geophys. Res.-Space, 113, A07S02, https://doi.org/10.1029/2007JA012756, 2008. a
Lyu, L. H. and Kan, J. R.: Ion leakage, ion reflection, ion heating and shock-front reformation in a simulated supercritical quasi-parallel collisionless shock, Geophys. Res. Lett., 17, 1041–1044, https://doi.org/10.1029/GL017i008p01041, 1990. a, b
Malkov, M. A.: Ion leakage from quasiparallel collisionless shocks: Implications for injection and shock dissipation, Phys. Rev. E, 58, 4911, https://doi.org/10.1103/PhysRevE.58.4911, 1998. a
Malkov, M. A., Sagdeev, R. Z., Dudnikova, G. I., Liseykina, T. V., Diamond, P. H., Papadopoulos, K., Liu, C.-S., and Su, J. J.: Ion-acoustic shocks with self-regulated ion reflection and acceleration, Phys. Plasmas, 23, 043105, https://doi.org/10.1063/1.4945649, 2016. a
Němeček, Z., Šafránková, J., Přech, L., Sibeck, D. G., Kokubun, S., and Mukai, T.: Transient flux enhancements in the magnetosheath, Geophys. Res. Lett., 25, 1273–1276, https://doi.org/10.1029/98GL50873, 1998. a
Omidi, N., Zhang, H., Sibeck, D., and Turner, D.: Spontaneous hot flow anomalies at quasi-parallel shocks: 2. Hybrid simulations, J. Geophys. Res.-Space, 118, 173–180, https://doi.org/10.1029/2012JA018099, 2013. a
Onsager, T. G., Winske, D., and Thomsen, M. F.: Ion injection simulations of quasi-parallel shock re-formation, J. Geophys. Res., 96, 21183–21194, https://doi.org/10.1029/91JA01986, 1991. a
Palmroth, M.: Vlasiator, Web site, available at: http://www.physics.helsinki.fi/vlasiator/, last access: 23 April 2020. a, b
Palmroth, M. and the Vlasiator team: Vlasiator: hybrid-Vlasov simulation code, Github repository, https://doi.org/10.5281/zenodo.3640593, version 4.0, last access: 23 April 2020. a
Palmroth, M., Archer, M., Vainio, R., Hietala, H., Pfau-Kempf, Y., Hoilijoki, S., Hannuksela, O., Ganse, U., Sandroos, A., von Alfthan, S., and Eastwood, J. P.: ULF foreshock under radial IMF: THEMIS observations and global kinetic simulation Vlasiator results compared, J. Geophys. Res.-Space, 120, 8782–8798, https://doi.org/10.1002/2015JA021526, 2015. a, b
Palmroth, M., Ganse, U., Pfau-Kempf, Y., Battarbee, M., Turc, L., Brito, T., Grandin, M., Hoilijoki, S., Sandroos, A., and von Alfthan, S.: Vlasov methods in space physics and astrophysics, Living Reviews in Computational Astrophysics, 4, 1, https://doi.org/10.1007/s41115-018-0003-2, 2018. a, b
Pfau-Kempf, Y.: Vlasiator – From local to global magnetospheric hybrid-Vlasov simulations, PhD thesis, University of Helsinki, available at: http://urn.fi/URN:ISBN:978-952-336-001-3 (last access: 15 May 2020), 2016. a
Pfau-Kempf, Y., Hietala, H., Milan, S. E., Juusola, L., Hoilijoki, S., Ganse, U., von Alfthan, S., and Palmroth, M.: Evidence for transient, local ion foreshocks caused by dayside magnetopause reconnection, Ann. Geophys., 34, 943–959, https://doi.org/10.5194/angeo-34-943-2016, 2016. a
Pfau-Kempf, Y., Battarbee, M., Ganse, U., Hoilijoki, S., Turc, L., von Alfthan, S., Vainio, R., and Palmroth, M.: On the Importance of Spatial and Velocity Resolution in the Hybrid-Vlasov Modeling of Collisionless Shocks, Front. Phys., 6, 44, https://doi.org/10.3389/fphy.2018.00044, 2018. a
Sandroos, A.: VLSV: file format and tools, Github repository, available at: https://github.com/fmihpc/vlsv/ (last access: 23 April 2020), 2019. a
Savoini, P. and Lembège, B.: Production of nongyrotropic and gyrotropic backstreaming ion distributions in the quasi-perpendicular ion foreshock region, J. Geophys. Res.-Space, 120, 7154–7171, https://doi.org/10.1002/2015JA021018, 2015. a
Savoini, P., Lembège, B., and Stienlet, J.: Origin of backstreaming electrons within the quasi-perpendicular foreshock region: Two-dimensional self-consistent PIC simulation, J. Geophys. Res.-Space, 115, A09104, https://doi.org/10.1029/2010JA015263, 2010. a
Savoini, P., Lembège, B., and Stienlet, J.: On the origin of the quasi-perpendicular ion foreshock: Full-particle simulations, J. Geophys. Res.-Space, 118, 1132–1145, https://doi.org/10.1002/jgra.50158, 2013. a
Scholer, M.: Diffuse ions at a quasi-parallel collisionless shock: Simulations, Geophys. Res. Lett., 17, 1821–1824, https://doi.org/10.1029/GL017i011p01821, 1990. a, b
Scholer, M. and Terasawa, T.: Ion reflection and dissipation at quasi-parallel collisionless shocks, Geophys. Res. Lett., 17, 119–122, https://doi.org/10.1029/GL017i002p00119, 1990. a, b
Schwartz, S. J. and Burgess, D.: Quasi-parallel shocks: A patchwork of three-dimensional structures, Geophys. Res. Lett., 18, 373–376, https://doi.org/10.1029/91GL00138, 1991. a
Schwartz, S. J., Thomsen, M. F., and Gosling, J. T.: Ions upstream of the Earth's bow shock: A theoretical comparison of alternative source populations, J. Geophys. Res., 88, 2039–2047, https://doi.org/10.1029/JA088iA03p02039, 1983. a
Schwartz, S. J., Burgess, D., Wilkinson, W. P., Kessel, R. L., Dunlop, M., and Lühr, H.: Observations of short large-amplitude magnetic structures at a quasi-parallel shock, J. Geophys. Res., 97, 4209–4227, https://doi.org/10.1029/91JA02581, 1992. a
Sckopke, N., Paschmann, G., Bame, S. J., Gosling, J. T., and Russell, C. T.: Evolution of ion distributions across the nearly perpendicular bow shock: Specularly and non-specularly reflected-gyrating ions, J. Geophys. Res., 88, 6121–6136, https://doi.org/10.1029/JA088iA08p06121, 1983. a
Su, Y., Lu, Q., Gao, X., Huang, C., and Wang, S.: Ion dynamics at supercritical quasi-parallel shocks: Hybrid simulations, Phys. Plasmas, 19, 092108, https://doi.org/10.1063/1.4752219, 2012. a
Sundberg, T., Boardsen, S. A., Slavin, J. A., Uritsky, V. M., Anderson, B. J., Korth, H., Gershman, D. J., Raines, J. M., Zurbuchen, T. H., and Solomon, S. C.: Cyclic reformation of a quasi-parallel bow shock at Mercury: MESSENGER observations, J. Geophys. Res.-Space, 118, 6457–6464, https://doi.org/10.1002/jgra.50602, 2013. a
Sundberg, T., Haynes, C. T., Burgess, D., and Mazelle, C. X.: Ion acceleration at the quasi-parallel bow shock: decoding the signature of injection, Astrophys. J., 820, 21, https://doi.org/10.3847/0004-637X/820/1/21, 2016. a, b, c, d, e, f, g
Thomas, V. A. and Winske, D.: Two dimensional hybrid simulation of a curved bow shock, Geophys. Res. Lett., 17, 1247–1250, https://doi.org/10.1029/GL017i009p01247, 1990. a, b
Thomsen, M. F., Schwartz, S. J., and Gosling, J. T.: Observational evidence on the origin of ions upstream of the Earth's bow shock, J. Geophys. Res., 88, 7843–7852, https://doi.org/10.1029/JA088iA10p07843, 1983. a
Tóth, G., Chen, Y., Gombosi, T. I., Cassak, P., Markidis, S., and Peng, I. B.: Scaling the Ion Inertial Length and Its Implications for Modeling Reconnection in Global Simulations, J. Geophys. Res.-Space, 122, 10336–10355, https://doi.org/10.1002/2017JA024189, 2017. a
Turc, L., Ganse, U., Pfau-Kempf, Y., Hoilijoki, S., Battarbee, M., Juusola, L., Jarvinen, R., Brito, T., Grandin, M., and Palmroth, M.: Foreshock Properties at Typical and Enhanced Interplanetary Magnetic Field Strengths: Results From Hybrid-Vlasov Simulations, J. Geophys. Res.-Space, 123, 5476–5493, https://doi.org/10.1029/2018JA025466, 2018. a, b, c, d, e
Turc, L., Roberts, O. W., Archer, M. O., Palmroth, M., Battarbee, M., Brito, T., Ganse, U., Grandin, M., Pfau-Kempf, Y., Escoubet, C. P., and Dandouras, I.: First Observations of the Disruption of the Earth's Foreshock Wave Field During Magnetic Clouds, Geophys. Res. Lett., 46, 12644–12653, https://doi.org/10.1029/2019GL084437, 2019. a, b
von Alfthan, S., Pokhotelov, D., Kempf, Y., Hoilijoki, S., Honkonen, I., Sandroos, A., and Palmroth, M.: Vlasiator: First global hybrid-Vlasov simulations of Earth's foreshock and magnetosheath, J. Atmos. Sol.-Terr. Phys., 120, 24–35, https://doi.org/10.1016/j.jastp.2014.08.012, 2014. a, b
Wilson III, L. B.: Low Frequency Waves at and Upstream of Collisionless Shocks, in: Low-Frequency Waves in Space Plasmas, Geophysical Monograph Series, American Geophysical Union (AGU), https://doi.org/10.1002/9781119055006.ch16, 2016. a
Wilson III, L. B., Sibeck, D. G., Breneman, A. W., Contel, O. L., Cully, C., Turner, D. L., Angelopoulos, V., and Malaspina, D. M.: Quantified energy dissipation rates in the terrestrial bow shock: 2. Waves and dissipation, J. Geophys. Res.-Space, 119, 6475–6495, https://doi.org/10.1002/2014JA019930, 2014a. a
Wilson III, L. B., Sibeck, D. G., Breneman, A. W., Contel, O. L., Cully, C., Turner, D. L., Angelopoulos, V., and Malaspina, D. M.: Quantified energy dissipation rates in the terrestrial bow shock: 1. Analysis techniques and methodology, J. Geophys. Res.-Space, 119, 6455–6474, https://doi.org/10.1002/2014JA019929, 2014b. a
Wu, M., Hao, Y., Lu, Q., Huang, C., Guo, F., and Wang, S.: The role of large amplitude upstream low-frequency waves in the generation of superthermal ions at a quasi-parallel collisionless shock: CLUSTER observations, Astrophys. J., 808, 2, https://doi.org/10.1088/0004-637X/808/1/2, 2015. a
Yang, Z. W., Lu, Q. M., and Wang, S.: The evolution of the electric field at a nonstationary perpendicular shock, Phys. Plasmas, 16, 124502, https://doi.org/10.1063/1.3275788, 2009. a
Zank, G. P., Rice, W. K. M., Le Roux, J., Cairns, I. H., and Webb, G. M.: The injection problem for quasiparallel shocks, Phys. Plasmas, 8, 4560, https://doi.org/10.1063/1.1400125, 2001. a





