A multi-fluid model of the magnetopause

Observation of the solar wind–magnetosphere boundary provides a unique opportunity to investigate the physics underlying the interaction between two collisionless magnetized plasmas with different temperature, density and magnetic field topology. Their mixing across the interface as well as the boundary dynamics are affected by the development of fluid (and kinetic) instabilities driven by large-scale inhomogeneities in particle and electromagnetic fields. Building up a realistic initial equilibrium state of the magnetopause according to observations is still a challenge nowadays. In this paper, we address the modeling of the particles and electromagnetic field configuration across the Earth's magnetopause by means of a three-fluid analytic model. The model relies on one hot and one cold ion population as well as a neutralizing electron population. The goal is to create an analytic model that is able to reproduce the observations as closely as possible. Some parameters of the model are set using a fitting procedure that aims to minimize their difference with respect to experimental data provided by the Magnetospheric MultiScale (MMS) mission. All of the other profiles, concerning the electron pressure and the relative densities of the cold and hot ion populations, are calculated in order to satisfy the fluid equilibrium equations. Finally, using a new tri-fluid code, we check the stability of the large-scale equilibrium model for a given experimental case and provide proof that the system is unstable to reconnection. This model could be of interest for the interpretation of satellite results and for the study of the dynamics at the magnetosphere–solar wind boundary.

1 Introduction

The solar wind–magnetosphere boundary, known as the magnetopause, is characterized by the presence of magnetic and velocity shears as well as jumps in magnetic and velocity magnitudes in addition to jumps in plasma density and temperature. These inhomogeneities are the sources of many plasma instabilities at different spatiotemporal scales (Labelle and Treumann, 1988) that, in turn, often trigger secondary instabilities at smaller scales. As an example, secondary instabilities such as magnetic reconnection, Kelvin–Helmholtz and/or Rayleigh–Taylor instability can efficiently develop on the shoulder of the primary instability; the Kelvin–Helmholtz instability at the low-latitude magnetopause is a prime example of such a case (see Faganello and Califano, 2017 and references therein).

All of these phenomena can cause significant entry of magnetosheath plasma mass (Paschmann, 1997), momentum (Dungey, 1961) and energy (Lee and Roederer, 1982) into the magnetosphere. The study of the magnetopause is of particular interest, as this system offers the unique opportunity to study a two-plasma large-scale interaction in conditions not achievable in the laboratory. The magnetopause physics is also of basic importance in studies addressing the Sun–Earth interaction, in particular concerning the impact of solar wind disturbances on the terrestrial environment and space-weather forecasting efforts (see for instance Baker and Lanzerotti, 2016). Modeling space plasmas using data provided by multi-spacecraft missions has been much developed during (and in preparation of) the “cluster era” (Büchner et al., 1998). Concerning the magnetopause data, one of the key points relates to the mixing between magnetospheric and magnetosheath plasmas and the resulting non-Maxwellian shape of the distribution functions (hereafter referred to as “dfs”) observed in these regions (Bosqued et al., 2001; Frey et al., 2003; Phan et al., 2005; Retinò et al., 2005). These dfs are often reminiscent of those observed in reconnection kinetic simulations (Nakamura and Scholer, 2000; Tanaka et al., 2008; Aunai et al., 2011). Some of these dfs can be compared using simple analytic models, as in the pioneering work by Cowley and Owen (1989). As the populations originating from the two different sides of the magnetopause differ with respect to density and temperature, modeling the mixing requires the use of at least a multi-population model. In the perspective of investigating the dynamics of the magnetopause mixing layer using a three-fluid numerical simulation, the main target of this paper is to build up a three-fluid equilibrium that is as realistic as possible to initialize the simulation.

The three-fluid model that we propose in the present paper aims to distinguish between ions of magnetospheric and magnetosheath origin. It must be considered as a first step towards a four-population model, which would also allow one to distinguish between the electrons from both origins. This simplification allows nonessential details related to the presence of two electron species, which are not likely to have a major role in structuring the large-scale equilibrium, to be avoided. In addition, note that for a correct modeling of the electrons in the magnetopause vicinity, one should also split the magnetospheric electrons into at least two subpopulations: one “cold” poorly measured population, carrying the density, and one “hot” population, carrying the pressure. Finally, starting from a previously existing two-fluid code, it is relatively straightforward to create a multi-ion one-electron code where the electrons only provide an “Ohm's law”. However, a fully multi-population code (i.e., including several electron populations) requires a radically different approach that is presently under investigation and is a matter for future work.

In the past, several multi-population models trying to simulate the plasma interaction between the magnetosheath and magnetosphere have been developed. In particular, for the modeling of tangential layers (i.e., without normal magnetic field and without normal velocity, $B_n=u_n=\mathrm{0}$), the kinetic models are by definition the most complete ones as they rely on a Vlasov equilibrium. Nevertheless, as these models are considerably more complicated than the fluid models, using the latter can be considered to be a necessary first step for modeling the magnetopause as closely to the observational data as possible. Note also that all of the equilibria built via dfs that are only single-valued functions of the particle invariants of motion (Channell, 1976) cannot really be considered to be “multi-population” models: they ignore the issue of accessibility (Whipple et al., 1984) and, therefore, cannot distinguish between particles of magnetospheric or magnetosheath origin. Some models (Roth et al., 1996; De Keyser and Roth, 1998) have partly accounted for the accessibility problem by considering functions of the invariants that are bi-valued. In recent years, new models have been developed by Belmont et al. (2012) and Dorville et al. (2015) that account for accessibility by considering more general multivalued dfs. Nevertheless, it must be kept in mind that all of these models involve many free parameters. In Dorville et al. (2015), the authors even emphasize that there is no general constraint for fixing the normal electric field profile in their kinetic model; thus, the normal electric field profile can be chosen in a fully arbitrary manner. Furthermore, even if a few profiles can be fixed in a more or less realistic way, all of the others depend on simple mathematical assumptions, which are largely arbitrary; therefore, the latter profiles generally still remain far from realistic.

A different approach to creating a large-scale configuration at the boundary between the magnetosheath and the magnetosphere is to run a global simulation that eventually reaches a steady state. This has been done recently utilizing hybrid and kinetic codes (Chen et al., 2017; Palmroth et al., 2018), although the question of the spatial resolution is then difficult to solve for investigating the internal structure of the magnetopause boundary. It will be interesting to compare the results obtained using the abovementioned methods with those obtained using the methods discussed in the present paper where the model instead relies on spacecraft data as the initial condition for the simulation.

In summary, the lack of realistic equilibria in the literature generally makes the initialization of the magnetopause studies difficult with respect to kinetic simulations. Recently the multi-population character of the medium has been taken into account by Dargent et al. (2017), although for a different purpose from that in this study. Using a particle-in-cell (PIC) code, they investigated the influence of cold magnetospheric ions on the development of magnetic reconnection. In this paper, the magnetospheric plasma includes two populations with different temperatures in order to account for the presence of the cold ions that are observed in the magnetosphere close to the magnetopause.

Multi-fluid models have been developed in various domains, although generally not for magnetopause studies. These studies address multispecies evolution involving chemical processes and collisions. They have been used to investigate planetary atmospheres (Modolo et al., 2006; Ma et al., 2007), the solar chromosphere (Alvarez Laguna et al., 2016) and basic plasma physics problems (e.g., drift turbulence in Shumlak et al., 2011).

In this paper, we present a new technique to create a three-fluid equilibrium that derives directly from satellite observations. The model assumes 1-D gradients in the normal direction and a tangential boundary (B_n=0) at the magnetopause. The magnetic and velocity shear are both taken into account in a realistic way. Profiles are chosen that best fit the data from the Magnetospheric MultiScale (MMS) mission (Burch et al., 2016), for which the time-to-space conversion has been performed using recent techniques presented in Manuzzo et al. (2019). As will be shown in Sect. 4, the method provides a cold and a hot contribution that are in qualitative agreement with observations, even if the model only uses the global ion macroscopic moments as inputs.

2 Observations

We use MMS data from 16 October 2015 at 13:05:34 + 40 s UT that occurred at [8.3, 8.5, −0.7] R_E in GSE frame, which embeds a magnetopause crossing. In Fig. 1, we plot the experimental data that the equilibrium model attempts to reproduce. This interval shows the standard signatures of the region where the magnetospheric and magnetosheath plasmas meet (magnetopause crossing): a reversal of the magnetic field and a change in the energy distributions.

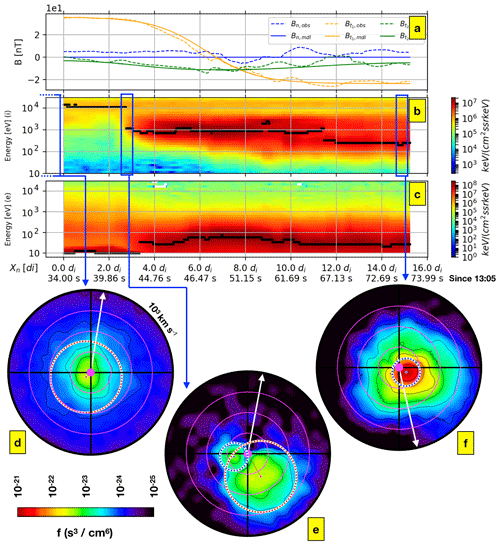
Figure 1 MMS data for the event on 16 October 2015 at 13:05:34 UT + 40 s. (a) Normal and tangential (to the magnetopause plane) components of the magnetic field. (b, c) Ion and electron spectrograms. The first abscissa is the spatial coordinate normal to the magnetopause X_n (see text), and the second abscissa is time. (d, e, f) Ion distribution functions (idfs) recorded by the Fast Plasma Investigation (FPI) instruments in the magnetosphere, in the overlapping region and in the magnetosheath, respectively. These idfs are projected on the tangential plane by integration over the normal component of the velocity.

In Fig. 1a–c, data are plotted as functions of a spatial coordinate X_n, which is the projection of the spacecraft path along the direction normal to the magnetopause (units of d_i,MSh with $d_{i,\mathrm{MSh}}\simeq \mathrm{70}$ km). Once the function X_n(t) is known, it allows for the recovery of the spatial profiles of all quantities of interest from the corresponding temporal series of the spacecraft magnetosheath–magnetosphere crossing, even with a variable velocity. For the sake of completeness, we also give the time corresponding to each given value of X_n in the abscissa of Fig. 1c. The spatial coordinate X(t) is determined by the integration of the velocity of the spacecraft with respect to the magnetic structure. In order to determine this spatial velocity, we use a new method from Manuzzo et al. (2019), which is an extension of the spatiotemporal difference (STD) method first proposed by Shi et al. (2006). The main difference with respect to the Shi model consists of taking the possible weak nonstationarities of the magnetic structure into account , i.e., assuming ${\partial }_{t,\mathrm{sc}}\mathit{B}={\partial }_{t,\mathrm{0}}\mathit{X}\cdot \mathrm{\nabla }\mathit{B}+{\partial }_{t,\mathrm{0}}\mathit{B}$ and not just ${\partial }_{t,\mathrm{sc}}\mathit{B}={\partial }_{t,\mathrm{0}}\mathit{X}\cdot \mathrm{\nabla }\mathit{B}$ (the indexes “sc” and “0” indicate the spacecraft frame and the frame where the intrinsic variation of the magnetopause structure is the smallest, respectively). This allows for some singularities in the results to be avoided.

Black points have been superimposed on the two spectrograms (Fig. 1b, c) to indicate their maxima. This allows one to more easily distinguish where the magnetosheath and the magnetospheric plasma interact, as indicated by discontinuities in the curve joining the maxima. The region where the two plasmas partially overlap in space is emphasized by a blue rectangle in Fig. 1b, which is centered at X_n∼3 d_i.

In Fig. 1d–f, we plot the 2-D ion distribution functions (idfs) in the plane tangential to the magnetopause. They are obtained by integration over the out-of-plane (normal) component of the velocity. Each plot is the average of five single idfs recorded within a ∼0.75 s long interval (equivalent to 0.5d_i). The radius of the distribution functions is 10³ km s⁻¹ and the purple full circle drawn at their centers determines the bottom limits of the energy of the FPI instrument (10 eV ∼ 53 km s⁻¹ for ions). The direction of the local magnetic field is indicated by a white arrow. In Fig. 1e (mixing region), one can observe that the idf contains two peaks that are emphasized by the blue and red dashed circles. These two circles have a diameter equal to the magnetosheath and magnetospheric thermal velocities, respectively. The same circles are shown for the magnetosheath and magnetospheric idfs in Fig. 1f and d. In these two asymptotic media, we see that there is only one single peak. Note that the idf shown in Fig. 1d was recorded a little earlier (10:20:00 UT + 2 s) during a “clear” observation of the magnetosphere and, therefore, allows the presence of magnetosheath particles when the spacecraft is too close to the magnetopause to be avoided. Conversely, Fig. 1e shows a mixture of the magnetosheath and magnetospheric populations at the same time. However, as the two peaks are close to each other and the distributions of the two populations are partly superposed, it is not possible to clearly separate the hot/cold contributions, which is a necessary input for the multi-population model to be built by a direct fit of this region. In the next section, we will explain a new method capable of separating the two particle components – even in such complex situations. Note that the electron spectrogram of Fig. 1c shows energy maxima that lay just at the bottom limit of the instrument (≃10 eV) in the magnetospheric region (X_n≤2d_i). This indicates the presence of cold electrons in the magnetosphere. The role of this poorly measured cold electron population is not relevant for the magnetopause pressure equilibrium, but it could be significant in the electron bulk velocity. However the electron population parameters will be not determined by a direct fit of the data nor will those of the two ion populations (cold/hot). Instead, they will be determined by another method based on the equilibrium equations, which we will describe in the next section.

3 The three-fluid model

3.1 Equilibrium equations

We present a three-fluid collisionless model here that includes two proton populations (one cold and one hot) and one electron population. The cold ion population models the ions of magnetosheath origin and disappears more and more on the magnetospheric side. Conversely, the hot population models the ions of magnetosphere origin and disappears on the magnetosheath side.

The continuity and ion momentum equations are derived from the first two moments of the Vlasov equation. We impose charge neutrality, and the displacement current is neglected. We assume isotropic pressures and adopt a polytropic closure for all populations. These equations are coupled to the electromagnetic field via the Faraday equation, and we use an Ohm's law that takes the electron pressure gradient into account but neglects electron inertia effects. The three-fluid system of equations reads as follows:

$$\begin{array}{}\text{(1a)}& {\displaystyle }& {\displaystyle }\sum _{\mathit{\alpha }}{n}_{\mathit{\alpha }}{q}_{\mathit{\alpha }}=\mathrm{0}\text{(1b)}& {\displaystyle }& {\displaystyle }\sum _{\mathit{\alpha }}{n}_{\mathit{\alpha }}{q}_{\mathit{\alpha }}{\mathit{U}}_{\mathit{\alpha }}=\mathrm{\nabla }\times \mathit{B}/{\mathit{\mu }}_{\mathrm{0}}\text{(1c)}& {\displaystyle }& {\displaystyle \frac{\partial n_{\mathit{\beta }}}{\partial t}}+\mathrm{\nabla }\cdot \left(n_{\mathit{\beta }}{\mathit{U}}_{\mathit{\beta }}\right)=\mathrm{0}\text{(1d)}& {\displaystyle }& {\displaystyle }\begin{array}{l}\frac{\partial \left(n_{\mathit{\beta }}{m}_{\mathit{\beta }}{\mathit{U}}_{\mathit{\beta }}\right)}{\partial t}+\mathrm{\nabla }\cdot \left(n_{\mathit{\beta }}{m}_{\mathit{\beta }}{\mathit{U}}_{\mathit{\beta }}{\mathit{U}}_{\mathit{\beta }}\right)+\mathrm{\nabla }\left(n_{\mathit{\beta }}{T}_{\mathit{\beta }}\right)\\ =n_{\mathit{\beta }}{q}_{\mathit{\beta }}\left(\mathit{E}+{\mathit{U}}_{\mathit{\beta }}\times \mathit{B}\right)\end{array}\text{(1e)}& {\displaystyle }& {\displaystyle \frac{\partial \left(n_{\mathit{\alpha }}{S}_{\mathit{\alpha }}\right)}{\partial t}}+\mathrm{\nabla }\cdot \left[{\mathit{U}}_{\mathit{\alpha }}\left(n_{\mathit{\alpha }}{S}_{\mathit{\alpha }}\right)\right]=\mathrm{0};S_{\mathit{\alpha }}=T_{\mathit{\alpha }}{n}_{\mathit{\alpha }}^{\mathrm{1}-\mathit{\gamma }}\text{(1f)}& {\displaystyle }& {\displaystyle \frac{\partial \mathit{B}}{\partial t}}=-\mathrm{\nabla }\times \mathit{E}\text{(1g)}& {\displaystyle }& {\displaystyle }\mathit{E}=-{\mathit{U}}_{\mathrm{e}}\times \mathit{B}+{\displaystyle \frac{\mathrm{1}}{n_{\mathrm{e}}{q}_{\mathrm{e}}}}\mathrm{\nabla }\left(n_{\mathrm{e}}{T}_{\mathrm{e}}\right),\end{array}$$

where the index α stands for “all populations”, and the index β represents “all ion populations”.

3.2 Determination of the fluid profiles

We aim to establish a tangential 1-D equilibrium to mimic the magnetopause observations previously presented as closely as possible. Assuming $\partial /\partial t$ = 0, this is done in three steps.

In step 1, we impose the magnetic field B as well as the density n_i, temperature T_i and velocity U_i profiles by fitting the data using a combination of hyperbolic tangents, as explained in Sect. 4. At this stage, the ion quantities are chosen without distinguishing between the cold and hot populations.

In step 2, we deduce the electron density n_e and velocity U_e using Eqs. (1a) and (1b), respectively. The temperature T_e is deduced from

$$\begin{array}{}\text{(2)}& P_{\mathrm{e}}=P_{\mathrm{tot}}-\left(P_{\mathrm{B}}+n_{\mathrm{i}}{T}_{\mathrm{i}}\right),\end{array}$$

where the total pressure, P_tot, has been imposed to be constant in order to fulfill the equilibrium conditions.

As far as P_e is concerned, we note that P_e is much smaller than P_i+P_B (see Fig. 2) and that it is difficult to estimate it precisely due to experimental uncertainties. As a consequence, the constant value of P_tot used in the model is taken as the maximum of the measured total pressure $P_{\mathrm{i}}+P_{\mathrm{B}}+P_{\mathrm{e}}$. Note that the total pressure is not really constant due to the abovementioned uncertainties on P_e and because the experimental structure may be slightly out of equilibrium. The modeled P_e is deduced from Eq. (2), with the choice for P_tot ensuring only positive values for P_e. Finally, the electric field E is deduced from the Ohm's Law, as in Eq. (1g).

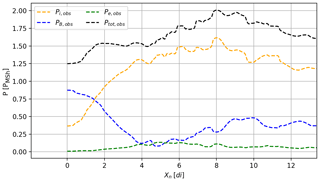
Figure 2 Comparison between P_e, P_i and P_B. The total pressure is indicated as P_tot. Numerical values are all normalized to the magnetosheath pressure P_MSh∼3200 eV cm⁻³.

In step 3, we now split the global proton population into two different populations, cold and hot (hereafter referred to as “ic” and “ih”, respectively) to distinguish the magnetospheric and magnetosheath populations. The densities (n_ic and n_ih), pressures (P_ic and P_ih) and currents (J_ic and J_ih) of the two ion populations add to form the total ion density, pressure and current as follows:

$$\begin{array}{}\text{(3a)}& {\displaystyle }& {\displaystyle }{n}_{\mathrm{i}}=n_{\mathrm{ic}}+n_{\mathrm{ih}}\text{(3b)}& {\displaystyle }& {\displaystyle }{n}_{\mathrm{i}}{T}_{\mathrm{i}}=n_{\mathrm{ic}}{T}_{\mathrm{ic}}+n_{\mathrm{ih}}{T}_{\mathrm{ih}}\text{(3c)}& {\displaystyle }& {\displaystyle }{n}_{\mathrm{i}}{\mathit{U}}_{\mathrm{i}}=n_{\mathrm{ic}}{\mathit{U}}_{\mathrm{ic}}+n_{\mathrm{ih}}{\mathit{U}}_{\mathrm{ih}}.\end{array}$$

The temperatures of the cold and hot ion populations, T_ic and T_ih, are assumed to be constant. As the global ion temperature profile T_i is known, their values are obtained from the satellite data using the following two limits:

$$\underset{x\to \mathrm{MSph}}{\lim }{T}_{\mathrm{ih}}=T_{\mathrm{i}};\underset{x\to \mathrm{MSh}}{\lim }{T}_{\mathrm{ic}}=T_{\mathrm{i}}.$$

The temperature ratio between the two populations is set by the value of the dimensionless parameter as follows:

$$\begin{array}{}\text{(4)}& \mathrm{{\rm Y}}\equiv {\displaystyle \frac{T_{\mathrm{ih}}}{T_{\mathrm{ic}}}}.\end{array}$$

Using Eq. (3b), the contributions of each population to density and pressure are fully determined by the T_i profile and the temperature ratio Υ:

$$\begin{array}{}\text{(5a)}& {\displaystyle }& {\displaystyle }\mathrm{\Gamma }\equiv {\displaystyle \frac{n_{\mathrm{ic}}}{n_{\mathrm{i}}}}={\displaystyle \frac{\mathrm{{\rm Y}}-\frac{T_{\mathrm{i}}}{T_{\mathrm{ic}}}}{\mathrm{{\rm Y}}-\mathrm{1}}}\text{(5b)}& {\displaystyle }& {\displaystyle }\mathrm{\Pi }\equiv {\displaystyle \frac{P_{\mathrm{ic}}}{P_{\mathrm{i}}}}={\left(\mathrm{1}+{\displaystyle \frac{\mathrm{1}-\mathrm{\Gamma }}{\mathrm{\Gamma }}}\mathrm{{\rm Y}}\right)}^{-\mathrm{1}}.\end{array}$$

The perpendicular currents and, thus, the corresponding velocities are fully determined by Eq. (1d). On the contrary, the parallel currents cannot be determined by the abovementioned system of equilibrium equations. Therefore, we will set them using a reasonable choice for the parameter ϕ which is equal to the ratio of the cold parallel ion current to the total parallel ion current as seen in the electron frame:

$$\begin{array}{}\text{(6)}& \mathit{\varphi }\equiv \mathrm{\Gamma }{\displaystyle \frac{({\mathit{U}}_{\mathrm{ic}}-{\mathit{U}}_{\mathrm{e}})\cdot \mathit{b}}{({\mathit{U}}_{\mathrm{i}}-{\mathit{U}}_{\mathrm{e}})\cdot \mathit{b}}}.\end{array}$$

The parallel components of the hot and cold ion velocities can have opposite directions; thus ϕ is defined in the $[-\mathrm{1},\mathrm{1}]$ range, whereas Γ and Π are defined in the [0,1] range. The reasonable choice for ϕ is suggested by the data and will be discussed in more details in the next section. In general, the asymptotic values of the cold and hot ion currents are chosen in agreement with the asymptotic values of n_ic and n_ih so that all of the corresponding values of the velocities U_ic and U_ih have reasonable values, although one of the two densities n_ic or n_ih tends to nearly zero on each side.

In order to implement this model into a numerical simulation, a compromise is necessary because the multi-fluid code cannot deal with a population having a zero density somewhere in the domain. To avoid this problem, we introduce the parameters ϵ^(c)≪1 and ϵ^(h)≪1, and we modify the initialization so that the cold and hot densities tend to ϵ^(h)n_i and (1−ϵ^(h))n_i on the magnetospheric side and to (1−ϵ^(c))n_i and ϵ^(c)n_i on the magnetosheath side. The temperatures are changed according to the following equations:

$$\begin{array}{}\text{(7a)}& {\displaystyle }& {\displaystyle }{T}_{\mathrm{ic}}={\displaystyle \frac{{\mathit{ϵ}}^{\left(c\right)}{T}_{\mathrm{i}}^{\mathrm{MSph}}-\left(\mathrm{1}-{\mathit{ϵ}}^{\left(h\right)}\right)T_{\mathrm{i}}^{\mathrm{MSh}}}{{\mathit{ϵ}}^{\left(c\right)}+{\mathit{ϵ}}^{\left(h\right)}-\mathrm{1}}}\text{(7b)}& {\displaystyle }& {\displaystyle }{T}_{\mathrm{ih}}={\displaystyle \frac{{\mathit{ϵ}}^{\left(h\right)}{T}_{\mathrm{i}}^{\mathrm{MSh}}-\left(\mathrm{1}-{\mathit{ϵ}}^{\left(c\right)}\right)T_{\mathrm{i}}^{\mathrm{MSph}}}{{\mathit{ϵ}}^{\left(c\right)}+{\mathit{ϵ}}^{\left(h\right)}-\mathrm{1}}},\end{array}$$

where T_ic and T_ih indicate the observed values corresponding to the model, and $T_{\mathrm{i}}^{\mathrm{MSph}}$ and $T_{\mathrm{i}}^{\mathrm{MSh}}$ indicate the temperatures corresponding to the magnetospheric and magnetosheath values of T_i. A similar correction is made for the ion velocities (see the following sections).

4 Data vs. analytic profiles

We apply the procedure to the case study introduced in Sect. 2. In Fig. 3, we compare the model field profiles with those obtained with the MMS data. The model profiles for the magnetic field, the ion temperature and density are obtained by a fit procedure (Fig. 3a, b, and c, respectively), whereas the others are calculated from the equilibrium equations. The fits are obtained by means of analytic functions. For a given quantity Q, the fitting functions have the following form:

$$\begin{array}{}\text{(8)}& Q=\sum _j{a}_{Q,j}+b_{Q,j}\tanh \left({\displaystyle \frac{X_n-c_{Q,j}}{d_{Q,j}}}\right),\end{array}$$

where X_n is the coordinate along the direction normal to the magnetopause (as discussed in Sect. 2). The parameters a_Q,j, b_Q,j, c_Q,j and d_Q,j are the free parameters shaping the analytic profiles, and j is the component index. The maximum value of j depends on the fitted quantity: the analytic profiles are considered to be good fits of the data if they correctly shape the large-scale configuration as well as the position and the length scale of the gradients within the magnetopause layer. An example of a “good fit” is given in Fig. 3a–c. It is worth noticing that the particle boundary, observed on density and temperature, has a length scale smaller than the magnetic boundary (by a ratio ≃0.25) and that its position is considerably shifted toward the magnetosphere with respect to the center of the magnetic jump. This may indicate the presence of a boundary layer, possibly made of magnetosheath plasma, that is observed on the magnetospheric side of the magnetopause (Hasegawa, 2012). Such features cannot be reproduced in the framework of a magnetohydrodynamic (MHD) equilibrium model. To the best of our knowledge, these features have not even been introduced in the context of a kinetic model.

In Fig. 3b, we show the temperature profiles as obtained with our model equilibrium. The total ion population temperature T_i has been obtained by a fit, and it is superposed onto the cold ion population temperature T_ic (blue curve) and the hot ion population temperature T_ih (red curve). The figure has been drawn using ϵ^(h)=0.35 and ϵ^(c)=0.05, which determine the values of T_ic and T_ih via Eqs. (7a) and (7b), respectively.

One observes that the global temperature is well fitted by the model outside the mixing region, but the fit is less accurate in the $\sim \mathrm{1.0}{d}_i\le X_n\le \sim \mathrm{2.5}{d}_i$ interval. In this interval, the real total ion temperature actually becomes larger than its magnetospheric asymptotic limit. Unfortunately this feature can not be reproduced by the present three-fluid model with hot and cold constant temperatures, as the Γ≥0 constraint forces the T_i profile to be lower than T_ih everywhere (see Eq. 5a). This little deviation is acceptable as the model mainly aims to reproduce the asymptotic trends, with the observed inner region most likely being out of equilibrium.

In Fig. 3c, we show the density profiles. As explained in the previous section, the hot and cold ion contributions to the total density n_i are computed by means of the Γ function, which is fixed once the global T_i profile and the temperature ratio Υ are fixed (Eq. 5a). In Fig. 3a–g, the two vertical (dashed black) lines indicate the limits of the region where $\mathrm{1}/\mathrm{4}\le \mathrm{\Gamma }\le \mathrm{3}/\mathrm{4}$. Note that the cold ion density rapidly falls to very low values in more or less ∼2 d_i (where d_i≃70 km is the ions inertial length measured in the magnetosheath), whereas the hot population density remains at nearly the same value over a longer interval (between 0 and 8 d_i).

The electron density and velocity profiles are obtained from the equilibrium equations. However, these quantities are not plotted here because their experimental counterparts are likely to be biased in the magnetosphere by the cold electron population, which is below the bottom energy threshold of the FPI instrument (as mentioned in Sect. 2). Conversely, in Fig. 3d, we plot the normal component of the electric field, which is obtained from the three-fluid model using Eq. (1g). We see that the electric field calculated by the model agrees quite well with the experimental field. As the electric field reflects the electron dynamics, this shows (independently of the electron measurements) that the electron dynamics is correctly accounted for in the model.

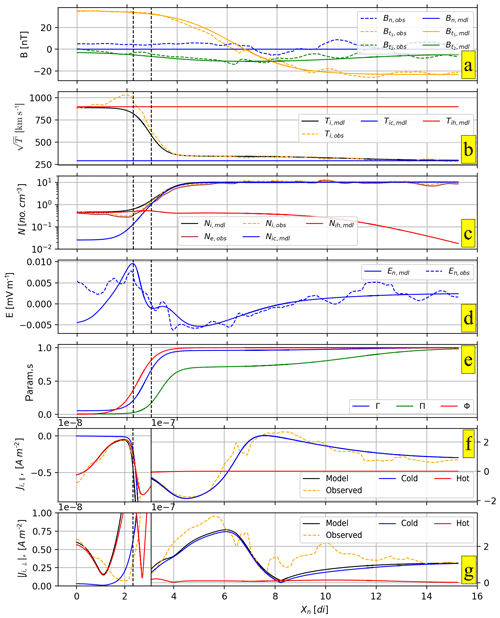
Figure 3 Comparison between the magnetopause profiles as observed by MMS on 16 October 2015 at 13:05:34 + 40 s UT and those used for the three-fluid model equilibrium. Satellite data are represented by dashed lines, and the extrapolated profiles used in the model are represented by continuous lines. The X_n coordinate represents the spatial coordinate normal to the magnetopause X_n. In the panels we show the magnetic field (a), the temperatures (b), the density (c), the normal component of the electric field (d), the parameter Γ, Π and Φ (e), and the parallel and perpendicular components of the ion current (f and g, respectively) as computed from particle data. The two vertical (black dashed) lines highlight the transition region ($\mathrm{1}/\mathrm{4}\le \mathrm{\Gamma }\le \mathrm{3.4}$). The blue and orange lines adopted for the electric and magnetic fields represent the normal and the tangential components of the fields. The square roots of the temperatures in panel (b) are plotted in velocity units in order to make the comparison with the idfs shown in Fig. (1) easier. For the sake of clarity, the curves shown in panels (f) and (g) have been multiplied by a factor of 10 in the $\mathrm{0.0}\le X_n\le \mathrm{3.0}$ interval.

The parallel components of the cold and hot ion currents are set by ϕ (Eq. 6). As long as there are no cold ions on the magnetospheric side and no hot ions on the magnetosheath side, the asymptotic constraints on ϕ would be

$$\underset{x\to \mathrm{MSph}}{\lim }\mathit{\varphi }=\mathrm{0};\underset{x\to \mathrm{MSh}}{\lim }\mathit{\varphi }=\mathrm{1}.$$

Nevertheless, owing to the compromises necessary to implement the model in the multi-population numerical simulation, the cold and hot densities actually take small but not strictly null values on both sides. To determine the corresponding parallel currents, corrections similar to Eqs. (7a) and (7b) are applied with the assumption that, on each side, the parallel velocities of the cold and hot populations, in the electron frame, are equal to each other and, therefore, equal to the global one. Under this assumption, it can be easily shown that the asymptotic values of Φ are equal to those of Γ:

$$\underset{x\to \mathrm{MSph}}{\lim }\mathit{\varphi }={\mathit{ϵ}}^{\left(h\right)};\underset{x\to \mathrm{MSh}}{\lim }\mathit{\varphi }=\mathrm{1}-{\mathit{ϵ}}^{\left(c\right)}.$$

Note that for the particular MMS event considered, the global ion parallel velocities are observed to be quasi-null on each side, so that the same asymptotic property holds for the velocities of the two populations.

Between the two limits above, a reasonable choice for the ϕ profile is that the length of its gradients is of the same order as the scale length of the density and temperature gradients, i.e., ∼ 1–2 d_i. The position of the main gradient of ϕ is set in order to separate the magnetopause thickness into two parts, each representing the length proportional to the gyro-radii of the two populations (their ratio is ≃2).

In Fig. 3e, we show the model profiles for Γ, Π and Φ. Because of the differences in temperature between the two components, the profile in Π (concerning the pressures) noticeably differs from the profile in Γ (concerning the densities).

Finally, in Fig. 3f and g, we show the results concerning the parallel and perpendicular components of the ion currents. Once more, one observes that the global ion current is well fitted with the exception of the perpendicular current in the mixing region, which is less accurate. This is due to the previously mentioned small inaccuracy in the modeled ion temperature in this region.

5 Numerical simulations

5.1 Setup

Here we give an example of a three-fluid numerical simulation with the aim of demonstrating the possibility of numerically studying the above system by starting from an equilibrium not far from a real one (not only qualitatively but also quantitatively). For the sake of simplicity, we limit the geometry (to 2-D) and the numerical code (to 3-D). A detailed numerical study relying on such an approach will be the focus of future work.

The three-fluid model introduced in this paper has been used to initialize a 2-D three-fluid numerical simulation of the interaction between the solar wind and the Earth's magnetopause. The numerical simulation is intended to mimic the MMS crossing on 16 October 2015 at 13:05:34 + 40 s UT. This simulation has been performed using a three-fluid numerical code that solves Eqs. (1a)–(1g). The code originates from a two-fluid 3-D parallel code largely used for the study of the interaction of the solar wind with the magnetosphere (see Fadanelli et al., 2018 and references therein). The three-fluid code adapts the new equations to the algorithm of the two-fluid code presented in Faganello et al. (2009). It advances in time using a standard third-order Runge–Kutta algorithm (Canuto, 1988). It uses sixth-order explicit finite differences along the periodic y direction and a sixth-order compact finite difference scheme with spectral like resolution for spatial derivative along the inhomogeneous x direction (see Lele, 1992 for the significance and technical details of compact finite differences with spectral like resolution). The numerical stability is guaranteed by means of a spectral filter along the periodic y direction and a spectral-like filtering scheme along the inhomogeneous x direction. The code is parallelized along the periodic y direction (Lele, 1992). The code has been validated by standard numerical tests. In particular, by separately selecting the two cold and hot ion populations, we have reproduced the propagation of ion acoustic and Alfvén waves.

To initialize the simulation presented in this paper, we take the model profiles represented in Fig. 3 as the initial equilibrium, including the few modifications for the cold and hot ion density components (with respect to the basic model) for computational reasons that are discussed at the end of Sect. 3. The three-fluid code handles a normalized version of the three-fluid set of equations (Eqs. 1a–1g) using the following characteristic quantities. Magnetic field and ion densities are normalized to their mean values in the magnetosheath (out of the magnetopause layer) B₀=B_MSh and n₀=n_MSh. Velocity is normalized to the corresponding Alfvén velocity $V_{\mathrm{0}}=V_{\mathrm{A},\mathrm{MSth}}=B_{\mathrm{0}}/\sqrt{\left({\mathit{\mu }}_{\mathrm{0}}{n}_{\mathrm{0}}{m}_i\right)}$, and time is normalized to the corresponding inverse ion gyro-frequency $t_{\mathrm{0}}=\mathrm{1}/{\mathrm{\Omega }}_{\mathrm{c},\mathrm{MSh}}=m_i/q_i{B}_{\mathrm{0}}$. The other normalization quantities are obtained from those just introduced: the lengths are normalized to l₀=V₀t₀ (i.e., the ion inertial length), the temperatures are normalized to $T_{\mathrm{0}}=m_i{V}_{\mathrm{0}}^{\mathrm{2}}$ and the electric field is normalized to E₀=V₀B₀.

The simulation box dimensions are given by L_x=160d_i and L_y=20π d_i, and the box is discretized using n_x=800 and n_y=320 grid points corresponding to $dx=dy=\mathrm{0.2}{d}_i$. We have checked that the equilibrium configuration remains stable for several thousand ion cyclotron times in the absence of an initial perturbation due to the very low values of the numerical noise and the high accuracy of the numerical method.

5.2 Results

The large-scale equilibrium configuration used to initialize the simulation is unstable with respect to the reconnection mode. At t=0 we add an initial perturbation $\mathit{\delta }\mathit{B}=\mathrm{\nabla }\times \mathit{A}$ to the equilibrium. The potential vector is given by a sum of random phase modes as follows:

$$\begin{array}{}\text{(9)}& \begin{array}{rl}{A}_l& =a\left(x\right)\sum _{k_y}\sum _{k_x}\mathit{\{}\cos \left[k_{x}x+k_{y}y+{\mathit{\varphi }}_{\mathrm{1}}(k_x,k_y)\right]\\ & +\cos \left[k_{x}x-k_{y}y+{\mathit{\varphi }}_{\mathrm{2}}(k_x,k_y)\right]\mathit{\}}/k,\end{array}\end{array}$$

where $k=\sqrt{k_x^{\mathrm{2}}+k_y^{\mathrm{2}}}$ and $\mathit{\varphi }\in [\mathrm{0},\mathrm{2}\mathit{\pi })$ are random phases, and a(x) is a Gaussian-like convolution profile in the inhomogeneous direction going to zero at both boundaries; a(x) is given by the following equation:

$$\begin{array}{}\text{(10)}& a\left(x\right)=a_{\mathrm{0}}{e}^{-{\left(\frac{x-x_{\mathrm{mp}}}{\mathrm{2}{L}_{\mathrm{mp}}}\right)}^{\mathrm{2}}},\end{array}$$

where $x_{\mathrm{mp}}=L_x/\mathrm{2}=\mathrm{60}$ and L_mp=1.66 are the position and the thickness of our magnetopause model, respectively, and a₀ is a small amplitude such that the maximum absolute value of the initial perturbation is $\sim {\mathrm{10}}^{-\mathrm{3}}$.

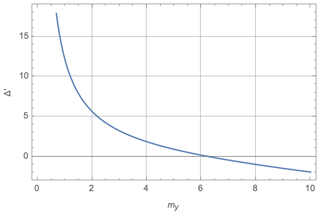
Figure 4 Δ^′ vs. the wave number m_y for an equilibrium magnetic field ∼tanh(x) (dimensionless). The unstable modes are those associated with positive values of Δ^′.

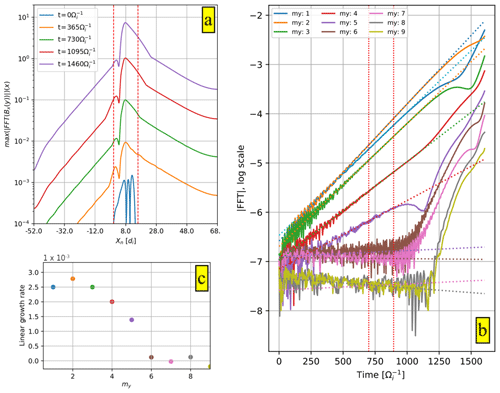
Figure 5 Development of the reconnection instability. (a) The modulus of the Fourier transform of δb_x along y vs. x at five fixed time instants. The plots correspond to the fastest growing mode, m=2, on a log scale. The two red dashed vertical lines indicate the space interval from Fig. 3. (b) The first five eigenmodes' growth vs. time. The orange curve corresponds to the most unstable mode, m=2, which is plotted in panel (a). (c) The growth rate values vs. k_y calculated by a best fit of the slopes in panel (b); the colors also correspond to those used in (b).

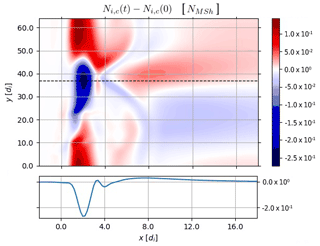
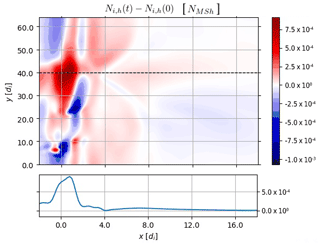
The simulation is run for about 1500 ion cyclotron times. Very rapidly, the initial perturbation reorganizes and sets up the reconnection eigenmodes that are identified by their wave number in the y periodic direction (each m wave number is easily recovered by taking the Fourier transform of the perturbation along the y direction at a given time). Following the classical reconnection theory (Furth et al., 1963) (but ignoring the density inhomogeneity), we have checked that our equilibrium is Δ^′ unstable for the first five eigenmodes. We recall here that the Δ^′ parameter depends on the equilibrium magnetic shear and the wavelength of the perturbation. It defines the instability threshold condition (${\mathrm{\Delta }}^{\prime }\ge \mathrm{0}$). The unstable modes can be deduced by looking at Fig. 4 where we plot Δ^′ as a function of the wave number m_y. We see that only the first five modes $m_y=\mathrm{1},\mathrm{\dots },\mathrm{5}$ correspond to a positive value of Δ^′, which is in agreement with the simulation where the m_y≥6 are stable in the linear phase (see discussion below). In Fig. 5a, we plot the profile of the fastest growing eigenmode (corresponding to m=2) of the x component of the magnetic field fluctuation δb_x. The plot is along the inhomogeneous x direction at five different times (see the legend) on a log scale. The two red vertical dashed lines indicate the spatial window of the equilibrium represented in Fig. 3. This shows that after an initial transient that is needed to set up the normal mode shape, the reconnection instability develops around the region where the magnetic field reverts, $\mathrm{0}\le x\le \mathrm{16}$ (see also Fig. 3). As the equilibrium is asymmetric, in particular regarding the cold and hot ion density that vary in a different location with respect to the point where the magnetic field inverts, the eigenmode is not symmetric considering the point where the magnetic field inverts, X_n≃6.4. To the best of our knowledge, this is the first time that the reconnection instability has been investigated in the framework of a three-fluid approach in a nonsymmetric equilibrium directly representing the large-scale configuration taken from a satellite data event. Our goal here is to present the possibility of setting up a “realistic” large-scale initial equilibrium configuration to be simulated by a three-fluid approach. The nonlinear development of the system and, in particular, the mixing efficiency will be the subject of future work. Still, in Fig. 5b, we plot the eigenmodes growth vs. time in normalized units (log scale). We see the exponential growth of the first five modes, $m_y=\mathrm{1},\mathrm{\dots },\mathrm{5}$. Modes with $m_y=\mathrm{6},\mathrm{7}$ are instead stable. The orange curve corresponds to the most unstable mode, m_y=2, which is plotted in panel (a). Despite the strong inhomogeneity of the system where, as discussed before, the magnetic inversion and the density variations occur at different locations, we see very clear exponential growth with a constant growth rate. The linear phase lasts until about t≃1000, after which the nonlinear phase begins. The growth rate values of the five unstable modes are reported in Fig. 5c, confirming the theoretical trend shown in Fig. 4. In particular, m_y=2 is the most unstable mode. In Fig. 6, we show the shaded iso-contours of the cold ion population, N_i,c, at the beginning of the saturated phase, t=1455. We see the formation of a hole structure corresponding to the region where the cold ion density grows and eventually reaches the asymptotic magnetosheath value. To show the cold density hole, we cut along the inhomogeneous x direction at y=38 (see dashed line in the bottom frame of Fig. 6). In Fig. 7, we show the same quantities for the hot ion fluctuations. We see “complementary” behavior in the sense that a bump is now generated more or less in correspondence with the cold ion hole. However, as already discussed, it is not the goal of this paper to study the nonlinear dynamics and mixing properties of the cold and hot ion populations. Our aim here is limited to presenting a method able to obtain a “realistic” three-fluid equilibrium starting from a set of satellite data that can be used as an initial condition for the investigation of the dynamics in the framework of a three-fluid approach.

Figure 6 Shaded iso-contours of the cold ion fluctuations, $N_{\mathrm{i},\mathrm{c}}-N_{\mathrm{i},\mathrm{c}}(t=\mathrm{0})$ at $t=\mathrm{1455}{\mathrm{\Omega }}_i^{-\mathrm{1}}$. The bottom panel shows a plot of the same quantities vs. x at y≃39, corresponding to the horizontal dashed line in the shaded iso-contours. Numerical values are normalized to the magnetosheath density N_MSh∼10 cm⁻³.

Figure 7 Same as in Fig. 6 but for the hot ion fluctuations, $N_{\mathrm{i},\mathrm{h}}-N_{\mathrm{i},\mathrm{h}}(t=\mathrm{0})$.

6 Conclusions

The huge number of spacecraft data available today offers a lot of information about the magnetopause, especially those from the MMS mission due to their high-resolution particle data. Thus, magnetopause modeling can now be improved in view of these observations, which show that this boundary is never the simple textbook boundary generally considered. Beyond the natural asymmetry in temperature and density between the magnetosphere and magnetosheath plasmas, the first important ingredient to consider is the strong velocity shear that arises at the boundary as well as the magnetic shear which is a defining property of the magnetopause. Furthermore, the gradients concerning the particles and those concerning the magnetic field generally have different locations and show different scale lengths. Therefore, the model also has to be able to take these characteristics into account.

In this paper, for the first time, we present a three-fluid equilibrium directly derived from data using a magnetopause crossing by MMS. The derivation of the model is based on a fit of the experimental data to the most reliable data, which is completed by a “realistic” solution of the equilibrium fluid equations for the others. The relative densities of the hot and cold ion populations calculated using the equilibrium equations provide an a posteriori check of our three-fluid model. In particular, this information helps to understand the different bulk quantities observed in the ion distribution functions (see Fig. 1d).

Furthermore, a preliminary study shows that the model can be implemented in a three-fluid numerical simulation, validating the correctness of the equilibrium solution. The detailed study of the long time evolution of the magnetopause instability will be the subject of future work.

It may seem contradictory to consider the data as characteristic of some magnetopause equilibrium and observe afterward that this equilibrium is not stable and should not last for long (even if the reconnection phenomenon is never “immediate”). To justify this point, one must understand that the main characteristics that are taken into account are the asymptotic values on each side and, in particular, the velocity shear between the magnetosheath and magnetosphere. These conditions are not changed by the instability. On the contrary, the positions and the scale of the different gradients can indeed be partly modified by the instability. We think that this is one of the interesting issues that can be investigated by the time evolution observed in the simulation. However the following questions are issues that will be resolved in future work: how is the system stability impacted? (A parametric study is needed.) How does the system change in time due to nonlinear effects? Will the simulation converge toward a new more stable equilibrium state representative of the real system?

Investigating the magnetopause stability and trying to understand topics such as when and where reconnection phenomena can be triggered and how the plasmas from both sides can be mixed are still currently challenging issues to attack using numerical simulations. However, knowing that the stability of a physical system is given by the specific initial equilibrium state, it must be kept in mind that the resulting nonlinear dynamics, in particular the mixing properties, also strongly depend on the choice of the initial equilibrium. As a consequence, it is very important to initialize a simulation with a configuration that is as realistic as possible. In most of the published literature, simulations have been initialized with relatively simple configurations, such as Harris sheets or modified Harris sheets, with little relationship to the real magnetopause. Therefore, the realistic three-fluid equilibrium presented in this paper should allow for this work to be taken a step further, and the same method could be applied to other experimental cases in the future.