Estimating the maximum of the smoothed highest 3-hourly aa index in 3 d by the preceding minimum for the solar cycle

Predicting the maximum intensity of geomagnetic activity for an upcoming solar cycle is important in space weather service and for planning future space missions. This study analyzed the highest and lowest 3-hourly aa index (aa_H∕aa_L) in a 3 d interval, smoothed by 363 d to analyze their variation with the 11-year solar cycle. It is found that the maximum of aa_H ($a{a}_{{\mathrm{H}}_{\max }}$) is well correlated with the preceding minimum of either aa_H ($a{a}_{{\mathrm{H}}_{\min }}$, r=0.85) or aa_L ($a{a}_{{\mathrm{L}}_{\min }}$, r=0.89) for the solar cycle. Based on these relationships, the intensity of $a{a}_{{\mathrm{H}}_{\max }}$ for solar cycle 25 is estimated to be $a{a}_{{\mathrm{H}}_{\max }}\left(\mathrm{25}\right)=\mathrm{83.7}\pm \mathrm{6.9}$ (nT), about 29 % stronger than that of solar cycle 24. This value is equivalent to the ap index of $a{p}_{\max }\left(\mathrm{25}\right)=\mathrm{47.4}\pm \mathrm{4.4}$ (nT) if employing the high correlation between ap and aa (r=0.93). The maximum of aa_L ($a{a}_{{\mathrm{L}}_{\max }}$) is also well correlated with the preceding $a{a}_{{\mathrm{H}}_{\min }}$ (r=0.80). The maximum amplitude of the sunspot cycle (R_m) is much better correlated with high geomagnetic activity ($a{a}_{{\mathrm{H}}_{\max }}$, r=0.79) than with low geomagnetic activity ($a{a}_{{\mathrm{L}}_{\max }}$, r=0.37). The rise time from $a{a}_{{\mathrm{H}}_{\min }}$ to $a{a}_{{\mathrm{H}}_{\max }}$ is weakly anti-correlated to the following $a{a}_{{\mathrm{H}}_{\max }}$ ($r=-\mathrm{0.42}$). Similar correlations are also found for the 13-month smoothed monthly mean aa index. These results are expected to be useful in understanding the geomagnetic activity intensity of solar cycle 25.

1 Introduction

Studying and predicting geomagnetic activity are important in both geophysics and space weather. Severe geomagnetic activity may cause intense geomagnetic storms (Gonzalez et al., 1989, 1994; Chen et al., 2019), leading to disruptions in communication and deviations of orbital motions of satellites (Yoshida and Yamagishi, 2010; Petrovay, 2020). Now that the old solar cycle 24 is over, satellite and spacecraft-related departments want to know the maximum intensity of both solar and geomagnetic activity in the new solar cycle 25 for planning future space missions.

Among various indices to quantitatively describe geomagnetic activity, the aa index (Mayaud, 1972), derived from the 3-hourly K index at two near-antipodal midlatitude stations in England and Australia, is the longest time series (since 1868) and has been widely used to analyze the long-term trend of global geomagnetic activity (Russell and Mulligan, 1995; Marat et al., 2017; Du, 2011b; El-Borie et al., 2019) and its correlation with both climate change (Cliver et al., 1998; Dobrica et al., 2009; Gavrilyeva et al., 2017) and solar activity (Echer et al., 2004; Prestes et al., 2006; Lukianova et al., 2009; Du, 2011a, c; Du and Wang, 2012a; Singh and et al., 2019). The minimum aa index (aa_min), at or near the minimum of the solar cycle, has been widely used to predict the maximum amplitude of the sunspot cycle (R_m), the so-called Ohl's precursor method (Brown and Williams, 1969; Ohl and Ohl, 1979; Du et al., 2009). But it is seldom used to directly predict the maximum aa index (aa_max) of an ensuing solar cycle.

The planetary geomagnetic index Ap (available since 1932, Bartels, 1963), derived from the average of the measurements at 13 observatories around the globe, is a daily measure of the response of geomagnetic field to variations in the interplanetary magnetic field (IMF) and the solar wind (Li, 1997; McPherron, 1999; Tsurutani et al., 2006). It is the main global magnetic index forecasted by government agencies (McPherron, 1999). Most works on forecasting the geomagnetic activity have been over short intervals, on the order of hours or days (McPherron, 1999; Abunina et al., 2013). In the earlier years, Kane (1988) pointed out that it is impossible to forecast long-term geomagnetic activity through analyzing the daily, monthly, and annual Ap and aa indices. Gordon (2015) demonstrated that long-term geomagnetic activity can only be predicted to within a limited threshold of accuracy due to the irregular trends and cycles in the annual data and nonlinear variability in the monthly series, through analyzing the aa index.

In this study, we analyze the relationship between the maximum aa index and its preceding minimum for the 11-year solar cycle. The data and parameters used in this study are described in Sect. 2. We find out the highest and lowest 3-hourly aa index (aa_H∕aa_L) in each 3 d interval, smoothed by 363 d (121 points) to analyze their variation with the solar cycle. In Sect. 3, it is found that the maximum of aa_H ($a{a}_{{\mathrm{H}}_{\max }}$) is well correlated with the preceding minimum of either aa_H ($a{a}_{{\mathrm{H}}_{\min }}$) or aa_L ($a{a}_{{\mathrm{L}}_{\min }}$) for the solar cycle (Sect. 3.1), which can be used to estimate the intensity of $a{a}_{{\mathrm{H}}_{\max }}$ for solar cycle 25. The maximum of aa_L ($a{a}_{{\mathrm{L}}_{\max }}$) is also found to be well correlated with the preceding $a{a}_{{\mathrm{H}}_{\min }}$ (Sect. 3.2). The rise time from $a{a}_{{\mathrm{H}}_{\min }}$ to $a{a}_{{\mathrm{H}}_{\max }}$ is only weakly anti-correlated to the following $a{a}_{{\mathrm{H}}_{\max }}$ (Sect. 3.3). Using the relationship between ap and aa, the maximum intensity of the ap index for solar cycle 25 is estimated (Sect. 3.4). Similar correlations are analyzed using the 13-month smoothed (with half weight at the two ends) monthly mean aa index (Sect. 4). Some conclusions are discussed and summarized in Sect. 5.

Figure 1 (a) The highest (aa_H) and (b) lowest (aa_L) 3-hourly aa index in each 3 d.

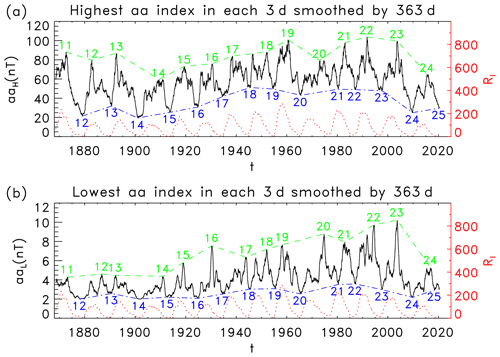
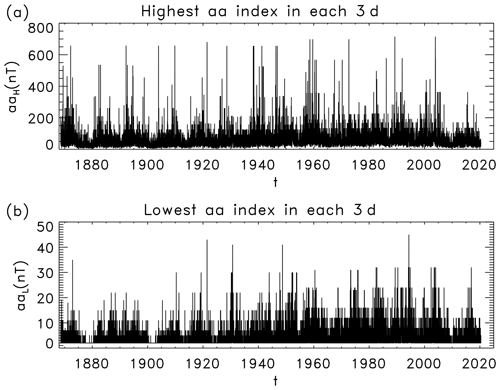
Figure 2 (a) The highest (aa_H) and (b) lowest (aa_L) 3-hourly aa index in each 3 d (black solid), smoothed by 121 points (363 d). The numbers in the figure represent the 11-year solar cycles. The upper dashed and lower dashed–dotted lines indicate the maxima and minima, respectively, of the solar cycle. The dotted red line shows the 13-month smoothed monthly mean sunspot number (R_I) for comparison.

2 Data

We use the 3-hourly aa index (in units of nT) since 1 January 1868 (updated to 10 October 2020) from the International Service of Geomagnetic Indices (ISGI; http://isgi.unistra.fr/, last access: 10 October 2020). We find out the highest and lowest aa index (aa_H∕aa_L) from 24 values of the 3-hourly aa index in each 3 d interval, as shown in Fig. 1. The values of aa_H are in the range [5, 715] nT, and those of aa_L are in the range [2, 45] nT.

It is seen in the figure that both aa_H and aa_L vary dramatically: the average absolute differences of the adjacent values are 36.7 and 2.5 nT, respectively. It is hard to see the variation in aa_H or aa_L with the solar cycle. In particular, most (63 %) values of aa_L are the minimum (2 nT). In order to analyze the long-term trend of aa with the solar cycle conventionally represented by the 13-month smoothed monthly mean sunspot number, both aa_H and aa_L are smoothed by w=121 points (363 d) using the following running smoothing technique:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}\stackrel{\mathrm{‾}}{x}\left(i\right)& ={\displaystyle \frac{\mathrm{1}}{w}}\sum _{j=-(w-\mathrm{1})/\mathrm{2}}^{(w-\mathrm{1})/\mathrm{2}}x(i+j),\\ i& =(w-\mathrm{1})/\mathrm{2},\mathrm{\dots },N_{\mathrm{0}}-(w-\mathrm{1})/\mathrm{2},\end{array}\end{array}$$

for x=aa_H and aa_L (N₀=18600). There are $N=N_{\mathrm{0}}-(w-\mathrm{1})=\mathrm{18480}$ data points left after removing the (w−1) incomplete smoothing points at the two ends of the series, as shown in Fig. 2 (solid). The smoothed monthly mean (w=13 months with half weight at the two ends) international sunspot number series (R_I; Clette et al., 2016),

$$\begin{array}{}\text{(2)}& R_{\mathrm{I}}\left(i\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{12}}}\left({\displaystyle \frac{R(i-\mathrm{6})}{\mathrm{2}}}+\sum _{j=-\mathrm{5}}^{\mathrm{5}}R(i+j)+{\displaystyle \frac{R(i+\mathrm{6})}{\mathrm{2}}}\right),\end{array}$$

of the second version (http://www.sidc.be/silso/datafiles, last access: 10 October 2020) is used for comparison (dotted), where R represents the (non-smoothed) monthly value (Petrovay, 2020). The smoothing width is selected to be w=121 points (363 d) as it is close to that (1 year = 12 months) used in the smoothing of R_I.

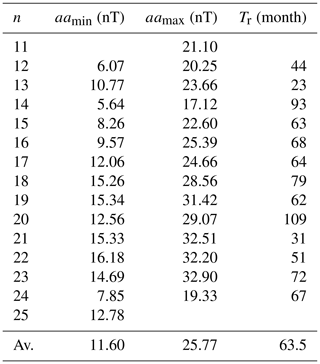
Table 1 The minimum ($a{a}_{{\mathrm{H}}_{\min }}$) and maximum ($a{a}_{{\mathrm{H}}_{\max }}$) of the 363 d smoothed highest 3-hourly aa index (aa_H) in each 3 d, the rise time from $a{a}_{{\mathrm{H}}_{\min }}$ to $a{a}_{{\mathrm{H}}_{\max }}$ (T_r), the minimum ($a{a}_{{\mathrm{L}}_{\min }}$) and maximum ($a{a}_{{\mathrm{L}}_{\max }}$) of 363 d smoothed lowest 3-hourly aa index (aa_L) in each 3 d, and the maximum (R_m) of 13-month smoothed monthly mean R_I for solar cycles 11–25.

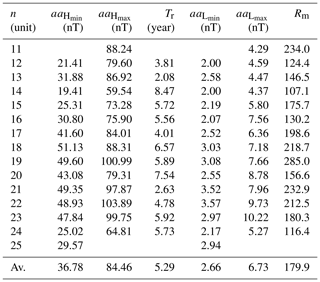
In panel a of the figure, the dashed (dashed–dotted) line indicates the maximum (minimum) of aa_H, $a{a}_{{\mathrm{H}}_{\max }}$ ($a{a}_{{\mathrm{H}}_{\min }}$). In panel b, the dashed (dashed–dotted) line indicates the maximum (minimum) of aa_L, $a{a}_{{\mathrm{L}}_{\max }}$ ($a{a}_{{\mathrm{L}}_{\min }}$). The value of $a{a}_{{\mathrm{H}}_{\max }}$ ($a{a}_{{\mathrm{L}}_{\max }}$) is the maximum of aa_H (aa_L) during the time period between two adjacent solar cycle minima (R_min) determined by the smoothed monthly mean R_I. The value of $a{a}_{{\mathrm{H}}_{\min }}$ ($a{a}_{{\mathrm{L}}_{\min }}$) is the minimum of aa_H (aa_L) during the time period between two adjacent maxima, $a{a}_{{\mathrm{H}}_{\max }}$ ($a{a}_{{\mathrm{L}}_{\max }}$). These parameters are displayed in Table 1, in which T_r is the rise time from $a{a}_{{\mathrm{H}}_{\min }}$ to $a{a}_{{\mathrm{H}}_{\max }}$ and R_m the maximum of R_I for the 11-year solar cycle. The last row denotes the averages of the parameters.

3 Result

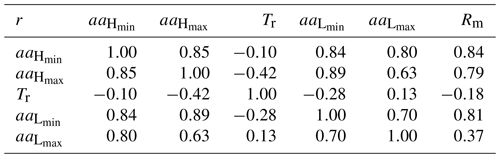
The correlation coefficients between the parameters in Table 1 are listed in Table 2 for comparison. It is seen in Table 2 that R_m is well correlated with $a{a}_{{\mathrm{H}}_{\min }}$ (r=0.84), $a{a}_{{\mathrm{H}}_{\max }}$ (r=0.79), and $a{a}_{{\mathrm{L}}_{\min }}$ (r=0.81) and positively correlated with $a{a}_{{\mathrm{L}}_{\max }}$ (r=0.37). This implies that the stronger the solar activity (R_I), the higher the geomagnetic activity (aa). But the maximum amplitude of sunspot cycle (R_m) is much better correlated with high geomagnetic activity ($a{a}_{{\mathrm{H}}_{\max }}$, r=0.79) than with low geomagnetic activity ($a{a}_{{\mathrm{L}}_{\max }}$, r=0.37), implying that low geomagnetic activity depends less on the solar activity than the high one does. The correlation between R_m and $a{a}_{{\mathrm{H}}_{\min }}$ ($a{a}_{{\mathrm{L}}_{\min }}$), r=0.84 (0.81), is related to Ohl's precursor method (Ohl and Ohl, 1979) for predicting R_m. Some other correlations are analyzed to estimate $a{a}_{{\mathrm{H}}_{\max }}$ (Sect. 3.1), $a{a}_{{\mathrm{L}}_{\max }}$ (Sect. 3.2), and T_r (Sect. 3.3).

Table 2 Correlation coefficients between the parameters in Table 1.

Figure 3 Scatter plots of $a{a}_{{\mathrm{H}}_{\max }}$ against $a{a}_{{\mathrm{H}}_{\min }}$ (a) and $a{a}_{{\mathrm{L}}_{\min }}$ (b).

3.1 Relationship between $a{a}_{{\mathrm{H}}_{\max }}$ and its preceding $a{a}_{{\mathrm{H}}_{\min }}/a{a}_{{\mathrm{L}}_{\min }}$

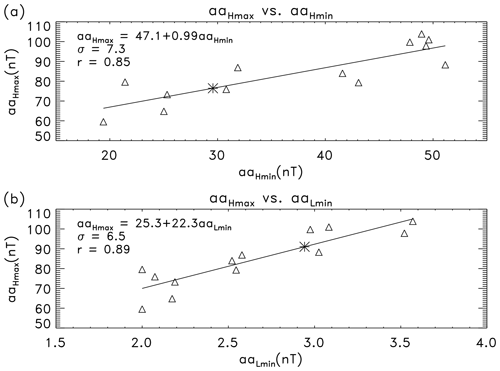
One can see in Table 2 that $a{a}_{{\mathrm{H}}_{\max }}$ is well correlated with its preceding $a{a}_{{\mathrm{H}}_{\min }}$ (r=0.85) and $a{a}_{{\mathrm{L}}_{\min }}$ (r=0.89), as shown in Fig. 3 for the scatter plots of $a{a}_{{\mathrm{H}}_{\max }}$ against $a{a}_{{\mathrm{H}}_{\min }}$ (a) and $a{a}_{{\mathrm{L}}_{\min }}$ (b). The solid lines represent the linear fits of $a{a}_{{\mathrm{H}}_{\max }}$ to $a{a}_{{\mathrm{H}}_{\min }}$ and $a{a}_{{\mathrm{L}}_{\min }}$ with the least-squares fit regression equations given by

$$\begin{array}{}\text{(3)}& {\displaystyle }a{a}_{{\mathrm{H}}_{\max }}=\mathrm{47.1}\pm \mathrm{7.1}+(\mathrm{0.99}\pm \mathrm{0.18})a{a}_{{\mathrm{H}}_{\min }},\mathit{\sigma }=\mathrm{7.3},\text{(4)}& {\displaystyle }a{a}_{{\mathrm{H}}_{\max }}=\mathrm{25.3}\pm \mathrm{9.5}+(\mathrm{22.3}\pm \mathrm{3.5})a{a}_{{\mathrm{L}}_{\min }},\mathit{\sigma }=\mathrm{6.5},\end{array}$$

where ± indicates the 1σ deviation of the fitting coefficient, and σ is the standard deviation of the regression.

Based on the above relationships, the minimum aa index (around the solar minimum) can be used as an indicator to estimate the following maximum. One can estimate $a{a}_{{\mathrm{H}}_{\max }}$ for solar cycle 25 by substituting the values of $a{a}_{{\mathrm{H}}_{\min }}$ (29.57 nT) and $a{a}_{{\mathrm{L}}_{\min }}$ (2.94 nT) into the above equations,

$$\begin{array}{}\text{(5)}& {\displaystyle }a{a}_{{\mathrm{H}}_{\max \mathrm{1}}}\left(\mathrm{25}\right)=\mathrm{76.4}\pm \mathrm{7.3}\left(\mathrm{nT}\right),\mathrm{from}a{a}_{{\mathrm{H}}_{\min }},\text{(6)}& {\displaystyle }a{a}_{{\mathrm{H}}_{\max \mathrm{2}}}\left(\mathrm{25}\right)=\mathrm{91.0}\pm \mathrm{6.5}\left(\mathrm{nT}\right),\mathrm{from}a{a}_{{\mathrm{L}}_{\min }}\end{array}$$

(labeled by asterisks in Fig. 3a and b). Since these values are derived by the fitting equations (Eq. 3) with similar correlation coefficients (0.85 and 0.89), we take their average,

$$\begin{array}{}\text{(7)}& \begin{array}{rl}a{a}_{{\mathrm{H}}_{\max }}\left(\mathrm{25}\right)& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left[a{a}_{{\mathrm{H}}_{\max \mathrm{1}}}\right(\mathrm{25})+a{a}_{{\mathrm{H}}_{\max \mathrm{2}}}(\mathrm{25}\left)\right]\\ & =\mathrm{83.7}\pm \mathrm{6.9}\left(\mathrm{nT}\right),\end{array}\end{array}$$

as an estimate of $a{a}_{{\mathrm{H}}_{\max }}\left(\mathrm{25}\right)$. It implies that the 363 d smoothed highest 3-hourly aa index in a 3 d interval during the maximum period of solar cycle 25 is estimated to be close to the average (84.46 nT) over the past cycles (Table 1) but higher than that (64.81 nT) of solar cycle 24 by about 29.2 %.

It should be pointed out that the above estimate may be an upper limit of $a{a}_{{\mathrm{H}}_{\max }}\left(\mathrm{25}\right)$ as the values of $a{a}_{{\mathrm{H}}_{\min }}\left(\mathrm{25}\right)$ and $a{a}_{{\mathrm{L}}_{\min }}\left(\mathrm{25}\right)$ may not be finally determined (refer to Discussion in Sect. 5). Although we are not quite sure if the current aa_H (aa_L), 30.69 (3.13) in April 2020, would decrease to a smaller value than that (29.57 (2.94)) used in the current work, there would not be significant variations in $a{a}_{{\mathrm{H}}_{\min }}$, aa_Lmiin, and the above estimate because solar cycle 25 (in terms of the smoothed monthly mean R_I) already started (December 2019) a few months ago.

3.2 Relationship between $a{a}_{{\mathrm{L}}_{\max }}$ and the preceding $a{a}_{{\mathrm{H}}_{\min }}$

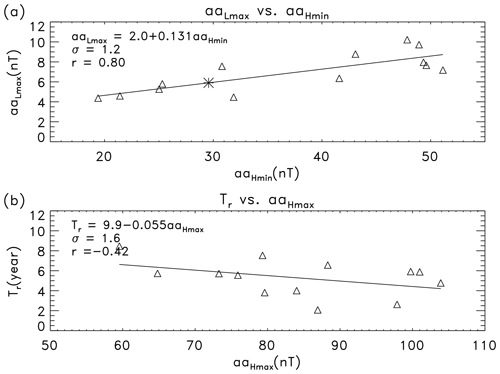
One can also see in Table 2 that $a{a}_{{\mathrm{L}}_{\max }}$ is well correlated with the preceding $a{a}_{{\mathrm{H}}_{\min }}$ (r=0.80) or $a{a}_{{\mathrm{L}}_{\min }}$ (r=0.70). Figure 4a shows the scatter plot of $a{a}_{{\mathrm{L}}_{\max }}$ against $a{a}_{{\mathrm{H}}_{\min }}$. The linear fitting equation of $a{a}_{{\mathrm{L}}_{\max }}$ to $a{a}_{{\mathrm{H}}_{\min }}$ (solid) is

$$\begin{array}{}\text{(8)}& a{a}_{{\mathrm{L}}_{\max }}=\mathrm{2.0}\pm \mathrm{1.2}+(\mathrm{0.131}\pm \mathrm{0.030})a{a}_{{\mathrm{H}}_{\min }},\mathit{\sigma }=\mathrm{1.2}.\end{array}$$

Substituting $a{a}_{{\mathrm{H}}_{\min }}\left(\mathrm{25}\right)=\mathrm{29.57}$ (nT) into this equation, one can estimate the 363 d smoothed lowest 3-hourly aa index in a 3 d interval during the maximum period of solar cycle 25, $a{a}_{{\mathrm{L}}_{\max }}=\mathrm{5.9}\pm \mathrm{1.2}$ (nT). This value is slightly lower than the average (6.73 nT) over the past cycles but higher than that (5.27 nT) of solar cycle 24 by 12.0 %.

3.3 Relationship between the rise time and the following maximum

Now, we analyze if the rise time of the aa geomagnetic index for the solar cycle is correlated with the following maximum so that it can be used to estimate the rise time, as is often the case in the solar (sunspot) cycle (Waldmeier, 1939).

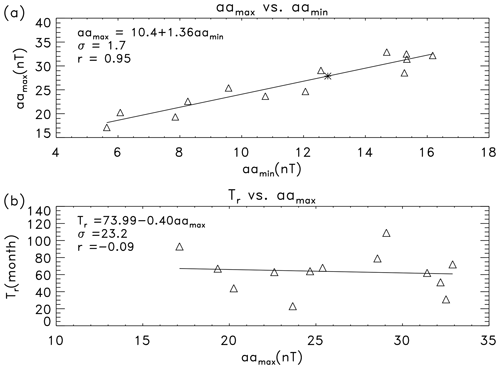
Figure 4b shows the scatter plot of the rise time (T_r) from $a{a}_{{\mathrm{H}}_{\min }}$ to $a{a}_{{\mathrm{H}}_{\max }}$ for the solar cycle against its following maximum ($a{a}_{{\mathrm{H}}_{\max }}$). The solid line indicates the linear fit of T_r to $a{a}_{{\mathrm{H}}_{\max }}$ by

$$\begin{array}{}\text{(9)}& T_{\mathrm{r}}=\mathrm{9.9}\pm \mathrm{3.0}-(\mathrm{0.055}\pm \mathrm{0.036})a{a}_{{\mathrm{H}}_{\max }},\mathit{\sigma }=\mathrm{1.6}\left(\mathrm{year}\right).\end{array}$$

The anti-correlation coefficient between T_r and $a{a}_{{\mathrm{H}}_{\max }}$, $r=-\mathrm{0.42}$ (at a confidence level of about 84 %), is so weak that it can hardly be used to estimate the rise time (T_r). If the rise time is computed from the minimum (R_min) of the sunspot cycle to $a{a}_{{\mathrm{H}}_{\max }}$, the correlation is even weaker, $r=-\mathrm{0.14}$.

Figure 4 Scatter plots of $a{a}_{{\mathrm{L}}_{\max }}$ against $a{a}_{{\mathrm{H}}_{\min }}$ (a) and T_r against $a{a}_{{\mathrm{H}}_{\max }}$ (b).

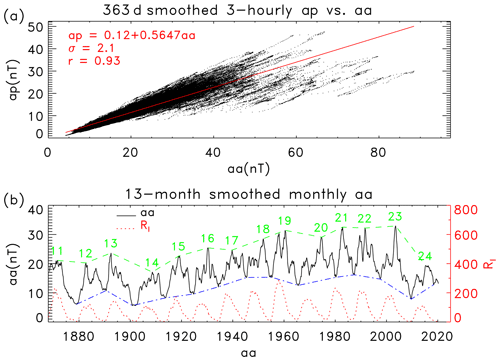
Figure 5 (a) Scatter plot of the 363 d smoothed 3-hourly ap against aa (dots) and the linear fit (solid). (b) The 13-month smoothed monthly mean aa (solid) and R_I (dotted). The numbers in the figure indicate the solar cycles. The upper dashed and lower dashed–dotted lines indicate the maximum (aa_max) and minimum (aa_min) of aa, respectively, for the solar cycle.

3.4 Relationship between ap and aa

Another important index often used to evaluate geomagnetic activity is the ap index (https://www.gfz-potsdam.de/en/kp-index, last access: 30 April 2018). Similar correlations as those for the aa index can also be obtained. But the ap index is available only from 1932 to April 2018. In this section, we employ the relationship between ap  and aa to estimate the maximum intensity of the ap index for solar cycle 25 from the previous result. Figure 5a shows the scatter plot of the 363 d smoothed 3-hourly ap against aa (dots). The solid line represents the linear fit of ap to aa by

$$\begin{array}{}\text{(10)}& ap=\mathrm{0.12}\pm \mathrm{0.01}+(\mathrm{0.5647}\pm \mathrm{0.0005})aa,\mathit{\sigma }=\mathrm{2.1}.\end{array}$$

It is obvious that ap is highly correlated with aa, r=0.93, as they are based on the same observations.

According to this equation, the estimated $a{a}_{{\mathrm{H}}_{\max }}\left(\mathrm{25}\right)=\mathrm{83.7}\pm \mathrm{6.9}$ (nT) in Sect. 3.1 is equivalent to $a{p}_{\max }\left(\mathrm{25}\right)=\mathrm{47.4}\pm \mathrm{3.9}\pm \mathrm{2.1}=\mathrm{47.4}\pm \mathrm{4.4}$ (nT), in which ±3.9 is derived from the uncertainty (±6.9) of $a{a}_{{\mathrm{H}}_{\max }}\left(\mathrm{25}\right)$, ±2.1 is the standard deviation of the regression, and $\sqrt{{\mathrm{3.9}}^{\mathrm{2}}+{\mathrm{2.1}}^{\mathrm{2}}}=\mathrm{4.4}$.

Table 3 Parameters of the 13-month smoothed monthly mean aa for the solar cycle.

4  Result for the 13-month smoothed monthly mean aa index

Finally, in this section, we simply analyze the previous correlations using the 13-month smoothed monthly mean aa index, as shown in Fig. 5b. The upper dashed and lower dashed–dotted lines indicate the maximum (aa_max) and minimum (aa_min) of the aa index, respectively, for the solar cycle. The value of aa_max is the maximum of aa during the time period between two adjacent solar cycle minima (R_min) determined by the smoothed monthly mean R_I (dotted). The value of aa_min is the minimum of aa during the time period between two adjacent maxima, aa_max. The parameters are listed in Table 3, in which T_r is the rise time from aa_min to aa_max.

Figure 6 Scatter plots of aa_max against aa_min (a) and T_r against aa_max (b).

Figure 6a shows the scatter plot of aa_max against aa_min (triangles). The solid line indicates the linear fit of aa_max to aa_min by

$$\begin{array}{}\text{(11)}& a{a}_{\max }=\mathrm{10.4}\pm \mathrm{1.7}+(\mathrm{1.36}\pm \mathrm{0.14})a{a}_{\min },\mathit{\sigma }=\mathrm{1.7}.\end{array}$$

The correlation coefficient between aa_max and aa_min is r=0.95 (at a confidence level greater than 99 %), slightly higher than that (r=0.85 (0.89)) for the correlation between $a{a}_{{\mathrm{H}}_{\max }}$ and $a{a}_{{\mathrm{H}}_{\min }}$ ($a{a}_{{\mathrm{L}}_{\min }}$) in Fig. 3 using the 363 d smoothed highest (lowest) 3-hourly aa index in a 3 d interval.

Substituting aa_min(25)=12.78 into this equation, one can estimate $a{a}_{\max }\left(\mathrm{25}\right)=\mathrm{27.9}\pm \mathrm{1.7}$ (asterisk in Fig. 6a), about 44 % higher than that (19.33) of solar cycle 24. This estimate is similar to the case in Sect. 3.1 that the estimate (91.0) of $a{a}_{{\mathrm{H}}_{\max }}\left(\mathrm{25}\right)$ from $a{a}_{{\mathrm{L}}_{\min }}$ in Eq. (5) is about 40 % higher than that (64.81 nT) of solar cycle 24 using the minimum of the 363 d smoothed lowest 3-hourly aa index in a 3 d interval.

Figure 6b shows the scatter plot of the rise time (T_r) from aa_min to aa_max against the maximum (aa_max). The data points are very scattered, and T_r is nearly uncorrelated to the following aa_max, $r=-\mathrm{0.09}$. Therefore, this correlation is unable to be used to estimate the rise time of aa_max.

5 Discussion and conclusions

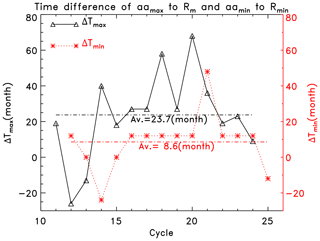
It is well known that the aa index is positively correlated with solar activity (as represented by R_I), since the latter is the main source of the former (Legrand and Simon, 1981; Feynman, 1982; Echer et al., 2004). In general, the stronger the solar activity, the higher the (aa) geomagnetic activity. However the relationship between aa and R_I is not a simple linear one (Borello-Filisetti et al., 1992; Mussino et al., 1994; Kishcha et al., 1999; Lockwood et al., 1999; Echer et al., 2004; Tsurutani et al., 2006; Du, 2011a, c, 2020). The aa index tends to lag behind R_I about 2–3 years around a solar cycle maximum (Wang et al., 2000; Echer et al., 2004) and (only) about 1 year around a solar cycle minimum (Legrand and Simon, 1981; Wang and Sheeley, 2009; Du, 2011b), as indicated in Fig. 7 for the time difference (ΔT_max) of the 13-month smoothed monthly mean aa_max to R_m (a) and that (ΔT_min) of aa_min to R_min (b). The intensity of geomagnetic activity can only be roughly evaluated from that of solar (sunspot) activity, as the linear correlation coefficient between the smoothed monthly mean aa and R_I is only 0.61 (Du, 2011c) or even lower (0.43) if using the non-smoothed series (Du, 2011b). In addition, future solar activity is also unknown at the current time, and so it can not be directly used to estimate future geomagnetic activity.

Figure 7 The time difference between aa_max and R_m (a) and that between aa_min and R_min (b).

There are many methods that can be used to predict the maximum amplitude of the sunspot cycle (R_m), such as (i) statistical methods, employing the relationship between the inter-cycle parameters (Thompson, 1988; Hathaway et al., 1994) or the early rising rate (Thompson, 1988; Cameron and Schüssler, 2008; Du and Wang, 2012b); (ii) functional methods, using mathematical functions of a few parameters (Hathaway et al., 1994; Du, 2011d) for extrapolating the following monthly values; (iii) geomagnetic precursor methods (Brown and Williams, 1969; Ohl and Ohl, 1979; Du et al., 2009), using the geomagnetic activity near the solar minimum; and (iv) solar precursor methods (Schatten et al., 1978; Pesnell and Schatten, 2018), using the previous cycle's polar field.

In contrast, there are fewer methods found to predict the maximum amplitude of the geomagnetic activity index for the 11-year solar cycle. Geomagnetic activity forecast has been over the order of hours or days (McPherron, 1999; Abunina et al., 2013). The annual or monthly prediction of geomagnetic activity is within a limited accuracy (over 20 %) due to irregular variation in the time series (McPherron, 1999; Gordon, 2015). In the earlier years, Kane (1988) even pointed out that it is impossible to forecast long-term geomagnetic activity through analyzing the time series of the Ap and aa index (refer also to Gordon, 2015). Geomagnetic activity near the solar minimum or at the decreasing phase of the solar cycle has been widely used to predict the maximum amplitude of the sunspot cycle but was seldom used to predict the maximum amplitude of the geomagnetic activity itself.

In the current work, we analyzed the highest (aa_H) and lowest (aa_L) 3-hourly aa index in each 3 d interval, smoothed by 363 d (121 points) to analyze their variation with the solar cycle represented by the 13-month smoothed monthly mean R_I. It is found that the maximum of aa_H ($a{a}_{{\mathrm{H}}_{\max }}$) is well correlated with the preceding minimum of either aa_H ($a{a}_{{\mathrm{H}}_{\min }}$, r=0.85) or aa_L ($a{a}_{{\mathrm{L}}_{\min }}$, r=0.89) for the 11-year solar cycle. So, these relationships can be used to estimate the maximum intensity of geomagnetic activity for the solar cycle by employing the time series itself, $a{a}_{{\mathrm{H}}_{\max }}\left(\mathrm{25}\right)=\mathrm{83.7}\pm \mathrm{6.9}$ (nT). It implies that the maximum intensity of geomagnetic activity for solar cycle 25 would be similar to the average over the past cycles but higher than that of solar cycle 24 by about 29.2 %. Certainly, this estimate may be an upper limit, as $a{a}_{{\mathrm{H}}_{\min }}$ and $a{a}_{{\mathrm{L}}_{\min }}$ may be finally determined a few months after the solar minimum (Fig. 7).

Similar results can also be obtained if using the ap index. However, the ap index is available only up to April 2018. So, we employed the relationship between ap and aa to estimate the maximum ap index for solar cycle 25: $a{p}_{\max }\left(\mathrm{25}\right)=\mathrm{47.4}\pm \mathrm{4.4}$ (nT). For the 13-month smoothed monthly mean aa index, the maximum aa index (aa_max) of the solar cycle is also well correlated to the preceding minimum (aa_min), with a correlation coefficient of r=0.95.

The well-known “Waldmeier effect” (Waldmeier, 1939), describing that the rise time of a solar cycle is well anti-correlated with the following maximum amplitude, has been widely used to estimate the rise or peak time of a solar cycle if the amplitude has been predicted. However, such a correlation is very weak for the geomagnetic activity index. The rise time (T_r) from $a{a}_{{\mathrm{H}}_{\min }}$ to $a{a}_{{\mathrm{H}}_{\max }}$ for the solar cycle is found to be only weakly anti-correlated to the following maximum ($a{a}_{{\mathrm{H}}_{\max }}$), $r=-\mathrm{0.42}$. This weak correlation may be related to the fact that the geomagnetic activity maximum (minimum) is not aligned to the solar (sunspot) activity maximum (minimum) in time (Fig. 7). In most cases, aa_max (aa_min) lags behind R_m (R_min). But in some other cases, aa_max (aa_min) precedes R_m (R_min). The weak correlation between the rise time and the following maximum of geomagnetic activity for the solar cycle can hardly be used to estimate the former.

According to the analysis above, the following conclusions may be summarized.

1. The 363 d smoothed highest (aa_H) and lowest (aa_L) 3-hourly aa index in a 3 d interval are analyzed, finding that the maximum of aa_H ($a{a}_{{\mathrm{H}}_{\max }}$) is well correlated with the preceding minimum of either aa_H ($a{a}_{{\mathrm{H}}_{\min }}$, r=0.85) or aa_L ($a{a}_{{\mathrm{L}}_{\min }}$, r=0.89) for the 11-year solar cycle. As a result, the maximum aa index for the current solar cycle 25 is estimated to be $a{a}_{{\mathrm{H}}_{\max }}\left(\mathrm{25}\right)=\mathrm{83.7}\pm \mathrm{6.9}$ (nT), about 29 % higher than that of solar cycle 24. This value is equivalent to the ap index of $a{p}_{\max }\left(\mathrm{25}\right)=\mathrm{47.4}\pm \mathrm{4.4}$ (nT) if using the relationship between ap and aa (Eq. 10).

2. The maximum ($a{a}_{{\mathrm{L}}_{\max }}$) of aa_L is also found to be well correlated with the preceding $a{a}_{{\mathrm{H}}_{\min }}$, r=0.80. Based on this correlation, $a{a}_{{\mathrm{L}}_{\max }}\left(\mathrm{25}\right)$ is estimated to be 5.9±1.2 (nT), about 12 % higher than that of solar cycle 24.

3. The maximum amplitude of the sunspot cycle (R_m) is much better correlated with high geomagnetic activity ($a{a}_{{\mathrm{H}}_{\max }}$, r=0.79) than with low geomagnetic activity ($a{a}_{{\mathrm{L}}_{\max }}$, r=0.37).

4. The rise time (T_r) from $a{a}_{{\mathrm{H}}_{\min }}$ to $a{a}_{{\mathrm{H}}_{\max }}$ is found to be weakly anti-correlated to the following maximum ($a{a}_{{\mathrm{H}}_{\max }}$) for the solar cycle, $r=-\mathrm{0.42}$ at the 84 % confidence level.

5. For the 13-month smoothed monthly mean aa index, the maximum aa index (aa_max) of the solar cycle is well correlated with the preceding minimum (aa_min, r=0.95). The rise time from aa_min to aa_max is nearly uncorrelated to the following maximum ($r=-\mathrm{0.09}$).