Strong southward and northward currents observed in the inner plasma sheet

It is generally believed that field-aligned currents (FACs) and the ring current (RC) are two dominant parts of the inner magnetosphere. However, using the Cluster spacecraft crossing the pre-midnight inner plasma sheet in the latitudinal region between 10 and 30^∘ N, it is found that, during intense geomagnetic storms, in addition to FACs and the RC, strong southward and northward currents also exist which should not be FACs because the magnetic field in these regions is mainly along the x–y plane. Detailed investigation shows that both magnetic-field lines (MFLs) and currents in these regions are highly dynamic. When the curvature of MFLs changes direction in the x–y plane, the current also alternatively switches between being southward and northward. To investigate the generation mechanism of the southward and northward current, we employed the analysis of energetic particle flux up to 1 MeV. For energetic particles below 40 keV, observations from Cluster CIS/CODIF (Cluster Ion Spectrometry COmposition and DIstribution Function analyzer) are used. However, for higher-energy particles, the flux is obtained by extrapolations of low-energy particle data through Kappa distribution. The result indicates that the most reasonable cause of these southward and northward currents is the curvature drift of energetic particles.

1 Introduction

Abundant current systems existing in the Earth's magnetosphere play a very important role in energy transformation in different regions (Kuijpers et al., 2014). Recently, through simulations and observations, numerous studies have shown that the inner-magnetosphere currents have a more complicated structure and distribution than originally thought. For example, in the low latitude, the magnetic-field geometry can be altered significantly into a tail-like shape during storm time (Tsyganenko et al., 2003). One or multiple banana currents can exist in the inner magnetosphere, which makes the link of the current systems more complicated (Liemohn et al., 2013). In the high latitudes, field-aligned currents (FACs) have more sophisticated structures except for the known large-scale region-1 and region-2 currents (Mishin et al., 1997; Dunlop et al., 2015a, b). Therefore, more work is still needed to reveal the true nature of these current systems.

The huge progress in satellite deployments makes it possible for direct observation of the inner-magnetosphere current system. It is believed that the magnetosphere and ionosphere are linked through a ring current (RC) and FACs (e.g., Le et al., 2004; Zhang et al., 2011). Therefore, many investigations are mainly focused on these two current systems, from high (e.g., Iijima and Potemra, 1976, 1978; Wang et al., 2006; Dunlop et al., 2015a) to low latitudes (e.g., Vallat et al., 2005; Shen et al., 2014; Yang et al., 2016). The region from low to middle latitudes, which is the key area for the inner-magnetosphere current link, however, has received less attention. Graphic plots and some statistical results (e.g., Le et al., 2004) show that FACs should be the dominant current in these areas. Through Cluster satellite observations, Vallat et al. (2005) pointed out that the RC could exist at middle (or even high) latitudes. Despite the results achieved by these various research efforts, there are still no findings enabling a conclusion about the complete current morphology in low and middle latitudes. For example, are FACs and the RC the only currents in these regions? If there are other currents, what is the corresponding generation mechanism for them? To address these questions, the current distribution and magnetic-field geometry during two storm events are investigated in the latitudinal regions from 10 to 30^∘ N.

In the following, we will use Cluster fluxgate magnetometer (FGM; Balogh et al., 1997) data to conduct the analysis for two reasons: (1) the polar orbit of Cluster offers an opportunity to go through both the low-latitude and middle-latitude regions and (2) the configuration of the four Cluster satellites makes it possible to calculate the current via Maxwell–Ampère's law and obtain the magnetic-field geometry. Moreover, in many previous works, it was thought that an asymmetric RC linked with the FACs, which is generally believed to occur during storm time, so storm events are our primary focus here.

Throughout this paper, solar magnetospheric (SM) coordinates are used. To better describe angles, spherical coordinates (θ, φ) in the SM frame are also defined; i.e., the polar angle θ (0^∘ $\le \mathit{\theta }\le \mathrm{180}$^∘) is the angle between the +z axis and the vector direction while the azimuthal angle φ (0^∘ $\le \mathit{\phi }\le \mathrm{360}$^∘) is rotated anticlockwise from the +x axis in the x–y plane when seen from +z axis. For current density analysis, the local cylindrical coordinate system (j_ρ, j_φ, j_z; Vallat et al., 2005) is also utilized. Where j_z is parallel to the +z axis, j_ρ represents the radial component of the current on the plane parallel to the x–y plane, oriented anti-earthward; j_φ points eastward, describing the RC.

2 Methodology

In this study, magnetic curvature analysis (MCA; Shen et al., 2003) and magnetic rotation analysis (MRA; Shen et al., 2007) are used; these techniques have the unique ability to reveal the three-dimensional geometric structure of the magnetic field directly as well as to provide more detailed magnetic-field-related parameters, such as the magnetic-field gradient; curvature; and the binormal of magnetic-field lines (MFLs), rotation rates, and current density. The magnetic unit vector $\widehat{\mathit{b}}=\mathit{B}/\left|\mathit{B}\right|$, curvature vector ${\mathit{\rho }}_{\mathrm{c}}({\mathit{\rho }}_{\mathrm{c}}=(\widehat{\mathit{b}}\cdot \mathrm{\nabla }\left)\widehat{\mathit{b}}\right)$, and the binormal vector $\widehat{\mathit{N}}(\widehat{\mathit{N}}=\widehat{\mathit{b}}\times {\widehat{\mathit{\rho }}}_{\mathrm{c}}/\left|\widehat{\mathit{b}}\times {\widehat{\mathit{\rho }}}_{\mathrm{c}}\right|)$ are orthogonal to each other in the analysis, and the radius of curvature is $R_{\mathrm{c}}=\mathrm{1}/{\mathit{\rho }}_{\mathrm{c}}$. The magnetic vector b has maximum, median, and minimum rotation rates of ${\mathit{\mu }}_{\mathrm{1}}^{\mathrm{1}/\mathrm{2}}$, ${\mathit{\mu }}_{\mathrm{2}}^{\mathrm{1}/\mathrm{2}}$, and ${\mathit{\mu }}_{\mathrm{3}}^{\mathrm{1}/\mathrm{2}}$ along ${\widehat{\mathit{e}}}^{\left(\mathrm{1}\right)}$, ${\widehat{\mathit{e}}}^{\left(\mathrm{1}\right)}$, and ${\widehat{\mathit{e}}}^{\left(\mathrm{2}\right)}$, respectively, where ${\widehat{\mathit{e}}}^{\left(\mathrm{1}\right)}$, ${\widehat{\mathit{e}}}^{\left(\mathrm{1}\right)}$, and ${\widehat{\mathit{e}}}^{\left(\mathrm{2}\right)}$ are the three characteristic eigenvectors of the magnetic field. Note that because the strong geomagnetic field in the region of interest will produce artificial currents in the basic MRA calculation (nonlinear contributions), the dipole field is subtracted when using the MRA method to minimize truncation error (Shen et al., 2014).

To make a comparison with the nondisturbed geomagnetic field, the local dipolar values of the magnetic-field strength, B_tDip; the radius of curvature, R_cDip; the magnetic-field gradient strength, |∇B_Dip|; and three rotation rates, ${\mathit{\mu }}_{\mathrm{1}}^{\mathrm{1}/\mathrm{2}}$, ${\mathit{\mu }}_{\mathrm{2}}^{\mathrm{1}/\mathrm{2}}$, and ${\mathit{\mu }}_{\mathrm{3}}^{\mathrm{1}/\mathrm{2}}$, are also presented. They are calculated (Shen et al., 2014) by using

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{\mathit{B}}_{\mathrm{tDip}}& =M{r}^{-\mathrm{3}}\sqrt{(\mathrm{1}+\mathrm{3}{\cos }^{\mathrm{2}}\mathit{\theta })},\\ R_{\mathrm{cDip}}& ={\displaystyle \frac{r}{\mathrm{3}}}\sqrt{(\mathrm{1}+\mathrm{3}{\cos }^{\mathrm{2}}\mathit{\theta }{)}^{\mathrm{3}}}/[\left|\sin \mathit{\theta }\right|\cdot (\mathrm{1}+{\cos }^{\mathrm{2}}\mathit{\theta }\left)\right],\\ \left|\mathrm{\nabla }{\mathit{B}}_{\mathrm{Dip}}\right|& =\mathrm{3}M{r}^{-\mathrm{4}}\\ & \cdot \sqrt{\mathrm{1}+{\cos }^{\mathrm{2}}\mathit{\theta }(\mathrm{7}+\mathrm{8}{\cos }^{\mathrm{2}}\mathit{\theta })}/\sqrt{(\mathrm{1}+\mathrm{3}{\cos }^{\mathrm{2}}\mathit{\theta })},\\ {\mathit{\mu }}_{\mathrm{1}}^{\mathrm{1}/\mathrm{2}}& ={\mathit{\mu }}_{\mathit{\theta }}^{\mathrm{1}/\mathrm{2}}=\mathrm{3}(\mathrm{1}+{\cos }^{\mathrm{2}}\mathit{\theta })/\left[r\right(\mathrm{1}+\mathrm{3}{\cos }^{\mathrm{2}}\mathit{\theta }\left)\right],\\ {\mathit{\mu }}_{\mathrm{2}}^{\mathrm{1}/\mathrm{2}}& ={\mathit{\mu }}_{\mathit{\varphi }}^{\mathrm{1}/\mathrm{2}}=\mathrm{3}\left|\cos \mathit{\theta }\right|/\left[r\sqrt{(\mathrm{1}+\mathrm{3}{\cos }^{\mathrm{2}}\mathit{\theta })}\right],\\ {\mathit{\mu }}_{\mathrm{3}}^{\mathrm{1}/\mathrm{2}}& ={\mathit{\mu }}_r^{\mathrm{1}/\mathrm{2}}=\mathrm{0},\end{array}\end{array}$$

where $M=m\cdot {\mathit{\mu }}_{\mathrm{0}}/\mathrm{4}\mathit{\pi }$ (with $m=\mathrm{7.78}\times {\mathrm{10}}^{\mathrm{22}}$ A m⁻² being the Earth's magnetic dipole moment) and r is the radial distance in SM coordinates.

3 Event analysis

The chosen events occurred on 12 April 2001 and 31 March 2001. These were the two largest storms from 2001 to 2004 during which the four Cluster satellites had a small (best) tetrahedron separation distance (≤1000 km). The minimum Dst indices for the two events were −271 and −387 nT, respectively. During the two events, Cluster was in the pre-midnight sector and traversed the RC region vertically from the Southern to Northern Hemispheres. The region of interest is in the Northern Hemisphere. Figure 1 gives the proton density and differential flux for H⁺, He⁺, and O⁺ during the analyzed interval, which are obtained from the Cluster Ion Spectrometer (CIS; Rème et al., 2001). The figure indicates that Cluster is mainly in the plasma sheet region (e.g., Vallat et al., 2005).

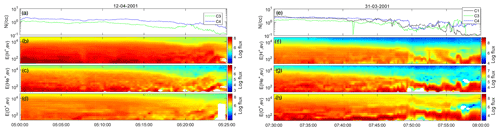
Figure 1 Cluster CIS data for 12 April 2001 (left) and 31 March 2001 (right) event. (a, e) The proton density variation for three satellites: C1 (black), C3 (green), and C4 (blue). (b–d, f–h) H⁺, He⁺, and O⁺ energy–time spectrograms in particle flux units ($\mathrm{ions}{\mathrm{cm}}^{-\mathrm{2}}{\mathrm{sr}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}{\mathrm{keV}}^{-\mathrm{1}}$) from C4.

3.1 12 April 2001 event

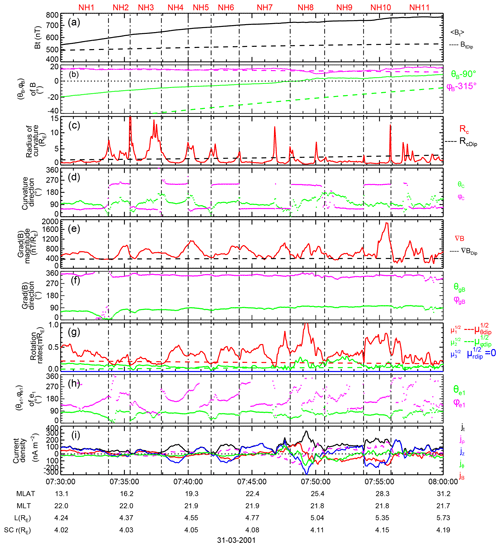
The time interval of interest for the first event is from 05:00 to 05:25 UT, with latitude ranging from 16.9 to 25.7^∘. Figure 2 presents some of the main physical quantities. Figure 2a shows the average magnetic field 〈B_t〉 detected from the four Cluster satellites and the local dipolar magnetic-field strength. It can be seen that the local magnetic field is enhanced in this area. Figure 2b indicates that the polar angle of the magnetic field is close to 90^∘, showing that the magnetic field lies approximately in the x–y plane. The polar angle and azimuthal angle of dipolar fields are also shown in dashed lines in Fig. 2b, which indicates a large deviation of the polar angle with observations. Figure 2c shows that the radius of curvature, R_c, has large variations. It is interesting to see that ϕ_c (the angle of R_c in Fig. 2d) changes direction alternately during the whole period. Therefore, eight regions (numbered from NH1 to NH8) were chosen according to the changes in the ϕ_c direction to investigate their features. The variations in some physical quantities are also summarized in Table 1. For ϕ_c and θ_e1, the average values (with a few large abnormal points removed) during this period are given. The “–” denotes values with large oscillations. For j_z, the maximum or minimum value during each interval is presented.

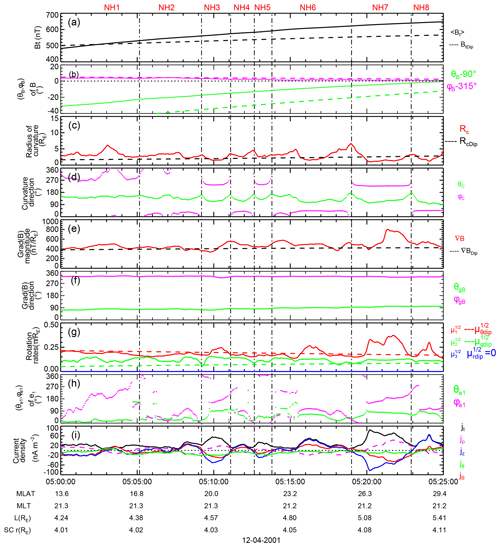
Figure 2 Geometry of the magnetic field and the current distribution in the Northern Hemisphere (NH) region on 12 April 2001. (a) Average magnetic strength B_t at the center of the Cluster tetrahedron (black solid line) and the calculated strength B_tDip of the dipole geomagnetic field (black dashed line). (b) Direction angles (θ_B, ϕ_B) of the magnetic field. 90 and 315^∘ are reduced respectively for θ_B and ϕ_B to better indicate the magnetic-field variation. The polar angle and azimuthal angle of dipolar fields are also show in dashed lines. (c) Radius of curvature, R_c (red solid line), and the calculated radius of curvature, R_cDip, of the dipole geomagnetic field (black dashed line). (d) Direction angles (θ_c, ϕ_c) of the curvature of the MFLs. (e) Value of the gradient of magnetic-field strength for the real magnetic field (red solid line) and dipole geomagnetic field (black dashed line). (f) Direction angles (θ_gB, ϕ_gB) of the gradient of magnetic-field strength. (g) Maximum, median, and minimum rotation rates of the measured magnetic field (solid lines) and dipole geomagnetic field (dashed lines). (h) Direction angles (θ_e1, ϕ_e1) of the maximum rotation rate. (i) Total current density j_t (black line) and the three components j_ρ (magenta line), j_φ (green line), and j_z (blue line) in local cylindrical coordinate system, respectively. The red line is the field-aligned component j_B (red line).

As shown in Fig. 2c, the radius of curvature of MFLs in the eight regions is more varied compared with that of the dipole field. Another feature observed in Fig. 2c is that R_c peaks at the vertical dashed lines. This is reasonable, since the curvature radius in the transition region should be larger than the region where the curvature radius has opposite directions. Figure 2d and the ϕ_c row in Table 1 give the average value of the azimuthal direction ϕ_c during each interval. This quantitatively reveals that ϕ_c alternatively varied between 30.3 and 51.9 and 230.3 and 292.0^∘. It is noted from Fig. 2d that, for some regions, the variation in polar angle θ_c has larger fluctuation (than azimuthal angle ϕ_c). This feature reflects larger changes of the magnetic field in z component. Figure 2g shows that ${\mathit{\mu }}_{\mathrm{1}}^{\mathrm{1}/\mathrm{2}}$ has an enhancement in each region, illustrating a stretched MFL structure. Figure 2h and row θ_e1 in Table 1 show that, for most regions, the largest value of the polar angle θ_e1 for ${\mathit{\mu }}_{\mathrm{1}}^{\mathrm{1}/\mathrm{2}}$ is close to 90^∘; therefore, the largest deviation of MFLs is along the x–y plane. Figure 2i indicates that the current oscillates and that the dominant current is along j_ρ and the north (or south) j_z direction, while j_φ is basically small compared with j_ρ and j_z. To show FACs, the j_B component is also given in Fig. 2i; it can be seen that the value of j_B is close to that of j_ρ because the direction of the magnetic field points approximately to the radial direction (see Fig. 2b). The maximum values for j_B and j_z were ∼40 and ∼80 nA m⁻², respectively. From Table 1 and Fig. 2, it is interesting to see that, from region NH1 to region NH8, the j_z component changed from positive (northward) to negative (southward) as ϕ_c varied from <50 to >230^∘.

Table 1 Variation in physical quantities for two storm events.

^a Storm events considered in this work.
^b The physical quantity ϕ_c is the average azimuthal direction of the curvature radius, θ_e1 is the average polar angle of maximum rotation rates of the magnetic field, and j_zm represents the maximum or minimum value of the j_z-current component.
^c−m Regions for each storm event.

3.2 31 March 2001 event

Another larger storm occurred between 07:30 and 08:00 UT on 31 March 2001. The event was once reported by Shen et al. (2014), but they only concentrated on the interval from approximately 07:00 to 07:25 UT. Observations are shown in Fig. 3 for the latitudinal region from 13.1 to 31.2^∘ N, the interval during the main phase of the storm. Here, 11 regions designated from NH1 to NH11 are divided also according to azimuthal direction changes of ϕ_c. The variations in some relative physical quantities are also shown in Table 1. From Fig. 3 and Table 1, it can be seen that these parameters behave the same as those of the first event, but with strong magnetic-field strength. Figure 3 indicates that the magnetic-field strength is stronger than that during the first event. The magnetic field is in the x–y plane (see Fig. 3b). The radius of curvature of MFLs (see Fig. 3c), the magnetic-field gradient (Fig. 3e), and the largest rotation rate (Fig. 3g) oscillates significantly and exhibits large deviations compared with those of the dipole field. Figure 3f shows that the magnetic-field gradient is in the x–y plane and directed toward the dayside. Figure 3h and row θ_e1 demonstrate that the largest variation in MFLs is near the x–y plane. In Fig. 3i, it is clear that the j_z component is the dominant current, with a maximum value of ∼300 nA m⁻². This value is more than triple that of the 12 April 2001 event. It is clear to see that the j_φ component is the smallest among these currents. Similar to first event, j_z is simultaneously observed to vary from northward to southward when φ_c changes direction.

Figure 3 Geometry of the magnetic field and the current distribution in the NH region on 31 March 2001. The format is the same as that of Fig. 2.

4 Discussion

During the 12 April 2001 and 31 March 2001 strong storm events, the Cluster satellites were located in the pre-midnight sector and crossed from ∼10 to ∼30^∘ N. In these regions, both the magnetic-field parameters and the current density fluctuated significantly. The MFLs, which were mainly in the x–y plane, severely deviated from the dipole field and changed (stretched) along the x–y plane. Figure 4 displays the total magnetic-field strength and its three components. It can be seen that the x and y components of the magnetic field have the largest fluctuations, which is consistent with the results obtained from Figs. 2 and 3. To further investigate the fluctuation, the continuous 1-D wavelet transform method is applied in the x and y component of the magnetic field. It is found that the ULF wave (ultra-low-frequency wave) covering a range of frequencies spanning from 4 to 10 mHz can be observed (not shown here), which is consistent with the typical current density variation in the ∼2–4 min period. Actually, the ULF wave in the plasma sheet region has been extensively reported in previous works (see Keiling, 2009, and references therein). Thus, it seems that ULF wave is a possible way to cause the variation in the curvature radius (and the field-aligned current).

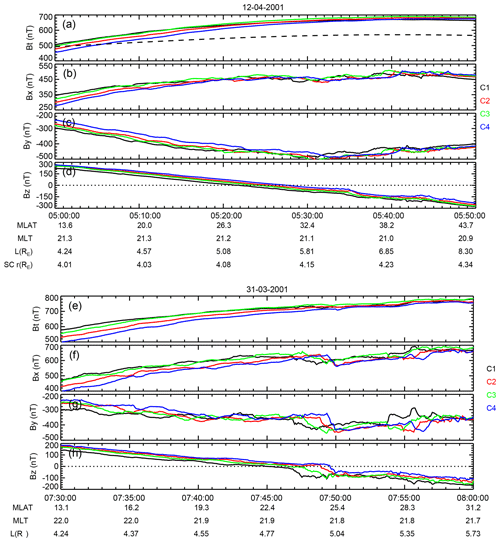
Figure 4 Magnetic field observed by the four Cluster satellites during 12 April 2001 and 31 March 2001 storm events.

The most obvious phenomenon in the two cases is the existence of three current systems, i.e., FACs, j_B, an azimuthal current, j_φ, and a northward (or southward) current, j_z. Among them, j_z is basically the strongest current component. In previous studies (e.g., Le et al., 2004; Vallat et al., 2005), the existence of j_B and j_φ has been proved. However, the occurrence of such a strong j_z in the inner plasma sheet has not been reported before. In the work of Vallat et al. (2005), they also found a southward current (see Fig. 14 and corresponding text). But it is in the equatorial ring current region (with no direction changes) and is mainly caused by an asymmetry between the ionospheric conductivities of the two hemispheres. It is very clear that the southward current in their paper is different than what we report here.

As introduced in previous studies (e.g., Parker, 1957), the current in the inner magnetosphere generally arises from gradient drifts as well as curvature drift and the gyromotion of energetic particles. They can be calculated by using the following (e.g., Lui et al., 1987; De Michelis et al., 1999):

$$\begin{array}{}\text{(2)}& {\displaystyle }{\mathit{j}}_{\mathrm{\nabla }}=P_{\perp }{\displaystyle \frac{\mathit{B}\times \mathrm{\nabla }\mathit{B}}{B^{\mathrm{3}}}},\text{(3)}& {\displaystyle }{\mathit{j}}_{\mathrm{C}}=-{\displaystyle \frac{P_{\parallel }}{B^{\mathrm{2}}}}{\mathit{\rho }}_{\mathrm{c}}\times \mathit{B},\text{(4)}& {\displaystyle }{\mathit{j}}_{\mathrm{G}}={\displaystyle \frac{\mathit{B}}{B^{\mathrm{2}}}}\times \left[\mathrm{\nabla }{P}_{\perp }-{\displaystyle \frac{P_{\perp }}{\mathit{B}}}\mathrm{\nabla }\mathit{B}-{\displaystyle \frac{P_{\perp }}{B^{\mathrm{2}}}}(\mathit{B}\cdot \mathrm{\nabla })\mathit{B}\right],\end{array}$$

where j_∇, j_C, and j_G represent the gradient current, curvature current, and gyromotion current, respectively, and P_⊥ and P_∥ are the pressure tensor components perpendicular and parallel to the magnetic field, which can be deduced from

$$\begin{array}{}\text{(5)}& {\displaystyle }{P}_{\perp }=\mathit{\pi }\sqrt{\mathrm{2}m}\int \int J\sqrt{\mathit{\epsilon }}{\sin }^{\mathrm{3}}\mathit{\alpha }\mathrm{d}\mathit{\alpha }\mathrm{d}\mathit{\epsilon },\text{(6)}& {\displaystyle }{P}_{\parallel }=\mathrm{2}\mathit{\pi }\sqrt{\mathrm{2}m}\int \int J\sqrt{\mathit{\epsilon }}{\cos }^{\mathrm{2}}\mathit{\alpha }\sin \mathit{\alpha }\mathrm{d}\mathit{\alpha }\mathrm{d}\mathit{\epsilon },\end{array}$$

where m is the mass of the particle, J is the differential flux intensity, and ε and α are the particle energy and pitch angle, respectively. Since the magnetic-field gradient ∇B and curvature ρ_c were obtained by using the MRA method, the above three currents can be calculated when the pressure tensor components are given.

For the two events in this study, both the magnetic field and magnetic-field gradient are directed toward the dayside. Therefore, the current deduced from B×∇B (the gradient drift current) should be small. To analyze the current contribution from gyromotion drift and curvature drift, we first show the three components of $-{\mathit{\rho }}_{\mathrm{c}}\times \mathit{B}$ for the two events in Fig. 5a and b. It is clearly seen that the $(-{\mathit{\rho }}_{\mathrm{c}}\times \mathit{B}{)}_z$ component is the dominate part and has the same variation trend as j_z. Therefore, the curvature drift current is a possible candidate. For gyromotion current, it originates from three terms, i.e., $\mathit{B}\times \mathrm{\nabla }{P}_{\perp }$, $-\mathit{B}\times \mathrm{\nabla }\mathit{B}$, and $-\mathit{B}\times (\mathit{B}\cdot \mathrm{\nabla })\mathit{B}$. Firstly, according to previous works (e.g., Lui et al., 1987; De Michelis et al., 1999), ∇P_⊥ is along the radial direction, which means that it has a similar direction with the magnetic field to the two events analyzed here. Thus, the contribution from $\mathit{B}\times \mathrm{\nabla }{P}_{\perp }$ should be small. Secondly, $-\mathit{B}\times \mathrm{\nabla }\mathit{B}$ is similar to the gradient drift current and can be negligible. Thirdly, since (B⋅∇)B has the same direction as ${\mathit{\rho }}_{\mathrm{c}}({\mathit{\rho }}_{\mathrm{c}}=(\widehat{\mathit{b}}\cdot \mathrm{\nabla })\widehat{\mathit{b}},\widehat{\mathit{b}}=\mathit{B}/\left|\mathit{B}\right|)$, according to Fig. 5a and b, the product of $-\mathit{B}\times (\mathit{B}\cdot \mathrm{\nabla })\mathit{B}$ (similar to ρ_c×B) will behave oppositely to j_z. Consequently, the gyromotion current has little possibility of contributing to a strong j_z. According to the above analysis, the most reasonable candidate for strong j_z should be the curvature drift.

Based on the above analysis, graphic plots are given in Fig. 5c and d to explain the possible generation mechanism for j_z. During the strong storm time, turbulence, e.g., ULF waves, results in the fluctuation of the MFLs; then, the radius of curvature of the MFLs decreases, leading to an increase in the curvature drift current. During this process, the direction of the magnetic field is nearly unchanged because the background field is very strong. However, the curvature will alternately change directions along with the variation in the MFLs, resulting in alternating variations in $-{\mathit{\rho }}_{\mathrm{c}}\times \mathit{B}$, i.e., leading to the oscillation of j_z.

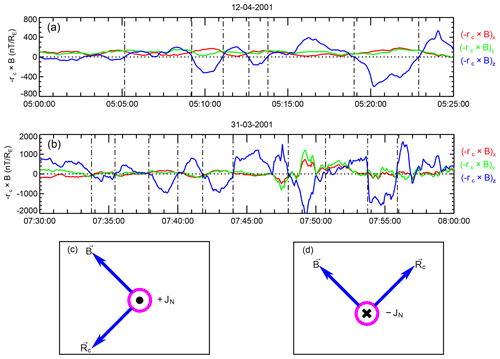
Figure 5 (a, b) The three components of $-{\mathit{\rho }}_{\mathrm{c}}\times \mathit{B}$ for two analyzed events. ρ_c is calculated from MRA method, and B is the averaged magnetic field measured by four Cluster spacecraft. (c, d) Graphic plots of the origin of the j_N current variation.

Figure 5a and b can only illustrate that the direction of $-{\mathit{\rho }}_{\mathrm{c}}\times \mathit{B}$ is consistent with northward current. To quantitatively check if the curvature current calculated through Eq. (3) is consistent with the result obtained from the MRA method, further investigation is necessary. The CIS/CODIF (Cluster Ion Spectrometry COmposition and DIstribution Function analyzer) can provide the differential flux intensity for energy below 40 keV. Through Eqs. (3), (5), and (6), the curvature current can be estimated. The results show that the main variation trend is consistent with result from MRA, but the intensity is very small (less than 1 nA m⁻²; not shown here). However, it should be noted that, for Cluster CIS/CODIF, only low-energy particle data are available; therefore, a large bias may exist when calculating the storm-time current. In contrast, much higher energy is used in previous studies (e.g., 1 MeV in the work of Lui et al., 1987). Cluster RAPID can provide energy spectrograms for the high-energy particle from ∼27.6 to ∼3056 keV. Unfortunately, there are no available data for the two analyzed events. The statistical study from Kronberg et al. (2015) proves that, in the near-Earth plasma sheet, higher-energy hydrogen and oxygen are greatly enhanced during geomagnetic activity. In the work of Ma et al. (2012), they also indicated that the flux for higher-energy particles could be comparable or larger than that of the low-energy particles.

Though, there is no available differential flux for high-energy particles on Cluster, the curvature current still can be estimated through simulations. Previous works have proved that the particle distribution in plasma sheet can be described as Kappa distribution functions (Pierrard and Lazar, 2010, and references therein):

$$\begin{array}{}\text{(7)}& f=N_{\mathrm{1}}{\left({\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }m{E}_{\mathrm{0}}{\mathit{\kappa }}_{\mathrm{1}}}}\right)}^{\mathrm{2}/\mathrm{3}}{\displaystyle \frac{\mathrm{\Gamma }({\mathit{\kappa }}_{\mathrm{1}}+\mathrm{1})}{\mathrm{\Gamma }({\mathit{\kappa }}_{\mathrm{1}}-\mathrm{1}/\mathrm{2})}}{\left(\mathrm{1}+{\displaystyle \frac{E}{{\mathit{\kappa }}_{\mathrm{1}}{E}_{\mathrm{0}}}}\right)}^{-{\mathit{\kappa }}_{\mathrm{1}}-\mathrm{1}},\end{array}$$

where N₁ and E₀ denote particle density and temperature, and κ₁ is a constant. For energy satisfying E≫E₀, Eq. (7) can be written as

$$\begin{array}{}\text{(8)}& f=a{E}^{-{\mathit{\kappa }}_{\mathrm{1}}-\mathrm{1}}.\end{array}$$

Since the differential flux intensity J and particle velocity distribution function f are related by J=fp², Eq. (8) is also the function of J, namely

$$\begin{array}{}\text{(9)}& J=a{p}^{\mathrm{2}}{E}^{-{\mathit{\kappa }}_{\mathrm{1}}-\mathrm{1}},\end{array}$$

where p is the momentum of the concerned particles, and a is a constant. Thus, with the known differential flux intensity from low-energy particle, the parameter a and κ₁ can be determined. Then, the differential flux intensity for high-energy particles (to 1 MeV) can be estimated using Eq. (9). Though particles are accelerated during the storm, we have confirmed that the Kappa distribution is still satisfied using CIS/CODIF observations (not shown here). However, it should be noted that, during the storm, a and κ₁ are no longer a constant but varied with time. Besides this, to check if the estimated high-energy particle differential flux (using low-energy particle data) is reasonable, we select a storm event that occurred on 20 April 2002, which has similar position with two analyzed events in this study, and has CIS/CODIF and RAPID observations at the same time. The result shows that the fitted result (from CIS/CODIF measurement) can basically reflect the main trend of the high-energy particles, which can demonstrate that our estimation used here is reasonable. During the storm time, currents calculated via energetic particle fluxes appear to still underestimate the current. As the particle flux fit method of calculating currents works so well for earlier in the time period, this undershoot during storm time might be indicative of additional energetic particle acceleration (a harder power law) in the parallel direction. This increased parallel pressure would result in the observed larger value of j_c.

Now, we can re-estimate the curvature current using Cluster CIS/CODIF observations for energy between 25 eV and 40 keV and simulation values for energy in the range >40 keV–1 MeV. Figure 6 shows the estimated z component of curvature current (the red dotted curve). It is close to result from MRA (the blue curve).

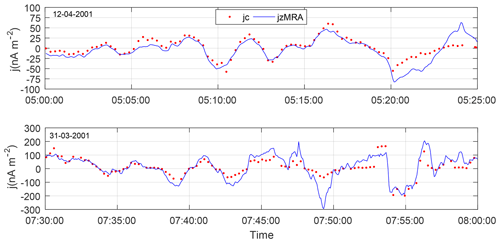
Figure 6 The z-component current density calculated from MRA method (the blue curve) and the estimated curvature current (the red dotted curve).

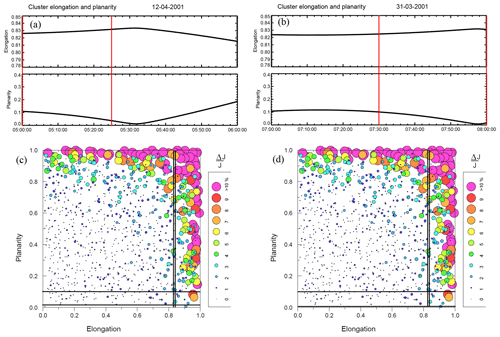
Figure 7 (a, b) Cluster elongation and planarity for two studied events. The red vertical lines demarcate the analyzed time interval. Panels (c) and (d) are taken from Robert et al. (1998) to evaluate the influence of the tetrahedron shape. Black lines mark the elongation and planarity obtained from panels (a) and (b).

It should be noted that both events analyzed here are in the Northern Hemisphere. Actually, we have checked that the southward and northward current also can be observed in the southern low and middle latitudes. Thus, such currents should be observable both in northern and southern inner plasma sheet during strong geomagnetic storm events.

According to previous analysis from plasma data (Baker et al., 2002; Korth et al., 2004; Vallat et al., 2005; Ohtani et al., 2007), most NH regions should correspond to the plasma sheet region. Using the T96 model (Tsyganenko, 1995, 1996), we tried to trace Cluster footprints in the Northern Hemisphere; it is found that the position is ∼55–60^∘ (not shown here), which just corresponds to the position of the FACs (Papitashvili et al., 2002; He et al., 2012). Because the MFL shapes in the plasma sheet were changed considerably, the particle motion in Earth's magnetic field will be altered correspondingly, which may affect the particle distribution in the polar and equatorial regions, hence leading to the variation in the FAC and RC distributions. These effects, however, need to be evaluated in future work.

When calculating current density using the MRA method, it should be noted that Cluster is not a regular tetrahedron shape around the perigee area but suffers from an elongation, which can produce an unnatural currents. These unnatural currents are included in our analysis and cannot be removed. To evaluate this component, methods from Robert et al. (1998) and Vallat et al. (2005) are used. Figure 7 gives the Cluster tetrahedron parameters for two analyzed events. Then, the current influence of the tetrahedron shape can be estimated as a function of elongation and planarity (Fig. 7c and d). It can be seen that the error caused by tetrahedron is never more than 30 %.

5 Summary

In this work, the magnetic-field geometry and current density in the inner plasma sheet during two intense geomagnetic storms were investigated. It is found that the magnetic field and current density highly fluctuated in this region. Generally, all three components of current can be observed during the analyzed interval. However, the northward (or southward) current is basically the strongest one. Detailed study shows that the MFLs align in the x–y plane; thus, the northward (or southward) current should not be FACs. This property has not been reported before.

The most prominent feature of the northward (or southward) current is the alternative changing of its direction, which is found to vary simultaneously with that of the curvature. To reveal the generation mechanism of the northward (or southward) current, gradient current, curvature current, and gyromotion current are analyzed. The results show that the curvature current has the same variation trend with the northward and southward current. Then, using low-energy particle observations from Cluster CIS/CODIF, combined with simulations based on Kappa distribution, the curvature current is calculated. It shows that the estimated curvature current coincides very well with the current density directly obtained from MCA and MRA. Therefore, the curvature drift of the energetic particle is the most reasonable mechanism of the southward and northward current.

For the two events analyzed in this work, we can observe ULF waves; this is consistent with the typical current density variation period. This turbulence excited during the strong storm can result in the decrease in curvature radius and changing of direction of MFLs, then leading to an increase in the curvature currents and variation in their direction.