Multi-point galactic cosmic ray measurements between 1 and 4.5 AU over a full solar cycle

The radiation data collected by the Standard Radiation Environment Monitor (SREM) aboard ESA missions INTEGRAL (INTErnational Gamma-Ray Astrophysics Laboratory), Rosetta, Herschel, Planck and Proba-1, and by the high-energy neutron detector (HEND) instrument aboard Mars Odyssey, are analysed with an emphasis on characterising galactic cosmic rays (GCRs) in the inner heliosphere. A cross calibration between all sensors was performed for this study, which can also be used in subsequent works. We investigate the stability of the SREM detectors over long-term periods. The radiation data are compared qualitatively and quantitatively with the corresponding solar activity. Based on INTEGRAL and Rosetta SREM data, a GCR helioradial gradient of 2.96 % AU⁻¹ is found between 1 and 4.5 AU. In addition, the data during the last phase of the Rosetta mission around comet 67P/Churyumov–Gerasimenko were studied in more detail. An unexpected yet unexplained 8 % reduction of the Galactic Comic Ray flux measured by Rosetta SREM in the vicinity of the comet is noted.

1 Introduction

The space radiation environment affects both manned and unmanned missions outside the Earth's protecting atmosphere and its magnetic field. Highly energetic particles can penetrate living tissue and a spacecraft's component materials, causing damage due to the deposition of energy. Major sources of this radiation are solar energetic particles (SEPs) and galactic cosmic rays (GCRs). This work focusses on the third source, the GCRs, and in particular on their variations in the inner heliosphere. The variation in galactic cosmic ray intensity depends on different physical processes: inward diffusion in the interplanetary magnetic field (IMF), adiabatic cooling, outward convection and deceleration in the solar wind plasma, drift along the heliospheric current sheet, and interaction with magnetic structures in shocks and in interplanetary coronal mass ejections (e.g. Potgieter, 2013; Moraal, 2013; Alania et al., 2014; Kozai et al., 2014; Giseler and Heber, 2016). The GCR intensity therefore varies with the solar wind velocity, the magnitude of the interplanetary magnetic field, solar activity, the heliospheric current sheet tilt angle and the solar polarity change. The study of the effects of GCRs on the Earth's atmosphere and climate is also a fascinating field of research (e.g Carslaw et al., 2002; Pierce, 2017; Frigo et al., 2018).

This work is based on the analysis of data collected by the Standard Radiation Environment Monitor (SREM) units on Rosetta, INTEGRAL (INTErnational Gamma-Ray Astrophysics Laboratory), Herschel, Planck and Proba-1 spacecraft and on data from the high-energy neutron detector (HEND) aboard Mars Odyssey. While INTEGRAL, Herschel, Planck and Proba-1 are located at around 1 AU from the Sun and HEND orbits Mars with an average heliocentric distance of 1.5 AU, Rosetta's heliocentric distance varied from 1 to 4.5 AU during its mission lifetime. This combined dataset provides a unique opportunity to determine the GCR flux measured over a range of distances of up to 3.5 AU and a time period of more than one solar cycle in interplanetary space. Of special interest are the Rosetta measurements close to comet 67P/Churyumov–Gerasimenko.

2 Instrument descriptions and datasets

2.1 The ESA radiation monitors

The SREM (e.g. Evans et al., 2008) is a particle detector developed to provide radiation information on a broad range of ESA space missions. SREM instruments have been installed on seven spacecraft so far, with two of them – Proba-1 and INTEGRAL – still operating at the time of writing. With its ability to measure high-energy charged particles (e.g. electrons and protons), it is able to provide valuable information regarding the near-platform radiation environment in short- and long-term periods. In addition, measurements are also a valuable resource for the improvement of space radiation environment models.

The SREM instrument consists of two detector heads with three silicon diode detectors, denoted as D1, D2 and D3. In the first of the two detector heads, the detectors D1 and D2 are arranged in a telescope configuration, with the main entrance covered by 2 mm of aluminium that provides a lower energy threshold of about 20 MeV for protons and about 1.5 MeV for electrons (Mohammadzadeh et al., 2003). Additionally, the detectors are separated from each other by another 1.7 mm of aluminium and 0.7 mm of tantalum, which sets the threshold for protons of up to roughly 39 MeV. Therefore, coincidence of D1 and D2 measures mostly high-energy protons. The opening window for the remaining detector head corresponding to detector D3 is covered with 0.7 mm of aluminium and provides therefore an energy threshold of about 0.5 MeV for electrons and about 10 MeV for protons, respectively. The opening angle of the telescope is ±20^∘. The detector electronics can operate with a detection rate up to 100 kHz with a corresponding dead-time correction below 20 %. The instrument itself is a box of 20 cm×12 cm×10 cm which weighs 2.6 kg, including the detector system and the supporting electronics. Measuring the incident radiation, the particle events are binned into 15 different channels which have different energy thresholds and discriminator levels. This allows differentiated insight into the energy ranges of the events. Table 1 displays the channels with corresponding logic, particles species and energy range. Channels TC1, S12, S13 (all D1) and TC2 (D2) are sensitive to both electrons and protons, where TC2 has the highest energy threshold of about 49 MeV for protons and about 2.8 MeV for electrons. With the channels S14, S15, C1–C3, S33 and S34 it is possible to measure mainly protons due to the given energy thresholds and the comparatively high discriminator levels. Channel S25 is dedicated to measuring the generally very low heavy ion flux due to its very high discriminator level. However, previous studies point to the fact that the heavy ion channel is most sensitive to protons (Lüdeke and Wyrwol, 2017). The coincidence channels C1 to C4 use both detector D1 and D2 simultaneously and measure mainly protons due to the high shielding provided by the layers made of aluminium and tantalum. The insensitivity of the C1, C2 and C3 channels to electrons arises from the high-energy deposit thresholds for these channels. The threshold for C4 is low enough to detect the electrons that can make it through the shielding. Channels TC3 and S32 to S34, based on detector D3, are sensitive to low-energy protons, with the sensitivity to electrons diminishing from S32 to S34. Nevertheless, one should keep in mind that all channels measure electrons as well as protons and that all channels are correlated. This means that it is possible to measure the same event in multiple channels. While the single-detector channels tend to measure particles in an omnidirectional way, the coincidence channels can be characterised to measure particles with a certain directionality. Therefore, there is a reduced number of degrees of freedom, since the particles are required to deposit energy in D1 and D2 simultaneously, and this is only possible if the particle trajectory crosses both detectors.

Table 1 List of SREM energy channels. The column “Bin” gives the name of the channel, and the column “Logic” names the corresponding detector (adapted from Evans et al., 2008). The study of the detector response to GCR indicates that the TC2 channels are mainly sensitive to energies between 200 MeV and 20 GeV.

2.2 HEND

In addition to the SREM monitors, we used data recorded by HEND (Boynton et al., 2004) aboard the Mars Odyssey spacecraft. It is composed of five separate sensors that provide measurements of neutrons in the energy range from 0.4 up to 15 MeV. In this study, only data from the outer scintillator (a veto counter used for anti-coincidence rejection of charged particles) in channels 9–16 are used (∼ 195 → 1000 keV). This sensor is very adequate for space weather studies, as it is sensitive to neutrons, charged particles and energetic photons (see more information in Sanchez-Cano et al., 2018). This instrument can be used also as a proxy for GCRs, as demonstrated in Zeitlin et al. (2010), since HEND measures secondary particles produced by the interactions of primary energetic GCR with the spacecraft, providing indirectly a measure of the cosmic rays (Zeitlin et al., 2010).

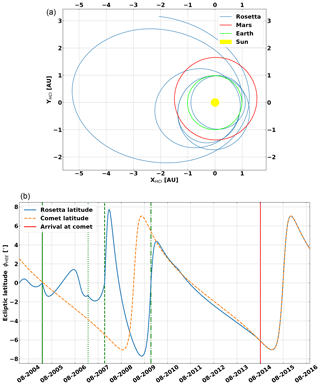
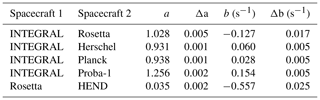
Figure 1 Orbital information for the used datasets. (a) Orbits of Earth (green), Mars (red) and Rosetta (blue) in HCI coordinates. (b) Ecliptic latitude in heliocentric Earth ecliptic (HEE) coordinate system: the solid green line indicates the first Rosetta Earth fly-by, the dotted green line indicates the Mars fly-by, the dashed green line indicates the second Earth fly-by and the dashed–dotted green line indicates the third Earth fly-by.

2.3 Orbits

Figure 1a shows the orbits of Earth (green), Mars (orange) and Rosetta (blue) in heliocentric inertial (HCI) coordinates. The HCI coordinate system is defined with its x axis pointing towards the solar-ascending note on the ecliptic, the z axis being aligned with the solar rotational axis and the y axis completing a right-handed Cartesian triad. At scales of astronomical units, we can assume that Earth's orbit is similar to INTEGRAL, Proba-1, Herschel and Planck's orbits and that the Mars' and Mars Odyssey's orbits also have a similar orbit around the Sun. Figure 1b illustrates the heliolatitudes travelled by the Rosetta mission, which describe how far the spacecraft and the comet travel out of the ecliptic plane. While the comet's components reflect its periodic nature, Rosetta's components do not, since it underwent a number of orbital changes to attain the same orbit as the comet. This was achieved with several gravity-assist fly-bys, which are indicated on the plot by vertical lines: three Earth gravity assists on 4 March 2005 (solid), 13 November 2007 (dashed) and 13 November 2009 (dashed–dotted) and a Mars gravity assist on 25 February 2007 (dotted), which all had a significant impact on the trajectory of the spacecraft. The final vertical line, in red, indicates the comet rendezvous on 6 August 2014.

2.4 Data processing

In this section, we explain the procedure of the GCR analysis. SREM channel TC2 was chosen to be the main channel for this study, having the highest proton energy threshold of the non-coincidence counters, with about 49 MeV. Since the GCR spectrum is dominated by very high-energy particles, it is therefore the most sensitive channel for these purposes. The TC2 channel could include a significant contribution from secondary particles induced by cosmic ray interaction with the spacecraft itself. As a first approximation, this contribution is expected to be minimised in the cross-calibration process. A full characterisation could be the topic of a follow-up study. As this study focusses on a count rate spectrum consisting of GCRs, it is necessary to clean the datasets from solar proton event (SPE) contamination by removing intervals containing SPE events. The times were chosen based on the ESA Solar Proton Event Archive (http://space-env.esa.int/index.php/Solar-Proton-Event-Archive.html, last access: 18 September 2019). Since the data in this archive are based on geostationary satellites, further SPEs detected by HEND and Rosetta at locations with a significant longitudinal difference with respect to the Earth's heliocentric longitude had to be removed manually. In practice, we removed peaks associated with SPEs in data when SPEs exceeded a local daily mean value of count rates (see http://space-env.esa.int/index.php/NOAA_SPE_Template.html?date=19971104 for more details, last access: 18 September 2019). The INTEGRAL dataset needed an additional processing to remove the signatures of Earth's inner-magnetospheric trapped-particle environment by only considering spacecraft altitudes above 60 000 km from the origin of the geocentric equatorial inertial (GEI) coordinate system.

The HEND data had to be processed in multiple steps. First, the SPEs were removed in a similar procedure as for the SREM data. Second, the reconfiguration of the anti-coincidence switch on HEND in 2012 had to be taken into account. This correction manifests itself in a constant offset of 750 counts from 19 October 2012, 16:02:54 UTC (J. J. Plaut, personal communication, 2018, and see http://pds-geosciences.wustl.edu/ody/ody-m-grs-2-edr-v1/odge1_xxxx/errata.txt, last access: 18 September 2019), which can be easily reversed. Finally, the data were converted from counts to counts per second by considering a collection interval of 19.7 s (Zeitlin et al., 2010).

2.5 Cross calibration between radiation monitors

A quantitative comparison between the measured count rates from different radiation monitors on spacecraft requires a cross-calibration exercise. All SREM instruments were calibrated against the INTEGRAL sensor, as INTEGRAL offers the longest baseline. HEND was then calibrated to the calibrated SREM aboard Rosetta. The calibration of Rosetta to INTEGRAL was based on their hourly averaged data of 3 d around Rosetta's three Earth fly-bys (similar space radiation environment during the fly-bys) on 4 March 2005, on 13 November 2007 and on 13 November 2009. A linear fit of the datasets is performed from which a fit function can be obtained. This is used to calibrate the Rosetta/SREM channel TC2 data. Figure 2 displays the 3-hourly averaged datasets with the corresponding standard error together with the linear fit. The data appear to be well aligned during the three chosen calibration periods, suggesting similar response to the GCR radiation environment and good stability over time between Rosetta and INTEGRAL. We associate the 2.8 % difference between INTEGRAL and Rosetta, taken from the gradient fit of 1.028±0.005, with differences in the sensitivity area of the two SREM detectors, noise levels, obstructions or different spacecraft mass distribution around the sensor head. We associate the GCR count rate changes over the years with the solar cycle (e.g. Heber and Potgieter, 2008; Potgieter, 2013), which is discussed in more depth below.

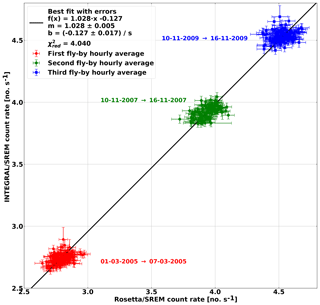
Figure 2 Cross calibration between INTEGRAL and Rosetta SREM instruments. Fitted data of Rosetta SREM and INTEGRAL SREM channel TC2 for the time around Rosetta's Earth fly-bys.

The fit yields the calibration function of the equation

$$\text{Count}\left(\text{INTEGRAL}\right)=\mathrm{1.028}\times \text{count}\left(\text{Rosetta}\right)-\mathrm{0.127}/s.$$

This function is then applied to the whole dataset of channel TC2.

Calibration of Planck/SREM, Herschel/SREM and Proba-1/SREM to INTEGRAL/SREM

Under the assumption that Planck, Herschel and INTEGRAL measure in a similar space radiation environment, excluding the INTEGRAL radiation belt passages, the calibration of Planck and Herschel to INTEGRAL is based on the whole channel TC2 dataset of the spacecraft at Lagrange point L2 to ensure the highest statistics and therefore the most accurate fit possible. The fit yields the following calibration functions:

$$\begin{array}{rl}& \text{Count}\left(\text{INTEGRAL}\right)=\mathrm{0.931}\times \text{count}\left(\text{Herschel}\right)+\mathrm{0.060}/s,\\ & \text{Count}\left(\text{INTEGRAL}\right)=\mathrm{0.938}\times \text{count}\left(\text{Planck}\right)+\mathrm{0.028}/s.\end{array}$$

Cross calibration with Proba-1 was carried out in a similar way to Planck and Herschel, although in this case, INTEGRAL counts were consistently higher than Proba-1 by a factor of 1.256. In addition to a possible active area difference, Proba-1's lower count rates can easily be explained by its low-altitude orbit, with the solid angle of Earth presenting a shielding for GCR fluxes. The fraction of the solid angle divided by 4π is equal to 21.2 %.

The fit yields the calibration function

$$\text{Count}\left(\text{INTEGRAL}\right)=\mathrm{1.256}\times \text{count}\left(\text{Proba-1}\right)+\mathrm{0.154}/s.$$

This function is applied to the whole dataset of Proba-1's channel TC2.

HEND

The HEND neutron monitor is calibrated with respect to SREM-Rosetta, which is calibrated with respect to INTEGRAL. Assuming a mean heliocentric distance of Mars at 1.5 AU, Rosetta data were used when the spacecraft was located at the same distance from the Sun, which happened seven times during the Rosetta cruise. These periods are indicated in Fig. 3, each covering ±3 d around the indicated time and being made up of hourly averaged data.

Figure 3 Cross calibration of Mars Odyssey HEND with Rosetta SREM, calibrated against INTEGRAL data. The seven groups of data correspond to the seven times Rosetta was 1.5 AU from the Sun.

The fit yields the calibration function

$$\text{Count}\left(\text{Rosetta}\right)=\mathrm{0.035}\times \text{count}\left(\text{HEND}\right)-\mathrm{0.557}/s.$$

This function is applied to the whole HEND dataset. It should be also noted that the shadow of Mars is not included in this study. The corresponding shielding is expected to be about 20 %.

Table 2 lists the fitting parameters for the generic function: count (spacecraft 1) $=a\times \text{count}\left(\text{spacecraft 2}\right)+b$.

Table 2 Fitting parameters for the function count (spacecraft 1) $=a\times \text{count}\left(\text{spacecraft 2}\right)+b$, including their uncertainties.

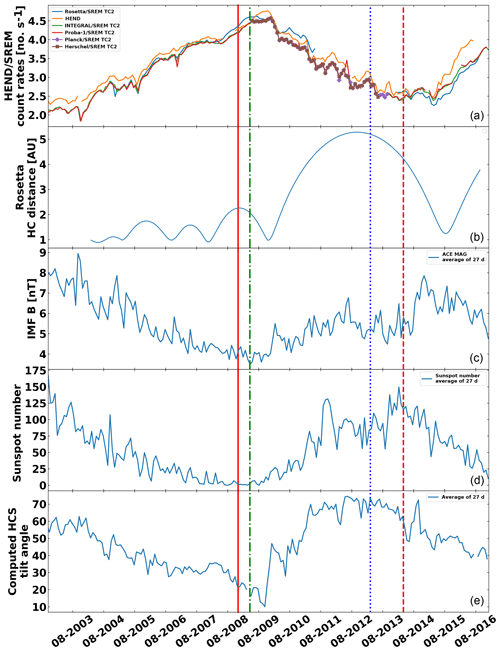
Figure 4 Temporal evolution of various datasets. (a) SREM and HEND count rates averaged over 27 d. (b) Rosetta heliocentric (HC) distances. (c) Interplanetary magnetic field measured by the MAG magnetometer aboard ACE at 1 AU. (d) Sunspot number. (e) Computed tilt angle of the heliospheric current sheet. The solid red vertical line indicates the minimum sunspot number, while the dashed vertical line indicates the maximum sunspot number. The dashed–dotted green vertical line indicates the peak of the Rosetta SREM count rate. The dotted blue line indicates the reversal of polarity of the average solar polar flux.

3 Data analysis

3.1 Overview of the data: GCR modulation

Having implemented the appropriate cross calibrations, a qualitative and quantitative comparison of the obtained datasets is possible. Data are averaged over 27 d in order to minimise longitudinal effects. Such longitudinal effects are illustrated in Appendix B. In the Fig. 4a, radiation data of Rosetta, INTEGRAL, Planck, Herschel, Proba-1 and HEND are shown. The SREM and HEND data are very well aligned throughout the whole epoch, although some differences stand out, in particular for HEND and Rosetta, which we associate with different heliospheric locations. The larger differences between HEND and INTEGRAL in 2015–2016 are not understood. The other panels display the Rosetta Heliocentric distances, the interplanetary magnetic field measured by the Advanced Composition Explorer (ACE) at 1 AU, the sunspot number and the computed tilt angle of the heliospheric current sheet. The peak count rate observed at Rosetta occurs in early 2009 (vertical green line), as the spacecraft passed through the aphelion of one of its orbits around the sun. This peak occurs during the long minimum solar activity and is well correlated with the minimum of the IMF of ∼ 4 nT. The HEND peak in late 2009 is coincident with the Rosetta peak, being about at the same heliocentric distance, and the Rosetta count rate is close to the values observed at 1 AU by INTEGRAL and Proba-1. The relative enhancement of the Rosetta count rate in 2010 is coincident with Rosetta's outbound leg, at heliocentric distances of ∼ 3.5 AU or more, shortly before rendezvous manoeuvres and hibernation, and again could be associated with the radial gradient of GCRs in the inner heliosphere. However, following hibernation exit in 2014, Rosetta's SREM count rates are similar to HEND even though Rosetta is ∼ 4.2 AU at this time. Shortly thereafter, surprisingly, the values dropped below the other measurements. This behaviour is discussed in Sect. 3.3.

Table 3 Radial gradients obtained for a given Rosetta-to-Sun distance, solar activity, interplanetary magnetic field and computed tilt angle for the mentioned periods. There are no obvious correlations between the radial gradient and the heliophysical parameters.

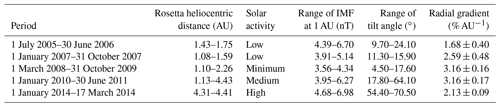
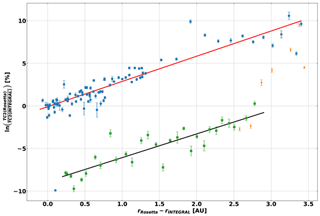
Figure 5 Logarithmic ratio of Rosetta and INTEGRAL SREM TC2 data drawn against the difference in heliocentric distance of Rosetta and INTEGRAL. The data in blue indicate the time before Rosetta's hibernation mode, the data in orange indicate the time right after hibernation mode until end of July 2014 and the data in green are from August 2014 until the end of the Rosetta mission in September 2016. The performed fits in red and black yield the corresponding radial gradients.

The count rates from all spacecraft display a long-term variation over ∼ 13 years, which we compare with various solar wind parameters. The IMF and solar wind measured by the ACE (Stone et a., 1998; Smith et al., 1998; McComas et al., 1998) along with the tilt of the heliospheric current sheet are plotted in the other panels of Fig. 4. The heliospheric current sheet (HCS) tilt is the maximum latitudinal extent of the HCS, computed using a potential field model applied to photospheric magnetic field observations (Hoeksema, 1995; Ferreira and Potgieter, 2003), showing the known solar cycle modulation of GCRs. In addition, the expected anticorrelation between GCR and IMF and sunspot number was analysed, and the result can be found in Appendix A. This anticorrelation is due to the modulation of GCR intensity. The GCR intensity decreases when the magnetic field and the solar activity increase due to the GCR diffusion in the solar wind. These “engineering” data are a new dataset that can be useful to study this modulation.

3.2 Helioradial gradient of cosmic rays

The availability of data from a family of instruments at different heliocentric distances allows the radial gradient of cosmic rays to be examined, providing an insight into the behaviour of the galactic cosmic ray propagation between 1 and 4.5 AU. The cosmic ray radial gradient is computed following the equation (Webber and Lockwood, 1991)

$$\begin{array}{}\text{(1)}& \text{Gr}=\ln (N_{\mathrm{2}}/N_{\mathrm{1}})/(r_{\mathrm{2}}-r_{\mathrm{1}}),\end{array}$$

where N is the count rate and r is the heliocentric radial distance at locations 1 and 2, where r₂>r₁. Since N values are count rates, Gr is an integral gradient.

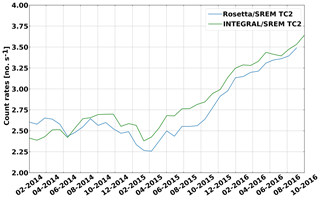
Figure 6 Zoom on the INTEGRAL and Rosetta SREM count rates during the period of the nominal Rosetta scientific mission. The Rosetta data clearly go below INTEGRAL in spring 2014.

The radial gradient was computed from the INTEGRAL and Rosetta dataset for selected periods of the Rosetta mission (e.g. in between planetary fly-bys), and the results are summarised in Table 3, which contains also some key heliophysical parameters.

Using Eq. (1) we consider the evolution of the radial gradient between Rosetta and INTEGRAL for the entire mission in Fig. 5, where the different coloured points indicate the different phase of the mission. Blue is pre-hibernation data, orange is January–July 2014 and green is July 2014–September 2016 data. A fit has been computed to the pre-hibernation data (red line) and the July 2014–September 2016 data (black line). During the pre-hibernation phase, the slope, which corresponds to the radial gradient, is found to be 2.96±0.12 % AU⁻¹. This positive gradient is mainly due to the inward diffusion of GCRs in an interplanetary magnetic field whose strength decreases with heliocentric distance. This result agrees well with previous studies for which the energy range can be compared with the TC2 range of ∼ 0.2–20 GeV (e.g. Vos and Potgieter, 2016 – range 0.1–10 GeV; Gieseler and Heber, 2016 – range 0.45–2 GeV). The slope during the comet phase (the start of this phase is marked by the red vertical bar in Fig. 1b) was found to be −2.8 % AU⁻¹ ± 0.12 % AU⁻¹. In Fig. 6, the count rate variation at Rosetta and INTEGRAL are shown. The drop in the count rate occurs during the approach phase, between February and May 2014. After that period (green points and black fit), the count rate variation and the ratio are in very good agreement with the expectation of a positive radial gradient of about 2.9 % AU⁻¹ (e.g. Vos and Potgieter, 2016; Gieseler and Heber, 2016).

3.3 Apparent attenuation of galactic cosmic ray flux in the vicinity of 67P

This section discusses the relative change in GCR counts at Rosetta compared to INTEGRAL during the comet phase of the mission in 2014. This change of behaviour can be observed in Fig. 6. The Rosetta counts, initially above INTEGRAL, rapidly decrease and remain below INTEGRAL for the rest of the time period. This change is illustrated in Fig. 5 by the black and red fits. A similar behaviour can be observed in all three channels or detectors of SREM. Comparing the two fits (red and black lines), the GCR fluxes after August 2014 are ∼ 8 % lower than expected from the pre-July 2014 data. We note that the count rates at Mars always stay higher than those registered near the Earth (see Fig. 4), even during the period shown in Fig. 6. This is consistent with a permanent positive GCR radial gradient and supports the reduction in the GCR rates at Rosetta compared to Earth being related to the comet approach.

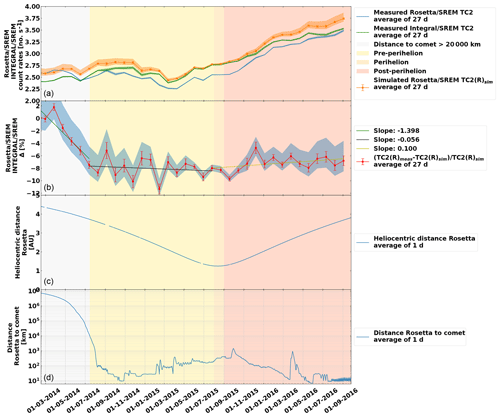
Figure 7 (a) INTEGRAL SREM data and measured and simulated Rosetta SREM data. (b) Computed GCR absorption. (c) Rosetta heliocentric distance. (d) Rosetta-to-nucleus distance. Colours in the background from left to right indicate different stages: when the Rosetta-to-comet distance was above 20 000 km (grey), the pre-perihelion phase (light yellow), the perihelion phase (darker yellow), and the post-perihelion phase (light red).

Another way of looking at this GCR attenuation during the Rosetta comet phase is to compute the ratio between the measured and the simulated Rosetta SREM TC2 count rate, assuming the calculated radial gradient during the Rosetta cruise phase. The results are displayed in Fig. 7. Figure 7b shows in particular the trend of the attenuation, which reaches a plateau of ∼ 8 %, which is relatively constant during the comet phase. For completeness, the Rosetta heliocentric and the spacecraft–comet distances are shown in Fig. 7c and d.

In order to discuss different reasons for this apparent attenuation, we looked for changes in environmental conditions. The attenuation effect coincides with the overall solar polarity change (the transition from an A<0 to an A>0 cycle). Previous studies have indicated a dependence of GCR fluxes with solar polarity (e.g. Potgieter et al., 2001), with radial gradients being smaller during A>0 cycles. Negative latitudinal gradients have been reported (e.g. Potgieter et al., 2001) but only for a fraction of 1 % ^∘−1 (Gieseler and Heber, 2016). During the comet phase, Rosetta moved from around −7.5 to +7.5^∘ heliolatitude, which could not account for the decrease in GCR fluxes. However, latitudinal gradients have only been reported during A<0 cycles, as opposed to the cycle 24, where A>0.

The decreasing ratio begins when Rosetta reaches around 20 000 km from the cometary nucleus and persists more or less at the same level until the end of the Rosetta mission. We cannot discern any anomalous Rosetta SREM instrumentation behaviour during the comet phase. For example, the period May–July 2014 coincided with several large rendezvous manoeuvres, where hundreds of kilograms of propellant material were used. A similar (in magnitude) series of manoeuvres were also implemented prior to hibernation in early 2011, suggesting that thruster-induced contamination or deterioration of the SREM detectors is not responsible. In addition, one would not expect the reduction of propellant within the fuel tanks to increase shielding. We note that INTEGRAL count rates are also consistent with Proba-1 measurements during this period, suggesting that both instruments are behaving nominally. For completeness, we checked that the separation with the Philae module in November 2014 did not have a noticeable effect.

We have considered the solid angle presented by the nucleus to have some impact on counts, with the comet angular size becoming as high as 30^∘ in November 2014 during lander delivery and ∼ 70^∘ in September 2016. However, for the majority of the time the angular size was < 10^∘ and insignificant (≪ 10^∘) when the “attenuation” began in early 2014, suggesting that the nucleus is not a major driver here.

Ground-based measurements of the comet indicate that cometary activity already began in February 2014 (Snodgrass et al., 2016), with Rosetta remote observations by the OSIRIS camera being able to resolve coma activity in March–April 2014, indicating a coma extent of around 1000 km at that time (Tubiana et al., 2015). However, it was not until August that the in situ instruments aboard Rosetta began to discern a coma signal, when the spacecraft got to within 100 km of the nucleus (Altwegg et al., 2015; Rotundi et al., 2015); thus, the transition in behaviour occurs before the spacecraft is immersed in the cometary coma. Nucleus activity and coma extent increases significantly in the subsequent months (e.g Hansen et al., 2016), yet with no corresponding change in the gradient of GCRs over this time. However, the potential shielding of the cometary gas and dust and associated plasma environment cannot be fully ruled out.

4 Discussion and concluding remarks

In this study, we have analysed data from the SREM instruments aboard several ESA spacecraft as well as the HEND instrument aboard Mars Odyssey. The combination of all these different instruments gives us multi-point observations of GCRs within the solar system, which constitute a very useful and rich dataset. It is important to note that the primary purpose of this dataset is engineering. However, the radiation monitors are highly valuable for pure scientific studies, as illustrated in this paper. Our first step was to calibrate the different SREM sensors aboard different spacecraft, such as Rosetta, INTEGRAL, Herschel, Planck and Proba-1. Then, the Rosetta data were also calibrated with respect to HEND aboard Mars Odyssey at Mars' distance.

In addition, the data are averaged over 27 d in order to avoid longitudinal effects. However, not doing so allows one to study time shifts between solar wind features between Earth and another location, as illustrated in Appendix B.

As a result, we have obtained a very useful dataset, which is totally calibrated, that gives us information of the evolution of GCRs with the solar cycle and heliocentric distance evolution. Some additional information regarding the GCR variability with respect to the interplanetary magnetic field (IMF) and sunspot number (SSN) can be found in the Appendix.

We have also demonstrated the value of the combination of such datasets in giving a broad view of the distribution of galactic cosmic rays in the inner heliosphere, both spatially and temporally. An important point has been the confirmation of the modulation of galactic cosmic rays with respect to solar activity as well as the anticorrelation with the interplanetary magnetic field. Also, thanks to the unique Rosetta trajectory within the inner solar system, the helioradial gradient of galactic cosmic rays between 1 and 4.5 AU was found to be 2.96 % AU⁻¹ (between 21 October 2004 and 21 May 2011), matching previous reports (e.g. Vos and Potgieter, 2016). This information provides insights into the behaviour of the galactic cosmic ray propagation within the inner heliosphere.

When considering the cometary phase of the Rosetta mission, from early 2014 to September 2016, the radial gradient changed, equivalent to an overall 8 % attenuation in the count rate, and reversed, with count rates at INTEGRAL being persistently greater than those at Rosetta, contrary to general expectations. We have considered several potential influences on these measurements to explain this observation, including heliospheric and more local environmental conditions. Although several aspects can be discounted for the GCR reduction in the comet environment, further work needs to be carried out on the nature of the overall cometary coma characteristics to quantify its potential impact along with heliospheric GCR modulation associated with the solar polarity changes. The combination of the extended minimum of solar cycle 23 with the weakest solar maximum (cycle 24) for a century, coincident with the time period under scrutiny, will also be examined.

In addition, other possible follow-up studies include a detailed temporal and spatial analysis of all the radiation datasets as well as short-scale variations in the GCR flux between close points, such as between Earth and Lagrange point L2 or when Rosetta did a fly-by to Earth and Mars.

Appendix A: Anticorrelation with interplanetary magnetic field and sunspot number

The anticorrelation between radiation monitor count rates and the IMF magnitude and sunspot number is evident (e.g. Cane et al., 1999; Potgieter, 2013; Mishra and Mishra, 2016, and reference therein) where the peak count rates at all spacecraft are coincident with the beginning of solar cycle 24 in December 2008. This period overall registered the highest overall GCR flux of the space age (Mewaldt et al., 2010), following one of the longest and deepest solar minimums for over a century. HEND and SREM counts subsequently decreased by around 50 % as the solar maximum was reached in April 2014. Figure A1 shows this anticorrelation for the Rosetta, INTEGRAL and HEND count rates, averaged over a solar rotation period (27 d).

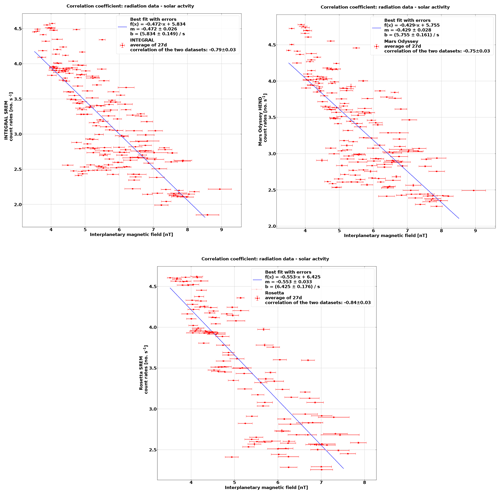
Figure A1 Anticorrelation of Rosetta, HEND and INTEGRAL radiation data with the IMF. The error bars for all data points correspond to the standard deviation.

Table A1 Correlation coefficients calculated based on 27 d averaged data from the radiation monitors.

The correlation coefficients, listed in Table A1, show the expected anticorrelation (e.g Cane et al., 1999; Belov, 2000; Utomo, 2017). IMF comparisons have a stronger correlation than the sunspot number at Rosetta, INTEGRAL and Proba-1 than Planck, Herschel and HEND. Planck and Herschel comparisons are over a shorter timescale during the rising phase of solar cycle 24, and HEND comparisons may be complicated by its indirect measurements of GCRs. Overall, however, the expected trends are present.

Appendix B: Time shift of solar wind features

GCR short temporal variations can be driven by coronal mass ejections (CMEs) and corotating interaction regions (CIRs; e.g. Moraal, 2013; Badruddin and Kumar, 2016; Sanchez-Cano et al., 2017; Witasse et al., 2017) and can influence the timing of signals at various locations in the heliosphere. To demonstrate this, we examine Rosetta and INTEGRAL data during the period from the middle until the end of 2007. In Fig. B1a, the count rates of channel TC2 of Rosetta (blue) and INTEGRAL (orange) are shown. The temporal delay in the measurement from the two spacecraft is clearly visible and decreases with time.

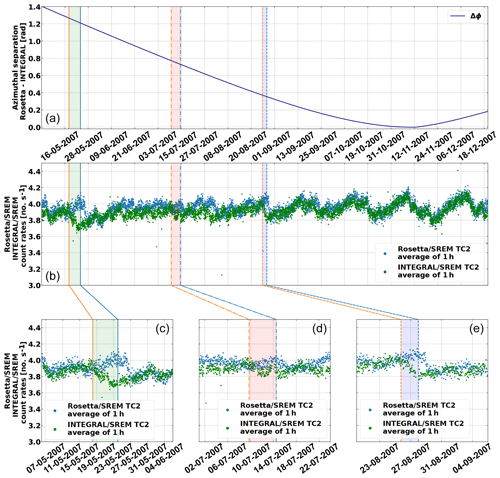
Figure B1 Solar wind feature shifts. (a) shows the azimuthal separation between Rosetta and INTEGRAL. (b) shows the count rates of channel TC2: the count rates of Rosetta SREM TC2 are plotted in blue, while INTEGRAL SREM data are plotted in green. (a) and (b) share the same x axis. (c–e) display a zoom of the three periods marked with vertical lines.

The other panels display a zoomed window of three periods, where correlated features or peaks are indicated in the corresponding datasets by straight, dashed–dotted and dashed vertical lines, with INTEGRAL in orange and Rosetta in blue. In May 2007, Rosetta was around 1.58 AU from the Sun and separated in longitude from the Earth by about 60^∘. In July 2007, Rosetta was around 1.55 AU from the Sun and longitudinally ∼ 45^∘ from Earth. Finally, in August 2007, Rosetta was around 1.4 AU and only ∼ 15^∘ from Earth longitudinally. The delay between INTEGRAL and Rosetta is 6 d and 2 h for the first event, 4 d and 18 h for the second event, and 2 d and 6 h for the third event in August 2007. These variations are related to the changing relative location and longitude of the spacecraft and Parker spiral configuration. In order to avoid these longitudinal effects, the data are averaged over 27 d (see Sect. 3.1).