the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Converging photospheric vortex flows close to the polarity inversion line of a fully emerged active region
Cristiano M. Wrasse
We report on the occurrence of vortexes in flow fields obtained from the evolution of the line-of-sight component of the photospheric magnetic field in a region around the polarity inversion line (PIL) of a fully emerged active region. Based on a local linear approximation for the flow field, we identify the presence of critical points and classify them according to the eigenvalues of the Jacobian matrix of the linear transformation. Converging vortexes are associated with the presence of a particular kind of critical point, known as the attracting focus. We identified 12 converging vortexes in the analyzed period and detected the occurrence of other types of critical points, which indicate the complexity of the flow field around the PIL. The detected vortexes show a clockwise preferred sense of rotation with approximately 67 % of the cases. A geometrical analysis of the velocity structures produced an average value of for the fractal dimension, which is very close to the one obtained for isotropic homogeneous turbulence (). This suggests that the flow around the PIL is turbulent in nature.
- Article
(5954 KB) - Full-text XML
- BibTeX
- EndNote
Horizontal flow fields in the solar photosphere have an important role in the concentration and dispersal of surface magnetic flux. To give some examples, surface flows are responsible for magnetic flux concentration at the border of the convection cells (magnetic network), they disperse the magnetic flux of active regions (turbulent diffusion) and they transport the magnetic flux to the poles (meridional flow). Horizontal flows may also contribute to magnetic energy and helicity injection into the upper atmosphere by twisting and interweaving the foot points of flux tubes, generating field-aligned currents and magnetohydrodynamic waves, and also may be responsible for the occurrence of magnetic reconnection by bringing together opposite magnetic polarity regions. Therefore, the investigation of photospheric horizontal motion patterns responsible for the evolution of magnetic features in the solar photosphere may give some clues for understanding how the combination of these two quantities, the magnetic field and flow field, influence the solar activity.
In this sense, vortex or rotational-motion patterns are particularly important for solar activity. In the quiet Sun, convective flows concentrate magnetic fields in the downdraft regions of the convective cells. The conservation of angular momentum forces the plasma to rotate around the center of the downdraft, generating small-scale vortexes. These vortexes have been extensively detected in observations of the photosphere (Brandt et al., 1988; Simon and Weiss, 1997; Attie et al., 2009; Bonet et al., 2010; Balmaceda et al., 2010; Vargas Domínguez et al., 2011) and also have been observed in the quiet Sun chromosphere as a signature of plasma moving along curly magnetic field lines in coronal holes (Wedemeyer-Böhm and Rouppe van der Voort, 2009). Simulations indicate that the vortexes occurring in strongly magnetized regions are closely connected with dissipation processes providing localized heating in the lower parts of the solar atmosphere (Moll et al., 2012), and observations usually associate vortex detection with bright points (Bonet et al., 2008).
On larger scales, rotational motions were observed in sunspots, and they are usually associated with energy and helicity buildup and later release by flare and/or coronal mass ejection (Brown et al., 2003; Hiremath and Suryanarayana, 2003; Hiremath et al., 2005; Yan and Qu, 2007; Yan et al., 2008, 2009, 2012; Min and Chae, 2009; Kazachenko et al., 2010; Zhu et al., 2012; Jiang et al., 2012; Vemareddy et al., 2012, 2016; Hardersen et al., 2013; Wang et al., 2014, 2016; Ruan et al., 2014; Gopasyuk, 2015; Li and Liu, 2015; Suryanarayana et al., 2015). The rotation of sunspots is usually very slow; this means that the evolution of the magnetic field in the corona associated with it would be slow as well. However, strong flares (M- or X-class) are sometimes associated with rapid (abnormal) sunspot rotation. At the moment there is not a defined mechanism to explain sunspot rotation. It is suggested that it could be a result of the interaction of the flux tube with photospheric flows, during or after its emergence, or the effect of the emergence of a twisted flux tube. Changes of rotational pattern of the sunspot after the flare occurrence were also observed (Liu et al., 2016; Bi et al., 2016), and they are associated with Lorentz forces. In this work, we investigate the properties of the flow field obtained from the evolution of photospheric magnetic features around the polarity inversion line (PIL) of a fully emerged active region (AR). We targeted the PIL, since it is the place where opposite polarity magnetic fields interact and where sharp changes are usually associated with the onset of flares (Severnyi, 1958; Wang et al., 1994; Kosovichev and Zharkova, 2001; Sudol and Harvey, 2005; Sharykin et al., 2017). We first focus on the detection and classification of critical points. Critical points are points where the velocity vanishes, and their importance resides in the fact that the flow may be directed to and rotate around these points, forcing opposite polarities to meet and annihilate there and contributing to the energetics of the solar atmosphere. The critical points are used to identify the presence of converging vortex flows in the region around the PIL. Finally, we investigate the geometric structure of the flow by calculating its the fractal dimension and use it as an indication that the flow around the PIL presents turbulent nature.
We selected as our target the AR NOAA 9289, located at the southern solar hemisphere. Figure 1 shows the full-disk line-of-sight (LOS) component of the photospheric magnetic field (Fig. 1a) and a close view of AR NOAA 9289 (Fig. 1b), as measured by the Michelson Doppler Imager (MDI) (Scherrer et al., 1995) on 2 January 2001 at 04:51:01 UT. The MDI instrument obtains images of the full disk of the Sun using a 1024×1024 pixel CCD camera, with a spatial resolution of 2 arcsec per pixel and a temporal resolution of 96 min. The noise level of the instrument is about 7.6 G (1 G) in the 96 min full-disk mode. In Fig. 1, the LOS magnetic field (BLOS) is saturated at ±100 G for a better visualization of the magnetic features. The AR consisted of a large bipolar magnetic field with a leading negative polarity and a following positive polarity region. From 31 December 2000 to 3 January 2001 the region was fully emerged, and its leading sunspot was seen rotating about 50∘ clockwise with an average speed of 0.56∘ h−1 (Zhu et al., 2012). This clockwise rotation may cause a shear in the polarity inversion line, increasing the energy and relative helicity flow out of the photospheric plane around that region. As shown in Fig. 1, there was a smaller bipolar AR close to AR NOAA 9289.
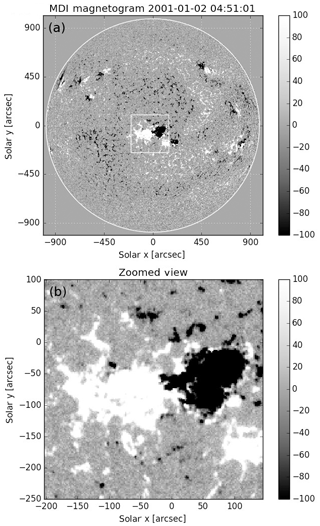
Figure 1Full-disk LOS magnetic field (a) and close view of AR NOAA 9289 (b) as measured by the MDI–SoHO (SoHO – Solar and Heliospheric Observatory) instrument on 2 January 2001 at 04:51:01 UT.
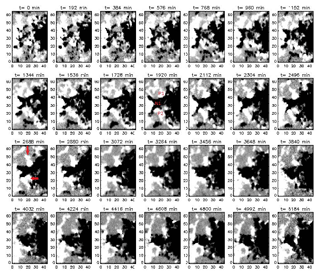
Figure 2Evolution of the LOS component of the magnetic field around the PIL for the period of 3.6 d starting on 31 December 2000 at 01:34:43 UT. The x and y axes show the spatial coordinates in pixel values, where each pixel corresponds approximately to 1.2 arcsec.
We focus on a region of approximately 54 arcsec×78 arcsec around the PIL and follow the evolution of BLOS for a period of 3.6 d starting on 31 December 2000 at 01:34:43 UT. Figure 2 displays the BLOS measurements with a cadence of 192 min. The x and y axes show the spatial coordinates in pixel values, where each pixel corresponds approximately to 1.2 arcsec. During this period, AR NOAA 9289 crossed the center of the solar disk, and the LOS component of the photospheric magnetic field is considered identical to component perpendicular to the photosphere. In case the AR is far from the disk center, a correction would be necessary to find the perpendicular component, since the LOS component does not correspond to the perpendicular component anymore. Visual inspection shows that initially the magnetic field around the PIL is very fragmented, with very small positive and negative polarity regions being randomly distributed. These fragmented polarities start to coalesce, forming a negative polarity region (N1), connected to the AR main negative polarity, and two smaller positive polarity regions, one north of the negative polarity (P1) and other south (P2). The positive polarities P1 and P2 coalesce with two smaller positive polarity regions that were located around them, indicated by red arrows in the figure. Later, the positive polarity P2 connects to the AR main positive polarity. During this process, it seems that the negative polarity (N1) deforms while the positive polarity (P1) protrudes into it, which could be a triggering mechanism for flare occurrence (Kusano et al., 2012; Toriumi et al., 2013). Finally, the negative polarity N1 starts to rotate clockwise around itself, and the positive polarity P1 starts to rotate in the same sense around N1, moving between N1 and the leading negative polarity. As discussed in Toriumi et al. (2013) for AR NOAA 11156, the evolution of the small-scale magnetic field around the PIL may increase the shear and contribute to the triggering of strong flares.
To determine the velocity field responsible for the changes observed in the BLOS component of the magnetic field, we used the local correlation tracking (LCT) technique (November and Simon, 1988). More specifically, we have used a Fourier-based local correlation tracking (FLCT) implementation described in Welsch et al. (2004). The LCT–FLCT velocity indicates the apparent movement of the foot point of the magnetic field lines. If we assume that the photospheric field is vertical due to the buoyancy of magnetic flux tubes, then a sequence of images will show the horizontal motion of the foot points of the magnetic flux tubes. The velocity is locally determined by cross correlating a small fraction of two subsequent images shifted by variable displacement. The shift having the highest correlation shows the relative displacement, and the tracking velocity is obtained by dividing this displacement by the time interval between two images of a sequence. This velocity is used as a proxy for the tangential plasma velocity.
Unfortunately, there are some issues regarding the LCT–FLCT method. As pointed by Démoulin and Berger (2003), if the flux tube is inclined when it rises through the solar atmosphere, the point where it crosses the photosphere moves horizontally. This apparent motion can be interpreted by the LCT–FLCT method as a proper horizontal motion, and Démoulin and Berger (2003) suggested a correction if the tangential component of the magnetic field and the vertical component of the velocity are known. Since in our case the AR does not emerge, i.e. has no vertical motions, this correction is not necessary. Another issue, pointed by Schuck (2005), is that LCT–FLCT does not permit any contraction, dilation or rotation of the magnetic fluid on the scale of the apodizing window. Schuck (2005, 2008) suggested combining the LCT–FLCT with the difference affine method, in a method called the difference affine velocity estimator (DAVE), to account for the convergence and divergence in the flow as well as for higher-order parametric profiles. Finally, the LCT–FLCT method considers that the vertical component of the magnetic field evolves according the advection equation, while in fact it evolves according the induction equation. Different methods for obtaining the horizontal velocity from the evolution of the normal component of the magnetic field that obey the induction equation are available (Welsch et al., 2004; Longcope, 2004; Schuck, 2008). However, they usually require extra information about the horizontal component of the magnetic field and the vertical component of the velocity or they impose some restrictions to the velocity field.
For the sake of simplicity, and because we have information only about the temporal evolution of BLOS, we decided to use the LCT–FLCT method even when we knew about the issues that the application of the method imply. We use the time of the sample of the BLOS component (≈192 min) and select a full-width half-maximum (FWHM) window of five pixels (≈6 arcsec) to perform the localized cross-correlation. In applying the LCT–FLCT method we considered BLOS to be a passive scalar and assumed that all the changes observed in Fig. 2 are due the horizontal displacement of the magnetic features, with no flux emergence or submergence.
2.1 Critical point detection and classification
Photospheric vortexes are important, since they can form twisted flux tubes, transporting magnetic energy and helicity to upper layers of the solar atmosphere in the process. They are usually detected by visual inspections and, since this may cause a bias in the analysis of vortexes, efforts in developing automated detection methods have been recently performed (Kato and Wedemeyer, 2017; Rempel et al., 2017; Giagkiozis et al., 2018). In this work, we intend to contribute to the development of automated methods of vortex detection by using a well-known method of detection and classification of critical points (Helman and Hesselink, 1989) to identify converging vortexes by associating them with a specific kind of critical point.
In a 2-D flow field the velocity vector is given at any point as . If we consider a linear vector field approximation, the velocity vector components can be written in terms of the (x,y) coordinate components as
and where the following equation,
is the Jacobian matrix of the transformation.
So, to represent the velocity vector in a linear approximation, we need to know the values of the constants a, b, c, d, e and f. To find the values of the constants, it is necessary to consider the velocity vector in at least three points around the region of interest (ROI) in order to solve the following linear system of equations:
for a, b and c, and the linear system of equations
for d, e and f. We solve the set of simultaneous linear equations of the form Ax=b by back-substitution using the IDL functions SVDC and SVSOL.
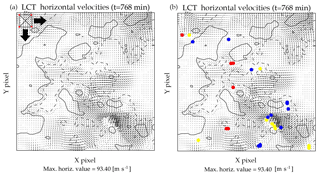
Figure 3(a) Illustration of the method for automatic search of critical points in a 2-D flow field. (b) Results obtained using the automatic search for the LCT flow field at t=768 min. The circles show the location of the suggested critical points, and the colors show their classification (blue is saddle point, red is attracting node or focus, and yellow is repelling node or focus).
Table 1Classification of critical points according to the values of the real (R) and imaginary (I) parts of the eigenvalues.

Once the linear representation of the field is available, we can use Eq. (1) to check if there is a critical point inside the ROI. Critical points may be interpreted as the fixed points of a map. Given the location of such a points and their types, the behavior of the orbit of the particles can be predicted around them. Also, critical points are the only points where the flow field lines are allowed to intersect. A critical point is characterized by a flow velocity given by . Then, in a linear vector field approximation, to find the coordinates of the critical point, we have to solve a matrix equation like
for x and y. The solution of this equation gives the (x,y) coordinates of the critical point if it exists.
From the eigenvalues of the Jacobian matrix, given by the solution of
we can classify the critical point according to Helman and Hesselink (1989), as presented in Table 1. We find the eigenvalues by first reducing the Jacobian matrix to the upper Hessenberg form using the ELMHES function in IDL and then returning the eigenvalues by applying the HQR function.
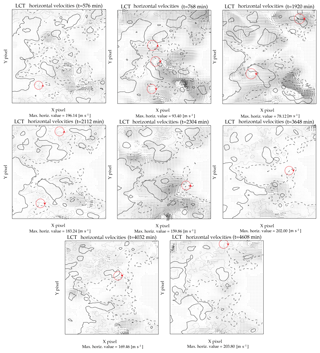
Figure 4Location of the detected vortex flows in the 2-D LCT flow fields obtained from the evolution of the magnetic structures around the PIL of a fully developed active region. The red circles indicate their location, and the arrows indicate the direction of rotation.
To automatically search for critical points, we scan the 2-D LCT–FLCT vector field using a rectangle of size (Δx, Δy). Figure 3a shows an illustration of the process for the vector field obtained at t=768 min. Using the information of the flow and the coordinates at three corners of the rectangle, we perform the calculations described previously to search for critical points and classify them. By choosing different corners we cover the whole area inside the rectangle, and after the calculation is finished we move the rectangle in the x direction by Δx and start the calculations again until the end of the line is reached. We then go to the next line by moving the rectangle Δy in the vertical direction until the complete 2-D flow field is covered. Figure 3b shows the result of this calculation, where the circles indicate the position of the suggested critical points. The different colors indicate the classification of the critical points: blue is the saddle point, red is attracting node or focus, and yellow is the repelling node or focus. The solid (dashed) contour line indicates the regions where BLOS equals the value of +100 G (−100 G).
The results are sensitive to the size of the rectangle and should be cross-checked by visual inspection, since the calculations may produce false positive cases or even miss some critical points. This cross-check may be performed with the original 2-D flow field, a renormalized one or any visualization that could facilitate the identification of the critical points like the line integral convolution (LIC) technique, for example.
2.2 Fractal dimension and the box-counting method
A fractal is defined as a set for which the Hausdorff–Besicovitch dimension (fractal dimension) exceeds the topological dimension (Mandelbrot, 1982). To calculate the fractal dimension of an image, we use the box-counting method. In this method, an image is covered by a sequence of grids of decreasing sizes, and for each of the grids we compute the number of square boxes intersected by the image, N(s), and the side length of the squares, s. The regression slope D of the straight line formed by plotting log (N(s)) against log (1∕s) indicates the degree of complexity, or fractal dimension, between 1 and 2 ():
Mandelbrot (1975) suggested that turbulent shapes require a proper geometrical description. For isoscalar surfaces in 3-D homogeneous turbulence, he argued for a fractal dimension , which corresponds to in two dimensions, if turbulence could be described as possessing Kolmogorov–Gauss scaling (Mandelbrot, 1975, 1982).
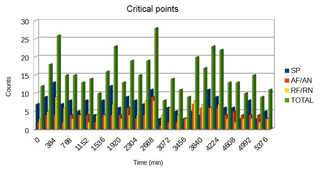
Figure 5Noncumulative counts of critical points detected on the 2-D LCT flows obtained from the evolution of the magnetic field around the PIL for the period of 3.6 d. The colors show their classification: blue is saddle point (SP), red is attracting node or focus (AN/AF), and yellow is repelling node or focus (RN/RF).

Figure 6Time evolution of the regions where the velocity is above the threshold value of v=23.6 m s−1, shown in black, for a period of 3.6 d starting on 31 December 2000 at 01:34:43 UT. The x and y axes show the spatial coordinates in pixel values, where each pixel corresponds approximately to 1.2 arcsec.
We apply the method described in Sect. 2 to identify and classify the critical points in the data cube containing the 2-D LCT–FLCT flow fields for the 3.6 d period starting on 31 December 2000 at 01:34:43 UT. Before we apply the method, each flow field is resampled to have 128×128 data points. We use a rectangle of 2×2 to scan the flow field, since this is the resolution necessary to detect the smallest structures in the flow field. We select only the critical points classified as an attracting focus and cross-check the results with a flow field normalized in a way that all the flow vectors have the same size. These critical points are associated with vortex flows converging to them.
Figure 4 shows the 2-D flow fields and the positions (red circles) where the presence of converging vortex flows were confirmed. We identified the occurrence of 12 converging vortexes in the LCT–FLCT flow field obtained from the evolution of the LOS photospheric magnetic field around the PIL for a period of 3.6 d. The arrows in Fig. 4 show the direction of rotation, with about 67 % (eight) of the cases rotating clockwise and 33 % (four) counterclockwise. This shows a preference for clockwise rotation in the set of converging vortexes detected around the PIL.
Our investigation also shows that critical points are always present in the LCT–FLCT flow fields for the period analyzed. Their total number varies with time, and saddle points are the most commonly detected type of critical point, with a total of 213 detected in the period of 3.6 d. Figure 5 shows a rough estimation of the noncumulative number of critical points computed for each time instant analyzed. This result probably reflects the complexity of the flow field around the PIL, since the lines connecting the critical points (separatrices) separate different flow regions. The detection method produced an accuracy of approximately 70 % in finding the critical points in the complex velocity fields obtained by LCT–FLCT.
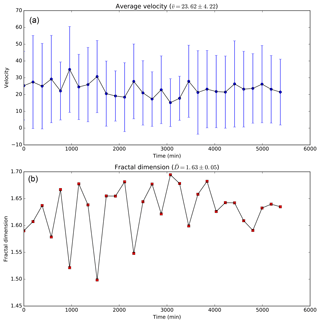
Figure 7Temporal evolution of the average velocity (a) and fractal dimension (b) for the flow around the PIL.
We also investigate the geometric aspect of the flow by calculating its fractal dimension. It describes how detail in a pattern changes with the scale at which it is measured and provides a measure of geometrical complexity (Mandelbrot, 1982). To perform this calculation we apply a mask to the flow field, selecting only the regions where the velocity amplitude is larger than v=23.6 m s−1. Figure 6 shows the time evolution of the distribution of the regions where the velocity amplitude is above the threshold, shown in black. We want to measure the fractal dimension of those structures. The selected threshold corresponds to the average of the velocities presented Fig. 7a.
The fractal dimension is calculated using the box-counting method described in Sect. 2. Figure 7b shows the results obtained for each time instant. They result in an average fractal dimension of . This fractal dimension is very close to the one obtained for homogeneous turbulence (), suggesting the occurrence of a turbulent flow around the PIL. Since fully developed turbulence consists of a hierarchy of eddies, we expect that vortex flows will be a common feature of the flow field around the PIL.
We have investigated the LCT–FLCT flow fields obtained from the evolution of BLOS in a region around the PIL for the presence of converging vortex flows. To perform this, we first look for the presence of critical points, using a linear approximation of the flow field, and classify them according to the eigenvalues of the Jacobian matrix of the linear transformation. Then, we sort a particular type of critical point called the attracting focus, which is associated with converging vortex flows. This procedure facilitates the visual identification of vortexes in the 2-D photospheric flow fields, and in our results we have identified a total of 12 converging vortexes in a period of 3.6 d. These converging vortexes show a clockwise preferred sense of rotation with approximately 67 % of the cases. The attracting focus is not the only kind of critical point detected, with the most common type being saddle points, with 213 detected in a 3.6 d period. These results reveal the complexity of the flow field around the PIL and suggest, together with previous results, that vortex flows are indeed a relatively common feature in the solar photosphere. By calculating the fractal dimension of the regions where the velocity is larger than a threshold value of v=23.6 m s−1, we obtain an average value of , which is very close to the values obtained for a homogeneous turbulence (). This reinforces the complexity of the flow around the PIL, suggesting that it presents a turbulent nature.
The data used in this work are made publicly available by the MDI–SoHO team. The algorithms used in this work may be provided upon request via e-mail (jeansantos@utfpr.edu.br).
JCS initiated the idea, selected the case study, prepared the data, and developed the algorithms to identify and classify the critical points and to calculate the fractal dimension. CMW contributed to the development of the algorithm to identify and classify the critical points and in the discussion of the results. All authors contributed to the discussion and the writing of the final paper.
The authors declare that they have no conflict of interest.
This article is part of the special issue “7th Brazilian meeting on space geophysics and aeronomy”. It is a result of the Brazilian meeting on Space Geophysics and Aeronomy, Santa Maria/RS, Brazil, 5–9 November 2018.
The authors would like to thank the anonymous referees for comments and suggestions, which helped to improve the quality of the article. This work was supported by the CNPq under the project 307653/2017-0. Jean C. Santos would like to thank the CNPq for the PCI-E2 postdoc fellowship under the individual project 300890/2017-6.
This research has been supported by the CNPq (grant no. 307653/2017-0).
This paper was edited by Marcos D. Silveira and reviewed by three anonymous referees.
Attie, R., Innes, D. E., and Potts, H. E.: Evidence of photospheric vortex flows at supergranular junctions observed by FG/SOT (Hinode), Astron. Astrophys., 493, L13–L16, https://doi.org/10.1051/0004-6361:200811258, 2009. a
Balmaceda, L., Vargas Domínguez, S., Palacios, J., Cabello, I., and Domingo, V.: Evidence of small-scale magnetic concentrations dragged by vortex motion of solar photospheric plasma, Astron. Astrophys., 513, L6, https://doi.org/10.1051/0004-6361/200913584, 2010. a
Bi, Y., Jiang, Y., Yang, J., Hong, J., Li, H., Yang, B., and Xu, Z.: Observation of a reversal of rotation in a sunspot during a solar flare, Nat. Commun., 7, 13798, https://doi.org/10.1038/ncomms13798, 2016. a
Bonet, J. A., Márquez, I., Sánchez Almeida, J., Cabello, I., and Domingo, V.: Convectively Driven Vortex Flows in the Sun, Astrophys. J., 687, L131, https://doi.org/10.1086/593329, 2008. a
Bonet, J. A., Márquez, I., Sánchez Almeida, J., Palacios, J., Martínez Pillet, V., Solanki, S. K., del Toro Iniesta, J. C., Domingo, V., Berkefeld, T., Schmidt, W., Gandorfer, A., Barthol, P., and Knölker, M.: SUNRISE/IMaX Observations of Convectively Driven Vortex Flows in the Sun, Astrophys. J., 723, L139–L143, https://doi.org/10.1088/2041-8205/723/2/L139, 2010. a
Brandt, P. N., Scharmer, G. B., Ferguson, S., Shine, R. A., and Tarbell, T. D.: Vortex flow in the solar photosphere, Nature, 335, 238–240, https://doi.org/10.1038/335238a0, 1988. a
Brown, D. S., Nightingale, R. W., Alexander, D., Schrijver, C. J., Metcalf, T. R., Shine, R. A., Title, A. M., and Wolfson, C. J.: Observations of Rotating Sunspots from TRACE, Sol. Phys., 216, 79–108, https://doi.org/10.1023/A:1026138413791, 2003. a
Démoulin, P. and Berger, M. A.: Magnetic Energy and Helicity Fluxes at the Photospheric Level, Sol. Phys., 215, 203–215, https://doi.org/10.1023/A:1025679813955, 2003. a, b
Giagkiozis, I., Fedun, V., Scullion, E., Jess, D. B., and Verth, G.: Vortex Flows in the Solar Atmosphere: Automated Identification and Statistical Analysis, Astrophys. J., 869, 169, https://doi.org/10.3847/1538-4357/aaf797, 2018. a
Gopasyuk, O. S.: Rotation of sunspots in active region NOAA 10930, Adv. Space Res., 55, 937–941, https://doi.org/10.1016/j.asr.2014.09.005, 2015. a
Hardersen, P. S., Balasubramaniam, K. S., and Shkolyar, S.: Chromospheric Mass Motions and Intrinsic Sunspot Rotations for NOAA Active Regions 10484, 10486, and 10488 Using ISOON Data, Astrophys. J., 773, 60, https://doi.org/10.1088/0004-637X/773/1/60, 2013. a
Helman, J. and Hesselink, L.: Representation and display of vector field topology in fluid flow data sets, Computer, 22, 27–36, https://doi.org/10.1109/2.35197, 1989. a, b
Hiremath, K. M. and Suryanarayana, G. S.: The flares associated with the abnormal rotation rates of the bipolar sunspots: Reconnection probably below the surface, Astron. Astrophys., 411, L497–L500, https://doi.org/10.1051/0004-6361:20031618, 2003. a
Hiremath, K. M., Suryanarayana, G. S., and Lovely, M. R.: Flares associated with abnormal rotation rates: Longitudinal minimum separation of leading and following sunspots, Astron. Astrophys., 437, 297–302, https://doi.org/10.1051/0004-6361:20042495, 2005. a
Jiang, Y., Zheng, R., Yang, J., Hong, J., Yi, B., and Yang, D.: Rapid Sunspot Rotation Associated with the X2.2 Flare on 2011 February 15, Astrophys. J., 744, 50, https://doi.org/10.1088/0004-637X/744/1/50, 2012. a
Kato, Y. and Wedemeyer, S.: Vortex flows in the solar chromosphere. I. Automatic detection method, Astron. Astrophys., 601, A135, https://doi.org/10.1051/0004-6361/201630082, 2017. a
Kazachenko, M. D., Canfield, R. C., Longcope, D. W., and Qiu, J.: Sunspot Rotation, Flare Energetics, and Flux Rope Helicity: The Halloween Flare on 2003 October 28, Astrophys. J., 722, 1539–1546, https://doi.org/10.1088/0004-637X/722/2/1539, 2010. a
Kosovichev, A. G. and Zharkova, V. V.: Magnetic Energy Release and Transients in the Solar Flare of 2000 July 14, Astrophys. J., 550, L105–L108, https://doi.org/10.1086/319484, 2001. a
Kusano, K., Bamba, Y., Yamamoto, T. T., Iida, Y., Toriumi, S., and Asai, A.: Magnetic Field Structures Triggering Solar Flares and Coronal Mass Ejections, Astrophys. J., 760, 31, https://doi.org/10.1088/0004-637X/760/1/31, 2012. a
Li, A. and Liu, Y.: Sunspot Rotation and the M-Class Flare in Solar Active Region NOAA 11158, Sol. Phys., 290, 2199–2209, https://doi.org/10.1007/s11207-015-0745-5, 2015. a
Liu, C., Xu, Y., Cao, W., Deng, N., Lee, J., Hudson, H. S., Gary, D. E., Wang, J., Jing, J., and Wang, H.: Flare differentially rotates sunspot on Sun's surface, Nat. Commun., 7, 13104, https://doi.org/10.1038/ncomms13104, 2016. a
Longcope, D. W.: Inferring a Photospheric Velocity Field from a Sequence of Vector Magnetograms: The Minimum Energy Fit, Astrophys. J., 612, 1181–1192, https://doi.org/10.1086/422579, 2004. a
Mandelbrot, B. B.: On the geometry of homogeneous turbulence, with stress on the fractal dimension of the iso-surfaces of scalars, J. Fluid Mech., 72, 401–416, https://doi.org/10.1017/S0022112075003047, 1975. a, b
Mandelbrot, B. B.: The fractal geometry of nature, W. H. Freeman and Company, New York, 1982. a, b, c
Min, S. and Chae, J.: The Rotating Sunspot in AR 10930, Sol. Phys., 258, 203–217, https://doi.org/10.1007/s11207-009-9425-7, 2009. a
Moll, R., Cameron, R. H., and Schüssler, M.: Vortices, shocks, and heating in the solar photosphere: effect of a magnetic field, Astron. Astrophys., 541, A68, https://doi.org/10.1051/0004-6361/201218866, 2012. a
November, L. J. and Simon, G. W.: Precise proper-motion measurement of solar granulation, Astrophys. J., 333, 427–442, https://doi.org/10.1086/166758, 1988. a
Rempel, E. L., Chian, A. C. L., Beron-Vera, F. J., Szanyi, S., and Haller, G.: Objective vortex detection in an astrophysical dynamo, Mon. Not. R. Astron. Soc., 466, L108–L112, https://doi.org/10.1093/mnrasl/slw248, 2017. a
Ruan, G., Chen, Y., Wang, S., Zhang, H., Li, G., Jing, J., Su, J., Li, X., Xu, H., Du, G., and Wang, H.: A Solar Eruption Driven by Rapid Sunspot Rotation, Astrophys. J., 784, 165, https://doi.org/10.1088/0004-637X/784/2/165, 2014. a
Scherrer, P. H., Bogart, R. S., Bush, R. I., Hoeksema, J. T., Kosovichev, A. G., Schou, J., Rosenberg, W., Springer, L., Tarbell, T. D., Title, A., Wolfson, C. J., Zayer, I., and MDI Engineering Team: The Solar Oscillations Investigation – Michelson Doppler Imager, Sol. Phys., 162, 129–188, https://doi.org/10.1007/BF00733429, 1995. a
Schuck, P. W.: Local Correlation Tracking and the Magnetic Induction Equation, Astrophys. J., 632, L53–L56, https://doi.org/10.1086/497633, 2005. a, b
Schuck, P. W.: Tracking Vector Magnetograms with the Magnetic Induction Equation, Astrophys. J., 683, 1134–1152, https://doi.org/10.1086/589434, 2008. a, b
Severnyi, A. B.: Nonstationary Processes in Solar Flares as a Manifestation of the Pinch Effect, Soviet Astronomy, 2, 310–325, 1958. a
Sharykin, I. N., Sadykov, V. M., Kosovichev, A. G., Vargas-Dominguez, S., and Zimovets, I. V.: Flare Energy Release in the Lower Solar Atmosphere near the Magnetic Field Polarity Inversion Line, Astrophys. J., 840, 84, https://doi.org/10.3847/1538-4357/aa6dfd, 2017. a
Simon, G. W. and Weiss, N. O.: Kinematic Modeling of Vortices in the Solar Photosphere, Astrophys. J., 489, 960–967, https://doi.org/10.1086/304800, 1997. a
Sudol, J. J. and Harvey, J. W.: Longitudinal Magnetic Field Changes Accompanying Solar Flares, Astrophys. J., 635, 647–658, https://doi.org/10.1086/497361, 2005. a
Suryanarayana, G. S., Hiremath, K. M., Bagare, S. P., and Hegde, M.: Abnormal rotation rates of sunspots and durations of associated flares, Astron. Astrophys., 580, A25, https://doi.org/10.1051/0004-6361/201423389, 2015. a
Toriumi, S., Iida, Y., Bamba, Y., Kusano, K., Imada, S., and Inoue, S.: The Magnetic Systems Triggering the M6.6 Class Solar Flare in NOAA Active Region 11158, Astrophys. J., 773, 128, https://doi.org/10.1088/0004-637X/773/2/128, 2013. a, b
Vargas Domínguez, S., Palacios, J., Balmaceda, L., Cabello, I., and Domingo, V.: Spatial distribution and statistical properties of small-scale convective vortex-like motions in a quiet-Sun region, Mon. Not. R. Astron. Soc., 416, 148–154, https://doi.org/10.1111/j.1365-2966.2011.19048.x, 2011. a
Vemareddy, P., Ambastha, A., and Maurya, R. A.: On the Role of Rotating Sunspots in the Activity of Solar Active Region NOAA 11158, Astrophys. J., 761, 60, https://doi.org/10.1088/0004-637X/761/1/60, 2012. a
Vemareddy, P., Cheng, X., and Ravindra, B.: Sunspot Rotation as a Driver of Major Solar Eruptions in the NOAA Active Region 12158, Astrophys. J., 829, 24, https://doi.org/10.3847/0004-637X/829/1/24, 2016. a
Wang, H., Ewell Jr., M. W., Zirin, H., and Ai, G.: Vector magnetic field changes associated with X-class flares, Astrophys. J., 424, 436–443, https://doi.org/10.1086/173901, 1994. a
Wang, R., Liu, Y. D., Wiegelmann, T., Cheng, X., Hu, H., and Yang, Z.: Relationship Between Sunspot Rotation and a Major Solar Eruption on 12 July 2012, Sol. Phys., 291, 1159–1171, https://doi.org/10.1007/s11207-016-0881-6, 2016. a
Wang, S., Liu, C., Deng, N., and Wang, H.: Sudden Photospheric Motion and Sunspot Rotation Associated with the X2.2 Flare on 2011 February 15, Astrophys. J., 782, L31, https://doi.org/10.1088/2041-8205/782/2/L31, 2014. a
Wedemeyer-Böhm, S. and Rouppe van der Voort, L.: Small-scale swirl events in the quiet Sun chromosphere, Astron. Astrophys., 507, L9–L12, https://doi.org/10.1051/0004-6361/200913380, 2009. a
Welsch, B. T., Fisher, G. H., Abbett, W. P., and Regnier, S.: ILCT: Recovering Photospheric Velocities from Magnetograms by Combining the Induction Equation with Local Correlation Tracking, Astrophys. J., 610, 1148–1156, https://doi.org/10.1086/421767, 2004. a, b
Yan, X. L. and Qu, Z. Q.: Rapid rotation of a sunspot associated with flares, Astron. Astrophys., 468, 1083–1088, https://doi.org/10.1051/0004-6361:20077064, 2007. a
Yan, X.-L., Qu, Z.-Q., and Kong, D.-F.: Relationship between rotating sunspots and flare productivity, Mon. Not. R. Astron. Soc., 391, 1887–1892, https://doi.org/10.1111/j.1365-2966.2008.14002.x, 2008. a
Yan, X.-L., Qu, Z.-Q., Xu, C.-L., Xue, Z.-K., and Kong, D.-F.: The causality between the rapid rotation of a sunspot and an X3.4 flare, Res. Astron. Astrophys., 9, 596–602, https://doi.org/10.1088/1674-4527/9/5/010, 2009. a
Yan, X. L., Qu, Z. Q., Kong, D. F., and Xu, C. L.: Sunspot Rotation, Sigmoidal Filament, Flare, and Coronal Mass Ejection: The Event on 2000 February 10, Astrophys. J., 754, 16, https://doi.org/10.1088/0004-637X/754/1/16, 2012. a
Zhu, C., Alexander, D., and Tian, L.: Velocity Characteristics of Rotating Sunspots, Sol. Phys., 278, 121–136, https://doi.org/10.1007/s11207-011-9923-2, 2012. a, b





