Kinematic models of the interplanetary magnetic field

Current knowledge on the description of the interplanetary magnetic field is reviewed with an emphasis on the kinematic approach as well as the analytic expression. Starting with the Parker spiral field approach, further effects are incorporated into this fundamental magnetic field model, including the latitudinal dependence, the poleward component, the solar cycle dependence, and the polarity and tilt angle of the solar magnetic axis. Further extensions are discussed in view of the magnetohydrodynamic treatment, the turbulence effect, the pickup ions, and the stellar wind models. The models of the interplanetary magnetic field serve as a useful tool for theoretical studies, in particular on the problems of plasma turbulence evolution, charged dust motions, and cosmic ray modulation in the heliosphere.

1 Introduction

The interplanetary magnetic field (IMF) is a spatially extended magnetic field of the Sun and forms together with the plasma flow from the Sun (referred to as the solar wind) a spatial domain of the heliosphere¹ around the Sun surrounded by the local interstellar cloud. Starting with the first direct measurements in the 1960s (Ness et al., 1964; Ness and Wilcox, 1964; Wilcox and Ness, 1965; Wilcox, 1968), the IMF is becoming increasingly more accessible in various places in situ in the solar system; e.g., the inner heliosphere (closer than the Earth orbit from the Sun) was covered by the Helios mission (Porsche, 1981; see monograph by Schwenn and Marsch, 1990, 1991), the outer heliosphere (beyond the Earth orbit) by Voyager (Stone, 1977; Kohlhase and Penzo, 1977; Stone, 1983), and the high-latitude region by the Ulysses mission (Wenzel and Smith, 1991; Wenzel et al., 1992).

In the lowest-order picture, the IMF has an Archimedean spiral structure, also referred to as the Parker spiral after Parker (1958), imposed by the solar wind expansion and the solar rotation, and exhibits spatial variation (e.g., sectors with the opposite directions of the radial component of the magnetic field, latitude dependence) and time variation (e.g., solar cycle dependence).

Typical values of the IMF magnitude (in the sense of the mean field) B₀ turn out to be of the order of 3–4 nT at the Earth orbit (1 astronomical unit, hereafter au). Long-term measurements of the IMF by the Ulysses spacecraft show that the field magnitude of about 3–4 nT is typical not only in the solar ecliptic plane but also in the high-latitude regions (Forsyth et al., 1996). Of course, irregular or transient phenomena (such as coronal mass ejections or co-rotating interaction regions) cause local, large-amplitude deviations from the mean field. Recent study by Henry et al. (2017) indicates that the IMF (at the Earth orbit) can be regarded as the Parker spiral type when the IMF is sufficiently inclined to the Earth orbital plane, either (1) B_x>0.4B and $B_y<-\mathrm{0.4}B$ or (2) $B_x<-\mathrm{0.4}B$ and B_y>0.4B, where B_x is the sunward component of the magnetic field (GSE-X direction), B_y is the dawn-to-dusk component of the field (GSE-Y direction), and B is the magnetic field magnitude. The IMF can be more radial and of the ortho-Parker spiral type (valid under $\left|B_x\right|>\mathrm{0.4}{B}_{\mathrm{t}}$, where B_t denotes the transverse component of the magnetic field to the radial direction from the Sun, $B_{\mathrm{t}}=\sqrt{B_y^{\mathrm{2}}+B_z^{\mathrm{2}}}$) or oriented more northward or southward $\left|B_z\right|>\mathrm{0.5}{B}_{\mathrm{t}}$.

Model construction of the IMF has immediate applications in the following plasma physical or astrophysical problems:

1. Solar wind turbulence.

   Plasma and magnetic field in interplanetary space develop into turbulence. Early in situ measurements in the 1960s have already shown that the frequency spectrum of the fluctuation of the IMF is a power law over a wide range of frequencies (typically in the MHz regime) (Coleman Jr., 1968), and the spectral index is close to $-\mathrm{5}/\mathrm{3}$ (Matthaeus et al., 1982; Tu and Marsch, 1995), known as the inertial-range spectrum of fluid turbulence. Properties of solar wind turbulence are extensively studied using in situ spacecraft such as Helios, Voyager, and Ulysses, and the observational properties are documented in reviews by, e.g., Tu and Marsch (1995), Petrosyan et al. (2010), and Bruno and Carbone (2013). Solar wind is the only accessible natural laboratory of turbulence in collisionless plasmas, relevant to astrophysical applications to interstellar turbulence. Knowledge on the IMF structure is an important ingredient in turbulence modeling. In particular, the large-scale inhomogeneity or velocity shear is the driver of turbulence when the solar wind plasma evolves into turbulence. For example, the mean-field models of turbulence explicitly need the large-scale structure as an input (Yokoi and Hamba, 2007; Yokoi, 2011).

2. Charged dust motion.

   Dust grains in interplanetary space have typically a length scale of nanometers to micrometers and are electrically charged by various processes, e.g., sticking of the ambient electrons onto the dust surface (which makes the dust charge state negative) or photo-electrons (which makes the charge state positive) (Shukla, 2001; Mann et al., 2014). Unlike the electrons or ions in the plasma, the charged dust grains undergo not only the gravitation attraction by the Sun and the planets and the Poynting–Robertson effect but also the electromagnetic interaction (Coulomb and Lorentz force). Combination of these forces results, e.g., in a long-time tilt of the orbital plane (on the timescale of 10 to 100 years), e.g., perihelion or aphelion shift from the solar ecliptic plane to the high-latitude region. Knowledge on the IMF structure is important because the orbital motion and the orbit drift can be tracked, either in a static IMF structure or in a time-evolving IMF structure (Grün et al., 1994; Mann et al., 2007, 2014; Czechowski and Mann, 2010; Lhotka et al., 2016).

3. Cosmic ray modulation.

   A cosmic ray consists mostly (more than 90 %) of protons. The spectrum of the cosmic ray is well characterized by a power law as a function of the particle energy (kinetic energy, strictly speaking) with a peak at about 1 GeV and a slope of about −2.7. The number flux of the cosmic ray can be measured by the neutron monitors and is known to be anti-correlated to the sunspot number variations with a period of about 22 years (cosmic ray modulation). The cosmic ray transport in the heliosphere is modeled by the convection–diffusion equation system, which can be treated both in a kinetic way based on the Boltzmann transport theory (Parker, 1965) and in a fluid–physical way using the continuity equation with the convection and diffusion terms (Duldig, 2001). See also the recent review by Potgieter (2013). The knowledge of the IMF is important because the cosmic ray exhibits charged particles undergo drift motions in a curved, inhomogeneous magnetic field (i.e., curvature drift and grad-B drift), as pointed out by, e.g., Isenberg and Jokipii (1979). In fact, the 22-year variation of the cosmic ray modulation (as measured by the neutron monitors on the Earth ground) can be explained and theoretically reconstructed by including the IMF structure (Kóta and Jokipii, 2001a; Burger et al., 2008; Miyahara et al., 2010).

Here we review various models of the IMF with an emphasis on the hydrodynamic approach and the analytic expression. This review is intended to complement a more comprehensive review by Owens and Forsyth (2013). We limit our review to the kinematic approach in the sense that the magnetic fields behave passively and are frozen-in into the given plasma flow. The review is organized in a concise way by primarily taking the kinematic approach. There is an increasing amount of literature and studies about the IMF, and the modeling approach is becoming diverse, e.g., hydrodynamic, hydromagnetic, and kinetic. We point out, however, that even in the simple kinematic approach, the IMF models are still illustrative and have various applications as introduced above.

We also limit our review to the analytic expression as much as possible. Analytic expression of the magnetic fields is a useful tool in space science and has been constructed for various plasma domains or plasma phenomena in the solar system other than the solar wind: solar corona (Banaszkiewicz et al., 1998), coronal mass ejection (CME) (Isavnin, 2017), Earth's magnetosphere (Katsiaris and Psillakis, 1987; Tsyganenko, 1990, 1995; Tsyganenko and Sitnov, 2007), and local interstellar medium surrounding the heliosphere (Röken, 2015). One can of course numerically solve the governing equations to reproduce the magnetic field and its dynamics more realistically, but the numerical treatment is not in the scope of this review.

The advantage of the analytic or semi-analytic expression is that one can implement the magnetic field models by themselves for the theoretical studies of the solar system plasma phenomena. Verification of the magnetic field models is possible using the existing in situ spacecraft data from, e.g., the Helios, Voyager, and Ulysses missions as well as the upcoming measurements in interplanetary space by Parker Solar Probe (Fox et al., 2016), BepiColombo's cruise in interplanetary space (Benkhoff et al., 2010), and Solar Orbiter (Müller et al., 2013).

2 Kinematic approach

We focus on the kinematic approach such that the flow pattern is given as an external field of a model field. The magnetic field is passive in the sense of the frozen-in field into the plasma. The reaction of the magnetic field onto the plasma motion (such as the Lorentz force acting on the plasma bulk flow) is not considered here.

2.1 Parker model

2.1.1 Thermally driven wind

In this section we review the formulation of the original Parker spiral model of the interplanetary magnetic field.

As suggested by Biermann (1951, 1957) the solar gas outflows into interplanetary space. The existence of the radial outflow of the solar gaseous material, nowadays known as the solar wind, and the spiral structure of the IMF associated with the solar rotation was predicted by Parker (1958) before the confirmation by in situ spacecraft measurements. It is worthwhile to note that the spiral structure in interplanetary space was also indicated in the comet tail study by Alfvén (1957) as a beam extending away from the Sun. The solar wind is mainly composed of protons, electrons, and helium alpha particles (there are, in addition, heavier ions from the Sun and pickup ions from the local interstellar medium) and streams radially away from the Sun far beyond the orbits of the planets over distances of about 100 au. The solar wind first encounters the termination shock located before the heliopause, a boundary layer between the solar plasma and the local interstellar medium at a distance of about 110–160 au. At the Earth orbit distance (1 au), the solar wind velocity typically ranges between 300 km s⁻¹ (referred to as the slow solar wind) and 700 km s⁻¹ (the fast solar wind). During the coronal mass ejection events, the solar wind speed can reach about 1400 km s⁻¹.

The Parker model treats the solar wind as a one-dimensional (in the radial direction), steady-state, isothermal thermally driven stream. Basic equations are the continuity equation,

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{d}{\mathrm{d}r}}\left(\mathit{\rho }{U}_{\mathrm{r}}{r}^{\mathrm{2}}\right)=\mathrm{0},\end{array}$$

the momentum balance,

$$\begin{array}{}\text{(2)}& U_{\mathrm{r}}{\displaystyle \frac{\mathrm{d}{U}_{\mathrm{r}}}{\mathrm{d}r}}+{\displaystyle \frac{\mathrm{1}}{\mathit{\rho }}}{\displaystyle \frac{\mathrm{d}p}{\mathrm{d}r}}+{\displaystyle \frac{{\mathrm{GM}}_{\odot }}{r^{\mathrm{2}}}}=\mathrm{0},\end{array}$$

and the adiabatic law or the equation of state,

$$\begin{array}{}\text{(3)}& p=\mathit{\rho }{c}_{\mathrm{s}}^{\mathrm{2}}.\end{array}$$

Here ρ denotes the mass density, U_r the radial component of the flow velocity, r the distance from the Sun, p the gas pressure, G the gravitational constant, M_⊙ the solar mass, and c_s the sound speed. Note that the sound speed is considered constant due to the assumption of the isothermal medium. Equations (1)–(3) can be reduced into the following form:

$$\begin{array}{}\text{(4)}& U_{\mathrm{r}}{\displaystyle \frac{\mathrm{d}{U}_{\mathrm{r}}}{\mathrm{d}r}}=\left({\displaystyle \frac{\mathrm{2}{c}_{\mathrm{s}}^{\mathrm{2}}}{r}}-{\displaystyle \frac{\mathrm{GM}}{r^{\mathrm{2}}}}\right){\left(\mathrm{1}-{\displaystyle \frac{c_{\mathrm{s}}^{\mathrm{2}}}{U_{\mathrm{r}}^{\mathrm{2}}}}\right)}^{-\mathrm{1}}.\end{array}$$

One sees immediately that Eq. (4) has a singularity at which U_r=c_s is satisfied. The flow speed reaches the sound speed (called the critical point or the sonic point) at

$$\begin{array}{}\text{(5)}& r_{\mathrm{c}}={\displaystyle \frac{{\mathrm{GM}}_{\odot }}{\mathrm{2}{c}_{\mathrm{s}}^{\mathrm{2}}}}.\end{array}$$

The critical point is located about 6 solar radii for a (coronal) temperature of 1 MK. Equation (4) exhibits difference types or classes of the flow velocity profile as a function of the distance from the Sun. Above all, a continuous flow acceleration over the sonic point meets the condition for the solar wind, i.e., acceleration in the subsonic domain (r<r_c) and further acceleration in the supersonic domain (r>r_c). See, e.g., Tajima and Shibata (2002) for a more detailed description about the Parker model. At a larger distance than the critical radius r_c, the flow velocity has an asymptotic form,

$$\begin{array}{}\text{(6)}& U_{\mathrm{r}}\simeq \mathrm{2}{c}_{\mathrm{s}}{\left(\ln {\displaystyle \frac{r}{r_{\mathrm{c}}}}\right)}^{\mathrm{1}/\mathrm{2}}.\end{array}$$

A comparison between the approximation of U_r using Eq. (6) and a numerical solution of Eq. (4) is shown in Fig. 1. The solution shown in red and obtained for T=1 MK perfectly agrees with the analytical solution shown in dashed black. The Parker model thus predicts that the solar corona expands radially outward at subsonic velocities close to the Sun (within the critical radius), and the coronal gas is gradually accelerated to supersonic velocities further out. Hereafter we also use an expression of U_sw for the magnitude of the solar wind velocity.

A more detailed analysis of the Parker model with the asymptotic solution of the flow velocity is presented by Summers (1978). A two-fluid model of the solar wind is presented by Summers (1982) as a hydrodynamic extension of the Parker model for the electron and the protons under the adiabatic law for each fluid type.

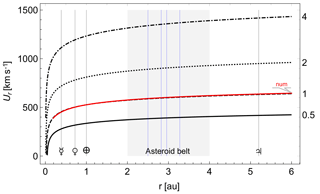
Figure 1 Radial solution of the solar wind U_r for different temperatures in megakelvin (right frame ticks). Vertical lines indicate the position of the planets; the dark-shaded region covers the region of main belt asteroids of the solar system, where blue lines mark the position of mean motion resonances of asteroids with planet Jupiter.

2.1.2 Spiral magnetic field

Using the angular velocity of the Sun, Ω_⊙, the radial, polar, and azimuthal components of the solar wind velocity are given in the HG (heliographic) frame of reference as follows:

$$\begin{array}{}\text{(7)}& {\displaystyle }& {\displaystyle }{U}_{\mathrm{r}}=U_{\mathrm{sw}},\text{(8)}& {\displaystyle }& {\displaystyle }{U}_{\mathit{\theta }}=\mathrm{0},\text{(9)}& {\displaystyle }& {\displaystyle }{U}_{\mathit{\varphi }}=-{\mathrm{\Omega }}_{\odot }r\sin \mathit{\theta }.\end{array}$$

A magnetic streamline satisfies the differential equation at a given polar angle θ,

$$\begin{array}{}\text{(10)}& {\displaystyle \frac{\mathrm{1}}{r\sin \mathit{\theta }}}{\displaystyle \frac{\mathrm{d}r}{\mathrm{d}\mathit{\varphi }}}\simeq {\displaystyle \frac{U_{\mathrm{r}}}{U_{\mathit{\varphi }}}}=-{\displaystyle \frac{U}{{\mathrm{\Omega }}_{\odot }r\sin \mathit{\theta }}}.\end{array}$$

We make use of a rough assumption that the flow speed is nearly constant over the critical radius beyond some distance r>r_c. The field-line equation (Eq. 10) has then the solution as

$$\begin{array}{}\text{(11)}& r-r_{\mathrm{0}}=-{\displaystyle \frac{U_{\mathrm{sw}}}{{\mathrm{\Omega }}_{\odot }}}\left(\mathit{\varphi }-{\mathit{\varphi }}_{\mathrm{0}}\right).\end{array}$$

Here, the magnetic field line passes through the coordinate at $\left(r_{\mathrm{0}},\mathit{\theta },{\mathit{\varphi }}_{\mathrm{0}}\right)$. The IMF is obtained from the divergence-free condition of the Maxwell equations,

$$\begin{array}{}\text{(12)}& \mathbf{\nabla }\cdot \mathit{B}=\mathrm{0}.\end{array}$$

That is, using the assumption of spherical symmetry, the IMF is expressed as

$$\begin{array}{}\text{(13)}& {\displaystyle }& {\displaystyle }{B}_{\mathrm{r}}=B_{\mathrm{0}}{\left({\displaystyle \frac{r_{\mathrm{0}}}{r}}\right)}^{\mathrm{2}},\text{(14)}& {\displaystyle }& {\displaystyle }{B}_{\mathit{\theta }}=\mathrm{0},\text{(15)}& {\displaystyle }& {\displaystyle }{B}_{\mathit{\varphi }}=-B_{\mathrm{0}}{\displaystyle \frac{{\mathrm{\Omega }}_{\odot }{r}_{\mathrm{0}}}{U_{\mathrm{sw}}}}{\displaystyle \frac{r_{\mathrm{0}}}{r}}\sin \mathit{\theta },\end{array}$$

where B₀ is the radial component of the magnetic field at a reference radius r₀.

The transformation into the stationary frame (HGI, heliographic inertial) yields the same expression of the magnetic field as Eqs. (13)–(15).

Note that, due to a Galilean transformation, the electric field has a convective contribution in the polar direction e_θ,

$$\begin{array}{}\text{(16)}& \mathit{E}=-\mathit{U}\times \mathit{B}=-U_{\mathrm{sw}}{B}_{\mathit{\varphi }}{\mathit{e}}_{\mathit{\theta }}.\end{array}$$

Realizations of the magnetic field lines in the Parker spiral model are shown for different (constant) solar wind speeds in Fig. 2. The angle between the magnetic field line and Earth's orbit is about 45^∘ for a typical solar wind speed of 400 km s⁻¹ and increases (becomes more radial) at a higher flow speed. Note that when considering the magnetohydrodynamic (MHD) effect, the above discussion is valid outside the Alfvén radius at which the flow speed reaches the Alfvén speed, $r_{\mathrm{A}}\simeq \mathrm{50}{R}_{\odot }=\mathrm{0.25}$ au, where R_⊙ is the solar radius.

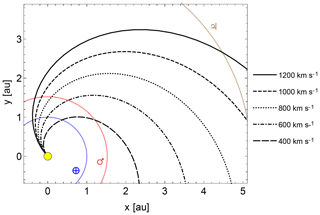
Figure 2 Streamlines in the Parker spiral model of interplanetary magnetic field around the Sun (a filled circle in yellow) in the heliospheric ecliptic plane up to 5 astronomical units (au) under different conditions of the solar wind speed. The orbit of the Earth is marked by a blue curve at a radius of 1 au, that of Mars by a red curve (1.5 au), and that of Jupiter by a green curve (5 au).

We rewrite Eqs. (13)–(15) into a simpler form as

$$\begin{array}{}\text{(17)}& {\displaystyle }& {\displaystyle }{B}_{\mathrm{r}}=B_{\mathrm{0}}{\left({\displaystyle \frac{r_{\mathrm{0}}}{r}}\right)}^{\mathrm{2}},\text{(18)}& {\displaystyle }& {\displaystyle }{B}_{\mathit{\varphi }}=-r_{\mathrm{0}}{B}_{\mathrm{0}}\left({\displaystyle \frac{r_{\mathrm{0}}}{r}}\right){\displaystyle \frac{{\mathrm{\Omega }}_{\odot }\cos \mathit{\vartheta }}{U_{\mathrm{sw}}}},\end{array}$$

where, again, $B_{\mathrm{0}}=B\left(r_{\mathrm{0}},\mathit{\theta },{\mathit{\varphi }}_{\mathrm{0}}\right)$ is the reference radial component of the magnetic field (Meyer-Vernet, 2012).

We note that in Eqs. (17)–(18) the latitude ϑ (measured from the Equator) is related to the polar angle θ (measured from the rotation axis) by $\mathit{\theta }=\mathit{\pi }-\mathit{\vartheta }$. By identifying or defining the radial and tangential components as B_R=B_r and B_T=B_ϕ, respectively, it is straightforward to transform the Parker spiral field into its radial (R), tangential (T), and normal (N) components as

$$\begin{array}{}\text{(19)}& {\displaystyle }& {\displaystyle }{B}_{\mathrm{R}}=B_{\mathrm{0}}{\left({\displaystyle \frac{r_{\mathrm{0}}}{r}}\right)}^{\mathrm{2}},\text{(20)}& {\displaystyle }& {\displaystyle }{B}_{\mathrm{T}}=-r_{\mathrm{0}}{B}_{\mathrm{0}}\left({\displaystyle \frac{r_{\mathrm{0}}}{r}}\right){\displaystyle \frac{{\mathrm{\Omega }}_{\odot }\sin \mathit{\theta }}{U_{\mathrm{sw}}}}.\end{array}$$

Note that the normal component vanishes, B_N=0, because the Parker model does not include the polar component like the dipolar field of the Sun.

2.1.3 Spiral angle

The distance to the surface on which an azimuthal angle of 45^∘ is realized (or B_θ≃B_r) is approximately located at

$$\begin{array}{}\text{(21)}& r\simeq {\displaystyle \frac{U_{\mathrm{sw}}}{{\mathrm{\Omega }}_{\odot }}}\sin \mathit{\theta }.\end{array}$$

Using the rotation period of the Sun of 25.38 d (equivalent to an angular velocity of $\mathit{\omega }=\mathrm{2.865}\times {\mathrm{10}}^{-\mathrm{6}}\mathrm{rad}{\mathrm{s}}^{-\mathrm{1}}$) and the flow speed U_sw≃430 km s⁻¹, the transition from the radially dominant to the azimuthally dominant magnetic field indeed happens around r=1 au. The transition distance is displayed as a function of the flow speed in Fig. 3 for three different solar rotation periods, 24.47, 25.38, and 26.24 d.

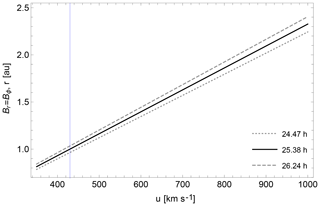
Figure 3 Heliocentric distance r in astronomical units (au) at which the spiral angle of the interplanetary magnetic field reaches 45^∘ to the radial direction from the Sun (B_r=B_ϕ). The curves are plotted as a function of the solar wind speed in units of km s⁻¹ for 3 different rotation rates, a period of 26.24 h (upper curve), 25.38 h (middle curve), and 24.47 h (lower curve). A typical value of the solar wind speed is 430 km s⁻¹ (shown by a vertical thin line).

Alternatively, the Parker spiral model can be formulated in terms of the spiral angle ψ:

$$\begin{array}{}\text{(22)}& \tan \mathit{\psi }={\displaystyle \frac{{\mathrm{\Omega }}_{\odot }(r-R_{\odot })\sin \mathit{\theta }}{U_{\mathrm{sw}}}}.\end{array}$$

In this setting, the magnetic field B is, by using the unit vectors in the radial direction e_r and in the azimuthal direction e_ϕ, given as

$$\begin{array}{}\text{(23)}& \mathit{B}=B_{\mathrm{0}}{\left({\displaystyle \frac{r_{\mathrm{0}}}{r}}\right)}^{\mathrm{2}}\left({\mathit{e}}_{\mathrm{r}}-\tan \mathit{\psi }{\mathit{e}}_{\mathit{\varphi }}\right).\end{array}$$

In this formulation the magnitude of the magnetic field is estimated as

$$\begin{array}{}\text{(24)}& B=B_{\mathrm{0}}{\left({\displaystyle \frac{r_{\mathrm{0}}}{r}}\right)}^{\mathrm{2}}\sqrt{\mathrm{1}+{\tan }^{\mathrm{2}}\mathit{\psi }}.\end{array}$$

2.1.4 Vector potential

The magnetic vector potential A for the Parker spiral magnetic field under the Coulomb gauge $\mathbf{\nabla }\cdot \mathit{A}=\mathrm{0}$ can analytically be evaluated (Bieber et al., 1987). The vector potential has the following form:

$$\begin{array}{}\text{(25)}& {\displaystyle }& {\displaystyle }{A}_r={\displaystyle \frac{\mathrm{2}a{\mathrm{\Omega }}_{\odot }}{\mathrm{3}{U}_{\mathrm{sw}}}}\left(\mathrm{1}-{\displaystyle \frac{\mathrm{3}x}{\mathrm{2}}}-x\ln \left(\mathrm{1}+x\right)\right),\text{(26)}& {\displaystyle }& {\displaystyle }{A}_{\mathit{\theta }}={\displaystyle \frac{\mathrm{2}a{\mathrm{\Omega }}_{\odot }}{\mathrm{3}{U}_{\mathrm{sw}}}}\sin \mathit{\theta }\left({\displaystyle \frac{x}{\mathrm{1}+x}}+\ln \left(\mathrm{1}+x\right)\right),\text{(27)}& {\displaystyle }& {\displaystyle }{A}_{\mathit{\varphi }}={\displaystyle \frac{a}{r\sin \mathit{\theta }}}\left(\mathrm{1}-x\right),\end{array}$$

where $x=\left|\cos \mathit{\theta }\right|$. Equations (25)–(27) correspond to the IMF in the following expression:

$$\begin{array}{}\text{(28)}& {\displaystyle }& {\displaystyle }{B}_{\mathrm{r}}={\displaystyle \frac{a}{r^{\mathrm{2}}}}{\displaystyle \frac{\cos \mathit{\theta }}{\left|\cos \mathit{\theta }\right|}},\text{(29)}& {\displaystyle }& {\displaystyle }{B}_{\mathit{\theta }}=\mathrm{0},\text{(30)}& {\displaystyle }& {\displaystyle }{B}_{\mathit{\varphi }}=-{\displaystyle \frac{a{\mathrm{\Omega }}_{\odot }}{U_{\mathrm{sw}}}}{\displaystyle \frac{\sin \mathit{\theta }\cos \mathit{\theta }}{\left|\cos \mathit{\theta }\right|}}.\end{array}$$

Here a is a free parameter proportional to the magnitude of the magnetic field in units of nT au² (for example, a=3.54 nT au² produces a magnetic field of 5 nT at 1 au). The polar component of the vector potential can be multiplied by a scalar function f(θ) to improve the accuracy of the model as A_θ→f(θ)A_θ.

Another formulation of the vector potential (again, under the Coulomb gauge) is to introduce a scalar potential as

$$\begin{array}{}\text{(31)}& {\mathrm{\Phi }}_{\mathrm{C}}=-{\displaystyle \frac{\mathrm{2}a{\mathrm{\Omega }}_{\odot }r}{\mathrm{3}u}}\left(\mathrm{1}-{\displaystyle \frac{\mathrm{3}x}{\mathrm{2}}}-x\ln \left(\mathrm{1}+x\right)\right),\end{array}$$

which yields the following vector potential (Webb et al., 2010):

$$\begin{array}{}\text{(32)}& \mathit{A}=a\left({\displaystyle \frac{\mathrm{1}-\left|\cos \mathit{\theta }\right|}{r\sin \mathit{\theta }}}{\mathit{e}}_{\mathit{\varphi }}-{\displaystyle \frac{f\left(\mathit{\theta }\right){\mathrm{\Omega }}_{\odot }\sin \mathit{\theta }}{U_{\mathrm{sw}}}}{\mathit{e}}_{\mathit{\theta }}\right).\end{array}$$

Of course, in both cases, Eqs. (25)–(27) and (32), the magnetic field is obtained by the definition of the vector potential as $\mathit{B}=\mathrm{\nabla }\times \mathit{A}$. The electrostatic potential for the convective electric field $\mathit{E}=-\mathit{U}\times \mathit{B}=-\mathrm{\nabla }\mathrm{\Phi }$ is

$$\begin{array}{}\text{(33)}& \mathrm{\Phi }=-a{\mathrm{\Omega }}_{\odot }\cos \mathit{\theta }.\end{array}$$

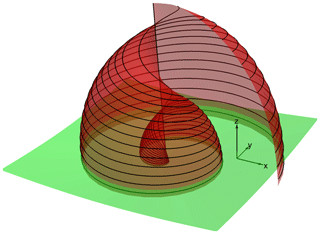
Figure 4 Magnetic field lines (black curves) in the Parker spiral model for different latitude angles θ from the rotation axis. Curves are defined as the intersection of the surfaces of the Euler potentials, ${\mathit{\alpha }}_{\mathrm{E}}=\mathrm{const}.$ and ${\mathit{\beta }}_{\mathrm{E}}=\mathrm{const}.$, as presented by Webb et al. (2010). Note that the spiral magnetic field lines are constructed with the radial component from the Sun and the azimuthal component around the rotation axis and do not contain the polar component (in the direction toward the rotation axis and perpendicular to the radial direction). The spiral field lines have an axial component along the rotation axis, but this is due to the radial component of the spiral field line (in the sense of being away from the rotation axis).

The magnetic field lines for the Parker spiral model are shown in Fig. 4. Black lines have been calculated by the intersection of the two surfaces of constant Euler potentials α_E, β_E (Webb et al., 2010):

$$\begin{array}{}\text{(34)}& {\mathit{\alpha }}_{\mathrm{E}}=-a\left|\cos \mathit{\theta }\right|,{\mathit{\beta }}_{\mathrm{E}}=\mathit{\varphi }+{\displaystyle \frac{{\mathrm{\Omega }}_{\odot }r}{U_{\mathrm{sw}}}}-{\mathrm{\Omega }}_{\odot }t.\end{array}$$

It is worth mentioning that the spiral magnetic field lines are constructed with the radial component from the Sun and the azimuthal component around the rotation axis and do not contain the polar component (in the direction toward the rotation axis and perpendicular to the radial direction) as in Eqs. (28)–(30). The Parker spiral field lines have an axial component along the rotation axis, but this is due to the radial component of the field line which has the axial component. For the sake of convenience one may set a value of unity to the variables a, t, Ω_⊙, and U_sw to provide the topology of the problem: α_E defines a cone (in green) that intersects a shell (in red) defined by β_E. Intersection lines define the magnetic field lines of the Parker model.

2.2 Generalization of the Parker model

The Parker spiral model well approximates the mean and large-scale structure of the interplanetary magnetic field of our solar system. However, it fails to describe the three-dimensional geometry and evolution in time on various scales.

2.2.1 Latitudinal dependence

The Parker model does not recognize the sign reversal of the dipolar magnetic field over the Northern Hemisphere and the Southern Hemisphere; the divergence-free nature of the magnetic field is not well represented. The hemispheric sign reversal can be incorporated into the Parker model as follows (Webb et al., 2010):

$$\begin{array}{}\text{(35)}& \mathit{B}={\displaystyle \frac{af\left(\mathit{\theta }\right)}{r^{\mathrm{2}}}}\left({\mathit{e}}_r-{\displaystyle \frac{{\mathrm{\Omega }}_{\odot }r\sin \mathit{\theta }}{U_{\mathrm{r}}}}{\mathit{e}}_{\mathit{\varphi }}\right).\end{array}$$

Here, the constant a and function f=f(θ) are given by

$$\begin{array}{}\text{(36)}& {\displaystyle }& {\displaystyle }a={\mathit{\sigma }}_{\mathrm{p}}{B}_{\mathrm{0}}{r}_{\mathrm{0}}^{\mathrm{2}},\text{(37)}& {\displaystyle }& {\displaystyle }f\left(\mathit{\theta }\right)=\mathrm{1}-\mathrm{2}H(\mathit{\theta }-\mathit{\pi }/\mathrm{2})={\displaystyle \frac{\cos \mathit{\theta }}{\left|\cos \mathit{\theta }\right|}},\end{array}$$

where ${\mathit{\sigma }}_{\mathrm{p}}=\pm \mathrm{1}$ defines the polarity of the magnetic field in the Northern Hemisphere of the Sun, and f(θ) is the Heaviside step function with the property $f\left(\mathit{\theta }\right)=+\mathrm{1}$ for $\mathrm{0}<\mathit{\theta }<\mathit{\pi }/\mathrm{2}$ and $f\left(\mathit{\theta }\right)=-\mathrm{1}$ for $\mathit{\theta }>\mathit{\pi }/\mathrm{2}$.

A more elaborated analytic model is proposed along with the Ulysses measurements over the solar polar regions (Zurbuchen et al., 1997; Forsyth et al., 2002). The three-dimensional model allows a nonzero field in the polar component and is expressed as

$$\begin{array}{ll}\text{(38)}& {\displaystyle }& {\displaystyle }{B}_{\mathrm{r}}=B_{\mathrm{0}}{\left({\displaystyle \frac{r_{\mathrm{0}}}{r}}\right)}^{\mathrm{2}},\text{(39)}& {\displaystyle }& {\displaystyle }{B}_{\mathit{\theta }}={\displaystyle \frac{B_{\mathrm{0}}{r}_{\mathrm{0}}^{\mathrm{2}}}{U_{\mathrm{sw}}r}}\mathit{\omega }\sin {\mathit{\beta }}_{\mathrm{F}}\sin \left(\mathit{\varphi }+{\displaystyle \frac{r{\mathrm{\Omega }}_{\odot }}{U_{\mathrm{sw}}}}-{\mathit{\varphi }}_{\mathrm{0}}\right),{\displaystyle }& {\displaystyle }{B}_{\mathit{\varphi }}=-{\displaystyle \frac{B_{\mathrm{0}}{r}_{\mathrm{0}}^{\mathrm{2}}}{U_{\mathrm{sw}}r}}[{\mathrm{\Omega }}_{\odot }\sin \mathit{\theta }-\mathit{\omega }(\cos {\mathit{\beta }}_{\mathrm{F}}\sin \mathit{\theta }+\\ \text{(40)}& {\displaystyle }& {\displaystyle }\sin {\mathit{\beta }}_{\mathrm{F}}\cos \mathit{\theta }\cos \left(\mathit{\varphi }+{\displaystyle \frac{r{\mathrm{\Omega }}_{\odot }}{U_{\mathrm{sw}}}}-{\mathit{\varphi }}_{\mathrm{0}}\right)\left)\right],\end{array}$$

where B₀ is the radial component of the magnetic field at the source surface located at heliospheric distance r=r₀, ω the differential rotation rate of the magnetic field line at foot points, β_F (the Fisk angle) the polar angle at which a field line originating in the rotational pole crosses the source surface and is related to the angle between the solar magnetic dipole axis and the rotation axis, and ϕ₀ the heliographic longitude of the plane defined by the rotation and magnetic axes. The source magnetic field is defined at r=r₀. The angle ϕ=ϕ₀ occurs in the plane defined by the rotation axis and the magnetic axis of the Sun. Angle β_F is the polar angle where the field line p crosses the source surface (from the heliographic pole). The angle β_F can be calculated in the model by Fisk (1996) for a given orientation α_F of the magnetic axis M and a given non-radial expansion. For the configuration discussed by Fisk (1996), the value of β_F is about 30^∘.

A model of latitudinal dependence of the magnetic field is constructed by employing the method of separation of the variable for an axisymmetric magnetohydrodynamic outflow (Lima et al., 2001). The radial and the azimuthal components of the magnetic field are proposed as

$$\begin{array}{}\text{(41)}& {\displaystyle }{\displaystyle }{B}_{\mathrm{r}}={\displaystyle \frac{B_{\mathrm{0}}}{r^{\mathrm{2}}}}\sqrt{\mathrm{1}+\mathit{\mu }{\sin }^{\mathrm{2}\mathit{ϵ}}\mathit{\theta }},\end{array}$$

$$\begin{array}{}\text{(42)}& {\displaystyle }{\displaystyle }{B}_{\mathit{\varphi }}=\mathit{\lambda }{B}_{\mathrm{0}}{\displaystyle \frac{{\sin }^{\mathit{ϵ}}\mathit{\theta }}{r}}\left({\displaystyle \frac{\frac{r^{\mathrm{2}}}{R_{\mathrm{s}}^{\mathrm{2}}}-\mathrm{1}}{\mathrm{1}-M_{\mathrm{A}}^{\mathrm{2}}}}\right),\end{array}$$

where ϵ is a free parameter, μ is the ratio of the flow kinetic energy (or energy density, strictly speaking) in the equatorial region to that in the polar region, and λ is the ratio of azimuthal to radial velocity (and also magnetic field) at the base of the wind. R_s is the radius of the star or the Sun. M_A is the Alfvén Mach number of the flow. The polar component of the magnetic field is assumed to vanish due to the assumption of the axial symmetry around the rotation axis.

2.2.2 Poleward component

The IMF can have a nonzero polar (or latitudinal) component, e.g., from the solar dipolar field. Generalization of the Parker model to the nonzero polar component case (B_θ≠0) is based on the analysis by Forsyth et al. (1996). Let ϕ_B be the azimuthal angle that the projection of the IMF vector onto the R–T plane makes with the R axis in the right-handed sense and δ_B be the meridional angle of the IMF to the R–T plane. These angles are defined in terms of the magnetic field components (Forsyth et al., 1996):

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\tan {\mathit{\varphi }}_B=B_{\mathrm{T}}/B_{\mathrm{R}},\\ \text{(43)}& {\displaystyle }& {\displaystyle }\sin {\mathit{\delta }}_B=B_{\mathrm{N}}/B,\end{array}$$

where $B=\sqrt{B_{\mathrm{R}}^{\mathrm{2}}+B_{\mathrm{T}}^{\mathrm{2}}+B_{\mathrm{N}}^{\mathrm{2}}}$.

The azimuthal angle of the spiral field ϕ_P that the tangent to the ideal Parker spiral magnetic field makes with the radially outward direction at a position in interplanetary space specified by radial position r and heliographic latitude δ is then given by

$$\begin{array}{}\text{(44)}& \tan {\mathit{\varphi }}_{\mathrm{P}}={\displaystyle \frac{U_{\mathit{\varphi }}-\mathrm{\Omega }r\cos \mathit{\delta }}{U_{\mathrm{r}}}}.\end{array}$$

On the assumption that U_ϕ is small, ϕ_P turns out to be negative. A magnetic field with a direction in agreement with the Parker spiral model will have either ϕ_B=ϕ_P in a region of outward polarity or ${\mathit{\varphi }}_B=\mathrm{180}{}^{\circ }+{\mathit{\varphi }}_{\mathrm{P}}$ in a region of inward polarity field. In both regions the Parker model predicts that an ideal magnetic field has a meridional angle ${\mathit{\delta }}_B=\mathrm{0}{}^{\circ }$ with respect to the R–T plane. Therefore, up to the second order in B_N the sine of the meridional angle δ_B according to the second equation in Eq. (43) is given by

$$\begin{array}{}\text{(45)}& \sin {\mathit{\delta }}_{\mathrm{B}}\simeq {\displaystyle \frac{B_{\mathrm{N}}}{\sqrt{B_{\mathrm{R}}^{\mathrm{2}}+B_{\mathrm{T}}^{\mathrm{2}}}}}.\end{array}$$

If we combine the first of Eq. (43) together with Eq. (45) and solve for B_T and B_N we find up to $\mathcal{O}\left(B_{\mathrm{N}}^{\mathrm{3}}\right)$:

$$\begin{array}{}\text{(46)}& {\displaystyle }& {\displaystyle }{B}_{\mathrm{T}}=-B_{\mathrm{0}}{\left({\displaystyle \frac{r_{\mathrm{0}}}{r}}\right)}^{\mathrm{2}}{\displaystyle \frac{\left(U_{\mathit{\varphi }}-r{\mathrm{\Omega }}_{\odot }\cos \mathit{\delta }\right)}{U_{\mathrm{r}}}},\text{(47)}& {\displaystyle }& {\displaystyle }{B}_{\mathrm{N}}=B_{\mathrm{0}}{\left({\displaystyle \frac{r_{\mathrm{0}}}{r}}\right)}^{\mathrm{2}}\sqrt{\mathrm{1}+{\displaystyle \frac{{\left(U_{\mathit{\varphi }}-r{\mathrm{\Omega }}_{\odot }\cos \mathit{\delta }\right)}^{\mathrm{2}}}{U_{\mathrm{r}}^{\mathrm{2}}}}}\sin {\mathit{\delta }}_B,\end{array}$$

where we substituted B_R by B_r in Eqs. (17)–(18),

$$\begin{array}{}\text{(48)}& B_{\mathrm{R}}=B_{\mathrm{0}}{\left({\displaystyle \frac{r_{\mathrm{0}}}{r}}\right)}^{\mathrm{2}}.\end{array}$$

Equations (46)–(48) provide a type of the Parker spiral magnetic field with the generalization to a nonzero normal component B_N≠0 parameterized by δ and δ_B. For ${\mathit{\delta }}_B=\mathrm{0}{}^{\circ }$ and ignoring the azimuthal component of the solar wind U_ϕ, the model reproduces the Parker model, i.e., Eqs. (17)–(18):

$$\begin{array}{}\text{(49)}& {\displaystyle }& {\displaystyle }{B}_{\mathrm{R}}=B_{\mathrm{0}}{\left({\displaystyle \frac{r_{\mathrm{0}}}{r}}\right)}^{\mathrm{2}},\text{(50)}& {\displaystyle }& {\displaystyle }{B}_{\mathrm{T}}=-\left({\displaystyle \frac{r_{\mathrm{0}}}{r}}\right)r_{\mathrm{0}}{B}_{\mathrm{0}}{\mathrm{\Omega }}_{\odot }\cos \mathit{\delta },\text{(51)}& {\displaystyle }& {\displaystyle }{B}_{\mathrm{N}}=\mathrm{0}.\end{array}$$

Another way of generalization is to use the power-law dependence using the power-law index κ as a free parameter (Lhotka et al., 2016),

$$\begin{array}{}\text{(52)}& {\displaystyle }& {\displaystyle }{B}_{\mathrm{R}}=B_{\mathrm{R}\mathrm{0}}{\left({\displaystyle \frac{r_{\mathrm{0}}}{r}}\right)}^{\mathrm{2}}{b}_{\mathrm{R}}\left(t\right),\text{(53)}& {\displaystyle }& {\displaystyle }{B}_{\mathrm{T}}=B_{\mathrm{T}\mathrm{0}}\left({\displaystyle \frac{r_{\mathrm{0}}}{r}}\right)b_{\mathrm{T}}\left(t\right),\text{(54)}& {\displaystyle }& {\displaystyle }{B}_{\mathrm{N}}=B_{\mathrm{N}\mathrm{0}}{\left({\displaystyle \frac{r_{\mathrm{0}}}{r}}\right)}^{\mathit{\kappa }}{b}_{\mathrm{R}}\left(t\right).\end{array}$$

Here, B_R0, B_T0, and B_N0 are the mean magnetic field. b_R, b_T, and b_N can be time-dependent such as the solar cycle (see Sect. 2.2.3). The power-law index κ is a free parameter and determines the dependence of B_N on the inverse distance from the Sun 1∕r.

2.2.3 Solar cycle dependence

The solar cycle is a periodic change in the sunspot number over 11 years. In the plasma physics sense, the solar cycle is more associated with the magnetic activity of the Sun with a period of 22 years (the magnetic polarity is reversed after one sunspot cycle). During solar maximum the entire magnetic field of the Sun flips, thus alternating the polarity of the field every solar cycle. The solar (magnetic) activity is diverse, such as solar radiation, ejections of solar material, and the number and the size of sunspots and the occurrence rate of solar eruptions. As a consequence, the periodic change in the solar magnetic field (or dipolar axis) affects the polarity of the IMF as well. To include the time-dependent effect Kocifaj et al. (2006) suggests the following magnetic field model:

$$\begin{array}{}\text{(55)}& {\displaystyle }& {\displaystyle }{B}_{\mathrm{R}}=B_{\mathrm{0}}{\left({\displaystyle \frac{r_{\mathrm{0}}}{r}}\right)}^{\mathrm{2}}\cos \left({\displaystyle \frac{\mathit{\pi }t}{\mathrm{11}\left[\mathrm{yr}\right]}}+{\mathit{\varphi }}_{\mathrm{0}}\right),\text{(56)}& {\displaystyle }& {\displaystyle }{B}_{\mathrm{T}}=-B_{\mathrm{0}}\left({\displaystyle \frac{r_{\mathrm{0}}}{r}}\right)\cos \mathit{\vartheta }\cos \left({\displaystyle \frac{\mathit{\pi }t}{\mathrm{11}\left[\mathrm{yr}\right]}}+{\mathit{\varphi }}_{\mathrm{0}}\right).\end{array}$$

Here, ϑ is again latitude with $\mathit{\theta }=\mathit{\pi }-\mathit{\vartheta }$. Note that the transverse direction (with a unit vector e_T) is constructed as ${\mathit{e}}_{\mathrm{T}}={\mathit{\omega }}_{\mathrm{mag}}\times {\mathit{e}}_{\mathrm{R}}$, where ω_mag is the magnetic axis of the Sun. If we assume that ω_mag coincides with the rotation axis of the Sun, Ω_⊙, then the relation $B_{\mathrm{T}}=-B_{\mathit{\varphi }}$ holds with B_ϕ given in Eqs. (17)–(18). However, in comparison with the second equation in Eqs. (17)–(18), the second equation in Eq. (35) differs by a factor $r_{\mathrm{0}}{\mathrm{\Omega }}_{\odot }/U_{\mathrm{r}}$ in addition to the inclusion of the time-dependent terms. However, assuming solar wind speed U_sw≃450 km s⁻¹ and solar rotation rate ${\mathrm{\Omega }}_{\odot }\simeq \mathrm{2}\mathit{\pi }/\mathrm{24.47}$ d⁻¹, this factor becomes close to unity at r₀=1 au.

2.2.4 Polarity and tilt angle

Two additional effects can further be incorporated into the IMF model, the polarity A_mag and the tilt angle θ_tilt. The polarity A_mag is defined such that a case of A_mag>0 corresponds to the magnetic fields pointing outward from the Sun in the Northern Hemisphere (the angle between the magnetic axis and the solar rotation axis is below 90^∘), and a case of A_mag<0 is in the opposite sense to A_mag>0. Using the polarity A, the Parker spiral magnetic field is given by the following equation (Jokipii and Thomas, 1981):

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathit{B}={\displaystyle \frac{A_{\mathrm{mag}}}{r^{\mathrm{2}}}}\left({\mathit{e}}_r-\mathrm{\Gamma }{\mathit{e}}_{\mathit{\varphi }}\right)\times \\ \text{(57)}& {\displaystyle }& {\displaystyle }\left\{\mathrm{1}-\mathrm{2}H\left[\mathit{\theta }-\left({\displaystyle \frac{\mathit{\pi }}{\mathrm{2}}}+{\mathit{\theta }}_{\mathrm{tilt}}\sin \left(\mathit{\varphi }-{\displaystyle \frac{r{\mathrm{\Omega }}_{\odot }}{U_{\mathrm{sw}}}}\right)\right)\right]\right\},\end{array}$$

where H is the Heaviside step function. Γ is defined as

$$\begin{array}{}\text{(58)}& \mathrm{\Gamma }={\displaystyle \frac{r{\mathrm{\Omega }}_{\odot }\sin \mathit{\theta }}{U_{\mathrm{sw}}}}.\end{array}$$

The polarity A_mag is expressed in units of magnetic flux (see Eq. 23). An equivalent formulation of Eq. (57) is as follows (Kota and Jokippii, 1983):

$$\begin{array}{}\text{(59)}& {\displaystyle }& {\displaystyle }\mathit{B}={\displaystyle \frac{A_{\mathrm{mag}}}{r^{\mathrm{2}}}}\left({\mathit{e}}_r-{\displaystyle \frac{r{\mathrm{\Omega }}_{\odot }\sin \mathit{\theta }}{U_{\mathrm{sw}}}}{\mathit{e}}_{\mathit{\varphi }}\right)\left[\mathrm{1}-\mathrm{2}H(\mathit{\theta }-{\mathit{\theta }}^{*})\right],\text{(60)}& {\displaystyle }& {\displaystyle }\cot {\mathit{\theta }}^{*}=-\tan {\mathit{\theta }}_{\mathrm{tilt}}\sin {\mathit{\varphi }}^{*},\end{array}$$

where ϕ^* is the azimuthal angle in the co-rotating frame at an angular speed of the solar rotation,

$$\begin{array}{}\text{(61)}& {\mathit{\varphi }}^{*}=\mathit{\varphi }+{\displaystyle \frac{r{\mathrm{\Omega }}_{\odot }}{U_{\mathrm{sw}}}}.\end{array}$$

The tilt angle θ_tilt is larger at near solar maximum and smaller at near solar minimum (Thomas and Smith, 1981) and typically varies from 75^∘ at high level of solar activity to 10 down to 3^∘ during solar minimum activity. A model of tilt angle variation over a 22-year solar cycle was constructed by Jokipii and Thomas (1981) and Kota and Jokippii (1983) as follows:

$$\begin{array}{}\text{(62)}& {\mathit{\theta }}_{\mathrm{tilt}}={\mathit{\theta }}_{\mathrm{t}\mathrm{0}}+{\mathit{\theta }}_{\mathrm{t}\mathrm{1}}\cos \left({\displaystyle \frac{\mathrm{2}\mathit{\pi }t}{T}}\right),\end{array}$$

where θ_t0=20^∘, θ_t1=10^∘, and T=11 yr. The tilt angle θ_tilt is set to be at sunspot maximum at t=0.

The wavy, flapping shape of the heliospheric current sheet is expressed by the equation for the polar angle as follows (Jokipii and Thomas, 1981):

$$\begin{array}{}\text{(63)}& {\displaystyle }& {\displaystyle }{\mathit{\theta }}_{\mathrm{cs}}={\displaystyle \frac{\mathit{\pi }}{\mathrm{2}}}+{\sin }^{-\mathrm{1}}\left[\sin {\mathit{\theta }}_{\mathrm{tilt}}\sin \left(\mathit{\varphi }-{\mathit{\varphi }}_{\mathrm{0}}+{\displaystyle \frac{r{\mathrm{\Omega }}_{\odot }}{U_{\mathrm{sw}}}}\right)\right],\text{(64)}& {\displaystyle }& {\displaystyle }\simeq {\displaystyle \frac{\mathit{\pi }}{\mathrm{2}}}+{\mathit{\theta }}_{\mathrm{tilt}}\sin \left(\mathit{\varphi }-{\mathit{\varphi }}_{\mathrm{0}}+{\displaystyle \frac{r{\mathrm{\Omega }}_{\odot }}{U_{\mathrm{sw}}}}\right).\end{array}$$

The approximation in Eq. (64) is valid for θ_tilt≪1 rad (up to about 30^∘).

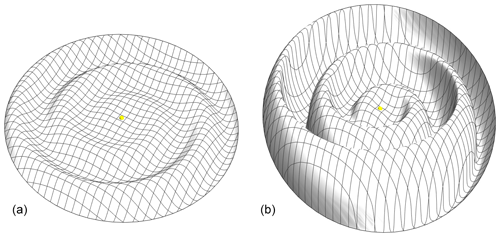
Figure 5 Shape of the “ballerina skirt” model of the heliocentric current sheet defined by $\cos {\mathit{\theta }}^{*}=\cos \mathit{\theta }$. Topology at t=0 and for θ_t0=5^∘ (a) and θ_t0=30^∘ (b).

A sketch of the topology of the heliospheric current sheet is shown in Fig. 5, where the magnetic field is discontinuous, i.e., for vanishing $\mathit{\theta }-{\mathit{\theta }}^{\ast }=\mathrm{0}$ in $H(\mathit{\theta }-{\mathit{\theta }}^{\ast })$. For small values of θ_tilt the sheet is close to the plane defined in terms of the solar equator (left) while for larger values (θ_tilt=20^∘) the wavy structure of the “ballerina skirt” is found to be much more pronounced.

The drift motion depends on the sign of qA_mag, a combination of the electric charge of the particle and the polarity of the solar magnetic field. During the period of qA_mag>0, the time variation of the cosmic ray flux shows a flatter maximum, while during qA_mag<0 the time variation of the cosmic ray flux shows a shape maximum; see, e.g. Jokipii and Thomas (1981) or Kota and Jokippii (1983).

A more refined magnetic field model is constructed by Burger et al. (2008), which offers an extension of the tilted heliospheric current sheet (with respect to the rotation axis) to the solar cycle dependence. The latitude-dependent magnetic field model is expressed as follows:

$$\begin{array}{ll}\text{(65)}& {\displaystyle }& {\displaystyle }{B}_{\mathrm{r}}=B_{\mathrm{0}}{\left({\displaystyle \frac{r_{\mathrm{0}}}{r}}\right)}^{\mathrm{2}},\text{(66)}& {\displaystyle }& {\displaystyle }{B}_{\mathit{\theta }}=B_{\mathrm{r}}{\displaystyle \frac{r}{U_{\mathrm{sw}}}}{\mathit{\omega }}^{\ast }\sin {\mathit{\beta }}^{\ast }\sin {\mathit{\varphi }}^{\ast },{\displaystyle }& {\displaystyle }{B}_{\mathit{\varphi }}=B_{\mathrm{r}}{\displaystyle \frac{r}{U_{\mathrm{sw}}}}[{\mathit{\omega }}^{\ast }\sin {\mathit{\beta }}^{\ast }\cos \mathit{\theta }\cos {\mathit{\varphi }}^{\ast }+\\ {\displaystyle }& {\displaystyle }\sin \mathit{\theta }\left({\mathit{\omega }}^{\ast }\cos {\mathit{\beta }}^{\ast }-{\mathrm{\Omega }}_{\odot }\right)+{\displaystyle \frac{\mathrm{d}{\mathit{\omega }}^{\ast }}{\mathrm{d}\mathit{\theta }}}\sin {\mathit{\beta }}^{\ast }\sin \mathit{\theta }\cos {\mathit{\varphi }}^{\ast }+\\ \text{(67)}& {\displaystyle }& {\displaystyle }{\mathit{\omega }}^{\ast }{\displaystyle \frac{\mathrm{d}{\mathit{\beta }}^{\ast }}{\mathrm{d}\mathit{\theta }}}\cos {\mathit{\beta }}^{\ast }\sin \mathit{\theta }\cos {\mathit{\varphi }}^{\ast }].\end{array}$$

Here

$$\begin{array}{}\text{(68)}& {\mathit{\varphi }}^{\ast }=\mathit{\varphi }-{\mathrm{\Omega }}_{\odot }t+{\displaystyle \frac{\mathrm{\Omega }(r-r_{\mathrm{0}})}{U_{\mathrm{sw}}}}+{\mathit{\varphi }}_{\mathrm{0}}.\end{array}$$

B₀ is again the radial component of the magnetic field at the reference radius r₀. The symbol β_F is the angle (the Fisk angle) between the virtual magnetic axis (p axis) and the rotation axis of the Sun, and ω is the differential rotation rate of the Sun. Both the angle β_F and ω are generalized to the latitude-dependent case by introducing the transition function F_t(θ) in the following way:

$$\begin{array}{}\text{(69)}& {\displaystyle }& {\displaystyle }{\mathit{\beta }}^{\ast }={\mathit{\beta }}_{\mathrm{F}}{F}_{\mathrm{t}}\left(\mathit{\theta }\right),\text{(70)}& {\displaystyle }& {\displaystyle }{\mathit{\omega }}^{\ast }=\mathit{\omega }{F}_{\mathrm{t}}\left(\mathit{\theta }\right).\end{array}$$

The transition function is constructed as follows (Burger et al., 2008):

$$\begin{array}{ll}{\displaystyle }{F}_{\mathrm{t}}& {\displaystyle }=\left|\tanh \left[{\mathit{\delta }}_{\mathrm{pol}}\mathit{\theta }\right]+\tanh \left[{\mathit{\delta }}_{\mathrm{pol}}\right(\mathit{\theta }-\mathit{\pi }\left)\right]\right.\\ \text{(71)}& {\displaystyle }& {\displaystyle }{\left.-\tanh \left[{\mathit{\delta }}_{\mathrm{eq}}\right(\mathit{\theta }-{\mathit{\theta }}_{\mathrm{b}}^{\prime }\left)\right]\right|}^{\mathrm{2}}\end{array}$$

for the northern high-latitude region ($\mathrm{0}\le \mathit{\theta }<{\mathit{\theta }}_{\mathrm{b}}^{\prime }$),

$$\begin{array}{}\text{(72)}& F_{\mathrm{t}}=\mathrm{0}\end{array}$$

for the equatorial or low-latitude region (${\mathit{\theta }}_{\mathrm{b}}^{\prime }\le \mathit{\theta }\le \mathit{\pi }-{\mathit{\theta }}_{\mathrm{b}}^{\prime }$), and

$$\begin{array}{ll}{\displaystyle }{F}_{\mathrm{t}}& {\displaystyle }=\left|\tanh \left[{\mathit{\delta }}_{\mathrm{pol}}\mathit{\theta }\right]+\tanh \left[{\mathit{\delta }}_{\mathrm{pol}}\right(\mathit{\theta }-\mathit{\pi }\left)\right]\right.\\ \text{(73)}& {\displaystyle }& {\displaystyle }{\left.-\tanh \left[{\mathit{\delta }}_{\mathrm{eq}}\right(\mathit{\theta }-\mathit{\pi }+{\mathit{\theta }}_{\mathrm{b}}^{\prime }\left)\right]\right|}^{\mathrm{2}}\end{array}$$

for the southern high-latitude region. ${\mathit{\theta }}_{\mathrm{b}}^{\prime }$ is the equatorward-limit polar angle of the coronal hole (characterized by open field lines) and is between 60 and 80^∘ from the solar rotation axis in Burger et al. (2008). The symbols δ_pol and δ_eq are the control parameters of the transition from the high-latitude magnetic fields (Fisk-type model) into the low-latitude fields (Parker-type model), e.g., ${\mathit{\delta }}_{\mathrm{pol}}={\mathit{\delta }}_{\mathrm{eq}}=\mathrm{5.0}$ proposed by Burger et al. (2008). The magnetic field model in Eqs. (65)–(67) represents a natural extension of the Parker model in that the case F_t=1 reproduces the model proposed by Zurbuchen et al. (1997) and the case F_t=0 reproduces the Parker model. The associated polar and azimuthal components of the flow velocity are

$$\begin{array}{ll}\text{(74)}& {\displaystyle }& {\displaystyle }{U}_{\mathit{\theta }}=r_{\mathrm{0}}{\mathit{\omega }}^{\ast }\sin {\mathit{\beta }}^{\ast }\sin {\mathit{\varphi }}_{\mathrm{\Omega }},{\displaystyle }& {\displaystyle }{U}_{\mathit{\varphi }}=r_{\mathrm{0}}({\mathit{\omega }}^{\ast }\sin {\mathit{\beta }}^{\ast }\cos \mathit{\theta }\cos {\mathit{\varphi }}_{\mathrm{\Omega }}+{\mathit{\omega }}^{\ast }\cos {\mathit{\beta }}^{\ast }\sin \mathit{\theta }+\\ {\displaystyle }& {\displaystyle \frac{\mathrm{d}\mathit{\omega }}{\mathrm{d}\mathit{\theta }}}\sin {\mathit{\beta }}^{\ast }\sin \mathit{\theta }\cos {\mathit{\varphi }}_{\mathrm{\Omega }}+\\ \text{(75)}& {\displaystyle }& {\displaystyle }{\mathit{\omega }}^{\ast }{\displaystyle \frac{\mathrm{d}{\mathit{\beta }}^{\ast }}{\mathrm{d}\mathit{\theta }}}\sin \mathit{\theta }\cos {\mathit{\varphi }}_{\mathrm{\Omega }}).\end{array}$$

The Fisk angle β_F is related to the tile angle of the heliospheric current sheet α_F by Burger et al. (2008):

$$\begin{array}{}\text{(76)}& \cos \left({\mathit{\alpha }}_{\mathrm{F}}+{\mathit{\beta }}_{\mathrm{F}}\right)=\mathrm{1}-\left(\mathrm{1}-\cos {\mathit{\theta }}_{\mathrm{mm}}^{\prime }\right){\displaystyle \frac{{\sin }^{\mathrm{2}}{\mathit{\alpha }}_{\mathrm{F}}}{{\sin }^{\mathrm{2}}{\mathit{\theta }}_{\mathrm{mm}}}},\end{array}$$

where θ_mm and ${\mathit{\theta }}_{\mathrm{mm}}^{\prime }$ are the equatorward (low-latitude) boundary of the polar coronal hole on the level of photosphere source surface in heliomagnetic coordinates, respectively. The boundary angles are expressed in heliographic coordinates as ${\mathit{\theta }}_{\mathrm{b}}={\mathit{\theta }}_{\mathrm{mm}}-{\mathit{\alpha }}_{\mathrm{F}}$ and ${\mathit{\theta }}_{\mathrm{b}}^{\prime }={\mathit{\theta }}_{\mathrm{mm}}^{\prime }-{\mathit{\alpha }}_{\mathrm{F}}$, respectively.

The tilt angles α_F and β_F and the boundary angles θ_b and ${\mathit{\theta }}_{\mathrm{b}}^{\prime }$ can be modeled in a time-dependent way when constructing the Fisk–Parker hybrid model (Burger et al., 2008) as a solar-cycle-dependent one: the time dependence of the tilt angle α_F is modeled as

$$\begin{array}{}\text{(77)}& {\mathit{\alpha }}_{\mathrm{F}}={\mathit{\alpha }}_{\min }+\left({\displaystyle \frac{\mathit{\pi }}{\mathrm{4}}}-{\displaystyle \frac{{\mathit{\alpha }}_{\min }}{\mathrm{2}}}\right)\left[\mathrm{1}-\cos \left({\displaystyle \frac{\mathit{\pi }}{\mathrm{4}}}T\left[\mathrm{yr}\right]\right)\right]\end{array}$$

for $\mathrm{0}\le T\left[\mathrm{yr}\right]\le \mathrm{4}$ yr and

$$\begin{array}{}\text{(78)}& {\mathit{\alpha }}_{\mathrm{F}}={\mathit{\alpha }}_{\min }+\left({\displaystyle \frac{\mathit{\pi }}{\mathrm{4}}}-{\displaystyle \frac{{\mathit{\alpha }}_{\min }}{\mathrm{2}}}\right)\left[\mathrm{1}-\cos \left({\displaystyle \frac{\mathit{\pi }}{\mathrm{7}}}\left(T\right[\mathrm{yr}]-\mathrm{11})\right)\right]\end{array}$$

for $\mathrm{4}<T\le \mathrm{11}\mathrm{yr}$, where ${\mathit{\alpha }}_{\min }=\mathit{\pi }/\mathrm{18}$ is an offset tilt angle. Time T is measured in units of years after a solar minimum. The time dependence of the boundary angles is

$$\begin{array}{}\text{(79)}& {\displaystyle }& {\displaystyle }{\mathit{\theta }}_{\mathrm{b}}={\displaystyle \frac{{\mathit{\theta }}_{\mathrm{b}\left(\min \right)}}{\mathrm{2}}}\left[\mathrm{1}+\cos \left({\displaystyle \frac{\mathit{\pi }}{\mathrm{4}}}T\left[\mathrm{yr}\right]\right)\right]\text{(80)}& {\displaystyle }& {\displaystyle }{\mathit{\theta }}_{\mathrm{b}}^{\prime }={\displaystyle \frac{{\mathit{\theta }}_{\mathrm{b}\left(\min \right)}^{\prime }}{\mathrm{2}}}\left[\mathrm{1}+\cos \left({\displaystyle \frac{\mathit{\pi }}{\mathrm{4}}}T\left[\mathrm{yr}\right]\right)\right]\end{array}$$

for $\mathrm{0}\le T\le \mathrm{4}\mathrm{yr}$ and

$$\begin{array}{}\text{(81)}& {\displaystyle }& {\displaystyle }{\mathit{\theta }}_{\mathrm{b}}={\displaystyle \frac{{\mathit{\theta }}_{\mathrm{b}\left(\min \right)}}{\mathrm{2}}}\left\{\mathrm{1}+\cos \left[{\displaystyle \frac{\mathit{\pi }}{\mathrm{7}}}\left(T\right[\mathrm{yr}]-\mathrm{11})\right]\right\}\text{(82)}& {\displaystyle }& {\displaystyle }{\mathit{\theta }}_{\mathrm{b}}^{\prime }={\displaystyle \frac{{\mathit{\theta }}_{\mathrm{b}\left(\min \right)}^{\prime }}{\mathrm{2}}}\left\{\mathrm{1}+\cos \left[{\displaystyle \frac{\mathit{\pi }}{\mathrm{7}}}\left(T\right[\mathrm{yr}]-\mathrm{11})\right]\right\}\end{array}$$

for $\mathrm{4}<T\le \mathrm{11}\mathrm{yr}$.

3 Further models and effects

3.1 Magnetohydrodynamic models

The models of the solar wind and the interplanetary magnetic field can be extended from kinematic or hydrodynamic treatments to magnetohydrodynamic (MHD) treatments. An overview of the MHD wind models is given by Tajima and Shibata (2002). Various magnetic effects are introduced in the MHD picture, e.g., the Alfvén velocity as a characteristic propagation speed (the Parker model, in contrast, recognizes the sound speed as a characteristic propagation speed) and the associated critical radius, collimation of the flow toward the rotation axis by magnetic pinching in the twisted field geometry.

3.1.1 One-dimensional treatment

An MHD model is proposed for an axisymmetric, one-dimensional, centrifugal-force-driven wind on the solar equatorial plane (Weber and Davis, 1967). Six variables are determined as a function of the radial distance (mass density, ρ; radial and azimuthal components of flow speed, U_r and U_ϕ; and that of the magnetic field, B_r and B_ϕ; and pressure p) using six equations (continuity equation, magnetic flux conservation, force balance, induction equation, adiabatic pressure, and energy conservation) and six integral constants (mass flux, magnetic flux, angular velocity of the Sun, Alfvén radius, entropy, and total energy). The Alfvén radius is defined as the radius at which the flow velocity reaches the Alfvén velocity in the radial component, $U_{\mathrm{r}}=V_{\mathrm{A},\mathrm{r}}$. At larger distances from the Sun, the solution is given asymptotically as

$$\begin{array}{}\text{(83)}& {\displaystyle }& {\displaystyle }\mathit{\rho }\propto r^{-\mathrm{2}},\text{(84)}& {\displaystyle }& {\displaystyle }{U}_{\mathrm{r}}\to U_{\mathrm{\infty }},\text{(85)}& {\displaystyle }& {\displaystyle }{B}_{\mathrm{r}}\propto r^{-\mathrm{2}},\text{(86)}& {\displaystyle }& {\displaystyle }{B}_{\mathit{\varphi }}\propto r^{-\mathrm{1}}.\end{array}$$

The magnetic field becomes more azimuthal and thus twisted with increasing distance, $B_{\mathit{\varphi }}/B_{\mathrm{r}}\propto r$.

The momentum balance equation by Parker (1958) is extended to including the effect of magnetic field and Alfvén wave heating rate (Alazraki and Couturier, 1971; Belcher, 1971; Woolsey and Cranmer, 2014; Comişel et al., 2015):

$$\begin{array}{ll}{\displaystyle }& {\displaystyle \frac{\mathrm{1}}{U}}{\displaystyle \frac{\mathrm{d}U}{\mathrm{d}r}}\left(U^{\mathrm{2}}-U_{\mathrm{c}}^{\mathrm{2}}\right)=-U_{\mathrm{c}}^{\mathrm{2}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}r}}\ln B-c_{\mathrm{s}}^{\mathrm{2}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}r}}\ln T\\ \text{(87)}& {\displaystyle }& {\displaystyle }+{\displaystyle \frac{Q_{\mathrm{A}}}{\mathrm{2}\mathit{\rho }(U+V_{\mathrm{A}})}}-{\displaystyle \frac{G{M}_{\odot }}{r^{\mathrm{2}}}}.\end{array}$$

Here Q_A denotes the Alfvén wave heating rate. U_c is the critical speed:

$$\begin{array}{}\text{(88)}& U_{\mathrm{c}}^{\mathrm{2}}=c_{\mathrm{s}}^{\mathrm{2}}+{\displaystyle \frac{W_{\mathrm{A}}}{\mathrm{4}\mathit{\rho }}}{\displaystyle \frac{\mathrm{3}U+V_{\mathrm{A}}}{U+V_{\mathrm{A}}}},\end{array}$$

where W_A is the energy density of the Alfvén waves including the perpendicular fluctuation components of the flow velocity δU_⟂ and that of the magnetic field δB_⟂,

$$\begin{array}{}\text{(89)}& W_{\mathrm{A}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathit{\rho }\mathit{\delta }{U}_{⟂}^{\mathrm{2}}+{\displaystyle \frac{\mathit{\delta }{B}_{⟂}^{\mathrm{2}}}{\mathrm{2}{\mathit{\mu }}_{\mathrm{0}}}}.\end{array}$$

3.1.2 Two-dimensional treatment

In the two-dimensional picture, the energy conservation (the generalized Bernoulli equation) and the conservation law perpendicular to the magnetic field (the generalized Grad–Shafranov equation) are derived using the force balance equation among the advection of the flow itself (flow nonlinearity such as steepening and eddies), the pressure gradient, the Lorentz force, and the gravitational attraction by the Sun, the mass flux conservation, the induction equation, and the adiabatic condition along the flow (Heinemann and Olbert, 1978; Sakurai, 1985; Lovelace et al., 1986). The generalized Grad–Shafranov equation cannot be solved analytically but needs to be solved numerically. It is found that the wind becomes collimated toward the rotation axis of the Sun (or the star) by the magnetic pinching of the spiral or twisted field. In fact, any stationary, axisymmetric magnetized wind collimates toward the rotation axis at large distances (Heyvaerts and Norman, 1989).

It is useful to introduce the poloidal–toroidal expression of the magnetic field in the two-dimensional MHD treatment:

$$\begin{array}{}\text{(90)}& {\mathit{B}}_{\mathrm{p}}=\mathbf{\nabla }\times \left(a{\mathit{e}}_{\mathit{\varphi }}\right)+B_{\mathit{\varphi }}{\mathit{e}}_{\mathit{\varphi }},\end{array}$$

where a denotes the magnetic stream function and e_ϕ is the unit vector in the azimuthal direction around the rotation axis. The poloidal fields B_p (the first term in Eq. 90) are obtained by a family of curves under $a=\mathrm{const}.$ We introduce the barred radius, which is the distance from the rotation axis, $\stackrel{\mathrm{‾}}{r}=r\sin \mathit{\theta }$. The flow velocity is decomposed by referring to the local magnetic field as

$$\begin{array}{}\text{(91)}& \mathit{U}={\displaystyle \frac{{\mathit{\alpha }}_{\mathrm{m}}\left(a\right)}{\mathit{\rho }}}\mathit{B}+{\stackrel{\mathrm{‾}}{r}}^{\mathrm{2}}\mathrm{\Omega }\left(a\right){\mathit{e}}_{\mathit{\varphi }},\end{array}$$

where the first term (denoted by U_p) is the flow velocity component parallel to the magnetic field in the frame rotating with the angular velocity Ω, and the second term (denoted by U_ϕ) is perpendicular to the magnetic field. The toroidal component of the magnetic field is determined by the angular momentum conservation,

$$\begin{array}{}\text{(92)}& \stackrel{\mathrm{‾}}{r}\left(U_{\mathit{\varphi }}-{\displaystyle \frac{B_{\mathit{\varphi }}}{{\mathit{\mu }}_{\mathrm{0}}a}}\right)=l=\mathrm{\Omega }{\stackrel{\mathrm{‾}}{r}}_{\mathrm{A}}^{\mathrm{2}}\left(a\right),\end{array}$$

where l is the specific angular momentum and ${\stackrel{\mathrm{‾}}{r}}_{\mathrm{A}}$ is the Alfvén radius at which the poloidal component of the flow velocity becomes equal to the Alfvén speed for the poloidal component of the magnetic field. Equation (92) is obtained from the (steady-state) MHD momentum equation and the flow velocity expression in Eq. (91). The magnetic stream function needs to be determined for the flow velocity and the poloidal component of the magnetic field. The magnetic stream function is numerically evaluated from the momentum equation (or force balance) perpendicular to the magnetic field by solving the following equation (Sakurai, 1985):

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathbf{\nabla }\cdot \left[\left({\displaystyle \frac{{\mathit{\alpha }}_{\mathrm{m}}^{\mathrm{2}}}{\mathit{\rho }}}-{\displaystyle \frac{\mathrm{1}}{{\mathit{\mu }}_{\mathrm{0}}}}\right){\displaystyle \frac{\mathbf{\nabla }a}{{\stackrel{\mathrm{‾}}{r}}^{\mathrm{2}}}}\right]=\mathit{\rho }(E^{\prime }-{\displaystyle \frac{\mathrm{1}}{{\mathit{\gamma }}_{\mathrm{p}}-\mathrm{1}}}{\displaystyle \frac{p}{\mathit{\rho }}}{\displaystyle \frac{K^{\prime }}{K}}+{\stackrel{\mathrm{‾}}{r}}^{\mathrm{2}}\mathrm{\Omega }{\mathrm{\Omega }}^{\prime })\\ {\displaystyle }& {\displaystyle }+{\displaystyle \frac{{\mathit{B}}_{\mathrm{p}}^{\mathrm{2}}}{\mathit{\rho }}}{\mathit{\alpha }}_{\mathrm{m}}{\mathit{\alpha }}_{\mathrm{m}}^{\prime }+D\left[{\displaystyle \frac{D}{{\mathit{\mu }}_{\mathrm{0}}}}{\mathrm{\Omega }}^{\mathrm{2}}{\stackrel{\mathrm{‾}}{r}}^{\mathrm{2}}{\mathit{\alpha }}_{\mathrm{m}}{\mathit{\alpha }}_{\mathrm{m}}^{\prime }-{\mathit{\alpha }}_{\mathrm{m}}^{\mathrm{2}}{\mathrm{\Omega }}^{\mathrm{2}}({\stackrel{\mathrm{‾}}{r}}_{\mathrm{A}}^{\mathrm{2}}{)}^{\prime }\right.\\ \text{(93)}& {\displaystyle }& {\displaystyle }\left.-{\mathit{\alpha }}_{\mathrm{m}}^{\mathrm{2}}\mathrm{\Omega }{\mathrm{\Omega }}^{\prime }\left({\stackrel{\mathrm{‾}}{r}}_{\mathrm{A}}^{\mathrm{2}}-{\stackrel{\mathrm{‾}}{r}}_{\mathrm{A}}\right)\right],\end{array}$$

where

$$\begin{array}{}\text{(94)}& D={\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}\mathit{\rho }\left({\stackrel{\mathrm{‾}}{r}}_{\mathrm{A}}^{\mathrm{2}}-r^{\mathrm{2}}\right)}{{\stackrel{\mathrm{‾}}{r}}^{\mathrm{2}}({\mathit{\mu }}_{\mathrm{0}}\mathit{\rho }{\mathit{\alpha }}_{\mathrm{m}}^{\mathrm{2}}-\mathit{\rho })}}\end{array}$$

and the prime $(\cdot {)}^{\prime }$ denotes the differentiation with respect to the magnetic stream function, d∕da. Equation (93) is the generalized Grad–Shafranov equation for the two-dimensional centrifugally driven wind. The density ρ follows the Bernoulli equation:

$$\begin{array}{}\text{(95)}& {\displaystyle \frac{U_{\mathrm{p}}^{\mathrm{2}}}{\mathrm{2}}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(U_{\mathit{\varphi }}-\mathrm{\Omega }\stackrel{\mathrm{‾}}{r}{)}^{\mathrm{2}}+{\displaystyle \frac{{\mathit{\gamma }}_{\mathrm{p}}}{{\mathit{\gamma }}_{\mathrm{p}}-\mathrm{1}}}{\displaystyle \frac{p}{\mathit{\rho }}}-{\displaystyle \frac{G{M}_{\cdot }}{r}}-{\displaystyle \frac{{\mathrm{\Omega }}^{\mathrm{2}}{\stackrel{\mathrm{‾}}{r}}^{\mathrm{2}}}{\mathrm{2}}}=E(a)\end{array}$$

under the polytropic or adiabatic equation of state

$$\begin{array}{}\text{(96)}& p=K\left(a\right){\mathit{\rho }}^{{\mathit{\gamma }}_{\mathrm{p}}}.\end{array}$$

In the two-dimensional MHD treatment of the flow, the wind becomes collimated toward the rotation axis by the pinch of toroidal fields (Sakurai, 1985), causing a nonzero poleward (northward or southward) component of the magnetic field.

3.2 More ingredients

Solar wind models can further be improved by considering turbulent diffusion and pickup ions.

3.2.1 Turbulent diffusion

Turbulence on smaller spatial scales serves as an energy sink to large-scale mean fields, which leads to the notion of turbulent diffusion (mean-field electrodynamics). To see this more clearly, one may decompose the magnetic field into a large-scale mean field B₀ and a fluctuating field δB (with the zero mean value), as well as the flow velocity:

$$\begin{array}{}\text{(97)}& {\displaystyle }& {\displaystyle }\mathit{B}={\mathit{B}}_{\mathrm{0}}+\mathit{\delta }\mathit{B},\text{(98)}& {\displaystyle }& {\displaystyle }\mathit{U}={\mathit{U}}_{\mathrm{0}}+\mathit{\delta }\mathit{U}.\end{array}$$

The induction equation for the large-scale magnetic field has then the frozen-in term for the large-scale fields B₀ and U₀ and the electromotive force term ℰ_em:

$$\begin{array}{}\text{(99)}& {\displaystyle \frac{\partial {\mathit{B}}_{\mathrm{0}}}{\partial t}}=\mathbf{\nabla }\times \left({\mathit{U}}_{\mathrm{0}}\times {\mathit{B}}_{\mathrm{0}}\right)+\mathbf{\nabla }\times {\mathcal{E}}_{\mathrm{em}}.\end{array}$$

The electromotive force is an averaged electric field coming from the coupling of the flow velocity fluctuations with the fluctuating magnetic field by the cross product:

$$\begin{array}{}\text{(100)}& {\mathcal{E}}_{\mathrm{em}}=〈\mathit{\delta }\mathit{U}\times \mathit{\delta }\mathit{B}〉.\end{array}$$

A widely used model in the mean-field electrodynamics is that the electromotive force depends on the large-scale quantities such as the large-scale magnetic field, the curl of the large-scale magnetic field, and the curl of the large-scale flow velocity. By introducing the proper transport coefficients α_t, β_t, and γ_t, the electromotive force is modeled as

$$\begin{array}{}\text{(101)}& {\mathcal{E}}_{\mathrm{model}}={\mathit{\alpha }}_{\mathrm{t}}{\mathit{B}}_{\mathrm{0}}-{\mathit{\beta }}_{\mathrm{t}}\mathbf{\nabla }\times {\mathit{B}}_{\mathrm{0}}+{\mathit{\gamma }}_{\mathrm{t}}\mathbf{\nabla }\times {\mathit{U}}_{\mathrm{0}}.\end{array}$$

After some algebra using Eqs. (99) and (101), one identifies that the term β_t∇×B₀ becomes nothing other than the diffusion term for the large-scale magnetic field (under the condition that the coefficient β_t is not negative):

$$\begin{array}{ll}{\displaystyle \frac{\partial {\mathit{B}}_{\mathrm{0}}}{\partial t}}=& {\displaystyle }\mathbf{\nabla }\times \left({\mathit{U}}_{\mathrm{0}}\times {\mathit{B}}_{\mathrm{0}}\right)+\mathbf{\nabla }\times \left({\mathit{\alpha }}_{\mathrm{t}}{\mathit{B}}_{\mathrm{0}}\right)+{\mathit{\beta }}_{\mathrm{t}}{\mathbf{\nabla }}^{\mathrm{2}}{\mathit{B}}_{\mathrm{0}}\\ \text{(102)}& {\displaystyle }& {\displaystyle }+\mathbf{\nabla }\times \left({\mathit{\gamma }}_{\mathrm{t}}\mathbf{\nabla }\times {\mathit{U}}_{\mathrm{0}}\right).\end{array}$$

The terms with α_t and γ_t in turn may amplify the large-scale magnetic field when the coefficients are in favor of field amplification (dynamo mechanism). The transport coefficients are theoretically estimated as follows:

$$\begin{array}{}\text{(103)}& {\displaystyle }& {\displaystyle }{\mathit{\alpha }}_{\mathrm{t}}=C_{\mathit{\alpha }}\mathit{\tau }(-h_{\mathrm{kin}}+h_{\mathrm{cur}}),\text{(104)}& {\displaystyle }& {\displaystyle }{\mathit{\beta }}_{\mathrm{t}}=C_{\mathit{\beta }}\mathit{\tau }\left(e_{\mathrm{kin}}+e_{\mathrm{mag}}\right),\text{(105)}& {\displaystyle }& {\displaystyle }{\mathit{\gamma }}_{\mathrm{t}}=C_{\mathit{\gamma }}\mathit{\tau }{h}_{\mathrm{crs}},\end{array}$$

where C_α, C_β, and C_γ are dimensionless scalar factors and are estimated as (Yoshizawa, 1998)

$$\begin{array}{}\text{(106)}& {\displaystyle }& {\displaystyle }{C}_{\mathit{\alpha }}\simeq \mathrm{0.02},\text{(107)}& {\displaystyle }& {\displaystyle }{C}_{\mathit{\beta }}\simeq \mathrm{0.05},\text{(108)}& {\displaystyle }& {\displaystyle }{C}_{\mathit{\gamma }}\simeq \mathrm{0.04}.\end{array}$$

The symbol τ denotes the turbulent correlation time length, and h and e represent the helicity and the energy quantities: h_kin the kinetic helicity density, h_cur the current helicity density, h_crs the cross helicity density, e_kin the turbulent kinetic energy density, and e_mag the turbulent magnetic energy density. The helicity density quantities and the energy density quantities are defined for the fluctuating field:

$$\begin{array}{}\text{(109)}& {\displaystyle }& {\displaystyle }{h}_{\mathrm{kin}}=〈\mathit{\delta }\mathit{U}\cdot \left(\mathbf{\nabla }\times \mathit{\delta }\mathit{U}\right)〉,\text{(110)}& {\displaystyle }& {\displaystyle }{h}_{\mathrm{cur}}={\displaystyle \frac{\mathrm{1}}{{\mathit{\mu }}_{\mathrm{0}}{\mathit{\rho }}_{\mathrm{0}}}}〈\mathit{\delta }\mathit{B}\cdot \left(\mathbf{\nabla }\times \mathit{\delta }\mathit{B}\right)〉,\text{(111)}& {\displaystyle }& {\displaystyle }{h}_{\mathrm{crs}}={\displaystyle \frac{\mathrm{1}}{\sqrt{{\mathit{\mu }}_{\mathrm{0}}{\mathit{\rho }}_{\mathrm{0}}}}}〈\mathit{\delta }\mathit{U}\cdot \mathit{\delta }\mathit{B}〉,\text{(112)}& {\displaystyle }& {\displaystyle }{e}_{\mathrm{kin}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\langle |\mathit{\delta }\mathit{U}{|}^{\mathrm{2}}\rangle ,\text{(113)}& {\displaystyle }& {\displaystyle }{e}_{\mathrm{mag}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}{\mathit{\mu }}_{\mathrm{0}}{\mathit{\rho }}_{\mathrm{0}}}}\langle |\mathit{\delta }\mathit{B}{|}^{\mathrm{2}}\rangle .\end{array}$$

Note that different definitions are possible for the helicity and energy density quantities. In the definition above (Eqs. 109–113) the fluctuating magnetic field is converted into the velocity dimension such as $\mathit{\delta }\mathit{B}/\sqrt{{\mathit{\mu }}_{\mathrm{0}}{\mathit{\rho }}_{\mathrm{0}}}$, and the energy density is represented as that per unit mass. The correlation time length τ can in the simplest case be modeled or represented by the eddy turnover time,

$$\begin{array}{}\text{(114)}& {\mathit{\tau }}_{\mathrm{ed}}={\displaystyle \frac{\mathrm{\ell }}{\mathit{\delta }U}}={\displaystyle \frac{e_{\mathrm{kin}}+e_{\mathrm{mag}}}{\mathit{\epsilon }}},\end{array}$$

where ε is the dissipation rate which needs to be obtained by solving an equation in the similar fashion to the turbulence energy (Yokoi et al., 2008). The estimate of timescale can be extended by including the Alfvén time effect into a synthesized timescale τ_s in the additive sense in the frequency domain as

$$\begin{array}{}\text{(115)}& {\displaystyle \frac{\mathrm{1}}{{\mathit{\tau }}_{\mathrm{s}}}}={\displaystyle \frac{\mathrm{1}}{{\mathit{\tau }}_{\mathrm{ed}}}}+\mathit{\chi }{\displaystyle \frac{\mathrm{1}}{{\mathit{\tau }}_{\mathrm{A}}}},\end{array}$$

where τ_A denotes the Alfvén time

$$\begin{array}{}\text{(116)}& {\mathit{\tau }}_{\mathrm{A}}={\displaystyle \frac{\mathrm{\ell }}{V_{\mathrm{A}}}}={\displaystyle \frac{|e_{\mathrm{kin}}+e_{\mathrm{mag}}{|}^{\mathrm{2}}}{\mathit{\epsilon }{V}_{\mathrm{A}}^{\mathrm{2}}}},\end{array}$$

with the length scale ℓ and the Alfvén speed V_A. The symbol χ is the weight factor for the Alfvén time and is estimated to be of the order 10² in the solar wind application (Yokoi et al., 2008). A more rigorous treatment is to solve two sets of equations, one for the large-scale mean fields and the other for the small-scale turbulent fields. This task can be achieved either analytically using the two-scale direct interaction approximation (Yokoi, 2006; Yokoi and Hamba, 2007; Yokoi et al., 2008) or numerically (Usmanov et al., 2012, 2014, 2016).

3.2.2 Pickup ions

Pickup ions from interstellar neutral hydrogen atoms are one of the ingredients to the solar wind and contribute to additional mass of the plasma, which results in deceleration of the solar wind expansion and in increase in the plasma temperature. Pickup ions originate in (1) charge exchange with the solar wind protons and (2) photoionization by the solar radiation. Steady-state MHD equations for the wind including pickup ions are introduced by Isenberg (1986) and Whang (1998) and are numerically implemented to simulation studies for a three-component fluid (thermal protons, electrons, pickup protons) by Usmanov and Goldstein (2006) and Usmanov et al. (2014) and for a four-component fluid by adding interstellar hydrogen (Usmanov et al., 2016).

The continuity equation in the one-fluid sense (mixture of electrons, solar wind protons, and pickup ions of interstellar origin) has a contribution from the photoionization as a source term and is written for the steady state as (Whang, 1998)

$$\begin{array}{}\text{(117)}& \mathbf{\nabla }\cdot \left(\mathit{\rho }\mathit{U}\right)=m_{\mathrm{p}}{q}_{\mathrm{ph}},\end{array}$$

where ρ and U denote the mass density and the flow velocity in the one-fluid sense, m_p the proton mass, and q_ph the pickup ion production rate by the photoionization process,

$$\begin{array}{}\text{(118)}& q_{\mathrm{ph}}={\mathit{\nu }}_{\mathrm{0}}\left({\displaystyle \frac{r_{\mathrm{0}}^{\mathrm{2}}}{r}}\right)n_{\mathrm{nt}}.\end{array}$$

Here ${\mathit{\nu }}_{\mathrm{0}}=\mathrm{0.9}\times {\mathrm{10}}^{-\mathrm{7}}$ s⁻¹ is the photoionization rate per hydrogen atom at the Earth orbit distance as reference r₀=1 au, and n_nt is the number density of neutral hydrogen (of interstellar origin). The one-fluid momentum equation in the steady state is approximated into (by neglecting higher-order terms) (Whang, 1998)

$$\begin{array}{ll}{\displaystyle }\mathit{\rho }\mathit{U}\cdot \mathit{U}+& {\displaystyle }\mathbf{\nabla }P-\mathit{\rho }\mathbf{\nabla }\left({\displaystyle \frac{G{M}_{\odot }}{r}}\right)-{\displaystyle \frac{\mathrm{1}}{{\mathit{\mu }}_{\mathrm{0}}}}(\mathbf{\nabla }\times \mathit{B})\times \mathit{B}=\\ \text{(119)}& {\displaystyle }& {\displaystyle }-(q_{\mathrm{ex}}+q_{\mathrm{ph}})m_{\mathrm{p}}\mathit{U}.\end{array}$$

Here q_ex is the pickup ion production rate by the charge exchange process,

$$\begin{array}{}\text{(120)}& q_{\mathrm{ex}}={\mathit{\sigma }}_{\mathrm{ex}}{n}_{\mathrm{sw}}{n}_{\mathrm{nt}}U,\end{array}$$

where σ_ex is the cross section of charge exchange between a hydrogen atom and the solar wind protons, and n_sw is the number density of solar wind protons.

3.3 Stellar wind and interstellar space

Various outflow models have been proposed for the stellar wind. For example, a wind model is constructed and numerically studied for the thermally driven hydrodynamic outflow from low-mass stars (Johnstone et al., 2015). A dead zone due to the magnetic dipole field effect can arise in the equatorial region (Keppens and Goedlbloed, 1999). A model is also constructed for the stellar winds around asymptotic giant branch (AGB) stars with dust grains by employing the MHD equation for the stellar wind plasma and the Euler equation for the dust grains under the gravity, the radiation pressure, and the drag force (Thirumalai and Heyl, 2010), showing the possibility of a stellar wind driven by dust grains. The mass-loss rate is observationally studied via stellar winds for subluminous stars (Krtička et al., 2016), in which the following flow velocity model is used for fitting with three parameters U₁, U₂, and γ_sw:

$$\begin{array}{ll}{\displaystyle }U=& {\displaystyle }\left[U_{\mathrm{1}}\left(\mathrm{1}-{\displaystyle \frac{R_{\mathrm{s}}}{r}}\right)+U_{\mathrm{2}}{\left(\mathrm{1}-{\displaystyle \frac{R_{\mathrm{s}}}{r}}\right)}^{\mathrm{2}}\right]\\ \text{(121)}& {\displaystyle }& {\displaystyle }\left\{\mathrm{1}-\exp \left[{\mathit{\gamma }}_{\mathrm{sw}}{\left(\mathrm{1}-{\displaystyle \frac{r}{R_{\mathrm{s}}}}\right)}^{\mathrm{2}}\right]\right\},\end{array}$$

where R_s is the stellar radius.

Stellar winds can be detected by the spectroscopic investigation. A line spectrum becomes distorted to blue-shifted absorption and red-shifted emission by the retarding stellar wind (away from the observer), known as the P Cygni profile. One type of the stellar wind models is the Lucy model (Lucy, 1971):

$$\begin{array}{}\text{(122)}& U=U_{\mathrm{t}}{\left[\mathrm{1}-{\displaystyle \frac{(\mathrm{1}-a_{\mathrm{sw}})R_{\mathrm{s}}}{r}}-a_{\mathrm{sw}}{\displaystyle \frac{R_{\mathrm{s}}^{\mathrm{2}}}{r^{\mathrm{2}}}}\right]}^{\mathrm{1}/\mathrm{2}},\end{array}$$

where a_sw is a free parameter with $-\mathrm{1}<a_{\mathrm{sw}}<\mathrm{1}$. Equation (122) satisfies the conditions of zero speed at the stellar surface (U=0 at r=R_s) and asymptotic behavior at very large distances from the star (U→U_t as r→∞). U_t is the terminal flow velocity. The flow speed increases monotonously as a function of the radius, U>0 and $\frac{\mathrm{d}U}{\mathrm{d}r}>\mathrm{0}$. The other type is a variant of the Lucy model (Kudritzki and Puls, 2000):

$$\begin{array}{}\text{(123)}& {\displaystyle \frac{U}{U_{\mathrm{t}}}}={\left(\mathrm{1}-b_{\mathrm{sw}}{\displaystyle \frac{R_{\mathrm{s}}}{r}}\right)}^{{\mathit{\beta }}_{\mathrm{sw}}},\end{array}$$

where the constant b_sw is the flow velocity at the inner boundary of the stellar wind. An even more simplified expression is (Lamers, 1998)

$$\begin{array}{}\text{(124)}& {\displaystyle \frac{U}{U_{\mathrm{t}}}}={\left(\mathrm{1}-{\displaystyle \frac{R_{\mathrm{s}}}{r}}\right)}^{{\mathit{\beta }}_{\mathrm{sw}}},\end{array}$$

where U_t is the asymptotic, termination flow speed. β_sw is a free parameter and is empirically chosen as $\mathrm{0.5}\le {\mathit{\beta }}_{\mathrm{sw}}\le \mathrm{4}$ (Sapar et al., 2003).

4 Summary and conclusions

There is an increasing amount of models for the interplanetary magnetic field. Starting with the Parker model, the magnetic field model can be extended to include the latitudinal dependence, the poleward component, the time dependence, and the polarity and tilt effect even in the analytic or semi-analytic treatment. Which model to choose would depend on the application, e.g., if the solar cycle is to be included or not, or if the latitudinal dependence is to be or not. In the temporal sense, cosmic ray diffusion has the shortest timescale, about 13 h for relativistic particles nearly at the speed of light to travel over 100 au distance in the heliosphere. In contrast, plasma turbulence evolves together with the solar wind, and the timescale is intermediate, being of the order or days; i.e., the solar wind travel time from the Sun to the Earth orbit, 1 au, is about 100 h or roughly 4 d. Charged dust motions and modulation of the cosmic ray flux in the heliosphere evolve on the longest timescale among the three applications, of the order of of years (secular variation of the orbital parameters).

The accuracy or the uncertainty of the reviewed models needs to be verified using in situ magnetic field measurements from the previous, current, and upcoming spacecraft missions. Above all, the magnetic field in the inner heliosphere will be extensively studied with Parker Solar Probe, BepiColombo (in particular, the cruise-phase measurements), and Solar Orbiter.

It is interesting to note that the analytic expression is also available for the coronal magnetic field (during the solar minimum) and the local interstellar magnetic field surrounding the heliosphere. Hence, naively speaking, one may expect to construct a more complete model of the magnetic field from the Sun to the local interstellar medium. Such a model, once smoothly and rationally connected from one region to another, enables one to improve the accuracy of theoretical studies on plasma turbulence evolution, charged dust motions, and diffusion of cosmic ray and energetic particles.

It is also worth noting the limits of the models. First, the magnetic fields are highly irregular in structure in the solar corona and at the solar surface. At some distance sufficiently close to the Sun, the interplanetary magnetic field should smoothly be connected to the coronal magnetic field. Second, the outer heliosphere has the termination shock and the heliopause, which are not included in the models in this review. Third, the solar variability includes not only the 11-year sunspot number variation or the 22-year magnetic structure variation, but also modulations of the solar cycle on long timescales such as 100 or even 1000 years.