On the ion-inertial-range density-power spectra in solar wind turbulence

A model-independent first-principle first-order investigation of the shape of turbulent density-power spectra in the ion-inertial range of the solar wind at 1 AU is presented. Demagnetised ions in the ion-inertial range of quasi-neutral plasmas respond to Kolmogorov (K) or Iroshnikov–Kraichnan (IK) inertial-range velocity–turbulence power spectra via the spectrum of the velocity–turbulence-related random-mean-square induction–electric field. Maintenance of electrical quasi-neutrality by the ions causes deformations in the power spectral density of the turbulent density fluctuations. Assuming inertial-range K (IK) spectra in solar wind velocity turbulence and referring to observations of density-power spectra suggest that the occasionally observed scale-limited bumps in the density-power spectrum may be traced back to the electric ion response. Magnetic power spectra react passively to the density spectrum by warranting pressure balance. This approach still neglects contribution of Hall currents and is restricted to the ion-inertial-range scale. While both density and magnetic turbulence spectra in the affected range of ion-inertial scales deviate from K or IK power law shapes, the velocity turbulence preserves its inertial-range shape in the process to which spectral advection turns out to be secondary but may become observable under special external conditions. One such case observed by WIND is analysed. We discuss various aspects of this effect, including the affected wave-number scale range, dependence on the angle between mean flow velocity and wave numbers, and, for a radially expanding solar wind flow, assuming adiabatic expansion at fast solar wind speeds and a Parker dependence of the solar wind magnetic field on radius, also the presumable limitations on the radial location of the turbulent source region.

1 Introduction

The solar wind is a turbulent flow with an origin in the solar corona. It is believed to become accelerated within a few solar radii in the coronal low-beta region. Though this awaits approval, it is also believed that its turbulence originates there. Turbulent power spectral densities in the solar wind have been measured in situ at around 1 AU for several decades already. They include spectra of the magnetic field (e.g. Goldstein et al., 1995; Tu and Marsch, 1995; Zhou et al., 2004; Podesta, 2011, for reviews, among others), but with improved instrumentation also of the fluid velocity (Podesta et al., 2007; Podesta, 2009; Šafránková et al., 2013), electric field (Chen et al., 2011, 2012, 2014a, b), temperature (Šafránková et al., 2016), and (starting with Celnikier et al., 1983, who already reported its main properties) also of the (quasi-neutral) solar wind density (Chen et al., 2012, 2013; Šafránková et al., 2013, 2015, 2016).

Complementary to the measurements in situ, the solar wind, ground-based observations of radio scintillations from distant stars, originally applied (Lee and Jokipii, 1975, 1976; Cordes et al., 1991; Armstrong et al., 1995) to the interstellar medium (ISM; for early reviews, e.g. Coles, 1978; Armstrong et al., 1981) and used for extra-heliospheric plasma diagnosis (cf., Haverkorn and Spangler, 2013), also provided information about the solar wind density turbulence (Coles and Harmon, 1989; Armstrong et al., 1990; Spangler and Sakurai, 1995; Harmon and Coles, 2005) mostly at solar radial distances $<\mathrm{60}{R}_{\odot }\approx \mathrm{0.25}$ AU in the innermost very low solar wind ($\mathrm{0.1}<{\mathit{\beta }}_{\mathrm{i}}<\mathrm{1}$; e.g. the model of McKenzie et al., 1995) region, which is of particular interest because it is the presumable source region of the solar wind, being accessible only remotely. Solar wind turbulence generated here seems to freeze¹ and is transported radially outward afterwards by the flow. Radio-phase scintillation of spacecraft signals from Viking, Helios, and Pioneer have been used early on (Woo and Armstrong, 1979) to determine solar wind density-power spectra in the radial interval ≤1 AU, reporting mean spectral Kolmogorov slopes $\sim -\mathrm{5}/\mathrm{3}$ with a strong flattening of the spectrum near the Sun at distances $<\mathrm{30}{R}_{\odot }$ where the slope flattens down to $\sim -\mathrm{7}/\mathrm{6}=-\mathrm{1.1}$, a finding which suggests evolution of the density turbulence with solar distance. In the ISM radio scintillation, observations covered a huge range of decades, from wavelength scales λ≈15 AU down to close to the Debye length λ_D≈50 m, suggesting an approximate Kolmogorov spectrum over 7 decades. From recent in situ Voyager 1 observations of ISM electron densities (Gurnett et al., 2013) a Kolmogorov spectrum has been inferred down to wavelengths of λ∼10⁶ m that is followed by an adjacent spectral intensity excess on the assumed kinetic scales for wavelengths λ≳λ_D (Lee and Lee, 2019).

Density fluctuations δN are generally inherent to pressure fluctuations δP. From fundamental physical principles, it follows that density turbulence does not evolve by itself. Through the continuity equation, it is related to velocity turbulence, which in its course requires the presence of free energy, being driven by external forces. It is primary, while turbulence in density, temperature, and the magnetic field is secondary (for a different claim, see Howes and Nielson, 2013; Nielson et al., 2013). Density turbulence may signal the presence of a population of compressive (magneto-acoustic-like) fluctuations in addition to the usually assumed (e.g. Biskamp, 2003; Howes, 2015) alfvénic turbulence, the dominant fluid–magnetic fluctuation family dealing with the mutually related alfvénic velocity and magnetic fields made use of in magnetohydrodynamic (MHD) theory based on Elsasser variables (Elsasser, 1950).

Inertial-range velocity turbulence is subject to Kolmogorov (Kolmogorov, 1941a, b, 1962) or Iroshnikov–Kraichnan (Iroshnikov, 1964; Kraichnan, 1965, 1966, 1967) turbulence spectra. (Regarding their generalisation to anisotropy with respect to any mean magnetic field, see Goldreich and Sridhar, 1995.) In the solar wind, Kolmogorov inertial-range spectra reaching down into the presumable dissipation range have been confirmed by a wealth of in situ observations (e.g. Goldstein et al., 1995; Tu and Marsch, 1995; Zhou et al., 2004; Alexandrova et al., 2009; Boldyrev et al., 2011; Matthaeus et al., 2016; Lugones et al., 2016; Podesta, 2011; Podesta et al., 2006, 2007; Sahraoui et al., 2009, and others). Since the mean fields $B_{\mathrm{0}},T_{\mathrm{0}},N_{\mathrm{0}},U_{\mathrm{0}}$ themselves obey pressure balance, one has the following for pressure balance among the turbulent fluctuations:

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\langle |\mathit{\delta }\mathit{B}{|}^{\mathrm{2}}\rangle }{B_{\mathrm{0}}^{\mathrm{2}}}}={\displaystyle \frac{\sqrt{\langle |\mathit{\delta }N{|}^{\mathrm{2}}\rangle }}{N_{\mathrm{0}}}}+{\displaystyle \frac{\sqrt{\langle |\mathit{\delta }T{|}^{\mathrm{2}}\rangle }}{T_{\mathrm{0}}}}.\end{array}$$

The angular brackets 〈…〉 indicate averaging over the spatial scales of the turbulence with respect to turbulent fluctuations. Alfvénic fluctuations (e.g. Howes, 2015, for a recent theoretical account of their importance in MHD turbulence) compensate separately due to their magnetic and velocity fluctuations being related; they do not contribute to extra compression. In order to infer the contribution of density fluctuations, one compares their spectral densities with those of the temperature δT or magnetic field δB. This requires normalisation to the means. Solar wind densities at 1 AU are of the order of N₀∼10 cm⁻³, while ion thermal speeds are of the order of v_i∼30 km s⁻¹. Moreover, mean plasma betas are of the order of β_i∼1 here. For checking pressure balance, measured density fluctuations can be compared with those two.

An example is shown in Fig. 1 based on solar wind measurements on 6 July 2012 (Šafránková et al., 2015, 2016). There is not much freedom left in choosing the mean densities and temperatures in Fig. 1. Densities at 1 AU barely exceed 10 cm⁻³. Electron temperatures are insensitive to those low-frequency density fluctuations. High mobility makes electron reaction isothermal.

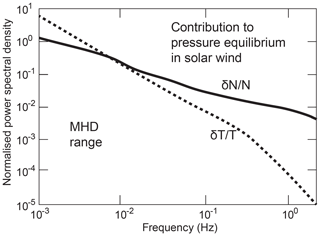
Figure 1 Normalised solar wind power spectra of turbulent temperature and density fluctuations. The curves are based on data from Šafránková et al. (2016) obtained on 6 July 2012 from the Bright Monitor of the Solar Wind (BMSW) instrument aboard the Spektr-R spacecraft. The solar wind conditions of these observations have been tabulated (Chen et al., 2014a). They indicate rather slow compared to medium conditions. The data have been rescaled and normalised to the main density N₀ and temperature T₀ in order to show their relative contributions to an assumed solar wind pressure balance. The interesting result is that in the lowest MHD frequency range density fluctuations are irrelevant with respect to pressure balance. At higher frequencies, however, the density fluctuations dominate the temperature fluctuations.

The data in Fig. 1 show the relative dominance of density fluctuations over ion temperature fluctuations under moderately low-speed solar wind conditions at all frequencies larger than the lowest accessible MHD frequencies. This is not surprising because one would not expect large temperature effects. Ion heating is a slow process which does not react to any fast pressure fluctuations caused by density or magnetic turbulence. It just shows that the turbulent thermal pressure is mainly due to density fluctuations over most of the frequency range. In the low-frequency MHD range the kinetic pressure of large-scale turbulent eddies dominates.

Inertial-range power spectra of turbulent density fluctuations are power laws. Occasionally they exhibit pronounced spectral excursions from their monotonic course prior to dropping into the dissipative range. Whenever this happens, the spectrum flattens or, in a narrow range of scales, even turns to positive slopes, sometimes dubbed spectral “bumps”. The reason for such spectral excesses still remains unclear. Similar bumps have also been seen in electric field spectra (e.g. Chen et al., 2012), where they have tentatively been suggested to indicate the presence of kinetic Alfvén waves which may be excited in the Hall-MHD (e.g. Huba, 2003) range as eigenmodes of the plasma. Models including Alfvén ion-cyclotron waves (Harmon and Coles, 2005) or kinetic Alfvén waves (Chandran et al., 2009) have been proposed to cause spectral flattening. Kinetic Alfvén waves may also lead to bumps if only β_i≪1. In fact, kinetic Alfvén waves possess a large perpendicular wave number $k_{⟂}{\mathit{\lambda }}_{\mathrm{i}}\sim \mathrm{1}$ of the order of the inverse ion-inertial length (e.g. Baumjohann and Treumann, 1996), the scale on which ions demagnetise. If sufficient free energy is available, they can thus be excited and propagate in this regime (e.g. Gary, 1993; Treumann and Baumjohann, 1997). Recently Wu et al. (2019) provided kinetic-theoretical arguments for kinetic Alfvén waves contributing to turbulent dissipation in the ion-inertial scale region. Causing bumps, the waves should develop large amplitudes on the background of general turbulence, i.e. causing intermittency. This requires the presence of a substantial amount of unidentified free energy, for instance in the form of intense plasma beams, which are very well known in relation to collisionless shocks both upstream and downstream (e.g. Balogh and Treumann, 2013). If kinetic Alfvén waves are unambiguously confirmed (see, e.g. Salem et al., 2012), the inner solar wind at ≲0.6 AU could be subject to the continuous presence of small-scale collisionless shocks, a assumption that is not unreasonable and which would be supported by observation of sporadic nonthermal coronal radio emissions (type I through type IV solar radio bursts).

In the present note we take a completely different model-independent point of view, avoiding reference to any superimposed plasma instabilities or intermittency (e.g. Chen et al., 2014b). We do not develop any “new theory” of turbulence. Instead, we remain in the realm of turbulent fluctuations, asking for the effect of ion inertia, with respect to ion demagnetisation in the ion-inertial Hall-MHD range, on the shape of the inertial-range power spectral density which will be illustrated referring to a few selected observations. To demonstrate pressure balance we refer to related magnetic power spectra, both measured in situ aboard spacecraft, which require a rather sophisticated instrumentation. Those measurements were anticipated by indirectly inferred density spectra in the solar wind (Woo, 1981; Coles and Filice, 1985; Bourgeois et al., 1985) and the interstellar plasma (Coles, 1978; Armstrong et al., 1981, 1990) from detection of ground-based radio scintillations.

In the next section we discuss the response of demagnetised ions to the presence of turbulence on scales between the ion and electron inertial lengths. We interpret this response as the consequence of electric field fluctuations in relation to the turbulent velocity field. The requirement of charge neutrality maps them to the density field via Poisson's equation. The additional contribution of the Hall effect can be separated. We then refer to turbulence theory, assuming that the mechanical inertial-range velocity–turbulence spectrum is either Kolmogorov (K) or Iroshnikov–Kraichnan (IK) and, in a fast-streaming solar wind under relatively weak conditions (Treumann et al., 2019), maps from wave number k into a stationary observer's frequency ω_s space via Taylor's hypothesis (Taylor, 1938).

In order to be more general, we split the mean flow velocity into bulk V₀ and large-eddy U₀ velocities, the latter being known (Tennekes, 1975) to cause Doppler broadening of the local velocity spectrum at a fixed wave number (reviewed and backed by numerical simulations by Fung et al., 1992; Kaneda, 1993). Imposing the theoretical K or IK inertial-range spectra, we then find the deformed power density spectra of density turbulence versus spacecraft frequency. We apply these to some observed spectral density bumps which we check on a measured magnetic power spectrum for pressure balance. The results are tabulated. Since bumpy spectra are rather rare, we also consider two more “normal” bumpless spectra. Such deformed density-power spectra which exhibit some typical spectral flattening were obtained under different solar wind conditions. The paper concludes with a brief discussion of the results.

2 Inertial-range ion response

Our main question concerns the cause of the occasionally observed scale-limited bumps in the turbulent density-power spectra, in particular their deviation from the expected monotonic inertial-range power law decay towards high wave numbers prior to entering the presumable dissipation range.

The philosophy of our approach is the following. Turbulence is always mechanical, i.e. in the velocity. It obeys a turbulent spectrum which extends over all scales of the turbulence. In a plasma, containing charged particles of different mass, these scales for the particles divide into magnetised, inertial, unmagnetised, and dissipative groups. On each of these intervals, the particles behave differently, reacting to the turbulence in the velocity. In the inertial range, the particles lose their magnetic property. They do not react to the magnetic field. They, however, are sensitive to the presence of electric fields, independent of their origin. Turbulence in velocity in a conducting medium in the presence of external magnetic fields is always accompanied by turbulence in the electric field due to gauge invariance, namely the Lorentz force. This electric field affects the unmagnetised component of the plasma, the ions in our case, which to maintain quasi-neutrality tend to compensate it. Below we deal with this effect and its consequences for the density-power spectrum.

2.1 Electric field fluctuations in the ion-inertial range

The steep decay of the normalised fluctuations in ion temperature above frequencies $>{\mathrm{10}}^{-\mathrm{1}}$ Hz is certainly due to the drop in ion dynamics at frequencies close to and exceeding the ion-cyclotron frequency, which at 1 AU distance from the Sun is of the order of $f_{\mathrm{ci}}={\mathit{\omega }}_{\mathrm{ci}}/\mathrm{2}\mathit{\pi }\sim \mathrm{1}$ Hz for a nominal magnetic field of ∼10 nT. In this range we enter the (dissipationless) ion-inertial or Hall (electron-MHD) domain where ions demagnetise, currents are carried by magnetised electrons, both species decouple magnetically, and Hall currents arise. At those frequencies, far below the electron $f_{\mathrm{e}}={\mathit{\omega }}_{\mathrm{e}}/\mathrm{2}\mathit{\pi }\sim \mathrm{35}$ kHz and (assuming protons) ion $f_{\mathrm{i}}={\mathit{\omega }}_{\mathrm{i}}/\mathrm{2}\mathit{\pi }\sim \mathrm{0.8}$ kHz plasma frequencies, ions and electrons couple mainly through the condition of quasi-neutrality, i.e. via the turbulent induction–electric field which becomes²

$$\begin{array}{ll}{\displaystyle }\mathit{\delta }\mathit{E}& {\displaystyle }=-\mathit{\delta }{\mathit{V}}_{⟂}\times {\mathit{B}}_{\mathrm{0}}-({\mathit{V}}_{\mathrm{0}}+{\mathit{U}}_{\mathrm{0}})\times \mathit{\delta }\mathit{B}-\\ {\displaystyle }& {\displaystyle }-{\displaystyle \frac{\mathrm{1}}{e{N}_{\mathrm{0}}}}{\mathit{B}}_{\mathrm{0}}\times \mathit{\delta }\mathit{J}+\\ \text{(2)}& {\displaystyle }& {\displaystyle }+\langle \mathit{\delta }\mathit{V}\times \mathit{\delta }\mathit{B}+{\displaystyle \frac{\mathrm{1}}{e{N}_{\mathrm{0}}}}\mathit{\delta }\mathit{J}\times ({\displaystyle \frac{\mathit{\delta }N}{N_{\mathrm{0}}}}{\mathit{B}}_{\mathrm{0}}-\mathit{\delta }\mathit{B})\rangle .\end{array}$$

For later use, we split the main velocity field $\langle \mathit{V}\rangle ={\mathit{V}}_{\mathrm{0}}+{\mathit{U}}_{\mathrm{0}}$ into the bulk flow (convection) V₀ and an advection velocity U₀. The latter is the mean velocity of a small number of large eddies which carry the main energy of the turbulence. Even for stationary turbulence, they advect the bulk of small-scale eddies around at speed U₀ (Tennekes, 1975; Fung et al., 1992).

The last three averaged nonlinear terms within the angular brackets 〈…〉 on the right are the nonlinear contributions of the fluctuations to the mean fields yielding an electromotive force which contributes to mean-field processes like convection, dynamo action, and turbulent diffusion. They vary only on the large mean-field scale. On the fluctuation scale they are constant and can be dropped, unless the turbulence is bounded, in which case boundary effects must be taken into account at the large scales of the system. Generally, in the solar wind this is not the case. The remaining three linear terms distinguish between directions parallel and perpendicular to the main magnetic field B₀. The third linear term is the genuine perpendicular Hall contribution. From Ampere's law for the current fluctuation ${\mathit{\mu }}_{\mathrm{0}}\mathit{\delta }\mathit{J}=\mathrm{\nabla }\times \mathit{\delta }\mathit{B}$ we have the following for the perpendicular and parallel components of the turbulent electric field:

$$\begin{array}{ll}{\displaystyle }\mathit{\delta }{\mathit{E}}_{⟂}& {\displaystyle }={\mathit{B}}_{\mathrm{0}}\times [\mathit{\delta }{\mathit{V}}_{⟂}-{\displaystyle \frac{U_{\mathrm{0}\Vert }}{B_{\mathrm{0}}}}\mathit{\delta }{\mathit{B}}_{⟂}-\\ {\displaystyle }& {\displaystyle }-{\displaystyle \frac{\mathrm{1}}{e{\mathit{\mu }}_{\mathrm{0}}{N}_{\mathrm{0}}}}(\mathrm{\nabla }\times \mathit{\delta }\mathit{B}{)}_{⟂}]-{\mathit{U}}_{\mathrm{0}⟂}\times \mathit{\delta }{\mathit{B}}_{\Vert }\\ \text{(3)}& {\displaystyle }\mathit{\delta }{\mathit{E}}_{\Vert }& {\displaystyle }=-{\mathit{U}}_{\mathrm{0}⟂}\times \mathit{\delta }{\mathit{B}}_{⟂}==⟹\mathrm{0}.\end{array}$$

The second of these equations is of no interest, because the low-frequency parallel electric field its right-hand side produces is readily compensated by electron displacements along B₀.

This leaves us with the fluctuating perpendicular induction field in the first Eq. (2). Here, any parallel advection U_0‖ attributes to the perpendicular velocity fluctuations from perpendicular magnetic fluctuations δB_⟂. On the other hand, any present parallel compressive magnetic fluctuations $\mathit{\delta }{\mathit{B}}_{\Vert }={\mathit{B}}_{\mathrm{0}}(\mathit{\delta }{B}_{\Vert }/B_{\mathrm{0}})$ contribute through perpendicular advection U_0⟂. In their absence, when the magnetic field is non-compressive, the last term disappears.

The complete Hall contribution to the electric field, viz. the last term in the brackets in Eq. (2), can be written as

$$\begin{array}{}\text{(4)}& \mathit{\delta }{\mathit{E}}_{⟂}^{\mathrm{H}}=-{\displaystyle \frac{B_{\mathrm{0}}}{e{\mathit{\mu }}_{\mathrm{0}}{N}_{\mathrm{0}}}}({\mathbf{\nabla }}_{⟂}\mathit{\delta }{B}_{\Vert }-{\mathrm{\nabla }}_{\Vert }\mathit{\delta }{\mathit{B}}_{⟂}).\end{array}$$

Even for $U_{\mathrm{0}\Vert }=\mathrm{0}$, it contributes through the turbulent fluctuations in the magnetic field. As both these contributions depend only on δB, we can isolate them for separate consideration. One observes that, in the absence of any compressive magnetic components δB_‖ and homogeneity along the mean-field ${\mathrm{\nabla }}_{\Vert }=\mathrm{0}$, there is no contribution of the turbulent Hall term to the electric induction field. In that case only velocity turbulence contributes. Below we consider this important case.

2.2 Relation to density fluctuations: Poisson's equation

Let us assume that advection by large-scale energy-carrying eddies is perpendicular ${\mathit{U}}_{\mathrm{0}}={\mathit{U}}_{\mathrm{0}⟂}$, and there are no compressive magnetic fluctuations $\mathit{\delta }{\mathit{B}}_{\Vert }=\mathrm{0}$. In Eq. (2) this reduces to considering only the first term containing the velocity fluctuations. We ask for its effect on the density fluctuations in the ion-inertial domain on scales where the ions demagnetise.

On scales in the ion-inertial range shorter than either the ion thermal gyroradius ${\mathit{\rho }}_{\mathrm{i}}=v_{\mathrm{i}}/{\mathit{\omega }}_{\mathrm{ci}}$ or – depending on the direction to the mean magnetic field B₀ and the value of plasma beta $\mathit{\beta }=\mathrm{2}{\mathit{\mu }}_{\mathrm{0}}{N}_{\mathrm{0}}{T}_{\mathrm{0}}/B_{\mathrm{0}}^{\mathrm{2}}$, with ${\mathit{\omega }}_{\mathrm{ci}}=e{B}_{\mathrm{0}}/m_{\mathrm{i}}$ ion-cyclotron and ${\mathit{\omega }}_{\mathrm{i}}=e\sqrt{N_{\mathrm{0}}/{\mathit{ϵ}}_{\mathrm{0}}{m}_{\mathrm{i}}}$ ion plasma frequency, respectively – inertial length ${\mathit{\lambda }}_{\mathrm{i}}=c/{\mathit{\omega }}_{\mathrm{i}}$, the ions demagnetise. Being non-magnetic, they do not distinguish between potential and induction–electric fields. They experience the induction field caused by the spectrum of velocity fluctuations as an external electric field which, in an electron-proton plasma, causes a charge density fluctuation eδN_i=eδN_e and thus a density fluctuation δN. Poisson's equation implies that

$$\begin{array}{}\text{(5)}& \mathrm{\nabla }\cdot \mathit{\delta }\mathit{E}={\displaystyle \frac{e}{{\mathit{ϵ}}_{\mathrm{0}}}}\mathit{\delta }N==⟹i\mathit{k}\cdot \mathit{\delta }{\mathit{E}}_k={\displaystyle \frac{e}{{\mathit{ϵ}}_{\mathrm{0}}}}\mathit{\delta }{N}_k.\end{array}$$

The right expression is its Fourier transform. For completeness we note that the Hall contribution to the Poisson equation in Fourier space reads

$$\begin{array}{}\text{(6)}& i{\mathit{k}}_{⟂}\cdot \mathit{\delta }{\mathit{E}}_{⟂k}^{\mathrm{H}}={\displaystyle \frac{B_{\mathrm{0}}}{e{\mathit{\mu }}_{\mathrm{0}}{N}_{\mathrm{0}}}}(k_{⟂}^{\mathrm{2}}\mathit{\delta }{B}_{\Vert k}-k_{\Vert }{\mathit{k}}_{⟂}\cdot \mathit{\delta }{\mathit{B}}_{⟂k})={\displaystyle \frac{e}{{\mathit{ϵ}}_{\mathrm{0}}}}\mathit{\delta }{N}_k^{\mathrm{H}}.\end{array}$$

Again it becomes obvious that absence of parallel (compressive) magnetic turbulence eliminates the first term in this expression, while purely perpendicular propagation eliminates the second term. Alfvénic turbulence, for instance, with $\mathit{\delta }{B}_{\Vert }=\mathrm{0}$ and $k_{⟂}=\mathrm{0}$, has no Hall effect on the modulation of the density spectrum, a fact which is well known. On the other hand, for perpendicular wave numbers $k=k_{⟂}$ only compressive Hall-magnetic fluctuations $\mathit{\delta }{B}_{\Vert k_{⟂}}$ contribute to the Hall fluctuations in the density $\mathit{\delta }{N}_{k_{⟂}}^{\mathrm{H}}$.

2.3 Relation between density and velocity power spectra

We are interested in the power spectrum of the turbulent density fluctuations in the proper frame of the turbulence.

Multiplication of the only remaining first term in the electric induction field Eq. (2) with wave number k selects wave numbers k_⟂ perpendicular to B₀. The combination of Eq. (2) and the Poisson equation then yields an expression for the power spectrum of the turbulent density fluctuations³ in wave-number space

$$\begin{array}{}\text{(7)}& \langle |\mathit{\delta }N{|}^{\mathrm{2}}{\rangle }_{k_{⟂}}=({\displaystyle \frac{{\mathit{ϵ}}_{\mathrm{0}}{B}_{\mathrm{0}}}{e}}{)}^{\mathrm{2}}{k}_{⟂}^{\mathrm{2}}\langle |\mathit{\delta }\mathit{V}{|}^{\mathrm{2}}{\rangle }_{k_{⟂}},\end{array}$$

where we from now on drop the index ⟂ on the velocity δV_⟂. Angular brackets again symbolise spatial averaging over the fluctuation scale. The functional dependence on the wave number is indicated by the index k_⟂. It is obvious that the power spectrum of density fluctuations in the ion-inertial Hall-MHD domain is completely determined by the power spectrum of the turbulent velocity⁴. This can be written as

$$\begin{array}{ll}{\displaystyle \frac{\langle |\mathit{\delta }N{|}^{\mathrm{2}}{\rangle }_{k_{⟂}}}{N_{\mathrm{0}}^{\mathrm{2}}}}& {\displaystyle }=\left({\displaystyle \frac{V_{\mathrm{A}}}{c}}{)}^{\mathrm{2}}\right({\displaystyle \frac{k_{⟂}}{{\mathit{\omega }}_{\mathrm{i}}}}{)}^{\mathrm{2}}\langle |\mathit{\delta }\mathit{V}{|}^{\mathrm{2}}{\rangle }_{k_{⟂}}\\ \text{(8)}& {\displaystyle }& {\displaystyle }={\displaystyle \frac{\langle |\mathit{\delta }\mathit{V}{|}^{\mathrm{2}}{\rangle }_{k_{⟂}}}{c^{\mathrm{2}}}}\left({\displaystyle \frac{V_{\mathrm{A}}}{c}}{)}^{\mathrm{2}}\right(k_{⟂}{\mathit{\lambda }}_{\mathrm{i}}{)}^{\mathrm{2}},\end{array}$$

where $V_{\mathrm{A}}^{\mathrm{2}}=B_{\mathrm{0}}^{\mathrm{2}}/{\mathit{\mu }}_{\mathrm{0}}{m}_{\mathrm{i}}{N}_{\mathrm{0}}$ is the squared Alfvén speed, and ${\mathit{\omega }}_{\mathrm{i}}^{\mathrm{2}}=e^{\mathrm{2}}{N}_{\mathrm{0}}/{\mathit{ϵ}}_{\mathrm{0}}{m}_{\mathrm{i}}$ is the squared proton plasma frequency. As expected, in order to contribute to density fluctuations, perpendicular scales ${\mathit{\lambda }}_{⟂}<{\mathit{\lambda }}_{\mathrm{i}}$ smaller than the ion-inertial length ${\mathit{\lambda }}_{\mathrm{i}}=c/{\mathit{\omega }}_{\mathrm{i}}$ are required, while in the long-wavelength range $k_{⟂}{\mathit{\lambda }}_{\mathrm{i}}<\mathrm{1}$, there is no effect on the spectrum. This is in agreement with the assumption that any spectral modification is expected only in the ion-inertial range.

The last equation is the main formal result. It is the wanted relation between the power spectra of density and velocity fluctuations. It contains the response of the unmagnetised ions to the mechanical turbulence.

2.4 Affected scale range

The density response demands that the ions are unmagnetised. This implies that $k_{⟂}{\mathit{\rho }}_{\mathrm{i}}<\mathrm{1}$, where ${\mathit{\rho }}_{\mathrm{i}}=v_{\mathrm{i}}/{\mathit{\omega }}_{\mathrm{ci}}={\mathit{\lambda }}_{\mathrm{i}}{v}_{\mathrm{i}}/V_{\mathrm{A}}$ is the ion gyroradius, with v_i as the thermal speed. Thus we have two conditions which must simultaneously be satisfied:

$$\begin{array}{}\text{(9)}& k_{⟂}{\mathit{\lambda }}_{\mathrm{i}}>\mathrm{1}\mathrm{and}{k}_{⟂}{\mathit{\lambda }}_{\mathrm{i}}>{\displaystyle \frac{V_{\mathrm{A}}}{v_{\mathrm{i}}}}\equiv {\mathit{\beta }}_{\mathrm{i}}^{-\frac{\mathrm{1}}{\mathrm{2}}}.\end{array}$$

For V_A<v_i the second condition is trivial. This is, however, a rare case, so the more realistic restriction is the opposite small ion-beta case when V_A>v_i and hence β_i<1. It must, however, be combined with another condition which requires that the wave numbers be smaller than the inverse electron gyroradius ${\mathit{\rho }}_{\mathrm{e}}=v_{\mathrm{e}}/{\mathit{\omega }}_{\mathrm{ce}}$. The relation between ρ_e and ρ_i is ${\mathit{\rho }}_{\mathrm{e}}^{\mathrm{2}}/{\mathit{\rho }}_{\mathrm{i}}^{\mathrm{2}}=m_{\mathrm{e}}{T}_{\mathrm{e}}/m_{\mathrm{i}}{T}_{\mathrm{i}}$. Moreover we have ${\mathit{\rho }}_{\mathrm{i}}/{\mathit{\lambda }}_{\mathrm{i}}=v_{\mathrm{i}}/V_{\mathrm{A}}$, and in addition, ${\mathit{\beta }}_{\mathrm{i}}=v_{\mathrm{i}}^{\mathrm{2}}/V_{\mathrm{A}}^{\mathrm{2}}=(T_{\mathrm{i}}/T_{\mathrm{e}}){\mathit{\beta }}_{\mathrm{e}}$. Using all these relations, we obtain finally that

$$\begin{array}{}\text{(10)}& \mathrm{1}<k_{⟂}^{\mathrm{2}}{\mathit{\lambda }}_{\mathrm{i}}^{\mathrm{2}}{\mathit{\beta }}_{\mathrm{i}}<{\displaystyle \frac{m_{\mathrm{i}}}{m_{\mathrm{e}}}}{\displaystyle \frac{T_{\mathrm{i}}}{T_{\mathrm{e}}}}\mathrm{for}{\mathit{\beta }}_{\mathrm{i}}<\mathrm{1}.\end{array}$$

This expression defines the marginal condition for the existence of a range in wave numbers where the ions respond to the spectrum of the turbulent electric field δE:

$$\begin{array}{}\text{(11)}& {\displaystyle \frac{T_{\mathrm{i}}}{T_{\mathrm{e}}}}\mathit{\gtrsim }{\displaystyle \frac{m_{\mathrm{e}}}{m_{\mathrm{i}}}}\sim \mathrm{0.001}.\end{array}$$

Because of the smallness of the right-hand side, this is a weak restriction. As expected, any effect on the density-power spectrum will disappear at wave numbers k_⟂ρ_e where the electrons demagnetise. On the other hand, the lower wave-number limit is a sensitive function of the external conditions. This becomes clear when writing it in the form

$$\begin{array}{}\text{(12)}& T_{\mathrm{e}}/T_{\mathrm{i}}{\mathit{\beta }}_{\mathrm{e}}<k_{⟂}^{\mathrm{2}}{\mathit{\lambda }}_{\mathrm{i}}^{\mathrm{2}}.\end{array}$$

The electron plasma beta in the solar wind is of the order of β_e≳O(1). However, the temperature ratio T_e∕T_i is variable and usually large, varying between a few and a few tens. Thus usually β_i<1. Figure 2 shows a graph of this dependence.

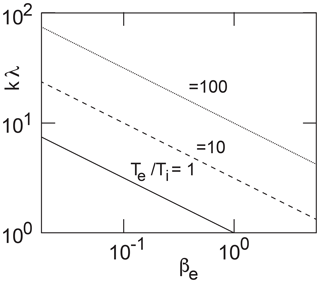
Figure 2 The range of permitted values of k_⟂λ_i as function of β_e for different ratios T_e∕T_i. Only the range above the lines is relevant. In the solar wind, usually T_e>T_i, implying that β_e>β_i (Newbury et al., 1998; Wilson III et al., 2018) unless the electrons become cooled by some process like emitting radiation, electron hole formation, or charge exchange.

2.5 Application to K and IK inertial-range models of turbulence

The power spectrum of the Poisson-modified ion-inertial-range density turbulence can be inferred once the power spectral density of the velocity is given. This spectrum must either be known a priori or requires reference to some model of turbulence.

We do not develop any model of turbulence here. In application to the solar wind we just make us, in the following, of the Kolmogorov (K) spectrum (or its anisotropic extension by Goldreich and Sridhar, 1995, abbreviated KGS) but will also refer to the IK spectrum, which both have previously been found to be of relevance in solar wind turbulence.

We shall make use of those spectra in two forms: the original ones which just assume stationarity and absence of any bulk flows and their modified advected extensions. The latter account for a distinction between a small number of large energy-carrying eddies with mean eddy vortex speed U₀ and bulk turbulence consisting of large numbers of small energy-poor eddies which are frozen to the large eddies. The large eddies stir the small-scale turbulence, forcing it into advective motion (Tennekes, 1975). This causes a Doppler broadening of the wave-number spectrum at fixed k and has been confirmed by numerical simulations (Fung et al., 1992; Kaneda, 1993). Below, it will be found that this advection cannot be resolved in bulk convective flow which buries the subtle effect of Doppler broadening. A probable counterexample is shown in Fig. 5.

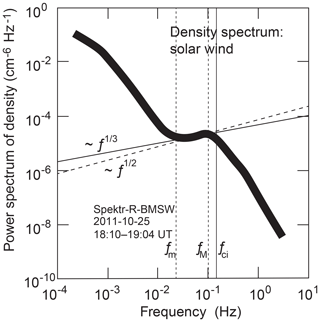
Figure 3 Solar wind power spectra of turbulent density fluctuations (based on BMSW data from Šafránková et al., 2013, obtained on 25 October 2011). Single point measurements were obtained with six Faraday cups with time resolution of 31 ms (∼30 Hz) under the following solar wind conditions: density $N\sim \mathrm{3}\times {\mathrm{10}}^{\mathrm{6}}$ m⁻³, mean magnetic field B₀∼8 nT, bulk speed V₀∼540 km s⁻¹, ion temperature T_i∼10 nT, Alfvén Mach number M_A∼6, and total β∼0.3, implying dilute low β (high M_A) and moderately fast flow conditions. The local thermal ion gyroradius is ${\mathit{\rho }}_{\mathrm{i}}\sim \mathrm{2.2}\times {\mathrm{10}}^{\mathrm{4}}$ m. The vertical line indicates the local ion-cyclotron frequency $f_{\mathrm{ci}}={\mathit{\omega }}_{\mathrm{ci}}/\mathrm{2}\mathit{\pi }\approx \mathrm{0.15}$ Hz. Plasma frequency is $f_{\mathrm{i}}={\mathit{\omega }}_{\mathrm{i}}/\mathrm{2}\mathit{\pi }\approx \mathrm{400}$ Hz. f_m and f_M are the approximate minimum and maximum frequencies of the bumpy range, respectively. The data were averaged over ∼1200 s measuring time and subsequently filtered (cf. Šafránková et al., 2016, for the description of the data reduction). The spectrum shown is the average spectrum with line width roughly corresponding to the largest spread of the filtered data in the logarithmic ordinate direction and applied to the whole spectrum. The power spectrum exhibits a (so-called) bump at intermediate frequencies of positive slopes ∼ω^⅓ or ∼ω^½. This is in agreement with it being caused by the response of the non-magnetic ions to the electric induction field of the turbulent mechanical fluctuations in the solar wind velocity in Kolmogorov (K; solid line) or Iroshnikov–Kraichnan (IK; dashed line) inertial-range turbulence. The large scatter in the data (weight of line) inhibits distinguishing between K and IK inertial-range velocity turbulence.

The stationary velocity spectrum of turbulent eddies at energy injection rate ϵ exhibits a broad inertial power law range in k (Kolmogorov, 1941a, b, 1962; Obukhov, 1941) which, between injection k_in and dissipation at k_d wave numbers, obeys the famous isotropic Kolmogorov power spectral density law in wave-number space:

$$\begin{array}{}\text{(13)}& \langle |\mathit{\delta }\mathit{V}{|}^{\mathrm{2}}{\rangle }_k\equiv {\mathcal{E}}_{\mathrm{K}}(k)=C_{\mathrm{K}}{\mathit{ϵ}}^{\frac{\mathrm{2}}{\mathrm{3}}}{k}^{-\frac{\mathrm{5}}{\mathrm{3}}}\mathrm{for}{k}_{\mathrm{in}}<k<k_{\mathrm{d}},\end{array}$$

with C_K≈1.65 as Kolmogorov's constant of proportionality (as determined by Gotoh and Fukayama, 2001, using numerical simulations). Clearly, in a fast-streaming solar wind, when straightforwardly mapping this K spectrum by the Taylor hypothesis (Taylor, 1938) into the stationary spacecraft frame, the spectral index is unchanged, and one trivially recovers the ${\mathit{\omega }}_{\mathrm{s}}^{-\frac{\mathrm{5}}{\mathrm{3}}}$ Kolmogorov slope in frequency space.

This changes drastically when referring to an advected K spectrum of velocity turbulence (Fung et al., 1992; Kaneda, 1993) which yields the above-mentioned spectral Doppler broadening at fixed k,

$$\begin{array}{ll}{\displaystyle }{\mathcal{E}}_{k{\mathit{\omega }}_k}^{\mathrm{ad}}& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{{\mathcal{E}}_{\mathrm{K}}\left(k\right)}{\sqrt{\mathrm{2}\mathit{\pi }}k{U}_{\mathrm{0}}}}\sum _{\pm }\exp [-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{{\mathit{\omega }}_{\pm }^{\mathrm{2}}}{(k{U}_{\mathrm{0}}{)}^{\mathrm{2}}}}],\\ \text{(14)}& {\displaystyle }{\mathit{\omega }}_{\pm }& {\displaystyle }={\mathit{\omega }}_k\pm {\mathrm{\ell }}_{\mathrm{K}}{k}^{\frac{\mathrm{2}}{\mathrm{3}}},\end{array}$$

which is due to decorrelation of the small eddies in advective transport, with ℓ_K∼O(1) being some constant. The k^⅔ dependence in the argument of the exponential results from advection k⋅δV of neighbouring eddies at velocity of $\mathit{\delta }V\propto k^{-\frac{\mathrm{1}}{\mathrm{3}}}$ (Tennekes, 1975; Fung et al., 1992). The frequency ω_k stands for the internal dependence of the turbulent frequency on the turbulent wave number k. It can be understood as an internal “turbulent dispersion relation”, which is neglected in turbulence theory.⁵ Then the advected power spectrum at large k is power law

$$\begin{array}{}\text{(15)}& {\displaystyle }{\mathcal{E}}_{k{\mathit{\omega }}_k}^{\mathrm{ad}}& {\displaystyle }\propto {\displaystyle \frac{{\mathcal{E}}_{\mathrm{K}}\left(k\right)}{k}}\exp (-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\cos }^{\mathrm{2}}{\mathit{\gamma }}_k)\sim k^{-\frac{\mathrm{8}}{\mathrm{3}}},\text{(16)}& {\displaystyle }{\mathit{\omega }}_{\pm }& {\displaystyle }\approx \mathit{k}\cdot {\mathit{U}}_{\mathrm{0}}=k{U}_{\mathrm{0}}\cos {\mathit{\gamma }}_k.\end{array}$$

In the stationary turbulence frame the power spectrum of turbulence in the velocity decays to $\propto k^{-\frac{\mathrm{8}}{\mathrm{3}}}$ with non-Kolmogorov spectral index $\mathrm{8}/\mathrm{3}\approx \mathrm{2.7}$.

It is of particular interest to note that solar wind turbulent power spectra at high frequency repeatedly obey spectral indices very close to this number. Boldly referring to Taylor's hypothesis where ω_s∝k, one might conclude then that a convective flow maps this spectral range of the advected turbulent K spectrum into the spacecraft frame where it appears as an ${\mathit{\omega }}_{\mathrm{s}}^{-\frac{\mathrm{8}}{\mathrm{3}}}$ spectrum.

If this is true, then the corresponding observed spectral transition (or break point) from the spectral K index $\sim \mathrm{5}/\mathrm{3}$ to the steeper index $\sim \mathrm{8}/\mathrm{3}$ observed in the large-wave-number power spectra indicates the division between large-scale energy-carrying, energy-rich turbulent eddies and the bulk of energy-poor small-scale eddies in the mechanical turbulence. It thus provides a simple explanation of the change in spectral index from $\sim \mathrm{5}/\mathrm{3}$ (K spectrum) to ≲3 (advected K turbulence spectrum) without invoking any sophisticated turbulence theory as well as having no effects of dissipation.

Inspecting the behaviour in the long-wavelength range, one finds that the exponential dependence $\exp (-{\mathrm{\ell }}_{\mathrm{K}}^{\mathrm{2}}/U_{\mathrm{0}}^{\mathrm{2}}{k}^{\frac{\mathrm{2}}{\mathrm{3}}})$ suppresses the spectrum here. This flattens the inertial-range spectrum towards small wave numbers k_in into the large-eddy range where it causes bending of the spectrum. The wave number at spectral maximum is

$$\begin{array}{}\text{(17)}& k_{\min }\mathit{\lesssim }{\mathrm{\ell }}_{\mathrm{K}}^{\mathrm{3}}/\mathrm{16}{U}_{\mathrm{0}}^{\mathrm{3}}\sqrt{\mathrm{2}}.\end{array}$$

Approaching from the Kolmogorov inertial range towards a smaller k, one observes flattening until k_min<k_in. In most cases this point will lie outside the observation range.

In the stationary turbulence frame the frequency spectrum is obtained when integrated with respect to k (Biskamp, 2003). It then maps the Doppler broadened advected velocity power spectrum (Fung et al., 1992; Kaneda, 1993) to the Kolmogorov law in the source-region frequency space:

$$\begin{array}{}\text{(18)}& \underset{k_{\mathrm{in}}}{\overset{k_{\mathrm{d}}}{\int }}\mathrm{d}k{\mathcal{E}}_{k{\mathit{\omega }}_k}^{\mathrm{ad}}\sim {\mathcal{E}}_{\mathrm{K}}^{\mathrm{ad}}\left(\mathit{\omega }\right)\propto {\mathit{\omega }}^{-\frac{\mathrm{5}}{\mathrm{3}}}.\end{array}$$

This mapping is independent of Taylor's hypothesis. It strictly applies only to the turbulent reference frame. When attempting to map it into the spacecraft frame via Taylor's Galilei transformation, referring to solar wind flow at finite V₀≠0, one must return to its wave-number representation in Eq. (11). This transformation, though straightforward, is obscured by the appearance of k in the exponential through ω_±. According to Taylor the turbulence frame frequency transforms as

$$\begin{array}{}\text{(19)}& {\mathit{\omega }}_k={\mathit{\omega }}_{\mathrm{s}}-k{V}_{\mathrm{0}}\cos \mathit{\alpha }.\mathit{\alpha }=\mathrm{\angle }(\mathit{k}\mathbf{,}{\mathit{V}}_{\mathrm{0}}).\end{array}$$

This is Taylor's Galilei transformation. Neglecting ω_k implies that ω_s=kV₀cos  α. The exponential reduces to

$$\begin{array}{}\text{(20)}& {\displaystyle }& {\displaystyle }\exp [-{\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}({\displaystyle \frac{{\mathit{\omega }}_k+k{V}_{\mathrm{0}}\cos \mathit{\alpha }\pm {\mathrm{\ell }}_{\mathrm{K}}{k}^{\frac{\mathrm{2}}{\mathrm{3}}}}{k{U}_{\mathrm{0}}}}{)}^{\mathrm{2}}]=\text{(21)}& {\displaystyle }& {\displaystyle }=\exp [-{\displaystyle \frac{\mathrm{1}}{\mathrm{4}(k{\mathit{\lambda }}_{\mathrm{i}}{)}^{\frac{\mathrm{2}}{\mathrm{3}}}}}({\displaystyle \frac{{\mathit{\lambda }}_{\mathrm{i}}^{\frac{\mathrm{1}}{\mathrm{3}}}{\mathrm{\ell }}_{\mathrm{K}}}{U_{\mathrm{0}}}}{)}^{\mathrm{2}}]\text{(22)}& {\displaystyle }& {\displaystyle }⟶\mathrm{1}-{\displaystyle \frac{\mathrm{1}}{\mathrm{4}(k{\mathit{\lambda }}_{\mathrm{i}}{)}^{\frac{\mathrm{2}}{\mathrm{3}}}}}({\displaystyle \frac{{\mathit{\lambda }}_{\mathrm{i}}^{\frac{\mathrm{1}}{\mathrm{3}}}{\mathrm{\ell }}_{\mathrm{K}}}{U_{\mathrm{0}}}}{)}^{\mathrm{2}},\end{array}$$

with ${\mathit{\lambda }}_{\mathrm{i}}^{\frac{\mathrm{1}}{\mathrm{3}}}\mathrm{\ell }/U_{\mathrm{0}}\equiv U_{\mathrm{\ell }}^{\mathrm{K}}/U_{\mathrm{0}}$ being a velocity ratio. The arrow holds for the ion-inertial range kλ_i>1 and $U_{\mathrm{\ell }}^{\mathrm{K}}/U_{\mathrm{0}}<\mathrm{1}$. The exponential expression leads to an advected K spectrum as observed by the spacecraft in frequency space:

$$\begin{array}{}\text{(23)}& {\mathcal{E}}_{{\mathit{\omega }}_{\mathrm{s}}}^{\mathrm{ad}}\propto {\mathit{\omega }}_{\mathrm{s}}^{-\frac{\mathrm{8}}{\mathrm{3}}}\exp [-{\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}({\displaystyle \frac{V_{\mathrm{0}}\cos \mathit{\alpha }}{{\mathit{\omega }}_{\mathrm{s}}{\mathit{\lambda }}_{\mathrm{i}}}}{)}^{\frac{\mathrm{2}}{\mathrm{3}}}\left({\displaystyle \frac{U_{\mathrm{\ell }}^{\mathrm{K}}}{U_{\mathrm{0}}}}{)}^{\mathrm{2}}\right],\end{array}$$

which, as before for large ω_s, is of the spectral index 8∕3. With decreasing spacecraft frequency ω_s, the exponential correction factor acts to suppress the spectrum. This corresponds to a spectral flattening towards smaller ω_s. It might even cause a spectral dip, depending on the parameters and velocities involved. The effect is strongest for aligned streaming and the eddy wave number. For α∼90^∘ one recovers the index 8∕3.

It is most interesting that spectral broadening, when transformed into the spacecraft frame in streaming turbulence, causes that strong of a difference between the original Kolmogorov and the advected Kolmogorov spectrum. This spectral behaviour is still independent of the Poisson modification, which we are going to investigate in the next section.

3 Ion-inertial-range density-power spectrum

Here we apply the Poisson-modified expressions to the theoretical inertial-range K and IK turbulence models. We concentrate on the inertial-range K spectrum and rewrite the result subsequently to the IK spectrum.

3.1 Inertial-range K and IK density-power spectrum

For the simple inertial-range K spectrum, we know from Eqs. (5) and (10) that

$$\begin{array}{}\text{(24)}& \langle |\mathit{\delta }N{|}^{\mathrm{2}}{\rangle }_{k_{⟂}}=C_{\mathrm{K}}({\displaystyle \frac{{\mathit{ϵ}}_{\mathrm{0}}{B}_{\mathrm{0}}}{e}}{)}^{\mathrm{2}}{\mathit{ϵ}}^{\frac{\mathrm{2}}{\mathrm{3}}}{k}_{⟂}^{\frac{\mathrm{1}}{\mathrm{3}}}\mathrm{for}{k}_{⟂\mathrm{in}}<k_{⟂}<k_{⟂\mathrm{d}}.\end{array}$$

This is a very simple wave-number dependence of the power spectrum of density turbulence, permitting (Treumann et al., 2019) Taylor's Galilei transformation into the spacecraft frame. Setting $k_{⟂}={\mathit{\omega }}_{\mathrm{s}}/V_{\mathrm{0}}\cos \mathit{\alpha }$ we immediately obtain

$$\begin{array}{}\text{(25)}& \langle |\mathit{\delta }N{|}^{\mathrm{2}}{\rangle }_{k_{⟂}}\propto {\mathit{\omega }}_{\mathrm{s}}^{\frac{\mathrm{1}}{\mathrm{3}}},\end{array}$$

with factor of proportionality $C_{\mathrm{K}}({\mathit{ϵ}}_{\mathrm{0}}{B}_{\mathrm{0}}/e{)}^{\mathrm{2}}({\mathit{ϵ}}^{\mathrm{2}}/V_{\mathrm{0}}\cos \mathit{\alpha }{)}^{\frac{\mathrm{1}}{\mathrm{3}}}$.

Following exactly the same reasoning when dealing with the IK spectrum, which has power index 3∕2, we obtain

$$\begin{array}{}\text{(26)}& \langle |\mathit{\delta }N{|}^{\mathrm{2}}{\rangle }_{k_{⟂}}\propto {\mathit{\omega }}_{\mathrm{s}}^{\frac{\mathrm{1}}{\mathrm{2}}}.\end{array}$$

Hence, the effect of the Poisson response of the plasma to the inertial-range power spectra of K and IK turbulence in the velocity is to generate a positive slope in the density-power spectrum when transformed by Taylor's Galilei transformation into the spacecraft frame.

We now proceed to the investigation of the effect of advection.

3.2 Advected Poisson-modified spectrum at V₀=0

Use of the advected power spectral density Eq. (11) of the velocity field for V₀=0 in the transformed Poisson equation, with $k\to k_{⟂}$ being perpendicular to the mean magnetic field B₀, yields the following for the non-convected advected turbulent ion-inertial-range Poisson-modified density-power spectrum in the stationary large-eddy turbulence frame:

$$\begin{array}{ll}{\displaystyle }\langle |\mathit{\delta }N{|}^{\mathrm{2}}{\rangle }_{{\mathit{\omega }}_k{k}_{⟂}}^{\mathrm{ad}}& {\displaystyle }={\displaystyle \frac{{\mathit{ϵ}}_{\mathrm{0}}^{\mathrm{2}}{B}_{\mathrm{0}}^{\mathrm{2}}}{e^{\mathrm{2}}}}{k}_{⟂}^{\mathrm{2}}\langle |\mathit{\delta }\mathit{V}{|}^{\mathrm{2}}{\rangle }_{{\mathit{\omega }}_k{k}_{⟂}}\\ {\displaystyle }& {\displaystyle }={\displaystyle \frac{{\mathit{ϵ}}_{\mathrm{0}}^{\mathrm{2}}{B}_{\mathrm{0}}^{\mathrm{2}}}{e^{\mathrm{2}}}}{k}_{⟂}^{\mathrm{2}}{\mathcal{E}}_{k_{⟂}{\mathit{\omega }}_k}^{\mathrm{ad}}\\ \text{(27)}& {\displaystyle }& {\displaystyle }\propto k_{⟂}^{-\frac{\mathrm{2}}{\mathrm{3}}}\sum _{\pm }\exp [-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{{\mathit{\omega }}_{\pm }^{\mathrm{2}}}{(k{U}_{\mathrm{0}}{)}^{\mathrm{2}}}}].\end{array}$$

Integration with respect to k_⟂ under the above assumption on ${\mathit{\omega }}_{\pm }\approx k_{⟂}{U}_{\mathrm{0}}$ yields the following for the Eulerian (Fung et al., 1992) density-power spectrum in frequency space ${\mathit{\omega }}_{\mathrm{\ell }}<\mathit{\omega }<{\mathit{\omega }}_u$ in the ion-inertial domain of the turbulent inertial range:

$$\begin{array}{}\text{(28)}& \langle |\mathit{\delta }N{|}^{\mathrm{2}}{\rangle }_{\mathit{\omega }}^{\mathrm{ad}}\sim {\mathit{\omega }}^{\frac{\mathrm{1}}{\mathrm{3}}},k_{\mathrm{ir}}^{\frac{\mathrm{2}}{\mathrm{3}}}{\mathit{ϵ}}^{\frac{\mathrm{1}}{\mathrm{3}}}={\mathit{\omega }}_{\mathrm{\ell }}<\mathit{\omega }<{\mathit{\omega }}_u.\end{array}$$

This is the proper frequency dependence of the advected turbulent density spectrum in the turbulence frame. Here $k_{\mathrm{ir}}\approx \mathrm{2}\mathit{\pi }{\mathit{\omega }}_{\mathrm{i}}/c$ (or 2πv_i∕ω_ci) is the wave number presumably corresponding to the lower end of the ion-inertial range. The upper bound on the frequency ω_u remains undetermined. One assumption would be that ω_u is the lower-hybrid frequency which is intermediate to the ion and electron cyclotron frequencies. At this frequency electrons become capable of discharging the electric induction field, thus breaking the spectrum to return to its Kolmogorov slope at increasing frequency.

In contrast to the Kolmogorov law, the Poisson-mediated proper advected density-power spectrum Eq. (18) increases with frequency in the proper stationary frame of the turbulence. This increase is restricted to that part of the inertial K range which corresponds to the ion-inertial scale and frequency range.

The case of an IK spectrum leads to an advected velocity spectrum

$$\begin{array}{}\text{(29)}& \langle |\mathit{\delta }\mathit{V}{|}^{\mathrm{2}}{\rangle }_{{\mathit{\omega }}_k{k}_{⟂}}\propto k_{⟂}^{-\frac{\mathrm{3}}{\mathrm{2}}},\end{array}$$

which yields

$$\begin{array}{ll}{\displaystyle }\langle |\mathit{\delta }N{|}^{\mathrm{2}}{\rangle }_{{\mathit{\omega }}_k{k}_{⟂}}^{\mathrm{ad}}& {\displaystyle }\propto k_{⟂}^{-\frac{\mathrm{1}}{\mathrm{2}}}\sum _{\pm }\exp [-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{{\mathit{\omega }}_{\pm }^{\mathrm{2}}}{(k{U}_{\mathrm{0}}{)}^{\mathrm{2}}}}],\\ \text{(30)}& {\displaystyle }{\mathit{\omega }}_{\pm }& {\displaystyle }={\mathit{\omega }}_k\pm {\mathrm{\ell }}_{\mathrm{IK}}{k}_{⟂}^{\frac{\mathrm{3}}{\mathrm{4}}}.\end{array}$$

Integration with respect to k_⟂ then gives the proper advected frequency spectrum in the stationary frame of IK turbulence:

$$\begin{array}{}\text{(31)}& \langle |\mathit{\delta }N{|}^{\mathrm{2}}{\rangle }_{\mathit{\omega }}^{\mathrm{ad}}\sim {\mathit{\omega }}^{\frac{\mathrm{1}}{\mathrm{2}}}.\end{array}$$

This proper IK density spectrum increases with frequency like the root of the proper frequency.

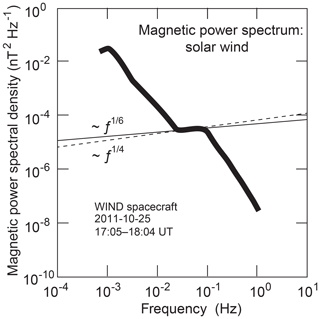
Figure 4 Solar wind power spectra of the turbulent magnetic field for the same time interval as in Fig. 3 measured by the WIND spacecraft (data from Šafránková et al., 2013), which was located at the Lagrange point L1. Line width accounts for the scatter of data. The magnetic turbulence spectrum exhibits a deformation similar to that in the density-power spectrum and the same frequency interval. The positive slope ∼ω^⅙ in the deformation confirms its origin from pressure balance. It indicates its nature being secondary to turbulence in density. The solid (dashed) line corresponds to an K (IK) velocity spectrum. The scatter of data was again substantial, thus inhibiting distinction between the two cases.

3.3 Taylor's Galilei-transformed Poisson-modified advected spectra

Turning to the fast-streaming solar wind, we find that with $k_{⟂}={\mathit{\omega }}_{\mathrm{s}}/V_{\mathrm{0}}\cos \mathit{\alpha }$ for the Poisson-modified advected and convected K density spectrum,

$$\begin{array}{}\text{(32)}& \langle |\mathit{\delta }N{|}^{\mathrm{2}}{\rangle }_{{\mathit{\omega }}_{\mathrm{s}}}^{\mathrm{K},\mathrm{ad}}\propto {\mathit{\omega }}_{\mathrm{s}}^{-\frac{\mathrm{2}}{\mathrm{3}}}\exp [-{\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}\left({\displaystyle \frac{V_{\mathrm{0}}\cos \mathit{\alpha }}{{\mathit{\omega }}_{\mathrm{s}}{\mathit{\lambda }}_{\mathrm{i}}}}{)}^{\frac{\mathrm{2}}{\mathrm{3}}}\right({\displaystyle \frac{U_{\mathrm{\ell }}^{\mathrm{K}}}{U_{\mathrm{0}}}}{)}^{\mathrm{2}}],\end{array}$$

where we again neglected the proper frequency dependence. This Taylor's Galilei-transformed density spectrum decays with increasing frequency, albeit at a weak power $\sim \mathrm{2}/\mathrm{3}$. At large frequency ω_s the exponent is 1, and the spectrum becomes $\propto {\mathit{\omega }}_{\mathrm{s}}^{-\frac{\mathrm{2}}{\mathrm{3}}}$. Towards smaller ω_s the spectrum flattens and assumes its maximum at

$$\begin{array}{}\text{(33)}& {\mathit{\omega }}_{\mathrm{sm}}^{\mathrm{K}}={\displaystyle \frac{\mathrm{3}}{\mathrm{8}}}\left({\displaystyle \frac{V_{\mathrm{0}}\cos \mathit{\alpha }}{{\mathit{\lambda }}_{\mathrm{i}}}}\right)({\displaystyle \frac{U_{\mathrm{\ell }}^{\mathrm{K}}}{U_{\mathrm{0}}}}{)}^{\mathrm{3}}.\end{array}$$

The same reasoning produces, for the Poisson-modified advected IK spectrum, the Taylor's Galilei-transformed spacecraft frequency spectrum

$$\begin{array}{}\text{(34)}& \langle |\mathit{\delta }N{|}^{\mathrm{2}}{\rangle }_{{\mathit{\omega }}_{\mathrm{s}}}^{\mathrm{IK},\mathrm{ad}}\propto {\mathit{\omega }}_{\mathrm{s}}^{-\frac{\mathrm{1}}{\mathrm{2}}}\exp [-{\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}\left({\displaystyle \frac{V_{\mathrm{0}}\cos \mathit{\alpha }}{{\mathit{\omega }}_{\mathrm{s}}{\mathit{\lambda }}_{\mathrm{i}}}}{)}^{\frac{\mathrm{3}}{\mathrm{4}}}\right({\displaystyle \frac{U_{\mathrm{\ell }}^{\mathrm{IK}}}{U_{\mathrm{0}}}}{)}^{\mathrm{2}}].\end{array}$$

Both advected K and IK spectra have negative slopes in spacecraft frequency ω_s. Like in the case of a K spectrum, this spectrum approaches its steepest slope of 1∕2 at large spacecraft frequencies ω_s, while in the direction of small frequencies, it flattens out to assume its maximum value at

$$\begin{array}{}\text{(35)}& {\mathit{\omega }}_{\mathrm{m}}^{\mathrm{IK}}=\left({\displaystyle \frac{\mathrm{7}}{\mathrm{8}}}{\displaystyle \frac{V_{\mathrm{0}}\cos \mathit{\alpha }}{{\mathit{\lambda }}_{\mathrm{i}}}}{)}^{\frac{\mathrm{3}}{\mathrm{2}}}\right({\displaystyle \frac{U_{\mathrm{\ell }}^{\mathrm{IK}}}{U_{\mathrm{0}}}}{)}^{\mathrm{3}}.\end{array}$$

In both cases of advected K and IK spectra the Taylor's Galilei transformation from the proper frame of turbulence into the spacecraft frame is permitted because it applies to the velocity and density spectra (Treumann et al., 2019). It maps the wave-number spectrum into the spacecraft frame frequency spectrum. However, in both cases we recover frequency spectra which decrease with frequency though weakly approaching the steepest slope at large frequencies. They flatten out towards low frequencies and may assume maxima only if these maxima are still in the inertial range of the advected K or IK spectrum. Only in this case does the spacecraft frequency spectrum exhibit a bump at their nominal maximum frequencies ω_sm. When the maximum frequency falls outside the ion-inertial range the bump will be absent, while the spectrum will be flatter than at large frequencies. Such flattened bumpless spectra have been observed. The next subsections provide examples of observed bumpy and bumpless spectra in the spacecraft frequency frame.

4 Application to selected observations in the solar wind

In the following two subsections we apply the above theory to real observations made in situ in the solar wind. We first consider density-power spectra exhibiting well-expressed spectral bumps of positive slope. We then show two examples where no bump is present but where the power spectra exhibit a scale-limited excess and consequently a scale-limited spectral flattening.

4.1 Observed bumpy solar wind power spectra of turbulent density

Figure 3 is an example of a density spectrum with respect to spacecraft frequency which exhibits a positive slope (or bump) on the otherwise negative slope of the main spectrum. The data in this figure were taken from published spectra (Šafránková et al., 2013) in the solar wind at an average bulk velocity of V₀≈534 km s⁻¹, density $N_{\mathrm{0}}\approx \mathrm{3}\times {\mathrm{10}}^{\mathrm{6}}$ m⁻³, and magnetic field B₀≈8 nT, yielding a super-alfvénic Alfvén Mach number M_A≈6, ion temperature T_i≲3 eV, and total plasma β≈0.3, i.e. low-beta conditions. The straight solid and broken lines drawn across this slope correspond to the predicted ∼ω^⅓ K and ∼ω^½ IK slopes under convection-dominated conditions. Both these lines fit the shape very well though it cannot be decided which of the inertial-range turbulence models provides a better fit, as the large scatter of the data mimicked by the line width inhibits any distinction. It is however obvious from Table 1 that advection plays no role in this case.

In order to check pressure balance between the density and magnetic field fluctuations, we refer to turbulent magnetic power spectra obtained at the WIND spacecraft Šafránková et al. (2013). WIND was located in the L1 Lagrange point. Magnetic field fluctuations were related in time to the Bright Monitor of the Solar Wind (BMSW) observations by the solar wind flow. In spite of their scatter, the data were sufficiently stationary for comparison to the density measurements.

Figure 4 shows the WIND magnetic power spectral densities. For transformation of the point cloud into a continuous line, we applied the same technique (Šafránková et al., 2016) as that for the density spectrum. The spectrum exhibits the expected positive slope in the BMSW frequency interval. The straight solid and broken lines along the positive slope correspond (within the uncertainty of the observations) to the root slopes of K and IK density inertial-range spectra $\langle |\mathit{\delta }B{|}^{\mathrm{2}}{\rangle }_{{\mathit{\omega }}_{\mathrm{s}}}\sim {\mathit{\omega }}_{\mathrm{s}}^{\frac{\mathrm{1}}{\mathrm{6}}}$ and $\sim {\mathit{\omega }}_{\mathrm{s}}^{\frac{\mathrm{1}}{\mathrm{4}}}$, respectively. The magnetic spectrum is the consequence of the K or IK density spectrum $\sim {\mathit{\omega }}_{\mathrm{s}}^{\frac{\mathrm{1}}{\mathrm{3}}}$ and $\sim {\mathit{\omega }}_{\mathrm{s}}^{\frac{\mathrm{1}}{\mathrm{2}}}$, respectively. Fluctuations in temperature do not, within experimental uncertainty, play any susceptible role. Comparing absolute powers is inhibited by the ungauged differences in instrumentation. (One may note that power spectral densities are positive definite quantities. Measuring their slopes is sufficient indication of pressure balance. Detailed pressure balance can only be seen when checking the phases of the fluctuations. Density and magnetic field would then be found in the antiphase.)

Table 1 K and IK ion-inertial-range spectral indices k^−a, $k^{-(a-\mathrm{2})}$, ${\mathit{\omega }}_{\mathrm{s}}^b$, and ${\mathcal{E}}_{\mathrm{Bs}}\sim {\mathit{\omega }}_{\mathrm{s}}^{b/\mathrm{2}}$ without and with advection.

4.2 The normal case: flattened density-power spectra without bump

The majority of observed density-power spectra in the solar wind do not exhibit positive slopes. Such spectra are of monotonic negative slope. In this sense they are normal. They frequently possess break points in an intermediate range where the slopes flatten. Two typical examples are shown in Fig. 5, combined from unrelated BMSW and WIND data (Šafránková et al., 2013; Podesta and Borovsky, 2010).

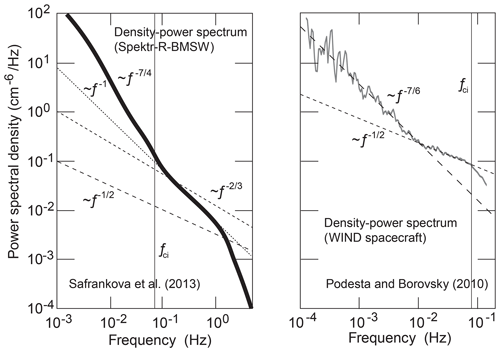
Figure 5 Two (redrawn on same scale) cases of normal solar wind density-power spectra measured by Spektr-R-BMSW (Šafránková et al., 2013) on 10 November 2011 and WIND (Podesta and Borovsky, 2010) on 4–8 January 1995 at different solar wind conditions. BMSW observations of 2011 were obtained under low-speed (∼370 km s⁻¹) moderately large total $\mathit{\beta }={\mathit{\beta }}_{\mathrm{i}}+{\mathit{\beta }}_{\mathrm{e}}\sim \mathrm{2.5}$, high Alfvénic Mach number M_A∼10, and mean-field B₀∼5 nT conditions. Density and temperature amounted to $N_{\mathrm{0}}\sim \mathrm{5}\times {\mathrm{10}}^{\mathrm{6}}$ m⁻³ and T_i∼10 eV, with ion-cyclotron f_ci∼0.08 Hz and plasma f_i∼500 Hz frequencies. WIND observations in L1 were obtained under high speed (∼640 km s⁻¹), β_i≲1, B₀∼6 nT, $N_{\mathrm{0}}\sim \mathrm{3.5}\times {\mathrm{10}}^{\mathrm{6}}$ m⁻³, T_i∼20 eV, and M_A∼9 conditions with similar cyclotron and plasma frequencies. In contrast to Fig. 3 these spectra do not exhibit regions of positive slope. Their spectral slope is interrupted by a flattened region. They share a range of spectral index $\sim -\mathrm{1}$, though in different frequency intervals, while the WIND spectrum exhibits a higher-frequency range of flat slope $\sim -\mathrm{1}/\mathrm{2}$ which is absent in the BMSW spectrum.

Their flattened spectral intervals each extend roughly over 1 decade in frequency. The BMSW spectrum is shifted by 1 order of magnitude in frequency to higher frequencies than the WIND spectrum. Its low-frequency part below the ion-cyclotron frequency f<f_ci has slope $\sim {\mathit{\omega }}^{-\frac{\mathrm{7}}{\mathrm{4}}}$, close to a K spectrum $\sim {\mathit{\omega }}^{-\frac{\mathrm{5}}{\mathrm{3}}}$. The slope of the flat section is $\sim {\mathit{\omega }}^{-\mathrm{1}}$ which is about the same as the slope of the entire low-frequency WIND spectrum before its spectral break. None of the Poisson-modified K or IK spectral slopes fit these flattened regions. At higher frequencies the BMSW spectrum steepens and presumably enters the dissipative range.

The slope of the WIND spectrum above its break point at frequency $\sim {\mathrm{10}}^{-\mathrm{2}}$ Hz decreases to $\sim {\mathit{\omega }}^{-\frac{\mathrm{1}}{\mathrm{2}}}$. This corresponds perfectly to an advected Taylor's Galilei-transformed IK spectrum, suggesting that WIND detected such a spectrum in the ion-inertial range which maps to those spacecraft frequencies. The pronounced ω⁻¹ spectrum at lower frequencies remains, however, unexplained for both spacecraft.

When crossing the cyclotron frequency f_ci, the WIND spectrum steepens. We also note that the normalised power spectral densities of WIND at $\langle |\mathit{\delta }N{|}^{\mathrm{2}}\rangle /N_{\mathrm{0}}^{\mathrm{2}}>\mathrm{0.3}$ and BMSW at $\mathrm{0.005}<\langle |\mathit{\delta }N{|}^{\mathrm{2}}\rangle /N_{\mathrm{0}}^{\mathrm{2}}<\mathrm{0.05}$ in the common slope $\sim {\mathit{\omega }}^{-\mathrm{1}}$ interval are roughly 2 orders of magnitude apart. This can hardly be traced back to the radial difference of 0.01 AU between L1 and 1 AU.

The obvious difference between the two plasma states is not in the Mach numbers but rather in β and V₀. The BMSW observed, under moderately high-β low-V₀ conditions, WIND under moderately low-β high-V₀ conditions at similar densities and Mach numbers. Because of the Galilean relation $k={\mathit{\omega }}_{\mathrm{s}}/V_{\mathrm{0}}\cos \mathit{\alpha }$, the high speed in the case of WIND seems responsible for the spectral shift in the ${\mathit{\omega }}_{\mathrm{s}}^{-\mathrm{1}}$ spectral range to lower than BMSW frequencies. This, however, comes up merely for a factor 2 which does not cover the frequency shift of more than 1 order of magnitude. Rather it is the angle between mean speed and the wave-number spectrum which displaces the spectra in frequency. If this is the case, then the WIND spectrum was about parallel to the solar wind velocity with WIND angle α≈0^∘, while the BMSW spectrum was close to being perpendicular with angle α≈90^∘, and it is the BMSW spectrum which has been shifted by Taylor's Galilei transformation into the high-frequency domain, while the WIND spectrum is about original. This may also be the reason why BMSW does not see the narrow, flattened spectral part while compressing the ${\mathit{\omega }}_{\mathrm{s}}^{-\mathrm{1}}$ part into just 1 order of magnitude in frequency. The near-perpendicular angle α will also be confirmed below in the bumpy BMSW spectral case.

5 Discussion

In this communication we dealt with the power spectra of density in low-frequency plasma turbulence. We did not develop any new theory of turbulence. We showed that, in the ion-inertial scale range of non-magnetised ions, the electric response of the ion population to a given theoretical turbulent K or IK spectrum of velocity may contribute to a scale-limited excess in the density fluctuation spectrum with a positive or flattened slope. We demonstrated that the obtained inertial-range spectral slopes within experimental uncertainty are not in disagreement with observations in the solar wind, but we could not decide between the models of turbulence. This may be considered a minor contribution only; it shows, however, that correct inclusion of the electrodynamic transformation property is important and suffices for reproducing an observational fact without any need to invoke higher-order interactions, any instability, or nonlinear theory. We also inferred the limitations and scale ranges for the response to cause an effect. However, a substantial number of unsolved problems remain. Below we discuss some of them.

5.1 Reconciling the spectral range

The main problem concerns the agreement with observations. Determination and confirmation of spectral slopes is a necessary condition. However, how should the observed frequency range be adjusted?

Inspecting Fig. 3, where we included the local ion-cyclotron frequency $f_{\mathrm{ci}}={\mathit{\omega }}_{\mathrm{ci}}/\mathrm{2}\mathit{\pi }$, we find the scale-limited positive slope (bump) of the density-power spectrum at spacecraft frequencies $f_{\mathrm{m}}\sim {\mathit{\omega }}_{\mathrm{m}}<{\mathit{\omega }}_{\mathrm{ci}}\sim \mathrm{0.22}$ Hz. According to Taylor, we have

$$\begin{array}{}\text{(36)}& {\mathit{\omega }}_{\mathrm{m}}=k_{\mathrm{m}}{V}_{\mathrm{0}}\cos {\mathit{\alpha }}_{\mathrm{m}},\mathrm{and}\mathrm{also}{k}_{\mathrm{m}}{\mathit{\lambda }}_{\mathrm{i}}>\mathrm{1},\end{array}$$

where α_m is the angle between k_m and velocity V₀, and ${\mathit{\lambda }}_{\mathrm{i}}=c/{\mathit{\omega }}_{\mathrm{i}}$. The first expression yields Taylor's Galilei-transformed wave number $k_{\mathrm{m}}\sim \mathrm{2.3}\times {\mathrm{10}}^{-\mathrm{6}}/\cos {\mathit{\alpha }}_{\mathrm{m}}$ m⁻¹. From the second, we have, with the observed ion plasma frequency, $k_{\mathrm{m}}\sim \mathrm{2}\mathit{\pi }\times {\mathrm{10}}^{-\mathrm{6}}$ m⁻¹. Hence we find that cos  α_m<0.37 or α_m>69^∘. The turbulent eddies are at highly oblique angles with respect to the flow velocity.

With angles of this kind the positive slope spectral range can be explained. The lower frequencies then correspond to eddies which propagate nearly perpendicular. Since our theory is generally restricted to wave numbers perpendicular to the ambient magnetic field, the eddies which contribute to the bumps are perpendicular to B₀ and highly oblique with respect to the flow. Similar arguments apply to the high-frequency excess in the WIND observations of Fig. 5. Referring to Table 1 this excess is explained as survival of the advected spectrum when Taylor's Galilei transformed into the spacecraft frame.

5.2 Radially convected spectra: effect of inhomogeneity

The assumption of Taylor's Galilei transformation in the way we used it (and is generally applied to turbulent solar wind power spectra) is valid only in stationary homogeneous turbulent flows of spatially constant plasma and field parameters⁶, which in the solar wind is not the case. It also assumes that wave numbers k are conserved by the flow⁷. Thus the above conclusion is correct only if the turbulence is generated locally and is transported over a distance where the radial variation of the solar wind is negligible. If it is assumed that the turbulence is generated in the innermost heliosphere at a fraction of 1 AU (e.g. McKenzie et al., 1995), any simple application of Taylor's Galilei transformation and thus the above interpretation break down.

Under the fast flow conditions of Fig. 3 it is reasonable to assume that the solar wind expands isentropically, denoting the turbulent source and spacecraft locations by indices q and s, respectively. The turbulent inertial range is assumed to be collisionless, dissipationless, and in ideal gas conditions. For simplicity assume that the expansion is stationary and purely radial. Under Taylor's assumption each eddy maintains its identity, which implies that the number of eddies is constant, and the eddy flux $F_s\left(r_s\right)/F_q\left(r_q\right)=r_q^{\mathrm{2}}/r_s^{\mathrm{2}}$, i.e. the turbulent power, decreases as the square of the radius. For the plasma we have the isentropic condition (e.g. Kittel and Kroemer, 1980, p. 174)

$$\begin{array}{}\text{(37)}& {\displaystyle \frac{T_s\left(r_s\right)}{T_q\left(r_q\right)}}=[{\displaystyle \frac{N_s\left(r_s\right)}{N_q\left(r_q\right)}}{]}^{\mathit{\gamma }-\mathrm{1}},\mathit{\gamma }={\displaystyle \frac{\mathrm{5}}{\mathrm{3}}},\end{array}$$

which gives $N_s\left(r_s\right)/N_q\left(r_q\right)=(r_q/r_s{)}^{\mathrm{3}}$, and thus $T_s\left(r_s\right)/T_q\left(r_q\right)=(r_q/r_s{)}^{\mathrm{2}}$. One requires that $k_q>{\mathit{\lambda }}_{\mathrm{i}q}^{-\mathrm{1}}={\mathit{\omega }}_{\mathrm{i}q}\left(r_q\right)/c$. By the same reasoning as that in the homogeneous case, one finds that

$$\begin{array}{ll}{\displaystyle \frac{f_{\mathrm{m}}}{f_{\mathrm{is}}}}& {\displaystyle }={\displaystyle \frac{k_{\mathrm{m}}{V}_{\mathrm{0}}}{{\mathit{\omega }}_{\mathrm{is}}}}\cos {\mathit{\alpha }}_{\mathrm{m}}\\ {\displaystyle }& {\displaystyle }=k_q{\mathit{\lambda }}_{\mathrm{i}q}{\displaystyle \frac{V_{\mathrm{0}}}{c}}({\displaystyle \frac{r_q}{r_s}}{)}^{\frac{\mathrm{3}}{\mathrm{2}}}\cos {\mathit{\alpha }}_{\mathrm{m}}\\ \text{(38)}& {\displaystyle }& {\displaystyle }\mathit{\gtrsim }{\displaystyle \frac{V_{\mathrm{0}}}{c}}({\displaystyle \frac{r_q}{r_s}}{)}^{\frac{\mathrm{3}}{\mathrm{2}}}\cos {\mathit{\alpha }}_{\mathrm{m}},\end{array}$$

inserting for the left-hand side and V₀, we find, with r_s=1 AU, that

$$\begin{array}{}\text{(39)}& r_q<{\displaystyle \frac{\mathrm{0.1}}{(\cos {\mathit{\alpha }}_{\mathrm{m}}{)}^{\frac{\mathrm{2}}{\mathrm{3}}}}}\mathrm{AU}.\end{array}$$

We conclude that under the assumption of isentropic expansion of the solar wind and Taylor's Galilei transport of turbulent eddies from the source region to the observation site at 1 AU, the generation region of the turbulent eddies which contribute to the bump in the K or IK density-power spectrum must be located close to the Sun. The marginally permitted angle α_m between wave number and mean flow is obtained by using r_q=1 AU, yielding α_m>47^∘, meaning that the flow must be oblique for the effect to develop, a conclusion already found above for homogeneous flow. These numbers are obtained under the unproven assumption that Taylor's Galilei transport conserves turbulent wave numbers in the inhomogeneous solar wind.

5.3 Ion gyroradius effect

So far we have referred to the inertial length as limiting the frequency range. We now ask, for the more stringent condition kρ_ic>1, that the responsible length be the ion gyroradius ${\mathit{\rho }}_{\mathrm{ic}}=v_{\mathrm{i}}/{\mathit{\omega }}_{\mathrm{ci}}$. In this case reference to the adiabatic conditions becomes necessary. We also need a model of the radial variation of the solar wind magnetic field. The field inside r_s=1 AU is about radial. Magnetic flux conservation yields the Parker model $B_s\left(r_s\right)=B_q\left(r_q\right)(r_q/r_s{)}^{\mathrm{2}}$. A more modern empirical model instead proposes a weaker radial decay of the power 5∕3 (for a review, e.g. Khabarova, 2013). With these dependences, we have

$$\begin{array}{}\text{(40)}& {\displaystyle }k{\mathit{\rho }}_s\left(r_s\right)& {\displaystyle }=k{\mathit{\rho }}_q\left(r_q\right){\displaystyle \frac{B_q\left(r_q\right)}{B_s\left(r_s\right)}}\sqrt{{\displaystyle \frac{T_{\mathrm{i}s}\left(r_s\right)}{T_{\mathrm{i}q}\left(r_q\right)}}}\text{(41)}& {\displaystyle }& {\displaystyle }=k{\mathit{\rho }}_q\left(r_q\right)({\displaystyle \frac{r_s}{r_q}}{)}^{\frac{\mathrm{2}}{\mathrm{3}}}>({\displaystyle \frac{r_s}{r_q}}{)}^{\frac{\mathrm{2}}{\mathrm{3}}},\end{array}$$

where the necessary condition kρ_q>1 has been used. Referring again to the observed minimum frequency f_m yields

$$\begin{array}{}\text{(42)}& {\displaystyle \frac{f_{\mathrm{m}}}{f_{\mathrm{ic},s}}}& {\displaystyle }={\displaystyle \frac{k_{\mathrm{m}}{V}_{\mathrm{0}}}{{\mathit{\omega }}_{\mathrm{ic},s}}}\cos {\mathit{\alpha }}_{\mathrm{m}}\text{(43)}& {\displaystyle }& {\displaystyle }=k{\mathit{\rho }}_q{\displaystyle \frac{V_{\mathrm{0}}}{v_{\mathrm{i}}}}\left({\displaystyle \frac{r_s}{r_q}}{)}^{\frac{\mathrm{2}}{\mathrm{3}}}\cos {\mathit{\alpha }}_{\mathrm{m}}\mathit{\gtrsim }{\displaystyle \frac{V_{\mathrm{0}}}{v_{\mathrm{i}}}}\right({\displaystyle \frac{r_s}{r_q}}{)}^{\frac{\mathrm{2}}{\mathrm{3}}}\cos {\mathit{\alpha }}_{\mathrm{m}}.\end{array}$$

Inserting for the frequency ratio $f_{\mathrm{m}}/f_{\mathrm{ic},s}\sim \mathrm{0.1}$ and the ratio of mean to thermal velocities $V_{\mathrm{0}}/v_{\mathrm{i}}\approx \mathrm{18}$, and setting r_s=1 AU, we obtain, for the source radius lying inside 1 AU,

$$\begin{array}{}\text{(44)}& \mathrm{1}\mathrm{AU}>r_{q\mathrm{m}}>\mathrm{300}(\cos {\mathit{\alpha }}_{\mathrm{m}}{)}^{\frac{\mathrm{3}}{\mathrm{2}}},\end{array}$$

which gives the result α_m≳89^∘ for the propagation angle obtained above. According to both these estimates eddy propagation is required to be quasi-perpendicular to the flow. This holds under the strong condition that the wave number is conserved during outward propagation.

5.4 Radial variation of wave number in expanding solar wind

The wave number $k\sim {\mathit{\lambda }}^{-\mathrm{1}}$ is an inverse wavelength. Let us assume that λ∼r stretches linearly when the volume expands, thereby reducing k hyperbolically. The eddies, which are frozen to the volume, also stretch linearly. In this case the ratio r_s∕r_q in Eq. (43) is raised to the power 1∕3, and we find instead that

$$\begin{array}{}\text{(45)}& r_{q\mathrm{m}}\mathit{\lesssim }({\displaystyle \frac{\cos {\mathit{\alpha }}_{\mathrm{m}}}{\mathrm{18}}}{)}^{\mathrm{3}}<\mathrm{1}\mathrm{AU}.\end{array}$$

This gives α_m≳87^∘ which is not too different from the above case. Thus the angle between mean speed and the turbulent wave number is close to perpendicular in order to reconcile the lower observed limit in spacecraft frequency with the wave number in the source region.

5.5 High-frequency limit for $f_{\mathrm{M}}\sim f_{\mathrm{ce},s}$

A similar reasoning can be applied to the upper frequency bound ω_M. Following the discussion in the Introduction, this bound is caused by the truncation of the ion-inertial range at large wave numbers when the scale approaches the electron scale, electron inertia takes over, and electrons demagnetise. The condition in this case is that kρ_e<1, which defines the maximum frequency ω_M.

We then have the following relation for the maximum wave number:

$$\begin{array}{}\text{(46)}& k{\mathit{\rho }}_{\mathrm{Me}}\left(r_s\right)=k{\mathit{\rho }}_{\mathrm{Me}}\left(r_q\right){\displaystyle \frac{B_q\left(r_q\right)}{B_s\left(r_s\right)}}\sqrt{{\displaystyle \frac{T_{\mathrm{e}s}\left(r_s\right)}{T_{\mathrm{e}q}\left(r_s\right)}}}<({\displaystyle \frac{r_s}{r_q}}{)}^{\frac{\mathrm{2}}{\mathrm{3}}}.\end{array}$$

From the maximum observed frequency, we find that, with f_M≲f_ce,s,

$$\begin{array}{ll}{\displaystyle \frac{f_{\mathrm{M}}}{f_{\mathrm{ce},s}}}& {\displaystyle }={\displaystyle \frac{k_{\mathrm{M}}{V}_{\mathrm{0}}}{{\mathit{\omega }}_{\mathrm{ce},s}}}\cos {\mathit{\alpha }}_{\mathrm{M}}\\ \text{(47)}& {\displaystyle }& {\displaystyle }=k{\mathit{\rho }}_q{\displaystyle \frac{V_{\mathrm{0}}}{v_{\mathrm{e}}}}\left({\displaystyle \frac{r_s}{r_q}}{)}^{\frac{\mathrm{2}}{\mathrm{3}}}\cos {\mathit{\alpha }}_{\mathrm{M}}\mathit{\lesssim }{\displaystyle \frac{V_{\mathrm{0}}}{v_{\mathrm{e}}}}\right({\displaystyle \frac{r_s}{r_q}}{)}^{\frac{\mathrm{2}}{\mathrm{3}}}\mathit{\lesssim }\mathrm{1},\end{array}$$

which, when inserting kρ_q≲1, adopting the main plasma parameters, and with maximum frequency $f_{\mathrm{M}}/f_{\mathrm{ce},s}\sim \mathrm{1}$ and r_s∼1 AU, yields

$$\begin{array}{}\text{(48)}& r_{q\mathrm{M}}>({\displaystyle \frac{V_{\mathrm{0}}}{v_{\mathrm{e}}}}{)}^{\frac{\mathrm{3}}{\mathrm{2}}}\mathrm{AU}\sim \mathrm{0.05}\mathrm{AU}.\end{array}$$

Taking the two results for this case together, the observations map to an angle of propagation α_m>49^∘ and places the turbulent source close to the Sun but outside 11 R_⊙≲r_q≲1 AU. It occurs only if the turbulence contains a dominant population of eddies obeying wave-number vectors k which are oblique to the mean flow velocity V₀. This is in agreement with our given estimate above on the theoretical limits and explains the relative rarity of its observation. Unfortunately, based on the observations, the desired location of the turbulent source region in space cannot be localised more precisely.

5.6 The observed case: $f_{\mathrm{m}}\sim \mathrm{0.1}{f}_{\mathrm{M}}\ll f_{\mathrm{ce},s}$

Reconciling the observed range of the bump poses a tantalising problem. Our theoretical approach would suggest that the bump develops between the two cyclotron frequencies of ions and electrons in the spacecraft frame. This would correspond to a range of the order of the mass ratio m_i∕m_e which would be 3 orders of magnitude. The actually observed range f_m≲f_s≲f_M is much narrower, being just 1 order of magnitude. Given the uncertainties of measurement and instrumentation this can be extended at most to the root of the mass ratio, which in a proton-electron plasma amounts to a factor of $f_{\mathrm{M}}/f_{\mathrm{s}}\sim \mathrm{43}$ only. In addition, unfortunately, the observed local maximum frequency in Fig. 3 is far less than the local electron cyclotron frequency $f_{\mathrm{M}}\ll f_{\mathrm{ce},s}$. The affected wave number and frequency ranges are very narrow and at the wrong place. Thus in the given version, the reasoning above does not apply. Already in the source region, the effect must be bound to a narrow domain in wave number. The mass ratio might suggest coincidence with the lower-hybrid frequency of a low-β proton-electron plasma which, when raised to the power 3∕2, yields

$$\begin{array}{}\text{(49)}& r_{q\mathrm{M}}\mathit{\gtrsim }\mathrm{0.6}\mathrm{AU},\end{array}$$

putting the source region substantially farther out to ≳45R_⊙.

The latter estimate is, however, quite speculative. Thus the narrowness of the observed bump in frequency poses a serious problem. Its solution is not obvious. The most honest conclusion is that little can be said about the observed upper frequency termination of the bump in Fig. 3 unless an additional assumption is made.

One may, however, argue that in a high-β_i plasma the gyroradius of the ions is large. The ions are non-magnetic, but the effect can arise only when the wavelength becomes less than the inertial length ${\mathit{\lambda }}_{\mathrm{m}}<{\mathit{\lambda }}_{\mathrm{i}}=c/{\mathit{\omega }}_{\mathrm{i}}$. Similarly the effect will disappear when the wavelength crosses the electron inertial length ${\mathit{\lambda }}_{\mathrm{M}}<{\mathit{\lambda }}_{\mathrm{e}}=c/{\mathit{\omega }}_{\mathrm{e}}$. The ratio of these two limits is ${\mathit{\lambda }}_{\mathrm{M}}/{\mathit{\lambda }}_{\mathrm{m}}=f_{\mathrm{M}}/f_{\mathrm{m}}=\sqrt{m_{\mathrm{i}}/m_{\mathrm{e}}}\approx \mathrm{43}$. This agrees approximately with the observation. This interpretation then identifies the range of the effect in spacecraft frequency and source wave number with the range between electron and ion-inertial lengths. Since both evolve radially with the ratio of the root of densities, the relative spectral width should not change from source to spacecraft.

In order to get an idea of the distance between source and spacecraft, we assume that in the interval between the minimum and maximum frequencies, the ion-cyclotron frequency is crossed. Hence the corresponding wave number is contained in the spectrum though it is invisible. This fact, however, enables us to refer to the difference in the ion-inertial length scale and the ion gyroradius. The total difference in frequency amounts to roughly 1 order of magnitude. The ratio of both lengths is ${\mathit{\rho }}_{\mathrm{i}}/{\mathit{\lambda }}_{\mathrm{i}}=\sqrt{{\mathit{\beta }}_{\mathrm{i}}}$, with β_i being the ion β. In isentropic expansion, the evolution of β_i, assuming a Parker model, is

$$\begin{array}{}\text{(50)}& ({\displaystyle \frac{{\mathit{\rho }}_{\mathrm{i}s}}{{\mathit{\rho }}_{\mathrm{i}q}}}{\displaystyle \frac{{\mathit{\lambda }}_{\mathrm{i}q}}{{\mathit{\lambda }}_{\mathrm{i}s}}}{)}^{\mathrm{2}}={\displaystyle \frac{{\mathit{\beta }}_{\mathrm{i}s}}{{\mathit{\beta }}_{\mathrm{i}q}}}\propto ({\displaystyle \frac{r_q}{r_s}}{)}^{\frac{\mathrm{5}}{\mathrm{3}}}.\end{array}$$

From observations we have a total β>1. We expect ρ_i≳λ_i and assume that β_i≳1. Figure 3 suggests a frequency ratio $f_{\mathrm{m}}/f_{\mathrm{M}}\sim {\mathit{\beta }}_{\mathrm{i}s}\sim \mathrm{0.7}$ larger than $\sqrt{m_{\mathrm{e}}/m_{\mathrm{i}}}\approx \mathrm{0.025}$. The affected frequency and wave-number ranges are limited from above when the scale approaches the electron gyroradius. In that case, the upper bound is not determined by the mass ratio alone. With the measured frequency ratio, the location of the source should then be outside a shortest distance of

$$\begin{array}{}\text{(51)}& r_q\mathit{\gtrsim }\mathrm{0.24}{\mathit{\beta }}_{\mathrm{i}q}\mathrm{AU}.\end{array}$$

This value corresponds to $>\mathrm{50}{\mathit{\beta }}_{\mathrm{i}q}{R}_{\odot }$ from the Sun. Since the source must lie inside r_q<1 AU, we conclude that β_iq≲4.15. This number is just an upper limit. It is consistent with model calculations (McKenzie et al., 1995) which predict β_iq<1 shifting the inner boundary of the turbulent source region further in.

5.7 Summary and outlook

In this paper, we considered the cases $V_{\mathrm{0}}=U_{\mathrm{0}}=\mathrm{0}$, $V_{\mathrm{0}}=\mathrm{0},U_{\mathrm{0}}\ne \mathrm{0}$, and V₀≠0 for K and IK velocity spectra, where V₀ is the velocity of the mean solar wind stream, and U₀ is the mean speed of the energy-carrying largest turbulent MHD vortices which advect the bulk of small-scale turbulence around (Tennekes, 1975). In the K and IK models of turbulence, they, in addition, play the role of the energy injectors. The resulting spectral slopes are given as b in the fourth column of Table 1. The input spectral power densities are ℰ_IK and ${\mathcal{E}}_{\mathrm{IK}}^{\mathrm{ad}}$. Each of them yields a different ion-inertial scale range power spectrum in k space and, consequently, also a different power law spectrum in ω_s space.

Table 1 shows that the ordinary spectra acquire positive slopes in wave number k in the frame of stationary and homogeneous turbulence in the turbulence frame. However, observations of this slope in frequency undermine this conclusion, suggesting that it is the ordinary K (IK) velocity turbulence (or if anisotropy is taken into account, the KGS) spectrum in the ion-inertial range which, when convected by the solar wind flow across the spacecraft, deforms the density spectrum. All advected spectra have, in contrast, a negative slope in frequency which in this form disagrees with observation of the spectral bumps.

The obtained advected slopes in the stationary turbulence frame are also too far away from the flattest notorious and badly understood negative slope ${\mathit{\omega }}_{\mathrm{s}}^{-\mathrm{1}}$ for being related. Their nominal K and IK slopes are $-\mathrm{2}/\mathrm{3}$ and $-\mathrm{1}/\mathrm{2}$, respectively. This implies that spacecraft observations interpreted as observing the local stationary turbulence do not, in the majority of cases, detect an advected convected spectrum in the ion-inertial K (IK) inertial range. They are, however, well capable of explaining the high-frequency flattened spectral excursion in the WIND spectrum which is shown in Fig. 5. It has the correct advective IK spectral index $-\mathrm{1}/\mathrm{2}$ when convected across the WIND spacecraft before the onset of spectral decay.

Generally the form of a distorted power spectrum in density depends on the external solar wind conditions. The reconciliation of these with the theoretical predictions and the observation of the spectral range of the distortion is a difficult, mostly observational task. We have attempted it in the discussion section. In particular the proposed bending of the power spectral density in the direction of lower frequencies requires identification of the maximum point of the advected spectrum in frequency and the transition to the undisturbed K or IK inertial ranges.

We tentatively tried taking thermodynamic effects in an expanding solar wind into account. This led to preliminary information about the angle between flow and the turbulent wave numbers which contribute to deformation of the spectrum. Some tentative information could also be retrieved in this case about the radial solar distance of the turbulent source region. When thermodynamics come in, one may raise the important question for the collisionless turbulent ion heating $\langle \mathit{\delta }{\dot{Q}}_{\mathrm{i}}\rangle =-\langle \mathit{\delta }{\dot{Q}}_{\mathrm{em}}\rangle =\langle \mathit{\delta }\mathit{J}\cdot \mathit{\delta }\mathit{E}\rangle$ in the ion-inertial range, the negative of the mean loss in electromagnetic energy density per time $\langle \mathit{\delta }{\dot{Q}}_{\mathrm{em}}\rangle$, proportional to the product of current vortices δJ and the turbulent electric field δE. Though of finite magnitude, it is second order. This is left for future investigation. Hall currents do not contribute to any heating.

So far we have not taken into account the contribution of Hall spectra. These affect the shape of the density spectrum via the Hall-magnetic field, a second-order effect indeed, though it might contribute to additional spectral deformation. Inclusion of the Hall effect requires a separate investigation with reference to magnetic fluctuations. On those scales the Hall currents should provide a free energy source internal to the turbulence, which is not included in K and IK theory.

Hall fields are closely related to kinetic effects in the ion-inertial range. Among them are kinetic Alfvén waves whose perpendicular scales $k_{⟂}\sim {\mathit{\lambda }}_{\mathrm{i}}^{-\mathrm{1}}$ agree with the scale of the ion-inertial range. Possibly they can grow on the expense of the Hall field which in this case plays the role of free energy for them. If they can grow to sufficiently large amplitudes, they contribute to further deforming K and IK ion-inertial-range density spectra.

Similarly, small-scale shock waves might evolve at the inferred high Mach numbers when turbulent eddies grow and steepen in the small-scale range. These necessarily become sources of electron beams, reflect ions, and transfer their energy in a kinetic-turbulent way to the particle population. Such beams act as sources of particular wave populations which contribute to turbulence, preferably at the kinetic scales of interest.

Inclusion of all these effects is a difficult task. It still opens up a wide field for investigation of turbulence on the ion-inertial scale not yet entering the (Treumann and Baumjohann, 2015) collisionless dissipation scale where electrons demagnetise as well and the current filaments dissipate their energy in the process of spontaneous collisionless reconnection as the most probable ultimate energy sink of otherwise collisionless turbulence. The scales of this dissipation process are still far away from any molecular scales. The resulting dissipation is justifiably anomalous.