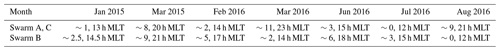Mitigation of ionospheric signatures in Swarm GPS gravity field estimation using weighting strategies

Even though ESA's three-satellite low-earth orbit (LEO) mission Swarm is primarily a magnetic field mission, it can also serve as a gravity field mission. Located in a near-polar orbit with initial altitudes of 480 km for Swarm A and Swarm C and 530 km for Swarm B and equipped with geodetic-type dual frequency Global Positioning System (GPS) receivers, it is suitable for gravity field computation. Of course, the Swarm GPS-only gravity fields cannot compete with the gravity fields derived from the ultra-precise Gravity Recovery And Climate Experiment (GRACE) K-band measurements. But for various reasons like the end of the GRACE mission in October 2017, data gaps in the previous months due to battery aging, and the gap between GRACE and the recently launched GRACE Follow-On mission, Swarm gravity fields became important to maintain a continuous time series and to bridge the gap between the two dedicated gravity missions. By comparing the gravity fields derived from Swarm kinematic positions to the GRACE gravity fields, systematic errors have been observed in the Swarm results, especially around the geomagnetic equator. These errors are already visible in the kinematic positions as spikes up to a few centimeters, from where they propagate into the gravity field solutions.

We investigate these systematic errors by analyzing the geometry-free linear combination of the GPS carrier-phase observations and its time derivatives using a combination of a Gaussian filter and a Savitzky–Golay filter and the Rate of Total Electron Content (TEC) Index (ROTI). Based on this, we present different weighting schemes and investigate their impact on the gravity field solutions in order to assess the success of different mitigation strategies. We will show that a combination of a derivative-based weighting approach with a ROTI-based weighting approach is capable of reducing the geoid rms from 21.6 to 12.0 mm for a heavily affected month and that almost 10 % more kinematic positions can be preserved compared to a derivative-based screening.

1 Introduction

Even though Swarm was designed as a magnetic field mission, Swarm has become important as a gravity mission to bridge the gap between GRACE and GRACE Follow-On (Lück et al., 2018). Thanks to the ultra-precise inter-satellite K-band measurements and high-quality accelerometer data, GRACE derived gravity field models are of superior quality, but due to battery aging starting in 2011 they started having gaps and eventually no more GRACE gravity fields were available since June 2017. The GRACE mission ended in October 2017 (JPL/NASA, 2017). GRACE Follow-On was launched on 22 May 2018. Due to a failure in the microwave instrument, a switchover to the backup system had to be performed; the science phase is expected to start in January 2019 (JPL/NASA, 2018). This has resulted in a gap of 1.5 years.

Recent comparisons of GRACE (K-band) gravity fields to Swarm (GPS-only) gravity fields showed two pronounced band-shaped artifacts of about 4 cm in geoid height along the geomagnetic equator when adopting a Gaussian filter of 400 km (Jäggi et al., 2016). Similar behavior of LEO-based GPS-only gravity fields was observed earlier in the computation of GOCE (Gravity Field And Steady-State Ocean Circulation Explorer) GPS-only gravity fields (Jäggi et al., 2015). In the GOCE case, only the ascending arcs (∼18 h magnetic local time – MLT) showed this behavior due to the dusk–dawn orbit configuration of the GOCE satellite (Bock et al., 2014). This special MLT is well known for a very pronounced equatorial ionization anomaly, equatorial spread F, as well as equatorial plasma bubbles (Whalen, 2000; Stolle et al., 2006). In this region, large gradients exist in the plasma density, which in turn may affect the tracking.

Usually for the GPS-based kinematic positioning the ionosphere-free linear combination

$$\begin{array}{}\text{(1)}& L_{\mathrm{IF}}={\displaystyle \frac{\mathrm{1}}{f_{\mathrm{1}}^{\mathrm{2}}-f_{\mathrm{2}}^{\mathrm{2}}}}\cdot (f_{\mathrm{1}}^{\mathrm{2}}{L}_{\mathrm{1}}-f_{\mathrm{2}}^{\mathrm{2}}{L}_{\mathrm{2}})\end{array}$$

is used, where f₁=1575.42 MHz and f₂=1227.60 MHz are the carrier frequencies and L₁ and L₂ are the two GPS carrier-phase observables. By forming this difference the first-order term of the ionospheric-phase advance cancels out. The remaining parts tend to be very small and were found to be negligible for the presented investigation (Jäggi et al., 2015).

The differences between the Swarm and GRACE gravity fields significantly improved with the tracking loop updates of the GPS receivers performed by ESA (Dahle et al., 2017; van den IJssel et al., 2016), which is an indicator that the high ionospheric activity affects the receiver tracking and in turn contaminates the ionosphere-free linear combination.

In contrast to the Sun-synchronous GOCE orbit, where only ascending arcs (close to 18 h MLT) were affected due to the dusk–dawn orbit geometry (Jäggi et al., 2011a), the Swarm orbit is evolving in MLT and therefore the dependency of the artifacts on magnetic local time can be examined. We use ionospheric information directly derived from the GPS measurements. Such an approach was already successfully applied by Jäggi et al. (2016) using epoch differences (a numerical approximation to compute the first time derivative) of the geometry-free linear combination

$$\begin{array}{}\text{(2)}& L_{\mathrm{GF}}=L_{\mathrm{1}}-L_{\mathrm{2}}.\end{array}$$

If the absolute value of the derivative exceeded 0.02 m s⁻¹, the GPS observations were rejected. Even though it successfully removed most of the signatures, the orbit was weakened due to the increased number of ambiguity parameters caused by gaps around the geomagnetic equator, as we will show later. In this article, we present a refined approach by using weighting strategies and assess whether higher-order time derivatives of L_GF may even represent a more adequate criterion to identify the problematic GPS data.

2 Impact of the ionosphere on GPS tracking performance

2.1 Swarm precise orbit determination

The precise orbit determination (POD) was performed using Development Version 5.3 of the Bernese GNSS software. We are following the procedure published in Jäggi et al. (2016). As external products, the final GPS orbits and the high-rate 5 s GPS satellite clock corrections are used which are provided by the Center Of Orbit Determination Europe (CODE). The Swarm Level-1b Receiver Independent Exchange Format (RINEX) 3 data (Gurtner and Estey, 2007) and Level-1b attitude data derived from the star tracker cameras are used. A final reduced-dynamic orbit with 6 min piecewise constant accelerations and a kinematic orbit are computed from undifferenced GPS carrier-phase observations. Code observations are only used for the initial clock synchronization. For the reduced-dynamic orbit, the gravity field model EGM2008 together with ocean tide model FES2004 are used. No non-gravitational forces were modeled. Both orbit types are computed for 24 h orbital arcs. Kinematic positions are essential for the gravity field determination as they contain no a priori information about the LEO's dynamics. Phase center variation (PCV) maps were generated in-flight using a residual approach. Ionosphere-free phase residuals larger than 4 cm compared to a screening orbit with 15 min piecewise constant accelerations are removed in the preprocessing. Usually for reduced-dynamic and kinematic orbit determination the phase observations have the same weight $p=\frac{{\mathit{\sigma }}_{\mathrm{0}}^{\mathrm{2}}}{{\mathit{\sigma }}^{\mathrm{2}}}$, where σ₀ is the a priori sigma for L1-phase observations of 1 mm and σ usually also equals 1 mm. For weighting, we will assign a specific σ to each observation. The ionosphere-free phase residuals, as shown in Figs. 2 and 7, were computed by using the screening orbit without rejecting large phase residuals. The same residuals were used to select the thresholds for weighting.

2.2 Systematic errors in kinematic positioning

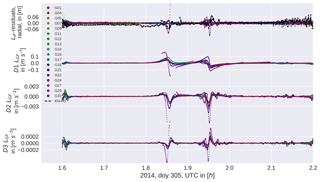
It was shown in earlier studies (Jäggi et al., 2016; Dahle et al., 2017) that the artifacts in the gravity field solutions are caused by the ionosphere. For that reason, we link fast-changing differences between kinematic positions and a reduced-dynamic orbit to the ambient plasma density. Swarm is equipped with Langmuir probes to directly measure in situ plasma density. Figure 1 shows a comparison between the measured plasma density and differences in kinematic positions to a reduced-dynamic orbit which offers more dynamical stiffness and is thus less susceptible to ionospheric disturbances. Especially around the sharp peak in plasma density, jumps of up to a few centimeters are observed in the orbit differences. If one compares this to the ionosphere-free GPS-phase residuals at the respective epochs (see Fig. 2 (top)), the epoch-wise variance over all GPS satellites becomes larger, thus indicating an inconsistency in the phase observables. The degradation occurs at the same epochs where the measured plasma density has its peaks (see Figs. 1 and 2, top curves). Because the GPS receiver moves with a large velocity (about 7.7 km s⁻¹), large gradients in the plasma density are clearly reflected in the geometry-free linear combination. Due to the different lines-of-sight to the tracked GPS satellites, this geometry-free linear combination has a large spatial variability.

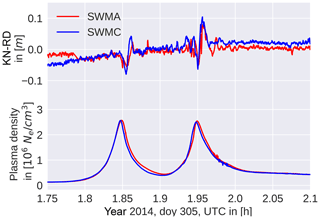
Figure 1 Orbit differences in the radial component between kinematic positions (KN) and a reduced-dynamic (RD) orbit fit (top) and plasma density during an equatorial pass.

In the following, we establish criteria for the occurrence of the degradation in the ionosphere-free phase residuals. We use numerical derivatives of the geometry-free linear combination because the degradation seems to be associated with rapid changes in plasma density and thus in the geometry-free linear combination. The geometry-free linear combination can be computed directly from the GPS RINEX file. No additional information, like an a priori orbit based on an underlying gravity field, is needed.

Figure 2 Phase residuals in reduced-dynamic positioning (top) and time derivatives of the geometry-free linear combination during one equatorial pass.

2.3 Radial variances

The covariance information of the kinematic point positioning may be used as an indicator for the quality of kinematic positions. Based on this, the kinematic positions may be weighted in the subsequent for gravity field determination. As shown by Jäggi et al. (2011b), however, this basically represents the geometry of the observation scenario. If kinematic positions have a high covariance, their impact on the gravity field solutions is small because they get properly weighted according to the covariance information. Because we saw in Sect. 2.2 that the spikes are associated with a spreading of the phase residuals, we compare the kinematic covariance with the epoch-wise standard deviation of the phase residuals over all satellites; see Fig. 3. We use magnetic latitude and magnetic local time because the phenomenon is most prominently visible around the magnetic equator in the evening hours. For the kinematic radial variances, we used the formal error propagation in the radial direction,

$$\begin{array}{ll}{\displaystyle }{\mathit{\sigma }}_r^{\mathrm{2}}& {\displaystyle }=(\mathrm{1}/r^{\mathrm{2}})\cdot (x^{\mathrm{2}}\cdot k_{xx}+y^{\mathrm{2}}\cdot k_{yy}+z^{\mathrm{2}}\cdot k_{zz}+\mathrm{2}\cdot x\cdot y\cdot k_{xy}\\ \text{(3)}& {\displaystyle }& {\displaystyle }+\mathrm{2}\cdot x\cdot z\cdot k_{xz}+\mathrm{2}\cdot y\cdot z\cdot k_{yz}),\end{array}$$

where x,y, and z are the coordinates in an Earth-fixed system and k_xy denotes the covariance between x and y, and $r=\sqrt{x^{\mathrm{2}}+y^{\mathrm{2}}+z^{\mathrm{2}}}$ is the geocentric distance. We use this to represent the quality of the 3-D positions in the radial direction, whereas we used the standard deviation of the phase residuals over all satellites at a certain epoch to identify the spreading. These values were binned, the mean of each box was computed, and for the purpose of visibility, the logarithm was used for the kinematic variances. The two figures look very different, especially around the polar regions where large phase residuals are more frequently observed. A different behavior can also be seen around the geomagnetic equator. In this region, the high standard deviation in phase residuals also affects earlier local times and slightly different latitudes than the high variances in kinematic positioning. For both plots, the same months (analyzed test period: 2015: January, March; 2016: February, March, June, July, August) were used and only kinematic positions with a minimum redundancy of five GPS satellites were used. No additional weighting or screening was performed.

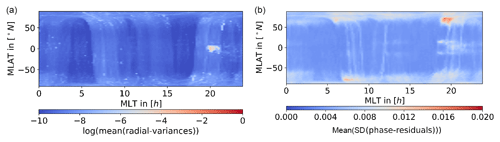
Figure 3 Radial variances (a) and spreading of phase residuals (b) binned in magnetic coordinates for the analyzed test period, 2015: January, March; 2016: February, March, June, July, August.

As shown by Xiong et al. (2016), the loss-of-lock events of the Swarm GPS receivers are highly correlated with bubble events. Whereas loss of lock corresponds to the worst case scenario, we saw in Fig. 3 that the kinematic radial variances also generally increase in the potential bubble regions, i.e., after sunset (18–22 h MLT) and near the geomagnetic equator. In this study, we extend the investigations by checking the radial variances of the unweighted and unscreened kinematic positions for Swarm for a long time span. As shown in the previous section, the phase residuals increase around the peaks in plasma density, indicating a potential degradation of the phase observables or a weaker geometry due to screened GPS observations or possible loss of locks.

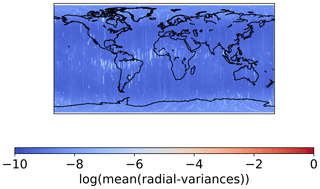
In Fig. 4 we binned the radial variances in 1^∘ lon × 1^∘ lat and formed the average using unweighted kinematic positions from November 2013 to December 2017 and all three Swarm satellites. Only positions with sufficient redundancy were used. Figure 4 shows that the geomagnetic equator is clearly visible showing the largest radial variances. If one reproduces this plot in MLT and Mlat (compare Fig. 3 (left)), a very pronounced peak around 18–22 h MLT becomes visible around 0^∘ Mlat. It should be noted that the time span used for Fig. 3 is given by the analyzed test period and by this it is shorter than in Fig. 4. Nevertheless, the observed patterns are almost identical to the results of Xiong et al. (2016) even if loss-of-lock events or data gaps for all GPS satellites are by construction not included in our figures. This again supports the statement that the GPS data quality suffers significantly from high activity in the magnetic-equatorial ionosphere at evening hours and, of course, due to equatorial plasma bubbles (see Fig. 3 (left)).

Figure 4 Radial variances binned for a longer time span in geographic coordinates, November 2013–December 2017.

2.4 Screened observations in preprocessing

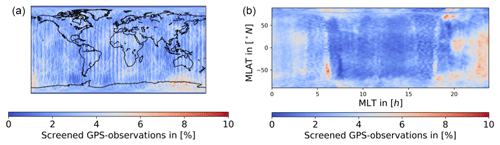
In the orbit processing, some observations are rejected in the preprocessing because they are considered to be outliers, or show large phase residuals, due to gaps, or small observation pieces. This screening is performed to avoid the propagation of data problems into the orbit solution. Even though this screening process applies especially in the nighttime hours, it does not seem to detect the observations responsible for the spikes in the kinematic positioning. The mean number of observations screened in the preprocessing is shown in Fig. 5. As before, only valid kinematic positions with enough redundancy were used and the mean difference between the number of observations in the RINEX file and the observations used for the final kinematic positioning is shown.

Figure 5 Average number of GPS observations screened in the preprocessing for the analyzed test period, 2015: January, March; 2016: February, March, June, July, August. (a) Geographic coordinates; (b) magnetic coordinates.

2.5 Computation of derivatives

Due to the noise of the geometry-free linear combination, the computation of meaningful derivatives is not straightforward. In order to obtain reliable derivatives, we use a combination of a Gaussian filter and a Savitzky–Golay filter. First, we smooth our data with the Gaussian filter, and then we apply the Savitzky–Golay filter to obtain the next-order derivative; we smooth again, etc. This approach allows us to keep the window size and the degree for the Savitzky–Golay filter low and by this reduce the sensitivity to noise in the higher-order derivatives. Before applying the filters, we use a jump and outlier detection with a threshold of 0.5 m s⁻¹ applied to epoch differences of the geometry-free linear combination. If larger jumps occur, the arcs were split to avoid any contamination of the derivatives. This action was also performed in case of gaps of one or more epochs in the 1 Hz RINEX data. For the Gaussian filter, we select a bandwidth of 10 s, a symmetrical window with a total width of 10.1 s, and a minimum number of 10 points. For the Savitzky–Golay filter, we choose a polynomial of degree 1, a symmetrical window with a total size of 12.5 s, and a minimum number of seven points. The parameters were determined empirically using an artificial signal (Fig. 6) and original Swarm RINEX data. Especially in case of the Gaussian filter, it is important to choose the parameters such that the window is almost fully populated (with the mentioned setting: max. one epoch missing) and symmetrically occupied. Otherwise, we may bias the smoothed points to the mean of the previous ones and forcing the derivatives to zero. If it was not possible to compute the derivative due to jumps, gaps or not enough data, the corresponding epochs were marked to set weights manually in a later stage. In our processing, we will assign a smaller weight to these epochs.

In Fig. 2 we show a short time series of phase residuals and the corresponding derivatives during one equatorial pass. It may be seen that the second and third time derivative are more focused on the epochs where the spikes occur than the first time derivative. The higher derivatives show comparatively larger amplitudes at the boundaries, which correspond to the polar regions, indicating that the quality of the derivatives might suffer from observation noise.

To check the consistency of the adopted differentiating schemes and to validate them, we simulated a signal including random jumps, observation gaps, and random noise. The signal was simulated by f(t)=sin ((100t)²) where t is measured in days. Gaussian noise with a standard deviation of 5 cm was selected. The number of jumps and the number of gaps was set to 40 and the locations were determined randomly. The jump sizes are given by a Gaussian random variable with a standard deviation of 5 m and the length of gaps in seconds is determined by a Poisson random variable with λ=100. The signal was chosen to be represented by a sinusoidal signal with frequencies changing as a function of time allowing to evaluate the performance of the differentiating scheme with frequency. In Fig. 6 we compare the following two cases. We compute the derivatives in the first case with an almost unsmoothed differentiating scheme using no Gaussian filter and only three points for the Savitzky–Golay filter, in contrast to the parameters mentioned above. If the smoothing is too weak, as one can see in the three-point case, the derivatives are very noisy. With the stronger smoothing one gets a dampening of the higher frequencies (approximately 10 %, 15 % and 25 % for the first, second and third derivative at 0.015 Hz), but in total the derivatives obtained represent the true derivative, as may be seen in Fig. 6. The gaps in the derivatives are given by artificial gaps in the data, but were further enlarged due to the minimum number of points restriction.

Figure 6 Tests on synthetic data. Red points show the true analytic noise-free derivative, green the computed derivatives from noisy data using the filter settings from Sect. 2.5 and blue points the three point derivative scheme. The noise in the second and third plot visible in the blue points exceeds the limit of the axis. The right side shows a zoom to compare the true derivative with the Gauss-SG filtered derivative.

3 Weighting of observations

3.1 AIUB standard screening

As a reference the AIUB standard screening is used, as published in Jäggi et al. (2016). It successfully removed the artifacts although the orbit quality was weakened and the number of ambiguities increased. Because it is a derivative-based approach, it can be used as a direct reference to our weighting solutions. In the AIUB standard screening the first time derivative of the geometry-free linear combination is computed without any smoothing using the half-difference of the previous and next epochs, which is equivalent to the three-point differentiating scheme shown in Sect. 2.5. Comparing this method to our differentiating scheme (compare Fig. 6), differences are visible, but both derivatives show similar amplitude and shape. If the absolute value of the first time derivative exceeded 2 cm s⁻¹, the observation was removed from the RINEX observations file. This introduces data gaps which are mostly responsible for the increased number of ambiguity parameters due to a very conservative setting up of new ambiguity parameters if data gaps are longer than 61 s. In cases where too many observations had to be removed, the kinematic positions could not be computed anymore.

3.2 Derivative-based weighting

In the derivative-based weighting schemes, we tested the first, second, and third time derivatives. As mentioned in Sect. 2.5, we use a combination of a Gaussian and a Savitzky–Golay filter. This additional effort is necessary due to the noise of L_GF. As shown in Sect. 2.5, already for the second time derivative using a classical three-point differentiation scheme, one would basically only see noise.

After numerically computing the time derivatives, we apply empirical thresholds. These thresholds were set by checking the amplitude of the derivatives, evaluating the performance on the gravity field level, and the threshold used by Jäggi et al. (2016). The thresholds were set to 2 cm s⁻¹ for $\left|\frac{\mathrm{d}{L}_{\mathrm{GF}}}{\mathrm{d}t}\right|$, 0.025 cm s⁻² for $\left|\frac{{\mathrm{d}}^{\mathrm{2}}{L}_{\mathrm{GF}}}{\mathrm{d}{t}^{\mathrm{2}}}\right|$ and 0.00075 cm s⁻³ for $\left|\frac{{\mathrm{d}}^{\mathrm{3}}{L}_{\mathrm{GF}}}{\mathrm{d}{t}^{\mathrm{3}}}\right|$.

If the time derivative at a certain epoch exceeds the threshold, an observation specific σ² of 21 mm² (standard σ²+20 mm²) is given to the observation instead of a standard unweighted σ² of 1 mm². This kind of extreme down-weighting is used to have a similar impact on the orbit as the standard screening, but because the observations stay in the RINEX observation file and also in the resulting normal equation system. No gaps and no additional ambiguities that would degrade the orbit are introduced. In case an observation epoch was too close to a gap or a jump and no derivative could be computed, the data point was down-weighted in addition assuming that the observation might be affected. The third time derivative suffers most from enlarged gaps due to non-computable derivatives. The gravity field recoveries based on correspondingly generated kinematic orbits turned out to be of inferior quality. For that reason, we focus on the first and second time derivative in the following sections.

For the first time derivative, we set the threshold to obtain similar results as with the AIUB standard screening to have a zero-test and to gain additional insight into the difference between screening and weighting. This is intended to directly assess the differences between screening and weighting.

3.3 ROTI-based weighting

The ROTI-based (Rate Of Total Electron Content (TEC) Index) weighting was used by Zehentner and Mayer-Gürr (2015) for the GOCE orbit processing where similar issues have been observed by Jäggi et al. (2015). ROTI is defined as

$$\begin{array}{}\text{(4)}& \mathrm{ROTI}=\sqrt{{\displaystyle \frac{\langle \mathrm{\Delta }{\mathrm{TEC}}^{\mathrm{2}}\rangle -\langle \mathrm{\Delta }\mathrm{TEC}{\rangle }^{\mathrm{2}}}{\mathrm{\Delta }{t}^{\mathrm{2}}}}}\end{array}$$

and is applied as a sliding window (Pi et al., 1997). The window size is set symmetrically with a width of 31 s. The differences to determine the ΔTEC were computed using the previous and the current epoch:

$$\begin{array}{}\text{(5)}& \mathrm{\Delta }\mathrm{TEC}\left(t_i\right)=\mathrm{TEC}\left(t_i\right)-\mathrm{TEC}\left(t_{i-\mathrm{1}}\right).\end{array}$$

In analogy to Sect. 3.2 points were down-weighted with a sigma square of 21 mm² if the number of data points was below a threshold of 10. For the ROTI approach, we tested two different scaling functions. First, we used the scaling function applied by Zehentner and Mayer-Gürr (2015) for GOCE which reads ${\mathit{\sigma }}^{\mathrm{2}}=max(\mathrm{1},\mathrm{20}\cdot \mathrm{ROTI})$ mm². This approach, however, turned out not to have an impact on the Swarm data. For our tests, we modified the weighting according to

$$\begin{array}{}\text{(6)}& {\mathit{\sigma }}_{\text{AIUB-ROTI}}^{\mathrm{2}}=max(\mathrm{1},\mathrm{60}\cdot \mathrm{ROTI}){\mathrm{mm}}^{\mathrm{2}}.\end{array}$$

Alternatively, Norbert Zehentner (personal communication, 2017) proposed for Swarm the following scaling function:

$$\begin{array}{}\text{(7)}& {\mathit{\sigma }}_{\text{GRAZ-ROTI}}^{\mathrm{2}}=\exp (\mathrm{20}\cdot \mathrm{ROTI}){\mathrm{mm}}^{\mathrm{2}}.\end{array}$$

In case the ROTI is small both approaches should return a σ² close to 1 mm². In case of high fluctuations, where ROTI becomes large, the second weights are much larger. The first set of weights will be referred to as AIUB-ROTI and the latter as Graz-ROTI. As one can see in Fig. 7 the ROTI weights are particularly pronounced in regions where the ionosphere-free phase residuals are large. ROTI turned out to be most effective in the polar regions due to the presence of plasma density fluctuations.

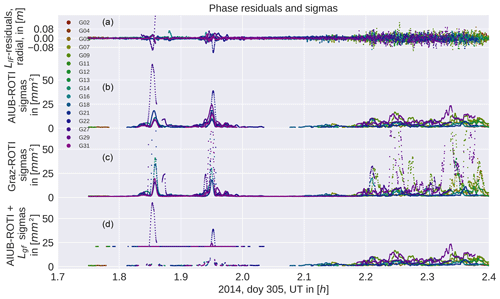
Figure 7 From (a) to (d): ionosphere-free phase residuals, AIUB-ROTI sigma squares, Graz-ROTI sigma squares, and AIUB-ROTI combined with the second derivative. Around 1.9 UT there is an equatorial pass and around 2.3 UT a polar pass. The ROTI sigma squares are larger at the polar region; the second derivative with a fixed sigma square (bottom) is only used near equatorial regions. Only sigma squares unequal to 1 mm² were plotted.

3.4 Geographical restriction of down-weighting

We are aiming to reduce the impact of the artifacts induced by the equatorial ionosphere on the gravity field models and consequently improve their quality. Some of our derivative-based approaches led to a degradation of the gravity fields in the polar regions as it will be shown in Sect. 4.2. To avoid this degradation we are limiting our derivative-based weighting to equatorial regions with a latitude between −50 and 50^∘ N. Due to the shape of the geomagnetic equator (which is located between roughly ±13^∘ latitude) and the equatorial ionization anomaly, which is located between −20 and 20 Mlat (Whalen, 2000), this covers all the equatorial ionosphere. For the ROTI approaches, no such limitation was performed due to the positive effect in the polar regions. The localized weighting will be referred to as equatorial (eq.).

3.5 Combination of methods

In the polar regions, the ROTI approach performs better; compare Fig. 8. The derivative-based approaches are more powerful in removing the equatorial artifact. Conclusively it is natural to combine both methods. Because the scaling function in case of the AIUB-ROTI provides less extreme weights, we decided to combine this one with the second derivative. This is achieved by taking the maximum of the AIUB-ROTI sigma square and the second derivative-based sigma square in the equatorial regions; compare Fig. 7.

4 Evaluation

4.1 Gravity field determination from kinematic positions

The celestial mechanics approach is used for gravity field determination as described in Jäggi et al. (2016, 2011a) and Beutler et al. (2010). In this procedure first 24 h arc a priori orbits are generated using the kinematic positions as pseudo-observations which are weighted epoch-wise using their formal covariance information. For the a priori orbits, the gravity field model EGM2008 and the ocean tide model FES2004 is applied. Empirical accelerations are used to compensate the non-gravitational forces. Swarm accelerometer data were not taken into account for the gravity field determination. The orbits are then expressed as truncated Taylor series including the empirical accelerations and the spherical harmonic coefficients of the gravity field. Daily normal equations (NEQ) are then set up, the empirical accelerations are pre-eliminated, and the daily NEQs are stacked in order to obtain monthly NEQ which eventually is inverted. By solving the NEQ corrections of the spherical harmonics coefficients with respect to the a priori gravity field are obtained. No regularization is applied in this article.

4.2 Swarm gravity field recovery

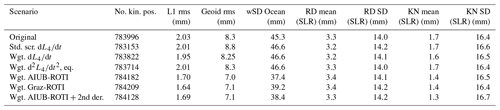
In order to validate our gravity field recovery results, we use the monthly JPL-GRACE-RL06 gravity field model as a reference field. Due to the ultra-precise K-band inter-satellite measurements, the GRACE gravity fields are of very high quality and essentially free from systematic ionospheric errors. GRACE GPS-only gravity fields are also free from systematic ionospheric errors, but in many observations are missing around the geomagnetic equation in the GRACE RINEX files (Jäggi et al., 2016, Fig. 12). In Fig. 8 (top left) we computed the geoid height differences between the JPL-GRACE-RL06 gravity field and a monthly Swarm GPS-only gravity field using the unweighted orbits. The differences were computed by taking the gravity fields up to degree and order 70 into account. The displayed month, March 2015, is heavily affected by the artifacts. The stripes around the geomagnetic equator are clearly visible with an amplitude of approximately 4 cm in geoid height when adopting a Gaussian filter radius of 400 km. In the case of the gravity fields obtained using the AIUB standard screening (top, right), these two bands have virtually disappeared.

As a first step, we compare the AIUB standard screening with the weighting based on the first derivative. This zero test shows similar performance as the standard AIUB screening, but especially in near Columbia and east of South America it seems to add some additional artifacts. Figure 13 explains the different behavior if we compare the number and location of the positions that were actually used for the gravity field recovery. The standard screening removes almost all positions in that specific area, in contrast to the weighting, where the positions are preserved, but minor artifacts appear instead.

We see that the second derivative has a similar performance when compared to the AIUB standard screening. In particular, the artifact in the Pacific region also vanished. In contrast to the standard screening, the noise seems slightly reduced, which may be seen in Fig. 8 and Tables 1 and 2 when comparing the geographically weighted rms of geoid height differences and the weighted standard deviation over the ocean. Using the second derivative with no geographical restrictions, we see some larger fluctuations around the polar regions. For this reason, we limit the second derivative-based weighting to the equatorial regions.

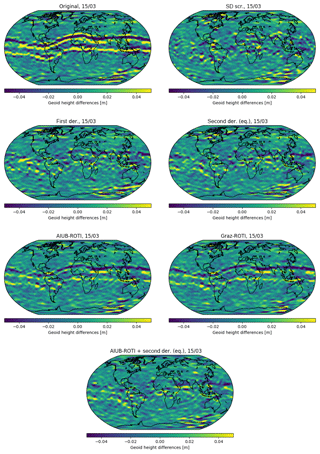
Figure 8 Geoid height differences between the monthly Swarm A gravity field to the corresponding JPL-GRACE-RL06 solution for March 2015. Gravity field differences were computed up to degree 70. The second derivative (eq.) based weighting was limited to the equatorial regions.

Table 1 Statistics and SLR residuals for Swarm A, March 2015.

Table 2 Statistics and SLR residuals for Swarm A, June 2016.

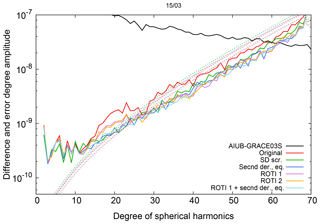
The ROTI approaches are not very successful in removing the two bands around the geomagnetic equator. In the polar regions, however, the ROTI-based gravity fields show reduced noise; see Fig. 8. The noise reduction of the ROTI approaches may be seen when comparing the geoid rms as well as the weighted standard deviation in Tables 1 and 2. This is supported by the difference degree amplitudes shown in Fig. 9. For degrees above 25, the difference degree amplitudes of both ROTI approaches are among the lowest. This implies that small-scale fluctuations are successfully reduced. A different result is obtained from the degrees between 15 and 25. In this spectral band, the performance of the derivative-based screening and weighting approaches clearly outperforms the ROTI solutions.

If one compares the AIUB screening to the second derivative, the AIUB screening shows a slightly better performance in the low degrees (<10), but in most of the higher degrees, the new approach shows a similar or even better performance. Eventually, we tested a combination of AIUB-ROTI and the second derivative limited to the Equator using the maximum sigma square of both approaches. The differences in the gravity field (see Fig. 8) still show some increased noise around the geomagnetic equator, but it is about the same level we had with the second derivative-based weighting. Especially in the region over Greenland, the gravity field benefits from the ROTI weighting. Looking again at the degree difference amplitudes, the light blue line is among the lowest for almost all degrees.

Figure 9 Difference (solid lines) and error (dashed lines) degree amplitude for monthly Swarm A gravity fields w.r.t. AIUB-GRACE03S, March 2015.

4.3 Weighted observations

It is our ambition to remove the equatorial artifact by down-weighting as few observations as possible. In the derivative-based cases we specified a clearly defined threshold which allows one to decide whether an observation needs to be down-weighted or not. However, the ROTI approach affects almost all epochs even if most of the weights are close to 1 mm². To evaluate how many epochs are heavily down-weighted, we, therefore, set thresholds to the ROTI derived weights to identify which observations are assigned strong weights. For representation purposes, we chose two different thresholds for ROTI-based weights: σ²>2 and σ²>5.

In Fig. 10 the percentage of weighted observations is illustrated in geomagnetic coordinates. Even though the first and second derivative-based weightings show similar performance, the weights based on the first derivative seem to act more specifically on the outer boundary of the ionization crests than the weights determined by the second time derivative. Using the second derivative is therefore beneficial if one assumes that the spikes in the kinematic positions are aligned with the sharp peaks in plasma density and are not on the flanks of the anomaly, which can be seen in Fig. 1. Evaluating the third time derivative one can see that a too large number of observations gets down-weighted. Almost every observation around the pole is affected if no limitation to the equatorial region is applied.

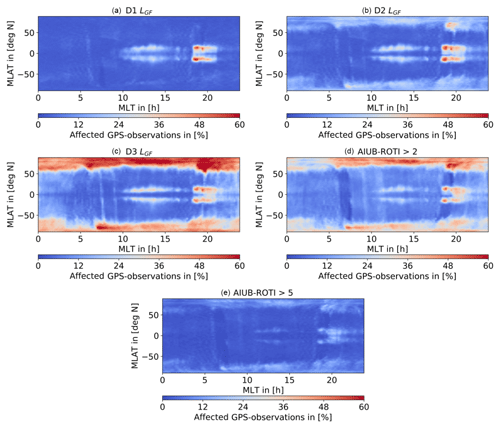
Figure 10 Percentage of weighted raw GPS measurements for the analyzed test period; 2015: January, March; 2016: February, March, June, July, August, binned to the corresponding LEO position. (a, b) D1 L_GF (a), D2 L_GF (b), (c, d) D3 L_GF (c), ROTI>2 (d), and (e) ROTI>5. Bin size 1^∘ Mlat×0.2 h MLT.

The ROTI weighting approach is, however, much more sensitive to fluctuations in the geometry-free linear combination as they occur on the poles or due to equatorial plasma bubbles, but it is not as successful in removing the equatorial artifact. If one compares the ratio of weighted observations in Fig. 10 for ${\mathit{\sigma }}_{\text{AIUB-ROTI}}^{\mathrm{2}}>\mathrm{2}$ (middle right) and ${\mathit{\sigma }}_{\text{AIUB-ROTI}}^{\mathrm{2}}>\mathrm{5}$ (bottom), the amount of weighted observations in the polar regions decreases significantly when the threshold is increased. This implies that for most observations only small sigma squares are applied. This explains why the dynamic ROTI weighting shows such a good performance around the poles. It is able to identify noisy observations and therefore reduce high-frequency noise in the gravity field solutions. The ROTI information is, therefore, to be used as a potential descriptor of the stochastic model of the GPS observations used for the positioning. Unfortunately, the systematically biased positions in the equatorial regions cannot reliably be identified by a high ROTI value. This may be seen in Fig. 10 when comparing the plots in the top row to the plot at the bottom.

Again, a benefit from using the second derivative instead of the first derivative may be seen. The number of weighted/screened positions is similar, but the difference and error degree amplitudes are reduced, especially in the higher degrees; see Fig. 9. Also, the geoid rms is reduced by 1.1 mm for March 2015, which is a heavily affected month; see Table 1.

4.4 Orbit

When analyzing the orbits, we see that the differences between kinematic and reduced-dynamic positions (see Fig. 11) are almost unaffected by the weighting. The spikes are still present even though their covariance information has changed as will be shown in Sect. 4.4 and 4.5. Low-frequency differences are introduced due to differently estimated empirical accelerations which are caused by down-weighting the problematic observations in the least-squares adjustment. This may be illustrated in particular by comparing the differences of the reduced-dynamic orbits to the unweighted reference; see Fig. 12 (left). The comparison reveals low-frequency differences of up to 1 cm amplitude for the ROTI-based approaches. Analyzing the kinematic positions on the right-hand side, one can see big differences around the polar regions and in the equatorial regions, too, of up to 10 cm. Such large differences are, however, only visible for very few epochs. In all four cases presented the differences are spatially very localized. Considering the Graz-ROTI weighting, one can see a jump in the radial component and the along track component in the kinematic positions. This is an indicator that the sigma squares introduced by the scaling function are too large. Such jumps also occur at other epochs for the Graz-ROTI, but in a few cases, they also occur in other weighting strategies when large sigma squares are applied.

In all the other cases, the differences, especially between the kinematic positions, are very small in between the polar regions and the equatorial anomaly.

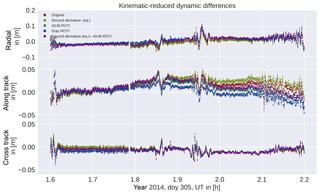
Figure 11 Kinematic minus reduced-dynamic positions in radial, along-track, and cross-track directions. For both kinematic and reduced-dynamic positions, the same weighting was applied.

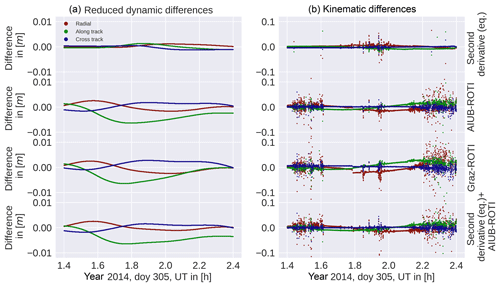
Figure 12 Differences between the unweighted positions of reduced-dynamic (a) and kinematic (b) orbits. All orbits were compared to the unweighted case. The second derivative-based weighting was limited to the equatorial region (eq.).

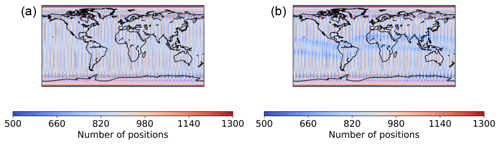
Figure 13 Number of kinematic positions for the analyzed test period. 2015: January, March; 2016: February, March, June, July, August, unscreened (a) and with AIUB standard screening (b). Binned in a 1^∘ × 1^∘ grid.

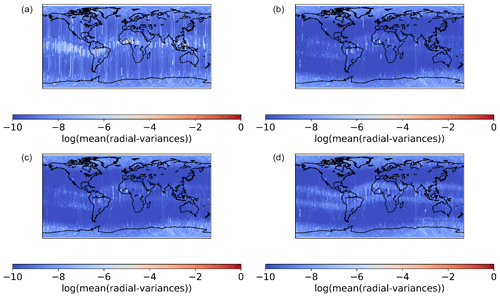
Figure 14 Radial variances for the analyzed test period, global. (a, b) AIUB standard screening (a) and AIUB-ROTI (b); (c, d) Graz-ROTI (c) and second derivative limited to the equatorial region (eq.) + AIUB-ROTI (d). The clearly visible ground track (a) is due to a large rms for Swarm A, 29 March 2015.

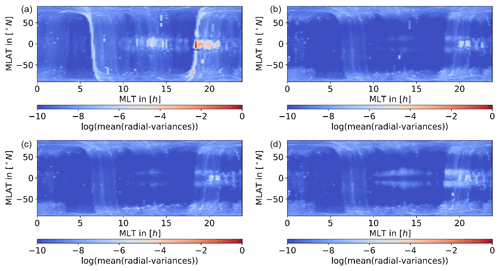
4.5 Covariances

The gravity field is not only determined by the used kinematic positions (pseudo-observations), but also by the adopted weights of the kinematic positions derived from their covariance information. To demonstrate how differently the weighting schemes affect the covariance information of the kinematic positions, we analyze the covariances of the kinematic positions as a function of their geographic and geomagnetic locations, respectively. The information was binned (1^∘ lat × 1^∘ lon for geographic coordinates and 1^∘ Mlat × 0.2 h MLT) and the mean of the radial variances (see Sect. 2.3) was computed. For better visibility, the logarithm of that mean was taken. As one can see that for the AIUB standard screening high radial variances are a single band along the geomagnetic equator, compare Figs. 14 and 15 top, left. A ground track is visible in the radial variances. This is connected to the Swarm A orbit on 20 March 2015. On this day the L1 rms of the kinematic orbit is 0.022108 m, which is approximately 10 times the usual rms. This is due to many screened observations and in turn short observation pieces. For comparison: using the second derivative weighting in addition to the AIUB-ROTI for the same day, the L1 rms is 0.001478 m. The other positions below and above the Equator do not show high covariances, but the number of positions is significantly decreased, as Fig. 13 illustrates. Between the two bands, the geometry of the observations is weakened, resulting in high variances. In the two bands, too many observations are affected by the screening, resulting in a significant loss of positions. For the combined weighting approach, we see two bands around the geomagnetic equator; compare with Figs. 14 and 15, bottom right. The positions between the two bands are of significantly better quality than the positions obtained using AIUB standard screening. As mentioned for the ROTI approaches, the highest variances result for areas of fluctuations such as the poles and equatorial regions around 18–22 h MLT, which are well known for equatorial plasma bubbles. This may be well recognized when plotting the covariances in geomagnetic coordinates (Fig. 15). Using the second derivative in addition to the ROTI (bottom right) results in higher covariances in the two bands around the geomagnetic equator; also, higher covariances in earlier MLT may be recognized. This illustrates the different sensitivities of the two approaches.

Figure 15 Radial variances in magnetic coordinates. (a, b) AIUB standard screening (a) and AIUB-ROTI (b); (c, d) Graz-ROTI (c) and second derivative limited to the equatorial region (eq.) + AIUB-ROTI (d).

4.6 Validation

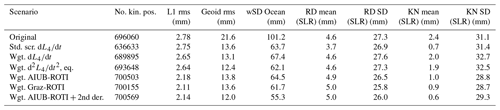
For an independent validation of the obtained orbits, we use satellite laser ranging (SLR) measurements and compute the differences between the SLR measurement and the GPS-based computed distances. As SLR stations, high-quality stations Graz (GRZL), Greenbelt (GODL), Haleakala (HA4T), Hartebeesthoek (HARL), Herstmonceaux (HERL), Matera (MATM), Mt Stromlo (STL3), Potsdam (POT3), Wettzell (SOSW), Wettzell (WETL), Yarragadee (YARL), and Zimmerwald (ZIML) are selected following the approach of Jäggi et al. (2016). An outlier threshold of 20 cm and an elevation cutoff of 10^∘ were applied. For March 2015 approximately 1400 normal points and for June 2016 1300 normal points are available. As additional criteria we use the L1-phase rms of the gravity field adjustment, the cos of latitude weighted rms of the geoid height differences with respect to a superior solution based on ultra-precise GRACE K-band measurements, and the cos of latitude weighted standard deviation above the ocean (Meyer et al., 2012); see Tables 1 and 2. It is interesting that we could preserve more positions in the ROTI weighted cases than in the case without weighting, now being kept with lower weight. The geoid rms of the gravity field solutions using unscreened and screened GPS observations is at the same level as the values published in Dahle et al. (2017). In the weighted scenarios for March 2015, the geoid rms is reduced when using the second derivative for weighting or when combining the second derivative derived weights with the AIUB-ROTI derived weights. For June 2016, the second derivative derived based weights lead to no difference in geoid rms. For this month, we obtain the smallest geoid rms when using ROTI derived weights. For both months, the geoid rms obtained when using the combination of the AIUB-ROTI derived weights and the second derivative derived weights is among the lowest. The ROTI approaches again tend to reduce the noise, which may be seen in the reduction of the geoid rms even if the geoid rms for March 2015 is slightly bigger compared to the second derivative. This might be due to the still existing artifacts around the geomagnetic equator. The fact that this improves significantly by combining the AIUB-ROTI with the second derivative supports this assumption. The same effect is visible for the weighted standard deviation above the oceans.

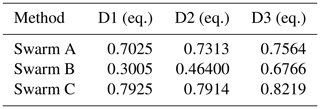
Table 3 Correlation coefficient between the relative number of weighted observations and the F10.7 index.

Regarding SLR, the mean offsets, as well as the standard deviations for the reduced-dynamic orbits, stay on a similar level. For the kinematic orbits, the mean and SLR standard deviations show a slight improvement if the ROTI approach is used.

In June 2016 the validation improves, but the orbits in June 2016 are not that much affected by the ionospheric activity. This is due to the less critical local times and a reduced F10.7 index which indicates less ionospheric activity; compare with Fig. 10 and Table 4. But even in that case, the ROTI approaches seem to be capable to improve the mean of the SLR residuals for the kinematic positions.

Figure 16 Percentage of screened position in comparison to the F10.7 and Kp indices.

Table 4 Local time at the middle of the month.

4.7 Weighted observations and F10.7/Kp index

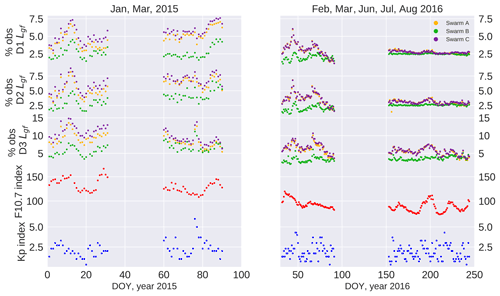
As shown by Jäggi et al. (2016) the amount of screened, or in our case weighted, observations depends on the ionospheric activity. The authors used the TEC to demonstrate this. In our study we compare the number of weighted observation to the F10.7 index as well as the Kp index. The first one is an indicator for the ionization, whereas the second is an indicator for the geomagnetic activity. As shown by Stolle et al. (2006), the probability of an equatorial plasma bubble is positively correlated with the F10.7 index. Equatorial plasma bubbles usually occur when there is high activity in the ionosphere. Previous studies connect bubbles to a strong vertical pre-reversal enhancement, fast changes in plasma density, an unstable E–F boundary, and strong gradients (Whalen, 2000; Kelley, 1989a; Stolle et al., 2006). This is, of course, harmful to the quality of GPS data, as one can see in Fig. 3 (left), where especially the bubble region shows high variances. So we expect a correlation between the F10.7 index and the number of weighted observations.

Secondly, the Kp index represents the disturbances in the geomagnetic field. Because the motion of ionospheric plasma is connected to the magnetic field (Kelley, 1989b), disturbances in the magnetic field may result again in errors in kinematic positioning. So we expect again a high number of affected observations under storm conditions. These comparisons are illustrated in Fig. 16. To avoid contamination due to the polar regions, we limit all three data sets to the equatorial regions (lat < 50^∘). The largest daily averaged Kp index in our time series is 6 on day 2015-076 (17 March 2015). On this day, there was a severe magnetic storm (class G4) with Kp up to 8. Especially in the second and third time derivative-based weightings, one can see a clear increase in the relative number of affected epochs. Most probably this is related to increased ionospheric fluctuations as they occur in storm conditions. In total, the percentage of weighted observations shows similar behavior to the F10.7 index. Some differences can be explained by the local time dependence. In total, as one can see in Table 3, the correlation between the percentage of weighted observations and the F10.7 index is quite strong (above 0.7) for Swarm A and Swarm C, but a lot weaker for Swarm B. The reason might be the higher altitude of Swarm B which leads to fewer free electrons and weaker gradients in the ray paths to the GPS satellites. In addition, Swarm B passes on different local times. In March 2015 the local times are comparable, resulting in very similar behavior (see Fig. 16). Towards the last months (July and August 2016), the local time of Swarm B is significantly different from the critical local times (18–2 h MLT), but in the same months Swarm A and Swarm C are inside the critical local times. Here we can clearly see the peak of the F10.7 index around day 200 in the percentage of weighted observations for Swarm A and Swarm C, but no signature is visible for Swarm B.

5 Conclusions

We showed that systematic errors up to 10 cm in difference between kinematic positions and a reduced-dynamic orbit are associated with sharp peaks in the plasma density. These errors propagate into the gravity field solutions derived from kinematic positions. When validating the monthly Swarm GPS-only gravity field solution to the corresponding JPL-GRACE-RL06 solution, band shaped residuals up to 4 cm in geoid height become visible. Furthermore, we showed that these systematics are associated with large phase residuals of 4–6 cm and can be identified using time derivatives of the geometry-free linear combination. Based on these time derivatives we developed weighting criteria and used already existing techniques such as the ROTI approach and the AIUB standard screening. We found that the second derivative-based weighting is very efficient in removing the artifacts around the geomagnetic equator. The ROTI approach improved the gravity fields in the polar regions. Eventually, we evaluated the different screening approaches and combined the ROTI approach with the derivative-based weighting to an even more effective approach. The improvement of the orbits is visible in the gravity fields as well as in the SLR residuals. For a heavily affected month (March 2015), the geoid rms was improved from 21.6 to 12.0 mm and the standard deviation of SLR residuals for the kinematic orbits was improved from 31.1 to 29.3 mm. How differently the weighting strategies apply to the observations is also visible in the covariance information of the kinematic positions. In turn, this covariance information is essential to improve the gravity field solutions. The number of weighted observations, especially in the derivative-based cases, has a significant correlation coefficient, between 0.70 and 0.82, with the F10.7 index representing the ionospheric activity, which is consistent with previous studies (Jäggi et al., 2016; Xiong et al., 2016).