“Diffusion” region of magnetic reconnection: electron orbits and the phase space mixing

The nonlinear dynamics of electrons in the vicinity of magnetic field neutral lines during magnetic reconnection, deep inside the “diffusion” region where the electron motion is nonadiabatic, has been numerically analyzed. Test particle orbits are examined in that vicinity, for a prescribed planar two-dimensional magnetic field configuration and with a prescribed uniform electric field in the neutral line direction. On electron orbits, a strong particle acceleration occurs due to the reconnection electric field. Local instability of orbits in the neighborhood of the neutral line is pointed out. It combines with finiteness of orbits due to particle trapping by the magnetic field, and this should lead to the effect of mixing in the phase space, and the appearance of dynamical chaos. The latter may presumably be viewed as a mechanism producing finite “conductivity” in collisionless plasma near the neutral line. That conductivity is necessary to provide violation of the magnetic field frozen-in condition, i.e., for magnetic reconnection to occur in that region.

Keywords. Magnetospheric physics (plasma sheet)

1 Introduction

The problem of magnetic reconnection in the vicinity of the neutral line for collisionless plasma has an extremely extensive literature; see, for example, the special issue of Space Science Reviews 2011 and the work (Hesse et al., 2011) and references therein. According to the prevailing ideas, the reconnection process proper occurs in the central part of a current sheet (CS) separating the regions with oppositely directed magnetic field, and is provided by processes on a very small electronic scale in the direction z perpendicular to the CS, where the role of finite conductivity in the generalized Ohm's law assumes the effect of the nongyrotropic component of the electron momentum flux (“pressure”) associated with the unmagnetized electron orbits on those small scales (Kuznetsova et al., 2001). The fields and fluxes of ions and electrons in the greater part of the “diffusion” region, at scales z of the order of the ion inertial length d_i, $z\sim d_{\mathrm{i}}=c/{\mathit{\omega }}_{\mathrm{pi}}$ (c is the speed of light, ${\mathit{\omega }}_{\mathrm{pi}}=\sqrt{\mathrm{4}\mathit{\pi }{n}_{\mathrm{i}}{e}^{\mathrm{2}}/m_{\mathrm{i}}}$ is the ion plasma frequency), but outside a very small region, where even the electrons cease to be magnetized and the nongyrotropic component of the electron momentum flux (“pressure”) appears, may be described in the Hall MHD terms. The scale of the “diffusion” region in the direction of plasma outflow (along the x direction parallel to the CS and lying in the magnetic field plane) and, correspondingly, the reconnection rate, are determined by the inflowing convection velocity times the reconnecting (B_x) component of the magnetic field. And those are “tied” into equations describing the system macroscopically. Such adjustment of the processes in the vicinity of the neutral line to external conditions occurs at two different levels, ionic and electronic. On a larger scale, in most of the “diffusion” region, for z∼d_i, the fields and fluxes of ions and electrons, as has been mentioned, are determined by the Hall MHD equations. At the smallest scale, in a region where the electrons are not magnetized and the electron pressure is nongyrotropic, the electron flux profile along the x direction is adjusted in such a way that the nongyrotropic electron pressure component is just sufficient to maintain the electric field that sets the reconnection rate on the neutral line, but is determined by the macroscopic flow.

By numerical simulation in models of different types it was found that the behavior of the system in the larger Hall region is quite similar for different types and intensity of dissipation in the smaller inner region. Moreover, the reconnection rate itself is insensitive to the nature and intensity of the dissipation (Hesse et al., 2001; Liu et al., 2017). A fairly simple qualitative explanation can be given to that. It turns out that the outflow of the electron fluid from the inner (dissipation) region has the character of a strong standing whistler wave. The phase velocity of the whistler ω∕k with which the outflow occurs is inversely proportional to the spatial scale, $\mathit{\omega }/k\sim k\sim \mathrm{1}/L$. This means that the electron flux from the dissipation region, which determines the magnetic reconnection rate, being the product of the velocity and thickness of the layer ∼L, is independent of this thickness. But it is just this scale that is regulated by the intensity of the dissipative effect: the resistivity η in the collisional case or the value of the nongyrotropic electron pressure in the collisionless one. Thus the layer structure adjusts to the magnetic reconnection rate, but does not affect it.

Note, however, that such a situation does not mean that the real nature of electron dynamics and corresponding features of electron orbits, which lie at its basis, may be thought insignificant.

Outside the diffusion region, the process of “magnetic annihilation” – the transformation of electromagnetic energy into the energy of plasma flows, meaning magnetic reconnection in the wider sense, is determined by ion motions, including those that are substantially nonadiabatic in thin layers adjacent to the diffusion region. As was pointed out in Domrin and Kropotkin (2007a, b, c), Kropotkin and Domrin (2009), and Kropotkin (2013), in that region the process is dominated by an “anisotropic” CS, the structure of which is determined by the specific ion orbits. This leads to ion anisotropy of a certain type, dependent on the distance from the central plane. However, inside the diffusion region the process of magnetic reconnection requires an “intermediary”, an additional link. This is the abovementioned Hall MHD structure, based on specific differences between the electron and ion orbits. And finally, deep inside this layer, in the nearest neighborhood of the neutral line, unmagnetized electron orbits determine the dynamics and structure of the reconnecting CS.

It is precisely the specific nature of such orbits, which in previous studies has remained mostly unidentified in a proper perspective, that this paper is devoted to. Basically, the numerical approach applied in this paper differs only weakly from that adopted in a number of earlier studies (Martin, 1986; Burkhart et al., 1991, and references therein). Moreover, the chaotic particle dynamics were then identified numerically by means of Lyapunov characteristic exponent analysis. However, the insight which appeared since that time, concerning the role of the electron zone in the “diffusion region”, on the one hand, and penetration of the nonlinear dynamics and dynamical chaos notions into this research area, on the other hand, has laid the way to a number of new results.

In this paper, the nonlinear dynamics of electrons moving in a magnetic field near its neutral line and in an electric field corresponding to the inflow of plasma into the reconnection zone has been studied numerically in a wide range of determining parameters (Sect. 2). Of course, these dynamics do not obey the adiabatic theory; its important property is a strong particle acceleration near the field neutral line. Another important feature of particle dynamics near the neutral line is pointed out in Sect. 3. Analysis of an equation governing such dynamics, involving the numerical results of Sect. 2, indicates an exponential divergence of orbits starting closely nearby. This feature of local instability, along with finiteness of the orbits in the phase space, in the general theory of nonlinear dynamical systems, should result in the appearance of stochastization, i.e., of dynamical chaos in the system. This is discussed in Sect. 4 in terms of the phenomenon of mixing in the phase space and formation of the collisionless energy dissipation mechanism. In this way we obtain a corroboration on the side of microscopic dynamics that the diffusion region should have a dissipation property in the macroscopic sense, i.e., provide the transformation of electromagnetic energy (a nonzero Poynting vector in the inflow region) into energy of accelerated particles.

2 Electron orbits: numerical simulation

We study test particle orbits in a prescribed field configuration. We use a two-dimensional model of magnetic field B(x,z) with a neutral line, $\mathit{B}(\mathrm{0},\mathrm{0})=\mathrm{0}$:

$$B_x=qbz;B_y=\mathrm{0};B_z={\displaystyle \frac{b}{\mathit{\kappa }}}\mathrm{arct}g\left(\mathit{\kappa }x\right).$$

Here the parameter q≥1 determines the opening angle, i.e., the angle between the separatrices dividing the magnetic fluxes near the neutral line, and also the value of a finite current density in the y direction, $j_y=cb\left[q-{\left(\mathrm{1}+{\mathit{\kappa }}^{\mathrm{2}}{x}^{\mathrm{2}}\right)}^{-\mathrm{1}/\mathrm{2}}\right]/\mathrm{4}\mathit{\pi }$. The normal component B_z goes to a constant for large values of x. In the calculations, dimensionless variables ($\mathit{\xi },\mathit{\eta },\mathit{\zeta },\mathit{\tau }$) are used:

$$x={\displaystyle \frac{mc}{Teb}}\mathit{\xi };y={\displaystyle \frac{mc}{Teb}}\mathit{\eta };z={\displaystyle \frac{mc}{Teb}}\mathit{\varsigma };t=T\mathit{\tau },$$

e and m being the electron charge and mass, respectively. Here T is an arbitrary timescale, which we choose based on the requirement of the best visibility in the presentation of results; see below. We also introduce the dimensionless parameter $k=\frac{Teb}{mc}\mathit{\kappa }$. In what follows, for convenience, we rename the variables ($\mathit{\xi },\mathit{\eta },\mathit{\zeta },\mathit{\tau }$) back to $\left(x,y,z,t\right)$, and k back to κ; then in dimensionless variables we have the equations of motion:

$$\begin{array}{}\text{(1)}& \begin{array}{l}\ddot{x}-{\displaystyle \frac{\mathrm{arct}g\left(\mathit{\kappa }x\right)}{\mathit{\kappa }}}\dot{y}=\mathrm{0};\\ \ddot{y}+{\displaystyle \frac{\mathrm{arct}g\left(\mathit{\kappa }x\right)}{\mathit{\kappa }}}\dot{x}-qz\dot{z}-\mathit{\epsilon }=\mathrm{0};\\ \ddot{z}+qz\dot{y}=\mathrm{0}.\end{array}\end{array}$$

Here

$$\begin{array}{}\text{(2)}& \mathit{\epsilon }=T^{\mathrm{3}}{\displaystyle \frac{e^{\mathrm{2}}b}{m^{\mathrm{2}}c}}{E}_{\mathrm{0}}\end{array}$$

is a dimensionless analog of the value $\frac{e}{m}{E}_{\mathrm{0}}$, where E₀=const is the intensity of the electric field directed along y. (At small z and x(0)→0 the motion along y occurs mainly under action of an accelerating force eE₀ so that $\mathrm{d}y/\mathrm{d}t\sim e{E}_{\mathrm{0}}t/m$. We obtain as a result that the equation $\frac{d^{\mathrm{2}}z}{\mathrm{d}{t}^{\mathrm{2}}}+\frac{eb}{mc}qz\frac{\mathrm{d}y}{\mathrm{d}t}=\mathrm{0}$ describes oscillations over z with their frequency square given approximately by the formula ${\mathit{\omega }}^{\mathrm{2}}=e^{\mathrm{2}}bq{E}_{\mathrm{0}}t/m^{\mathrm{2}}c$. Therefore, requiring that in the time interval T of the equation set integration, there should be many oscillations, and we obtain the condition $\mathit{\epsilon }={\mathit{\omega }}^{\mathrm{2}}{T}^{\mathrm{2}}=e^{\mathrm{2}}bq{E}_{\mathrm{0}}{T}^{\mathrm{3}}/m^{\mathrm{2}}c\gg \mathrm{1}$. As to the magnitude $\stackrel{\mathrm{̃}}{z}$ of oscillations, we have $\stackrel{\mathrm{̃}}{z}\sim v_z/\mathit{\omega }$. The value of velocity v_z at the beginning of the oscillation regime is given by an estimate $v_z\sim c{E}_{\mathrm{0}}/B_x\sim c{E}_{\mathrm{0}}/\mathrm{2}bz$. It follows that ${\stackrel{\mathrm{̃}}{z}}^{\mathrm{2}}\sim \frac{c{E}_{\mathrm{0}}}{\mathrm{2}b\mathit{\omega }}=\frac{m^{\mathrm{2}}{c}^{\mathrm{2}}}{\mathrm{2}q{e}^{\mathrm{2}}{b}^{\mathrm{2}}{T}^{\mathrm{2}}}\sqrt{\mathit{\epsilon }}$, and for the dimensionless magnitude we have an estimate ${\stackrel{\mathrm{̃}}{\mathit{\varsigma }}}^{\mathrm{2}}={\left(ebT/mc\right)}^{\mathrm{2}}{\stackrel{\mathrm{̃}}{z}}^{\mathrm{2}}=\sqrt{\mathit{\epsilon }}/\mathrm{2}q$. It is seen that taking the ε value to be quite large we can obtain a demonstrable representation of the system dynamics at small x(0), at those times when the particle arrives in close vicinity of the magnetic field neutral line.)

Equations (1) must be supplemented by initial conditions, i.e., by setting the values x(0), y(0), z(0), $\dot{x}\left(\mathrm{0}\right)$, $\dot{y}\left(\mathrm{0}\right)$, $\dot{z}\left(\mathrm{0}\right)$. In the planar geometry, without loss of generality we assume y(0)=0.

We have studied a set of possible orbits over a wide range of parameters, including the values κ, q, ε and initial values of coordinates and velocities. To illustrate the typical results here, we have chosen the values of the magnetic field parameters $\mathit{\kappa }=\mathrm{0.002},q=\mathrm{2}$.

In the simplest situation, it can be assumed that a flow of plasma with cold electrons arrives at the CS. Then, if an electron starts somewhere away from the CS, it must be postulated that its velocity v^′(0) in the local reference frame (that moving with the plasma bulk velocity) is zero. Thus we have two conditions: ${\mathit{E}}_{\mathrm{0}}+\left[\mathit{v}\left(\mathrm{0}\right)\times \mathit{B}\left(\mathrm{0}\right)\right]/c=\mathrm{0}$, and (v(0)B(0))=0. In the dimensionless variables this leads to the following relations:

$$\begin{array}{}\text{(3)}& \begin{array}{l}\dot{x}\left(\mathrm{0}\right)={\displaystyle \frac{\mathrm{arct}g\left(\mathit{\kappa }x\left(\mathrm{0}\right)\right)}{\mathit{\kappa }}}{\displaystyle \frac{\mathit{\epsilon }}{q^{\mathrm{2}}{z}^{\mathrm{2}}\left(\mathrm{0}\right)+{\mathrm{arctg}}^{\mathrm{2}}\left(\mathit{\kappa }x\left(\mathrm{0}\right)\right)/{\mathit{\kappa }}^{\mathrm{2}}}};\\ \dot{y}\left(\mathrm{0}\right)=\mathrm{0};\\ \dot{z}\left(\mathrm{0}\right)=-qz\left(\mathrm{0}\right){\displaystyle \frac{\mathit{\epsilon }}{q^{\mathrm{2}}{z}^{\mathrm{2}}\left(\mathrm{0}\right)+\mathrm{arct}{g}^{\mathrm{2}}\left(\mathit{\kappa }x\left(\mathrm{0}\right)\right)/{\mathit{\kappa }}^{\mathrm{2}}}}.\end{array}\end{array}$$

For this simplest situation, it can be easily seen how the dimensionless parameters that determine the orbit of interest should be chosen. Since we will further investigate the dependence of the orbit features on the initial value x(0) starting with x(0)=0, there is actually only a pair of such dimensionless parameters, z(0) and  ε. For an arbitrary timescale T, it is to be assumed that the time a particle takes to reach the plane z(0)=0 must be much less than this scale: $z\left(\mathrm{0}\right)/\frac{c{E}_{\mathrm{0}}}{bz\left(\mathrm{0}\right)}\ll T$ (here z(0) has the original meaning, with the dimension of length). Then, taking into account Eq. (2) and using our reverse renaming of variables, the condition  ε≫z²(0) is obtained. Accordingly, we shall first consider the electron orbits at  ε=50 000 and specifying the initial value of the coordinate z(0)=50.

For solution of the Equation set (1) with corresponding initial conditions and for graphical presentation of results, the Wolfram Mathematica package has been used. Accuracy of the codes applied in Mathematica calculations was of course adequately verified by the Wolfram team long ago; it is quite sufficient for the presented graphics. In our work, in some cases that accuracy has been tested by means of varying the parameters used.

First of all, let us turn to the case x(0)=0. According to Eq. (3) we have $\dot{x}\left(\mathrm{0}\right)=\mathrm{0}$, and it is clear that the orbit remains in the plane x=0, while in the y direction an unlimited acceleration takes place. The corresponding time profile z(t) is shown in Fig. 1a. Apparently, this is a “Speiser” orbit oscillating near the neutral layer, complicated by acceleration in the electric field $E_y=E_{\mathrm{0}}=\mathrm{const}$. This acceleration occurs at an almost constant rate from the moment t_c when the particle reaches the neighborhood of the neutral line, as can be seen from Fig. 1b. Acceleration is unlimited in time.

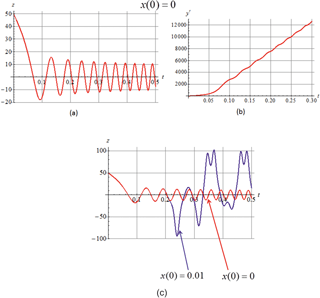
Figure 1 (a) Oscillations over z at x(0)=0. (b) Time dependence of the velocity $\dot{y}\left(t\right)$ at x(0)=0. (c) Comparison of the initial time dependence z(t) for x(0)=0 (red curve) and x(0)=0.01 (blue curve).

Now consider the results of numerical calculations relating to how the electron orbits in general look and how their character changes when the initial conditions change. From a large number of calculations performed, here we illustrate several characteristic series.

Consider in more detail the orbits discussed above: we set again ε=50 000 and  z(0)=50, and let the initial displacement x from the plane x=0 be very small, x(0)=0.01.

An initial course of the z(t) function is shown in Fig. 1c, for the starting case x(0)=0 (red curve) and for x(0)=0.01 (blue curve). The initial motion to the z=0 plane and the first meandering “Speiser” oscillations in these two cases are indistinguishable. But then we see a sharp departure of a particle from the “Speiser” orbit; the oscillation pattern completely changes. This may be generally viewed as manifestation of local instability in the phase space, as we discuss below, in Sect. 3.

The orbit for x(0)=0.01 in projection onto the (x,z) plane is shown in Fig. 2a, in projection onto the (y,z) plane in Fig. 2b, and in projection onto the (x,y) plane in Fig. 2c. Here we see an initial fast drift motion of a particle toward the neighborhood of the neutral line, without shifting along the x and y directions. Then the particle moves along the “Speiser” section of the orbit, oscillating in the z direction and crossing the z=0 plane many times, and simultaneously shifting along the x and y directions. Having reached nearly $x\simeq \mathrm{150},y\simeq \mathrm{600}$ position, the particle again sharply changes the motion pattern: oscillations begin along the field lines, with a fast Larmor rotation around them, with reflection from mirror points, and with a relatively slow motion from one field line to another, i.e., the drift in the electric field and in the nonuniform and curved magnetic field. (This of course is just a qualitative description in the familiar terms of magnetic trapping in the mirror field configuration; no adiabaticity concept is in general applicable here.)

Having presented in Fig. 2d a plot of time dependence for the particle kinetic energy $m\left[{\dot{x}}^{\mathrm{2}}\left(t\right)+{\dot{y}}^{\mathrm{2}}\left(t\right)+{\dot{z}}^{\mathrm{2}}\left(t\right)\right]/\mathrm{2}$ (in arbitrary units), we see that at first, when the particle moves to the z=0 plane, this energy remains small, and then the particle is very quickly accelerated by the electric field E₀ on the “Speiser” section of the orbit, and after this the energy remains almost constant, only slightly increasing with each new intersection of the z=0 plane. The fast acceleration occurring on the “Speiser” portion of the orbit is now limited in time, in contrast to the case x(0)=0.

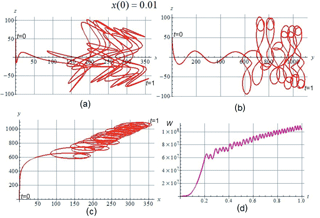
Figure 2 The orbit pattern at x(0)=0.01: (a) projected to the (x,z) plane, (b) projected to the (y,z) plane, (c) projected to the (x,y) plane. (d) Time dependence of the kinetic energy.

The orbits of electrons that are “cold” at the start retain a similar character up to the values x(0)∼1. However, for larger x(0) values, the situation changes significantly. We present for comparison the corresponding plots for the x(0)=10 case. The orbit in projection onto the (x,z) plane is shown in Fig. 3a, in projection onto the (y,z) plane in Fig. 3b, and in projection onto the (x,y) plane in Fig. 3c. Figure 3d demonstrates the time dependence of the kinetic energy. It is seen that there is no “Speiser” section here, but the orbit remains finite over z, oscillating between the reflection points, with a gradual energy gain. At the first intersection of the z=0 plane, a particularly fast acceleration occurs.

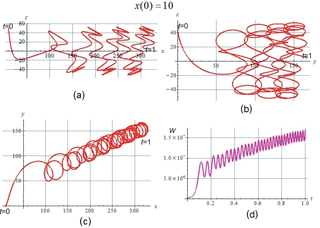
Figure 3 The orbit pattern at x(0)=10: (a) projected to the (x,z) plane, (b) projected to the (y,z) plane, (c) projected to the (x,y) plane. (d) Time dependence of the kinetic energy.

With an even greater initial distance from the x=0 plane, x(0)=100, the orbit has again a pattern different from the previous ones. The corresponding plots are shown in Fig. 4a–c. Here the orbit crosses the z=0 plane only once, and then leaves it winding around a field line; this is accompanied by slow drift motions in the direction transverse to that of magnetic field in the central plane. Acceleration occurs only at this one-time intersection, and the kinetic energy achieved is much less than in the previous calculations, where acceleration occurs during multiple intersections of the z=0 plane; see the plot in Fig. 4d.

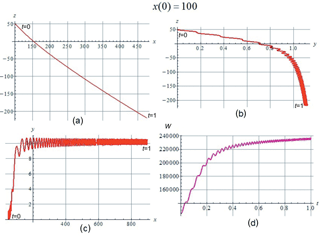
Figure 4 The orbit pattern at x(0)=100: (a) projected to the (x,z) plane, (b) projected to the (y,z) plane, (c) projected to the (x,y) plane. (d) Time dependence of the kinetic energy.

When specifying nonzero initial speeds ${\mathit{v}}^{\prime }\ne \mathrm{0}$ in the local frame moving with the plasma bulk velocity, orbits appear that do not intersect the z=0 plane at all, and there is no acceleration. This behavior corresponds to the familiar pattern of electric drift in the vicinity of the neutral line, and arises with a small oscillatory component of the particle velocity characteristic of “cold” electrons: the electric drift forms particle orbits along hyperbolas orthogonal to the magnetic field line hyperbolas.

So, in general, for all variations of the parameters, we observe the same effect: acceleration of electrons by the electric field when they appear in the vicinity of the neutral line; the picture is somewhat different for a single or multiple intersection of the neutral plane. At very small x(0), there is a distinctly “Speiser” section of the orbit, on which a particularly fast acceleration takes place.

3 Local instability

We return to the case of an orbit starting very close to the x=0 plane. Let us turn to the first equation of the set Eq. (1) in Sect. 2. We have first set x(0)=0 and based on the numerical result that, beginning at some t=t_c, the velocity v_y increase is very close to linear; see Fig. 1b. For values of x(0)≠0 that are small compared to κ⁻¹ (the diffusion region scale in the x direction), κx(0)≪1, and returning to the initial variables, we then have

$$\ddot{x}={\displaystyle \frac{e}{mc}}{v}_y{B}_z={\displaystyle \frac{e^{\mathrm{2}}b}{m^{\mathrm{2}}c}}{E}_{\mathrm{0}}x\left(t-t_{\mathrm{c}}\right)={\displaystyle \frac{x\left(t-t_{\mathrm{c}}\right)}{{\mathit{\tau }}^{\mathrm{3}}}},$$

where

$$\mathit{\tau }={\left({\displaystyle \frac{e^{\mathrm{2}}b}{m^{\mathrm{2}}c}}{E}_{\mathrm{0}}\right)}^{-\mathrm{1}/\mathrm{3}}={\left({\displaystyle \frac{eb}{mc}}\right)}^{-\mathrm{2}/\mathrm{3}}{\left({\displaystyle \frac{c}{b}}{E}_{\mathrm{0}}\right)}^{-\mathrm{1}/\mathrm{3}}.$$

Note that the above equation is the Airy equation. In our dimensionless variables it takes the form

$$\ddot{x}-\mathrm{45}\mathrm{000}xt=\mathrm{0}.$$

(Here the coefficient 45 000 is taken from the numerical calculation of $\dot{y}\left(t\right)$ according to Eq. 1.) Departure from the x=0 plane is described by the Airy function of the second kind $x\left(t^{\prime }\right)=x\left(\mathrm{0}\right)\mathrm{Bi}\left(\mathrm{10}\times {\mathrm{45}}^{\mathrm{1}/\mathrm{3}}{t}^{\prime }\right)$ (where $t^{\prime }=t-t_{\mathrm{c}}$) with an exponential asymptotic. This is shown in Fig. 5a, which presents the results of calculating the above Airy function (blue curve) and of the numerical solution of the Equation set (1) for x(t) (red curve). (In the Figure x(0)=0.01 is adopted.)

Now for any small deviation $\mathit{\xi }\left(t\right)=x_{\mathrm{1}}\left(t\right)-x\left(t\right)$, for a pair of orbits starting at small initial x(0)≠0 and x₁(0)≠0, we obtain the same governing equation, and the following argument may be applied to such a deviation.

On a small time interval Δt the coefficient at x  in the equation, equal to $\mathit{\kappa }=\frac{e^{\mathrm{2}}b}{m^{\mathrm{2}}c}{E}_{\mathrm{0}}t=\left(t/\mathit{\tau }\right){\mathit{\tau }}^{-\mathrm{2}}$ changes by $\left(\frac{e^{\mathrm{2}}b}{m^{\mathrm{2}}c}{E}_{\mathrm{0}}\right)\mathrm{\Delta }t=\left(\mathrm{\Delta }t/\mathit{\tau }\right){\mathit{\tau }}^{-\mathrm{2}}$, and its relative variation is $\mathrm{\Delta }\mathit{\kappa }/\mathit{\kappa }\sim \mathrm{\Delta }t/t$. If the coefficient κ remained constant, there would exist an exponentially increasing solution $\sim \exp \left({\mathit{\kappa }}^{\mathrm{1}/\mathrm{2}}t\right)$. The exponent is equal to ${\mathit{\kappa }}^{\mathrm{1}/\mathrm{2}}t={\left(\frac{e^{\mathrm{2}}b}{m^{\mathrm{2}}c}{E}_{\mathrm{0}}\right)}^{\mathrm{1}/\mathrm{2}}{t}^{\mathrm{3}/\mathrm{2}}={\left(t/\mathit{\tau }\right)}^{\mathrm{3}/\mathrm{2}}$, and on the time interval Δt it changes by $\frac{\mathrm{3}}{\mathrm{2}}{\mathit{\tau }}^{-\mathrm{3}/\mathrm{2}}{t}^{\mathrm{1}/\mathrm{2}}\mathrm{\Delta }t$.

So if we fix some time moment t≫τ, then on the time interval from t to t+Δt the exponent changes by $\frac{\mathrm{3}}{\mathrm{2}}{\mathit{\tau }}^{-\mathrm{3}/\mathrm{2}}{t}^{\mathrm{1}/\mathrm{2}}\mathrm{\Delta }t=\frac{\mathrm{3}}{\mathrm{2}}{\left(t/\mathit{\tau }\right)}^{\mathrm{1}/\mathrm{2}}\left(\mathrm{\Delta }t/\mathit{\tau }\right)\gg \mathrm{\Delta }t/\mathit{\tau }$. Therefore if the double inequality $t\gg \mathrm{\Delta }t\gg \mathit{\tau }$ holds, we obtain a very large value of the exponential multiplier $\exp \left(\frac{\mathrm{3}}{\mathrm{2}}{\mathit{\tau }}^{-\mathrm{3}/\mathrm{2}}{t}^{\mathrm{1}/\mathrm{2}}\mathrm{\Delta }t\right)\gg \mathrm{1}$ along with a small variation of κ (that coefficient remains almost constant, $\mathrm{\Delta }\mathit{\kappa }/\mathit{\kappa }\sim \mathrm{\Delta }t/t\ll \mathrm{1})$, i.e., at every t≫τ a fast, exponential divergence of orbits x(t) and x₁(t) occurs. In other words, if we take a pair of closely neighboring orbits at a moment t, then during particle motion along them at later times, earlier than the dynamical equation form changes considerably, the particles will diverge at an exponentially large distance.

In such a situation we may speak of the presence of a local instability in the system, in the vicinity of the magnetic field neutral line.

A clear confirmation of instability at $x\left(\mathrm{0}\right)=\dot{x}\left(\mathrm{0}\right)=\mathrm{0}$ is shown in Fig. 5b, where the orbits starting at different small |x(0)| values are shown projected onto the z=0 plane. Here the orbit sections from t=0 to t=0.2 are shown in red, from t=0.2 to t=0.4 – in green, and from t=0.4 to t=0.45 – in blue.

Note that the diverging orbits turn out to be limited (generally speaking, in the phase space) because of cyclotron rotation.

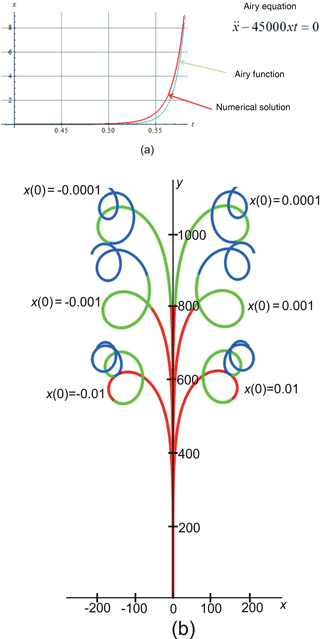
Figure 5 (a) Time dependence x(t) at small x(0)≠0. (b) Orbits starting at various small values of x(0), projected to the plane z=0.

Figure 6 (a) Oscillations over z on the “cucumber” orbit. (b) The “cucumber” orbit projected to the z=0 plane. (c) Oscillations over z on the “ring” orbit. (d) The “ring” orbit projected to the z=0 plane.

4 Discussion and conclusions

As has been shown earlier (see, e.g., Burkhart, 1990), the motion of an electron in the neutral line vicinity being nonadiabatic, is described by nonlinear equations, and on the orbit there is a “Speiser” meander section on which a fast particle acceleration occurs, in the electric field corresponding to the inflow of plasma into the reconnection area. This should result in a strong conversion of energy of the electromagnetic field into energy of the electron flows.

We point out here that this effect is accompanied by another one which is very important from the point of view of a general theory of nonlinear dynamical systems.

It is well known that even in the case of a relatively simple system of low dimension, there may exist such domains in its phase space, where the orbits are stochastic. We point out that an electron in our model field, in the neutral line vicinity is just such a system.

Consider a pair of orbits in the X phase space (with dimension n) starting at closely located points X(0) and X₁(0) so that $\mathit{\xi }\left(\mathrm{0}\right)={\mathit{X}}_{\mathrm{1}}\left(\mathrm{0}\right)-\mathit{X}\left(\mathrm{0}\right)\to \mathrm{0}$. We then can linearize the equation set of the dynamical system and obtain a set of linear equations for the small increment ξ(t). Let A be the matrix of coefficients of that equation set. The general solution of the equation set may be presented as a superposition of n fundamental particular solutions {ξ_j(t)}:

$$\mathit{\xi }\left(t\right)=\sum _j{C}_j{\mathit{\xi }}_j\left(t\right),$$

where the C_j constants are determined from the projection of the initial increment ξ(0) onto the {ξ_j(0)} vector basis. In the simplest case when the matrix of coefficients A is independent of time, all the vector components ξ_j(t) are exponential in time, ξ_j(t)∼exp (λ_jt). The parameters λ_j are Lyapunov's exponents of the system. Generally, the time dependence of the fundamental particular solutions {ξ_j(t)} is more complicated than exponential. However, keeping in mind that the A(t) matrix does not unlimitedly grow with time, for large times we can write |ξ_j(t)|=Φ_j(t)exp (λ_jt), where the Φ_j(t) function has a slower growth rate than exponential.

Turning back to our case, we have seen in Sect. 3 that in the neutral line vicinity there is an area in the phase space where local instability acts. It means that the distance ξ between neighboring orbits in the x direction increases exponentially: on a time interval Δt it increases so that $\mathit{\xi }\left(t+\mathrm{\Delta }t\right)/\mathit{\xi }\left(t\right)=\exp \left(\frac{\mathrm{3}}{\mathrm{2}}{\mathit{\tau }}^{-\mathrm{3}/\mathrm{2}}{t}^{\mathrm{1}/\mathrm{2}}\mathrm{\Delta }t\right)\gg \mathrm{1}$. We conclude that a maximum positive Lyapunov's exponent should exist, ${\mathit{\lambda }}^{\left(m\right)}\ge \frac{\mathrm{3}}{\mathrm{2}}{\mathit{\tau }}^{-\mathrm{3}/\mathrm{2}}{t}^{\mathrm{1}/\mathrm{2}}$.

Note that the existence of local instability, in the terms of a positive Lyapunov characteristic exponent, was first pointed out for this problem in Martin (1986).

As has been noted earlier, the local instability of orbits takes place along with finiteness of motion in the phase space due to the particle trapping by the magnetic field. From the general theory of nonlinear dynamical systems (see, e.g., Tabor, 1989; Ott, 2002; Usikov et al., 1988) it then follows that the system possesses the corresponding Kolmogorov–Synai entropy of the order of the maximum positive Lyapunov exponent, h∼λ^(m). This means that correlation decay occurs on the timescale

$${\mathit{\tau }}_{\left(\mathrm{corr}\right)}\le {\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}{\mathit{\tau }}^{\mathrm{3}/\mathrm{2}}{t}^{-\mathrm{1}/\mathrm{2}}\sim \left({\displaystyle \frac{mc}{eb}}\right){\left({\displaystyle \frac{b}{c{E}_{\mathrm{0}}}}\right)}^{\mathrm{1}/\mathrm{2}}{t}^{-\mathrm{1}/\mathrm{2}}.$$

This leads to the effect of mixing in the phase space, and to the appearance of dynamical chaos on some particular sites in the phase space.

In the case of a somewhat similar situation, a one-dimensional current sheet with a 2B₀ change of the tangential magnetic field component across the sheet and a nonzero constant normal component B_n=const (and without an electric field), the feature of orbit stochastization was demonstrated long ago in Chen and Palmadesso (1986). In that model, there are “slow” nonlinear oscillations on “cucumber” orbits, coexisting with “fast” oscillations containing both spiral and meander regions (Büchner and Zelenyi, 1986). If the defining parameter $\mathit{\kappa }=\left(B_{\mathrm{n}}/B_{\mathrm{0}}\right){\left(L/{\mathit{\rho }}_{\mathrm{0}}\right)}^{\mathrm{1}/\mathrm{2}}$ (L is the transverse scale of the current sheet, ρ₀ is the Larmor radius in the field B₀) is small, then there is a stochastization mechanism associated with the intersection of the separatrix between two different types of fast oscillations, spiral and meander (Büchner and Zelenyi, 1986; Timofeev, 1978; Neishtadt, 1987). And with the increase of the parameter κ, according to Malova and Sitnov (1989), stochastization additionally occurs due to overlapping resonances of the fast and slow oscillations.

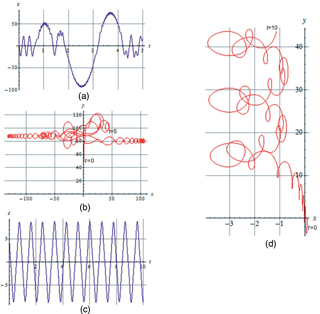
If in the model we are considering, with a nonuniform B_n field, with a neutral line of the magnetic field, we set the electric field E₀ equal to zero, then the nature of orbits described in these previous works is basically preserved (see Fig. 6a–d), supplemented only by the particle displacement over y due to the drift in the B_n field, nonuniform over x. Therefore, the same mechanisms of stochasticity must operate.

However, in the model considered here, in the presence of a reconnection electric field, those effects, as we have seen, are supplemented by the local instability effect near the neutral line. A qualitative explanation may be given following the notions of, for example, Usikov et al. (1988) concerning the role in the effect of stochasticity generation which is played by a separatrix existing in the phase space of a nonlinear system. “Slow” oscillations over x occur within certain limits from x_min up to x_max. If x_min corresponds to the position of the neutral line of the magnetic field, a separatrix arises on which the period of “slow” oscillations tends to infinity. Accordingly, a “phase space fluid drop” of this “slow” variable is stretched in phase (and compressed in action), and phase mixing occurs (e.g., Usikov et al., 1988). Combined with the finiteness of the orbits, this provides a mechanism of stochastization.

According to modern knowledge (see, for example, Gaspard, 1998) macroscopic transport processes in multiparticle systems may be viewed as being based on microscopic particle dynamics, which demonstrates the properties of dynamical chaos. Accordingly, the above argument seems to indicate the presence of collisionless “dissipation” of the Landau damping type (Mouhot and Villani, 2011). As this mathematical research shows, the phenomenon of damping can be interpreted in terms of the transfer of regularity from kinetic variables to spatial ones, and not as a transformation of energy; phase mixing is the clue mechanism.

Thus we obtain an indication of the fundamental dynamical basis of the collisionless magnetic reconnection process, which at the macroscopic level, considering the thin “diffusion” region near the neutral line, looks like a process involving a finite “conductivity” in collisionless plasma.

Now we note an analysis somewhat similar to ours was recently carried out in Zenitani and Nagai (2016). A set of electron orbits passing in the vicinity of the magnetic field neutral line has been identified there under conditions when this field itself, as well as the electric field and the plasma characteristics, is determined in numerical simulation of the entire three-dimensional plasma system. Modeling was carried out by means of a particle-in-cell code applied to a time-dependent spontaneous magnetic reconnection process in which an electric field arises in a self-consistent manner as a result of development of an initially small perturbation, rather than being arbitrarily given, as is done here.

Electron orbits are grouped in this work according to some of their basic characteristics. There are classes of orbits qualitatively corresponding to those obtained by us, with “Speiser” sections and fast acceleration in the vicinity of the neutral line. Along with them, orbits of a substantially different type, named “Speiser orbits without intersection of the central plane”, were obtained. Those orbits appear due to the fact that in the model (Zenitani and Nagai, 2016) there are such electric fields that are absent here: the polarization field E_z and the parallel field E_∥. Such fields actually arise during magnetic reconnection, due to the Hall plasma dynamics indicated in Sect. 1.

However, the approach used in Zenitani and Nagai (2016) does not allow the systematic tracing of how the orbit nature and the acceleration gained by an electron depend on the distance to the neutral line, as we have done here. This dependence could not be traced down to very small x(0) values where the local instability appears. So the local instability of orbits in the vicinity of the neutral line was not identified; this has been done here for the first time. As indicated above, combined with the finiteness of motion in the phase space due to the particle trapping by the magnetic field, this instability serves as the basis for the effect of the phase space mixing and the appearance of dynamical chaos.

One more important point, which has a wider relation to particle-in-cell (PIC) codes, is that the formation of a small-scale (fractal) stochastic structure in the phase space cannot be reproduced in numerical simulation by means of a large particle-in-cell code. But namely such a structure is apparently responsible for the dissipative behavior of the system in the vicinity of the magnetic field neutral line, in a thin electronic “diffusion layer”. True, this flaw of PIC codes may be partly overcome if the particle number per cell becomes sufficiently large, since as this number increases the size of super-particles in the PIC method decreases.

An additional comment should be made here, in particular in relation to self-consistent models of magnetic reconnection. In fact it is just assumed that any electron orbit under study is located deep inside the small electron diffusion region. There is no attempt to relate the adopted dimensionless parameters to physical scales characteristic for that domain. True, this is an ambiguous task since those scales depend in particular on the (numerical) model adopted for such a comparison. In any case it is reasonable to postulate that such a small electron diffusion region exists. Note, however, that if the current carried by unmagnetized electrons themselves were large, then the magnetic field configuration would be more complicated: it would have a spatial scale of the same order as the electron oscillations about the neutral plane of the CS. Then a study based on test particle orbits in a prescribed field would be inapplicable. So another assumption, implicitly made, is that the currents forming the magnetic field configuration, are carried mainly by ions, and not by unmagnetized electrons; correspondingly, the field configuration spatial scales are sufficiently large. This actually is the case for the existing self-consistent models of magnetic reconnection (e.g., Hesse et al., 2011; Bessho et al., 2014; Liu et al., 2017). This may also eliminate the problem with those electric fields mentioned above which appear in self-consistent models, the polarization field E_z and the parallel field E_∥. Those fields vary on a large ionic scale; in particular, the polarization field is associated with the Hall electric current (Hoshino, 2005). Also, in the numerical simulation (Egedal et al., 2012) it was found out that the parallel fields operate in spatial regions that exceed the regular electron diffusion region scale by orders of magnitude. And then, since unlike the reconnection field E₀, those fields must go to zero at z→0, they might be neglected in the small electron diffusion region.

Magnetic reconnection in collisionless plasma may be considered as a complex of two main problems. The first problem is fast energy conversion. As has been shown in earlier studies and has been pointed out in the Introduction, this may be understood as a result of “magnetic field annihilation” dominated by an “anisotropic” thin current sheet, the structure of which is determined by the specific ion orbits. The second problem is that of a nonzero electric field E≠0 on the magnetic field neutral line B=0. This is shown here to be directly connected with specific features of electron motion. Electrons are accelerated by the electric field, $\mathrm{d}\left|v_y\right|/\mathrm{d}t>\mathrm{0}$ in the “electron diffusion region” where they are “demagnetized”. The resulting |v_y| produces a repulsing Lorentz force acting in the x direction, and a local instability appears. Combined with finite dimensions of the electron orbit in the phase space (due to magnetic trapping) this leads to orbit stochastization. The latter may presumably be viewed as a mechanism producing finite “conductivity” in collisionless plasma near the neutral line.