Araucaria growth response to solar and climate variability in South Brazil

In this work, the Sun–Earth–climate relationship is studied using tree growth rings of Araucaria angustifolia (Bertol.) O. Kuntze collected in the city of Passo Fundo, located in the state of Rio Grande do Sul (RS), Brazil. These samples were previously studied by Rigozo et al. (2008); however, their main interest was to search for the solar periodicities in the tree-ring width mean time series without interpreting the rest of the periodicities found. The question arises as to what are the drivers related to those periodicities. For this reason, the classical method of spectral analysis by iterative regression and wavelet methods are applied to find periodicities and trends present in each tree-ring growth, in Southern Oscillation Index (SOI), and in annual mean temperature anomaly between the 24 and 44^∘ S. In order to address the aforementioned question, this paper discusses the correlation between the growth rate of the tree rings with temperature and SOI. In each tree-ring growth series, periods between 2 and 7 years were found, possibly related to the El Niño/La Niña phenomena, and a ∼ 23-year period was found, which may be related to temperature variation. These novel results might represent the tree-ring growth response to local climate conditions during its lifetime, and to nonlinear coupling between the Sun and the local climate variability responsible to the regional climate variations.

Keywords. History of geophysics (solar–planetary relationships) – meteorology and atmospheric dynamics (climatology; palaeoclimatology)

1 Introduction

In Brazil, dendrochronological/dendroclimatic studies are still incipient (Fritts, 1976; Schöngart et al., 2002, 2004; Rigozo et al., 2007a, b, 2008; Lisi et al., 2008; Oliveira et al., 2009; Prestes et al., 2011, 2014; Andreacci et al., 2013; Pagotto et al., 2015; Lorensi and Prestes, 2016; Lorensi, 2016; Perone et al., 2016), considering the great biodiversity and continental dimension of Brazil when compared to South American countries such as Chile and Argentina. However, these kinds of studies have become more numerous in the recent years (Rigozo et al., 2007a, b, 2008; Lisi et al., 2008; Oliveira et al., 2009; Prestes et al., 2011, 2014; Andreacci et al., 2013; Pagotto et al., 2015; Lorensi and Prestes, 2016; Lorensi, 2016; Perone et al., 2016).

However, the study of solar variations related to the energy flux entering the Earth's atmosphere is predominantly observational, and it has also only recently been undertaken. This fact limits understanding their effects on climate, and the possibility of long-term climate prediction. For these reasons, it is necessary to understand the solar variations, and other geophysical phenomena in the distant past to try to predict the future.

Tree-ring time series are witnesses of the environment and climate that influenced their growth in the past (Fritts, 1976; Kononov et al., 2009; Muraki et al., 2015); therefore they can be used for climate studies in local regions and for particular time periods without instrumental measurements. Tree growth lasts from germination to death, and it is influenced by several simultaneous environmental factors. Temperature, precipitation, and solar radiation play an important role, especially for species located in regions with highly contrasted season conditions. These environmental factors induce different growth rate causing different cell size over time, which allows direct visual identification, i.e., the tree growth rings. The thickness variation of yearly tree rings reflects the specimen sensitivity to the environmental factors of where it grows. Depending of the conditions and the species, some of these environmental factors may prevail over others.

Tree-ring data have been used to reconstruct the climate (e.g., Case and MacDonald, 1995; Jacoby et al., 2003; D'Arrigo et al., 2001; Salzer and Kipfmueller, 2005; Shao et al., 2005; Therrell et al., 2006; Lorensi and Prestes, 2016), and there is evidence of solar influence on these data in timescales of decades to centuries. In addition, there is evidence of solar cycles in living and fossil tree-ring time series (Mori, 1981; Ammons et al., 1983; Nordemann et al., 2005; Raspopov et al., 2011; Prestes et al., 2011, 2014; Dorotovič et al., 2014; Perone et al., 2016).

Rigozo et al. (2008) used 12 tree-ring thickness time series from Passo Fundo (Brazil) to search for solar activity periodicities; however they did not present a study about the rest of the periodicities found in the Passo Fundo records. The goal of this article is to confirm the nonlinear character of the solar activity and their correlation (if any) with the variability of climate conditions using the same records previous studied by Rigozo et al. (2008). This article will focus on the rest of the periodicities found by Rigozo et al. (2008), but it will also re-analyze the periodicities of 11, 22, 54, 80, and 208 years through iterative regression analysis in order to obtain a deeper understanding of the effects of solar activity, climate, and geophysical phenomena in South Brazil.

2 Location and data sets

2.1 Passo Fundo, Rio Grande do Sul, Brazil

In the city of Passo Fundo located in South Brazil (52^∘11^′ W, 28^∘16^′ S; altitude of 740 m), the climate can be classified as humid subtropical (Cfa in the Köppen climate classification), where the coldest month is on average above 0 ^∘C (32 ^∘F) and the highest average temperature is above 22 ^∘C (71.6 ^∘F). There is no significant precipitation difference between seasons, with annual rainfall reaching 1746 mm. However, there is excessive rainfall during El Niño years (an increase in rainfall of 30–40 %) and drought during the La Niña years (an decrease in rainfall of 10–30 %). In Rio Grande do Sul, the excessive rainfall during El Niño years is more pronounced due to a higher frequency of cold fronts during the warm phase of El Niño–Southern Oscillation (ENSO); see Gelcer et al. (2013) for more details. These persistent climate anomalies can last from 6 months up to 1.5 years as discussed by Berlato and Fontana (2003).

2.2 Dendrochronological series

The dendrochronological series are used in the present work for study the Sun–Earth-climate relationship. These series are obtained from trees located in the region of South Brazil. The tree samples from Araucaria angustifolia species are collected in Passo Fundo, RS, Brazil. These samples were previous used by Rigozo et al. (2008) to identify solar maximum epoch imprints in the tree rings.

All the Araucaria angustifolia samples were collected in 2005 in Passo Fundo, in the environs of the Passo Fundo National Forest (PFNF). The PFNF is a Brazilian conservation site, which is the best-preserved Araucaria forest area in Brazil. The forest coverage is higher in the PFNF than the grassland due to the Protected Area Management Plan. The samples were collected from 12 different trees, and from each tree, four different radius samples were chosen. Then, these data were averaged. The comprehensive procedure of tree-ring sample preparation mandated that (i) the samples should be dried under shady/enclosure conditions; (ii) the samples should be sanded with 50–600 grit sandpaper in order to highlight ring growth; (iii) the best sample radius based on growth-ring morphology should be selected; (iv) the growth rings should be labeled; and finally (v) the growth-rings should be measured.

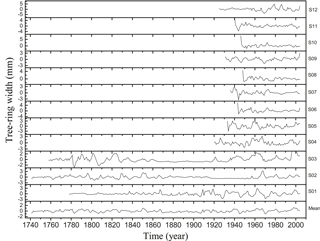
Figure 1 Mean time series of growth ring thickness of trees from Passo Fundo, Rio Grande do Sul, after removing their long trend curves.

The time series were obtained using a tree-ring measuring table (Lintab III) with an accuracy of 0.01 mm. In the first step, the growth-rings were identified and demarcated. In this part of the laboratory procedure, the tree rings were properly indicated, i.e., without any false or missing rings being considered. In the second step as previously explained by Rigozo et al. (2008), the tree-ring thickness chronology was obtained averaging the 12 chosen different tree-ring samples, and each sample was averaged using the different radii of four individual tree-ring samples. The mathematical function that represents its individual growth trend was subtracted from each tree series sample, in order to determine the individual residual dendrochronology (see Fig. 1 in Rigozo et al., 2008). For more information about the sample methodology preparation and the sample correlations; see Rigozo et al. (2008). The 12 dendrochronological series are shown in Fig. 1. However, it only presents the residual tree-ring thickness time series, which are a modified version of the Fig. 1 in Rigozo et al. (2008), i.e., without the long trends.

Moreover, the tree-sample ages were determined by the ring-counting. As the samples were collected from live trees in 2005, the last year of ring formation is 2004. In samples of Araucaria angustifolia, the counting of growth rings is usually used to provide an estimation of tree age (Oliveira et al., 2009; Santos et al., 2015; Lorensi and Prestes, 2016).

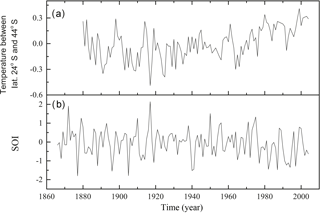
We also used the most recent continuous series from climate drivers. In Fig. 2, these series are shown as follows: (a) the annual mean temperature anomaly between 24 and 44^∘ S in the interval 1880–2004 (obtained from Goddard Institute for Space Studies, NASA, https://data.giss.nasa.gov/, last access: January 2017) and (b) Southern Oscillation Index (SOI) in the interval 1866–2004 (obtained from https://crudata.uea.ac.uk/cru/data/soi/, last access: January 2017). The SOI is an index used to represent the ENSO phenomena.

Figure 2 (a) Annual mean temperature anomaly between 24 and 44^∘ S. (b) Southern Oscillation Index (SOI).

3 Methodology

3.1 Iterative regression method (ARIST)

An iterative regression method (ARIST) is used to search for periodicities embedded in tree growth ring time series, and it was used successfully by Rigozo et al. (2008) for identify solar maximum epoch imprints in these tree rings as mentioned before. This method is an iterative least square fit, and it uses a simple sine function with three unknown parameters, a₀ = amplitude, a₁ = angular frequency and a₂ = phase (Wolberg, 1967; Rigozo and Nordemann, 1998; Rigozo et al., 2005). The starting point of this method is the so-called conditional function $F=Y-a_{\mathrm{0}}\sin (a_{\mathrm{1}}t+a_{\mathrm{2}})$, where Y is the observed signal, t is the time, and a₀, a₁, and a₂ are the three unknown parameters described above; see Rigozo et al. (2005) for more details on how to determine the initial values of a₀, a₁, and a₂.

Every periodicity embedded in the time series corresponds to a set of three parameter values, where the periodicity is determined by applying the iterative process to the original time series with the limiting condition of maintaining the angular frequency a₁ inside a restricted domain of the allowed interval of angular frequencies. Moreover, this method provides the standard deviation for each parameter obtained by the iterative least square fit of the time series. Rigozzo et al. (2005) describe this methodology in detail and compare it to other classical spectral analyses.

The advantage of this method over the Fourier method is that it is able to find periodicities associated with long trends. In other words, it fits senoidal functions in the signal. In addition, if only a segment of a sine function fits the original signal, it is possible to determine the period of this trend using ARIST. On the other hand, in the Fourier method, long trends are bounded by the finite length of the time series.

3.2 Wavelet method

The wavelet transform is an useful tool for non-stationary signal analysis. It permits the local identification of spectral content of a certain time series in time and in space (Kumar and Foufoula-Georgiou, 1997; Torrence and Compo, 1998; Percival and Walden, 2000).

The continuous wavelet transform (CWT) of a time series is defined as the convolution between the series and the scaled and translated version of the chosen wavelet function. By varying the wavelet timescale and translating the scaled versions of the wavelet mother, it is possible to build a two-dimensional spectrogram showing the time versus frequency (period), and how they vary with time.

The CWT of a time series f is defined by the integral transform,

$$\begin{array}{ll}\text{(1)}& {\displaystyle }& {\displaystyle }W(a,b)=\int f\left(t\right){\displaystyle \frac{\mathrm{1}}{\sqrt{a}}}{\mathit{\psi }}^{*}\left({\displaystyle \frac{t-b}{a}}\right)\mathrm{d}t,{\displaystyle }& {\displaystyle }a>\mathrm{0},a\in \mathbb{R},\end{array}$$

where * represents the complex conjugate and the pre-factor |a|^½ is introduced in order to guarantee that all the scaled functions ${\left|a\right|}^{\frac{\mathrm{1}}{\mathrm{2}}}\mathit{\psi }\left(\frac{t}{a}\right)$ have the same energy in the 𝕃²(ℝ) sense. This function W(a,b) represents the wavelet coefficients that is a function of both time and frequency (time b and scale a).

In this work, we used an updated version of the CWT algorithm of Torrence and Compo (1998). The Morlet wavelet function is chosen because it represents the best compromise between time and frequency concentration as established by Heisenberg's uncertainty principle; see Kumar and Foufoula-Georgiou (1997) for more details. It is important to mention that due to the limitation of the signal length, the border effects are treated here using the symmetrization method; see chapter 8 of Strang and Nguyen (1996) for more details. This method assumes that signals can be recovered outside their original support by symmetric boundary value replication. This method has the disadvantage of introducing discontinues at the borders; however, it works well in general. Moreover, there is no loss of response due to wavelet truncation, and the cone of influence is not needed.

The wavelet cross-correlation is also used because the wavelet cross power indicates the scale of high correlation between two time series with indices 1 and 2 (see Torrence and Compo, 1998; Percival and Walden, 2000, for more details). Therefore, the wavelet cross-correlation to study the correlation between a pair of data sets as a function of scale a and time t is given by

$$\begin{array}{}\text{(2)}& \mathcal{C}(a,t)={\displaystyle \frac{{\mathcal{W}}_{\mathrm{1}}(a,t){\mathcal{W}}_{\mathrm{2}}^{*}(a,t)}{(\int {\mathcal{W}}_{\mathrm{1}}(a,t{)}^{\mathrm{2}}\mathrm{d}t\int {\mathcal{W}}_{\mathrm{2}}(a,t{)}^{\mathrm{2}}\mathrm{d}t{)}^{\frac{\mathrm{1}}{\mathrm{2}}}}},\end{array}$$

where ${\mathcal{W}}_i(a,t)=\left|W_i(a,t)\right|-\stackrel{\mathrm{‾}}{\left|W_i(a,t)\right|}$, W_i are the wavelet coefficients, and $\stackrel{\mathrm{‾}}{W_i}$ is the arithmetic mean in time for i=1 or 2.

The wavelet cross-correlation will allow us to check the interaction between two sets of dendrochronological data for each considered timescale.

4 Results and discussion

The Sun is both an element and a climate forcing. Therefore, solar cycles presented in the dendrochronological series will be re-analyzed because many periods found in these series may be possibly due to a combination of solar cycle harmonics. As for example, the periods of ∼ 17 to ∼ 18 years (Saros cycle) and ∼ 30 to ∼ 35 years (Brückner cycle) can also be found in the climatological series. Moreover, Gusev (2011) discussed that the climatic variations are forced oscillations driven by solar forcing, and consequently, it implies the existence of intrinsic climatic oscillations related to solar activity. As aforementioned, the main focus of this paper is to study the nonlinear behavior of the solar activity and their correlation with the variability of climate conditions. Due to this fact, we will divide Sect. 4 into two subsections: solar influences and climate influences.

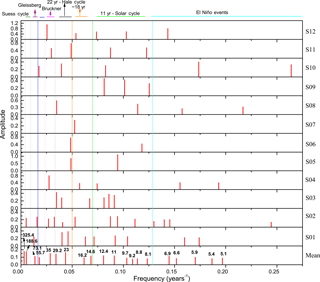
Figure 3 Amplitude spectra for each tree-ring thickness sample at a confidence of 95 % from S01 to S12 (top 12 panels) and the average of them (bottom panel).

4.1 Solar influences

The amplitude spectra for each tree-ring thickness time series using the ARIST at a confidence level of 95 % are shown in Fig. 3. These spectra are related to the tree-ring thickness time series shown in Fig. 1.

It is possible to see the presence of some well-known periodicities related to the solar activity. The solar activity presents several sub-intervals including the Schwabe cycle which corresponds to a period bandwidth of 8–13 years, the cycle of ∼ 11 years related to the sunspot number variability, and the Hale cycle of 20–29 years related to the magnetic solar cycle of 22 years. The Gleissberg cycle of 70–90 years can also been seen (Kivelson and Russell, 1995; Hoyt and Schatten, 1997). This spectral analysis of each tree individual sample related to the solar activity was not done by Rigozo et al. (2008).

Several authors (e.g., Currie, 1973; Radoski et al., 1975; Courtillot et al., 1977; Clúa de Gonzalez et al., 1993; Juckett, 2001; Prestes et al., 2006, 2011) applied different analysis techniques (Fourier analysis, maximum entropy, and multitaper method) to determine the spectral content of the sunspot number time series. Their main results include a low period cycle of 5.5 years; a variable solar cycle of 11 years, which may appear with lower or higher periods between ∼ 8 and ∼ 13 years depending upon on the decadal time interval used in the analysis; and a cycle of ∼ 90 years, which is also frequently present in the sunspot number series (Herman and Goldberg, 1978). Considering the solar cycles from 11 to 22, an average period of 9.67 years can be found; therefore, it explains why the period may vary between 9 and 11 years (Kivelson and Russell, 1995).

In dendrochronological series, similar results were found by many authors (Murphy, 1990, 1991; Rigozo et al., 2004; Nordemann et al., 2005; Vincent et al., 2007; Muraki et al., 2011; Wang and Zhang, 2011; Lorensi, 2016). Murphy (1990, 1991) analyzed tree-ring time series obtained in Australia and Taiwan and found periods related to the solar cycle of 11 years between 9.3 and 13.3 years, and between 11.1 and 13.6 years, respectively. In the South Brazil region, Rigozo et al. (2004) studied tree rings collected in Concórdia, and they found periods of 10.6 and 83.4 years, which corresponds to the solar cycle of 11 years and the Gleissberg cycle of ∼ 80 years, respectively. Nordemann et al. (2005) performed a study using tree-ring chronology obtained in Brazil and Chile. The Brazilian tree samples showed periodicities of 79, 51.3, 23.7, and 10.5 years relating to solar activity, while the tree-ring samples collected in Chile showed periodicities of 197, 89.6, 50.3, 11.8, and 10.5 years. Another study using Araucaria angustifolia samples collected in General Carneiro, Irani, and Fazenda Rio Grande in South Brazil was performed by Lorensi (2016). In this study, periodicities related to solar cycle of 11 years, 22 years, and longer periods such as the Gleissberg cycle were found. Muraki et al. (2011) studied tree-ring growth using 391-year-old cedar samples collected in Japan, and they found periodicities of 25 and 12 years. These authors concluded that tree growth rate can be influenced by solar activity. Periodicities between 20 and 28 years were also found by Muraki et al. (2011) in Araucaria columnaris samples from New Caledonia. Wang and Zhang (2011) found periodicities around 204, 73, 20.5, 11.2–11.1, and 5.3–5.1 years performing spectral analysis using samples from the mountains of Tibet, which correspond to Suess, Gleissberg, Hale cycle and second harmonic of the Schwabe cycle, respectively.

In Rigozo et al. (2008), the periodicities found in the tree rings collected in Passo Fundo were also mainly attributed to the solar variability. The periods between 8.1 and 12.4 years were related to solar cycle of 11 years, while the period of 23.0 year was related to the Hale cycle. They suggested that the period of 55.7 years might be related to the fourth harmonic of the Suess cycle as discussed by Damon et al. (1997). On the other hand, they suggested that the period of 73.1 years was attributed to the Gleissberg cycle, and the period of 188.6 years was attributed to the Suess cycle of 200 years. In the bottom panel of Fig. 3, all the aforementioned periodicities related to solar activity can be observed, in addition to each of the 12 dendrochronological series obtained in Passo Fundo, although they are not so evident as in their average series.

For a paleoclimatic study, Raspopov et al. (2011) used fossil trees of ∼ 70 000 years old (380 rings) and ∼ 12 000 years old (120 rings). Using the fossil of ∼ 70 000 years old, the researchers found periodicities of 8–10, 20–22, and 100–120 years that correspond to Schwabe, Hale, and Gleissberg cycles, respectively. Using a ∼ 12 000-year-old fossil, periodicities of 4, 9–12 (Schwabe cycle), 17 (lunar cycle), and 31–34 years (Brückner cycle) were found.

Fossil trees of ∼ 50 000 years and living trees obtained in Chile were analyzed by Roig et al. (2001). They found similar spectral periodicities between these two data sets, such as 136–153, 81–94, and 47–53 years and periods of 35, 24, 17.8, 11.8, 6.6, 5.1, 4.58, 4.3, 3.7, 3.2, and 2.77 years. This indicates that similar factors may affect the radial growth of these trees since the end of the Pleistocene. These authors related the periods of 81–94, 24, and 11.8 years to the solar modulation.

However, the cycles of 7 and 8 years found in the tree-ring chronological series could be related to two beating solar/climatic cycles as discussed by Hoyt and Schatten (1997). It is well known that a combination of wave oscillation patterns between various forcing frequencies can be obtained as a response of the nonlinearity interactions as discussed by Le Treut and Ghil (1983). The nonlinearity wave oscillation patterns are the response to additive and multiplicative periodic forcing f_o, so they are composed of the harmonic of the forcing f_h and their combination, for example f_o+f_h, f_o−f_h, and f_o+2f_h, among many others.

For Raspopov et al. (2000, 2001), the Brückner cycle is a result of solar activity nonlinear effects in the terrestrial environment. They found that the combination of the Gleissberg cycle (∼ 90 years) and the Hale cycle (22 years) may result in the Brückner cycle ($(\mathrm{1}/\mathrm{22})-(\mathrm{1}/\mathrm{90})\cong \mathrm{1}/\mathrm{30}$) or in the Saros lunar cycle ($(\mathrm{1}/\mathrm{90})+(\mathrm{1}/\mathrm{22})\cong \mathrm{1}/\mathrm{17}$). Therefore, Raspopov et al. (2000, 2001) concluded that the periods of between ∼ 17 and ∼ 18 and ∼ 30 and ∼ 35 years might also be a result of solar activity nonlinear effect in atmospheric processes. Kurths et al. (1993) showed that the combinations of two periods of 12.6 and 17.1 year could generate periods of 7.3 and 47.9 years as mathematical described by the following equations: $(\mathrm{1}/\mathrm{12.6})+(\mathrm{1}/\mathrm{17.1})\cong \mathrm{1}/\mathrm{7.3}$, and $(\mathrm{1}/\mathrm{12.6})-(\mathrm{1}/\mathrm{17.1})\cong \mathrm{1}/\mathrm{47.9}$.

Once more, in the average chronology obtained in Passo Fundo (bottom panel of Fig. 3), we observe that the period of 6.6 and 35 years may be the beat period (the rate of alternation between constructive and destructive wave interference) results from the periods of 11 and 16.2 years, [$(\mathrm{1}/\mathrm{11})+(\mathrm{1}/\mathrm{16.2})\cong \mathrm{1}/\mathrm{6.6}$] and [$(\mathrm{1}/\mathrm{11})-(\mathrm{1}/\mathrm{16.2})\cong \mathrm{1}/\mathrm{35}$], respectively, as discussed by Raspopov et al. (2000, 2001). In the same way, the periods of 17.5 and 33.5 years may also be a result from the beat period of 23 and 73.1 years, [$(\mathrm{1}/\mathrm{23})+(\mathrm{1}/\mathrm{73.1})\cong \mathrm{1}/\mathrm{17.5}$] and [$(\mathrm{1}/\mathrm{23})-(\mathrm{1}/\mathrm{73.1})\cong \mathrm{1}/\mathrm{33.5}$], respectively.

Moreover, Gusev (2011) analyzed the natural climatic oscillations driven by solar activity. The author verified that variations in climatic parameters do not always occur synchronously with the corresponding 11- and 22-year solar cycles. Based on this analysis, we apply a period bandwidth filter of 8–13 years in the tree-ring width average and in the sunspot number series, as shown in Fig. 4. We observe that the phase shift between tree rings and sunspot variations is variable, and it changes with time from 0 to 180^∘. The phase shift occurs when there is a significant change in the sunspot number amplitude, as can be observed in Dalton minimum (1794–1824). Therefore, our result of tree-ring width and solar variation analysis behaves in the same way as reported by Gusev (2011).

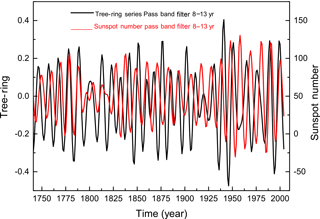
Figure 4 Signals filtered of the mean width of tree-ring series and sunspot number between 8 and 13 years.

In addition, Gusev (2011) and Gusev and Martin (2012) showed that the profile features between climatic parameters and sunspot number can be reproduced by a forced oscillation equation using a driving force term that describes the variation of the sunspot number with a period varying from 16 to 70 years. This forced oscillation equation also describes the presence of natural climatic oscillations with periods above 30 years, which possibly correspond to the Brückner cycle usually observed in the variations of some climatic parameters such as precipitation and temperature.

It is also possible that the correlation and the phase shift between tree-ring width and the sunspot number series can be due to the modulation of the cloudiness (Dengel et al., 2009). This modulation can be caused by the cosmic ray ionization, which increases the diffuse radiation, and consequently, makes the photosynthetic production more efficient (see Urban et al., 2007; Dengel et al., 2009, and references therein). Inoue et al. (1979) showed that the tree growth is greater when it is not under extremely shady conditions compared to full daylight conditions. Their study was based on the daily photosynthetic production of each plant using Araucaria angustifolia specimen in the juvenile stage. However, the ratio of the strength between the effect of cosmic rays and the climate (UV light) may be about 1 : 10, and therefore the effect of cosmic rays is minor.

Figure 5 Amplitude spectra of the (a) annual mean temperature anomaly between 24 and 44^∘ S; (b) SOI. The significance level is 95 %.

4.2 Climate influences

Other period intervals observed in Fig. 3 may also be related to the climate influences, such as the El Niño and La Niña phenomena, which correspond to a period bandwidth of 2–7 years in each tree-ring amplitude spectrum. This phenomenon modifies global climate activity; however it does not have well-defined regularity (Oliveira, 1999).

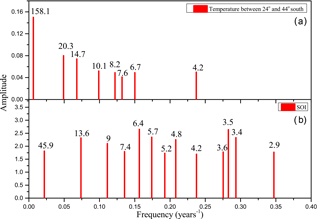
For this reason, spectral analysis using the ARIST is performed, in order to verify a possible cause–effect relationship between the periods found in the annual mean temperature and the SOI series, as shown in Fig. 5. The periods between 8.2 and 10.1 years in the temperature data may be related to solar cycle of 11 years, while the period of 20.3 years may be related to the Hale cycle. The period of 158.1 years may be related to the second harmonic of the 328 years found by Rigozo et al. (2008) in the sunspot number data. The lower periods of 4.2, 6.7, and 7.6 years in the temperature data can be attributed to the effects of the El Niño events because they are related to the periods of 4.2, 6.4, and 7.4 years in the SOI data. These results agree with the El Niño model discussed by Guilyardi (2006). In that paper, the El Niño model is assessed in terms of the two modes: first – the sea surface temperature mode, which implies low-amplitude El Niño events with a frequency of 2–3 years; second – the thermocline mode, which involves the western Pacific circulation, and consequently, implies large-amplitude El Niño events with a frequency of 4–5 years.

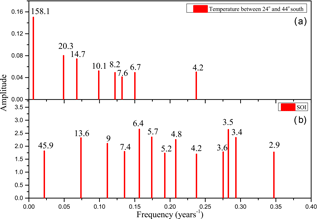
Figure 6 Morlet cross-wavelet map between the annual mean temperature anomaly, between 24 and 44^∘ S, and the tree-ring average chronology. The contour plot represents the significance levels for 95 %. Panel (b) presents the global wavelet spectrum, which is defined as the wavelet coefficients power average for each scale, i.e., it corresponds to a Fourier spectrum.

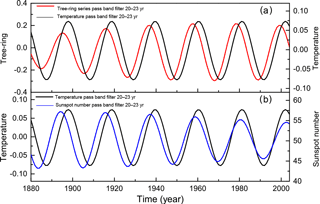
Figure 7 (a) Signals filtered of the mean width of tree-ring series and annual mean temperature anomaly (from 24 to 44^∘ S); (b) annual mean temperature anomaly (from 24 to 44^∘ S) and sunspot number, between 20 and 23 years.

As discussed by Rigozo et al. (2008), it is possible to quantify every frequency detected (P_i) in the signal by obtaining a power fraction (fP, where $fP=\frac{P_i}{\sum P_i}$) of this frequency related to the total spectrum (sum of all powers found). Therefore, Table 1 presents the power fraction of every frequency signal found in relation to the total signal spectrum for both the annual mean temperature and the SOI presented in Fig. 5. We observe that 25 % of the fP of the annual mean temperature (between 4.2 and 7.6 years) is related to the SOI periodicities (between 2.9 and 7.4 years). In other words, the El Niño phenomenon represents a total of 25 % of the spectral temperature signal. This result is consistent with the study on trees 391-year-old trees in Japan of Muraki et al. (2011), who found lower periods than the solar cycles and related them to ENSO events.

Table 1 Power fraction of the frequency found in the mean width of tree-ring series and annual mean temperature anomaly and SOI signals.

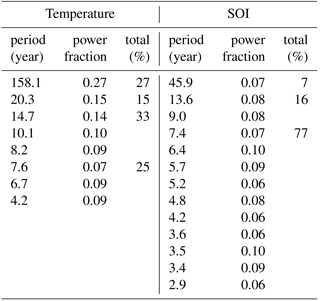
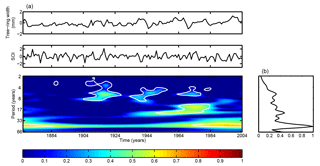
Figure 8 Morlet cross-wavelet map between tree-ring average chronology collected in Passo Fundo and the SOI. The contour plot represents the significance levels for 95 %. Panel (b) presents the global wavelet spectrum, which is defined as the wavelet coefficients power average for each scale, i.e., it corresponds to a Fourier spectrum.

In order to correlate the influence of the temperature on the tree-ring width growth, the Morlet cross-wavelet transform was performed in the annual mean temperature anomaly (from 24 to 44^∘ S) and tree-ring average chronology was collected in Passo Fundo (Fig. 6). The results show lower periods, between 4 and 8 years, occurring during 1910–1935, and the period of ∼ 12 years appears between 1944 and 1974, while the period of ∼ 22 years is present during the entire data interval. Some studies showed that the periodicities of 11, 22, and 90 years found in temperature time series are related to the solar activity (Raspopov et al., 2004; Gusev, 2011; Gusev and Martin, 2012). Moreover, we observe the strong relationship between the temperature and tree-ring growth in ∼ 1917, when the lowest temperature value is observed. This decrease in temperature is also followed by a decrease of the tree-ring growth.

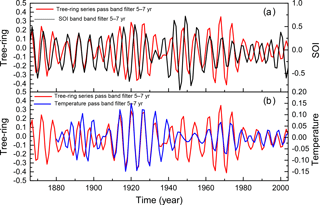
Figure 9 (a) Signals filtered of the mean width of tree-ring series and annual mean temperature anomaly (from 24 to 44^∘ S); (b) annual mean temperature anomaly (from 24 to 44^∘ S) and sunspot number, between 5 and 7 years.

Similar to the analysis done in Fig. 4, Fig. 7 shows the tree-ring time series, the annual mean temperature anomaly (from 24 to 44^∘ S) series, and the sunspot number series filtered using a period bandwidth of 20 to 23 years. A lag of 3 years between the tree-ring growth and the temperature during 1880 to 2004 is observed, whereas between the temperature and the sunspot, the phase variably shifts with time, changing from 4 years to 0 along the interval studied. The reverse behavior is observed between the tree rings and the sunspot number which corresponds to the red line and blue line in Fig. 7, respectively. We can see that the phase shifts with time from 0 to 4 years. The results of the Morlet cross-wavelet scalogram of SOI and tree-ring chronology obtained in Passo Fundo are shown in Fig. 8. These results indicate mainly a presence of periods between 4 and 8 years during the time interval of ∼ 1910 to ∼ 1925, ∼ 1930 to ∼ 1955, and ∼ 1965 to ∼ 1975; and a period of ∼ 17 years during ∼ 1945 to ∼ 1985. The same kind of result was found by Rigozo et al. (2003) using wavelet techniques. They studied the periodicities of ENSO presented in the tree rings in the region of South Brazil, and they found periods between 2 and 8 years in their data showing non-stationary behavior.

The time series of tree-ring growth from Passo Fundo, the SOI, and the temperature anomaly (from 24 to 44^∘ S) are usually filtered in the interval of 5–7 years, in order to find better correlations in their global wavelet spectrum and cross-wavelet analysis. This interval is chosen because it may be related to the El Niño/La Niña events. It is well known that during the occurrence of El Niño events, an excess of precipitation occurs in the South Brazil region, and the northern parts of Argentina and Uruguay. In contrast, the lowest level of precipitation takes place during the occurrence of La Niña (Rao and Hada, 1990; Grimm et al., 1998).

Figure 9a shows the tree-ring and the SOI series filtered between 5 and 7 years, while Fig. 9b shows the tree-ring and the temperature anomaly series filtered by the same bandwidth filter. The series of tree-ring growth and SOI show a phase and anti-phase shift throughout the years of 1866 and 2004. In the intervals of 1866–1900 and 1959–1982, these series are in phase, whereas in the intervals of 1900–1930 and 1982–2004, they are in anti-phase. In the interval of 1930–1959, there is a lag of one year between these two series. Similar behavior is observed between the series of tree-ring growth and temperature anomaly. These series of tree-ring growth and temperature anomaly are in anti-phase during the intervals of 1880–1906 and 1937–1950, and in phase during the intervals of 1906–1937 and 1950–2004.

Comparing the SOI to the temperature anomaly (black and blue curve in Fig. 9a and b, respectively), we observe that in the interval 1880–1930, both series are in anti-phase. This fact indicates that during the El Niño events (SOI negative) there is an increasing temperature tendency due to the highest precipitation levels. Rampelotto et al. (2012) showed that the rainfall and the temperature variability in Santa Maria, RS (29^∘41^′ S, 53^∘48^′ W) is related to the SOI variation, especially during El Niño events. Souza Echer et al. (2008) also found that the precipitation at Pelotas, RS (31^∘46^′19^′′ S, 52^∘20^′33^′′ W) is strongly influenced by the ENSO phenomenon. In summary, analyzing both graphs in Fig. 9, we observe that both the SOI and the temperature have strong influence on the araucaria growth in this region of Brazil, mainly when the temperature anomaly presents its greatest amplitude as shown in the interval of 1906–1937.

5 Conclusions

In this paper, 12 araucaria dendrochronological series from Passo Fundo are analyzed using the ARIST. Also, the global wavelet spectrum and the cross-wavelet analyses are performed in order to identify the non-stationary characteristics in tree-ring, temperature and SOI data. The principal results may be summarized as follows:

• i.

  There is evidence of the solar cycle influence related to the cycles of Schwabe (∼ 11 years), Hale (∼ 22 years), and Gleissberg (∼ 70 to ∼ 90 years) in each dendrochronological series, and also in the dendrochronological average series.

• ii.

  The cycles of ∼ 18 years (Saros lunar cycle) and of ∼ 30 to ∼ 35 years (Brückner climatic cycle) may be a combination between the Gleissberg cycle and the Hale cycle; they may be a result of the nonlinear effects of the solar activity in the terrestrial environment.

• iii.

  There is evidence in the temperature and in the SOI analysis that some of their natural climatic oscillation may be driven by solar activity.

• iv.

  In total, 25 % of the temperature spectral content is related to the periodicities between ∼ 4 and ∼ 7 years, which are related to the El Niño/La Niña phenomena.

• v.

  A 20–23-year bandwidth period is found in the dendrochronological series, and it is well correlated with the temperature anomaly (from 24 to 44^∘ S), but it has a phase lag of ∼ 3 years.

• vi.

  In addition, the rainfall and the temperature variability in Passo Fundo seem to also be related to the SOI variation (sometimes in phase or in anti-phase) for the bandwidth corresponding to the El Niño/La Niña phenomena.

In summary, these results indicate that the variability in tree-ring growth of Araucaria angustifolia is closely related to the variation of temperature and precipitation. This fact is possibly due to the nonlinear effects of Sun variability, and to the El Niño–Southern Oscillation in the climate system over South Brazil. Therefore, it should be further investigated.