the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Determination of gravity wave parameters in the airglow combining photometer and imager data
Prosper K. Nyassor
Ricardo Arlen Buriti
Igo Paulino
Amauri F. Medeiros
Hisao Takahashi
Cristiano M. Wrasse
Delano Gobbi
Mesospheric airglow measurements of two or three layers were used to characterize both vertical and horizontal parameters of gravity waves. The data set was acquired coincidentally from a multi-channel filter (Multi-3) photometer and an all-sky imager located at São João do Cariri (7.4∘ S, 36.5∘ W) in the equatorial region from 2001 to 2007. Using a least-square fitting and wavelet analysis technique, the phase and amplitude of each observed wave were determined, as well as the amplitude growth. Using the dispersion relation of gravity waves, the vertical and horizontal wavelengths were estimated and compared to the horizontal wavelength obtained from the keogram analysis of the images observed by an all-sky imager. The results show that both horizontal and vertical wavelengths, obtained from the dispersion relation and keogram analysis, agree very well for the waves observed on the nights of 14 October and 18 December 2006. The determined parameters showed that the observed wave on the night of 18 December 2006 had a period of min, with the horizontal wavelength of 235.66 ± 11.78 km having a downward phase propagation, whereas that of 14 October 2006 propagated with a period of min with a horizontal wavelength of km, and with an upward phase propagation. The observation of a wave taken by a photometer and an all-sky imager allowed us to conclude that the same wave could be observed by both instruments, permitting the investigation of the two-dimensional wave parameter.
Keywords. Atmospheric composition and structure (airglow and aurora) – electromagnetics (wave propagation) – history of geophysics (atmospheric sciences)
- Article
(2996 KB) - Full-text XML
- BibTeX
- EndNote
Propagation of atmospheric gravity waves in the upper atmosphere is extremely unstable. The vertical component of the propagating gravity wave is a very vital aspect in investigating the coupling dynamics between different regions of the atmosphere (Hocking, 1996). Due to the exponential decay of density with altitude and conservation of energy, gravity wave amplitudes increase exponentially with altitude, whereas dissipation processes like wave saturation and wave interaction with other waves and background wind limit the growth of the amplitude of the wave (Fritts and Alexander, 2003). Some studies on gravity wave saturations revealed that the momentum is transferred into the background wind, thereby depositing the wave energy into the background atmosphere (e.g. Fritts, 1984; Smith et al., 1987; Dewan and Good, 1986; Fritts and Alexander, 2003).
Measurements of gravity waves with periodicity in the mesosphere and lower thermosphere (MLT) region require passive airglow observation of the sky in a two-dimensional form with relatively high temporal resolution (in a few minutes). Among several gravity wave observational techniques, such as radio frequency and optical measurements, airglow observations using a photometer and all-sky imagers have been effectively used (Hecht et al., 1987; Taylor et al., 1991, 2009; Takahashi et al., 1992; Taori and Taylor, 2006). Airglow emissions are prominent physical phenomena used to further study the vertical and horizontal parameters of gravity waves. According to Takahashi et al. (2011), the airglow emission layers that have been extensively used to monitor wave activity in the MLT region are OI5577 (hereafter OI), O2(0–1) band (hereafter O2), NaD-line (hereafter NaD) and OH(6–2) band (hereafter OH) at their respective peak emission altitudes of 97, 94, 90 and 87 km. Simultaneous observation of multiple airglow emissions is one of the techniques used to investigate the vertical propagation of gravity waves. For this technique to be feasible, the vertical wavelengths of the wave must be larger than the thickness of the airglow emission layer (Ghodpage et al., 2014). According to Noxon (1978) and Taori et al. (2005), such observational data can be used to compute the amplitude growth and the propagation characteristics of gravity waves.
In the present study, we investigated gravity wave parameters propagating vertically through OI, O2, NaD and OH emissions, their phase difference and variability of the amplitudes of the oscillations. Using the dispersion relation of gravity waves, the horizontal and vertical wavelengths are estimated for the observed short period oscillations (Vadas and Liu, 2009). The discussion will be focused on the similar periodicity observed within the three emission layers; the amplitude growth and the propagation direction.
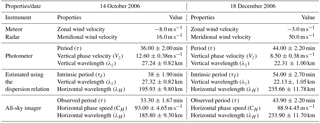
The instruments used for the present study are the multi-channel filter photometer (Multi-3), the all-sky imager and the meteor radar at São João do Cariri, located geographically at 7.4 ∘ S and 36.5∘ W. Among the listed instruments, the photometer is the main instrument used in observing the vertical parameters of the waves of interest, whereas the all-sky imager and the meteor radar were co-located instruments used to observe the horizontal parameters and the wind velocity respectively.
2.1 Photometer
A multi-channel tilting filter photometer (Multi-3) with five interference filters was used to measure the OI, O2, NaD and OH mesospheric airglow emissions. The observations were made between January 2001 and December 2007, resulting in 1051 nights of clear sky. Out of 1051 nights, only 389 nights present similar periods in at least two emission layers, of which 24 nights present similar periods in three emission layers.
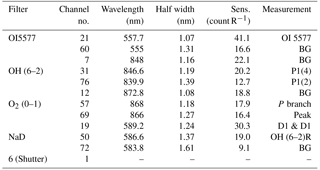
The background continuum intensity (R nm−1) and the line intensity (R) were measured in obtaining the zenith sky spectrum by tilting the filters relative to their optical axes in which a scan of about 8 nm wavelength was made. The mesospheric component of the OI557.7 nm was estimated by subtracting the ionospheric F region component computed as 20 % of the simultaneously observed OI630.0 nm intensity (Silverman, 1970). The time interval between the observation cycle was approximately 2 min, thereby making the temporal resolution 2 min. The photometer characteristics, spectral resolution and sensitivity, are summarised in Table 1.
A MgO white screen illuminated by a laboratory standard lamp (Eppley 8315, 100 W Tungsten filament lamp) was used to calibrate the absolute sensitivity (counts/Rayleigh) of the photometer. The estimated error in the absolute intensity for OI was approximately 5 and 10 % for OH(6–2) and O2 due to the increased systematic error in calibration. For rotational temperature (TOH), the instrumental error determined was ±3 K (Takahashi et al., 1998).
The usual observation scheme was undertaken with a period of 13 nights per month focused around the time of new moon with more than 6 h of uninterrupted observation time per night. In this work, a database of OI, O2, NaD and OH was analysed to find the similar periodicities in the propagating gravity waves in each emission altitude. More details on the multi-channel filter photometer can be found in Kirchhoff (1984), Buriti et al. (2001, 2004), and Wrasse et al. (2004).
2.2 All-sky imager
An all-sky imager in São João do Cariri was used. Images of OH (Meinel), OI5577, OI6300 and OI7774 airglow emission layers were taken by this equipment. With regards to the present work, only the OH Meinel airglow image corresponding to the selected coincident photometer observation was used.
The airglow all-sky imager is an optical instrument made of a fast fish-eye (f∕4) lens and a telecentric lens system, a filter wheel, a charged coupled device (CCD) camera, and a set of lenses for reconstruction of the images on the CCD. The entire system is microcomputer-based controlled. The CCD camera has an area of 6.04 cm2, with a 1024 × 1024 back-illuminated pixel array of 14 bits per pixel. In order to enhance the signal-to-noise ratio, the images were binned on-chip down to a resolution of 512 × 512. The high quantum efficiency, low dark noise (0.5 electrons pixel−1 s−1), low readout noise (15 electron rms) and high linearity (0.05 %) of this device enable it to measure airglow emissions (Medeiros et al., 2001). More details about the São João do Cariri imager have been reported by Medeiros et al. (2005).
2.3 Meteor radar
A SKiYMET all-sky interferometric meteor radar using an antenna array composed of two-element reception yagi antennas and three-element transmitting yagi antenna (five antennas) was used to observe winds in the mesosphere. This radar operates at a frequency of 35.24 MHz with a maximum output power of 12 kW. The radar measures the radial velocity by transmitted radiation scattered from meteor trails and the differences in the phase of the signal received by each possible pairing of antennas determines the position of the trail. This radar also measures the temperature at the height of the meteor peak count rates, but this parameter was not used in this work. The range is obtained by the delay between the transmitted and received signal. The least-square fitting technique applied to all the radial velocities measured in a given time/height bin was used to determine the zonal, meridional and vertical velocity components. Vertical velocities are normally very small and are therefore ignored. The respective temporal and vertical resolutions of this radar are typically 60 min and 2–3 km. More details on the radar have been published elsewhere (Hocking, 1996, 2001; Buriti et al., 2008).
2.4 Methodology and data analysis
2.4.1 Photometer time series
The first step considered before processing the photometer time series data was the background intensity variation. This variation gives the degree of contaminants composed of artificial light sources, clouds or astronomical lights. The time range with high contaminants is eliminated, which leads to the reduction of the time duration of the observation period.
Secondly, high-frequency oscillations are removed by taking three-point running means. Since gravity waves are modulated by tidal waves (Preusse et al., 2008; Takahashi et al., 1999), the effects of tides are eliminated by constructing a harmonics for ter-diurnal and semi-diurnal tides. The harmonics (H) used is expressed mathematically by
where A, B and C are the unknown amplitude, x is the time of observation, ϕ is the phase and T is the period. Subtracting the harmonics from the average (smoothed) intensity, the residual (only gravity waves) time series is obtained. The residual is then subjected to a Lomb–Scargle periodogram and wavelet spectrogram to obtain the observed gravity wave period. Using the least-square fitting method and the wavelet spectrogram, the amplitude and the phase were estimated. The vertical phase velocity (Vz) was then estimated from the quotient of the difference between the higher and lower emission layers observed and their corresponding phase, expressed by Eq. (2):
Multiplying the period obtained by the vertical phase speed, the vertical wavelength was obtained using Eq. (3).
Using the intrinsic period, the horizontal wavelength was calculated by using the dispersion relation for gravity waves (Gossard and Hooke, 1975),
where m is the vertical wavenumber, H is the scale height, N is the buoyancy frequency and ωI is the intrinsic frequency. By scale analysis, the effect of the Coriolis parameter is ignored due to the period of observation and the location of the observation site. From the horizontal wavenumber, kH, the horizontal wavelength is estimated using Eq. (5),
The intrinsic frequency, ωI, was estimated by finding the difference between the vertical observed period obtained from Lomb–Scargle and the estimated background wind frequency using Eq. (6).
where ωI is the intrinsic frequency, ω0 is the observed frequency, UH is the velocity of the background wind and kH is the horizontal wavenumber estimated from the horizontal wavelength obtained from the keogram analysis.
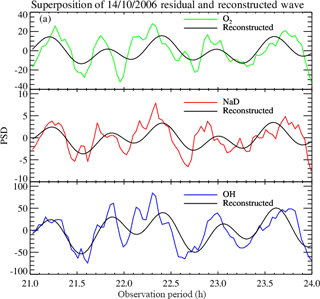
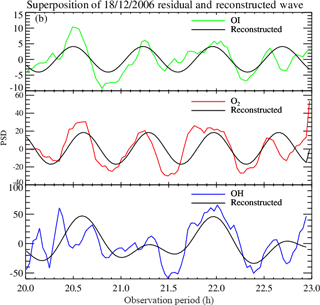
Figure 3The superposition of the 14 October 2006 residual wave and the reconstructed wave with two harmonics.
2.4.2 All-sky image
The co-located all-sky images were analysed using the keogram analysis from which the horizontal parameters of the same wave are obtained. The keogram simply separates the image of the oscillation under study into meridional and zonal components. The wave parameters are then obtained from the geometrical relationship between the components. For this study we used the keogram analysis to obtain the horizontal wave parameters such as the horizontal wavelength, the period and the direction of propagation of the wave observed by the photometer. Details on the methodology of the keogram analysis can be found in Paulino et al. (2011), with more details in Figueiredo et al. (2018). The co-located meteor radar is operated in a routine base providing information on zonal and meridional wind velocities which aided in the estimation of the intrinsic wave frequency.
3.1 Airglow photometer
Out of the 7 years of data used, we found two nights which present similar periods of oscillations in the airglow emission layers in the photometer data and images from the all-sky imager. Due to cloud contaminations, only 3 h of observed data were used for the selected nights. On 14 October, observations made between 21:00 and 23:00 local time (LT) were used in the present study, whereas on 18 December, observations between 20:00 and 22:00 LT were used. Similar periodic oscillations were found in the co-located airglow images and the spectral characteristics of these oscillations were estimated and studied.
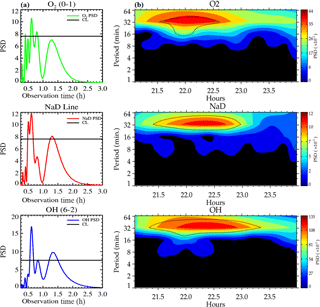
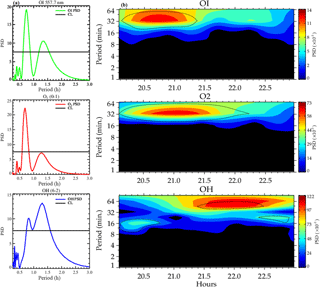
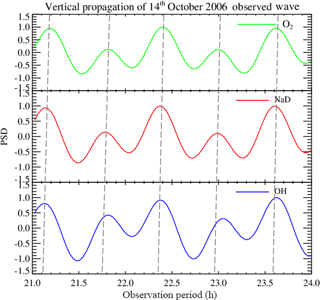
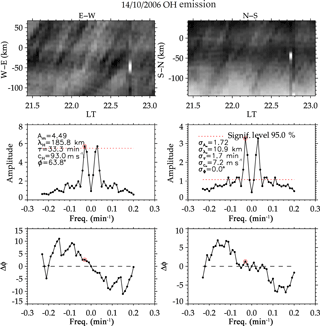
The gravity wave period estimated using Lomb–Scargle on the night of 14 October 2006 in the O2, NaD and OH airglow emission layers presented two major peaks with confidence levels greater than 95 %; Fig. 1a shows the Lomb–Scargle periodogram; the first peak presented a period of ∼ 0.60 ± 0.03 h (36 ± 2.00 min) and ∼ 1.33 ± 0.07 h (79.80 ± 4.00 min) for the second peak. To confirm the true presence of the second peak, we subjected this period to the Horne and Baliunas test (Horne and Baliunas, 1986). According to the Horne and Baliunas test, spectral leaked frequencies may have significant height, which might appear as a true signal. The Horne and Baliunas test is used to test the originality of the frequencies with lower power spectral density (PSD). This was done by subtracting a sinusoid with frequency corresponding to the most significant peak from the data (Ferraz-Mello, 1981) and recomputing the periodogram. If the second peak (the so-called ghost frequency) still exists, it implies the second peak is a true signal. The Horne and Baliunas test was done to verify the true existence of the periodicities obtained in the Lomb–Scargle periodograms (Fig. 1a) for the cases presented, but the test plots are not shown here. Since the photometer data is almost evenly distributed, wavelet analysis (Torrence and Compo, 1998) (as shown in Fig. 1b) of the same residual data was applied to confirm the periods observed in the Lomb–Scargle analysis. Comparing these two techniques, we affirm that the periods are true.
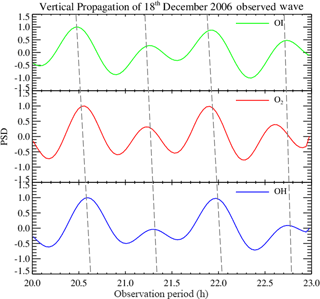
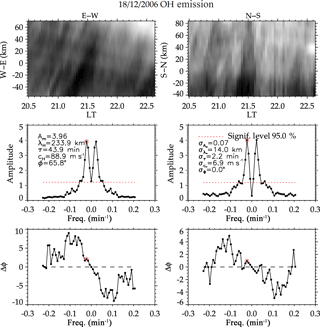
Similarly, Fig. 2a and b show the same analysis for the waves observed on 18 December 2006. It is noted that, for the OI and O2 emission layers, the oscillation periods of ∼ 0.73 ± 0.04 (43.80 ± 2.20 min) and ∼ 1.33 ± 0.10 h (79.80 ± 4.00 min) were obtained in which the highest peak was ∼ 0.73 ± 0.04 h (43.80 ± 2.20 min). On the other hand, the OH emission layer had the highest peak at ∼ 1.33 ± 0.10 h (79.80 ± 4.00 min) and the lowest at 0.73 ± 0.10 h. Due to this inversion, the 1.33 ± 0.10 h (79.80 ± 4.00 min) period dominated in the wavelet spectrogram, as shown in Fig. 2b, whereas the 0.73 ± 0.10 h period was not seen.
In order to confirm the result estimated from the residual time, an artificial wave was reconstructed using the amplitude, phase and observed period as presented in Table 3 to evaluate the obtained result. To achieve that, the reconstructed waves of two harmonics were overplotted on the residual photometer data as shown in Figs. 3 and 4.
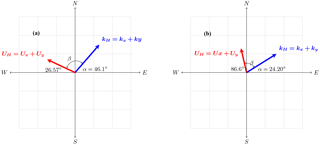
Figure 11Vector diagram of the wave with respect to the background wind for (a) 14 October 2006 and (b) 18 December 2006 observation.
The amplitude (Rayleigh), phase (hour) and observed period (hour) obtained from the least-square fitting approach and Lomb–Scargle are shown in Table 2 for 14 October and 18 December 2006 observation, respectively.
3.2 Vertical propagation
From Table 2, we observed on the night of 14 October that O2 lags NaD by ∼ 0.10 ± 0.00 h (6.20 ± 0.00 min) with a vertical phase velocity (Vz) of km h−1 (10.75 ± 0.32 m s−1) and vertical wavelength (λz) of 23.22 ± 0.67 km, whilst NaD also lags behind OH by ± 0.05 ± 0.00 h (3.05 ± 0.09 min) with a vertical phase velocity (Vz) of 59.04 ± 1.77 km h−1 (16.40 ± 0.49 m s−1) and vertical wavelength (λz) of 35.42 ± 1.06 km. Considering the three emission layers, O2 lags behind OH by 0.15 ± 0.01 h (9.25 ± 0.46 min) with a vertical phase velocity (Vz) of 45.41 ± 1.36 km h−1 (12.60 ± 0.38 m s−1) and vertical wavelength (λz) of 27.24 ± 0.82 km. Based on the wave parameters obtained we plot the harmonic analysis of 14 October, which is shown in Fig. 5. From Fig. 5, one can see that there is a tendency of phase delay from OH to O2, indicating an upward phase propagation. According to the gravity wave propagation theory, upward phase propagation means downward energy propagation (Nappo, 2013).
Considering only two emission layers, i.e. O2 and NaD, and NaD and OH, we found the average of their sum for the phase velocities and vertical wavelengths to be 48.88 ± 1.47 km h−1 (13.57 ± 0.41 m s−1) and 31.33 ± 0.94 km respectively. Comparing these with the values obtained from the direct three emission layer estimation, it is noted that there is a slight difference between the computed values. These differences can be attributed to the difference in the assumed emission altitudes of the two layers and the background wind at that layer. Statistically, the linear fitting of the altitude of the three emission layers against their respective phase has a coefficient of determination of 0.96.
Referring to Table 2 for 18 December 2006, it was revealed that, OI leads O2 by h (6.82 ± 0.34 min) with a vertical phase velocity (Vz) of 26.40 ± 0.79 km h−1 (7.31 ± 0.22 m s−1) and vertical wavelength (λz) of 19.36 ± 0.77 km while O2 leads OH by ∼ 0.21 ± 0.01 h (4.27 ± 0.21 min) with vertical phase velocity (Vz) of 32.78 ± 1.31 km h−1 (9.10 ± 0.36 m s−1) and vertical wavelength (λz) of 23.93 ± 1.00 km. Considering the three emission layers; OI leads OH by h (19.63 ± 0.98 min) with a vertical phase velocity (Vz) of 30.56 ± 1.38 km h−1 (8.49 ± 0.38 m s−1) and vertical wavelength (λz) of 23.21 ± 1.05 km. This shows that, the wave is having an upward energy propagation (a downward phase propagation). Thus, taking the average of the two emission layers, OI versus O2, and O2 versus OH, we found that the phase velocity and vertical wavelength were 29.59 ± 1.33 km h−1 (8.22 ± 0.37 m s−1) and 21.64 ± 0.97 km respectively. Comparing these with the values obtained from the three emission layers direct estimation, slight variations between the values were noted. These variations can be due to the assumed altitudes between the emission layers and the background wind at that layer. Statistically, the linear fit of the three emission layers (altitude against their corresponding phase) have a coefficient of determination of 0.97. Figure 6 shows the downward phase propagation of the 18 December 2006 observed wave.
3.3 Keogram analysis
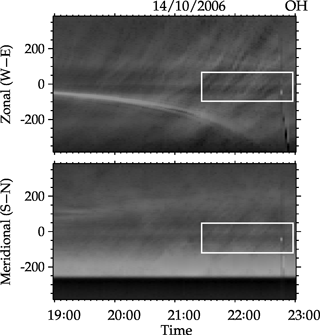
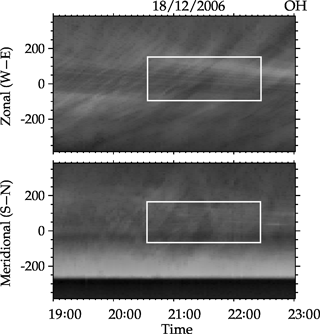
Figures 7 and 8 are the OH NIR co-located keogram developed from the unwarped images obtained from the all-sky imager of the same waves observed in the photometer data on 14 October and 18 December 2006. The results of the spectral analysis obtained are shown in Figs. 9 and 10.
For the case of 14 October 2006 (Fig. 9), the period of the horizontal component of the wave is 0.55 ± 0.03 h (33.30 ± 1.70 min) propagating at 334.80 ± 16.74 km h−1 (93.00 ± 7.30 m s−1) and having a horizontal wavelength of 185.80 ± 10.09 km with an azimuthal angle of 64∘ suggesting that, the horizontal component of the wave is northeastward.
Similarly, Fig. 10 shows the result from the all-sky image of 18 December 2006. The intrinsic period of the horizontal component of the wave is 0.73 ± 0.04 h (43.90 ± 2.20 min) propagating at 88.90 ± 6.90 m s−1 with a horizontal wavelength of 233.90 ± 14.00 km moving at 65.8∘ from the azimuth and showing that the wave on this day is propagating northeastward. To estimate the influence of the background wind, coincident meridional and zonal wind velocities were taken from the Meteor radar.
The coincident measurement of the horizontal component of the wave using the all-sky imager and the background wind velocity from the Meteor radar jointly gave the general insight about the interaction of the wave with the background wind. The background wind velocity was smoothed by a 3 h running average. Using the zonal and meridional wind velocities, the magnitude and the direction of the winds were also estimated. With these two parameters, the angle (β) that the wind made with the wave was found to be 89.6∘, indicating that the wind was moving northwestward. By using the projection method of the dot product (Dray and Manogue, 2006), the intrinsic frequency obtained using Eq. (6) was found to be s−1 (38.19 min) and the observed frequency to be s−1 (33.30 min) for the case of 14 October 2006. This value was confirmed using the inner product method, where the angle (), their respective wind velocity and wave numbers were used in this estimation. The inner product method also yielded the same result for the intrinsic frequency. From the dispersion relation for gravity waves (Eq. 4), the estimated value for the horizontal wavelength (λH) is 195.93 ± 9.80 km.
For 18 December 2006, the angle (β) that the wind made with the wave was found to be 69.2∘. By using the projection method of the dot product, the intrinsic frequency was found to be s−1 (54.00 min), whereas the observed frequency was s−1 (43.90 min). Applying the same inner product approach used earlier, we found that the angle (α) the wave made with the azimuth was 24.2∘. This agreed with the estimated value obtained using the projection method. Their respective wind and wave numbers were used in this estimation. The inner product method also yielded the same result for the intrinsic frequency. From the dispersion relation for gravity waves, the estimated value for the horizontal wavelength is 235.66 ± 11.78 km. The estimated values from our analysis for the two cases are shown in Table 3.
The simultaneous observation of similar gravity wave periods within the three airglow emission layers in the photometer data suggests a vertical propagation of the same gravity wave. The observed waves propagated through the emission altitudes OH (87 km), NaD (90 km) to O2 (94 km) for the case of 14 October 2006, whereas that of 18 December 2006 propagated through OH (87 km), O2 (94 km) to OI (97 km). From our observation, the amplitude growth reflects theory and agrees reasonably with previous observational works done (e.g. Taori et al., 2007; Taori and Kamalakar, 2013; Takahashi et al., 2011; Ghodpage et al., 2014).
Using the wind data from the meteor radar, the intrinsic frequency of the vertical (either upward or downward) phase propagation was estimated using Eq. (6). With the estimated intrinsic frequency, the horizontal wavelength was estimated using the dispersion relation of gravity waves (Vadas and Liu, 2009) and compared to the horizontal wavelength obtained from the keogram analysis of the simultaneously observed OH images. Both the analytical and numerical results of the horizontal wavelength agree reasonably, hence suggesting that the same wave was observed by the photometer and the all-sky imager. The observations of the same wave in both instruments allow the investigation of the two-dimensional properties of the waves.
From the case study on the night of 14 October and 18 December 2006, we observed two different wave propagation modes, one had an upward phase propagation while the other had a downward phase propagation. The latter is well known as upward propagation of gravity wave (Fritts and Alexander, 2003). However, the former can not be explained by the upward propagating gravity waves. In order to further investigate the present case we have to know more about the background atmosphere (wind and temperature, for example).
The data used to produce the results of this manuscript were obtained from the Observatório de Luminescência Atmosférica da Paraíba at São João do Cariri, which is supported by the Universidade Federal de Campina Grande and Instituto Nacional de Pesquisas Espaciais. If someone would like to access these data, please contact either Amauri F. Medeiros (afragoso@df.ufcg.edu.br) or Cristiano M. Wrasse (cristiano.wrasse@inpe.br).
The authors declare that they have no conflict of interest.
This article is part of the special issue “Space weather connections to near-Earth space and the atmosphere”. It is a result of the 6∘ Simpósio Brasileiro de Geofísica Espacial e Aeronomia (SBGEA), Jataí, Brazil, 26–30 September 2016.
This work has been supported by Coordeção de Aperfeiçoamento de
Pessoal de Nível Superior (CAPES) and Conselho Nacional de
Desenvolvimento Cinetífico e Tecnóligo (CNPq). Also we
acknowledge, Christopher Torrence of the National Snow and Ice Data Center,
CIRES, CU Boulder and Gilbert P. Compo of CIRES, University of Colorado &
Physical Sciences Division, NOAA ESRL Boulder, Colorado for their significant
contribution in their guidance to the Wavelet Analysis used in this work. Igo
Paulino thanks the CNPq for the grant with number 303511/2017-6. Finally, a
special thanks goes to both the reviewers and editor, who have tremendously
helped to improve this paper through their comments and constructive
criticism.
The topical editor, Christoph
Jacobi, thanks M. Sivakandan and one anonymous referee for help in evaluating
this paper.
Buriti, R., Takahashi, H., and Gobbi, D.: First results from mesospheric airglow observations at 7.5∘ S, Revista Brasileira de Geofísica, 19, 169–176, 2001. a
Buriti, R., Takahashi, H., Gobbi, D., de Medeiros, A., Nepomuceno, A., and Lima, L.: Semiannual oscillation of the mesospheric airglow at 7.4∘ S during the PSMOS observation period of 1998–2001, J. Atmos. Sol.-Terr. Phy., 66, 567–572, 2004. a
Buriti, R. A., Hocking, W. K., Batista, P. P., Medeiros, A. F., and Clemesha, B. R.: Observations of equatorial mesospheric winds over Cariri (7.4∘ S) by a meteor radar and comparison with existing models, Ann. Geophys., 26, 485–497, https://doi.org/10.5194/angeo-26-485-2008, 2008. a
Dewan, E. and Good, R.: Saturation and the “universal” spectrum for vertical profiles of horizontal scalar winds in the atmosphere, J. Geophys. Res.-Atmos., 91, 2742–2748, 1986. a
Dray, T. and Manogue, C. A.: Journal of Online Mathematics and Its Applications The Geometry of the Dot and Cross Products, 6, 1–13, 2006. a
Ferraz-Mello, S.: Estimation of periods from unequally spaced observations, Astron. J., 86, 619–624, 1981. a
Figueiredo, C., Takahashi, H., Wrasse, C., Otsuka, Y., Shiokawa, K., and Barros, D.: Medium scale traveling ionospheric disturbances observed by detrended total electron content maps over BrazilMedium scale traveling ionospheric disturbances observed by detrended total electron content maps over Brazil, J. Geophys. Res.-Space, 123, 2215–2227, 2018. a
Fritts, D. C.: Gravity wave saturation in the middle atmosphere: A review of theory and observations, Rev. Geophys., 22, 275–308, 1984. a
Fritts, D. C. and Alexander, M. J.: Gravity wave dynamics and effects in the middle atmosphere, Rev. Geophys., 41, 1–64, 2003. a, b, c
Ghodpage, R., Taori, A., Patil, P., Gurubaran, S., Sharma, A., Nikte, S., and Nade, D.: Airglow measurements of gravity wave propagation and damping over Kolhapur (16.5∘ N, 74.2∘ E), Int. J. Geophys., 2014, 1–9, 2014. a, b
Gossard, E. and Hooke, W.: Waves in the Atmosphere, 456 pp., 1975. a
Hecht, J., Walterscheid, R., Sivjee, G., Christensen, A., and Pranke, J.: Observations of wave-driven fluctuations of OH nightglow emission from Sondre Stromfjord, Greenland, J. Geophys. Res.-Space, 92, 6091–6099, 1987. a
Hocking, W.: Dynamical coupling processes between the middle atmosphere and lower ionosphere, J. Atmos. Terr. Phys., 58, 735–752, 1996. a, b
Hocking, W.: Middle atmosphere dynamical studies at Resolute Bay over a full representative year: Mean winds, tides, and special oscillations, Radio Sci., 36, 1795–1822, 2001. a
Horne, J. H. and Baliunas, S. L.: A prescription for period analysis of unevenly sampled time series, Astrophys. J., 302, 757–763, 1986. a
Kirchhoff, V.: Elementos básicos sobre fotômetros de filtro inclinável, 1984. a
Medeiros, A. F., Taylor M. J., Takahashi, H., Batista, P. P., and Gobbi, D.: An unusual airglow wave event observed at Cachoeira Paulista 23∘ S, Adv. Space Res., 27, 1749–1754, https://doi.org/10.1016/S0273-1177(01)00317-9, 2001.
Medeiros, A., Fechine, J., Buriti, R., Takahashi, H., Wrasse, C., and Gobbi, D.: Response of OH, O2 and OI5577 airglow emissions to the mesospheric bore in the equatorial region of Brazil, Adv. Space Res., 35, 1971–1975, 2005. a
Nappo, C. J.: An introduction to atmospheric gravity waves, Academic Press, 2013. a
Noxon, J.: Effect of internal gravity waves upon night airglow temperatures, Geophys. Res. Lett., 5, 25–27, 1978. a
Paulino, I., Takahashi, H., Medeiros, A., Wrasse, C., Buriti, R., Sobral, J., and Gobbi, D.: Mesospheric gravity waves and ionospheric plasma bubbles observed during the COPEX campaign, J. Atmos. Sol.-Terr. Phys., 73, 1575–1580, 2011. a
Preusse, P., Eckermann, S. D., and Ern, M.: Transparency of the atmosphere to short horizontal wavelength gravity waves, J. Geophys. Res.-Atmos., 113, 1–16, 2008. a
Silverman, S.: Night airglow phenomenology, Space Sci. Rev., 11, 341–379, 1970. a
Smith, S. A., Fritts, D. C., and Vanzandt, T. E.: Evidence for a saturated spectrum of atmospheric gravity waves, J. Atmos. Sci., 44, 1404–1410, 1987. a
Takahashi, H., Sahai, Y., Batista, P. P., and Clemesha, B. R.: Atmospheric gravity wave effect on the airglow O2 (0, 1) and OH (9, 4) band intensity and temperature variations observed from a low latitude station, Adv. Space Res., 12, 131–134, 1992. a
Takahashi, H., Batista, P., Buriti, R., Gobbi, D., Nakamura, T., Tsuda, T., and Fukao, S.: Simultaneous measurements of airglow oh emissionand meteor wind by a scanning photometer and the muradar, J. Atmos. Sol.-Terr. Phys., 60, 1649–1668, 1998. a
Takahashi, H., Batista, P., Buriti, R., Gobbi, D., Nakamura, T., Tsuda, T., and Fukao, S.: Response of the airglow OH emission, temperature and mesopause wind to the atmospheric wave propagation over Shigaraki, Japan, Earth Planet. Space, 51, 863–875, 1999. a
Takahashi, H., Onohara, A., Shiokawa, K., Vargas, F., and Gobbi, D.: Atmospheric wave induced O2 and OH airglow intensity variations: effect of vertical wavelength and damping, Ann. Geophys., 29, 631–637, https://doi.org/10.5194/angeo-29-631-2011, 2011. a, b
Taori, A. and Kamalakar, V.: Airglow measurements of wave damping at upper mesospheric altitudes over a low latitude station in India, Indian Journal of Radio and Space Physics (IJRSP), 42, 371–379, 2013. a
Taori, A. and Taylor, M.: Characteristics of wave induced oscillations in mesospheric O2 emission intensity and temperatures, Geophys. Res. Lett., 33, 1–5, 2006. a
Taori, A., Taylor, M. J., and Franke, S.: Terdiurnal wave signatures in the upper mesospheric temperature and their association with the wind fields at low latitudes (20∘ N), J. Geophys. Res.-Atmos., 110, 1–12, 2005. a
Taori, A., Guharay, A., and Taylor, M. J.: On the use of simultaneous measurements of OH and O2 emissions to investigate wave growth and dissipation, Ann. Geophys., 25, 639–643, https://doi.org/10.5194/angeo-25-639-2007, 2007. a
Taylor, M. J., Espy, P., Baker, D., Sica, R., Neal, P., and Pendleton Jr, W.: Simultaneous intensity, temperature and imaging measurements of short period wave structure in the OH nightglow emission, Planet. Space Sci., 39, 1171–1188, 1991. a
Taylor, M. J., Pautet, P.-D., Medeiros, A. F., Buriti, R., Fechine, J., Fritts, D. C., Vadas, S. L., Takahashi, H., and São Sabbas, F. T.: Characteristics of mesospheric gravity waves near the magnetic equator, Brazil, during the SpreadFEx campaign, Ann. Geophys., 27, 461–472, https://doi.org/10.5194/angeo-27-461-2009, 2009. a
Torrence, C. and Compo, G. P.: A practical guide to wavelet analysis, B. Am. Meteorol. Soc., 79, 61–78, 1998. a
Vadas, S. L. and Liu, H.: Generation of large-scale gravity waves and neutral winds in the thermosphere from the dissipation of convectively generated gravity waves, J. Geophys. Res.-Space, 114, 1–25, 2009. a, b
Wrasse, C. M., Takahashi, H., and Gobbi, D.: Comparison of the OH(8–3) and (6–2) band rotational temperature of the mesospheric airglow emissions, Revista Brasileira de Geofísica, 22, 223–231, 2004. a