Plasma flow patterns in and around magnetosheath jets

The magnetosheath is commonly permeated by localized high-speed jets downstream of the quasi-parallel bow shock. These jets are much faster than the ambient magnetosheath plasma, thus raising the question of how that latter plasma reacts to incoming jets. We have performed a statistical analysis based on 662 cases of one THEMIS spacecraft observing a jet and another (second) THEMIS spacecraft providing context observations of nearby plasma to uncover the flow patterns in and around jets. The following results are found: along the jet's path, slower plasma is accelerated and pushed aside ahead of the fastest core jet plasma. Behind the jet core, plasma flows into the path to fill the wake. This evasive plasma motion affects the ambient magnetosheath, close to the jet's path. Diverging and converging plasma flows ahead and behind the jet are complemented by plasma flows opposite to the jet's propagation direction, in the vicinity of the jet. This vortical plasma motion results in a deceleration of ambient plasma when a jet passes nearby.

Keywords. Magnetospheric physics (magnetosheath; MHD waves and instabilities; solar wind–magnetosphere interactions)

1 Introduction

Plasma jets defined as transient increases in dynamic pressure are a very common phenomenon in the subsolar magnetosheath (Němeček et al., 1998; Savin et al., 2008; Karlsson et al., 2012; Plaschke et al., 2016). In particular, the magnetosheath region downstream of the quasi-parallel shock is permeated by magnetosheath jets. Correspondingly, subsolar jet occurrence is found to be controlled – almost exclusively – by the cone angle of the interplanetary magnetic field (IMF), i.e., the angle between the IMF and the Earth–Sun line, while other solar wind parameters or their variability only play a minor role (Archer et al., 2012; Archer and Horbury, 2013; Plaschke et al., 2013). A substantial fraction of jets is believed to originate from bow shock ripples or undulations (Hietala and Plaschke, 2013), which are common at the reforming, patchy, quasi-parallel bow shock (Schwartz and Burgess, 1991; Omidi et al., 2005). At inclined shock surfaces, the solar wind plasma is compressed, but less decelerated and thermalized, leading to entities of dense and fast plasma inside the magnetosheath (Hietala et al., 2009, 2012). Other generation mechanisms are related to IMF discontinuities, discontinuity-related hot flow anomalies (HFAs), and spontaneous HFAs originating from foreshock cavitons (Lin et al., 1996a, b; Savin et al., 2012; Zhang et al., 2013; Kajdič et al., 2013; Omidi et al., 2013; Archer et al., 2014; Chu et al., 2017).

Due to their mechanisms of generation, jets are more prevalent closer to the bow shock (Plaschke et al., 2013). Nevertheless, large-scale jets with a cross-sectional diameter of over 2 R_E (Earth radii) have been found to impact the subsolar magnetopause at relatively high rates (with respect to other transients) of once every 21 min, on average, and once every 6 min when the IMF cone angle is low (under 30^∘). These impact rates are even more remarkable when taking into account that jets of smaller scale occur more often and that typical jet scales are on the order of 1 R_E (Karlsson et al., 2012; Archer et al., 2012; Hietala et al., 2012; Plaschke et al., 2013, 2016; Gunell et al., 2014). When jets impact the magnetopause, the consequences can be substantial. Due to their excess dynamic pressure, they will indent the magnetopause locally, generating surface waves on the boundary and inner magnetospheric compressional waves (Glassmeier and Heppner, 1992; Plaschke et al., 2009; Shue et al., 2009; Amata et al., 2011; Plaschke and Glassmeier, 2011; Archer et al., 2013a, b). In addition, local reconnection may perhaps be triggered at the magnetopause (Hietala et al., 2012). In the magnetosphere, the radiation belt electron population may be modified by magnetopause shadowing (Elkington et al., 2003; Turner et al., 2012). Consequences may even be seen on the ground, in the form of increased ionospheric convection, geomagnetic field variations, and possibly “throat” aurora observations (Hietala et al., 2012; Dmitriev and Suvorova, 2012; Archer et al., 2013b; Han et al., 2017).

Consequences of jets are not only restricted to the magnetopause and the magnetosphere. Also within the magnetosheath, jets are expected to alter ambient plasma due to their excess velocity. Simulation results by Karimabadi et al. (2014) show that fast jets push slower ambient magnetosheath plasma out of their way. As a result, that ambient plasma performs an evasive motion around jets, such that it is further slowed down or even pushed in a sunward direction in the vicinity of jets. Thereby, jets may create anomalous flows, stir the plasma in the magnetosheath, and hence be a source of additional turbulence. Note, however, that these simulations were 2-D, which may affect the flow patterns.

A first observational indication for this plasma motion has recently been reported by Plaschke et al. (2017). Within an interval of repeated jet observations downstream of the quasi-parallel bow shock by the Magnetospheric Multiscale (MMS) spacecraft (Burch et al., 2016), a high plasma velocity variability is seen, which includes sunward plasma flows in the subsolar magnetosheath. Unfortunately, due to the close MMS spacecraft configuration on the order of a few tens of kilometers (i.e., much smaller than the typical jet scale sizes), it could not be directly proven that the sunward flows were indeed caused by the nearby passage of high-speed jets. This is the primary aim of this paper, to ascertain whether or not jets cause evasive motion of the plasma in the magnetosheath.

2 Data sets

To achieve this goal, we need observations of jets by multiple spacecraft (at least spacecraft pairs) that feature separations on the order of typical jet cross-sectional scales, so that the jet and the plasma outside can be monitored simultaneously. The orbits of the five Time History of Events and Macroscale Interactions during Substorms (THEMIS) spacecraft turn out to be ideally suited (Angelopoulos, 2008). In particular, the inner three THEMIS spacecraft (THA, THD, and THE) regularly traverse the dayside magnetosheath at the required distances from one another when their orbit apogees are located in the subsolar local time sector.

A data set of 2859 subsolar magnetosheath high-speed jets already exists that we can use for this study; ion velocity, density and dynamic pressure measurements of one of them are shown as an example in Fig. 1. The data set was created for a statistical study by Plaschke et al. (2013), based on 4 years (2008 to 2011) of five THEMIS spacecraft measurements (THA to THE, each spacecraft treated separately as a single spacecraft). Here we briefly recall the steps that led to the compilation of the jet data set; the selection process is explained in more detail in section 2 of Plaschke et al. (2013).

First, THEMIS measurements at geocentric distances between 7 and 18 R_E, taken inside a 30^∘ wide cone with the tip at Earth and open towards the Sun, were preselected. From these measurements, magnetosheath intervals were selected: (i) where THEMIS ion density measurements exceeded twice the solar wind density (see panel b of Fig. 1) as given by the OMNI high-resolution solar wind data set (King and Papitashvili, 2005); (ii) where the differential ion energy flux of 1 keV ions exceeded that of 10 keV ions; and (iii) where THEMIS magnetometer (Auster et al., 2008), electrostatic analyzer (McFadden et al., 2008), and OMNI IMF, ion density, ion velocity, and plasma beta data were available. Note that the OMNI data are already propagated to the bow shock nose. Averages over 5 min of OMNI measurements preceding any time of interest were used to account for the additional propagation delays to the locations of the THEMIS spacecraft. Therewith, 6960 intervals with durations exceeding 2 min were obtained, comprising in total 2736.9 h of magnetosheath measurements.

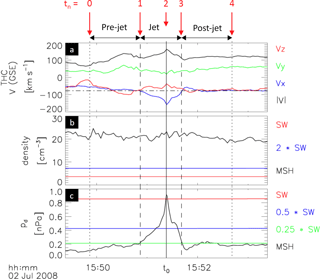
Figure 1 Figure showing a magnetosheath high-speed jet observed by THC. From top to bottom: (a) ESA ion velocity measurements in GSE, (b) ESA ion density measurements in black and (twice the) solar wind density measurements by OMNI in red (blue), (c) dynamic pressure p_d,x measured by THC (black) as well as (1∕4 and 1∕2) the solar wind value in red (green and blue). On top, the pre-jet, jet, and post-jet intervals are marked; normalized times are given in red. Figure modified from Fig. 1 in Plaschke et al. (2013).

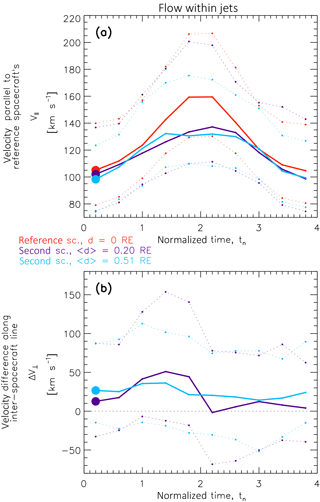
Figure 2 Cases where second spacecraft observed jets. The top panel (a) shows v_∥ and the bottom panel (b) shows Δv_⟂ values. Median and (upper and lower) quartile values are depicted with solid and dotted lines, respectively. Red lines correspond to reference spacecraft measurements; purple and blue lines correspond to second spacecraft measurements for d<0.4 R_E (〈d〉=0.20 R_E) and d>0.4 R_E (〈d〉=0.51 R_E), respectively. Initial median values pertaining to normalized times t_n=0…0.4 are depicted by bold circles.

Second, within these subsolar magnetosheath data intervals, jets were identified as follows: (i) the dynamic pressure in the geocentric solar ecliptic (GSE) x-direction ($p_{\mathrm{d},x}=\mathit{\rho }{v}_x^{\mathrm{2}}$) shall be larger than half the respective solar wind value p_d,sw (see panel c of Fig. 1). The interval where $p_{\mathrm{d},x}>p_{\mathrm{d},\mathrm{sw}}/\mathrm{4}$ shall be denoted as a jet interval of length t_jet. Start and end times of that interval shall be denoted with t_jet,s and t_jet,e, respectively, and the time of maximum $p_{\mathrm{d},x}/p_{\mathrm{d},\mathrm{sw}}$ shall be denoted with t₀ (all these times are marked with vertical lines in Fig. 1). (ii) The observing spacecraft shall be located in the magnetosheath (as defined above) between $t_{\mathrm{jet},\mathrm{s}}-\mathrm{1}$ min and $t_{\mathrm{jet},\mathrm{e}}+\mathrm{1}$ min. Intervals between $t_{\mathrm{jet},\mathrm{s}}-\mathrm{1}$ min and t_jet,s and between t_jet,e and $t_{\mathrm{jet},\mathrm{e}}+\mathrm{1}$ min are called pre-jet and post-jet intervals, respectively (see the top of Fig. 1). (iii) The ion velocity v_x shall be negative within the jet interval, and shall surpass v_x(t₀)∕2 at least once within both pre-jet and post-jet intervals (see panel a of Fig. 1). Therewith we ensure that jets propagate towards the magnetopause and are associated with significant, localized enhancements in velocity. By applying these criteria, Plaschke et al. (2013) identified 2859 jets in total in the preselected magnetosheath data.

Plaschke et al. (2016) go on to identify jet observations by one THEMIS spacecraft (denoted as the reference spacecraft at position r_ref) for which additional observations by another THEMIS spacecraft (second spacecraft at r_sec) are available in a plane perpendicular to the jet propagation direction. That latter direction shall be given by the ion velocity v measured by the reference spacecraft at time t₀. In detail, it is ascertained whether there is a second spacecraft such that the angle between

$$\begin{array}{}\text{(1)}& \mathit{d}={\mathit{r}}_{\sec }-{\mathit{r}}_{\mathrm{ref}}\end{array}$$

and v is between 80 and 100^∘ at times t₀. The second spacecraft shall be located in the magnetosheath between $t_{\mathrm{0}}\pm (t_{\mathrm{jet}}+\mathrm{1}$ min). These criteria are fulfilled for 561 jets. For 101 of those, there are even two “secondary” spacecraft measurements available (i.e., all three THEMIS spacecraft were located appropriately in the magnetosheath). Hence, we obtain 662 observations by pairs of jet observing reference spacecraft and context providing second spacecraft in the subsolar magnetosheath. Plaschke et al. (2016) call the data set comprising these 662 cases the two spacecraft (2SC) data set (see Sect. 3 of that paper for more details).

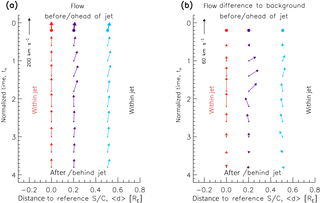
Figure 3 Visualization of velocities depicted in Fig. 2; cases where second spacecraft observed jets. Left panel (a): arrows show median velocity components v_∥ (upwards) and Δv_⟂ (to the right) corresponding to different normalized times t_n. Red arrows are based on reference spacecraft measurements. Purple and blue arrows show median v_∥ and Δv_⟂ for second spacecraft at two different distances 〈d〉=0.20 R_E and 〈d〉=0.51 R_E. Initial values pertaining to normalized times t_n=0…0.4 are depicted by bold arrows/circles. Right panel (b): derived from (a) by subtracting those initial flow values, i.e., the respective background flows in the magnetosheath.

3 Analysis and results

A jet is observed by the reference spacecraft in each of the 662 cases; i.e., there are defined times $t_{\mathrm{jet},\mathrm{s}}-\mathrm{1}$ min, t_jet,s, t₀, t_jet,e, and $t_{\mathrm{jet},\mathrm{e}}+\mathrm{1}$ min. We identify normalized times t_n=0…4, such that t_n=0 and t_n=4 correspond to $t_{\mathrm{jet},\mathrm{s}}-\mathrm{1}$ min and $t_{\mathrm{jet},\mathrm{e}}+\mathrm{1}$ min, respectively. Times t₀ are associated with t_n=2. For the jet shown in Fig. 1, the normalized times are given on top of the figure in red.

In order to characterize the flow patterns in and around jets, we use the ion velocities v measured by the pairs of THEMIS spacecraft: (i) in the direction of v as seen by the reference spacecraft (v_ref), which at t_n=2 corresponds to the jet direction as observed by the reference spacecraft, and (ii) in the direction d, which is approximately perpendicular to v_ref, at least at t_n=2. We denote ion velocity measurements along v_ref with v_∥, and along d as v_⟂. The difference of the latter measurements

$$\begin{array}{}\text{(2)}& \mathrm{\Delta }{v}_{⟂}=v_{⟂,\sec }-v_{⟂,\mathrm{ref}}\end{array}$$

indicates whether the flow along the inter-spacecraft line is divergent (Δv_⟂ positive) or convergent (Δv_⟂ negative).

3.1 Flow pattern inside jets

First, we look into the plasma flow within jets. Therefore, we select those cases of the 2SC data set where second spacecraft observed simultaneously a jet, i.e., where times t₀ (t_n=2) as seen by the reference spacecraft were within a jet interval observed by second spacecraft. This holds for 230 cases. We divide this group into cases where $\left|\mathit{d}\right|=d<\mathrm{0.4}{R}_{\mathrm{E}}$ and cases where d>0.4 R_E. There are 84 and 146, respectively, and their median distances 〈d〉 are 〈d〉=0.20 R_E and 〈d〉=0.51 R_E. Furthermore, we divide the normalized time sequence (between t_n=0 and 4) into 10 intervals of 0.4 time units each. For each group of cases and time interval, we compute median v_∥ and Δv_⟂ values, as well as upper and lower quartiles thereof. These are displayed in Fig. 2.

In the top panel (a), v_∥ is shown as a function of normalized time t_n. The median velocity v_∥ as seen by the reference spacecraft (red solid line) increases from just over 100 to about 160 km s⁻¹. That velocity is computed from all 662 2SC cases, as it does not depend on second spacecraft observations; the same applies to the reference spacecraft observations shown in Figs. 3, 4, and 5. In normalized time, the maximum in v_∥ is symmetric around t_n=2. Second spacecraft at different distances d (but still within the jets that the reference spacecraft are in) see corresponding increases in v_∥ (purple and blue lines). However, the peak median v_∥ values are lower (less than 140 km s⁻¹). This is expected, since we use the ion velocity vectors measured by the reference spacecraft as reference directions for v_∥. Hence, reference/second spacecraft measurements of v_∥ are necessarily equal to/lower than the full modulus of the ion velocity at the respective spacecraft locations.

In the bottom panel (b) of Fig. 2, Δv_⟂ values are shown. Almost all median values (solid lines) are positive. Hence, in general, we observe diverging flows, as expected in the subsolar magnetosheath due to the velocity deviation imposed on the solar wind plasma when passing the curved bow shock. In agreement with expectations, this effect is larger for larger spacecraft separations d, as evidenced by the initial (t_n=0…0.4) median Δv_⟂ values that are depicted by bold circles. With respect to the variations in Δv_⟂, a clear bipolar pattern is apparent. Divergence of plasma flows first increases ahead of t_n=2. After t_n=2, the divergence becomes notably smaller, before returning to pre-jet levels. At t_n=2.2 even slightly negative median Δv_⟂ values (converging flows) are observed, for 2SC cases with d<0.4 R_E (〈d〉=0.20 R_E, solid purple line).

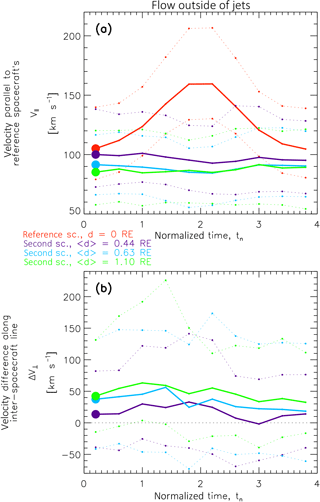
Figure 4 Cases where second spacecraft did not observe jets. The top panel (a) shows v_∥ and the bottom panel (b) shows Δv_⟂ values. Median and (upper and lower) quartile values are depicted with solid and dotted lines, respectively. Red lines correspond to reference spacecraft measurements; purple, blue, and green lines correspond to second spacecraft measurements for 〈d〉=0.44 R_E, 〈d〉=0.63 R_E, and 〈d〉=1.10 R_E, respectively. Initial median values pertaining to normalized times t_n=0…0.4 are depicted by bold circles.

The data from Fig. 2 are visualized in Fig. 3a. The median velocities v_∥ and Δv_⟂ yield the vertical and horizontal components of the arrows. Red arrows correspond to reference spacecraft median v_∥ observations, purple and blue arrows to the median velocity measurements by second spacecraft. Note that the normalized time increases from the top to the bottom of the figure. Hence, earlier observations corresponding to the front side of the jets are on top, while later observations (rear side) are shown at the bottom.

Figure 3b is directly derived from Fig. 3a by subtracting the background magnetosheath flows, i.e., the initial median values pertaining to normalized times t_n=0…0.4. Hence, it depicts and emphasizes the jet-induced changes in plasma flow with respect to the magnetosheath background. Clearly, the change from flow divergence to convergence around t_n=2 can be observed (arrows pointing right, then left). This change coincides with an overall flow velocity increase in the direction of v_ref (upward pointing arrows), not only at the reference spacecraft, but also at the jet-crossing second spacecraft locations.

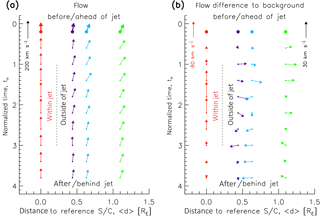
Figure 5 Visualization of velocities depicted in Fig. 4; cases where second spacecraft did not observe jets. Left panel (a): arrows show median velocity components v_∥ (upwards) and Δv_⟂ (to the right) corresponding to different normalized times t_n. Red arrows are based on reference spacecraft measurements. Purple, blue, and green arrows show median v_∥ and Δv_⟂ for the second spacecraft at three different distances 〈d〉=0.44 R_E, 〈d〉=0.63 R_E, and 〈d〉=1.10 R_E. Initial values pertaining to normalized times t_n=0…0.4 are depicted by bold arrows/circles. Right panel (b): derived from (a) by subtracting those initial flow values, i.e., the respective background flows in the magnetosheath. Note that the arrow scales in panel (b) are different for reference and second spacecraft measurements.

3.2 Flow pattern outside jets

Similar to Fig. 2, Fig. 4 shows velocities v_∥ and Δv_⟂ for median distances 〈d〉=0.44 R_E (spacecraft distances d<0.55 R_E, 202 cases), 〈d〉=0.63 R_E ($\mathrm{0.55}{R}_{\mathrm{E}}<d<\mathrm{0.85}{R}_{\mathrm{E}}$, 122 cases), and 〈d〉=1.10 R_E ($\mathrm{0.85}{R}_{\mathrm{E}}<d<\mathrm{1.7}{R}_{\mathrm{E}}$, 67 cases), derived from spacecraft pair observations where second spacecraft did not observe jets while the reference spacecraft did. Apparently, results for v_∥ are very different when comparing Figs. 2a and 4a. Second spacecraft outside jets do not observe an increase in v_∥, but rather a decrease close to t_n=2. This decrease is slight in the v_∥ medians, but quite pronounced in their upper quartiles.

Again, in general, median v_∥ are smaller and median Δv_⟂ values are larger for larger distances 〈d〉, as evidenced for instance by the values pertaining to t_n=0…0.4 that are depicted by bold circles in both panels of Fig. 4.

In the median Δv_⟂ data pertaining to the smallest distances d (solid purple line in bottom panel b), the bipolar pattern of increasing/decreasing flow divergence over jet passages can be recognized well. This bipolar pattern is also clearly visible in the corresponding upper and lower quartile data, similar to what is seen inside the jet (see Fig. 2b). However, in comparison, that pattern seems to be slightly shifted towards larger normalized times: the minimum in median Δv_⟂ is reached at t_n=3, where it becomes slightly negative (converging flows). With larger distances d from the reference spacecraft, a clear bipolar pattern is not apparent any more. However, we still see an increase in Δv_⟂ from t_n=0 to about t_n=1…1.4. That increase starts earlier for more distant spacecraft. Thereafter, Δv_⟂ essentially decreases to lower levels with respect to t_n=0 (bold circles). Similar to Fig. 3, the data from Fig. 4 are visualized in Fig. 5.

Figure 5b depicts how the magnetosheath flow is altered by the nearby passage of a jet. As in Fig. 3b, the divergence and later convergence of plasma flows can be clearly seen. However, in the v_ref direction, magnetosheath plasma outside of jets is decelerated rather than accelerated around t_n=2, as evidenced by slightly downward pointing arrows.

4 Discussion

The results obtained in the previous section allow for the following interpretation. When a high-speed jet penetrates slower magnetosheath plasma, it acts as a plough. The plasma immediately ahead of the fastest jet (core) region (i) will be accelerated in jet propagation direction and thereby contribute to the jet, and (ii) will be pushed to the side (increased divergence of plasma) to make way for the faster jet plasma. This is consistent with increases in both v_∥ and Δv_⟂ around t_n=1 as shown in Figs. 2 and 3. The passage of the core jet plasma creates a wake region to which relatively slower plasma is taken in, leading to a minimum in Δv_⟂ (less diverging or even converging plasma) and a decrease from the maximum in v_∥ between t_n=2 and 3 (again, Figs. 2 and 3). The situation is illustrated in an exaggerated and simplified manner in Fig. 6: see the thin and thick arrows along the trajectory of the “second spacecraft inside jet” that resemble those in Figs. 3a and b, respectively. Note that Fig. 6, similar to Figs. 3b and 5b, does not show any non-jet-related, i.e., general, differences in v_∥ between reference and second spacecraft, as well as generally positive Δv_⟂ levels that increase with d, which should be attributed to the common divergence of plasma flows in the subsolar magnetosheath.

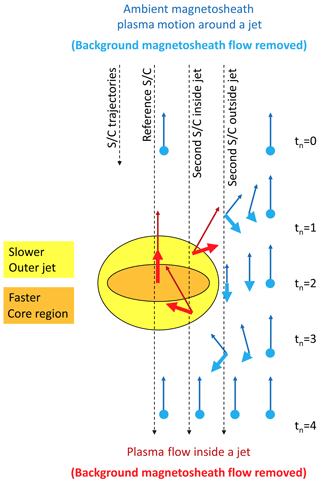
Figure 6 Sketch of plasma flow patterns inside (red) and outside (blue) a magnetosheath jet. The flows are depicted by thin solid arrows resembling those in Figs. 3a and 5a. Differences from the background magnetosheath flow are illustrated by thick arrows and dots in lighter colors (compare to Figs. 3b and 5b). The jet plasma itself is shown to be layered, with slower plasma (in yellow) outside a faster core region (in orange). The upper part corresponds to the magnetosheath ahead of the jet (t_n=0), whereas the lower part of the sketch depicts the trailing magnetosheath region (t_n=4).

Pushing plasma out of the region ahead of the core jet region needs to have repercussions also on the plasma that is not directly in the jet's way, but in the vicinity of the propagation path. It will also be pushed away from that path ahead of the jet, consistent with an increase in Δv_⟂ before t_n=2 in Fig. 4b. Likewise, behind the jet, plasma streaming into the wake region will also lead ambient plasma outside of the jet's way to follow suit, thereby decreasing Δv_⟂ after t_n=2, in agreement with observations. The plasma motion out/into the jet's way ahead/behind it needs to be closed by plasma motion from the region ahead to the region behind the jet. That plasma motion is opposite to the jet's direction of propagation and to the regular magnetosheath plasma motion, to which it is superposed. As a result, the ambient plasma motion in v_ref direction (i.e., v_∥) should exhibit a local minimum on the jet passage at t_n=2, as illustrated by the thin arrows in Fig. 6 along the trajectory “second spacecraft outside jet”. This can be seen in Fig. 4a. Note, however, that this minimum in median v_∥ is very shallow and far from exhibiting the sunward plasma motion (negative v_∥) in the ambient magnetosheath, seen in simulations by Karimabadi et al. (2014) as a reaction to jet penetration. Not even the lower quartiles of second spacecraft v_∥ measurements become negative.

In the frame of reference of the background magnetosheath flow (Figs. 3b, 5b, and thick arrows in Fig. 6), the plasma motion in and around jets is clearly vortical. In that respect, jets may be comparable to bursty bulk flows, as those cause somewhat similar plasma flows while ploughing through slower ambient plasma in the tail of the magnetosphere (e.g., Kauristie et al., 2000; Birn et al., 2004; Keiling et al., 2009; Panov et al., 2010).

There are also similarities in plasma motion with the laminar flow of an incompressible medium around a sphere or cylinder, in the sub-(magneto)-sonic regime applicable to most jets (Plaschke et al., 2013). In agreement with this interpretation, the change around t_n=2 from more to less diverging (even converging) flows, between maximum and minimum in Δv_⟂, occurs on longer timescales when observing ambient plasma further away from the jet (see Fig. 4b); these changes are fastest inside the jet (see Fig. 2b). In fact, observations of the second spacecraft not traversing the jet and being distant from the reference spacecraft hardly exhibit the full bipolar Δv_⟂ signature between t_n=0 and t_n=4 (blue and green lines/arrows in Figs. 4b and 5b). Increases in divergence seem to start earlier than at t_n=0. And at t_n=4, median Δv_⟂ values are still not recovering from the decreasing trend. Hence, the plasma motion of jet evasion starts earlier and is concluded later for plasma elements that are further away from the jet's path.

Lastly, it should be mentioned that the evasive plasma motion and, in general, the flow patterns in and around jets may be dependent on particular properties of those jets. For instance, it seems reasonable to assume that the cross-sectional scale size of jets, perpendicular to their propagation direction, may affect the evasive plasma motion, as it correlates with the amount of plasma that needs to be displaced. Unfortunately, it is impossible from two-spacecraft measurements to determine that perpendicular scale size for individual jets. Hence, any possible effect on plasma flow patterns associated therewith cannot be addressed in this paper. These and other effects dependent on jet properties remain to be studied in the future.

5 Summary and conclusions

We have performed a statistical study of plasma flows in and around magnetosheath high-speed jets, based on 662 cases in which one THEMIS spacecraft observed a jet and another nearby THEMIS spacecraft provided context to that observation. We find direct evidence for the following behavior: magnetosheath high-speed jets accelerate slower plasma ahead of them in their propagation path and push it to the side. After passage, plasma that is slower than the fastest jet plasma fills the wake region of the jet along its path. This evasive motion of slower plasma to give way to the jet core plasma is found to occur similarly in the ambient magnetosheath, near but not on a jet's path. In the frame of reference of the background magnetosheath flow, the plasma clearly performs a vortical motion. Divergent and convergent flows out of and towards the jet's path are complemented by flows in the opposite direction to the jet's propagation direction. These flows are superposed to the usual background flow of ambient plasma in the magnetosheath (mostly in the direction of propagation), thereby slowing plasma down. That deceleration is, however, small on average, so that no sunward flows become apparent in the statistical (median) results, contrary to simulations by Karimabadi et al. (2014) and case study observations by Plaschke et al. (2017).