Proton plasma asymmetries between the convective-electric-field hemispheres of Venus' dayside magnetosheath

Proton plasma asymmetries with respect to the convective electric field (E) are characterized in Venus' dayside magnetosheath using measurements taken by an ion mass-energy spectrometer and a magnetometer. Investigating the spatial structure of the magnetosheath plasma in this manner provides insight into the coupling between solar-wind protons and planetary ions. A previously developed methodology for statistically quantifying asymmetries is further developed and applied to an existing database of proton bulk-parameter measurements in the dayside magnetosheath. The density and speed exhibit mild asymmetries favoring the hemisphere in which E points towards the planet, while the magnetic-field-strength asymmetry favors the opposite hemisphere. The temperature perpendicular to the background magnetic field has a mild asymmetry favoring the hemisphere in which E points away from the planet; the temperature parallel to the background magnetic field and the temperature anisotropy present no significant asymmetries. Deflection of the solar wind due to momentum exchange with planetary ions is revealed by the O⁺ Larmor-radius trends of the asymmetries of the bulk-velocity components perpendicular to the upstream solar-wind flow. This interpretation is enabled by comparisons to experimental and numerical studies of solar-wind deflection at Mars, highlighting the benefits of comparative planetology studies.

1 Introduction

Unmagnetized bodies like Venus and Mars experience a closer interaction with the solar wind than those with an intrinsic magnetic field (Russell et al., 2016; Futaana et al., 2017). The upstream interplanetary magnetic field (IMF) B_IMF and convective electric field $\mathit{E}=-{\mathit{v}}_{\mathrm{SW}}\times {\mathit{B}}_{\mathrm{IMF}}$ (where v_SW is the solar-wind velocity; see Fig. 1) influence several phenomena, such as the plasma boundary morphology (Phillips et al., 1986; Zhang et al., 1991b; Edberg et al., 2009; Chai et al., 2015; Signoles et al., 2023), pick-up-ion dynamics (Barabash et al., 2007a, b; Brain et al., 2016; Jarvinen et al., 2016), and plasma wave activity (Du et al., 2010; Delva et al., 2011; Ruhunusiri et al., 2017; Xiao et al., 2018). In particular, the structure of the magnetosheath, the region where the solar wind transfers momentum and energy to the planet's magnetosphere (Longmore et al., 2005; Lucek et al., 2005; Haaland et al., 2017), is responsive to the configuration of the upstream electromagnetic fields. For example, the orientation of B_IMF with respect to the bow-shock normal affects solar-wind proton flows and temperature anisotropies (Halekas et al., 2017; Rojas Mata et al., 2023). More generally, observational studies of the magnetosheath's properties at bodies across the Solar System reveal significant dependencies on (magnetic) longitude, commonly referred to as dawn–dusk or $q_{⟂}/q_{\parallel }$ asymmetries (Dubinin et al., 2008; Dimmock and Nykyri, 2013; Walsh et al., 2014; Haaland et al., 2017; Carbary et al., 2017; Palmaerts et al., 2017; Behar et al., 2018; Rojas Mata et al., 2023). Investigating the physics behind these asymmetries has meaningfully advanced our fundamental understanding of the solar-wind interaction with the different bodies.

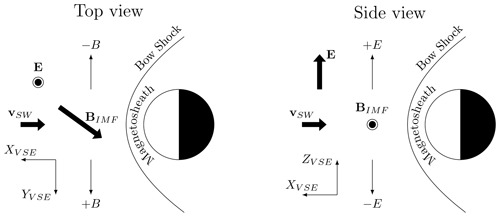
Figure 1 Configuration of electromagnetic fields around Venus. The solar-wind velocity v_SW and interplanetary magnetic field B_IMF define the direction of the convective electric field $\mathit{E}=-{\mathit{v}}_{\mathrm{SW}}\times {\mathit{B}}_{\mathrm{IMF}}$. We indicate the ±E and ±B hemispheres as well as the coordinate axes of the Venus–Sun–electric-field reference frame described in Sect. 2.1. The magnetosheath is the region downstream of the bow shock containing shocked solar-wind and planetary particles.

In contrast, few studies investigate analogous solar-wind plasma asymmetries at unmagnetized bodies as a function of latitude, i.e., between the hemispheres in which the convective electric field points away from (+E) or towards (−E) the body. At Mars, Dubinin et al. (2018) found that the magnetosheath plasma in the +E hemisphere is slower and more deflected in the direction opposite to E. Romanelli et al. (2020) determined that this asymmetry decreases with respect to the solar-wind density and increases with respect to the cross-flow component of B_IMF, which is consistent with a two-fluid description of mass loading by pick-up ions. Similar analyses based on plasma data at Venus have not been found, while magnetometer-based investigations found that the magnitude of B_IMF throughout the magnetic barrier is greater in the +E hemisphere (Phillips et al., 1986; Zhang et al., 1991b; Du et al., 2013; Xiao et al., 2018). Additionally, at both planets, B_IMF wraps asymmetrically (e.g., more tightly in the −E hemisphere) in the magnetosheath and magnetotail (Zhang et al., 2010; Du et al., 2013; Dubinin et al., 2019, 2021; Zhang et al., 2022). Other studies that mention differences between the ±E hemispheres instead focus on the dynamics of pick-up-ion escape (Barabash et al., 2007b, a; Dubinin et al., 2011; Xu et al., 2023), which has been linked to the B_IMF asymmetries at Venus (Luhmann et al., 1985; Phillips et al., 1987).

In parallel, numerical studies of the plasma environment around unmagnetized bodies have investigated topics such as hemispheric asymmetries, plasma boundary morphology, and pick-up-ion dynamics (Brecht and Ferrante, 1991; Moore et al., 1991; Shimazu, 1999; Kallio et al., 2011). For example, recent hybrid models (Kallio et al., 2006; Jarvinen et al., 2013, 2016) reproduce observed ±E asymmetries concerning plasma velocities and magnetic fields as well as indicating that the dynamics of pick-up ions depend on their upstream Larmor radius:

$$\begin{array}{}\text{(1)}& r_{L,i}={\displaystyle \frac{m_i}{q_i}}{\displaystyle \frac{\left|{\mathit{v}}_{\mathrm{SW}}\right|B_y}{B_{\mathrm{IMF}}^{\mathrm{2}}}},\end{array}$$

where m_i is the ion mass, q_i is the ion charge, and B_y is the cross-flow component of B_IMF. Although the asymmetries and pick-up ions may be linked, their exact interdependence remains unresolved, as asymmetries arise even if planetary ions (O⁺ and H⁺) are not included in the simulation (Brecht, 1990; Jarvinen et al., 2013). Additionally, few studies directly compare global simulations to local spacecraft data; therefore, how well the models quantitatively reproduce the measured spatial structure of the plasma environment is not fully determined.

The above illustrates the opportunity to develop new insight into magnetosheath physics by comparing observations and simulations not only at a single body but also across different bodies (i.e., Venus, Mars, and even comets). To this end, in this paper, we characterize the proton plasma asymmetries between the +E and −E hemispheres of Venus' dayside magnetosheath. We apply and extend the methodology developed by Rojas Mata et al. (2023) to statistically quantify asymmetries. In Sect. 2, we overview the data set used as well as the methodology for quantifying parameter asymmetries; our results follow in Sect. 3. We discuss connections to relevant numerical and observational studies in Sect. 4 and present concluding remarks in Sect. 5.

2 Data and methodology

2.1 Dayside magnetosheath database

For this study, we use a database of proton plasma bulk-parameter measurements in Venus' dayside magnetosheath (Rojas Mata and Futaana, 2023). Based on measurements taken by the Ion Mass Analyser (IMA) instrument (Barabash et al., 2007c) and the Magnetometer (MAG) (Zhang et al., 2006) aboard the Venus Express (VEX) mission (Svedhem et al., 2007), the database includes densities, velocities, and both perpendicular and parallel temperatures for 1181 locations in the magnetosheath along with corresponding upstream solar-wind conditions for the 597 orbits spanned. These bulk parameters result from bi-Maxwellian gyrotropic fits to IMA's velocity-distribution-function (VDF) measurements (Bader et al., 2019; Rojas Mata et al., 2022). Using fits instead of taking velocity-space moments “has the advantage of compensating for an incomplete sampling of the VDF due to IMA's limited field of view” (Rojas Mata et al., 2022), although only to a reasonable degree of blockage. Therefore, a variety of physical, statistical, and instrument-based criteria filtered out scans whose measurements were not adequately represented by a bi-Maxwellian model, either due to blockage or other reasons. As detailed in Rojas Mata et al. (2023), the special database of Rojas Mata and Futaana (2023) was constructed by manually searching for orbits with identifiable dayside bow-shock crossings in order to properly classify IMA scan locations. Further manual selection yielded the 597 orbits which have well-defined solar-wind conditions based on the medians of measurements immediately upstream of the dayside bow-shock crossing.

To characterize asymmetries between the ±E hemispheres of the magnetosheath, we use the Venus–Sun–electric-field (VSE) reference frame. The +X_VSE axis points against the solar-wind velocity, whose aberration we correct for using each orbit's upstream measurements (Rojas Mata et al., 2023). The +Y_VSE axis points along the cross-flow component of B_IMF, making +Z_VSE point along the upstream convective electric field E. The ±E hemispheres then correspond to the north (+Z_VSE) and south (−Z_VSE) hemispheres of this reference frame. The spatial coverage of the measurements in this reference frame is decently uniform except for limited coverage on the dayside close to the subsolar point caused by VEX's orbit geometry (see the “subsolar-wind hole” in Fig. 4 of Rojas Mata et al., 2023).

2.2 Statistically quantifying asymmetries

As VEX's highly elliptical, quasi-polar orbit led to the sampling of opposing VSE hemispheres under different solar-wind conditions, measurement-by-measurement pairing is not possible in order to quantify spatial asymmetries. Rojas Mata et al. (2023) addressed this challenge by developing a methodology that uses distributions of ratios of estimated measurement distributions as measures of the plasma parameter asymmetries. The technique also quantifies the variability in the asymmetries, provides flexibility for analyzing spatially binned data, and does not rely on models for the distributions. We refer the reader to the aforementioned reference for a full discussion of the methodology; here, we briefly overview the steps for quantifying the spatial asymmetry of a parameter a (e.g., speed or magnetic-field strength) between hemispheres H1 and H2:

1. Normalize the measurements of a by their corresponding value in the upstream solar wind, i.e., $\widehat{a}=a/a_{\mathrm{SW}}$.

2. Approximate the probability distribution function (PDF) of $\widehat{a}$ in each hemisphere using Gaussian kernel density estimates.

3. Draw 𝒪(10⁶) random samples each of ${\widehat{a}}_{\mathrm{H}\mathrm{1}}$ and ${\widehat{a}}_{\mathrm{H}\mathrm{2}}$ using the estimated PDFs.

4. Compute the distribution of $\stackrel{\mathrm{‾}}{a}={\widehat{a}}_{\mathrm{H}\mathrm{1}}/{\widehat{a}}_{\mathrm{H}\mathrm{2}}$ by pairing the samples.

In this work, $H\mathrm{1}=+E$ hemisphere and $H\mathrm{2}=-E$ hemisphere of the dayside magnetosheath. The process can also be applied to binned data (e.g., between two bins centered at corresponding latitudes in each hemisphere), so we also compute asymmetries with the measurements sorted in 15° wide latitudinal bins with a 50 % overlap. Note that such binning means that we average over radial distance and longitude. The bulk statistical quantities (e.g., medians) derived from the distribution of $\stackrel{\mathrm{‾}}{a}$ are superior products to those calculated by the alternative method of taking the ratio of the quantity between corresponding bins or hemispheres; such a method has higher uncertainty and worse reproducibility (Brody et al., 2002).

3 Results

3.1 Scalar parameters

In Fig. 2, we present the medians of the magnetosheath measurements (panels a–f) and of their normalized values (panels g–l) as of function of VSE latitude. The “error” bars indicate the first and third quartiles of the measurement distributions in each bin; rather than uncertainty, these values reflect the spread of the distributions and how they shift across bins. Bins centered less than 60° (45°) from the central parallel contain more than 70 (100) scans each. Bins 75° or farther from the central parallel contain far fewer scans (<25); thus, these data may have lower statistical reliability. Including them or not in the subsequent analysis, however, does not affect the final results and conclusions.

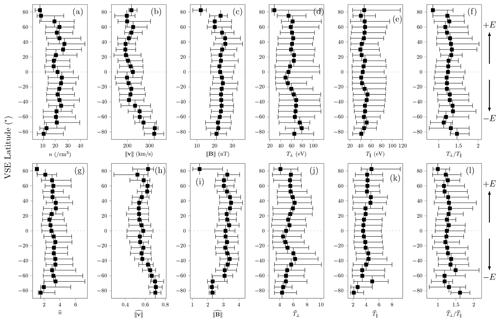
Figure 2 Proton parameters in the dayside magnetosheath as a function of latitudinal distance from the central parallel. Panels (a)–(f) show unnormalized values, whereas panels (g)–(l) are normalized by the solar-wind value. Positive VSE latitude corresponds to the +E hemisphere, whereas negative VSE latitude corresponds to the −E hemisphere. Markers indicate medians, while error bars correspond to the first and third quartiles.

The plasma speed appears lower closer to the central parallel (Fig. 2h), which is consistent with the expectation of higher deceleration closer to the near-sub-solar-wind region (Spreiter and Alksne, 1966; Spreiter et al., 1970). Other parameters do not seem to exhibit clear trends as a function of latitude, especially given their wide variability. In Fig. 3, we display the median parameter asymmetries as a function of latitudinal distance from the central parallel. Additionally, the top marker in each plot indicates the overall asymmetry calculated using data across all latitudes in each hemisphere. Most parameters exhibit weak or insignificant asymmetries except in the bins above 60°, which again contain far fewer measurements and may be less statistically reliable. The plasma speed is slightly higher (∼6 %) in the −E hemisphere (Fig. 3b), while the IMF magnitude seems more symmetric but still favors the +E hemisphere by ∼5 % (Fig. 3c). This contrasts with previous observations of clearly higher speeds in the −E hemisphere and stronger magnetic fields in the +E hemisphere (Phillips et al., 1986; Zhang et al., 1991b; Du et al., 2013; Dubinin et al., 2018; Xiao et al., 2018; Xu et al., 2023). Meanwhile, the ∼10 % lower density observed at lower latitudes in the +E hemisphere (Fig. 3a) may relate to plasma depletion in the magnetic barrier (Zwan and Wolf, 1976; Zhang et al., 1991a; Luhmann, 1995). However, even if we did not average over radial distance, the spatial resolution of the IMA scans (0.2–0.3 R_V, where R_V is the Venus radius) is insufficient to properly discern this effect given the expected thickness of such a plasma depletion layer (less than 1000 km). As a function of latitude, both temperatures (Fig. 3d, e) appear quite symmetric; the parallel temperature has no overall asymmetry, while the perpendicular temperature favors the +E hemisphere by ∼5 %. The temperature anisotropy (Fig. 3f) exhibits more variability, but there is no significant asymmetry overall.

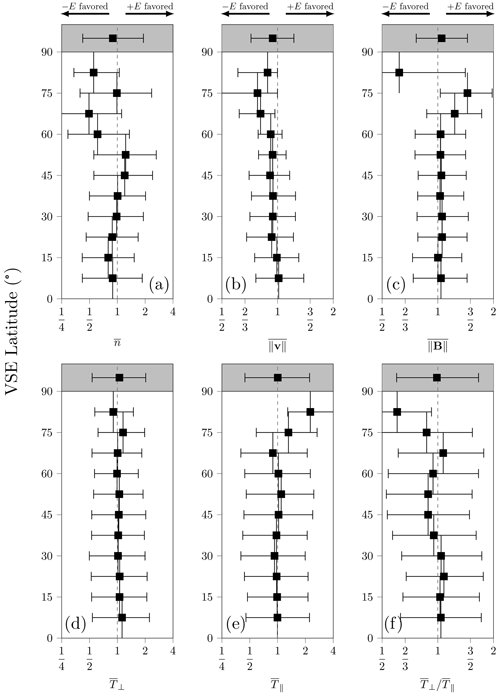
Figure 3 Proton parameter asymmetries as a function of latitudinal distance from the central parallel. The marker at the top corresponds to the overall asymmetry across all latitudes for each hemisphere. The asymmetry favors the +E hemisphere if $\stackrel{\mathrm{‾}}{a}>\mathrm{1}$ or the −E hemisphere if $\stackrel{\mathrm{‾}}{a}<\mathrm{1}$. Markers indicate medians, while error bars correspond to the first and third quartiles. Note the varying horizontal scales.

These results contrast with the asymmetries between the magnetosheath plasma downstream of different bow-shock geometries (see Fig. 6 in Rojas Mata et al., 2023). Those asymmetries are more significant and exhibit trends with respect to the upstream Alfvén Mach number. This indicates that the convective electric field has little influence on average magnetosheath properties, especially compared with the bow-shock geometry. We also did not find significant trends with any upstream parameter (e.g., density, speed, or Alfvén Mach number). Despite the potential connection between ±E asymmetries and pick-up-ion dynamics, we found no significant dependencies on the upstream O⁺ Larmor radius. However, as varying the upstream Larmor radius changes the direction of the pick-up-ion trajectories (Jarvinen et al., 2016), analyzing the components of the bulk velocity likely yields more informative results on the matter. This requires us to reevaluate our methodology to make it adequate for quantities which are not strictly positive.

Figure 4 Distributions of the proton bulk-velocity components in the +E (a, b, c) and −E (d, e, f) hemispheres. Black represents data with $r_{\mathrm{L},{\mathrm{O}}^{+}}<\mathrm{0.75}{R}_{\mathrm{V}}$, dark gray represents all $r_{\mathrm{L},{\mathrm{O}}^{+}}$, and light gray represents $r_{\mathrm{L},{\mathrm{O}}^{+}}>\mathrm{1.58}{R}_{\mathrm{V}}$. The markers indicate the median for each distribution along with the respective first and third quartiles as the error bars. The arrow indicates increasing $r_{\mathrm{L},{\mathrm{O}}^{+}}$.

3.2 Bulk-velocity components

Figure 4 presents (1) the measurement distributions of v_x, v_y, and v_z in the +E and −E hemispheres and (2) the distributions for the data subsets corresponding to large (above the third quartile 1.58 R_V) and small (below the first quartile 0.75 R_V) upstream O⁺ Larmor radius $r_{\mathrm{L},{\mathrm{O}}^{+}}$ (the median for all data is 1.09 R_V). We also indicate the median (marker) and quartiles (error bars) for each distribution at the top of each plot. Note that only v_x can be normalized by its upstream value, as the solar wind points solely along X_VSE; therefore, we only consider unnormalized measurements. As expected, v_x is negative and larger than the other components. v_y is unevenly distributed about zero due to a previously observed asymmetry in the proton flow in the Venus Solar Orbit (VSO) frame attributed to the planet's orbital motion (Lundin, 2011). As VEX only sampled the northern VSO hemisphere, this asymmetry does not average out when converting into the VSE frame, leading to mostly positive (negative) values in the +E (−E) hemisphere. Finally, while the sign of v_z is mostly as expected for each hemisphere, IMA's field of view combined with the spacecraft's orientation may occasionally lead to measurements with the “wrong” sign. However, such interpretation assumes that v_z should always be positive (negative) in the +E (−E) hemisphere. We did not find analogous studies presenting distributions of v_z (Romanelli et al., 2020, only discusses means), so we cannot compare our findings to related work to gauge how justified this assumption is. Regardless, reviewing the measurements to correct v_z (if required at all) is beyond the scope of this work; our methodology and the equal impact of systematic errors on both hemispheres mitigate potential errors anyway.

v_x does not vary significantly with $r_{\mathrm{L},{\mathrm{O}}^{+}}$ in the +E hemisphere. In the −E hemisphere, the small $r_{\mathrm{L},{\mathrm{O}}^{+}}$ measurements have a sudden dip around −100 km s⁻¹ (possibly a random sampling artifact) which, if not present, would also make v_x insensitive to $r_{\mathrm{L},{\mathrm{O}}^{+}}$. Both v_y and v_z follow opposite trends with respect to $r_{\mathrm{L},{\mathrm{O}}^{+}}$, regardless of hemisphere: v_y becomes more positive as $r_{\mathrm{L},{\mathrm{O}}^{+}}$ increases, whereas v_z becomes more negative. The solar wind thus seems to deflect towards the +Y_VSE and −Z_VSE directions as $r_{\mathrm{L},{\mathrm{O}}^{+}}$ increases. As pick-up ions are more common in the +E hemisphere (Phillips et al., 1987; Barabash et al., 2007b; Jarvinen et al., 2013), quantifying asymmetries of v_y and v_z as a function of $r_{\mathrm{L},{\mathrm{O}}^{+}}$ may clarify how these trends relate to the momentum exchange between solar-wind protons and planetary ions. Previously, ratios provided easily interpretable measures of asymmetry for positive scalar parameters such as density or temperature. However, the measurement distributions of v_y and v_z have positive and negative portions; thus, while the methodology from Sect. 2.2 can still be applied, the resulting distributions of parameters ratios are more difficult to interpret. An alternative is to use a sum instead of a ratio as the measure of asymmetry; Romanelli et al. (2020) did so to study ±E asymmetries in v_z at Mars. As the average v_z was primarily positive in the +E hemisphere and negative in the −E one, summing the values between the hemispheres always gave the difference in the magnitude of this component. We therefore modify the procedure from Sect. 2.2 to use sums of unnormalized parameters as our measure of asymmetry, i.e., $\stackrel{\mathrm{‾}}{a}=a_{\mathrm{H}\mathrm{1}}+a_{\mathrm{H}\mathrm{2}}$ instead of $\stackrel{\mathrm{‾}}{a}={\widehat{a}}_{\mathrm{H}\mathrm{1}}/{\widehat{a}}_{\mathrm{H}\mathrm{2}}$. Now $\stackrel{\mathrm{‾}}{a}>\mathrm{0}$ indicates a +E-favored asymmetry and $\stackrel{\mathrm{‾}}{a}<\mathrm{0}$ a −E-favored one. For our data, the “bodies” of the v_y and v_z distributions have opposite signs in opposite hemispheres, so the bodies of the sum distributions provide reliable measures of average asymmetries. However, as this is not true for the “tails” of the distributions, the sum distributions may be artificially wide.

Adopting these modifications, we present the medians of the v_y and v_z asymmetries across all latitudes in each hemisphere in Fig. 5. Again, the error bars indicate the first and third quartiles of the distributions. We also show the results for the data subsets corresponding to large and small upstream O⁺ Larmor radius. The v_y asymmetry decreases with increasing O⁺ Larmor radius, suggesting that the underlying mechanism deflecting the solar wind in the y direction either disappears or affects both hemispheres more evenly as $r_{\mathrm{L},{\mathrm{O}}^{+}}$ increases. Meanwhile, the v_z asymmetry favors the +E hemisphere for small $r_{\mathrm{L},{\mathrm{O}}^{+}}$ and the −E hemisphere for large $r_{\mathrm{L},{\mathrm{O}}^{+}}$. This switch in the hemisphere that the asymmetry favors may be connected to how much E×B-drift and finite-Larmor-radius dynamics affect momentum transfer between planetary and solar-wind ions for different $r_{\mathrm{L},{\mathrm{O}}^{+}}$. We note that these trends do not arise when splitting the data by high and low values for $\left|\mathit{v}\right|$, $\left|{\mathit{B}}_{\mathrm{IMF}}\right|$, or B_y – the individual parameters which comprise $r_{\mathrm{L},{\mathrm{O}}^{+}}$.

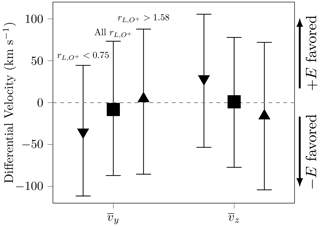
Figure 5 Proton bulk-velocity component asymmetries as a function of upstream O⁺ Larmor radius. For each parameter, the left marker is for $r_{\mathrm{L},{\mathrm{O}}^{+}}<\mathrm{0.75}$, the middle is for all $r_{\mathrm{L},{\mathrm{O}}^{+}}$, and the right is for $r_{\mathrm{L},{\mathrm{O}}^{+}}>\mathrm{1.58}$. The asymmetry favors the +E hemisphere if $\stackrel{\mathrm{‾}}{a}>\mathrm{0}$ or the −E hemisphere if $\stackrel{\mathrm{‾}}{a}<\mathrm{0}$. Markers indicate the median for each distribution along with the respective first and third quartiles as the error bars.

4 Discussion

Our interpretation of these Larmor-radius-dependent trends of solar-wind deflection at Venus benefits from comparisons with observations at Mars and comets; such comparative studies place the discussion into a broader context of solar-wind interactions with unmagnetized atmospheric bodies (see, e.g., Luhmann et al., 1987; Fedorov et al., 2008; Holmstrom and Wang, 2015; Jarvinen et al., 2016). However, as mentioned before, few studies provide quantitative characterizations of plasma asymmetries between the ±E hemispheres, let alone investigate dependencies on Larmor radius. This is understandable, as the Larmor radii of pick-up ions at these bodies are commonly larger than the obstacle radius. Thus, the particle motion is studied in the large-Larmor-radius limit in which other parameters are relevant. This contrasts with the range of $r_{\mathrm{L},{\mathrm{O}}^{+}}$ that we observe at Venus (about 0.4–2.4 R_V), which means the data likely cover mixed dynamical regimes. This is illustrated by simulations in which pick-up-ion species with Larmor radii similar to the planet radius experience both E×B-drift and finite-Larmor-radius dynamics (Jarvinen et al., 2016). Fundamental differences like these complicate but do not impede drawing beneficial insight from comparisons between these bodies.

4.1 Comparison to Mars

We first compare our results to Romanelli et al. (2020)'s analysis of ±E asymmetries in the z component of the proton bulk velocity in Mars' magnetosheath. This component was greater in magnitude in the −E hemisphere, coinciding with what we observe for large $r_{\mathrm{L},{\mathrm{O}}^{+}}$ at Venus. Using a two-species ion fluid description, the authors derived an analytic expression “suggesting a dependence between the SW flow asymmetry on the $\left(e{B}_y\right)/\left(n_{\mathrm{SW}}{m}_p\right)$ external factor”, where m_p is the proton mass and n_SW is the solar-wind density. The measured distributions of ${\stackrel{\mathrm{‾}}{v}}_z$ indeed confirm this predicted dependence of the asymmetry on B_y, n_SW, and $\left(e{B}_y\right)/\left(n_{\mathrm{SW}}{m}_p\right)$. We do not observe similar trends with respect to these parameters in the v_z asymmetry at Venus, simply verifying that the assumptions based on a large Larmor radius for planetary ions at Mars are not applicable. The authors did not investigate trends with upstream Larmor radius, thereby impeding further comparison with our analysis. Unfortunately, no other studies have characterized proton plasma magnetosheath asymmetries at Mars; given the abundance of plasma data provided by missions like Mars Express (Chicarro et al., 2004; Barabash et al., 2006) or MAVEN (Jakosky et al., 2015; Halekas et al., 2015), future work could provide new beneficial insight into the v_z asymmetry (or that of any parameter) by applying our methodology at Mars.

4.2 Comparison to simulations

As with observational work, existing numerical studies have not characterized ±E asymmetries in the magnetosheath plasma as a function of upstream Larmor radius. Nevertheless, Jarvinen et al. (2016)'s global hybrid simulations of planetary ion dynamics at Venus and Mars provide pertinent results to contextualize our observations. The authors simulated the planets' plasma environment not only under their respective nominal upstream conditions (“Venus nominal” and “Mars nominal”) but also with the heliodistance of each planet interchanged (“Mars at Venus” and “Venus at Mars”). By analyzing test particle trajectories of planetary ions with $m/q=\mathrm{1}$, 4, 16, and 32 (i.e., H⁺, He⁺, O⁺, and O${}_{\mathrm{2}}^{+}$) released at an altitude of 0.2 planet radii (see Figs. 6–9 in Jarvinen et al., 2016), the authors investigated different factors affecting the E×B-drift and finite-Larmor-radius dynamics of escaping ions. All runs feature stronger magnetic fields and O⁺ ions concentrated in the +E hemisphere.

The key difference in the four cases simulated is the increasing upstream O⁺ Larmor radius of 0.7, 1.2, 3.0, and 5.3 planet radii (see Table 2 in Jarvinen et al., 2016), the parameter chosen as a “first approximation of how important the finite-Larmor-radius effects are for the dynamics of escaping planetary ions” (Jarvinen et al., 2016). As $r_{\mathrm{L},{\mathrm{O}}^{+}}$ increases in the simulations, the O⁺ trajectories in the +E hemisphere align more along the +Z_VSE axis; the pick-up ions accelerate less in the −Y_VSE direction and more in the +Z_VSE direction. With less pick-up-ion motion along the Y_VSE axis, differences in the solar-wind v_y distributions between the ±E hemispheres should decrease, which is precisely the trend that we see in the data in Fig. 5. Simultaneously, the solar-wind v_z distributions in both hemispheres should become more negative, which we see in Fig. 4c, f. As v_z is mostly positive in the +E hemisphere and negative in the −E one, the v_z asymmetry becomes more −E favored as $r_{\mathrm{L},{\mathrm{O}}^{+}}$ increases, as shown in Fig. 5a. Therefore, despite our Venus data not spanning the same range of $r_{\mathrm{L},{\mathrm{O}}^{+}}$ as the simulations, it seems the Larmor-radius-dependent trends in the ±E asymmetries are consistent with varying momentum exchange between planetary O⁺ and solar-wind protons.

Still unexplained, however, is why the v_z asymmetry is +E favored for small $r_{\mathrm{L},{\mathrm{O}}^{+}}$. We have so far only considered momentum exchange with heavy pick-up ions, yet the simulations show that the dynamics of lighter ions (like H+) are significantly different because they experience more E×B-drift dynamics than finite-Larmor-radius effects. Light ions concentrate in the −E hemisphere, so their effect would be to deflect the solar wind towards the +Z_VSE axis. Due to their smaller mass, this may only be noticeable when the heavier ions also experience more E×B-drift dynamics so that their contribution to momentum exchange in the Z_VSE direction is reduced or more even between hemispheres. New simulations expanding upon the results in Jarvinen et al. (2016) and simultaneously quantifying plasma asymmetries could provide clarity on this matter.

5 Conclusions

Using measurements taken by Venus Express' ion mass-energy spectrometer and magnetometer, we characterized proton bulk-parameter asymmetries between the ±E hemispheres of Venus' dayside magnetosheath. The main results are as follows:

1. Speed has a weak asymmetry favoring the −E hemisphere (∼6 %), whereas the magnetic-field strength slightly favors the +E hemisphere by ∼5 %. Previous studies have found stronger asymmetries for these two parameters.

2. No significant asymmetries exist in the parallel temperature or the temperature anisotropy. The density asymmetry favors the −E hemisphere by ∼10 %, while the perpendicular temperature favors the +E hemisphere by ∼5 %.

3. The y and z components of the bulk velocity and their asymmetries exhibit trends with the upstream O⁺ Larmor radius. Comparison to simulations and Mars studies suggests that these trends may be consistent with deflection due to momentum exchange with planetary ions.

Our comparative analysis certainly has limitations yet nevertheless demonstrates the appeal of directly characterizing space plasmas across bodies of different scales. In addition to Venus and Mars, comets could be included in the analysis – for example, by considering the solar-wind deflection at comet 67P/Churyumov–Gerasimenko (Behar et al., 2018). New numerical and observational analyses of the plasma environment at all of these bodies via a uniform methodology would provide further insight into the phenomena discussed here. For example, identifying the parameters controlling the various asymmetries and characterizing their effect under equivalent upstream conditions could provide a more fundamental perspective of the solar-wind interaction with unmagnetized obstacles.