Relativistic kinematic effects in the interaction time of whistler-mode chorus waves and electrons in the outer radiation belt

Whistler-mode chorus waves propagate outside the plasmasphere, interacting with energetic electrons in the outer radiation belt. This leads to local changes in the phase space density distribution due to energy or pitch angle diffusion. The wave–particle interaction time (T_r) is crucial in estimating time-dependent processes such as the energy and pitch angle diffusion. Although the wave group and particle velocities are a fraction of the speed of light, the kinematics description of the wave–particle interaction for relativistic electrons usually considers the relativistic Doppler shift in the resonance condition and relativistic motion equation. This relativistic kinematics description is incomplete. In this paper, to the literature we add a complete relativistic description of the problem that relies on the relativistic velocity addition (between the electron and the wave) and the implications of the different reference frames for the estimates of the interaction time. We use quasi-linear test particle equations and the special relativity theory applied to whistler-mode chorus waves parallel propagating in cold-plasma magnetosphere interaction with relativistic electrons. Also, we consider that the resonance occurs in the electron's reference frame. At the same time, the result of such interaction and their parameters are measured in the local inertial reference frame of the satellite. The change pitch angle and the average diffusion coefficient rates are then calculated from the relativistic interaction time. The interaction time equation is consistent with previous works in the limit of non-relativistic interactions (T_nr). For the sake of application, we provide the interaction time and average diffusion coefficient D_aa for four case studies observed during the Van Allen Probes era. Our results show that the interaction time is generally longer when applying the complete relativistic approach, considering a non-relativistic calculation. From the four case studies, the ratio $T_{\mathrm{r}}/T_{\mathrm{nr}}$ varies in the range 1.7–3.0 and $D_{\mathrm{aa}}/D_{\mathrm{aa}}^{\mathrm{nr}}$ in the range 1.9–5.4. Accurately calculating the interaction time with full consideration of special relativity can enhance the modeling of the electron flux in Earth's outer radiation belt. Additionally, the change in pitch angle depends on the time of interaction, and similar discrepancies can be found when the time is calculated with no special relativity consideration. The results described here have several implications for modeling relativistic outer-radiation-belt electron flux resulting from the wave–particle interaction. Finally, since we considered only one wave cycle interaction, the average result from some interactions can bring more reliable results in the final flux modeling.

1 Introduction

The inner magnetosphere's outer radiation belt is filled mainly with electrons in a broad energy range, from tens of kiloelectronvolts (keV) to megaelectronvolts (MeV), distributed in several pitch angles. In the equatorial region, the loss cone instability (for a detailed description, see Lakhina et al., 2010, and references therein), caused by the electron's source population (tens of electronvolts (eV) to tens of keV) anisotropy, produces whistler-mode chorus waves (Tsurutani and Smith, 1974, 1977; Shprits et al., 2007, 2008; Lakhina et al., 2010; Lam et al., 2010; Tsurutani et al., 2013). Chorus waves are very low frequency (VLF) (from hundreds of hertz (Hz) to a few kilohertz (kHz)) in whistler mode and propagate as discrete wave packets.

In the magnetosphere, the whistler-mode chorus waves can be observed either at low frequency, i.e., $\mathrm{0.1}{\mathrm{\Omega }}_{\mathrm{ce}}<\mathit{\omega }<\mathrm{0.5}{\mathrm{\Omega }}_{\mathrm{ce}}$ (when the emission occurs in frequencies lower than half the electron gyrofrequency (Ω_ce)), or high frequency ($\mathrm{0.5}{\mathrm{\Omega }}_{\mathrm{ce}}<\mathit{\omega }<\mathrm{0.9}{\mathrm{\Omega }}_{\mathrm{ce}}$) (Artemyev et al., 2016). At the frequency ω=0.5Ω_ce, chorus waves are likely to interact with low-energy electrons due to Landau resonance, which causes damping (Tsurutani and Smith, 1974; Bortnik et al., 2006). The wave vector can be oriented quasi-parallel to the ambient magnetic field (θ≤ 45^∘) when exhibiting right-handed circularly polarized emission (Artemyev et al., 2016) or oblique (45^∘ < θ≤ 50^∘) and very oblique (θ> 50^∘) to the ambient magnetic field (Artemyev et al., 2016; Hsieh et al., 2020, 2022, and references therein). In the latter case, the electric field is elliptically polarized (Verkhoglyadova et al., 2010).

Chorus waves are observed outside the plasmasphere, mainly at the dawn side of the magnetosphere. Often, they interact with the electron seed population (hundreds of keV) and accelerate them to MeV energies (Thorne et al., 2005; Tu et al., 2014; Santolik et al., 2009; Reeves et al., 2003, 2013; Jaynes et al., 2015; da Silva et al., 2021; Lejosne et al. , 2022; Hua et al., 2022) or diffuse in pitch angle scattering (Horne and Thorne, 2003; Horne et al., 2003; Alves et al., 2016; Zhang et al., 2017; Liu et al., 2020; Guo et al., 2021), which may cause electrons to precipitate into the atmosphere. The wave–particle interaction succeeds when the resonance condition is satisfied, which implies a balance among the wave frequency, electron's energy, plasma density, and ambient magnetic field strength (${\mathit{\omega }}_{\mathrm{pe}}/{\mathrm{\Omega }}_{\mathrm{e}}$), as shown by Horne et al. (2003).

In the magnetosphere, the kinematics description of the wave–particle interaction for relativistic electrons usually considers the relativistic Doppler shift in the resonance condition (e.g., Thorne et al., 2005; Summers et al., 1998) and the relativistic motion equation (e.g., Omura, 2021). Often, the resonant kinetic energy of the electrons results from the resonance condition and the motion equation, together with the wave group velocity (e.g., Omura, 2021; Hsieh et al., 2022; Summers et al., 2012; Glauert and Horne, 2005; Lyons et al., 1972). The wave–particle interaction time (T_r) is a crucial parameter in estimating time-dependent processes such as the energy and pitch angle diffusion coefficients (Walker, 1993; Lakhina et al., 2010; Tsurutani et al., 2013; Hsieh et al., 2020, 2022); however, the relativistic kinematics description mentioned above is incomplete to calculate this parameter. In this paper, to the latter approach we add a complete relativistic description of the problem: the relativistic velocity addition (between the electron and the wave) and the implications of the different reference frames for the estimates of the change in pitch angle and the diffusion coefficient.

We calculate the parameters for four case studies to give a quantitative comparison between the complete relativistic description and a non-relativistic approach (used here as an approximation to calculate the interaction parameters). The interaction time is calculated using the test particle equations (Tsurutani and Smith, 1974; Lakhina et al., 2010; Horne et al., 2003; Bortnik et al., 2008) along with the special relativity theory applied to whistler-mode chorus waves propagating in the cold-plasma magnetosphere (where group velocity is  0.3c to 0.5c) and energetic electrons (with energy ∼ 0.1 to 2 MeV). We consider that the resonance occurs in the electron's reference frame. At the same time, the result of such interaction and their parameters are measured in the local inertial reference frame of the satellite.

We considered parallel propagating whistler-mode chorus waves linearly interacting with relativistic electrons to derive first the group velocity equation, then the resonant relativistic kinetic energy, and finally the interaction time. Thus, we calculate the change pitch angle and the diffusion coefficient rates. We use the Van Allen Probes measurement of wave parameters, ambient magnetic field, density, electron fluxes, and equatorial pitch angle to apply the interaction time equation. A complete calculation of these parameters can improve relativistic outer-radiation-belt electron flux variation models.

2 Wave–particle interaction in the radiation belt

2.1 Group velocity for parallel and oblique propagation

The inner magnetosphere plasma density is a fundamental parameter to determine the wave dispersion relation (and group velocity) involved in the Doppler shift cyclotron resonance condition (see density implications to the resonant diffusion surfaces; e.g., Horne and Thorne, 2003). Recent space missions have provided density measurement with a confidence level of 10 % under quiet geomagnetic conditions (Zhelavskaya et al., 2016). Outside the plasmasphere, while magnetospheric convection increases, the plasma density can vary from very low density (∼ 1 cm⁻³) to increased density values (∼ 50 cm⁻³). Despite the fact that Lakhina et al. (2010) and Tsurutani and Lakhina (1997) estimated the change in pitch angle for non-relativistic electrons and chorus waves, both propagating parallel to the ambient magnetic field in a dense plasma, i.e., X≫Y², there is still no estimate for low-density plasma conditions such as those observed by recent missions. Several works have shown that plasma density varies due to the magnetospheric activity under different solar wind drivers (e.g., see discussions in Li et al., 2014; Sicard-Piet et al., 2014; Allison et al., 2021), leading to an additional difficulty in imposing simplifications in the calculation of parameters related to the ambient electron plasma density. In this work, we are interested in whistler-mode chorus waves, which occur in frequencies higher than the ion cyclotron frequency; besides the wave–particle interaction outside the plasmasphere, the dispersion relation for this case is obtained from the solution of the Appleton–Hartree equation (Bittencourt, 2004). Thus, the whistler-mode chorus wave group velocity in the magnetosphere is calculated by the solution of the dispersion relation $\mathit{\eta }\left(\mathit{\omega }\right)=kc/\mathit{\omega }$ in a cold plasma, neglecting ion contributions:

$$\begin{array}{}\text{(1)}& \mathit{\eta }\left(\mathit{\omega }\right)={\left[\mathrm{1}-{\displaystyle \frac{X(\mathrm{1}-X)}{\begin{array}{c}(\mathrm{1}-X)-\frac{\mathrm{1}}{\mathrm{2}}{Y}^{\mathrm{2}}{\sin }^{\mathrm{2}}\mathit{\theta }+\\ \sqrt{{\left(\frac{\mathrm{1}}{\mathrm{2}}{Y}^{\mathrm{2}}{\sin }^{\mathrm{2}}\mathit{\theta }\right)}^{\mathrm{2}}+(\mathrm{1}-X{)}^{\mathrm{2}}{Y}^{\mathrm{2}}{\cos }^{\mathrm{2}}\mathit{\theta }}\end{array}}}\right]}^{\mathrm{1}/\mathrm{2}},\end{array}$$

where $X={\mathit{\omega }}_{\mathrm{pe}}^{\mathrm{2}}/{\mathit{\omega }}^{\mathrm{2}}$, and $Y={\mathrm{\Omega }}_{\mathrm{ce}}/\mathit{\omega }$, where ω_pe is the plasma frequency, and θ is the wave normal angle (WNA). The WNA is defined as the angle between the wave vector k and the ambient magnetic field B₀. The positive signal in the square root in the denominator is chosen because we consider the ordinary right circularly polarized (RCP) wave propagation mode (Helliwell, 1965). We take the derivative of Eq. (1) to evaluate the group velocity ($v_{\mathrm{g}}\equiv \mathrm{d}\mathit{\omega }/\mathrm{d}k$) for a given whistler-mode chorus wave propagating at a given angle, such that θ can be chosen among parallel, quasi-parallel, and oblique classification, related to the ambient magnetic field in any plasma density:

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{v_{\mathrm{g}}}{c}}={\displaystyle \frac{\mathrm{1}}{\mathit{\eta }+\mathit{\omega }\mathrm{d}\mathit{\eta }/\mathrm{d}\mathit{\omega }}}.\end{array}$$

For whistler-mode chorus waves propagating outside plasmapause, where density can vary from ∼ 1 to ∼ 20 cm⁻³, the usual high-dense plasma approximation (e.g., see Bittencourt, 2004; Artemyev et al., 2016) is often inconvenient under disturbed geomagnetic conditions. Thus, we solve Eq. (2) for low electron density conditions. The wave group velocity and the maximum wave propagation frequency are significantly lowered as the WNA becomes oblique, as shown in Fig. 1, because the ambient refractive index is not isotropic.

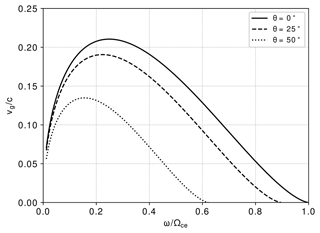
Figure 1 Group velocity $v_{\mathrm{g}}/c$ as a function of whistler-mode chorus wave frequency to the plasma gyrofrequency for the propagation of three different wave normal angles. This group velocity is the full solution of Appleton–Hartree for whistler waves propagating in low-density plasma media at any orientation. The Van Allen Probes apogee orbit provides plasma parameters used in the calculation, B₀=150 nT and low density n=2 cm⁻³.

2.2 Wave–particle cyclotron resonance condition

The whistler-mode chorus waves are generated near the geomagnetic equator, where they are often observed propagating at frequency ω, parallel to the field lines (Tsurutani and Lakhina, 1997; Santolik et al., 2009; Lakhina et al., 2010). Also, oblique chorus waves are observed at high latitudes (Omura, 2021; Artemyev et al., 2016) and can resonantly interact with electrons elsewhere (Mourenas et al., 2015).

Electrons undergoing a bouncing motion parallel to the magnetic field lines see a relativistic Doppler shift in the wave frequency from its frame of observation:

$$\begin{array}{}\text{(3)}& \mathit{\omega }-\mathit{k}\cdot {\mathit{v}}_{\mathrm{e}}=n{\displaystyle \frac{{\mathrm{\Omega }}_{\mathrm{ce}}}{\mathit{\gamma }\left(v_{\mathrm{e}}\right)}},\end{array}$$

where the vector v_e is the electron velocity, ${\mathrm{\Omega }}_{\mathrm{ce}}\equiv e{B}_{\mathrm{0}}/m_{\mathrm{e}}$, and $\mathit{\gamma }\left(v_{\mathrm{e}}\right)=(\mathrm{1}-v_{\mathrm{e}}^{\mathrm{2}}/c^{\mathrm{2}}{)}^{-\mathrm{1}/\mathrm{2}}$. The resonant cyclotron harmonics are given by the integer number n, with n=0 corresponding to the Landau resonance condition. The gyrofrequency low-order harmonics $n=\pm \mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{\dots }$ are often observed for oblique wave vector propagation (Artemyev et al., 2016; Orlova et al., 2012; Subbotin et al., 2010; Lorentzen et al., 2001). If they are positive, the resonance is said to be normal; otherwise, it is anomalous (Tsurutani and Lakhina, 1997). The pitch angle scattering and energy diffusion occur when whistler-mode chorus wave group velocity and the relativistic electron propagation velocity fulfill the resonance condition in Eq. (3) (Tsurutani and Lakhina, 1997; Shprits et al., 2008; Lakhina et al., 2010).

The scalar product in Eq. (3) is calculated for an electron resonant speed and wave propagating in a dispersive media with phase (group) velocity given by Eq. (1) (Eq. 2). Henceforth, we consider linear wave–particle interactions, in which parallel whistler-mode chorus waves propagate in the same direction to the electron's velocity vector or opposite to it. From Eq. (3), we can obtain the electron speed for which the resonant condition is fulfilled in terms of the wave and plasma parameters. We call this the resonant relativistic electron's speed

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{v_{\mathrm{e}}}{c}}={\displaystyle \frac{\mathit{\eta }\cos \mathit{\delta }+\left(n{\mathrm{\Omega }}_{\mathrm{ce}}/\mathit{\omega }\right){\left[{\mathit{\eta }}^{\mathrm{2}}{\cos }^{\mathrm{2}}\mathit{\delta }+\left(n^{\mathrm{2}}{{\mathrm{\Omega }}_{\mathrm{ce}}}^{\mathrm{2}}/{\mathit{\omega }}^{\mathrm{2}}-\mathrm{1}\right)\right]}^{\mathrm{1}/\mathrm{2}}}{{\mathit{\eta }}^{\mathrm{2}}{\cos }^{\mathrm{2}}\mathit{\delta }+n^{\mathrm{2}}{{\mathrm{\Omega }}_{\mathrm{ce}}}^{\mathrm{2}}/{\mathit{\omega }}^{\mathrm{2}}}}.\end{array}$$

Measured in the satellite reference frame. In the above equation, δ is the angle between the wave and electron velocity vectors. It equals α or π−α for co-propagating and counter-propagating waves, respectively. The dispersion relation η(ω) is chosen according to the application. Here we consider the dispersion relation given by Eq. (1). In plasma wave propagation, the electron plasma density is a determinant parameter in calculating wave group velocity. However, obtaining wave group velocity from the Appleton–Hartree solution in this environment can be challenging (Anderson et al., 1992). We use plasma density data from the EMFISIS instrument (Kletzing et al., 2013) on board the Van Allen Probes mission to calculate the wave–particle time of interaction. However, a more precise measurement is still challenging. The Van Allen Probes in situ measurements (ambient density, magnetic field) are used in Eq. (4) to calculate typical values of the resonant kinetic energy

$$\begin{array}{}\text{(5)}& K_{\mathrm{res}}={\displaystyle \frac{m{c}^{\mathrm{2}}}{\sqrt{\mathrm{1}-v_{\mathrm{e}}^{\mathrm{2}}/c^{\mathrm{2}}}}}-m{c}^{\mathrm{2}},\end{array}$$

of electrons that resonantly interact with the wave frequency in a given plasma condition and wave propagation direction. The resonance condition allows for different harmonics, represented by n, to fulfill the condition shown in Eq. (3) (see, e.g., Camporeale, 2015, for a discussion of resonant interaction). For a matter of example, we choose to solve Eq. (5) for the parallel whistler-mode chorus waves counter-propagating and co-propagating to the electron's velocity vector. The equatorial electron pitch angle in this example is 40^∘. In Fig. 2, the resonant kinetic energies are calculated for the gyrofrequency harmonic $n=+\mathrm{5}$, ambient magnetic field B₀=150 nT, and electron plasma density n_e=2.0 cm⁻³. From Eq. (4), we can obtain the equation presented by Summers et al. (2012) if we use their notation¹ $v_{\mathrm{e}}=v_{\mathrm{R}}+v_{⟂}$.

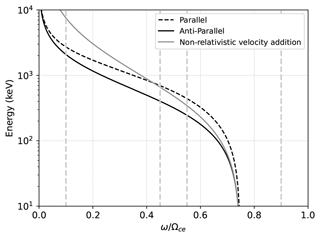
Figure 2 Comparison of the electron resonant kinetic energy (keV) as a function of whistler-mode chorus wave frequency normalized by the electron gyrofrequency propagating parallel and antiparallel to the ambient magnetic field (B₀=150 nT). The wave–particle resonance condition depends on the wave dispersion relation ($\mathit{\omega }/\mathit{k}$), calculated from Eq. (2), with $n=+\mathrm{5}$. The vertical lines delimitate the low-band whistler-mode chorus wave frequency corresponding to $\mathrm{0.1}{f}_{\mathrm{ce}}\le f\le \mathrm{0.45}{f}_{\mathrm{ce}}$ and the high-band $\mathrm{0.55}{f}_{\mathrm{ce}}\le f\le \mathrm{0.90}{f}_{\mathrm{ce}}$ as a fraction of the electron gyrofrequency. Plasma parameters are the same as those used in Fig. 1.

3 Relativistic interaction time

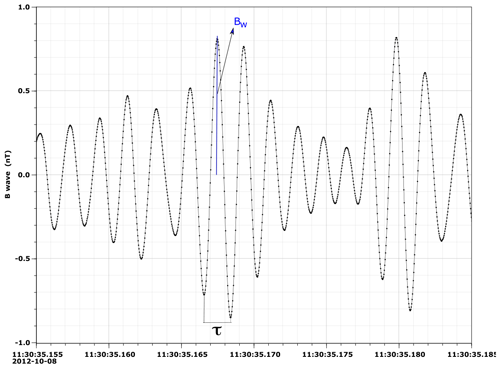
The wave–particle interaction holds as the resonance condition prevails; after that, the interaction is ended. Thus, the interaction time T can be defined as the time elapsed by the resonant electron passing through the wave subelement with duration τ (Hsieh et al., 2020; Lakhina et al., 2010). Alternatively, one can also define it as the time needed for the phase difference between the wave and particle to change by 1 rad (Tsurutani and Lakhina, 1997; Walker, 1993). In the following calculations, we consider the former definition.

In order to calculate the interaction time, one needs to define two reference frames to work on a relativistic kinematic scenario. The first one is the satellite frame (S) in which the measurement of the relevant physical quantities (including T) takes place, and the second one is the frame of the electron guiding center (S^′) in which the interaction occurs (see Fig. 3). In this article, we consider the definition of the electron guiding center as the center of a circular orbit around the magnetic field line (Baumjohann and Treumann, 1997). To justify the use of an inertial frame associated with the satellite, consider, for instance, the maximum acceleration achieved by the satellite at the perigee (data from satellite orbit can be found, e.g., in Mauk et al., 2013), it is 8.2 m s⁻². The interaction time between the electron and the wave is of the order of 10⁻³ s. Since the period of the satellite is 537.1 min, its acceleration is nearly constant during the interaction. Therefore, the change in the speed of the satellite in its orbit during one interaction time is around $\mathrm{8.2}\times {\mathrm{10}}^{-\mathrm{3}}\mathrm{m}{\mathrm{s}}^{-\mathrm{1}}$ which is 6 orders of magnitude smaller than the speed of the satellite at the perigee 9.8 km s⁻¹. Similarly, the spin period of the satellite is 11 s (Breneman et al., 2022), which leads to a change in angle of about 1.8 arcmin through the interaction time relative to one wave cycle. Thus, for the purposes of the present article, it is reasonable to consider the satellite to be an inertial reference frame during the interaction time relative to one wave cycle. Moreover, it is a standard approach in the literature to consider the satellite to be an inertial reference frame.

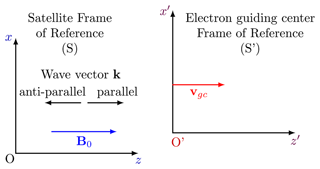
Figure 3 Illustration of the two reference frames used in calculating the interaction time in Sect. 3. The electron guiding center frame of reference (S^′) has a velocity v_gc with respect to the satellite frame of reference (S). This velocity parallels the ambient magnetic field B₀. Thus, the angle between the wave vector k and v_gc equals the WNA, and it is 0^∘ for parallel and 180^∘ for antiparallel propagating waves.

The relative velocity between S and S^′ is the electron guiding center velocity v_gc. The guiding center electron velocity is related to the electron's speed by the pitch angle α by the relation v_gc=v_ecos α. Since v_gc is parallel to the ambient magnetic field B₀, the angle between v_gc and the wave vector coincides with the WNA given by θ. In S^′ the interaction time can be written as

$$\begin{array}{}\text{(6)}& T^{\prime }={\displaystyle \frac{L^{\prime }}{v_{\mathrm{g}}^{\prime }}},\end{array}$$

where L^′ and $v_{\mathrm{g}}^{\prime }$ are the wave subelement's scale size and the wave's group velocity in this same frame. If v_gc is much smaller than the speed of light, one can relate the group velocity in both frames $v_{\mathrm{g}}^{\prime }$ and v_g simply by the vector addition formula of v_g and v_gc. However, in the general case for which the electrons are relativistic, this is no longer true, and one needs to use the relativistic formula of the addition of velocities (for a description of the relativistic addition of velocities, see, e.g., Chap. 11 in Jackson, 1999). Therefore, we have

$$\begin{array}{}\text{(7)}& v_{\mathrm{g}}^{\prime }={\displaystyle \frac{\sqrt{v_{\mathrm{g}}^{\mathrm{2}}+v_{\mathrm{gc}}^{\mathrm{2}}-\mathrm{2}{v}_{\mathrm{g}}{v}_{\mathrm{gc}}\cos \mathit{\theta }-{\left(\frac{v_{\mathrm{g}}{v}_{\mathrm{gc}}\sin \mathit{\theta }}{c}\right)}^{\mathrm{2}}}}{\mathrm{1}-\frac{v_{\mathrm{g}}{v}_{\mathrm{gc}}}{c^{\mathrm{2}}}\cos \mathit{\theta }}},\end{array}$$

where θ is the angle (in the S frame) between v_g and v_gc.

Another relativistic effect to consider in the transition from one frame to another is the Lorentz–FitzGerald contraction. If L₀ is the scale size of the wave in its proper reference frame, in the S^′ frame, we have

$$\begin{array}{}\text{(8)}& L^{\prime }={\displaystyle \frac{L_{\mathrm{0}}}{\mathit{\gamma }\left(v_{\mathrm{g}}^{\prime }\right)}},\end{array}$$

where the Lorentz factor is

$$\begin{array}{}\text{(9)}& \mathit{\gamma }\left(v_{\mathrm{g}}^{\prime }\right)={\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{1}-\frac{{v_{\mathrm{g}}^{\prime }}^{\mathrm{2}}}{c^{\mathrm{2}}}}}}.\end{array}$$

In the same fashion, the scale size of the wave in the S frame is

$$\begin{array}{}\text{(10)}& L={\displaystyle \frac{L_{\mathrm{0}}}{\mathit{\gamma }\left(v_{\mathrm{g}}\right)}},\end{array}$$

and after combining Eqs. (8) and (10) we obtain

$$\begin{array}{}\text{(11)}& L^{\prime }={\displaystyle \frac{\mathit{\gamma }\left(v_{\mathrm{g}}\right)}{\mathit{\gamma }\left(v_{\mathrm{g}}^{\prime }\right)}}L.\end{array}$$

Note that if we have, for instance, $v_{\mathrm{g}}^{\prime }>v_{\mathrm{g}}$, the subelement's wave scale size in the S^′ frame is smaller than the scale size measured in the satellite frame. The difference between the two sizes is more considerable when the electron's speed is higher.

Substituting the above equation in Eq. (6) we have

$$\begin{array}{}\text{(12)}& T^{\prime }={\displaystyle \frac{\mathit{\gamma }\left(v_{\mathrm{g}}\right)}{\mathit{\gamma }\left(v_{\mathrm{g}}^{\prime }\right)}}{\displaystyle \frac{L}{v_{\mathrm{g}}^{\prime }}}.\end{array}$$

Finally, the time dilation effect is the third relativistic kinematic effect. The interaction time in the S frame can be obtained from the above expression in the S^′ frame by multiplying Eq. (12) by a new Lorentz factor γ(v_gc). The final equation is

$$\begin{array}{}\text{(13)}& T={\displaystyle \frac{\mathit{\gamma }\left(v_{\mathrm{gc}}\right)\mathit{\gamma }\left(v_{\mathrm{g}}\right)}{\mathit{\gamma }\left(v_{\mathrm{g}}^{\prime }\right)}}{\displaystyle \frac{L}{v_{\mathrm{g}}^{\prime }}}.\end{array}$$

Therefore, if we use Eq. (7) together with Eq. (13), we obtain the expression of the interaction time with all quantities measured in the S frame. The final expression contemplates all the relativistic kinematic effects.

Additionally, a comparison of the time of interaction calculated through Eq. (13) with the time calculated without considering any relativistic correction is shown in Fig. 4 for parallel propagating waves and 80^∘ pitch angle electrons. According to our results, the non-relativistic time is underestimated, even for low-energy electrons. This happens due to the wave group velocity being very high in the magnetospheric density conditions. Thus the relativistic addition velocity should be considered whatever the resonant electron energy.

The influence of these three relativistic kinematic effects on the time of interaction can be analyzed by plotting each term in Eq. (13) as a function of the electron resonant energy or wave frequency (not shown). Regarding the contribution of each term, we obtain that the main contribution comes from the $L/v_{\mathrm{g}}^{\prime }$ ratio, which differentiates from the non-relativistic equation by the relativistic velocity addition ($v_{\mathrm{g}}^{\prime }$). Moreover, the difference in time due to the γ factor is 20 % for parallel wave propagation at any resonant electron energy, and it becomes more significant at kinetic energy higher than 1 MeV.

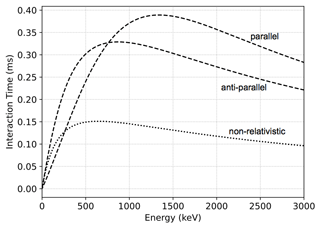
Figure 4 Comparison of time of interaction (ms) as a function of electron resonant kinetic energy (keV) calculated using Eq. (13) (dashed lines) and the non-relativistic approach (dotted line) for parallel and antiparallel wave propagation. Plasma parameters are B_am=166 nT, τ=1.8 ms, and n_e=3.0 cm⁻³.

4 Case studies: application of interaction time to estimate the change in pitch angle and diffusion coefficient rates

4.1 Calculations of the change in pitch angle and diffusion coefficient rates

The interaction time derived in the last section is usually longer than that calculated without a more complete relativistic description, as shown in the example of Fig. 4. In this section, we compare the complete relativistic description and the non-relativistic interaction time, applied to calculate the pitch angle diffusion coefficient (D_aa) computed from the change in pitch angle. The change in pitch angle can be calculated using the test-particle approach as done by Tsurutani and Lakhina (1997) and, later on, Lakhina et al. (2010).

Let us start with the Lorentz equation

$$\begin{array}{}\text{(14)}& {\displaystyle \frac{d\mathit{p}}{\mathrm{d}t}}=q_{\mathrm{e}}\left(\mathit{E}+{\mathit{v}}_{\mathrm{e}}\times \mathit{B}\right),\end{array}$$

where B is the sum of the wave magnetic field B_w and the ambient magnetic field B₀; the wave electric field is $\mathit{E}=(\mathit{\omega }/k){\mathit{B}}_{\mathrm{w}}\times \widehat{k}$; and $q_{\mathrm{e}}=-e$ and p=γ(v_e)m_ev_e are the electron charge and momentum, respectively. For the WNA, let us consider the simple case for which θ=0. Considering B₀ in the +z direction of a local Cartesian coordinate system associated with the S frame, we have the following components of Eq. (14):

$$\begin{array}{}\text{(15)}& {\displaystyle \frac{\mathrm{d}{p}_x}{\mathrm{d}t}}=q_{\mathrm{e}}\left[{\displaystyle \frac{\mathit{\omega }}{k}}{B}_y+\left(v_y{B}_{\mathrm{0}}-v_z{B}_y\right)\right],\end{array}$$

$$\begin{array}{}\text{(16)}& {\displaystyle \frac{\mathrm{d}{p}_y}{\mathrm{d}t}}=q_{\mathrm{e}}\left[-{\displaystyle \frac{\mathit{\omega }}{k}}{B}_x-\left(v_x{B}_{\mathrm{0}}-v_z{B}_x\right)\right],\end{array}$$

$$\begin{array}{}\text{(17)}& {\displaystyle \frac{\mathrm{d}{p}_z}{\mathrm{d}t}}=q_{\mathrm{e}}\left(v_x{B}_y-v_y{B}_x\right).\end{array}$$

The electron momentum can be written as $\mathit{p}={\mathit{p}}_{⟂}+{\mathit{p}}_{\parallel }$, where ${\mathit{p}}_{⟂}\equiv p_x\widehat{i}+p_y\widehat{j}$ is the momentum orthogonal to the ambient magnetic field, and ${\mathit{p}}_{\parallel }\equiv p_z\widehat{k}$ is parallel to it. Therefore, the pitch angle can be obtained from $\tan \mathit{\alpha }=p_{⟂}/p_{\parallel }$, and we obtain the following formula for a small change in α:

$$\begin{array}{}\text{(18)}& \mathrm{\Delta }\mathit{\alpha }={\displaystyle \frac{p_{\parallel }\mathrm{\Delta }{p}_{⟂}-p_{⟂}\mathrm{\Delta }{p}_{\parallel }}{p^{\mathrm{2}}}}.\end{array}$$

Combining Eqs. (15), (16), and (17) with the above equation, it is straightforward to show that

$$\begin{array}{}\text{(19)}& \mathrm{\Delta }\mathit{\alpha }={\displaystyle \frac{q_{\mathrm{e}}{B}_{\mathrm{w}}\sin \mathit{\varphi }}{\mathit{\gamma }\left(v_{\mathrm{e}}\right)m_{\mathrm{e}}}}\left({\displaystyle \frac{\mathit{\omega }}{k}}{\displaystyle \frac{\cos \mathit{\alpha }}{v_{\mathrm{e}}}}-\mathrm{1}\right)\mathrm{\Delta }t,\end{array}$$

where ϕ is the angle between the wave magnetic field and the orthogonal component of the electron momentum.

If we further consider a resonant interaction, as given by Eq. (3), we finally obtain a fully relativistic equation for a small change in the pitch angle due to a wave–particle interaction

$$\begin{array}{}\text{(20)}& \mathrm{\Delta }\mathit{\alpha }={\displaystyle \frac{{\mathrm{\Omega }}_{\mathrm{ce}}}{\mathit{\gamma }\left(v_{\mathrm{e}}\right)}}{\displaystyle \frac{B_{\mathrm{w}}}{B_{\mathrm{0}}}}\sin \mathit{\varphi }\left[{\displaystyle \frac{\mathit{\omega }{\cos }^{\mathrm{2}}\mathit{\alpha }}{\left(n{\mathrm{\Omega }}_{\mathrm{ce}}/\mathit{\gamma }\left(v_{\mathrm{e}}\right)-\mathit{\omega }\right)}}+\mathrm{1}\right]\left[\mathrm{\Gamma }{\displaystyle \frac{v_{\mathrm{g}}}{v_{\mathrm{g}}^{\prime }}}\right]\mathit{\tau },\end{array}$$

where we used the definition $\mathrm{\Gamma }\equiv \frac{\mathit{\gamma }\left(v_{\mathrm{gc}}\right)\mathit{\gamma }\left(v_{\mathrm{g}}\right)}{\mathit{\gamma }\left(v_{\mathrm{g}}^{\prime }\right)}$, and Δt=T is the time of interaction given by Eq. (13).

Equation (20) is in the context of quasi-linear regimes for the calculation of change in pitch angle. The change in the electron's pitch angle derived in Eq. (20) considers the interaction with one chorus wave subelement with a constant time duration (τ). It is consistent with the non-relativistic approach such as Eq. (3.6) in Kennel and Petschek (1966), Eq. (11) in Tsurutani and Lakhina (1997), and Eq. (11) in Lakhina et al. (2010), which considered the relativistic resonant condition and the non-relativistic equation of motion. In the limit for non-relativistic electrons, γ(v_e)∼ 1 and T_r equal to Δt in Kennel and Petschek (1966) and Tsurutani and Lakhina (1997) or to τ in Lakhina et al. (2010). In addition, Allanson et al. (2022) show the exact equation for pitch angle scattering and second-order equations for weak turbulence and non-linear regimes. However, considering the quasi-linear wave–particle regime, Eq. (20) is similar to Eq. (S3) in Allanson et al. (2022).

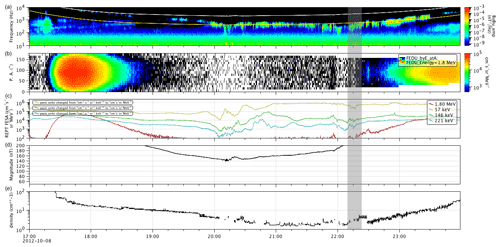
Figure 5 Case 1. Panels show from (a) to (e) the whistler-mode chorus waves' spectrum, the interpolated 1.8 MeV electron flux pitch angle distribution, the relativistic and low-energy electron fluxes, the ambient magnetic field, and the local plasma density. The parameters shown in the shaded region were used to calculate the interaction time, change in pitch angle, and diffusion coefficient for the resonant electrons energy shown in Table 1.

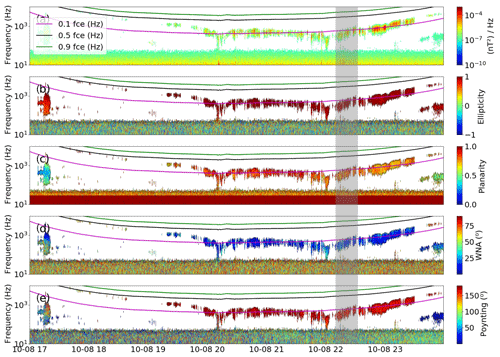
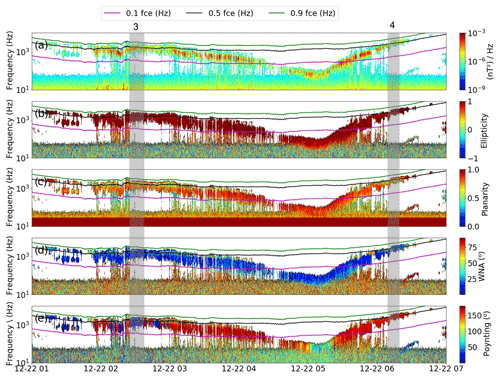
Figure 6 Case 1. Panels show the whistler-mode chorus waves' (a) spectrum of the magnetic field, (b) ellipticity, (c) planarity, (d) WNA (wave normal angle), and (e) the polar angle of the Poynting vector. In all panels, the values of 0.1 fce (electron cyclotron frequency) (Hz), 0.5 fce (Hz), and 0.9 fce (Hz) are shown by the pink, black, and green lines, respectively. The parameters shown by the shaded region were used to calculate the interaction time, change in pitch angle, and diffusion coefficient for the resonant electrons energy shown in Table 1.

The pitch angle diffusion coefficient (D_aa) can be estimated from the change in the pitch angle as by Kennel and Petschek (1966):

$$\begin{array}{}\text{(21)}& D_{\mathrm{aa}}={\displaystyle \frac{\langle (\mathrm{\Delta }\mathit{\alpha }{)}^{\mathrm{2}}\rangle }{\mathrm{2}\mathrm{\Delta }t}}.\end{array}$$

To solve Eq. (21), we considered that the time duration of a chorus subelement (τ) is not constant. Santolik et al. (2004), and later Lakhina et al. (2010), expressed the chorus subelement time duration as a power law distribution, such as τ^−β, in which τ can vary from 1 to 100 ms and the power law index varies in a range of 2–3. In the present estimate, we choose a fixed index (equal to 2) in the power law. The pitch angle diffusion coefficient averaged in time duration of the whistler-mode chorus waves emphasizes the relevance of the interaction time in the calculation. As a consequence of such construction, a limitation of this approach is that other averaged effects, such as spectrum fluctuation (Kennel and Petschek, 1966) or random phase (Li et al., 2015), bounce orbit (Lyons et al., 1972; Glauert and Horne, 2005), and ensemble contributions (Tao et al., 2011, 2012), affecting the pitch angle diffusion coefficient have to be considered separated. Then, we estimate the average 〈D_aa〉 from the average 〈Δα〉 for four case studies described in the following.

4.2 Case studies analysis

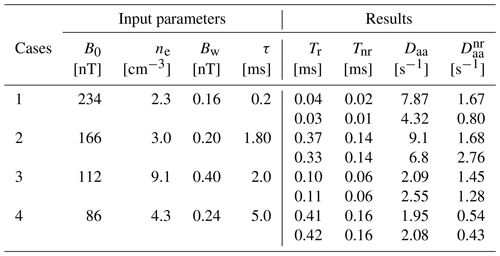
The ambient magnetic field magnitude (B₀), electron plasma density (n_e), wave frequency (f_w), wave magnetic field maximum amplitude (B_w), and one wave cycle period (τ) are the input parameters used in the estimation of resonant kinetic energy (Eq. 5), the relativistic interaction time (T_r) (Eq. 13), the change in pitch angle (Eq. 20), and the pitch angle diffusion coefficient (D_aa) (Eq. 21). The inputs and results are summarized in Table 1 for the studied cases 1 and 2 (Tu et al., 2014) and 3 and 4 (Liu et al., 2020; Guo et al., 2021). Besides T_r and D_aa calculated using the special relativity theory approach, we compare the results with a non-relativistic approach for the determinant parameters T_nr and $D_{\mathrm{aa}}^{\mathrm{nr}}$.

The Van Allen Probes provide in situ measurement from the ambient plasma, relativistic electrons, and wave parameters (see instrument details in the Appendix). For the four case studies, we plot the time evolution of the radial phase space density (PSD) profiles in inbound/outbound regions of probes A or B, which allows for the identification of the local relativistic electron loss and/or local low-energy acceleration (in a given L^*) in the outer radiation belt. These measurements are analyzed concomitant with whistler-mode chorus wave activities to investigate the local contribution of pitch angle diffusion driven by whistler-mode chorus waves to the electron flux variability. The pitch angle diffusion is due wave–particle interaction. The (anti)parallel propagating chorus wave can interact with relativistic electrons from different energies through at least one wave cycle τ. The several electrons' energy are allowed to participate in the interaction because of the harmonic resonant number n on the left-hand side of Eq. (3) (see Allison et al., 2021, and references therein).

Table 1 Input parameters used in the equations of Sects. 2, 3, and 4 to calculate the chorus wave–particle time of interaction and the pitch angle diffusion coefficient for cases 1 to 4. K_res=1 MeV, and the initial equatorial pitch angle is 60^∘. For each case, the first (second) line shows results for parallel (antiparallel) propagating waves and electrons. The subscripts r and nr mean relativistic and non-relativistic, respectively.

Cases 1 and 2 (Tu et al., 2014) – from 8 October 2012 (dropout). Cases 3 and 4 (Liu et al., 2020) – 22 December 2014, 00:00–06:00 (UTC).

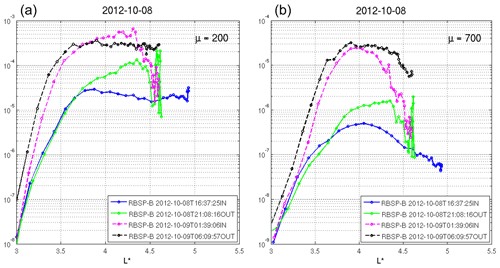
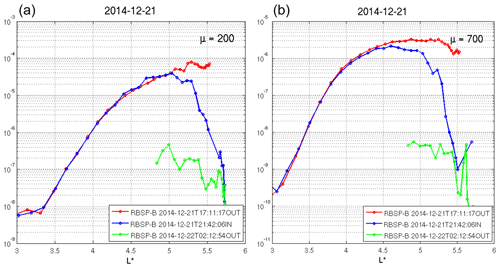
Figure 7 Case 1. Time evolution of phase space density (PSD $[c/(\mathrm{cm}\mathrm{MeV}){)}^{\mathrm{3}}{\mathrm{sr}}^{-\mathrm{1}}$]) radial profiles at fixed first adiabatic invariant, μ=200 MeV G⁻¹ (a) and μ=700 MeV G⁻¹ (b), and second (K=0.11 $G^{\mathrm{1}/\mathrm{2}}{R}_E$) adiabatic invariant for both inbound and outbound parts of the RBSP-B orbit. Period of analysis: 8 October 2012 from 16:37 UT through the interval of interest.

The four case studies are described in a sequence of three figures each. These plots show the ambient plasma and wave parameters used in the calculations and also the PSD analyses. The sequence of plots is described in the following. First, Figs. 5 (Figs. A1 and D1) show, from top to bottom, the whistler-mode chorus waves' spectrum, the interpolated 1.8 MeV electron flux pitch angle distribution, the relativistic and low-energy electron stacked fluxes, the magnitude of the ambient magnetic field, and the local plasma density. Second, Fig. 6 (Figs. B1 and E1) shows from panels (b)–(e), respectively, the whistler-mode chorus waves' ellipticity, planarity, wave normal angle, and the polar angle of the Poynting vector. The wave parameters were calculated according to Santolik et al. (2003), and the ambient electron density was provided according to Zhelavskaya et al. (2016). Finally, Fig. 7 (Figs. C1 and F1) shows the time evolution of PSD ($[c/(\mathrm{cm}\mathrm{MeV}\left){)}^{\mathrm{3}}{\mathrm{sr}}^{-\mathrm{1}}\right]$) as a function of L^* calculated through the magnetic field model (TS04) (Tsyganenko and Sitnov, 2005) for μ=200 and 700 MeV G⁻¹. The values of μ correspond to electron energy of 0.37 and 0.92 MeV, respectively, at $L^{*}=\mathrm{5}$. In these figures, we can identify the order of magnitude and energy level of the events in the same period when chorus waves are observed. In all the case studies, the whistler-mode chorus wave events were selected regarding their ellipticity (ϵ∼ 1), planarity of the magnetic field polarization (≥0.8), wave normal angle (WNA ∼ 0), and Poynting vector orientation (∼ 0 or 180^∘). The shaded area in the plots shows the in situ parameters used in calculations summarized in Table 1.

In cases 1 (8 October 2012 from 22:00 to 22:30 UT, Figs. 5 and 6) and 2 (29 June 2012 at 11:00 UT, Figs. A1 and B1), we consider the plasma parameters measured by probe A as it closes to the perigee, where the ambient magnetic field is higher than in the apogee, but the plasma density is low. Under these conditions, the bouncing 1 MeV electrons can interact with the 2 kHz whistler-mode chorus waves as they propagate parallel and antiparallel to each other. The chorus subelement was chosen in case 1 (2) in the instant concomitant with the change in the 57–1800 (1800) keV electron flux energy levels.

To confirm the local variations of the electron flux concomitant with chorus activity, we analyze the PSD for case 1 (2). Figure 7 shows two significant locally growing electron PSD peaks at $L^{*}=\mathrm{4.3}$ and fixed μ=200 and μ=700 MeV G⁻¹, above 370 keV (see green and magenta curves in panels a and b). A local electron flux decrease between $L^{*}=\mathrm{3.9}$ and 4.3 is observed near 06:09 UT on 9 October 2012 for energies close to 0.6 MeV (see the black curve in panel a), while for energies from above 0.6 MeV a slight electron flux increase is observed (black curve the panel b). Case 2 is shown in Fig. C1. It presents a local loss of electrons from 09:06 UT close to $L^{*}=\mathrm{4.6}$ and fixed μ=200 and 700 MeV G⁻¹ (blue curve in panel left and right), which can be caused by the pitch angle scattering driven by chorus waves. Curiously, the electron acceleration is observed from 09:06 UT at $L^{*}\le \mathrm{4.2}$ for both fixed μ, with a major proportion in μ=700 MeV G⁻¹.

Once the wave–particle interaction is confirmed, we proceed to the calculation of T_r, and thus the D_aa, as shown in Table 1. In cases 1 and 2, the relativistic interaction time can be 3 times higher than the non-relativistic calculation; i.e., $T_{\mathrm{r}}/T_{\mathrm{nr}}$ varies from 1.7 to 3.0. Since the electron plasma frequency ratio is low ($\mathrm{2.0}\le {\mathit{\omega }}_{\mathrm{pe}}/{\mathrm{\Omega }}_{\mathrm{ce}}\le \mathrm{3.3}$), the whistler-mode chorus wave–particle interaction is favored (Horne et al., 2003), so the D_aa reaches up to ∼ 8 s⁻¹. According to our calculation, if the non-relativistic approach is used just for one wave cycle, it may lead D_aa to an underestimation of 20 %, as obtained for the ratio $D_{\mathrm{aa}}/D_{\mathrm{aa}}^{\mathrm{nr}}$ calculated for the antiparallel (parallel) case 1 (2).

In cases 3 and 4 (observed on 22 December 2014, shown in the shaded areas in Fig. D1 at 02:30 and 06:00 UT), the ambient magnetic field is lower than the previous cases, as probe A travels to the apogee. Probe A shows a minor decrease at the 60^∘ equatorial pitch angle relativistic outer-radiation-belt electron flux, concomitant to low-intensity chorus waves detected in the $\mathrm{0.1}{\mathrm{\Omega }}_{\mathrm{ce}}<\mathit{\omega }<\mathrm{0.45}{\mathrm{\Omega }}_{\mathrm{ce}}$ (and at ω<0.1Ω_ce, in case 4) frequency range. Figure E1 panels (b) and (c) show that the waves found a denser magnetosphere (see Table 1); thus the wave group velocity is lowered, compared to the previous events. The WNA in panel (d) remained close to zero, indicating parallel or antiparallel propagation to the ambient magnetic field line. Also, the polar angle of the Poynting vector in panel (e) confirms an alternation between antiparallel propagation (180^∘) in the shaded region for case 3 and quasi-parallel (0^∘) propagation in case 4.

Additionally, in Fig. F1 the PSD analysis presented shows the local electron flux decrease close to $L^{*}=\mathrm{5}$ (μ=200 MeV G⁻¹) and $L^{*}=\mathrm{4.5}$ (μ=700 MeV G⁻¹) near 21:42 UT on 21 December 2014 (blue curves in panels a and b). An expressive electron flux decrease (more than 3 orders of magnitude) is observed again near 02:12 UT on 22 December 2014 for energies from 0.37 MeV (green curves in panels a and b). This second electron flux decrease is also discussed in Fig. D1.

The ratio $T_{\mathrm{r}}/T_{\mathrm{nr}}$, in cases 3 and 4 for (anti)parallel propagation, is in the range ∼ 1.7 and 2.6, respectively. Despite these cases, the wave group velocities being lower than the previous cases and the electron plasma frequency ratio (${\mathit{\omega }}_{\mathrm{pe}}/{\mathrm{\Omega }}_{\mathrm{ce}}\ge \mathrm{7}$) being higher than the previous cases, the relativistic approach is an important consideration to improve the diffusion coefficient rates since $D_{\mathrm{aa}}/D_{\mathrm{aa}}^{\mathrm{nr}}$ is still significant, reaching ∼ 5 in a case study with a lower wave group velocity.

5 Conclusions

In this article, we consider the kinematics of special relativity to derive a consistent formula to calculate the interaction time equation applied to the wave–particle interaction between whistler-mode chorus waves and high-energy electrons. In the magnetosphere, the whistler wave's group velocity magnitude reaches a fraction of the speed of light. As these waves propagate, they can interact with high-energy electrons bouncing in the magnetic field lines. This problem pertains to the domain of Special Relativity, as it involves high magnitudes of velocities in the interactions. Several previous works described the wave–particle interaction using a quasi-linear theory for propagating waves interacting with non-relativistic (such as Kennel and Petschek, 1966; Walker, 1993; Tsurutani and Lakhina, 1997) and relativistic electrons (Hsieh et al., 2022; Lakhina et al., 2010; Horne et al., 2003). However, relativistic kinematics is not thoroughly described. In this context, we use first-order solutions such as those established by Lakhina and Tsurutani (2010), aiming to improve the calculation of the interaction time in a quasi-linear wave–particle interaction regime.

Through the derivation, we considered that the wave–particle interaction occurs in the electron's reference frame, and the change in electron flux pitch angle is measured in the satellite reference frame. Also, the scale factor length contraction and the time dilatation effects are considered to relate the parameters from one reference frame to the other, as well as the relativistic transformation of velocities.

Considering four case studies, we used the equations derived in Sects. 2, 3, and 4 to compare the magnitude of the interaction time and the pitch angle scattering diffusion coefficient calculated with a complete relativistic description and a non-relativistic approach. Results for this set of events show that the complete relativistic calculation led to an interaction time (T_r) up to 3 times longer than the non-relativistic approach. Furthermore, D_aa can be up to 5 times higher when a complete relativistic approach is used to compute the estimation.

In addition, the interaction time significantly depends on the wave group velocity and the relativistic addition velocity, besides the initial pitch angle and gyrofrequency harmonic. The main difference we observe using a more complete relativistic description is that the interaction time is often longer than that calculated with a non-relativistic description; it can be up to 3 times longer. Consequently, the diffusion coefficients can be more than 5 times higher compared to a non-relativistic approach. Regarding the applicability of the results shown here, Eqs. (5), (13), and (21) are consistent with the non-relativistic approach previously described by Kennel and Petschek (1966), Tsurutani and Lakhina (1997), and Lakhina et al. (2010) for wave–particle interaction in linear regimes. The linear interactions correspond to the most often wave–particle events observed in the magnetosphere since, according to Zhang et al. (2018), the weak turbulence in plasma and non-linear events occurrence rates is around 10 % to 15 % considering the average occurrence of whistler-mode chorus waves. Moreover, several difficulties arrive in calculating the trapping time in non-linear interactions using in situ measurements (e.g., Omura, 2021; Omura et al., 2008) since these events have a solution of the wave–particle interaction equation based on, at least, second-order terms in wave amplitude (e.g., Allanson et al., 2022; Artemyev et al., 2023; Omura, 2021; Osmane et al., 2016; Bortnik et al., 2008). Despite the limitations of the presented model, our results (i.e., Eq. 13) can be applied as a first-order approach to non-linear regimes (e.g., Hsieh et al., 2021) to estimate the interaction time from in situ measurements. This estimate is relevant to determine the energy gain of electrons undergoing a wave–particle interaction (Hsieh et al., 2021), although the interaction time is known to be shorter than the trapping time (Hsieh et al., 2021; Bortnik et al., 2008).

In summary, comparing our results with the Lakhina et al. (2010) methodology for pitch-angle scattering, we find that relativistic effects result in larger pitch-angle diffusion. Our results indicate that more accurate descriptions of pitch-angle scattering by whistler waves (e.g., through the Kennel and Engelman, 1966 or Hamiltonian methods, Artemyev et al., 2021) can also potentially be significantly affected by the addition of relativistic effects. Accurate calculation of the interaction time with full consideration of special relativity can enhance the modeling of the electron flux in Earth's outer radiation belt. This approach improves the estimation of wave–particle interaction time and pitch angle diffusion coefficient.

Appendix A: Case studies

The instruments on board the Van Allen Probes measuring the case study parameters are from the Electric and Magnetic Field Instrument Suite and Integrated Science (EMFISIS) (Kletzing et al., 2013), which provides the chorus waves' power spectrum density and other waves' parameters. The pitch angle distribution of relativistic electrons is provided by the Relativistic Electron Proton Telescope (REPT) (Baker et al., 2013), and the low-energy electron flux is measured by the Magnetic Electron Ion Spectrometer (MagEIS) (Blake et al., 2013). Both REPT and MagEis data are available at https://rbsp-ect.newmexicoconsortium.org/data_pub/ (Boyd et al., 2023). Also, data from the MagEIS instrument on board Van Allen Probe B are available at https://rbspgway.jhuapl.edu/psd (last access: 2 October 2023). The Electric Field and Waves (EFW) instrument (Wygant et al., 2013) provides the ambient magnetic field magnitude.

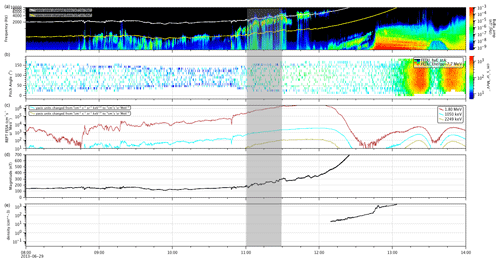
Figure A1 Case 2. Panels show from (a) to (e) the whistler-mode chorus waves' spectrum, the interpolated 1.8 MeV electron flux pitch angle distribution, the relativistic and low-energy electron fluxes, the ambient magnetic field, and the local plasma density for the whistler-mode chorus waves observed on 29 June 2013. The parameters shown in the highlighted area were used to calculate the time of interaction and change in pitch angle for the energy of the resonant electrons shown in Table 1.

Cases 1 and 2 are related to the whistler-mode chorus waves magnetic field spectrum, the interpolated 1.8 MeV electron flux pitch angle distribution, the relativistic and low-energy electron fluxes, the ambient magnetic field, and the local plasma density. Also shown are the whistler-mode chorus waves' ellipticity, planarity, WNA (wave normal angle), and the polar angle of the Poynting vector. The parameters are taken from the period highlighted in the gray-shaded area. They are used to calculate the time of interaction and change in pitch angle for the energy of the resonant electrons shown in Table 1.

Also, for cases 1 and 2, we selected some periods of interest to confirm that wave–particle interaction takes place during these events. We show in this section the measurements of the time evolution of phase space density (PSD) radial profiles at fixed first adiabatic invariant, μ=200 and μ=700 MeV G⁻¹, and second ($K=\mathrm{0.11}{G}^{\mathrm{1}/\mathrm{2}}{R}_E$) adiabatic invariant for both inbound and outbound parts of the RBSP-B orbit.

Appendix B

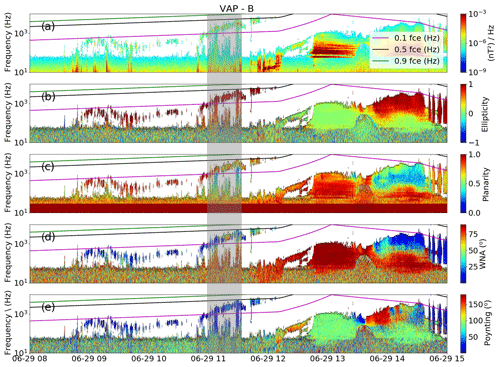
Figure B1 Case 2. Panels from 29 June 2013 show the whistler-mode chorus waves' (a) spectrum of the magnetic field, (b) ellipticity, (c) planarity, (d) WNA (wave normal angle) and (e) the polar angle of the Poynting vector. In all panels, the values of 0.1 fce (Hz), 0.5 fce (Hz), and 0.9 fce (Hz) are shown by the pink, black, and green lines, respectively. The parameters shown from the gray-shaded period are used to calculate the time of interaction and change in pitch angle for the resonant electrons energy shown in Table 1.

Appendix C

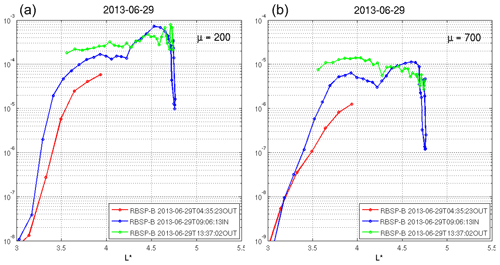
Figure C1 Case 2. Time evolution of phase space density (PSD) radial profiles at fixed first adiabatic invariant, μ=200 MeV G⁻¹ (a) and μ=700 MeV G⁻¹ (b), and second ($K=\mathrm{0.11}{G}^{\mathrm{1}/\mathrm{2}}{R}_E$) adiabatic invariant for both inbound and outbound parts of the RBSP-B orbit. Period of analyses: 29 June 2013 at 04:35:23 to 13:37:02 UT.

Appendix D

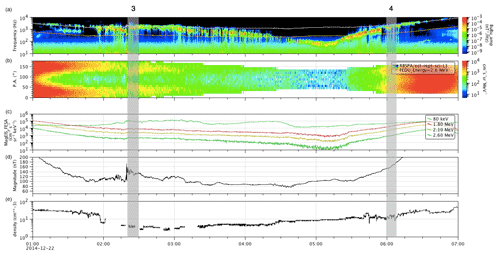
Figure D1 Case 3 and 4. Panels show from (a) to (e) the whistler-mode chorus waves' spectrum, the interpolated 1.8 MeV electron flux pitch angle distribution, the relativistic and low-energy electron fluxes, the ambient magnetic field, and the local plasma density observed on 21–22 December 2014. The parameters shown in the highlighted area were used to calculate the time of interaction and change in pitch angle for the energy of the resonant electrons shown in Table 1.

Appendix E

Figure E1 Case 3 and 4. Same as Fig. B1 but for 21–22 December 2014.

Appendix F

Figure F1 Same as Fig. C1 but for both inbound and outbound parts of the RBSP-B orbit in the period of analyses: 21 December 2014 at 17:11:17 UT to 22 December 2014 at 02:12:54 UT.

Appendix G

Figure G1 The high-resolution magnetic field measurement related to the event on 8 October 2012. A similar plot was made for the other three studied events. The figure identifies the maximum instantaneous wave magnetic field amplitude B_w and the one wave cycle period τ.