Forcing mechanisms of the migrating quarterdiurnal tide

We used a nonlinear mechanistic global circulation model to analyze the migrating quarterdiurnal tide (QDT) in the middle atmosphere with focus on its possible forcing mechanisms: the absorption of solar radiation by ozone and water vapor, nonlinear tidal interactions, and gravity wave–tide interactions. We show a climatology of the QDT amplitudes, and we examine the contribution of the different forcing mechanisms to the QDT amplitude. To this end, we first extracted the QDT from the model tendency terms and then removed the respective QDT contribution from the different tendency terms. We find that the solar forcing mechanism is the most important one for the QDT; however, the nonlinear and gravity wave forcing mechanisms also play a role in autumn and winter, particularly at lower and middle latitudes in the mesosphere and lower thermosphere. Furthermore, destructive interference between the individual forcing mechanisms is observed. Therefore, tidal amplitudes become even larger in simulations with the nonlinear or gravity wave forcing mechanisms removed.

1 Introduction

The dynamics of the upper mesosphere and lower thermosphere (MLT) are strongly influenced by atmospheric waves, especially solar tides (Forbes, 1982a, b; Forbes et al., 1994; Manson et al., 1989; Hagan et al., 1995; Jacobi et al., 1999; Pancheva et al., 2002; Yiğit and Medvedev, 2015). Tides are global-scale oscillations with periods of a solar day (24 h) and its harmonics (12, 8 and 6 h), which mainly result from the absorption of solar radiation by water vapor in the troposphere and ozone in the stratosphere (Chapman and S., 1970; Andrews et al., 1987; Xu et al., 2012). Because of the decrease in density and conservation of energy, the tidal amplitudes increase with height (Chapman and S., 1970; Andrews et al., 1987) and reach a maximum in the MLT region before they dissipate. Tides with larger periods like diurnal tides (DTs), semidiurnal tides (SDTs) and terdiurnal tides (TDTs) usually have larger amplitudes than short-period tides like the quarterdiurnal tide (QDT). This is why the QDT has attracted less attention in the past than the relatively well understood DTs, SDTs and TDTs.

There are few observational and model studies available on the QDT; however, the QDT has been observed from satellites. Therefore, Azeem et al. (2016) analyzed temperature data from the near-infrared spectrometer (NIRS) onboard the International Space Station (ISS) and from the Sounding of the Atmosphere using Broadband Emission Radiometry (SABER) instrument onboard the Thermosphere Ionosphere Mesosphere Energetics Dynamics (TIMED) satellite. They obtained an amplitude of the QDT that grew from ∼5 K near an altitude of 100 km to ∼30 K near an altitude of 130 km. Liu et al. (2015) also used measurements from SABER/TIMED temperature data to analyze the QDT in the MLT as well as its global structure and seasonal variability. They compared their results with different Hough modes. In their study, they noticed that between an altitude of 70 and 90 km at the Equator and at low latitudes, the (4,6) Hough mode dominated; above 90 km, more than one Hough mode is visible, but the (4,6) mode remains predominant. The SABER/TIMED data also show a meridional structure with three amplitude maxima between 4^∘ S and 4^∘ N: two of these maxima are centered at 3^∘ and one is centered above the Equator. This structure is also seen in the analyses by Azeem et al. (2016) with two additional maxima at about 6^∘ in both hemispheres. Jacobi et al. (2019) analyzed QDT signatures in lower ionospheric sporadic E occurrence rates. They mainly found maxima during early and late winter at middle latitudes, which coincided with modeled vertical shear QDT maxima of the zonal wind.

The QDT has also been observed in radar wind measurements in the MLT region (e.g., Sivjee and Walterscheid, 1994; Smith et al., 2004; Jacobi et al., 2017b; Guharay et al., 2018). Guharay et al. (2018) analyzed the variability of the QDT in the MLT over Brazilian low-latitude stations and found QDT wind amplitudes that reach 2 ms⁻¹ with a maximum during late summer and fall. Jacobi et al. (2017b) analyzed MLT (80–100 km) radar data from Collm (51^∘ N, 13^∘ E) and Obninsk (55^∘ N, 37^∘ E). They found maximum amplitudes in winter with a long-term mean monthly mean zonal amplitude of 7 ms⁻¹. Bispectrum analysis of the Collm data showed that nonlinear interaction is a possible forcing mechanism, especially in winter and in the upper height gates accessible to the radar (Jacobi et al., 2018). MLT radar observations were also performed at Esrange (68^∘ N, 21^∘ E) by Smith et al. (2004). They observed maximum monthly mean amplitudes during winter that can exceed 5 ms⁻¹. They also presented simulations of the QDT using a mechanistic model, which supported the results from the radar at Esrange and Collm, showing similar timing and magnitude of the seasonal peak amplitude. Furthermore, Smith et al. (2004) analyzed the forcing mechanisms of the QDT and showed that the solar forcing mechanism is the most important. Nevertheless, there is also a possible influence from a nonlinear interaction between different tides that may cause an additional QDT to the solar-forced QDT. The theory of nonlinear interactions between tides was described by Teitelbaum and Vial (1991). Accordingly, a pure nonlinear QDT wave (period of 6 h) is generated when a nonlinear interaction occurs between two SDTs (periods of 12 h) or between a TDT and a DT (periods of 8 and 24 h). Similarly, it holds for the wave number k, that a k=4 wave can be formed by a nonlinear interaction between two existing waves with k=2 or between waves with k=1 and k=3. Another possible source of tides is the interaction between gravity waves and tides. For example, Miyahara and Forbes (1991) demonstrated such a mechanism for the TDT, although without consideration of the QDT. Simulations of gravity wave–tide interactions were performed by Ribstein and Achatz (2016), but they did not analyze higher harmonics than the SDT. Liu et al. (2006) showed nonlinear interactions between atmospheric tides at midlatitude radar measurements, as well as an interaction between tides and gravity waves from a bicoherence spectrum analysis. This was mainly found for the upper height gates considered.

To summarize, there is some indication that the QDT is a regular phenomenon especially visible in the MLT, but the database is sparse and there is no final and quantitative information about the role of its different forcing mechanisms. Therefore, in this paper, we analyze the migrating QDT in the middle atmosphere with the help of a mechanistic global circulation model, and we focus on possible forcing mechanisms, i.e., the absorption of solar radiation by ozone and water vapor, nonlinear tidal interaction, and gravity wave–tide interaction. This is carried out by separately analyzing these forcing mechanisms and their relative contribution to the QDT tidal amplitudes. The paper is structured as follows: the model and experiments are described in Sect. 2; the QDT model climatology is presented, and the results of the runs with different forcing mechanisms excluded are shown in Sect. 3; and finally, the results are discussed and summarized in Sect. 4.

2 Description of the model and the experiments

The Middle and Upper Atmosphere Model (MUAM; Pogoreltsev, 2007; Pogoreltsev et al., 2007) is used to investigate the forcing mechanisms of migrating QDTs with wave number 4. MUAM is a 3-D, primitive equation, mechanistic global circulation model based on the earlier Cologne Model of the Middle Atmosphere–Leipzig Institute for Meteorology (COMMA-LIM), described by Jakobs et al. (1986), Fröhlich et al. (2003b) and Jacobi et al. (2006). Recent versions of the MUAM model are described by Lilienthal et al. (2017), Lilienthal et al. (2018), Lilienthal and Jacobi (2019), Jacobi et al. (2019) and Samtleben et al. (2019). The model reaches from the surface at 1000 hPa to a log-pressure height of 160 km, with a constant scale height of H=7 km and a vertical resolution of 2.842 km. In the lowermost 30 km, i.e., in the lowest 10 model levels, the zonal mean temperatures are nudged to monthly mean zonal mean ERA-Interim reanalysis temperatures (ERA-Interim, 2018; Dee et al., 2011). The wave propagation remains unaffected by nudging, as this only alters the zonal mean. Above 30 km, the background winds can develop freely in the model and are only affected by the zonal mean temperature nudging below. In contrast to other model experiments (e.g., Pogoreltsev et al., 2007; Pogoreltsev, 2007; Lilienthal et al., 2017; Samtleben et al., 2019), we do not include planetary wave forcing at the lower boundary to avoid undesired wave coupling with tides. In our experiments, we perform ensemble runs with 11 members using ERA-Interim data from 2000 to 2010 in order to describe interannual variability.

The solar heating through absorption, including water vapor, carbon dioxide, ozone, oxygen and nitrogen, in the middle atmosphere is parameterized following Strobel (1978). We do not intend to perform an ozone- and CO₂-dependent trend analysis, so we leave both constant in all simulations. Ozone is implemented as a monthly mean zonal mean field for the year 2005 up to an altitude of 50 km taken from MERRA-2 (Modern-Era Retrospective Analysis for Research and Applications, version 2) reanalysis data (MERRA-2, 2019; Gelaro et al., 2017) for each of the ensemble members. Above 50 km, the ozone mixing ratio is assumed to decrease exponentially. In the ensemble runs, the CO₂ mixing ratio is chosen according to the Mauna Loa Observatory data for 2005 as a global constant up to 80 km and an exponential decrease above this level (e.g., 380 ppm for February 2005; NOAA ESRL Global Monitoring Division, 2018; Thoning et al., 1989). Extreme ultraviolet (EUV) and chemical heating (Riese et al., 1994) are included (Fröhlich et al., 2003a).

The diurnal cycle of solar radiation absorption leads to self-consistent forcing of tidal harmonics such as DT, SDT, TDT and QDT. The model is unable to produce non-migrating tides, because it contains no 3-D fields of ozone and water vapor – it only contains zonal means. In contrast to the version by Ermakova et al. (2017) and Jacobi et al. (2017a), latent heat release is not included here. We used a horizontal resolution of $\mathrm{2.5}{}^{\circ }\times \mathrm{5.625}{}^{\circ }$ for the model, which differs from the version of, e.g., Lilienthal et al. (2017) and Lilienthal et al. (2018), in order to be able to better resolve the meridional structure of the QDT. In an earlier model version with a 5^∘ meridional resolution, essentially only one maximum was seen in the QDT amplitudes per hemisphere (Jacobi et al., 2019), whereas satellite observations (Azeem et al., 2016; Liu et al., 2015) show a more detailed meridional structure. Furthermore, from the linear theory, including the QDT meridional structure representation by Hough modes, another result was expected, as shown by Azeem et al. (2016).

The gravity wave routine, which is used in this model version, is an updated linear Lindzen-type parameterization (Lindzen, 1981; Jakobs et al., 1986), as described by Fröhlich et al. (2003b) and Jacobi et al. (2006). This parameterization is based on waves initialized at an altitude of 10 km that are traveling in eight directions with a phase speed between 5 and 30 ms⁻¹. These waves do not effectively propagate beyond the lowermost thermosphere; therefore, the Lindzen-type routine is coupled through the eddy diffusion coefficient with a modified nonlinear parameterization, following Yiğit et al. (2008, 2009), which is initiated with gravity waves of higher horizontal phase speeds. The individually excited gravity waves are clearly separated by their different phase velocities. The distribution of tendency terms from both gravity wave routines can be summed up to the total acceleration of the mean flow through gravity waves. More information about the gravity wave parameterization included in MUAM is given in Lilienthal et al. (2017) and Lilienthal et al. (2018).

The model uses a time step of 120 s and starts with a spin-up time of 120 model days. In that time, the heating rates are zonally averaged, which means there are no tides. After that, a further 90 model days are simulated with zonally variable heating rates so that tidal forcing is introduced. The declination in this model version is fixed to the 15th day of the respective month. The following results are analyzed from the last 30 model days. In this time period, the tidal amplitudes remain almost constant and show only small day-to-day variations. Lower atmospheric mean temperatures are nudged during the entire model run. However, as only zonal means are modified, tidal forcing and propagation remains possible.

Solar tides, including the QDT, may be generated by three different mechanisms, namely solar heating, nonlinear tide–tide interactions, and gravity wave–tide interactions. More details on these forcing mechanisms and how they are represented in the MUAM model are described by Lilienthal et al. (2018). Here, we essentially follow their approach by removing different forcing mechanisms. To this end, we used a Fourier transform and removed the wave number 4 (which is equivalent to the migrating QDT, as there are no non-zonal structures except for the migrating tides in our MUAM version) amplitude from the respective forcing term during each time step and at each model grid point. To remove the solar forcing mechanism, the wave number 4 heating was removed from the radiation parameterization scheme. To remove the nonlinear tide–tide interactions, we separated the nonlinear terms, which are essentially the advection terms in the momentum equation and the temperature equation, as was done in Lilienthal et al. (2018). We then removed the wave number 4 in these terms. As these advection terms are responsible for wave–wave interactions, this strategy effectively removes the QDT forcing through nonlinear interaction. To remove gravity wave–tide interactions, the total acceleration and heating through gravity wave oscillations of wave number 4 are removed. Table 1 shows an overview of our simulations in which different forcing mechanisms are eliminated separately: (i) SOL, which had no gravity wave–tide interactions and no nonlinear interactions; (ii) NLIN, which had no solar forcing mechanism and no gravity wave–tide interactions; and (iii) GW, which had no solar forcing and no nonlinear interactions. Effectively, these experiments represent model runs with only solar (SOL), nonlinear (NLIN) and gravity wave (GW) forcing of the QDT. Furthermore, two experiments were performed where only one process was removed, namely (iv) NO_NLIN with removed nonlinear interactions, and (v) NO_GW without gravity wave–tide interaction. In addition, a reference (REF) run was performed with all forcing mechanisms enabled.

Table 1 Overview on the different model experiments.

3 Results

3.1 Reference simulation and QDT climatology

In the reference run (REF), all forcing mechanisms (direct solar, gravity wave–tide interactions and nonlinear interactions) are included. Results from this experiment will be described here in comparison with results from the literature. For an overview of the seasonal cycle of the QDT, Fig. 1 shows the QDT temperature and wind amplitudes at a height of about 101 km. In the Northern Hemisphere, amplitudes increase in autumn and winter in the latitude ranges from 20 to 40^∘ N and from 50 to 70^∘ N, respectively. Maximum wind amplitudes in the Northern Hemisphere are seen in February and October; for the meridional wind, the largest amplitudes are found in the 20–40^∘ N range, whereas the largest zonal wind and temperature QDT amplitudes during these months are seen at 50–70^∘ N. In the Southern Hemisphere maximum amplitudes also appear during autumn and winter (April to October) between 20–40 and 50–70^∘ S. The higher latitude maximum is more strongly expressed than in the Northern Hemisphere.

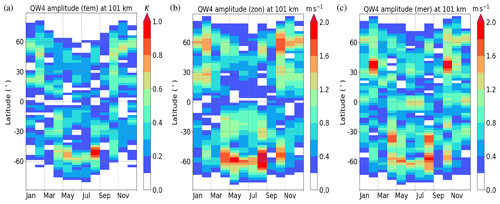
Figure 1 REF monthly mean QDT amplitudes at an altitude of 101 km. From left to right: (a) temperature, (b) zonal wind and (c) meridional wind.

Liu et al. (2015) showed a climatology of QDT temperature amplitudes from SABER/TIMED satellite data between 50^∘ N and 50^∘ S over 10 years. The amplitudes presented by Liu et al. (2015) show maxima near 30^∘ N and 30^∘ S and above the Equator. Their QDT temperature amplitudes reach values from 0.5 to 1.0 K between 70 and 90 km, and the amplitudes reach up to 4 K on an annual and long-term average at higher altitudes. Thus, the amplitudes observed by Liu et al. (2015) are larger than those in the MUAM simulation.

The maxima in February, April, May and August at 40^∘ N from MUAM simulations in Fig. 1a agree with the satellite measurements analyzed by Liu et al. (2015). Our simulated maximum in October, in comparison, does not appear in the SABER/TIMED data. Moreover, the extrema at about 10^∘ N in June, September and October, as reported by Liu et al. (2015), do not match with the MUAM results, because the amplitudes in the model are much smaller than the amplitudes observed by satellites.

Model simulations of the QDT temperature amplitudes at an altitude of 100 km by Smith et al. (2004) show a similar seasonal and latitudinal amplitude maximum distribution as seen in the MUAM results. Again, however, the amplitudes in the model simulations from Smith et al. (2004) are larger than in the MUAM results. Amplitudes in the MUAM simulations tend to underestimate other results by a factor of about 2 or 3. One reason for this is that water vapor in MUAM is implemented as zonal mean and not as a 3-D field, and latent heat is also not included as a QDT source in the model. In addition, the amplitudes of other tides (DT, SDT and TDT) are also too small compared with observations (Lilienthal et al., 2018); thus, nonlinear interaction processes are possibly underestimated. Figure S5 in the Supplement shows the DT and SDT zonal wind amplitudes for February and October from the MUAM REF simulation as well as the climatology from the Global Scale Wave Model (GSWM, 2020). The latitude-dependent structure and the increase of the amplitudes with altitude is correctly reproduced by the MUAM model. However, the maxima of the DT and SDT amplitudes in MUAM are sometimes more than 50 % lower than those of the GSWM at low- and midlatitudes. Furthermore, comparison with radar measurements (e.g., Manson et al., 1989; Pokhotelov et al., 2018) shows that the amplitudes of the DT and SDT are underestimated in MUAM.

Meteor radar measurements of zonal wind QDT amplitudes at 50^∘ N by Jacobi et al. (2017b, 2018) show maxima in January and February as well as in April and May, which is analogous to the MUAM simulations. The maxima in autumn, seen in Fig. 1b, are also supported by their measurements. Moreover, the temporal and spatial distribution of zonal wind amplitudes by Smith et al. (2004) show good similarity in with the MUAM simulations, as is also the case for the meridional wind amplitudes in our study (Fig. 1c).

Ensemble simulations, which contain the solar, nonlinear and gravity wave forcing mechanisms for all wave numbers, are useful as a reference for all experiments because they represent a QDT that can be compared with observations. The results in the following are given as means of the 11 ensemble members. As the largest amplitudes are found in February and October in the Northern Hemisphere (see Fig. 1), we selected these months for further analysis. In Fig. 2, the background climatology for the MUAM zonal mean circulation is shown for February (Fig. 2a, b) and October (Fig. 2c, d), for the temperature (Fig. 2a, c) and zonal wind (Fig. 2b, d) parameters. The data are the model results for the years 2000–2010 (shown using color coding), i.e., with the respective ERA-Interim reanalysis zonal mean temperatures used for nudging, and are presented with the corresponding standard deviations (shown using contour lines).

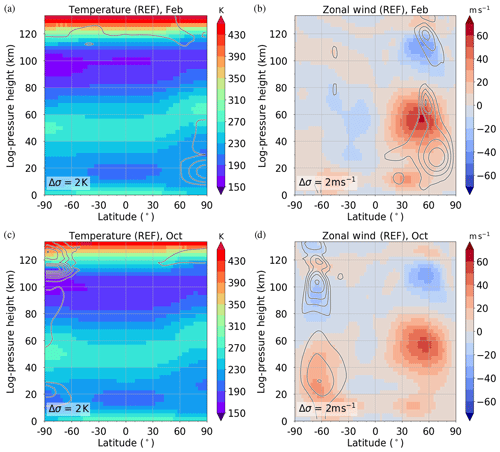
Figure 2 Panels (a) and (c) show the REF zonal mean temperature, and panels (b) and (d) show zonal wind for (a, b) February and (c, d) October conditions. Results are an average of 11 ensemble members (shaded color). Standard deviations σ are 2 K for temperature and 2 ms⁻¹ for zonal wind.

The model zonal wind climatology agrees reasonably well with earlier empirical climatologies such as COSPAR International Reference Atmosphere (CIRA-86; Fleming et al., 1990) or the radar-based Global Empirical Wind Model (GEWM; Portnyagin et al., 2004; Jacobi et al., 2009) and the satellite-based URAS Reference Atmosphere Project (URAP Swinbank and Ortland, 2003). In February, the easterly jet of the summer hemisphere is weaker than the abovementioned climatologies. The same is true for the equatorial easterly winds in October. The model temperature shows general agreement with the empirical CIRA-86 climatology. In February the stratopause and mesopause temperatures above the Equator and at low latitudes are about 10 K lower than those predicted by the CIRA-86 climatology. These differences are not seen in the comparison for October. MUAM produces a year-to-year variability (standard deviation σ) especially in the areas of the strongest jets of the northern midlatitudes in February (up to σ(u)=8 ms⁻¹) and at the southern midlatitudes in October (up to σ(u)=10 ms⁻¹). The reason for this is the annual variability in the formation of the polar vortex, which affects the strength of the jets and the temperature at the high and midlatitudes. This variability causes fluctuation of a few Kelvin (K) or meters per second (ms⁻¹). Elsewhere, the standard deviation is very small and mostly amounts to less than σ(T)=2 K (σ(u)=2 ms⁻¹, σ(v)=0.5 ms⁻¹).

In comparison with the more recent Horizontal Wind Model (HWM14; Drob et al., 2015), the westerly wind jet in February in the middle atmosphere midlatitudes is much stronger (+20 ms⁻¹) in the MUAM simulation. The easterly wind jet in the mesosphere, in contrast, is much weaker (−35 ms⁻¹) in the MUAM simulation than predicted by HWM14. Furthermore, the mesospheric wind reversal is found at higher altitudes in HWM14 (100 km) than in the MUAM (80 km) simulation, especially in the Northern Hemisphere. Similarly, the wind jets in the mesopause and lower thermosphere region are much weaker in the MUAM run than in HWM14. Better agreement is seen for October regarding the strength of the wind jets. However, in contrast to February, the wind reversal in October is higher in MUAM (80 km) than in HWM14 (70 km).

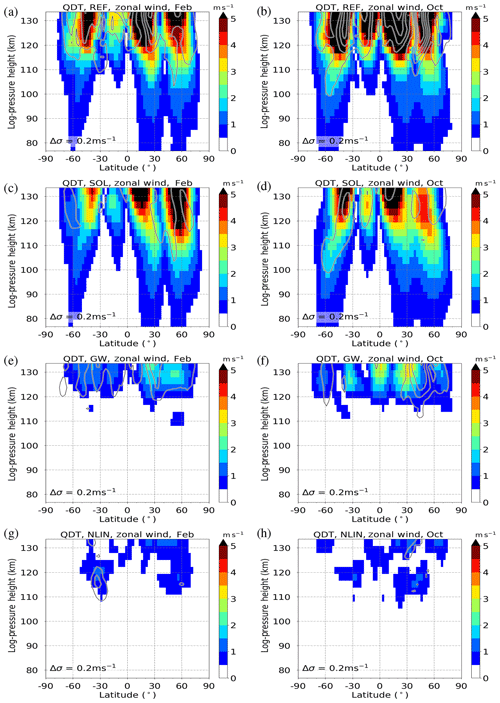
All QDT forcing terms, including the solar forcing, nonlinear forcing and the forcing resulting from gravity wave–tide interactions, are shown in Fig. 3 (thermal parameters) and Fig. 4 (wind parameters) for February (a, c, ,e ,g) and October (b, d, f, h). All of these forcing terms in the MUAM tendency equations are scaled by the factor $\exp [-z(\mathrm{2}H{)}^{-\mathrm{1}}]$ in order to account for the growth rate of the amplitudes with altitude due to decreasing density. Thus, the figures show the source regions of the QDT. However, from the parameters shown in Figs. 3 and 4, no statement about the propagation conditions of the QDT is possible because the tide might be trapped in the source region and be unable to propagate upwards (Lilienthal et al., 2018). In general, the QDT in situ forcing in February and October shows a similar global distribution.

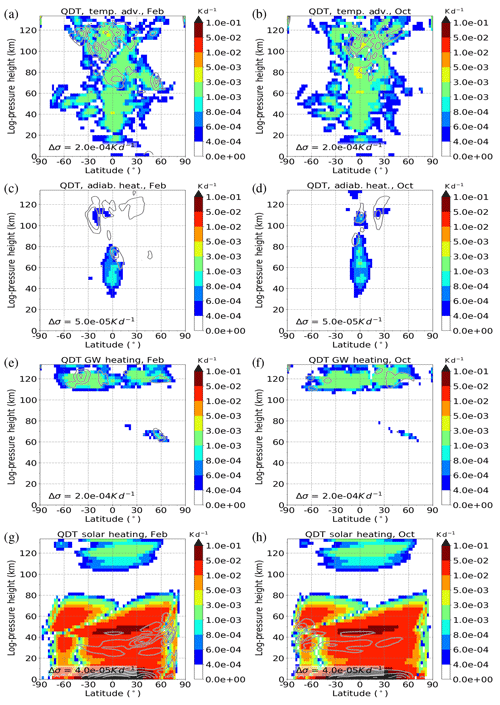
Figure 3 Quarterdiurnal component of thermal tendency terms in the REF simulation for February conditions (a, c, e, g) and October conditions (b, d, f, h). Amplitudes are scaled by $\exp [-z(\mathrm{2}H{)}^{-\mathrm{1}}]$. Results are an average of the 11 ensemble members (shaded color). Standard deviations (σ) are added as gray contour lines. Panels (a) and (b) show temperature advection (nonlinear component), panels (c) and (d) show adiabatic heating (nonlinear component), panels (e) and (f) show heating due to gravity wave activity (tendency term from gravity wave parameterization), and panels (g) and (h) show solar heating (tendency term from solar radiation parameterization). Note that the color scales are different and that the scale in panels (g) and (h) is not linear.

Figure 3 shows temperature advection (Fig. 3a, b), the nonlinear component of adiabatic heating (Fig. 3c, d), the heating related to dissipating gravity waves (Fig. 3e, f), and direct solar heating (Fig. 3g, h). Note the different color scales in Fig. 3 to cover the maxima of all forcing terms. The thermal forcing of the QDT is dominated by direct solar heating in the troposphere and stratosphere (Fig. 3g, h). This is due to the absorption of solar radiation by water vapor in the troposphere and ozone in the stratosphere. In the mesosphere (80–110 km) nonlinear wave–wave interactions (Fig. 3a, b) play the most important role and show maxima at the Equator in the stratosphere, mesosphere and lower thermosphere. Nonlinear adiabatic heating (Fig. 3c, d) maximizes in the upper stratosphere and mesosphere at the Equator. However, this forcing is about 1 order of magnitude smaller than the nonlinear forcing and, therefore, will be disregarded in the following. In the lower thermosphere, the strongest QDT generation second to solar heating takes place through gravity wave heating (Fig. 3e, f). Nevertheless, nonlinear effects continue to occur, and they are partly comparable in magnitude to the gravity wave forcing.

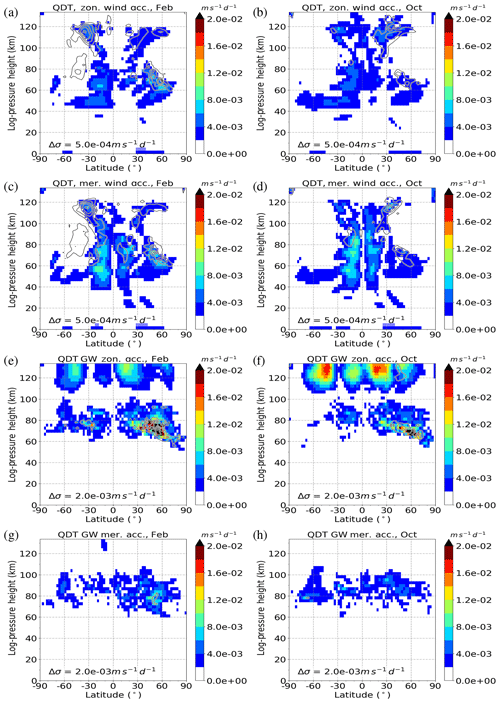
Figure 4 Quarterdiurnal component of zonal and meridional wind acceleration terms in the REF simulation for February conditions (a, c, e, g) and October conditions (b, d, f, h). Amplitudes are scaled by $\exp [-z(\mathrm{2}H{)}^{-\mathrm{1}}]$. Results are an average of the 11 ensemble members (shaded color). Standard deviations (σ) are added as gray contour lines. Panels (a) and (b) show the zonal wind advection (nonlinear component), panels (c) and (d) show the meridional wind advection (nonlinear component), panels (e) and (f) show the zonal acceleration due to gravity waves, and panels (h) and (h) show the meridional acceleration due to gravity waves (tendency terms from gravity wave parameterization). Note that the color scales are different.

Figure 4 shows QDT acceleration terms in the momentum equations and, thus, refers to the wind parameters. The data are again scaled by $\exp [-z(\mathrm{2}H{)}^{-\mathrm{1}}]$ according to energy conservation. The different panels show the zonal (Fig. 4a, b) and meridional wind advection (Fig. 4c, d) as well as the zonal (Fig. 4e, f) and meridional (Fig. 4g, h) acceleration due to gravity waves. In the troposphere, stratosphere and large parts of the mesosphere, the nonlinear forcing of both the zonal (Fig. 4a, b) and meridional (Fig. 4c, d) QDT wind dominates over the gravity wave forcing (Fig. 4e, f, g, h). Near the mesopause, gravity wave zonal and meridional forcing is more important than the nonlinear forcing in zonal and meridional wind. The zonal gravity wave forcing becomes relatively strong above 60 km at the northern middle latitudes. The gravity wave forcing plays a major role above 110 km, where it dominates over other nonlinear forcings. In the meridional component, the wind advection (Fig. 4c, d) outweighs the gravity wave forcing (Fig. 4g, h) at almost all altitudes.

3.2 Separation of quarterdiurnal generation mechanisms

To quantify the effect of each forcing mechanism on the QDT, we performed simulations with various forcing terms switched off (see Table 1). For the months of February and October, the QDT amplitudes and phases of the simulations REF, SOL, GW and NLIN are shown in Figs. 5–8 (Fig. 5a and b show temperature, and Fig. 7a and b show zonal wind). Note that amplitudes are not scaled in contrast to the forcing terms in Figs. 3 and 4. In October, the amplitudes tend to be a little stronger than in February (Fig. 5), and the amplitudes generally increase with height. In the REF run, there are four maxima for temperature and zonal wind. At an altitude of 100 km, amplitudes up to 0.5 K in temperature and 1.5 ms⁻¹ in zonal wind are achieved. Thus, the modeled amplitudes are much smaller than those reported from measurements (e.g., Liu et al., 2015; Azeem et al., 2016; Jacobi et al., 2017b; Guharay et al., 2018), i.e., satellite measurements reveal temperature amplitudes of 5–10 K, depending on season and altitude, whereas radar data suggest wind amplitudes of 2.5–5 ms⁻¹.

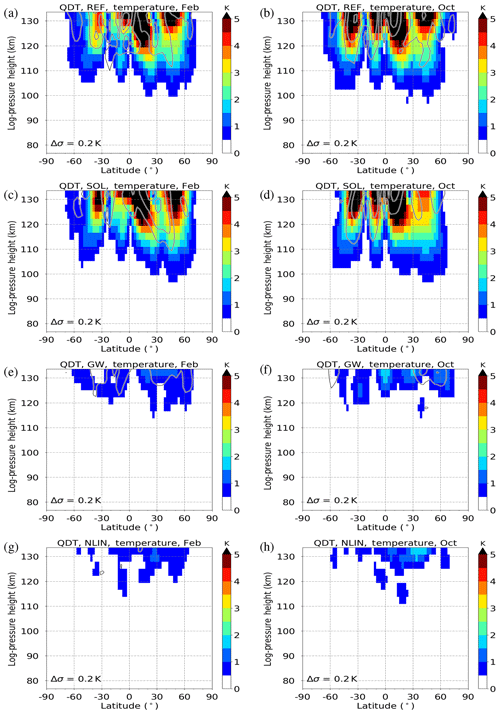
Figure 5 Simulations of zonal mean QDT amplitudes for temperature (colors), showing (a, c, e, g) February and (b, d, f, h) October conditions. Panels (a) and (b) show the REF run with all forcing mechanisms enabled, panels (c) and (d) show the SOL run with only the direct solar forcing mechanism enabled, panels (e) and (f) show the GW run with only the gravity wave forcing mechanism enabled, and panels (g) and (h) show the NLIN run with only the nonlinear forcing mechanism enabled. Standard deviations σ are added as gray contour lines.

In Fig. 5c and d, the SOL simulations for February and October are shown for temperature; in Fig. 7c and d, they are shown for zonal wind. In this run, the gravity wave forcing mechanism and the nonlinear forcing mechanism were removed from the terms of the model tendency equation, as described in Sect. 2. The QDT amplitudes in the SOL run look very similar to those of the REF run in terms of amplitude magnitude and distribution. This agrees well with Fig. 3g and h, showing that direct solar forcing is the strongest forcing mechanism and dominates the QDT in situ generation. On closer examination, the midlatitudes of both hemispheres show even larger temperature and zonal wind amplitudes in the SOL run than in the REF run, in particular during February. Conversely, amplitudes during October tend to be slightly decreased in the SOL simulation but with similar global structure to those of the REF simulation. The GW run only contains the gravity wave forcing and shows only small amplitudes for the temperature (Fig. 5e, f; up to 2 K) and zonal wind (Fig. 7e, f; up to 3.5 ms⁻¹) compared with the REF and SOL simulations. Similar to the REF simulation, amplitudes gradually increase with height, and maxima are located at northern low latitudes of the lower thermosphere; however, they are negligible below 115 km. This is most likely due to the fact that gravity wave–tide interactions mainly take effect in the lower thermosphere (see Figs. 3 and 4).

Figures 5g and h and 7g and h show the QDT amplitudes for the NLIN run. This simulation contains only the forcing of nonlinear interactions. The amplitudes for the temperature component (Fig. 5g, h) are comparable to those of the GW run with a maximum of 2 K. For the zonal wind component (Fig. 7g, h), the amplitudes are even smaller than in the GW run with less than 1.5 ms⁻¹. Therefore, we cannot derive a clear meridional structure of the nonlinear QDT. Keeping in mind that nonlinear tidal interactions mainly occur in the mesosphere (see Figs. 3 and 4), one may conclude that QDTs generated by this mechanism are trapped near their forcing region and cannot propagate further upward.

In addition, a NO_NLIN run was performed in which only quarterdiurnal nonlinear interactions were removed. The amplitudes of the NO_NLIN simulation are even larger than those in the REF simulation. This fact is also seen for the SOL simulations compared with the REF run. Larger amplitudes are also partly visible for the NO_GW simulation, with only interactions between tides and gravity waves removed in the model tendency terms. The amplitudes (Figs. S1, S3) and phases (Figs. S2, S4) of these simulations are shown in the Supplement, because amplitude and phase differences are rather small compared with the REF simulation. Similar behavior has been reported by Smith et al. (2004), who removed the nonlinear QDT forcing in their model and concluded that tidal interactions reduced rather than enhanced the QDT amplitude. In the following, this is investigated in more detail by analyzing phase differences between the differently generated QDTs. In this way, we intend to reveal possible interactions between these waves.

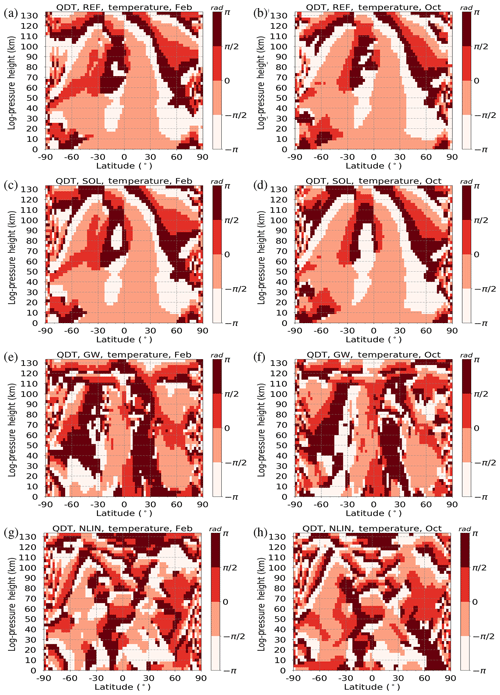
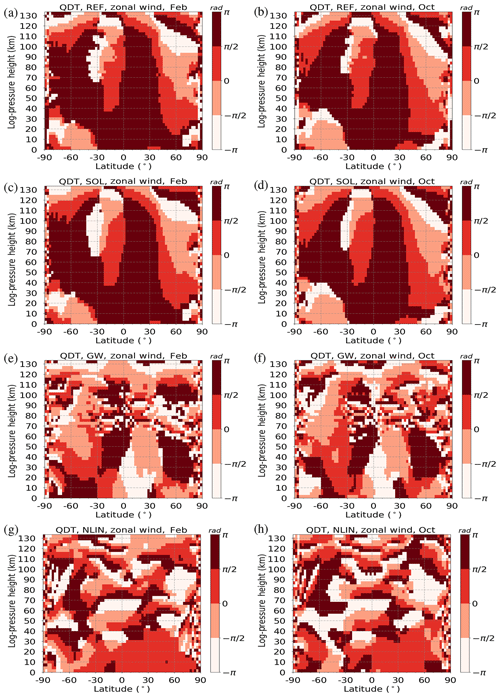
Figure 6 Simulations of zonal mean QDT phases for temperature (colors), showing (a, c, e, g) February and (b, d, f, h) October conditions. Panels (a) and (b) show the REF run with all forcing mechanisms enabled, panels (c) and (d) show the SOL run with only the direct solar forcing mechanism enabled, panels (e) and (f) show the GW run with only the gravity wave forcing mechanism enabled, and panels (g) and (h) show the NLIN run with only the nonlinear forcing mechanism enabled. Standard deviations σ are added as gray contour lines.

Figure 7 Same as Fig. 5 but for QDT zonal wind amplitudes.

The corresponding phases of the REF simulation can be found in Fig. 6a and b for temperature and in Fig. 8a and b for zonal wind. The corresponding vertical wavelength can be determined at any latitude from the vertical phase gradient. The wavelength is defined by the vertical distance between two points with identical phases and should cover a complete span of phases. According to theory, an upward propagating wave must have a negative phase gradient. At latitudes with large amplitudes, the vertical wavelengths tend to also be larger. In the opposite case, the wavelengths are smaller when the amplitudes are small. In February, the wavelengths reach 100 km or more. In October, phases are very similar. Both months show large areas with constant phases, especially at low latitudes.

Figure 8 Same as Fig. 6 but for QDT zonal wind phases.

Moreover, the QDT phases for the temperature (Fig. 6c, d) and the zonal wind (Fig. 8c, d) component of the SOL simulation are almost identical to the results of the REF run. The phases of the GW run (Figs. 6d, f and 8d, f) clearly differ from the REF run, i.e., vertical wavelengths are shorter and the phase position and distribution have also changed. Looking at the QDT phases of the NLIN run for temperature (Fig. 6g, h) and zonal wind (Fig. 8g, h), the associated vertical wavelengths are again smaller compared with the GW run, based on a more irregular phase distribution.

In Fig. 9, we present QDT amplitude differences between the NO_NLIN and REF simulations, which are scaled by density to highlight the actual source region of the waves. Here, the red (blue) areas denote larger amplitudes in NO_NLIN (REF) simulations. This means that the run with one forcing removed has larger amplitudes than the REF run in red areas. We conclude that the removed nonlinear forcing must have destructively interfered with other QDT from other forcings (such as solar or gravity wave forcing). The NLIN run (only nonlinear forcing) is expected to show small QDT amplitudes because of the weak nonlinear forcing. Without destructive interference, the NO_NLIN (without nonlinear forcing) simulation should show larger amplitudes than the NLIN run but smaller amplitudes than the REF run, because one forcing (nonlinear) is missing. Figure 9a and c show the temperature component, and Fig. 9b and d show the zonal wind component in February and October, respectively. Furthermore, the hatched areas denote destructive interference between the QDTs of NLIN and SOL, which are defined by their phases differences $\mathrm{\Delta }\mathrm{\Phi }={\mathrm{\Phi }}_{\mathrm{NLIN}}-{\mathrm{\Phi }}_{\mathrm{SOL}}$:

$$\begin{array}{}\text{(1)}& \mathrm{120}{}^{\circ }\le \mathrm{\Delta }\mathrm{\Phi }\le \mathrm{240}{}^{\circ }.\end{array}$$

In the case of a superposition of such destructively related NLIN and SOL waves, the amplitude of NO_NLIN is expected to be larger than in REF, because the nonlinear (NLIN) and solar (SOL) QDT of the REF run act against each other. Indeed, we observe regions for temperature (Fig. 9a, c) and zonal wind (Fig. 9b, d) in which the amplitudes in the NO_NLIN run are larger than in the REF simulation, and destructive interference between the nonlinear and solar QDT concurrently corresponds to these positive amplitude differences. Thus, we can conclude that the nonlinearly excited part of the QDT weakens the pure solar QDT amplitude in the REF simulation. The effect is more pronounced for the zonal wind than for temperature.

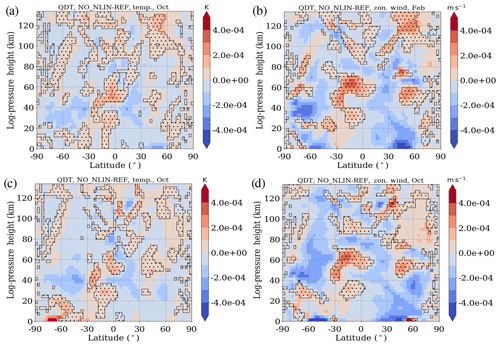
Figure 9 Difference of QDT amplitudes between NO_NLIN and REF simulation, scaled by $\exp [-z(\mathrm{2}H{)}^{-\mathrm{1}}]$. Red denotes larger NO_NLIN simulation amplitudes, and blue denotes larger REF simulation amplitudes. Areas of destructive interference ($\mathrm{120}{}^{\circ }\le \mathrm{\Delta }\mathrm{\Phi }\le \mathrm{240}{}^{\circ }$) between NLIN and SOL phases are hatched. Panels (a) and (c) show temperature, and panels (b) and (d) show zonal wind for (a, b) February conditions and (c, d) October conditions.

In addition to the interaction between nonlinear and solar QDT, an interaction between gravity-wave-induced QDT and solar QDT is also possible. For this reason, we show the respective results in Fig. 10, which is comparable to Fig. 9. Colors denote the differences between the NO_GW and the REF simulation, which are again scaled by the growth rate of the amplitudes with altitude. Red (blue) colors denote larger NO_GW (REF) amplitudes. Areas of destructive interference (see Eq. 1 with $\mathrm{\Delta }\mathrm{\Phi }={\mathrm{\Phi }}_{\mathrm{GW}}-{\mathrm{\Phi }}_{\mathrm{SOL}}$) between the phases from the NO_GW and SOL run are hatched. The difference between the NO_GW and the REF runs shows that the amplitudes in the NO_GW simulation are sometimes larger than in the REF run. This often happens in areas where destructive interference can be detected, but it is less well pronounced than in Fig. 9 for the nonlinear–solar QDT interaction. This means that the QDT owing to gravity wave–tide interactions also tends to act against the solar QDT which leads to a decline in QDT amplitude in the REF simulation for temperature and zonal wind, where both forcing mechanisms are present. The interaction between GW and NLIN QDT is not shown separately because they were found to be negligible.

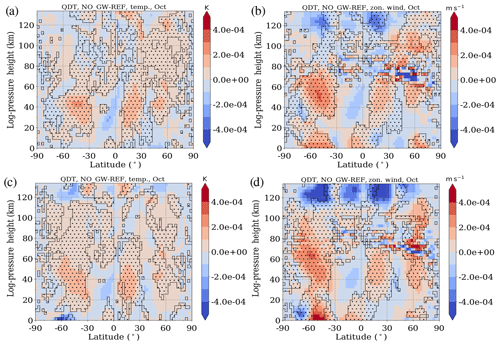
Figure 10 Difference of QDT amplitudes between the NO_GW and REF simulations, scaled by $\exp [-z(\mathrm{2}H{)}^{-\mathrm{1}}]$. Red denotes larger NO_GW simulation amplitudes, and blue denote larger REF simulation amplitudes. Areas of destructive interference ($\mathrm{120}{}^{\circ }\le \mathrm{\Delta }\mathrm{\Phi }\le \mathrm{240}{}^{\circ }$) between the GW and SOL phases are hatched. Panels (a) and (c) show temperature, and panels (b) and (d) show zonal wind for (a, b) February and (c, d) October conditions.

4 Discussion and conclusion

The results of the REF simulation show a consensus in the climatology and global structure of QDT in comparison with observations and other model studies. The amplitudes of the MUAM are relatively small for the QDT with up to 2.5 ms⁻¹ in the zonal wind at an altitude of 101 km and 5.0 ms⁻¹ at an altitude of 120 km in spring and autumn. For example, QDT amplitudes obtained from meteor radar measurements (Jacobi et al., 2017b) are up to 3 times larger than in the MUAM simulations. However, it is a known issue that numerical models tend to underestimate the tides in some regions and seasons (e.g., Smith, 2012; Pokhotelov et al., 2018).

In our simulations, the meridional structure of QDT amplitudes shows three to four maxima in both the temperature and zonal wind component. These are located at low (10–30^∘) and middle latitudes (40–70^∘) of the respective hemisphere. These maxima at low and midlatitudes are also present in the NIRS and SABER temperature measurements (Liu et al., 2015; Azeem et al., 2016). Meteor radar measurements at northern midlatitudes (Jacobi et al., 2017b) confirm our QDT wind maxima in winter, spring and autumn. The maximum of the QDT wind amplitudes at low latitudes has been proven by meteor radar measurements over Brazil (Guharay et al., 2018). They show maxima below 100 km in spring and autumn as in the MUAM simulations.

In the present paper, we focused on forcing mechanisms of the QDT. To this end, we first compared all possible sources of the migrating QDTs in our simulations following the approach of Lilienthal et al. (2018). These are (i) the absorption of solar radiation by water vapor and ozone, (ii) nonlinear tidal interactions between migrating DTs and TDTs and the self-interaction of migrating SDTs, and (iii) nonlinear interactions between gravity waves and tides. To our knowledge, this is the first time that the global distribution of quarterdiurnal in situ forcing from a numerical model has been presented. In summary, the solar forcing dominates in the troposphere and stratosphere, the nonlinear forcing predominates in the mesosphere, and the gravity wave forcing mainly takes place in the mesosphere and thermosphere. These results do not allow us to draw conclusions on the upward propagation of the QDT, as they only show local excitation.

For this reason, we adapt the idea of Smith et al. (2004), who performed simulations with individual forcing mechanisms removed. In addition to Smith et al. (2004), we also consider gravity wave–tide interactions. Some of our simulations are designed in a way that only a single forcing mechanism remains and the other two sources are removed (SOL, NLIN and GW), whereas in other simulations only one of the sources was removed (NO_NLIN and NO_GW).

As a result, we find that the solar forcing mechanism is the most important and dominant of all forcing mechanisms, as the removal of direct quarterdiurnal solar heating (GW and NLIN runs) leads to a significant decrease in the QDT amplitude. Smith et al. (2004) came to the same conclusion when they removed the quarterdiurnal solar forcing in their simulations.

We also showed that the amplitudes resulting from the gravity wave forcing mechanism (GW) are smaller than the resulting amplitudes of the direct solar forcing (SOL), but they are larger than those from the nonlinear forcing mechanisms (NLIN). In agreement with the results of Smith et al. (2004), nonlinear tidal interactions seem to play a minor role in the total QDT amplitudes, although we found distinct sources of nonlinear quarterdiurnal in situ excitation in the mesosphere (see above). This allows for the conclusion that the QDT from local nonlinear forcing mechanisms can not propagate and is, to a large degree, trapped in the vertical domain. Significant nonlinear QDT amplitudes only exist in the thermosphere. In the temperature component, QDT amplitudes of the NLIN and GW simulations are comparable in magnitude. In the zonal wind component, they are smaller in NLIN than in GW. For the GW and NLIN simulations, we note relatively short vertical wavelengths, accompanied by small QDT amplitudes, compared with the SOL and REF runs. Therefore, we can state that if the amplitudes are small, the vertical wavelength is also shorter. Lilienthal et al. (2018) found a similar relation for the vertical wavelengths of the TDT.

In the SOL simulation, which only contains the solar forcing, we see that the amplitudes are larger than in the REF run in some cases. A similar feature was observed by Smith et al. (2004). Here, we compare phase and amplitude differences between our different simulations to investigate the physical explanation behind this. We find that the amplitudes in simulations with removed forcing mechanisms (NO_NLIN and NO_GW) increase compared with the REF simulation in the same areas where destructive phase relations between the differently generated QDTs are detected. This leads to the conclusion that QDTs that are excited by different mechanisms counteract rather than enhance each other. Therefore, removing an individual forcing mechanism in NO_NLIN or NO_GW also avoids the destructive interference, and the remaining QDT can propagate freely, resulting in larger amplitudes.

This destructive relation appears to be more clear between the nonlinear tidal forcing and the direct solar forcing than between the gravity wave-induced forcing and the solar forcing. Note, however, that nonlinear tidal interactions generally have a smaller impact on the QDT than gravity wave–tide interactions, as described above. We do not present phase relations between the nonlinear and gravity wave forcing because these were found to be small. Apparently, the dominating solar forcing has to be involved in the destructive phase relation. In future, an implementation of a latent heat release parameterization according to Ermakova et al. (2019) and Jacobi et al. (2017a) and 3-D ozone (Suvorova and Pogoreltsev, 2011) and water vapor (Ermakova et al., 2017) fields into the model is planned, which may help to increase tidal amplitudes towards more realistic magnitudes. Another important issue is the careful treatment of gravity waves, because we demonstrated that gravity waves are the most important source of QDTs above the mesopause. In MUAM, gravity waves are currently implemented via two coupled parameterizations. These two parameterizations could be replaced by the original whole atmosphere scheme, as provided by Yiğit et al. (2008). Furthermore, a sensitivity study with respect to the strength of the individual forcing terms may contribute to a better understanding of the forcing mechanisms and interactions, thereby showing their impact on QDT amplitudes and the background circulation. Further examination of dominating Hough modes may help explain the different meridional structures at different altitudes.