A case study of the large-scale traveling ionospheric disturbances in the eastern Asian sector during the 2015 St. Patrick's Day geomagnetic storm

This study presents a comprehensive observation of the large-scale traveling ionospheric disturbances (LSTIDs) in the eastern Asian sector during the 2015 St. Patrick's Day (17 March 2015) geomagnetic storm. For the first time, three dense networks of GPS receivers in China and Japan are combined together to obtain the two-dimensional (2-D) vertical total electron content (VTEC) perturbation maps in a wider longitudinal range than previous studies in this region. Results show that an LSTID spanning at least 60^∘ in longitude (80–140^∘ E) occurs as a result of possible atmospheric gravity waves (AGWs) propagating from high to lower latitudes at around 09:40–11:40 UT (universal time), and the crest of this LSTID shows a tendency of dissipation starting from the eastern side. The manifestation of the 2-D VTEC perturbation maps is in good agreement with the recordings from two high-frequency Doppler sounders and the iso-frequency lines from eight ionosondes. Then, the propagation parameters of the LSTIDs are estimated by applying least-square fitting methods to the distinct structures in the 2-D VTEC perturbation plots. In general, the propagation parameters are observably longitudinally dependent. For example, the propagation direction is almost due southward between 105 and 115^∘ E, while it is slightly southwest and southeast in the western and eastern sides of this region. This feature is probably related to the regional geomagnetic declination. The mean values of the period, trough velocity (V_t), crest velocity (V_c), and wavelength of the LSTIDs in the studied longitudinal bands are 74.8±1.4 min, 578±16 m s⁻¹, 617±23 m s⁻¹, and 2691±80 km, respectively. Finally, using the VTEC map data from the Madrigal database of the MIT Haystack Observatory, the characteristics of the ionospheric disturbances over the European sector (30–70^∘ N, 10–20^∘ E) are also studied. The results are very different from those in the eastern Asian sector in parameters like the occurrence time, oscillation period, and propagation velocities.

1 Introduction

During the geomagnetic storm, the solar wind energy is impulsively or continually injected into the earth polar region, making the atmospheric and ionospheric states deviate greatly from their background levels (Fuller-Rowell et al., 1994; Mendillo and Narvaez, 2009). In general, the response of the ionosphere to the geomagnetic storm is classified by a variety of different features, one of which being the large-scale traveling ionospheric disturbance (LSTID) that is the wave-like perturbation mainly propagating equatorward from high latitudes. Traveling ionospheric disturbances (TIDs) are classified into LSTIDs and medium-scale TIDs, and they are considered to be the ionospheric manifestation of the presence of atmospheric gravity waves (AGWs) stimulated by different sources. LSTIDs are mainly caused by joule heating or Lorenz drag forcing in the auroral regions during a geomagnetic storm period (Hines, 1960; Richmond and Roble, 1979; Hocke and Schlegel, 1996).

In earlier years, the acquisition of the continuous evolution of LSTIDs on a global scale was limited by the availability of the ionospheric observations. In order to obtain the propagation characteristics of LSTIDs, researchers needed to organize their findings from limited ionospheric observations, for example, the foF2 data from sparsely distributed ionosondes. In the 1980s, the GPS (Global Positioning System) method was introduced into the ionospheric study (Klobuchar, 1986; Lanyi and Roth, 1988; Coster and Gaposchkin, 1989). With the dense and worldwide distributed GPS receivers, some characteristic ionospheric phenomena, like TIDs (Saito et al., 1998; Tsugawa et al., 2004; Ding et al., 2007), ionospheric storms (Ho et al., 1996), and ionospheric responses to solar flares (Afraimovich, 2000; Zhang and Xiao, 2005), were revisited frequently and new results were obtained.

The propagation characteristics of LSTIDs are always topics of great research interest (Hunsucker, 1982; Ho et al., 1996; Balthazor and Moffett, 1999; Afraimovich et al., 1998, 2000; Shiokawa et al., 2002; Tsugawa et al., 2003, 2004; Ding et al., 2008, 2014; Borries et al., 2009, 2017; Habarulema et al., 2015, 2016, 2018; Zakharenkova et al., 2016; Figueiredo et al., 2017; Pederick et al., 2017; Cherniak and Zakharenkova, 2018; Lyons et al., 2019). Based on limited GPS stations measurements, Afraimovich et al. (1998) proposed a radio interferometry method to roughly estimate horizontal propagation velocities and phase front angles of TIDs. Furthermore, the worldwide or local dense distribution of the GPS receivers networks facilitates the acquisition of the global or regional total electron content (TEC) perturbation maps with high spatial and temporal resolutions to reveal the detailed propagating characteristics of TIDs (Ho et al., 1996; Saito et al., 1998; Tsugawa et al., 2004; Borries et al., 2009; Ding et al., 2012). With more than 60 GPS receivers distributed worldwide, Ho et al. (1996) studied the global distribution of TEC perturbations during a magnetic storm. They identified a TID propagating from the northern sub-auroral region to lower latitudes at a speed of about 460 m s⁻¹. The GPS Earth Observation Network (GEONET) in Japan is one of the densest GPS receiver networks on the Earth, and two-dimensional (2-D) TEC perturbations over Japan can be mapped with the GEONET observations. With these high-resolution TEC perturbation maps, the spatial structures and temporal evolutions of a TID in the nighttime midlatitude ionosphere over Japan were revealed clearly (Saito et al., 1998). Since then, with this dense GPS network, the characteristics of LSTIDs over Japan are carefully studied through case and statistical analysis, and some propagation features of TIDs in this region are revealed (Saito et al., 2001; Shiokawa et al., 2002; Tsugawa et al., 2003, 2004, 2006).

For the LSTID with scales of thousands of kilometers, the extensive spatial coverage of ionospheric observations is undoubtedly useful for capturing its propagation features. In recent years, the GPS data from densely distributed GPS stations in China were used to study LSTIDs in this region (Ding et al., 2012, 2013, 2014; Song et al., 2013). Based on the GPS data from the Crustal Movement Observation Network of China (CMONOC), Ding et al. (2012) obtained temporal continuous 2-D imaging of ionospheric disturbances during the geomagnetic storm on 28 May 2011 and found two LSTIDs moving southwestward with the front width of at least 1600 km during different storm stages. In addition, through the comparative climatological study of LSTIDs over North America and China, the different time dependencies of LSTID occurrence over two longitudinal sectors were revealed statistically (Ding et al., 2014). These studies further emphasize the effectiveness of the large-coverage, high-resolution ionospheric observations from GPS networks in revealing the structures of the ionospheric disturbances.

The propagating direction of the LSTID during the geomagnetic storm has always been focused on for the LSTID studies. From case and statistical studies about LSTIDs during geomagnetic storms over the eastern Asia region conducted by Chinese and Japanese scientists independently, the dominant propagating direction of LSTID in China and Japan is a little different. It mainly propagates southwest in the Chinese region (Ding et al., 2014), while it mainly propagates southeast in the Japanese region (Tsugawa et al., 2004). Although the geomagnetic declination is considered to be one of the main factors responsible for the propagation direction of LSTID based on different LSTID studies, the LSTID studies concerning the same geomagnetic storm using both Chinese and Japanese GPS networks together have not been reported yet.

During the period of 17–18 March 2015, the strongest geomagnetic storm in the 24th solar cycle occurred, and LSTIDs were detected and analyzed in different longitudinal sectors (Ramsingh et al., 2015; Borries et al., 2016; Zakharenkova et al., 2016; Habarulema et al., 2018). Meanwhile, two high-frequency (HF) Doppler sounders in Chinese midlatitudes operated by the China Meridional Project (Wang, 2010) recorded large ionospheric HF Doppler shifts after 10:00 UT (universal time), which seem to indicate the LSTIDs in the Asian region between 09:00 and 12:00 UT that were reported by Habarulema et al. (2018). In this study, the multi-network of densely distributed GPS receivers, the HF Doppler sounder stations, and an ionosonde network are used to conduct a more comprehensive study on the propagating characteristics of the disturbances in the eastern Asian region, especially on the characteristics of the dominant propagating direction over China and Japan.

2 Data and methods

Figure 1 illustrates the locations of ground-based receivers used in this study from four Global Navigation Satellite Systems (GNSS) networks, distinguished by colors. They are the Chinese Meteorological GNSS Network (CMGN), CMONOC, GEONET, and International GNSS Service (IGS). These receivers are selected through data quality checking and regional restriction (10–60^∘ N, 70–150^∘ E), and the numbers of used stations are 259, 220, 1300, and 31 for CMGN, CMONOC, GEONET, and IGS, respectively. The sample rate of all GPS data is 30 s. Combining the carrier phase and pseudo-range measurements in two L-band frequencies of GPS, the vertical TEC (VTEC) can be obtained. In the calculation, the height of the ionospheric thin shell is set to be 400 km, and the cutoff elevation angle is 30^∘. The detailed process of the TEC calculation from GPS data can be found in our previous studies (Zhang et al., 2009, 2010).

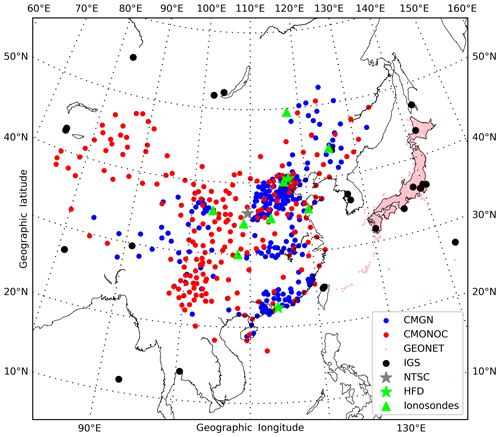
Figure 1 Locations of the GPS stations of different networks (colored dots), the HF Doppler sounder stations (green stars), the National Time Service Center of China (gray stars), and the ionosonde stations (green triangles) that are used in this study.

Different methods were used for extracting the TEC perturbations related to LSTIDs in previous research (Wan et al., 1997; Afraimovich et al., 2000; Shiokawa et al., 2002; Nicolls et al., 2004; Tsugawa et al., 2004; Ding et al., 2007). Afraimovich et al. (2000) suggested that the LSTID characteristics in TEC can be determined by removing the trend with three- to five-order polynomials, which is introduced by the motion of satellites and background variations in ionosphere. For a similar purpose, Shiokawa et al. (2002) subtracted a running average of TEC over 1 h from the raw TEC, and a series of 2-D TEC perturbation maps was obtained with more than 1000 GPS receivers in Japan. Ding et al. (2007) developed another method of obtaining the 2-D TEC perturbation maps by expressing the VTEC as a one-order function of local time and latitude. According to their argument, this method is sufficient for removing background trends for continuous observation of a GPS receiver–satellite pair without introducing artificial perturbations. After comparing the results of these methods, a method similar to Ding et al. (2007) is conducted in this study in which the VTEC is treated as a function of UT, longitude (Long), and latitude (Lat), i.e.,

$$\begin{array}{}\text{(1)}& {\displaystyle }{\mathrm{VTEC}}_{\mathrm{0}}={\mathrm{C}}_{\mathrm{0}}+{\mathrm{C}}_{\mathrm{1}}\mathrm{UT}+{\mathrm{C}}_{\mathrm{2}}\mathrm{Long}+{\mathrm{C}}_{\mathrm{3}}\mathrm{Lat},\text{(2)}& {\displaystyle }\mathrm{VTECP}=\mathrm{VTEC}-{\mathrm{VTEC}}_{\mathrm{0}},\end{array}$$

in which VTEC₀ is the background change and VTECP is VTEC perturbation. Then, the obtained VTECP data are reorganized into pixels which are bounded by 10–60^∘ N, 70–150^∘ E, and with a spatiotemporal resolution of 1^∘ longitude × 1^∘ latitude × 10 min. The pixel value is the average of all VTECPs in this pixel. After these steps, the featured ionospheric disturbances are expected to appear in a series of 2-D VTECP maps.

As a comparison, the VTEC map from the Madrigal database of the MIT Haystack Observatory is used to reveal the ionospheric disturbances in the European sector (30–70^∘ N, 10–20^∘ E). This database provides worldwide VTEC values in 1^∘ latitude × 1^∘ longitude pixels with a temporal resolution of 5 min (Rideout and Coster, 2006) and has good data coverage in the European sector. VTEC maps with such a high spatiotemporal resolution are suitable for revealing the structures of traveling ionospheric disturbances (Zhang et al., 2017).

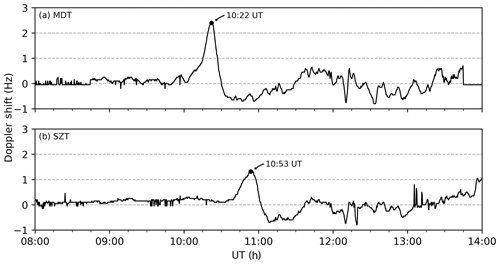
The Doppler shift data observed at two HF Doppler sounder stations in China are collected, which are MDT (40.4^∘ N, 116.9^∘ E) and SZT (22.6^∘ N, 114.1^∘ E). The sounding system continuously receives electromagnetic waves with a stabilized frequency of 10 MHz transmitted by the National Time Service Center (NTSC; 35.7^∘ N, 109.6^∘ E) to detect the ionospheric disturbances through the Doppler shifts of this standard frequency. These shifts are considered to be caused by ionospheric variations, mainly around the reflecting point of the electromagnetic wave in the ionosphere. According to the geometrical relationships, the locations of the reflecting point for MDT and SZT are 38.0^∘ N, 113.2^∘ E, and 29.2^∘ N, 111.8^∘ E, respectively. These stations are marked in Fig. 1 with colored stars.

In this study, ionograms from eight ionosonde stations in Chinese middle latitudes are used to derive the iso-frequency lines, which vary as a function of universal time and virtual height. The sample rate of the ionograms is 15 min. These ionosondes belong to the China Research Institute of Radio Wave Propagation (CRIRP), and their locations are marked with green triangles in Fig. 1. The virtual height data are manually scaled by us from these ionograms, with professional scaling software provided by CRIRP to reduce possible errors of auto-scaling (Krankowski et al., 2011; Habarulema and Carelse, 2016). During the scaling, we limited the frequency to less than 7 MHz. In addition, the space environment data for this event are from OMNI dataset, which is downloaded from the FTP service of the NASA Goddard Space Flight Center.

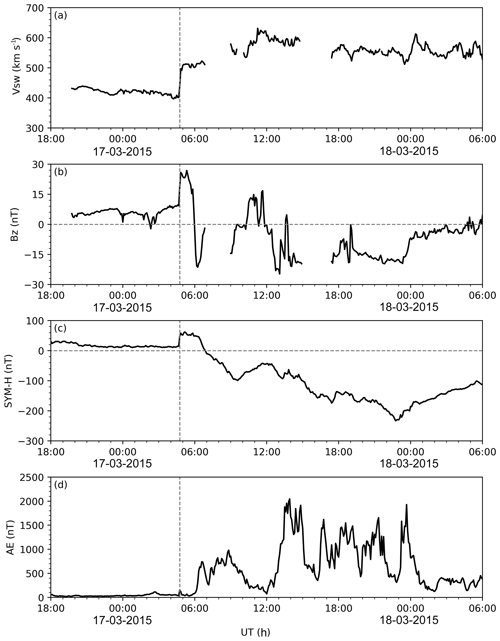
Figure 2 Temporal variations in (a) the solar wind speed (V_sw), (b) the IMF B_z component, (c) the SYM-H index, and (d) the AE index between 18:00 UT, 16 March 2015, and 06:00 UT, 18 March 2015. The occurrence of SSC is shown with vertical dashed lines.

Figure 3 Temporal variations in the HF Doppler shift records from (a) MDT and (b) SZT between 08:00 and 14:00 UT, 17 March 2015.

3 Results

3.1 Observations

Figure 2 shows the variations in solar wind speed (Fig. 2a), the interplanetary magnetic field (IMF) B_z component (Fig. 2b), the SYM-H index (Fig. 2c), and  the AE index from the OMNI dataset (Fig. 2d), and the time range is from 18:00 UT, 16 March 2015, to 06:00 UT, 18 March 2015. It should be noted that the solar wind magnetic field and plasma data are time shifted to the bow shock nose to better support the studies of coupling between the solar wind and magnetosphere. It can be seen clearly that a geomagnetic storm occurred on 17 March 2015, with the sudden storm commencement (SSC) at ∼ 04:45 UT, which is characterized by a sharp increase (marked with vertical dashed lines) in the solar wind speed, B_z, and SYM-H index. The main phase of the storm can be roughly divided into two stages. The first stage is from ∼ 06:00 UT, when the IMF B_z component first turns southward, to ∼ 12:00 UT, when the B_z turns southward again after turning back northward for about 2 h. After ∼ 12:00 UT, the B_z is southward for most of the time until it enters the recovery phase. The SYM-H and AE indices show a similar two-stage feature as the B_z. SYM-H decreases after ∼ 06:00 UT, reaches the first minimum at ∼ 09:30 UT, and increases to a local maximum at ∼ 12:00 UT. Then, it gradually decreases with small oscillations and reaches the minimum value of −233 nT at ∼ 22:45 UT. Correspondingly, the AE index exhibits the first increase period between 06:00 and 12:00 UT, with the maximum intensity of ∼1000 nT, and the second period between 12:00 and 02:00 UT of the next day, during which the AE increases much larger with several peaks. This storm is the strongest one in the 24th solar cycle (Astafyeva et al., 2015).

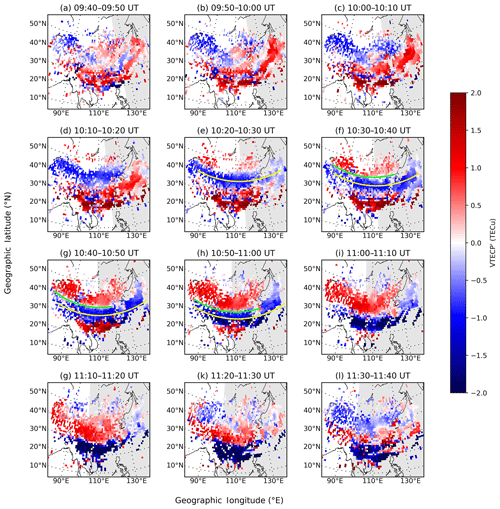
Figure 4 A series of 2-D VTECP^′ maps over the eastern Asian sector from the period of 09:40–09:50 to 11:30–11:40 UT on 17 March 2015. The gray areas represent the nightside. The color bar represents the VTECP^′ (units: TECu), which is transformed from the original VTECP value with Eq. (3) for a more viewer-friendly color map. The green and yellow lines illustrate the least-square fittings (order two) for wavefronts.

During the first stage of the main phase, disturbances are observed successively at MDT and SZT Doppler sounder stations. Figure 3 illustrates the variations in the Doppler shift records at (Fig. 3a) MDT and (Fig. 3b) SZT between 08:00 and 14:00 UT on 17 March 2015. It shows that two distinct positive shifts occur at about 10:22 and 10:53 UT. Shortly after this, it exhibits two negative shifts but with much smaller amplitudes. Supposing that these successive disturbances indicate a propagating perturbation, according to the estimated locations of the reflecting points that are mentioned above and the occurrence time of the two positive peaks, the approximate speed of this perturbation is about 535 m s⁻¹. This value is much larger than the speed of the movement of the ionospheric negative storm that usually occurs in the middle latitudes due to storm-induced equatorward wind (Buonsanto, 1999), and the ionospheric storm is not serious in the Asian sector during this period (Astafyeva et al., 2015). Considering the magnitude of the speed and the time interval of the positive–negative variations, the recorded perturbations probably reflect an equatorward-propagating LSTID in the eastern Asian sector.

To confirm this, Fig. 4 presents a sequence of 2-D VTECP maps between 09:40 and 11:40 UT on 17 March 2015 with the method described in Sect. 2. The gray areas represent the nightside. The raw value of VTECP has already been converted into VTECP^′ with the equation

$$\begin{array}{}\text{(3)}& {\mathrm{VTECP}}^{\prime }=\mathrm{sgn}\left(\mathrm{VTECP}\right)\cdot {\log }_{\mathrm{10}}\left(\mathrm{abs}\left(\mathrm{VTECP}\right)+\mathrm{1}\right).\end{array}$$

The raw amplitude of VTECP above 30^∘ N is ∼2 TECu (1 TECu =10¹⁶ electrons m⁻²) while the raw amplitude of VTECP below 30^∘ N reaches ∼10 TECu. Thus, transforming Eq. (3) provides a better color map for 2-D VTECP plots by sharpening the edges between positive and negative values and reducing the differences of VTECP in middle and low latitudes. Consequently, it should be noted that the amplitude of the wave-like variation does not represent the true wave amplitude but an “artificial” one. The yellow lines illustrate the least-square fitting results for all the negative pixels within certain rectangular areas bounded by longitudes and latitudes. The green lines are similar but for pixels with the bottom 5 % absolute VTECP^′ values in selected areas (see Sect. 3.2 for a detailed example). These lines mark the approximate locations of the wavefronts.

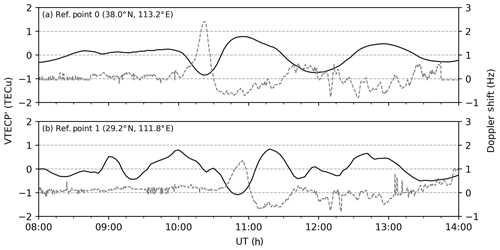
Figure 5 Temporal variations in mean VTECP^′ near the Doppler reflection points between 08:00 and 14:00 UT, 17 March 2015. Doppler shift recordings in Fig. 3 are plotted with dashed lines for comparison.

A large-scale wave-like perturbation can be seen clearly in Fig. 4. The first relatively distinct wave structure emerges during the 10:10–10:20 UT period (Fig. 4d), while its sign can already be observed as early as 09:40–09:50 UT (Fig. 4a) in the northwestern part of China. During 10:20–10:30 UT (Fig. 4e), a negative band occurs across both the Chinese–Japanese sector between around 30 and 45^∘ N, which gradually propagates to lower latitudes in the following minutes. During 10:30–10:40 UT (Fig. 4f), the first clear wavefront of the positive band appears, which also shows an equatorward movement for at least half an hour. Finally, there seems to be no distinct wave structure following the positive band. Considering the spatiotemporal characteristics of this perturbation, it can be preliminarily identified as an LSTID. By the way, it is interesting to note that the positive bands do not extend to the Japanese sector in Fig. 4h and i, and the corresponding VTECP^′ amplitudes seem smaller in the eastern side than in the western side. This may be related to the fact that the Japanese sector has already entered the nightside.

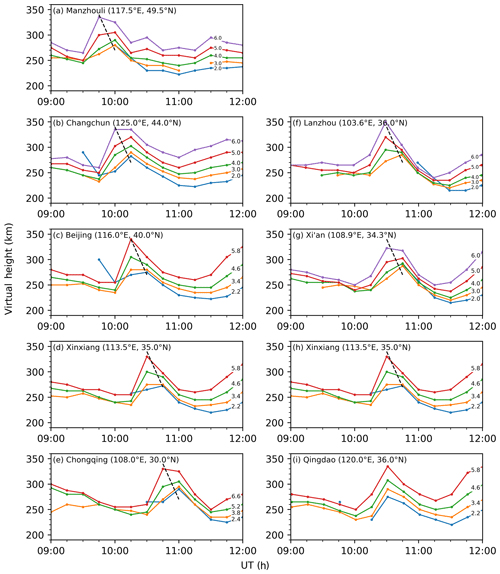
Figure 6 Temporal variations in the virtual height for iso-frequency lines from eight ionosondes between 08:00 and 12:00 UT, 17 March 2015. Frequencies are depicted on each iso-frequency line. The time resolution is 15 min for all stations. The black dashed lines indicate the downward phase change.

Both the negative and positive bands exhibit more complex variations when they enter the equatorial ionospheric anomaly (EIA) region between 20 and 30^∘ N. On the one hand, the amplitude of VTECP^′ is relatively larger than those in the higher latitudes. On the other hand, it seems that the equatorward propagation of the negative band decelerates significantly in this area, which is especially shown in Fig. 4g–l. Such complex features are probably related to the various physical processes in this region. Ding et al. (2012) suggested that LSTIDs experience severe dissipation in southern China region due to viscosity and heat conductivity at low latitudes, which may account for the weakening of the equatorward-propagating wave-like structures. Besides this, Pradipta et al. (2016) studied the interaction of the auroral LSTIDs from opposite hemispheres near the dip equator during the 26 September 2011 geomagnetic storm. Their results show that such interaction may bring much complexity to the TEC perturbations near the dip equator.

Our observations of the Doppler shift and VTECP^′ maps are in good agreement. To show it clearly, Fig. 5 shows the variations in the mean VTECP^′ data near the Doppler reflection points with the same time range of Fig. 3. Doppler shift recordings in Fig. 3 are also plotted with dashed lines for comparison. It can be seen that the troughs at around 10:20 UT in Fig. 5a and 10:50 UT in Fig. 5b correspond well to the two distinct crests in Fig. 3. In addition, the variations in the VTECP^′ between 11:00 and 14:00 UT are also in a good negative correlation with the Doppler shift observations for each reflecting point. It should be noted that the variation in VTECP^′ at the reflecting point 1 exhibits more variability than that at the reflecting point 0, especially at around 09:00, 10:00, and 12:00 UT. Considering that point 1 (29.2^∘ N, 111.8^∘ E) is approaching the EIA region, the causes for VTEC perturbations are more complicated, as mentioned above. This feature is consistent with the observations of the 2-D VTECP^′ maps in Fig. 4.

Ionospheric parameters from ionograms have been extensively used since early TID studies. Recently, ionograms and iso-frequency lines with different sampling rates were used in TID studies (Klausner et al., 2009; Ding et al., 2012, 2013; Pradipta et al., 2016; Ramsingh et al., 2015; Habarulema et al., 2018). Figure 6 presents the temporal variations in the virtual height for each iso-frequency line. The name and location of the corresponding ionosonde stations are given in each subplot. The frequency is marked on the right side for each line. In the left column, the results of five stations are arranged in order from high to lower latitudes, and the right column shows the recordings of four stations in the same latitudinal belt. We can see clearly that a distinct uplift of the virtual height occurs at 09:45 UT at Manzhouli station, and it gradually moves equatorward from high to lower latitudes (Fig. 6a–e). Meanwhile, there is no clear phase difference for the stations on the right column. This means that the ionospheric disturbance roughly moves along the meridian line in this longitudinal sector (around 115^∘ E), which corresponds to the results of the 2-D VTECP^′ map. Moreover, although the time resolution of 15 min is relatively low, it can still be identified that the crests in the higher iso-frequency lines appear earlier than those in the lower ones. Such trends (marked with black dashed lines) indicate a downward vertical phase velocity, which is one of the typical characteristics of the TID and AGW (Hine, 1960; Hocke and Schlegel, 1996). It should be noted that the downward trend is not much clear for certain station, especially the one in Qingdao. This may be attributed to the 15 min sampling interval.

3.2 Estimating propagation parameters

In preparation for estimating the propagation parameters of this LSTID, Fig. 7 shows a detailed example of the wavefront fitting method with the VTECP^′ map in Fig. 4g (10:40–10:50 UT). The reason for choosing this period is that the structure of the wavefront is relatively clear, and the boundary between the trough and crest of this LSTID can still be partly identified in the Japanese sector. The green line is the least-square fitting for the green dots, of which the absolute VTECP^′ values are close to zero (bottom 5 %) among all the dots in a certain region (30–40^∘ N, 75–140^∘ E). The wave-propagating azimuth (marked with arrows) can be estimated with the normal direction of this fitting line. The estimated azimuths are listed in Table 1 in the second column.

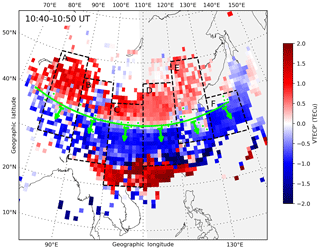
Figure 7 A detailed example of the wavefront fitting method. Green dots indicate the data points for least-square fitting. Green arrows depict the propagation orientations in different longitudes. Dashed black rectangles mark the areas for generating TLPs in Fig. 8.

It can be seen clearly that the TID moves due south around 110^∘ E, and in the western and eastern regions, the propagation direction is slightly southwest and southeast. It should be noted that, although the morphology of this TID is continuously changing as it moves from high to lower latitudes in the studied region, the longitudinal dependences of azimuths of all fitting lines in Fig. 4e, f, g, and h are similar.

In order to derive the phase speed, period, and wavelength of this LSTID, the time–latitude plots (TLPs) of VTECP^′ are obtained for six longitudinal bands, which are marked with dashed rectangles A–F in Fig. 7. For each band, the VTECP^′ data are averaged along the latitude for every 6 min, and the results as a function of UT and latitude are illustrated correspondingly in Fig. 8a–f. As mentioned above, the VTECP^′ variation related to EIA is rather complex. Considering that EIA is mainly a low-latitudinal phenomenon, only values over 30^∘ N are used to estimate the speed. The 30^∘ N indicates the boundary of EIA and is marked with dashed lines in Fig. 8.

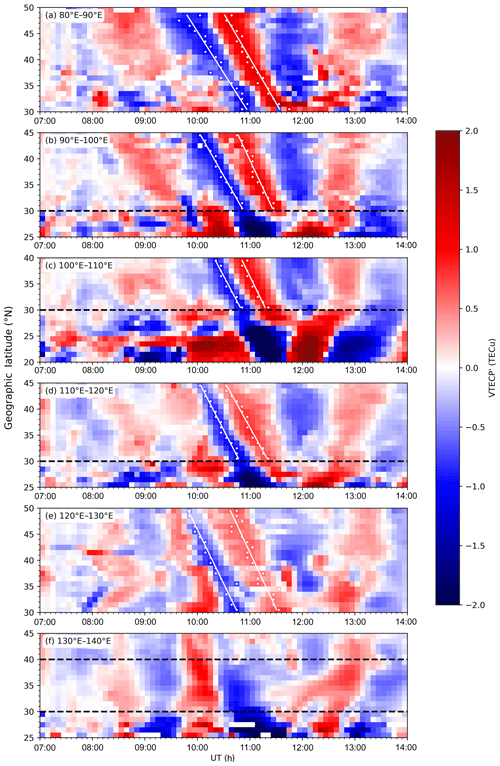
Figure 8 TLPs of VTECP^′ for different longitudinal bands between 07:00 and 14:00 UT. White dots give the data points for linear fitting, and the fitting results are marked with white lines; 30^∘ N in (b–d) and (f) is marked with black dashed lines, which indicate the boundary of EIA, and 40^∘ N is marked in (f).

As expected, the most distinctive structures in all panels are the pair of negative and positive bands between about 10:00 and 12:00 UT, which correspond to the perturbations moving from high to lower latitudes shown in Fig. 4. The structures in the 130–140^∘ E are not quite clear, which may be due to the lack of data in some parts of this area, but the trough around 10:40 UT can still be identified. To estimate the meridional speeds of these perturbation patterns, the linear least-square method is used to fit the pairs of troughs and crests. The data points for the linear fitting (white dots) are the minimum and maximum values around the trough and crest. The speeds for the wave trough (V_t) and crest (V_c) can be derived based on the slopes of the fitting lines. Moreover, the period of the wave can be estimated through the time interval between the trough and crest in TLPs. To be specific, for each longitudinal region, the averaged values of the time intervals along all latitudinal bins is set to be half of the period of the wave in this region. As for the estimation of wavelength, note that the studied area is ∼20^∘ in latitude, which is roughly one wavelength, and thus makes it difficult to estimate the wavelength directly from the 2-D VTECP^′ map. Thus, the wavelength is derived from the multiplication of speed and period.

However, those speed, period, and wavelength are the projections on longitudes. After adjusted by the propagation azimuths that were calculated above, the final results of the estimated parameters are listed in Table 1. It can be seen that these parameters show certain longitudinal dependence. It should be noted that the data coverage is relatively lower in the eastern and western boundaries of the investigated region. This may impact the accuracy of the estimation of the LSTID properties in these areas. On the whole, the mean values and standard deviations of the period, V_t, V_c, and wavelength are 74.8±1.4 min, 578±16 m s⁻¹, 617±23 m s⁻¹, and 2691±80 km, respectively. These parameters are typical for an LSTID. V_t and V_c overlap, although only marginally, considering the error ranges. Meanwhile, the mean V_c is slightly larger than the mean V_t, which seems like the wave behind pushing the wave ahead. In general, the speeds of the trough and crest of the LSTID should be rather similar, since they are induced by the same gravity wave. However, the wave properties might change with time being dependent on the forcing from the background condition, especially for LSTIDs covering a large spatial region. This might explain the differences.

In addition, it is interesting to note that V_t is in reasonable agreement with the result of 535 m s⁻¹ derived from the Doppler recordings. To show it more specifically, we estimated the speed and direction of the LSTID using the same TLP method as Fig. 8 but in 111–114^∘ E and 29–38^∘ N (corresponding to the reflecting points). The results are 562±59 m s⁻¹ and 0.2^∘, respectively. In general, the LSTID velocity estimated from ground-based stations tends to be larger than the actual velocity, since these stations, in most cases, are not in perfect alignment with the propagation direction of the LSTID (Afraimovich et al., 1998; Habarulema et al., 2013). Such good agreement between VTECP^′ and HF Doppler results may be attributed to the fact that the reflecting points (29.2^∘ N, 111.8^∘ E; 38.0^∘ N, 113.2^∘ E) of the Doppler sounders are in a narrow longitudinal band and the direction of the LSTID's propagation is also almost due south between 111 and 114^∘ E.

As mentioned above, the VTECP^′ in the EIA region seems to exhibit different features compared to that in the middle latitudes. It can be seen from Fig. 8c that VTECP^′ in the EIA region also shows a periodic variation, but it seems to have a longer period and time duration than the LSTID. These disturbances are probably related to the complex variations in VTEC after 08:00 UT (around dusk). Besides this, the perturbations at 20^∘ N around 12:00 and 13:00 UT show patterns of poleward movement. Habarulema et al. (2018) identified TIDs in the Asian–Australian sector during the same storm period. It provides clear examples of TIDs crossing the dip equator from the Southern Hemisphere to the Northern Hemisphere at around 09:00–12:00 UT. Their analysis shows that these TIDs may not have exceeded 30^∘ N. Such a poleward feature was also detected in other longitudinal sectors during this storm (Zakharenkova et al., 2016) and other storms (Pradipta et al., 2016; Jonah et al., 2018). In addition, Ding et al. (2013) studied the poleward-propagating LSTIDs in southern China during a medium-scale storm in 2011. They attributed their observations to the excitation of secondary LSTIDs during the dissipation of primary disturbances from the lower atmosphere. Besides this, the poleward-moving disturbances may also be induced by the variation in the equatorial electrojet, as pointed out by Chimonas (1970) and more recently by Habarulema et al. (2016). A detailed investigation of this phenomenon is not the focus of this work.

4 Discussion

Our results show that the propagation parameters of the LSTID in the eastern Asian sector during the St. Patrick's Day storm are longitudinally dependent. Among these parameters, the longitudinal dependence of the propagation azimuth of an LSTID receives much attention in previous works. In general, earlier studies suggested that there are four main factors that affect the direction of a polar-originating LSTID, including the velocity of the background neutral wind (Hines, 1960; Morton and Essex, 1978; Maeda and Handa, 1980), the structure and evolution of the source region in the auroral oval (Maeda and Handa, 1980; Hunsucker, 1982; Ding et al., 2007), the Coriolis force (Maeda and Handa, 1980; Balthazor and Moffett, 1999; Afraimovich et al., 2000; Tsugawa et al., 2004; Ding et al., 2013), and the declination of the geomagnetic field (Tsugawa et al., 2004; Borries et al., 2009).

The Coriolis force effect is generally believed to contribute to the clockwise shift of the propagation direction of the LSTIDs (Afraimovich et al., 2000; Tsugawa et al., 2004; Ding et al., 2013), The observations of the shift (10–20^∘ on average) are consistent with the calculation by Maeda and Handa (1980) and the model simulation by Balthazor and Moffett (1999). However, in our study, the shift of the propagation direction is not systematic westward, which means the variability in the LSTID azimuth in our observation cannot be attributed to the Coriolis force, at least not to it alone.

Table 1 The estimated propagation parameters of the LSTID and the corresponding standard errors. The second column contains the propagation directions, which are measured clockwise from the south. V_t and V_c represent the speed estimated with a certain wave trough and crest. Dir. stands for direction.

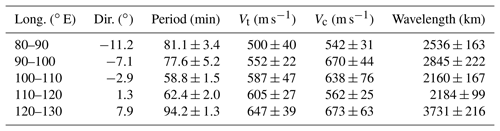
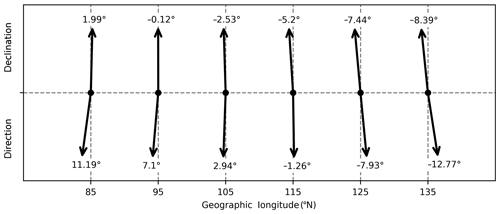
Figure 9 The sketch of (upper) the geomagnetic declination angles and (lower) the propagation directions in different longitudes on the wavefront fitted in Fig. 7. The propagation directions are measured clockwise from the south.

The structure and movement of the source region for the LSTID in the auroral oval are another candidate for explaining the longitudinal dependence of the propagation direction of the LSTID. Previous studies suggested that the westward movement of enhanced electrojets in the auroral arc is an important cause of the westward shift of the LSTID propagation direction at high latitudes (Hunsucker, 1982; Ding et al., 2007). The change of the propagation direction of LSTIDs as they move from high to middle latitudes during the superstorm of 29 October 2003 over North America was explained by Ding et al. (2007) as being related to a change in the position of the electrojet enhancement area near the auroral oval. Nevertheless, since the structure and the evolution process of the source region during storm period are complicated, more cases and modeling studies are needed to find a clear connection between it and the propagation direction of LSTIDs.

In general, the velocity of the neutral wind is much less than that of the LSTIDs, and the thermospheric wind velocity in the same latitudinal belt with a limited longitudinal extension should exhibit little variance. Thus, the contribution of the background wind on the change of the propagating direction would be limited in the absence of the geomagnetic field. However, a combined effect of magnetic declination and zonal wind can cause F-region electron density differences between two sides of the zero declination (Zhang et al., 2011). During storm periods, the enhanced zonal winds (Fuller-Rowell et al., 1994) can intensify these differences (Thomas et al., 2016). As a result, the geomagnetic declination is considered to be an important factor that affects the propagation direction of the LSTID. Some researchers studied the predominant propagation direction of LSTIDs during storm periods in different longitudinal sectors and suggested that, statistically speaking, the predominant directions of LSTIDs in Europe, China, and Japan are primarily southward, south to west, and south to east, respectively (Nicolls et al., 2004; Tsugawa et al., 2004; Borries, 2009; Ding et al., 2013). These results are all consistent with the corresponding geomagnetic declination in each sector.

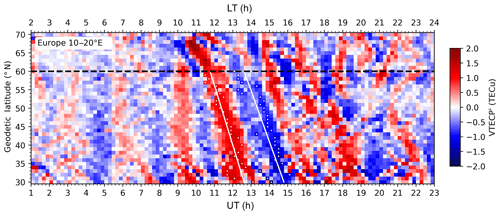
Figure 10 The TLP of VTECP^′ for the European sector (30–70^∘ N, 10–20^∘ E) between 01:00 and 23:00 UT. White lines and dots are similar to those in Fig. 8. The black dashed line depicts 60^∘ N.

In the longitudinal region of 70–150^∘ E, the geomagnetic declination angles change from northeast in the western side to northwest in the eastern side. This characteristic seems to show some kind of consistency with the azimuth results in Table 1. To illustrate such connection quantitatively, Fig. 9 depicts the geomagnetic declination on the wavefront in different longitudes in Fig. 7 (Fig. 9a) and the propagation direction (azimuth – 180^∘) of the LSTID at the same spot (Fig. 9b). The connection between these two parameters is quite obvious in this event. This result proves that the propagation of LSTIDs in different longitudes is probably influenced by the orientation of the geomagnetic field lines in the eastern Asian sector. In addition, the tendency of field-aligned propagation of the LSTID indicates that it is driven by the neutral winds, since the winds push the plasma up and down along the magnetic field lines. There is no evidence, such as simultaneous perturbations at all latitudes in other cases (Borries et al., 2016; Zakharenkova et al., 2016), to show that the LSTID in the Chinese–Japanese sector is affected by the prompt penetration electric field (PPEF) during the same period. Besides, considering the relatively low data coverage in the eastern and western sides of the studied region, it should be noted that our speculation needs to be verified with more observational data and numerical simulation to reduce uncertainty in our propagation estimation and to figure out the detailed physical processes.

During the 2015 St. Patrick's Day storm, LSTIDs in the European–African, American, and Asian–Australian sectors were detected and analyzed with TEC observations (Borries et al., 2016; Zakharenkova et al., 2016; Habarulema et al., 2018). It shows clearly in their results that the European sector also exhibits LSTIDs around 11:00 UT. As a comparison, we also analyzed these LSTIDs, but with VTEC data from the Madrigal database of the MIT Haystack Observatory. To derive the VTECP, a narrow longitudinal band (30–70^∘ N, 10–20^∘ E) is selected, and the VTEC data with the same latitude at the same time are averaged. At each latitude bin, the averaged VTEC forms a time series, and the temporal resolution is set to 12 min with bin averaging. Then, a running mean with a 1.5 h window is conducted for each time series, and their difference is taken as the VTECP. The result is plotted in Fig. 10 as a TLP. The fitting lines are obtained with the same method as those in Fig. 8.

Figure 10 is basically consistent with previous results (Borries et al., 2016; Zakharenkova et al., 2016), such as the synchronous perturbations around 04:45 and 09:15 UT and the LSTID structures between 10:00 and 17:00 UT. Moreover, our result shows that the VTECP^′ behavior between 60 and 70^∘ N is quite different from that between 30 and 60^∘ N. The pattern around 10:00 UT seems to represent a TID with smaller speed. Considering that the physical processes are more complex in such high latitudes (Foster et al., 2014), we only focus on the perturbations below 60^∘ N. The speeds estimated from the most distinct crest and trough are $\sim \mathrm{500}\pm \mathrm{51}$ and $\sim \mathrm{427}\pm \mathrm{55}$ m s⁻¹, respectively, and the estimated period is $\sim \mathrm{4.0}\pm \mathrm{0.2}$ h. It is clear that the appearances of the LSTIDs are different in the European and eastern Asian sectors during the same period for the same storm event. Borries et al. (2016) presented a detailed study on the LSTID in Europe during this storm. It is suggested that the perturbation occurring around 11:00 UT is special, since it is impacted by PPEF and wind at the same time. Comparatively, the LSTID in the Chinese–Japanese sector seems to be only driven by winds. This may partly account for the difference of LSTIDs between the eastern Asian and European sectors. Besides, such a difference may also be related to the location or structure of the joule heating source in the auroral oval or the difference of the background TEC in the two sectors. For better understanding this difference, more studies on the joule heating source are needed.

5 Summary

Using data from four GPS receiver networks (CMGN, CMONOC, GEONET, and IGS), together with recordings of two HF Doppler sounders and eight ionosondes, we provide comprehensive and detailed observation results of the LSTIDs in the eastern Asian sector during the 2015 St. Patrick's Day storm. The GPS receiver networks in China and Japan are combined together to produce 2-D VTEC perturbation maps in order to give a wider image of the LSTID structures in eastern Asia. As a comparison, the ionospheric disturbances in the European sector are also studied with VTEC data from the Madrigal database. The propagation parameters of the LSTIDs are estimated. The main results can be summarized as follows:

1. An LSTID occurs as a result of possible AGWs propagating from high to lower latitudes around 09:40–11:40 UT, which spans over 60^∘ in longitude, and the crest of this LSTID is characterized by a clear tendency to dissipate starting from the eastern side. These features are in good agreement with observations by HF Doppler sounders and ionosondes.

2. The propagation orientation is almost due southward around 105–115^∘ E, and it tends to slightly shift westward and eastward in the western and eastern parts of the studied area. This is suggested to be influenced by the regional declination of the geomagnetic field lines.

3. The propagation parameters in different longitudinal bands are estimated. These parameters show certain longitudinal differences. On the whole, the mean values and standard deviations of the period, V_t, V_c, and wavelength are 74.8±1.4 min, 578±16 m s⁻¹, 617±23 m s⁻¹, and 2691±80 km, respectively.

It should be noted that our results show certain consistency with previous research focusing on the Chinese or Japanese sector for different LSTID events. Nevertheless, the longitudinal dependence shown in our results should be examined further with more case studies based on large longitudinal and high-resolution coverage of GPS data.