the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Notes on the correlation between sudden stratospheric warmings and solar activity
Ekaterina Vorobeva
A correlation between solar activity and normalized occurrence rate of sudden stratospheric warmings (SSWs) has been found. As a proxy for solar activity, the 10.7 cm solar radio flux has been used. In order to find the correlation, we derived a normalized occurrence rate of major sudden stratospheric warmings (MSSWs) based on both the ERA-40/ERA-Interim dataset and NCEP data. Based on this distribution, we calculated the correlation coefficient, which amounts to 0.63, with a significance of 90.68 %, for ERA-40/ERA-Interim, and 0.55 for the NCEP–NCAR-I reanalysis, with a significance of 83.80 %. Additionally, we calculate correlation coefficients for Lyman-alpha flux and sunspot numbers with the analogous method for the same period.
- Article
(300 KB) - Full-text XML
- BibTeX
- EndNote
In the middle of the last century, Scherhag (1952) and Scrase (1953) independently found an incident of sudden stratospheric warming (SSW). A corresponding mesospheric cooling was found shortly after (Quiroz, 1969). The SSW effect is manifested in the sudden and short (several days) increase in temperature (up to 60 K) in the stratosphere and joint cooling in the mesosphere at high and middle latitudes during winter. One can find a more strict definition of SSW in reviews on this subject (e.g. Butler et al., 2015). According to current knowledge (see e.g. Shepherd et al., 2014; Zülicke et al., 2018; and references therein) the genesis of the effect goes from mesopause at high latitudes toward stratosphere at middle latitudes with a peak of intensity around 65∘ N. There are two types of sudden stratospheric warmings: minor warmings and major warmings. Minor warmings also consist of the temperature increase, but at 10 hPa it is about 30 K smaller than for major warmings. The main difference is that, unlike in the major warming, during the minor one, the zonal wind weakens but does not reverse the direction (e.g. Labitzke, 1981). In this study, we consider just the major sudden stratospheric warming (MSSW) effect.
SSW events play a rather important role in atmospheric investigations not only because these pronounced events have impacts on all processes in the middle atmosphere but also because they provide a natural examination of our understanding of atmospheric interactions. The first step to understanding the nature of SSWs was the theory of propagation of planetary waves (PWs) by Charney and Drazin (1961), who derived the dispersion relationship for vertically propagating Rossby waves. The theoretical explanation was proposed by Dickinson (1968a, b, 1969a, b) and consists of an interaction of PWs which penetrate into the winter middle atmosphere and affect general mean circulation when they dissipate. Steady dissipating waves can weaken the zonal mean flow and maintain the winter stratosphere above radiative equilibrium temperatures (Dickinson, 1969b). This theory was confirmed by model simulations (Matsuno, 1970, 1971). Currently, this explanation is generally accepted; nevertheless, we should note that there are alternatives. For example, based on model simulations, Peters (1985a, b) found that SSW-like effects may occur due to non-linear wave–wave interactions. However, the role of wave–wave interaction during SSWs has not been clear until the present time. Recently, Gavrilov et al. (2017) have touched upon this problem.
Since SSWs have been observed and modelled in numerous works (e.g. Holton, 1976; Schoeberl, 1978; Tao, 1994; Siskind et al., 2005; Smith et al., 2011; and references therein), the topic has attracted genuine interest in all fields of atmospheric science. Using a 3-D model, Sonnemann et al. (2006) studied the distributions of minor chemical species in the mesopause region in times of SSWs. The most-detailed investigation of the variability of the hydroxyl airglow layer during SSWs has been represented in the work of Shepherd et al. (2010). The response of OH* and the infrared atmospheric band has been found by satellite observations (Gao et al., 2011), and Shepherd et al. (2014) investigated the impact of this phenomenon on distributions of CO and NOx based on a joint analysis of model simulation and satellite observations. The impact of SSWs on the secondary ozone layer has been highlighted in the work of Tweedy et al. (2013) based on model simulations and in the work Smith et al. (2009) based on the SABER instrument on board the TIMED satellite. The temperature and dynamic structure of the mesopause region during sudden stratospheric warmings were investigated by reanalysis data (Siskind et al., 2010) and based on a global circulation model (Zülicke and Becker, 2013). A large number of works are devoted to the role and propagations of gravity waves in times of SSWs (Limpasuvan et al., 2011, 2012; McLandress et al., 2013; de Wit et al., 2014; Ern et al., 2016). Recently, an effect on the troposphere (Hinssen et al., 2011) and equatorial latitudes has been found (Bal et al., 2017). More about SSWs and related fields can be found in reviews of this subject (e.g. Holton, 1980; McIntyre, 1982; Plumb, 2010; Butler et al., 2015).
Solar irradiance strongly affects the Earth's atmosphere and climate (Seppälä et al., 2014); hence, naturally, the question of what the effect of solar variations is on the SSW occurrence rate arises. The strongest solar variation is the 11-year solar cycle. Labitzke and van Loon (1990) did not find any significant correlation between the 11-year solar cycle and MSSWs based on their analysis of the 10.7 cm solar radio flux. Nevertheless, Labitzke (2004, and references therein) showed that such a correlation exists for MSSW events distributed by phases of QBO (quasi-biennial oscillation). This is partially in contradiction with the work of Sonnemann and Grygalashvyly (2007), who found such a correlation without considering a relation to QBO phases based on an analysis of Lyman-alpha flux and sunspot numbers. The reason for the discrepancy is either the difference in fluxes or methods.
We decided to narrow this gap in the knowledge and conduct an analysis of the solar radio flux at 10.7 cm (F10.7). However, based on SSW statistics and F10.7 data, we derived a normalized occurrence rate for MSSW events. The data, method, and results are described in Sect. 2; the discussion is presented in Sect. 3 followed by concluding remarks in the last section.
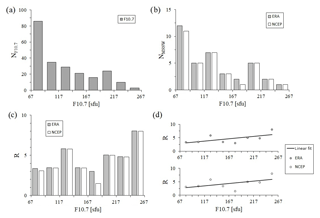
Figure 1(a) Monthly mean F10.7 values between 1958 and 2013 of 4 months between December and March; (b) the number of MSSWs depending on F10.7 values; (c) normalized occurrence rate of MSSWs depending on F10.7 values; (d) correlation analysis for the normalized occurrence rate of MSSWs and F10.7 values.
We investigate the statistical connection between MSSWs and solar activity. As a proxy for solar activity, we use the 10.7 cm solar radio flux (http://lasp.colorado.edu/lisird/data/noaa_radio_flux/, last access: 31 March 2019). Because MSSWs are phenomena that commonly occur from December until March (Charlton et al., 2007; Charlton and Polvani, 2007), we calculated monthly mean values of F10.7 for December, January, February, and March through the entire period from 1958 to 2013. The lowest mean F10.7 value did not fall below 67 solar flux units (sfu). The uppermost value did not exceed 267 sfu. We chose a difference of 25 sfu for the flux subdivision (eight subintervals) and calculated a number of monthly mean F10.7 values which fell into each subinterval (Fig. 1a).
Next, we calculated the mean F10.7 values for the month prior to the MSSWs' central day (the day when zonal mean zonal wind at 10 hPa becomes negative). In this study, we used two databases of central day. The first database combines the central day of MSSW events from the ERA-40 reanalysis for the period 1958 to 1979 (14 events) and ERA-Interim reanalysis for the period 1979 to 2013 (23 events) (Butler et al., 2017). The central days of the NCEP–NCAR-I reanalysis (35 events) (Butler et al., 2017) were used as the second database. Then, we calculated the number of MSSWs that occurred in each F10.7 subinterval (Fig. 1b) based on two databases of central day. The dependence of MSSWs on F10.7 is rather negative (Fig. 1b), but we should take into account that the distribution of wintertime monthly averaged values of F10.7 is non-uniform. The values corresponding to low solar activity occur most often, and values corresponding to high solar activity are rare. Hence, for calculations of correlation between MSSW and F10.7, the number of MSSWs for a given solar activity should be normalized by the duration of the solar activity in the respective phase. A detailed description of this procedure is presented in Sonnemann and Grygalashvyly (2007). We calculated the MSSWs' occurrence rate normalized by the occurrence rate of F10.7 values as shown in Sonnemann and Grygalashvyly (2007):
where and are the number of F10.7 values and the number of MSSWs in subinterval i, respectively. Note that calculation by Eq. (1) entails a statistical uncertainty which decreases with the number of solar cycles.
Figure 1c illustrates the dependence between the normalized occurrence rate of MSSWs and the values of F10.7 according to Eq. (1) for ERA and NCEP–NCAR-I databases. We conducted the correlation analysis for the normalized occurrence rate of MSSWs and the F10.7 values with eight subdivisions (Fig. 1d). The correlation coefficient equals 0.63 for the ERA case and 0.55 for the NCEP–NCAR-I case. The significance amounts to 90.68 % and 83.80 % for ERA and NCEP–NCAR-I, respectively. The results demonstrate a distinct statistical connection between the normalized MSSW events and the F10.7 values. Our correlation coefficients are smaller than those of Sonnemann and Grygalashvyly (2007), probably because we use different solar proxies, subdivisions, and periods.
A possible explanation for the correlation is the impact of solar activity either on the strength and activity or on propagation conditions of PWs (e.g. Arnold and Robinson, 1998; Fröhlich and Jacobi, 2004). Recently, Koval et al. (2018) found that solar activity might affect meridional temperature gradients and consequently change the vertical structure of the zonal wind and PWs' propagation conditions. This may point to a potential explanation. Another one possibility to explain obtained correlation is the interaction of cosmic rays (which anti-correlate with solar activity) with the atmosphere and, particularly, with the stratosphere, which have an impact on climate (see Fig. 7 in Usoskin, 2017; Fig. 3 in Seppälä et al., 2014; and corresponding discussions). In addition, a variation in the ozone concentration over a solar cycle (Keating et al., 1987; Hartogh et al., 2011) could influence the occurrence rate of MSSWs by changing the thermal structure of the middle atmosphere.
The separation of the effects of long-term changes in a solar cycle and long-term changes of anthropogenic greenhouse gases (GHGs) and ozone-depleting substances (ODSs) on the middle atmosphere remains an unsolved problem. In general, the joint decline of the solar cycle and the growth of GHGs and ODSs may produce bias in correlation. However, according to current knowledge, there is no statistically significant impact of anthropogenic changes on the frequency of SSWs (e.g. Butchart et al., 2000; SPARC CCMVal, 2010; Mitchell et al., 2012; Hansen et al., 2014, Ayarzagüena et al., 2018). Moreover, some of the recent works show the enhancement of the frequency of SSWs under forcing of GHGs and ODSs (e.g. Huebener et al., 2007; Charlton-Perez et al., 2008; Bell et al., 2009; Schimanke et al., 2013; Ayarzagüena et al., 2013). Thus, the joint effect of the negative trend in solar cycle strength and the positive trend of GHGs may just reduce positive correlation but cannot be its cause.
The 10.7 cm solar radio flux is not the only proxy for solar activity. Most used proxies, which differ by nature from the F10.7, are Lyman-alpha flux and sunspot numbers (Bruevich et al., 2014; Mei et al., 2018), as well as 3.2, 8, 15, and 30 cm solar fluxes (Dudok de Wit et al., 2014; Vaishnav et al., 2019). Thus, the information about correlation coefficients for the same database and method potentially can be useful to identify possible reasons of correlation. Hence, such correlation coefficients with corresponding significance are calculated and stored in the Table 1. We have not found any clear dependence of either correlation coefficients or significance on solar radio flux wavelength.
We investigated the statistical relationship between solar activity and the occurrence rate of major sudden stratospheric warmings (MSSWs). For this purpose, the 10.7 cm solar radio flux has been used as a proxy for solar activity. The calculations have been performed based on two datasets of central day (NCEP–NCAR-I and combined ERA) for the period from 1958 to 2013. The analysis of calculations was based on the normalized MSSW occurrence rate. The analysis revealed a positive correlation between MSSW events and solar activity with a correlation coefficient equal to 0.63 for the ERA dataset and 0.55 for the NCEP–NCAR-I dataset. Note that the correlation is necessary but is not a sufficient condition for a relationship between the two phenomena. The nature of the correlation is still not clear, and further investigations in this direction are necessary.
The F10.7 and Lyman-alpha solar flux data are available at http://lasp.colorado.edu/lisird/ (University of Colorado, 2019). The sunspot number data are accessible at https://www.ngdc.noaa.gov/stp/solar/ssndata.html (NOAA's National Centers for Environmental Information, 2019). The 3.2, 8, 15, and 30 cm solar flux data are available at https://spaceweather.cls.fr/services/radioflux/ (Dudok de Wit et al., 2014).
The author declares that there is no conflict of interest.
The author is grateful to her teachers Valentine A. Yankovsky, Gustav Shved, and Eugene L. Genikhovich.
This paper was edited by Andrew J. Kavanagh and reviewed by one anonymous referee.
Arnold, N. F. and Robinson, T. R.: Solar cycle changes to planetary wave propagation and their influence on the middle atmosphere circulation, Ann. Geophys., 16, 69–76, https://doi.org/10.1007/s00585-997-0069-3, 1998.
Ayarzagüena, B., Langematz, U., Meul, S., Oberlander, S., Abalichin, J., and Kubin, A.: The role of climate change and ozone recovery for the future timing of major stratospheric warmings, Geophys. Res. Lett., 40, 2460–2465, https://doi.org/10.1002/grl.50477, 2013.
Ayarzagüena, B., Polvani, L. M., Langematz, U., Akiyoshi, H., Bekki, S., Butchart, N., Dameris, M., Deushi, M., Hardiman, S. C., Jöckel, P., Klekociuk, A., Marchand, M., Michou, M., Morgenstern, O., O'Connor, F. M., Oman, L. D., Plummer, D. A., Revell, L., Rozanov, E., Saint-Martin, D., Scinocca, J., Stenke, A., Stone, K., Yamashita, Y., Yoshida, K., and Zeng, G.: No robust evidence of future changes in major stratospheric sudden warmings: a multi-model assessment from CCMI, Atmos. Chem. Phys., 18, 11277–11287, https://doi.org/10.5194/acp-18-11277-2018, 2018.
Bal, S., Schimanke, S., Spangehl, T., and Cubasch, U.: Variable influence on the equatorial troposphere associated with SSW using ERA-Interim, J. Earth Syst. Sci., 126, 1–13, https://doi.org/10.1007/s12040-017-0802-6, 2017.
Bell, C. J., Gray, L. J., Charlton-Perez, A. J., Joshi, M. M., and Scaife, A. A.: Stratospheric communication of El Nino teleconnections to European winter, J. Climate, 22, 4083–4096, https://doi.org/10.1175/2009JCLI2717.1, 2009.
Bruevich, E. A., Bruevich, V. V., and Yakunina, G. V.: Changed Relation between Solar 10.7-cm Radio Flux and some Activity Indices which describe the Radiation at Different Altitudes of Atmosphere during Cycles 21–23, J. Astrophys. Astron., 35, 1–15, https://doi.org/10.1007/s12036-014-9258-0, 2014.
Butchart, N., Austin, J., Knight, J. R., Scaife, A. A., and Gallani, M. L.: The response of the stratospheric climate to projected changes in the concentrations of well-mixed greenhouse gases from 1992 to 2051, J. Climate, 13, 2142–2159, https://doi.org/10.1175/1520-0442(2000)013<2142:TROTSC>2.0.CO;2, 2000.
Butler, A. H., Seidel, D., Hardiman, S., Butchart, N., Birner, T., and Match, A.: Defining sudden stratospheric warmings, B. Am. Meteorol. Soc., 96, 1913–1928, https://doi.org/10.1175/BAMS-D-13-00173.1, 2015.
Butler, A. H., Sjoberg, J. P., Seidel, D. J., and Rosenlof, K. H.: A sudden stratospheric warming compendium, Earth Syst. Sci. Data, 9, 63–76, https://doi.org/10.5194/essd-9-63-2017, 2017.
Charlton, A. J. and Polvani, L. M.: A new look at stratospheric sudden warmings. Part I. Climatology and modeling benchmarks, J. Climate, 20, 449–469, https://doi.org/10.1175/JCLI3996.1, 2007.
Charlton, A. J., Polvani, L. M., Perlwitz, J., Sassi, F., Manzini, E., Shibata, K., Pawson, S., Nielsen, J. E., and Rind, D.: A new look at stratospheric sudden warmings. Part II. Evaluation of model simulations, J. Climate, 20, 470–488, https://doi.org/10.1175/JCLI3994.1, 2007.
Charlton-Perez, A. J., Polvani, L. M., Austin, J., and Li, F.: The frequency and dynamics of stratospheric sudden warmings in the 21st century, J. Geophys. Res., 113, D16116, https://doi.org/10.1029/2007JD009571, 2008.
Charney, J. G. and Drazin, P. G.: Propagation of planetary-scale disturbances from the lower into the upper atmosphere, J. Geophys. Res., 66, 83–109, https://doi.org/10.1029/JZ066i001p00083, 1961.
de Wit, R. J., Hibbins, R. E., Espy, P. J., Orsolini, Y. J., Limpasuvan, V., and Kinnison, D. E.: Observations of gravity wave forcing of the mesopause region during the January 2013 major Sudden Stratospheric Warming, Geophys. Res. Lett., 41, 4745–4752, https://doi.org/10.1002/2014GL060501, 2014.
Dickinson, R. E.: On the exact and approximate linear theory of vertically propagating planetary Rossby waves forced at a spherical lower boundary, Mon. Weather Rev., 96, 405–415, 1968a.
Dickinson, R. E.: Planetary Rossby waves propagating vertically through weak westerly wind wave guides, J. Atmos. Sci., 25, 984–1002, 1968b.
Dickinson, R. E.: Vertical propagation of planetary Rossby waves through an atmosphere with Newtonian cooling, J. Geophys. Res., 74, 929–938, 1969a.
Dickinson, R. E.: Theory of planetary wave-zonal flow interaction, J. Atmos. Sci., 26, 73–81, 1969b.
Dudok de Wit, T., Bruinsma, S., and Shibasaki, K.: Synoptic radio observations as proxies for upper atmosphere modelling, J. Space Weather Space Clim., 4, A06, https://doi.org/10.1051/swsc/2014003, 2014.
Dudok de Wit, T., Bruinsma, S., and Shibasaki, K.: Synoptic radio observations as proxies for upper atmosphere modelling, available at: https://spaceweather.cls.fr/services/radioflux/ (last access: 12 March 2019), 2014.
Ern, M., Trinh, Q. T., Kaufmann, M., Krisch, I., Preusse, P., Ungermann, J., Zhu, Y., Gille, J. C., Mlynczak, M. G., Russell III, J. M., Schwartz, M. J., and Riese, M.: Satellite observations of middle atmosphere gravity wave absolute momentum flux and of its vertical gradient during recent stratospheric warmings, Atmos. Chem. Phys., 16, 9983–10019, https://doi.org/10.5194/acp-16-9983-2016, 2016.
Fröhlich, K. and Jacobi, C.: The solar cycle in the middle atmosphere: changes of the mean circulation and of propagation conditions for planetary waves, Rep. Inst. Meteorol. Univ. Leipzig, 34, 106–117, 2004.
Gao, H., Xu, J., Ward, W., and Smith, A. K.: Temporal evolution of nightglow emission responses to SSW events observed by TIMED/SABER, J. Geophys. Res., 116, D19110, https://doi.org/10.1029/2011JD015936, 2011.
Gavrilov, N. M., Koval, A. V., Pogoreltsev, A. I., and Savenkova, E. N.: Numerical Simulation of Wave Interactions during Sudden Stratospheric Warming, Izvestiya Atmos. Ocean. Phys., 53, 674–685, https://doi.org/10.1134/S0001433817060044, 2017.
Hansen, F., Matthes, K., Petrick, C., and Wang, W.: The influence of natural and anthropogenic factors on major stratospheric sudden warmings, J. Geophys. Res.-Atmos., 119, 8117–8136, https://doi.org/10.1002/2013JD021397, 2014.
Hartogh, P., Sonnemann, G. R., Grygalashvyly, M., and Jarchow, C.: Ozone trends in the mid-latitude stratopause region based on microwave measurements at Lindau (51.66∘ N, 10.13∘ E), the ozone reference model, and model calculations, Adv. Space Res., 47, 1937–1948, https://doi.org/10.1016/j.asr.2011.01.010, 2011.
Hinssen, Y., van Delden, A., and Opsteegh, T.: Influence of sudden stratospheric warmings on tropospheric winds, Meteorol. Z., 20, 259–266, https://doi.org/10.1127/0941-2948/2011/0503, 2011.
Holton, J. R.: A semi-spectral numerical model for wave-mean flow interactions in the stratosphere: Application to sudden stratospheric warmings, J. Atmos. Sci., 33, 1639–1649, https://doi.org/10.1175/1520-0469(1976)033<1639:ASSNMF>2.0.CO;2, 1976.
Holton, J. R.: The dynamics of sudden stratospheric warmings, Annu. Rev. Earth Planet. Sc., 8, 169–190, 1980.
Huebener, H., Cubasch, U., Langematz, U., Spangehl, T., Niehorster, F., Fast, I., and Kunze, M.: Ensemble climate simulations using a fully coupled ocean-troposphere-stratosphere general circulation model, Philos. T. R. Soc. A, 365, 2089–2101, https://doi.org/10.1098/rsta.2007.2078, 2007.
Keating, G. M., Pitts, M. C., Brasseur, G., and De Rudder, A.: Response of the middle atmosphere to short-term solar untraviolett variations, 1. Observations, J. Geophys. Res., 92, 889–902, 1987.
Koval, A. V., Gavrilov, N. M., Pogoreltsev, A. I., and Shevchuk, N. O.: Propagation of stationary planetary waves to the thermosphere at different levels of solar activity, J. Atmos. Sol.-Terr. Phy., 173, 140–149, https://doi.org/10.1016/j.jastp.2018.03.012, 2018.
Labitzke, K.: Stratospheric-mesospheric midwinter disturbance: A summary of characteristics, J. Geophys. Res., 86, 9665–9678, https://doi.org/10.1029/JC086iC10p09665, 1981.
Labitzke, K.: On the signal of the 11-year sunspot cycle in the stratosphere over the Antarctic and its modulation by the Quasi-Biennial Oscillation, J. Atmos. Sol.-Terr. Phy., 66, 1151–1157, https://doi.org/10.1016/j.jastp.2004.05.011, 2004.
Labitzke, K. and van Loon, H.: The state of the atmosphere on the Northern Hemisphere at solar maximum, July 1989–February 1990, Beilage zur Berliner Wetterkarte, SO 6/90, in: Meteorolog. Abh., FU-Berlin, Band 64, No. 4, 1990.
Limpasuvan, V., Alexander, M. J., Orsolini, Y. J., Wu, D. L., Xue, M., Richter, J. H., and Yamashita, C.: Mesoscale simulations of gravity waves during the 2008–2009 major stratospheric sudden warming, J. Geophys. Res., 116, D17104, https://doi.org/10.1029/2010JD015190, 2011.
Limpasuvan, V., Richter, J. H., Orsolini, Y. J., Stordal, F., and Kvissel, O.-K.: The roles of planetary and gravity waves during a major stratospheric sudden warming as characterized in WACCM, J. Atmos. Sol.-Terr. Phy., 78–79, 84–98, https://doi.org/10.1016/j.jastp.2011.03.004, 2012.
Matsuno, T.: Vertical propagation of stationary planetary waves in the winter northern hemisphere, J. Atmos. Sci., 27, 871–883, https://doi.org/10.1175/1520-0469(1970)027<0871:VPOSPW>2.0.CO;2, 1970.
Matsuno, T.: A dynamical model of the stratospheric sudden warming. J. Atmos. Sci., 28, 1479–1494, https://doi.org/10.1175/1520-0469(1971)028<1479:ADMOTS>2.0.CO;2, 1971.
McIntyre, M. E.: How well do we understand the dynamics of stratospheric warmings?, J. Meteorol. Soc. Jpn., 60, 37–65, https://doi.org/10.2151/jmsj1965.60.1_37, 1982.
McLandress, C., Scinocca, J. F., Shepherd, T. G., Reader, M. C., and Manney, G. L.: Dynamical control of the mesosphere by orographic and nonorographic gravity wave drag during the extended northern winters of 2006 and 2009, J. Atmos. Sci., 70, 2152–2169, https://doi.org/10.1175/JAS-D-12-0297.1, 2013.
Mei, Y., Deng, H., and Wang, F.: On midrange periodicities in solar radio flux and sunspot areas, Astrophys. Space Sci., 363, 84, https://doi.org/10.1007/s10509-018-3306-1, 2018.
Mitchell, D. M., Osprey, S. M., Gray, L. J., Butchart, N., Hardiman, S. C., Ciarlton-Perez, A. J., and Watson, P.: The effect of climate change on the variability of the Northern Hemisphere stratospheric polar vortex, J. Atmos. Sci., 69, 2608–2618, https://doi.org/10.1175/JAS-D-12-021.1, 2012.
NOAA's National Centers for Environmental Information: Sunspot Numbers, available at: https://www.ngdc.noaa.gov/stp/solar/ssndata.html, last access: 4 March 2019.
Peters, D.: Zur resonanten Wechselwirkung von planetaren Wellen in einem Zweischichtenmodell unter Berücksichtigung der externen Anregung einer Welle. Tiel1: Der Amplitudenverlauf, Z. Meteorol., 35, 239–251, 1985a.
Peters, D.: Zur resonanten Wechselwirkung von planetaren Wellen in einem Zweischichtenmodell unter Berücksichtigung der externen Anregung einer Welle. Tiel2: Die zonal gemittelte Bewegung, Z. Meteorol., 35, 252–256, 1985b.
Plumb, R. A.: Planetary waves and the extratropical winter stratosphere, Stratos. Dyn. Transp. Chem., Geophys. Monogr. Ser., 190, 23–41, 2010.
Quiroz, R. S.: The warming of the upper stratosphere in February 1966 and the associated structure of the mesosphere, Mon. Weather Rev., 97, 541, https://doi.org/10.1175/1520-0493(1969)097<0541:TWOTUS>2.3.CO;2, 1969.
Scherhag, R.: Die explosionsartige Stratosphärenerwärmung des Spätwinters 1951/1952, Ber. Deut. Wetterdienst, 6, 51–63, 1952.
Schimanke, S., Spangehl, T., Huebener, H., and Cubasch, U.: Variability and trends of major stratospheric warmings in simulations under constant and increasing GHG concentrations, Clim. Dynam., 40, 1733–1747, https://doi.org/10.1007/s00382-012-1530-x, 2013.
Schoeberl, M. R.: Stratospheric warmings: Observations and theory, Rev. Geophys., 16, 521–538, https://doi.org/10.1029/RG016i004p00521, 1978.
Scrase, F. J.: Relatively high stratospheric temperatures of February 1951, Meteorol. Mag., 82, 19–27, 1953.
Seppälä, A., Matthes, K., Randall, C. E., and Mironova, I. A.: What is the solar influence on climate? Overview of activities during CAWSES-II, Prog. Earth Planet. Sc., 1, 24, https://doi.org/10.1186/s40645-014-0024-3, 2014.
Shepherd, M. G., Cho, Y.-M., Shepherd, G. G., Ward, W., and Drummond, J. R.: Mesospheric temperature and atomic oxygen response during the January 2009 major stratospheric warming, J. Geophys. Res., 115, A07318, https://doi.org/10.1029/2009JA015172, 2010.
Shepherd, M. G., Beagley, S. R., and Fomichev, V. I.: Stratospheric warming influence on the mesosphere/lower thermosphere as seen by the extended CMAM, Ann. Geophys., 32, 589–608, https://doi.org/10.5194/angeo-32-589-2014, 2014.
Siskind, D. E., Coy, L., and Espy, P.: Observations of stratospheric warmings and mesospheric cooling by the TIMED SABER instrument, Geophys. Res. Lett., 32, L09804, https://doi.org/10.1029/2005GL022399, 2005.
Siskind, D. E., Eckermann, S. D., McCormack, J. P., Coy, L., Hoppel, K. W., and Baker, N. L.: Case studies of the mesospheric response to recent minor, major, and extended stratospheric warmings, J. Geophys. Res., 115, D00N03, https://doi.org/10.1029/2010JD014114, 2010.
Smith, A. K., López-Puertas, M., García-Comas, M., and Tukiainen, S.: SABER observations of mesospheric ozone during NH late winter 2002–2009, Geophys. Res. Lett., 36, L23804, https://doi.org/10.1029/2009GL040942, 2009, 2009.
Smith, A. K., Garcia, R. R., Marsh, D. R., and Richter, J. H.: WACCM simulations of the mean circulation and trace species transport in the winter mesosphere, J. Geophys. Res., 116, D20115, https://doi.org/10.1029/2011JD016083, 2011.
Sonnemann, G. R. and Grygalashvyly, M.: The relationship between the occurrence rate of major stratospheric warmings and solar Lyman-alpha flux, J. Geophys. Res., 112, D20101, https://doi.org/10.1029/2007JD008718, 2007.
Sonnemann, G. R., Grygalashvyly, M., and Berger, U.: Impact of a stratospheric warming event in January 2001 on the minor constituents in the MLT region calculated on the basis of a new 3D-model LIMA of the dynamics and chemistry of the middle atmosphere, J. Atmos. Sol.-Terr. Phy., 68, 2012–2025, https://doi.org/10.1016/j.jastp.2006.04.005, 2006.
SPARC CCMVal: SPARC report on the evaluation of chemistry-climate models, SPARC-Report No. 5, WCRP-132,WMO/TD-No. 1526, SPARC CCMVal, SPARC Office, Zurich, Switzerland, 2010.
Tao, X.: Wave-mean flow interaction and stratospheric warming in an isentropic model, J. Atmos. Sci., 51, 134–153, 1994.
Tweedy, O. V., Limpasuvan, V., Orsolini, Y. J., Smith, A. K., Garcia, R. R., Kinnison, D., Randall, C. E., Kvissel, O.-K., Stordal, F., Harvey, V. L., and Chandran, A.: Nighttime secondary ozone layer during major stratospheric sudden warmings in specified-dynamics WACCM, J. Geophys. Res.-Atmos., 118, 8346–8358, https://doi.org/10.1002/jgrd.50651, 2013.
University of Colorado: Lasp Interactive Solar Irradiance Datacenter, available at: http://lasp.colorado.edu/lisird/, last access: 6 March 2019.
Usoskin, I. G.: A history of solar activity over millennia, Living Rev. Sol. Phys., 14, 1–97, https://doi.org/10.1007/s41116-017-0006-9, 2017.
Vaishnav, R., Jacobi, C., and Berdermann, J.: Long-term trends in the ionospheric response to solar EUV variations, Ann. Geophys. Discuss., https://doi.org/10.5194/angeo-2019-34, in review, 2019.
Zülicke, C. and Becker, E.: The structure of the mesosphere during sudden stratospheric warmings in a global circulation model, J. Geophys. Res., 118, 2255-2271, https://doi.org/10.1002/jgrd.50219, 2013.
Zülicke, C., Becker, E., Matthias, V., Peters, D. H. W., Schmidt, H., Liu, H.-Li, de la Torre-Ramos, H., and Mitchell, D. M.: Coupling of stratospheric warmings with mesospheric coolings in observations and simulations, J. Climate, 31, 1107–1133, https://doi.org/10.1175/JCLI-D-17-0047.1, 2018.






