Validation and application of optimal ionospheric shell height model for single-site estimation of total electron content

We recently proposed a method to establish an optimal ionospheric shell height model based on the international GNSS service (IGS) station data and the differential code bias (DCB) provided by the Center for Orbit Determination in Europe (CODE) during the time from 2003 to 2013. This method is very promising for DCB and accurate total electron content (TEC) estimation by comparing to the traditional fixed shell height method. However, this method is basically feasible only for IGS stations. In this study, we investigate how to apply the optimal ionospheric shell height derived from IGS station to non-IGS stations or isolated GNSS receivers. The intuitive and practical method to estimate TEC of non-IGS stations is based on optimal ionospheric shell height derived from nearby IGS stations. To validate this method, we selected two dense networks of IGS stations located in regions in the US and Europe. Two optimal ionospheric shell height models are established by two reference stations, namely GOLD and PTBB, which are located at the approximate center of two selected regions. The predicted daily optimal ionospheric shell heights by the two models are applied to other IGS stations around these two reference stations. Daily DCBs are calculated according to these two optimal shell heights and compared to respective DCBs released by CODE. The validation results of this method are as follows. (1) Optimal ionospheric shell height calculated by IGS stations can be applied to its nearby non-IGS stations or isolated GNSS receivers for accurate TEC estimation. (2) As the distance away from the reference IGS station becomes larger, the DCB estimation error becomes larger. The relation between the DCB estimation error and the distance is generally linear.

1 Introduction

Dual-frequency GPS signal propagation is affected effectively by ionospheric dispersive characteristics. Taking advantage of this property, ionospheric total electron content (TEC) along the path of signal can be estimated by differencing the pseudorange or carrier phase observations from dual-frequency GPS signals. Carrier phase leveling or smoothing of code measurement is widely adopted to improve the precision of absolute TEC observations (Mannucci et al., 1998; Horvath and Crozier, 2007). In general, it is considered that the derived TEC in carrier phase leveling or smoothing technique consists of slant TEC (STEC), the combination differential code bias (DCB) of satellite and receiver, multipath effects and noise. The DCB is usually considered as the main error source and could be as large as several TEC units (TECu) (Lanyi and Roth, 1988; Warnant, 1997).

For TEC and DCB estimations, mapping functions with a single-layer model (SLM) assumption have been intensively studied for many years. Sovers and Fanselow (1987) firstly simplified the ionosphere to a spherical shell. They set the bottom and the top side of the ionospheric shell as h−35 and h+75 km, where h is taken to be 350 km above the surface of the earth and allowed to be adjusted. In this model, the electron density was evenly distributed in the vertical direction. Based on this model, Sardón et al. (1994) introduced the Kalman filter method for real-time ionospheric vertical TEC (VTEC) estimation, which can also be a promising prediction of DCBs under adverse conditions (antispoofing, ionospheric disturbances). Klobuchar (1987) assumed that STEC equals VTEC multiplied by the approximation of the standard geometric mapping function at the mean vertical height of 350 km along the path of STEC. Lanyi and Roth (1988) further developed this model into a single thin-layer model and proposed the standard geometric mapping function and the polynomial model. The single thin-layer model assumed that the ionosphere is simplified by a spherical thin shell with infinitesimal thickness. Clynch et al. (1989) proposed a mapping function in the form of a polynomial by assuming a homogeneous electron density shell between altitudes of 200 and 600 km. Mannucci et al. (1998) presented an elevation scaling mapping function derived from the extended slab mode. There are also many modified mapping functions according to the standard geometric mapping function. Schaer (1999) proposed the modified standard mapping function using a reduced zenith angle. Rideout and Coster (2006) presented a new mapping function which replaces the influence of the shell height by an adjustment parameter and set the shell height as 450 km. Smith et al. (2008) modified the standard mapping function by using a complex factor. Based on the electron density field derived from the international reference ionosphere (IRI), Zus et al. (2017) recently developed an ionospheric mapping function at fixed height of 450 km with dependence on time, location, azimuth angle, elevation angle, and different frequencies.

The ionospheric shell height is considered to be the most important parameter for a mapping function, and the shell height is typically set to a fixed value between 350 and 450 km (Lanyi and Roth, 1988; Mannucci et al., 1998). Birch et al. (2002) proposed an inverse method to estimate the shell height by using simultaneous VTEC and STEC observations and suggested the shell height is preferably a value between 600 and 1200 km. Nava et al. (2007) utilized multiple stations to obtain a shell height estimation method by minimizing the mapping function errors; this method is referred as the “coinciding pierce point” technique. Their results indicated that the suitable shell heights for the midlatitude is 400 and 500 km during the geomagnetic undisturbed conditions and disturbed conditions, respectively. In the case of the low latitude, the shell height at about 400 km is suitable for both quiet and disturbed geomagnetic conditions. Jiang et al. (2018) applied this technique to estimate the optimal shell height for different latitude bands. In their case, the optimal layer height is about 350 km for the entire globe. Brunini et al. (2011) studied the influence of the shell height by using an empirical model of the ionosphere and pointed out that a unique shell height for whole region does not exist. Li et al. (2018) applied a new determination method of the shell height based on the combined international GNSS service (IGS) Global Ionospheric Maps and the two methods mentioned above to the Chinese region and indicated that the optimal shell height in China ranges from 450 to 550 km. Wang et al. (2016) studied the shell height for a grid-based algorithm by analyzing goodness of fit for STEC. Lu et al. (2017) applied this method to different VTEC models and investigated the optimal shell heights at solar maximum and at solar minimum.

In the recent study by Zhao and Zhou (2018), a method to establish an optimal ionospheric shell height model for single-station VTEC estimation has been proposed. This method calculates the optimal ionospheric shell height in order to minimize the difference between the estimated DCB and the DCB released by the Center for Orbit Determination in Europe (CODE). Five optimal ionospheric shell height models were established by the proposed method based on the data of five IGS stations at different latitudes and the corresponding DCBs provided by CODE during 2003 to 2013. For the five selected IGS stations, the results have shown that the optimal ionospheric shell height models improve the accuracies of DCB and TEC estimation compared to a fixed ionospheric shell height of 400 km in a statistical sense. We also found that the optimal ionospheric shell height shows 11- and 1-year periods and is correlated to the solar activity, which indicated the connection of the optimal shell height with ionospheric physics.

While the proposed optimal ionospheric shell height model is promising for DCB and TEC estimation, this method also can be implemented to isolated GNSS receivers not belonging to IGS stations, if we can get the long-term observations and reference values of DCB from the isolated GNSS receivers. By considering the spatial correlation of ionospheric electron density, it is intuitive and practical to adopt the optimal ionospheric shell height of a nearby IGS station to the non-IGS stations. So whether an optimal ionospheric shell height model can improve the TEC∕DCB estimation of nearby stations needs to be verify.

The purpose of this study is to investigate the feasibility of applying the optimal ionospheric shell height model derived from IGS station to nearby non-IGS GNSS receivers for accurate TEC and DCB estimation. By selecting two different regions in the US (Region I) and Europe (Region II) with dense IGS stations, we calculate the daily DCBs of 2014 by using the optimal ionospheric shell heights derived from data from 2003 to 2013 of two central stations in two regions. We also try to find the DCB estimation error and its relation to the distance away from the central reference station.

2 Method

In Zhao and Zhou (2018), we proposed a concept of optimal ionospheric shell height for accurate TEC and DCB estimation. Based on daily data of a single site, this approach searches for a daily optimal ionospheric shell height, which minimizes the difference between the DCBs calculated by the VTEC model for a single site and reference values of DCB. For a single site, its long-term daily optimal ionospheric shell heights can be estimated and then modeled. In our case, the polynomial model (Wild, 1994; Komjathy, 1997) is applied to estimate satellite and receiver DCBs, and the DCBs provided by CODE are used as the reference.

In the polynomial model, the VTEC is considered as a Taylor series expansion in latitude and solar hour angle, which is expressed as follows:

$$\begin{array}{}\text{(1)}& {\displaystyle }{T}_{\mathrm{V}}(\mathit{\phi },S)=\sum _{i=\mathrm{0}}^m\sum _{j=\mathrm{0}}^n{E}_{ij}(\mathit{\phi }-{\mathit{\phi }}_{\mathrm{0}}{)}^i(S-S_{\mathrm{0}}{)}^j,\end{array}$$

where T_V denotes VTEC. φ and S denote the geographic latitude and the solar hour angle of ionospheric pierce point (IPP), respectively; φ₀ and S₀ denote φ and S at the center of the cover region of IPP in 1 day. E_ij is the model coefficient, and m and n denote the orders of the model. A polynomial model fits the VTEC over a period of time. In our case, a VTEC model is generated over 3 h of time, therefore eight VTEC models are applied per day. DCB is considered as constant in one day. Since our analysis is based on long-term single-site data, we set m and n to 4 and 3, respectively. Huang and Yuan (2014) applied the polynomial model with the same orders to TEC estimation.

Based on the thin shell approximation, the observation equation can be written as follows:

$$\begin{array}{}\text{(2)}& {\displaystyle }{T}_{\mathrm{os}}^{\mathrm{PRN}}(\mathit{\phi },S)=T_{\mathrm{V}}(\mathit{\phi },S)\cdot f\left(z\right)+DC{B}^{\mathrm{PRN}},\end{array}$$

where $T_{\mathrm{os}}^{\mathrm{PRN}}$ is slant TEC calculated by carrier phase smoothing, the superscript PRN denotes the GPS satellite, DCB^PRN denotes the combination of GPS satellite and receiver DCB, and z denotes the zenith angle of IPP. According to Lanyi and Roth (1988), the standard geometric mapping function f(z) is expressed as follows:

$$\begin{array}{}\text{(3)}& {\displaystyle }f\left(z\right)=\mathrm{1}/\cos \left(z\right),\end{array}$$

$$\begin{array}{}\text{(4)}& {\displaystyle }z=\arcsin {\displaystyle \frac{R_{\mathrm{E}}\cdot \cos \mathit{El}}{R_{\mathrm{E}}+h}},\end{array}$$

where R_E denotes the earth's radius, El denotes the elevation angle, and h denotes the thin ionospheric shell height. Note that h also affects the location of the IPP.

To estimate DCBs, the method above requires a definite thin shell height value. Conversely, if we get the daily solutions of DCBs, the optimal ionospheric shell height can be estimated. The optimal ionospheric shell height is assumed to be between 100 and 1000 km and is defined as the shell height with the minimum difference between DCB^PRN and the reference values. This optimization problem can be written as follows:

$$\begin{array}{}\text{(5)}& \begin{array}{c}\text{min}\\ \mathrm{100}<h<\mathrm{1000}\end{array}\text{mean}\left(\left|\mathit{D}\mathit{C}{\mathit{B}}_{\mathrm{ref}}-\mathit{D}\mathit{C}\mathit{B}\right|\right)\text{ s.t. }\mathit{T}=\mathbf{\Phi }\cdot \mathit{E}+\mathit{\theta }\cdot \mathit{D}\mathit{C}\mathit{B},\end{array}$$

where h is the daily optimal ionospheric shell height, DCB_ref denotes the vector of the reference values of DCBs, s.t. is the abbreviation for subject to, $\mathit{T}=\mathrm{\Phi }\mathbf{\cdot }\mathit{E}+\mathit{\theta }\cdot \mathit{D}\mathit{C}\mathit{B}$ is the matrix form of all the observation equations in one day, T denotes the vector of T_os, E corresponds to the coefficients of the models and contains E_ij, DCB is the vector of DCB^PRN, Φ is the coefficient matrix of E and contains $(\mathit{\phi }-{\mathit{\phi }}_{\mathrm{0}}{)}^i(S-S_{\mathrm{0}}{)}^{j}f\left(z\right)$, and θ is the coefficient matrix of DCB and contains only 1 and 0 s. E and DCB are unknown.

After the method above is applied to 11-year data, the estimated optimal ionospheric shell heights can be modeled by a Fourier series, which is expressed as follows:

$$\begin{array}{}\text{(6)}& {\displaystyle }h\left(x\right)=a_{\mathrm{0}}+\sum _{n=\mathrm{1}}^k\left(a_n\cos {\displaystyle \frac{\mathrm{2}n\mathit{\pi }x}{L}}+b_n\sin {\displaystyle \frac{\mathrm{2}n\mathit{\pi }x}{L}}\right),\end{array}$$

where k is the order of Fourier series and is set to 40, a_n and b_n are the model coefficients, x is the time, and L is the time span which is equal to 4018 d. The maximum frequency of the model is 40 ∕ L ≈0.01 per day, which corresponds to a period of 100 d. By the least-squares method, the model coefficients can be estimated.

This model can be applied to neighboring stations' DCB estimations. Instead of fixed shell height, this model provides a predicted optimal ionospheric shell height. Note that, while in the establishment and application of the model, the VTEC model, mapping function and elevation cut-off angle are constant, all of them affect the optimal ionospheric shell height.

3 Experiment and results

The previous section introduced a method to establish a daily optimal ionospheric shell height model based on a single site with reference values of DCBs. To analyze the improvement of DCB estimation by this model for the reference station and other neighboring stations, we present two experiments to evaluate and validate this method by using IGS stations located in the US and Europe. To ensure the accuracy and consistency of DCB, we only select IGS stations with pseudorange measurements of P1 code, and whose receiver DCBs have been published by CODE.

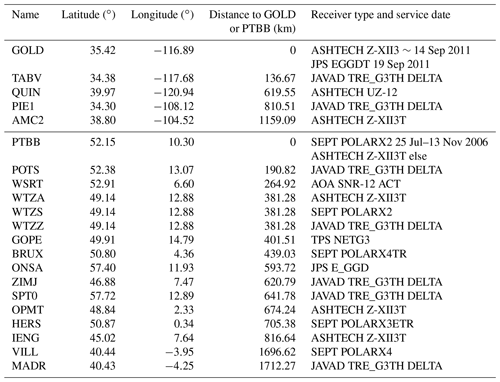
Figure 1 shows the location and distribution of the selected IGS stations in two regions. Table 1 shows the information of the geographical location, distance to reference station in each region and receiver types of all stations. Based on the RINEX data of the GOLD station in Region I and the PTBB station in Region II during the period of 2003–2013, two separate optimal ionospheric shell height models for each region are established by the aforementioned method. Then the model is applied to estimate DCB in 2014 for all the other stations in each region. Note that the reference stations GOLD and PTBB are marked with black triangles in the figure. The other neighboring stations are located in different orientations of GOLD and PTBB with different distances, which range from 136 to 1159 km for region I and range from 190 to 1712 km for region II. In the table, the receiver type is corresponding to 2003–2014 for GOLD and PTBB, and 2014 for the other stations. In region I, the receiver type of GOLD was changed once in September 2011. The five selected stations used four receiver types in 2014; TABV and PIE1 had the same receiver type. In region II, there are 9 receiver types for the 16 stations. The receiver type of PTBB has changed twice in 2006.

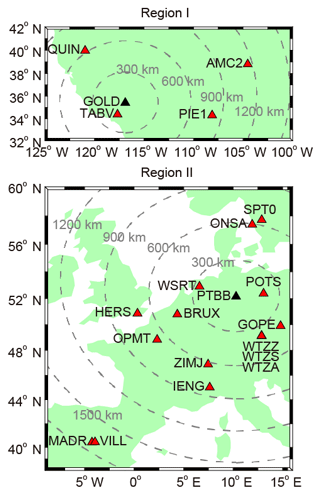
Figure 1 Geographical location of the selected IGS stations in the US region (Region I) and Europe region (Region II). The black triangle in each plot is the reference station.

Table 1 Information for the stations.

Table 2 Statistical results of mean and RMS of average ΔDCB in 2014.

Figure 2 shows the estimated daily optimal ionospheric shell height of GOLD and PTBB during the period from 2003 to 2013. The left panel shows the variation in the daily optimal ionospheric shell height and the fitting result by Eq. (6). From the overall trend, the variations in daily optimal ionospheric shell height for both stations appear as wave-like oscillations during the 11-year period. In the right panel, the statistical results are fitted by a normal distribution. The mean and the standard deviation (SD) of the normal distribution are 714.3 and 185.4 km for GOLD, respectively. The mean and SD values for PTBB are 416.4 and 184.1 km, respectively. At the end of 2010, a gap appears, because the DCB provided by CODE is simultaneously anomalous for both stations (Zhao and Zhou, 2018), and the data during this period are abandoned.

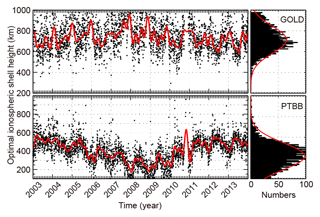
Figure 2 Variation in the daily optimal ionospheric shell height (black) and the fitting result (red).

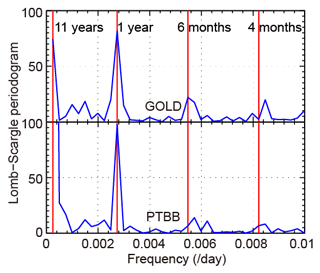
Figure 3 shows the amplitude spectra of the daily optimal ionospheric shell height of the two reference stations estimated by the Lomb–Scargle analysis (Lomb, 1976; Scargle, 1982). As can be found in Fig. 3, the peaks correspond to 11-year, 1-year, 6-month and 4-month cycles. The amplitudes of 11- and 1-year cycles are more evident than other periods in both stations. As mentioned earlier, 0.01 per day is about the maximum frequency of Eq. (6). Higher frequencies would not be useful because of their small amplitudes. This result shows that the optimal ionospheric shell height of GOLD and PTBB is periodic, and the 40th order of Fourier series is suitable for modeling its variation.

Figure 3 Lomb–Scargle spectra of the daily optimal ionospheric shell height.

We establish two optimal ionospheric shell height models for each region from the 40th-order Fourier series based on the 11-year data of GOLD and PTBB. To investigate the availability zone of the optimal ionospheric shell height model, we apply the models to the stations of each region as shown in Fig. 1 and Table 1. Based on the predicted daily optimal ionospheric shell heights in 2014 calculated by the model at GOLD or PTBB, each station is applied to estimate DCB separately in 2014 using Eqs. (1)–(4). The difference in DCBs in all stations in each region calculated using the optimal ionospheric shell height model at the reference stations and DCBs provided by CODE is then compared to the difference in DCBs calculated using a fixed ionospheric shell height (400 km) and DCBs released by CODE.

The results of this comparison are shown in Fig. 4. The panels for the stations are arranged by their distances to reference stations, and this is also applied to Table 2; from the top panels to the bottom panels, the distance of the corresponding station to the reference station gradually increases. The left and right panels show the daily differences and the histograms of the statistical results in 2014, respectively. For all of the stations, the daily average differences of DCBs calculated using the optimal ionospheric shell height model are reduced compared to those using the fixed ionospheric shell height. For GOLD and TABV, the improvement is substantial; the daily average ΔDCB is close to zero. For the other stations, the median daily average ΔDCB is negative, but smaller in absolute value than using the fixed shell height. This result shows the improvement of the model seems to be related with the distance to GOLD. Data gaps in the figure correspond to days when data from that station are not available. Figure 5 is the same format as Fig. 4 and shows the results of Region II. Comparing to the results of fixed ionospheric height, Fig. 5 also indicates that the ΔDCB calculated using the optimal ionospheric shell heights at PTBB is on average smaller than that calculated using fixed ionospheric shell height. Both Fig. 4 and 5 show that the accuracy of DCB estimation can be improved using optimal ionospheric heights from reference stations.

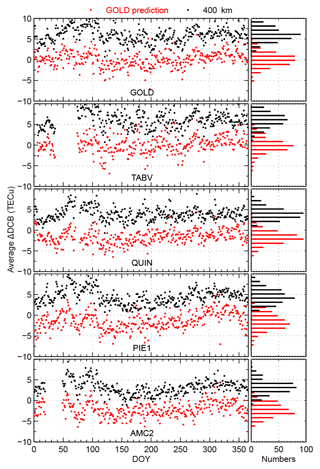
Figure 4 Comparisons of the average ΔDCB calculated using the predicted optimal ionospheric shell heights (red dots) and those using the fixed ionospheric shell height (black dots) in 2014 for stations in Region I.

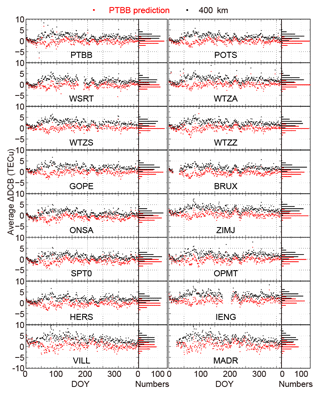
Figure 5 Comparisons of the average ΔDCB calculated using the predicted optimal ionospheric shell heights (red dots) and those using the fixed ionospheric shell height (black dots) in 2014 for stations in Region II.

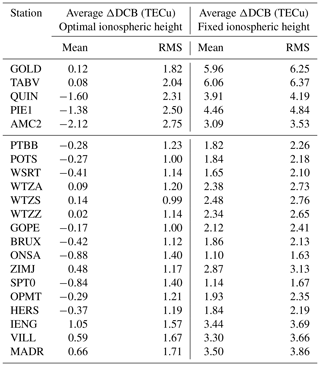
Table 2 shows the quantitative statistical results of average ΔDCB in 2014. For all the stations in each region, the mean values and the root mean squares (RMSs) using the optimal ionospheric shell height model are smaller than those using the fixed ionospheric height. For Region I, the improvements in GOLD and TABV are the most significant. Their mean values are reduced to 0.12 and 0.08 TECu, respectively; the root mean squares are reduced by 4.43 and 4.33 TECu, respectively. For Region II, the improvements in DCB estimation are the most obvious for WTZZ, with the mean value of ΔDCB decreasing from 2.34 to 0.02. We could note that TABV and WTZZ station are quite close to the reference stations in each region.

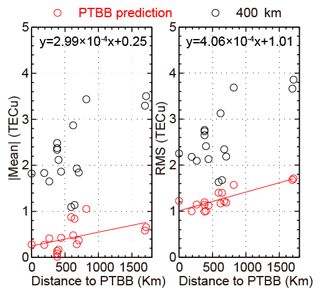
Figures 6 and 7 show the relation between the statistical results of average ΔDCB and the distance to the reference stations in each region. The left and the right panels in each figure show the relation of the absolute mean value and the root mean square, respectively, with the distance to GOLD or PTBB. For all of the stations, the optimal ionospheric shell height model improves the accuracies of DCB estimation compared to the fixed ionospheric shell height in a statistical sense; both of the absolute mean values and the root mean squares become smaller. For the optimal ionospheric shell height model, the absolute mean values show a positive correlation with the distance to reference station GOLD or PTBB in each region, as well as the root mean squares. By using the linear regression, for Region I, the absolute mean value increases at a rate of about 1.84 TECu per 1000 km and starts at about 0.05 TECu. The RMS value increases at a rate of about 0.75 TECu per 1000 km and starts at about 1.87 TECu. According to the fitting results, the absolute mean value and the RMS are less than 1 and 2.25 TECu in the region around GOLD with a radius of 500 km, and less than 2 and 2.62 TECu for the region with a radius of 1000 km. For Region II, the absolute mean value increases at a rate of about 0.30 TECu per 1000 km and start at about 0.25 TECu. The RMS value increases at a rate of about 0.41 TECu per 1000 km and starts at about 1.01 TECu. According to the fitting results, the absolute mean value and the RMS are less than about 0.40 and 1.21 TECu in the region around PTBB with a radius of 500 km, and less than about 0.55 and 1.42 TECu for the region with a radius of 1000 km. For the two regions, the RMSs show stronger linear relations with distance than the means.

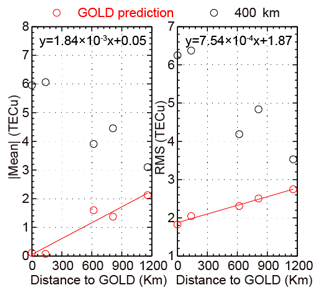
Figure 6 Relation of the accuracy for DCB estimation with the distance to GOLD. The red lines are the linear fitting results.

Figure 7 Relation of the accuracy for DCB estimation with the distance to PTBB. The red lines are the linear fitting results.

4 Summary

In this study, we implement and validate a method to transfer the optimal ionospheric shell height derived for IGS stations to non-IGS stations or isolated GNSS receivers. We establish two optimal ionospheric shell height models by the 40th-order Fourier series based on the data of IGS stations GOLD and PTBB in two separate regions. These two models are applied to the stations in each region, where the distance to GOLD ranges from 136 to 1159 km and the distance to PTBB ranges from 190 to 1712 km. The main findings are summarized as follows:

1. The optimal ionospheric shell height model improves the accuracy of DCB estimation compared to the fixed shell height for all of the stations in a statistical sense. These results indicate the feasibility of applying the optimal ionospheric shell height derived from IGS stations to other neighboring stations. The IGS stations can calculate and predict the daily optimal ionospheric shell height and then release this value to the nearby non-IGS stations or isolated GNSS receivers.

2. For other stations in each region, the error of DCB by the optimal ionospheric shell height increases linearly with the distance to the reference station GOLD or PTBB. For the mean and the RMS of the daily average ΔDCB, in region I, the slopes are about 1.84 and 0.75 TECu per 1000 km; in region II, the slopes are about 0.30 and 0.41 TECu per 1000 km. These results indicate the horizontal spatial correlation of regional ionospheric electron density distribution. For the different region, the error at 0 km (i.e., the error for the reference station) is different, which should also be considered, and the quality of the DCB estimations also depends on the quality of the optimal shell height model at the reference stations themselves.

Due to a requirement of this experiment, we only analyze two regions in midlatitude because of the insufficiency of long-term P1 data. We also ignore the orientation of isolated GPS receivers to the reference station.