GREEN: the new Global Radiation Earth ENvironment model (beta version)

GREEN (Global Radiation Earth ENvironment) is a new model (in beta version) providing fluxes at any location between $L^{\ast }=$ 1 and $L^{\ast }=$ 8, all along the magnetic field lines, for all local times and for any energy between 1 keV and 10 MeV for electrons and between 1 keV and 800 MeV for protons. This model is composed of global models (AE8 and AP8, and SPM for low energies) and local models (SLOT model, OZONE and IGE-2006 for electrons, and OPAL and IGP for protons). GREEN is not just a collection of various models; it calculates the electron and proton fluxes from the most relevant existing model for a given energy and location. Moreover, some existing models can be updated or corrected in GREEN. For examples, a new version of the SLOT model is presented here and has been integrated in GREEN. Moreover, a new model of proton flux in geostationary orbit (IGP) developed a few years ago is also detailed here and integrated in GREEN. Finally a correction of the AE8 model at high energy for L^∗ < 2.5 has also been implemented. The inputs of the GREEN model are the coordinates of the points and the date (year, month, day, UTC) along an orbit, the particle species (electron or proton) and the energies. Then GREEN provides fluxes all along the given orbit, depending on the solar cycle and other magnetic parameters such as L^∗, B_mirror and B_eq.

1 Introduction

The well-known NASA AP8 and AE8 models (Sawyer and Vette, 1976; Vette, 1991) are commonly used in the satellite industry to specify the radiation belt environment. Unfortunately, there are some limitations in the use of these models, primarily due to the covered energy range, but also because in some regions of space there are discrepancies between the predicted average values and the measurements. Moreover, the new US models AE9 and AP9 were developed a few years ago (Ginet et al., 2013). These models are better than AE8 and AP8 in some cases but need to be improved in some regions of radiation belts. Therefore, our aim is to develop a radiation belt model, covering a large region of space and energy, from low Earth orbit (LEO) altitudes to geostationary Earth orbit (GEO) and above, and from plasma to relativistic particles. The aim for the first version of this new model is to correct the AP8 and AE8 models where they are deficient or not defined. Ten years ago we developed the IGE-2006 model for geostationary orbit electrons (Sicard-Piet et al., 2008). This model has proven to be more accurate than AE8 and is used commonly in the industry, covering a broad energy range, from 1 keV to 5 MeV. From then, a proton model for geostationary orbit, called IGP, was also developed for material applications and is presented in this paper. These models in geostationary orbit were followed by the OZONE model (Bourdarie et al., 2009), covering a narrower energy range but the whole outer electron belt; the SLOT model (Sicard-Piet et al., 2014) to assess average electron values for 2 < L^∗ < 4; and finally the OPAL model (Boscher et al., 2014), which provides high-energy proton flux values at low altitudes. As most of these models were developed using more than a solar cycle of measurements – these ones being checked, cross-calibrated and filtered – we have no doubt that the obtained averages are more accurate than AP8 and AE8 for these particular locations. These local models were validated along different orbits with independent data sets or measurements of space environment effects.

Figure 1 Input and output parameters of the GREEN model.

Obviously, the ideal would be to develop a unified global model across many L^∗ and energies rather than combining “submodels”. However, radiation belts are made of several regions with different dynamics and several populations (low energies and high energies) with different behavior. So it is easier to develop local models for each region and each energy range.

In order to develop a new global model, called GREEN (Global Radiation Earth ENvironment), with GREEN-e for electrons and GREEN-p for protons, we will use a cache file system to switch between models, in order to obtain the most reliable value at each location in space and each energy point. Of course, the way the model is developed is well suited to future enhancement with new models developed locally or under international partnerships. The first beta version of the GREEN model is presented in this paper.

2 Development of the model

2.1 Main principles

GREEN is a new model composed of different global and local models. The first step of the development was to define a list of the most relevant models in the case of electrons and another one for protons. These two lists can be expanded and modified at any time. GREEN-e is composed of AE8 (Vette, 1991), the SLOT model (Sicard-Piet et al., 2014), OZONE (Bourdarie et al., 2009), IGE-2006 (Sicard-Piet et al., 2008) and SPM for the lower energies (Ginet et al., 2013). GREEN-p is composed of AP8 (Sawyer and Vette, 1976), OPAL (Boscher et al., 2014) and SPM (Ginet et al., 2013). The second step was to define a 3-D grid in energy (Ec), B_local∕B_eq (with B_local the local magnetic field and B_eq the equatorial magnetic field) and L^∗. This grid represents the global architecture of GREEN. This 3-D grid (Ec, B_local∕B_eq, L) is the same as the one used for the physical model Salammbô (Herrera et al., 2016, and references therein) with 133 steps in L^∗ (between $L^{\ast }=$ 1 and $L^{\ast }=$ 8), 133 steps in B_local∕B_eq and 49 steps in energy and has not been chosen randomly. After verification, this grid allows the results of the most binding model (for example OPAL) to be reproduced as best as possible. Obviously the energy grid is different for GREEN-e and GREEN-p. Then, fluxes from each model integrated in GREEN are calculated on this 3-D grid. Taking into account that some local models that compose GREEN give only flux integrated in energy, only this kind of flux is provided by GREEN (cm⁻² s⁻¹). Finally, a priority order of the different models is established according to space location and energy to provide the most reliable value of flux. The last step is to calculate flux for a given energy and a given location by interpolating in the 3-D grid of the most reliable model.

Figure 2 Energy and L coverage of the different models integrated in GREEN-e.

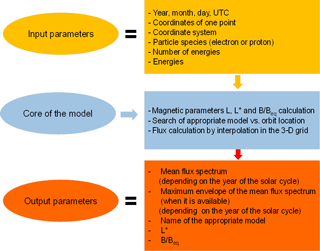
Figure 1 is a scheme describing all the input parameters, the core of the model and all the output parameters of GREEN. One of the features of GREEN is that it provides fluxes depending on the year of the solar cycle and not just two states as in the case of AE8 (AE8 MIN and AE8 MAX). Moreover, when it is possible, GREEN also provides the maximum envelope of the mean flux, depending also on the year of the solar cycle, due to the variation from one solar cycle to another (as explained in detail for IGE-2006; Sicard-Piet et al., 2008).

2.2 GREEN-e

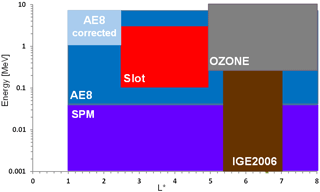
In this section, the electron part of GREEN, GREEN-e, is described in detail. Figure 2 represents energy and L coverage of the different models integrated in GREEN-e. It is important to keep in mind that most of the models are defined in terms of L^∗ calculated with International Geomagnetic Reference Field (IGRF) + Olson–Pfitzer magnetic field models, except AE8. Indeed, when AE8 is used, the L parameter must be calculated with the Jensen and Cain magnetic field model (Vette, 1991).

2.2.1 AE8 and SPM

As mentioned in Fig. 2, AE8 and SPM are used by default. This is the case for the SPM model at low energy (< 30 keV) except in geostationary orbit when IGE-2006 is preferred and for AE8 at higher energy (> 30 keV) outside the coverage of the SLOT model, OZONE and IGE-2006. SPM is a model with no solar cycle dependence; thus electron fluxes resulting from this model are considered constant throughout the solar cycle. For AE8, two versions exist: AE8 MAX for the solar maximum and AE8 MIN for the solar minimum. It is common to consider a full solar cycle of 11 years with 4 years of solar minimum (2 years before the minimum and 2 years after) and 7 years of solar maximum. Thus, in GREEN, when AE8 is the preferred model, the appropriate version of AE8 (MIN or MAX) is taken according to the year chosen by the user.

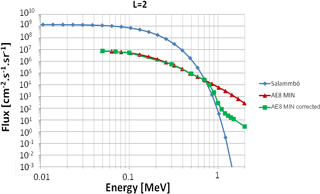
The inner zone of electron radiation belts is a region in which interest has grown in recent years thanks to data from the Van Allen Probes (Li et al., 2015; Claudepierre et al., 2017). As mentioned in this figure, for L < 2.5 and energy greater than a few hundred kiloelectron volts, we choose to use a corrected version of AE8. Indeed, in a previous study, Boscher at al. (2018) showed that high-energy electron fluxes (greater than a few hundred kiloelectron volts) predicted by AE8 are overestimated in the region for L^∗ < 2.5. It is difficult to estimate the error made by AE8, but this study aims at showing that in this region and for high energy the physical model Salammbô provides electron fluxes in agreement with in situ measurements. Thus, in this version of GREEN-e model, AE8 fluxes have been corrected, that is to say, divided by a given factor, calculated using the Salammbô model. The Salammbô model is not perfect everywhere, but it has been proven that the decrease of electron flux with energy is good (Boscher et al., 2018). Thus, when electron fluxes from AE8 are higher than those provided by Salammbô, they are divided by the ratio between the both, up to a factor 100, in order to limit the correction (Fig. 3). This correction is not perfect but does allow better estimation of high-energy electron flux in the region L^∗ < 2.5.

Figure 3 Electron fluxes provided by Salammbô in blue (average of years during solar minimum), by AE8 MIN in red and AE8 MIN corrected in green at L= 2.

2.2.2 SLOT model

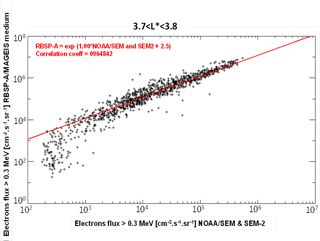
Figure 4 Example of correlation between NOAA-POES and Van Allen Probe-A flux for electrons > 0.3 MeV and for L^∗ between 3.7 and 3.8.

Figure 2 shows also that the SLOT model is available from $L^{\ast }=$ 2.5 to $L^{\ast }=$ 5 and for energies from 100 keV to 3 MeV. The SLOT model developed in 2013 (Sicard-Piet et al., 2014) was a model that reflects the mean flux at each point along the magnetic field lines. This first version has been updated in 2017 and is described here. As explained in a previous paper (Sicard-Piet et al., 2014), the SLOT model is based on the correlation between the flux dynamics in LEO orbit with NOAA-POES (Polar Operational Environmental Satellites) data and the flux all along the magnetic field line. The first change in the model is its spatial extension: the upper spatial limit of the SLOT model is now $L^{\ast }=$ 5 as opposed to $L^{\ast }=$ 4 before. Then, taking into account new measurements such as those from the Van Allen Probes (MagEIS), correlation factors all along the magnetic field line have been recalculated, between $L^{\ast }=$ 2.5 and $L^{\ast }=$ 5. An example of the correlation between NOAA-POES data and Van Allen Probe-A measurements is plotted in Fig. 4 for electrons with energy > 0.3 MeV and for L^∗ between 3.7 and 3.8. This kind of correlation is made with all data used in the model and listed in Sicard-Piet et al. (2014) plus the Van Allen Probes. As explained by Sicard-Piet et al. (2014), these correlation factors are multiplied with the NOAA-POES data in order to obtain mean electron fluxes between > 0.1 and > 3 MeV along all magnetic field lines between $L^{\ast }=$ 2.5 and $L^{\ast }=$ 5 (Fig. 5). An equatorial pitch angle distribution shape based on a sine function is assumed and constrained by data all along the magnetic field lines between $L^{\ast }=$ 2.5 and $L^{\ast }=$ 5 (Fig. 5).

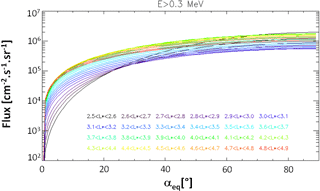
Figure 5 Electron fluxes along magnetic field lines (90^∘ corresponds to the Equator) for energy > 0.3 MeV and for all L^∗ intervals of the SLOT model (in color).

The most significant change in this new version of the SLOT model is the dependence of fluxes on the solar cycle. In order to have dependence on the solar cycle in GREEN-e, we have to study in detail the dynamics of the measurements from all NOAA-POES spacecraft. As an example of this solar cycle dependence, > 300 keV electron fluxes vs. time from all NOAA-POES data is plotted in Fig. 6. This figure shows clearly a correlation between the dynamics of NOAA-POES electron fluxes and the solar cycle (F10.7). The dynamics have been studied for four energy channels: > 0.1, > 0.3, > 1 and > 3 MeV.

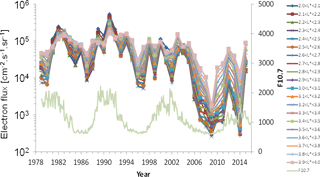
Figure 6 Electron > 300 keV fluxes vs. time (1978–2015) from all NOAA-POES data for each L^∗ interval defined in the SLOT model. F10.7 is also represented in green.

Then, the flux dynamics over time between 1978 and 2015 have been represented in the 11 years of the solar cycle, from year −6 to year 4, with year 0 being the solar minimum. The fluxes vs. year of the solar cycle in NOAA-POES orbit for electrons > 1 MeV and for each L^∗ interval is plotted in Fig. 7. This modulation with the solar cycle has been defined in LEO orbit for the four energy channels of the SLOT model and has been applied to the mean flux all along the magnetic field lines, from low altitude to the Equator.

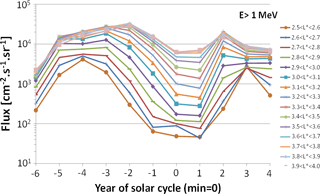
Figure 7 Electron > 1 MeV fluxes vs. year of the solar cycle from all NOAA-POES data for each L^∗ interval defined in the SLOT model.

Finally, in order to take into account the modulation of flux from one solar cycle to another, this new version of the SLOT model provides mean flux for a given year of the solar cycle as well as the maximum flux of the three solar cycles used in the model for this given year.

Figure 8 Energy and L coverage of the different models integrated in GREEN-p.

Thus, the new version of the SLOT model provides electron fluxes from 0.1 to 3 MeV for all altitudes with L^∗ between 2.5 and 5 with a dependence on the solar cycle.

Figure 9 Example of proton flux spectrum (cm⁻² s⁻¹ sr⁻¹) resulting from OPAL-V2 (in blue) and AP8 MIN (in green).

2.2.3 OZONE model

OZONE is valid for L^∗ > 4 and for energies greater than 300 keV. In geostationary orbit, OZONE agrees with IGE-2006 results; consequently OZONE will be used for energies > 300 keV in GEO orbit. The version of OZONE developed in 2009 (Bourdarie et al., 2009) was already dependent on the solar cycle, so the model was not modified before integration in GREEN-e.

2.2.4 IGE-2006 model

IGE-2006 is a specification model developed exclusively for geostationary orbit (Sicard-Piet et al., 2008). This orbit is at a fixed altitude but is represented by a large L^∗ range, between 5.7 and 7.1. As explained in Sicard-Piet et al. (2008), fluxes provided by IGE-2006 come from averaged fluxes measured by all available Los Alamos National Laboratory (LANL) spacecraft. In this version of GREEN-e, fluxes will be considered as a constant in this L^∗ range. IGE-2006 is solar cycle dependent, so the model was not modified before integration in GREEN-e.

2.3 GREEN-p

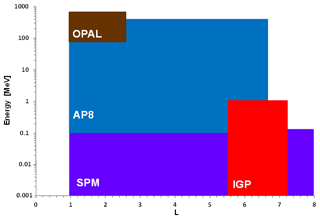
In this section, the proton part of GREEN, GREEN-p, is described in detail. Figure 8 represents energy and L coverage of the different models integrated in GREEN-p. It is important to keep in mind that most of the models are defined in terms of L^∗ calculated with IGRF + Olson–Pfitzer (Olson and Pfitzer, 1977) magnetic field models, except AP8. Indeed, when AP8 is used, the L parameter must be calculated with the Jensen and Cain magnetic field model for AP8 MIN and the Goddard Space Flight Center (GSFC) model for AP8 MAX (Sawyer and Vette, 1976).

2.3.1 OPAL

The first version of OPAL was a model valid for protons > 80 MeV and for altitude lower than 800 km, depending on the solar cycle (Boscher et al., 2014). This year, a new version of OPAL has been developed at ONERA, using ICARE-NG measurements on board Jason-2 and Jason-3 (Boscher et al., 2011). Now OPAL-v2 provides proton fluxes for energy between 80 and 800 MeV up to the orbit of Jason spacecraft (1336 km). It is important to keep in mind that input parameters of OPAL are the radio flux F10.7 of the Sun and the magnetic field of the given year. As OPAL depends on the radio flux F10.7, an input of OPAL is the date. So, for a given date chosen by the user in the past, the real F10.7 value is used to calculate proton fluxes. But for a given date in the future, it is not so easy because the F10.7 value is unknown. Consequently, a statistical study has been done on F10.7 values from 1947 to now in order to define a mean F10.7 value for each of the 11 years of a solar cycle. Thus, for a given date chosen by the user in the future, the year of the solar cycle is predicted (from year −6 to year +4, with 0 being the year of the minimum), according to which the corresponding mean F10.7 value is used in OPAL to calculate proton fluxes. Moreover, added to the mean proton fluxes, OPAL provides an upper envelope considering the variation from one solar cycle to another. Taking into account that high-energy proton fluxes are anticorrelated with F10.7 values, this upper envelope is calculated using the minimum F10.7 value measured since 1947 for each year of the solar cycle.

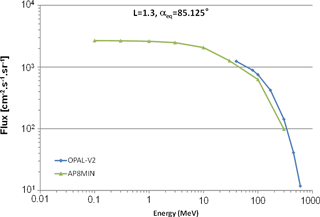
Figure 9 represents an example of a proton flux spectrum (cm⁻² s⁻¹ sr⁻¹) at $L^{\ast }=$ 1.3 near the magnetic equator (α_eq= 85.125^∘) resulting from OPAL-V2 (in blue) and AP8 MIN (in green). We can observe that, for this L^∗ value, fluxes from OPAL-V2 are slightly higher than those from AP8 MIN. This new version of OPAL has been integrated in GREEN-p.

2.3.2 IGP

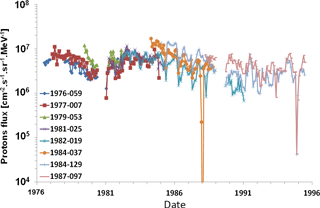
On board the Los Alamos National Laboratory satellites, from July 1976 (launch of the satellite: 1976-059) to June 1995 (end of the measurements on board: 1984-129 and 1987-097), there was a detector named CPA (Charged Particle Analyzer), which covered the energy range 80 keV–300 MeV (Higbie et al., 1978; Baker et al., 1979). To cover a larger energy range, we also used the measurements of the MPA (Magnetospheric Plasma Analyzer) detector on board LANL satellites being launched between September 1989 (launch of the satellite: 1989-046) and November 1995 (McComas et al., 1993). These measurements cover roughly the energy range, 0.1–38 keV.

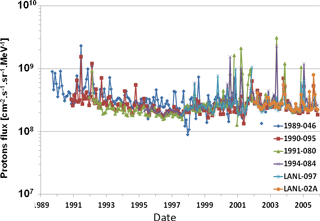
Figure 10 Monthly average 1 keV proton flux measured in GEO by the detector MPA on board the different LANL satellites.

Figure 11 Monthly average 80 keV proton flux measured in GEO by the detector CPA-LoP on board the different LANL satellites.

MPA measurements

MPA measurements are globally of good quality. The temporal resolution is 86 s most of the time, but it can be doubled (172 s) for short periods of time. The detector aged with time; it drifted. This drift is compensated for over time, but after several years it is impossible to measure the highest energies anymore (typically after 10 years, it is impossible to obtain measurements above 10 keV). For the development of a proton specification model, data between 1 and 32 keV have been used. Fluxes below 1 keV have not been used, due to uncertainties in the spacecraft potential determination. Thus, we determined monthly averages of the proton flux for each satellite. These monthly averages were made in order to analyze possible solar cycle or seasonal effects (linked to the magnetic field or to its activity). An example is given for the 1 keV protons in Fig. 10. Some points as high as 2.3 × 10⁹ MeV⁻¹ cm⁻² s⁻¹ sr⁻¹ observed in June 1991 could be due to the effect of magnetic activity, a particular contamination during that period or a (or several) bad point(s). Apart from these, no seasonal effect is observed in the flux curve; if there is a solar cycle effect, it is very low. As the flux does not vary with time, an average spectrum was deduced from all the measurements, taking into account the number of points for each satellite.

CPA measurements

The CPA instrument is in fact made of two different instruments: CPA-LoP and CPA-HiP, which respond respectively to protons in the range 73–512 keV and 400 keV–300 MeV. The measurements are also globally of high quality. The time resolution of the instrument is 10 s, which means that the number of points is much higher. A monthly average for each channel was produced. An example of this average is plotted in Fig. 11 for 80 keV protons for each available LANL spacecraft. From that figure, it appears that there is no seasonal variation in the 80 keV proton flux; if there is a solar cycle one, it should be small in the range covered by CPA-LoP (less than a factor of 2). We must note in this figure a few low flux values which lie below the general tendency of the curve; it is suspected that they are due to gain switches for that particular channel and that satellite. We have not removed them, as the total average is not affected by these points.

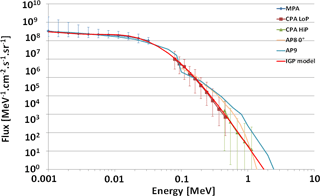
Figure 12 Total spectrum of trapped protons deduced from MPA and CPA measurements on board different LANL satellites and from the model. Fluxes from AP8 and AP9 are provided for comparison.

As for MPA, a global average of all the points was performed, in order to obtain a global spectrum of protons from 1 keV up to 1 MeV in geostationary orbit. Above 1 MeV, data were not used because of the contamination by protons from solar flares.

IGP model

Combining the part of the spectrum from MPA and CPA up to around 1 MeV leads to Fig. 12. The average fluxes are plotted, together with an error bar which corresponds to the maximum and minimum values obtained in the monthly averages from the full time period and all spacecraft. Though a gap exists between the two instruments, it appears that both parts of the spectrum are consistent: at low energy the spectrum is very flat; it falls very quickly for energies greater than 50 keV. We also compared in this figure the obtained spectrum with AP8 (for longitude 0^∘, AP8 MAX and MIN being equal in this region) (Sawyer and Vette, 1976). For unidirectional flux comparison, we divided the AP8 flux by 4π, the environment being nearly isotropic in geosynchronous orbit for trapped particles. We can see that the obtained spectrum is nearly consistent with AP8. In fact, near 1MeV, the main problem is distinguishing trapped particles from untrapped ones (solar protons and cosmic rays). That may explain part of the difference. Globally, while the obtained spectrum is nearly a power law, AP8 is more an exponential law, with characteristic energy around 100 keV.

We tried to determine an empirical formula with all the average flux values. For the high-energy part, we used a kappa function with 9 keV characteristic energy and = 5.45, not far from what was obtained by Christon et al. (1991) in the plasma sheet. An exponential part (with 2 keV characteristic energy) was added at low energy to fit the total spectrum:

$${\displaystyle }\mathrm{flux}=\mathrm{4}\times {\mathrm{10}}^{\mathrm{8}}\exp (-E/\mathrm{0.002})+\mathrm{7}\times {\mathrm{10}}^{\mathrm{10}}E{\left(\mathrm{1}+{\displaystyle \frac{E}{\mathrm{5.45}x\mathrm{0.009}}}\right)}^{-\mathrm{6.45}},$$

where E is the energy in megaelectron volts (MeV) and the flux in MeV⁻¹ cm⁻² s⁻¹ sr⁻¹.

Figure 13 Electron fluxes vs. L^∗ and energy in 1996 and 2003 provided by the GREEN-e model.

The model result is compared to the average spectrum in Fig. 12. This spectrum is very useful for deducing surface material degradation for satellites in geostationary orbit. It also can be used for dynamic physical modeling of the radiation belt proton to set a boundary condition.

This model is compared to the NASA AP9-SPM one (Ginet et al., 2013; Roth et al., 2014) also in Fig. 12. The NASA AP8 model was limited to energies greater than 100 keV. In geostationary orbit, the low-energy part comes from the same measurements we used: the MPA detector on board the LANL spacecraft and the two models are very close (the difference can be due to the interpolation used between channels). In AP9-SPM, the obtained spectrum is extrapolated to around 100 keV, but it is possible that our way to connect the two parts of the model has to be improved. With AP9-SPM, the two parts of the spectrum do not match. Obviously, there is a discontinuity at around 100 keV. At higher energy levels, the spectra from AP8 and AP9 are not too different, up to around 500 keV. Above this value, AP9 exceeds AP8 by a growing factor. The main problem for such energies is distinguishing trapped and untrapped particles in the measurements. We know from magnetospheric shielding calculations that for this energy range both particles can be observed depending on the viewing direction. Looking to the east, trapped particles from the radiation belts are observed; looking to the west, only cosmic rays and solar protons coming from outside the magnetosphere are observed. That is why in our analysis no points were extracted for E > 1.14 MeV. The model just gives an extrapolation (reasonable as a power law). It is really difficult to validate the IGP model with other data, because good proton data are extremely rare in GEO orbit, due to contamination by electrons measurements and solar protons.

Figure 14 Electron fluxes vs. L^∗ and energy in 1996 and 2003 provided by the GREEN-e model with a simple smooth function.

3 Results and validation

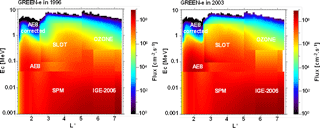
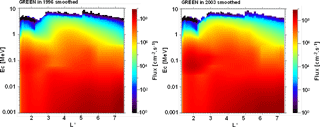
Once each of the local models has been integrated into GREEN, we are able to calculate fluxes at any location between $L^{\ast }=$ 1 and $L^{\ast }=$ 8 all along the magnetic field lines and for any energy between 1 keV and 10 MeV for electrons and between 1 keV and 800 MeV for protons. Figure 13 gives examples of electron fluxes provided by the GREEN-e model in 1996 (solar minimum) and in 2003 (solar maximum) vs. L^∗ and energy at the Equator. The different models used are also mentioned on the plot. This figure shows clearly the influence of the solar cycle on the electron flux, particularly in the Slot region where fluxes are higher during solar maximum. Moreover, we can note that discontinuities exist at the interface of the different models and have to be removed or at least smoothed in the future versions of GREEN-e. There are several ways to attenuate these discontinuities. The first one is to apply a simple smooth function to the 3-D grid of GREEN. An example of results obtained with this kind of smooth function is represented in Fig. 14. This figure shows that the discontinuities are clearly attenuated but the error on the electron flux can remain significant at the interface of the models. The second method would be to apply a more complex smooth function, for example by using our physical model, Salammbô. But the way to do that needs to be well thought out and defined. The third method, the best but the hardest, would be to improve the different models close to their boundaries, with new measurements for example. If each model on one side and the other of an interface provides a flux closer to a real flux, discontinuities will be removed. The different methods of attenuating discontinuities will be investigated in detail in the future versions of the GREEN model.

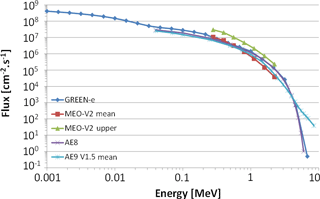
Figure 15 Electron spectrum from GREEN-e (in blue) in a whole solar cycle compared to the mean (in red) and upper (in green) flux provided by the MEO-V2 model.

Now that the results of GREEN-e have been presented, it is important to validate them. For the validation, results from GREEN will be presented without any smooth functions. The first validation is done in medium Earth orbit (MEO) by comparing electron fluxes provided by GREEN-e and by other models: the MEO-V2 model (Sicard-Piet et al., 2006), AE8, and AE9 and AP9 (v1.5). MEO-v2 model is not used in GREEN-e and is a good way to validate it. Figure 15 represents the electron spectrum from GREEN-e in blue, from the MEO-V2 model in red for the mean flux and in green for the upper envelope, and from AE8 in purple for a whole solar cycle. Results from AE9 and AP9 (v1.5 mean) are also plotted in light blue. This figure shows that electron fluxes provided by the GREEN-e model are coherent with those resulting from the MEO-V2 model: equal or slightly higher than mean MEO-V2 fluxes and lower than upper envelope fluxes. Fluxes from GREEN are also coherent with AE8 and AE9, except for energies greater than 5 MeV, where AE9 provides electron fluxes higher than GREEN and AE8.

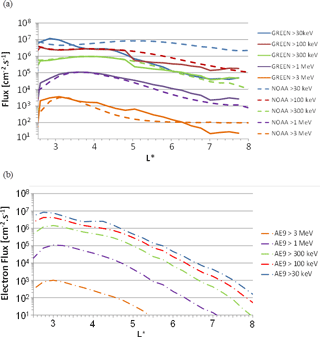
Figure 16 (a) Mean electron fluxes in LEO orbit between 1999 and 2010 from NOAA-POES measurements (in dashed lines) and from one solar cycle in GREEN-e (in full lines) for several energy channels. (b) Electron fluxes in LEO orbit (820 km, 98^∘) from AE9 v1.5 mean.

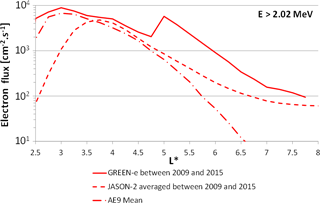
Figure 17 Mean electron fluxes in Jason-2 orbit between 2009 and 2015 from GREEN-e (in full line), Jason-2 measurements (in dashed line) and AE9 mean v1.5 (dash-dotted line) for E > 2.02 MeV electrons.

In order to validate fluxes in other orbits, a comparison between GREEN-e results and NOAA-POES measurements is done in LEO orbit. Figure 16 represents (i) mean electron fluxes between 1999 and 2010 from NOAA-POES measurements (in dashed lines) for several energy channels (> 30, > 100, > 300 keV, > 1 and > 3 MeV) and fluxes from GREEN-e, calculated based on a full solar cycle, and (ii) electron fluxes resulting from the AE9 v1.5 mean. This figure shows that beyond $L^{\ast }=$ 2.5 fluxes resulting from GREEN-e are in agreement with NOAA-POES data, with less than a factor 3 between the two, particularly in the L range of the SLOT model (2.5 < L^∗ < 5), which is based on these data. At high energy (> 3 MeV) for L^∗ > 6, POES data seem to reach the background of the instrument, probably due to cosmic particle measurements, while fluxes from the GREEN-e model continue to decline while L^∗ increases. We can note that for low energy (∼ 30 keV) there is a big difference between GREEN-e and NOAA-POES measurements and that for some L^∗ values this flux is lower than > 100 keV, which is not usual. It is important to keep in mind that for low energy (∼ 30 keV), electron fluxes in GREEN-e come from AE8, while fluxes for higher energies come from the SLOT model and OZONE. This energy channel (∼ 30 keV) would be a track of improvement of GREEN. Moreover, fluxes below $L^{\ast }=$ 2.5 are not plotted in the figure because it is well known that NOAA-POES data are contaminated by very high energy protons at low L^∗ values (Evans and Greer, 2000). We can also note that there are significant differences between GREEN-e and AE9 above $L^{\ast }=$ 4.5. In LEO orbit, the higher the value of L^∗, the further away from the Equator and the more the electron fluxes differ between AE9 and GREEN. So it seems that, near the Equator, GREEN and AE9 are coherent, but it is no longer the case at the end of the magnetic field lines for low pitch angles.

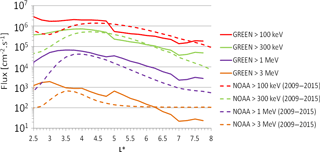
Figure 18 Mean electron fluxes in LEO orbit between 2009 and 2015 from NOAA-POES measurements (in dashed lines) and from GREEN-e (in full lines) for several energy channels.

The same kind of comparison has been made between GREEN-e results and Jason-2 data for E > 2.02 MeV electrons for L^∗ > 2.5 between 2009 and 2015 and is plotted in Fig. 17. The period 2009 to 2015 corresponds to years 0, 1, 2, 3, 4, −5 and −6 of the solar cycle (0 is the year of the minimum). In Fig. 17, fluxes are an average of results from GREEN-e for these years of the solar cycle. Electron fluxes from AE9 (mean v1.5) are also plotted. This graph shows first that there is a discontinuity in the GREEN-e model at $L^{\ast }=$ 5, at the interface between the SLOT model and OZONE. It is clear that some efforts must be made to remove this kind of discontinuity in the next version of GREEN. We can also mention the significant difference between AE9 and GREEN at L^∗ > 4.5 as in the case of Fig. 16. However, what we want to highlight with this plot is the difference between GREEN-e results and Jason-2 measurements for low L^∗ values (L^∗ < 3.5). Electron flux measured by Jason-2 at this energy level is much lower than the one provided by GREEN and AE9 in this region, while Fig. 16 showed a very good correlation between GREEN, AE9 and NOAA measurements in the same region (L^∗ < 3.5). Why was there an agreement between the results of GREEN and NOAA that no longer appears with the Jason-2 measurements? Is this due to the difference of altitude between the two spacecraft (800 km for NOAA and 1336 km for Jason-2)?

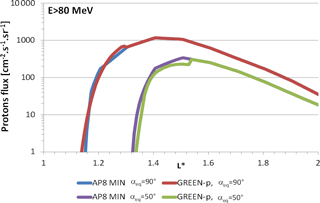
Figure 19 Proton fluxes vs. L^∗ resulting from GREEN-p and AP8 MIN at two magnetic latitudes corresponding to α_eq= 90^∘ and α_eq= 50^∘ for E > 80 MeV protons.

In order to illustrate the reason for this difference between Jason-2 measurements and GREEN and AE9 results, Fig. 18 has been plotted. It is the same figure as Fig. 16 but not during the same period of time: 2009 to 2015 for Fig. 18 as opposed to 1999 to 2010 for Fig. 16. This figure shows that the comparison between in situ measurements and GREEN results depends on the period of time. If the period of time of in situ measurements is long enough (several solar cycles) or is representative of a mean flux, data will easily be compared to GREEN results. On the other hand, if the period of time of in situ measurements is too short compared to a solar cycle or is during a very quiet solar cycle, which is the case for Jason-2 measurements, comparison with GREEN flux will not be so easy. So the difference of flux at L^∗ < 3.5 between GREEN-e and Jason-2 data in Fig. 17 or between GREEN-e and NOAA-POES data in Fig. 18 is clearly due to the period of time, which corresponds to very quiet years, not representative of a mean solar cycle.

Concerning the model GREEN-p, it is much less finalized than the electron version GREEN-e because only the OPAL model, which has a narrow spatial coverage, has been implemented in addition to AP8 and SPM. It is really difficult to measure protons of energy around megaelectron volts in the radiation belts because of the predominant presence of the electrons which very often contaminate the data. Thus, due to a lack of good-quality data in sufficient numbers, it is difficult to develop a model of protons for energies around megaelectron volts. Some efforts will be made in the near future to improve the modeling of megaelectron-volt protons in GREEN-p and compare the results with measurements from GPS or THEMIS for example.

However, we can still present an example of results from GREEN-p and compare them to AP8, even if only OPAL-V2 is integrated in the global model. Figure 19 represents proton fluxes vs. L^∗ resulting from GREEN-p and AP8 MIN at two magnetic latitudes corresponding to α_eq= 90^∘ and α_eq= 50^∘, for E > 80 MeV protons. This figure shows that fluxes from GREEN-p come from OPAL-V2 up to $L^{\ast }=$ 1.3 for α_eq= 90^∘ and up to $L^{\ast }=$ 1.5 for α_eq= 50^∘ and from AP8 beyond. At very low L^∗, when AP8 and OPAL-V2 are available, some small differences appear in the flux. At α_eq= 50^∘ fluxes for GREEN-p are slightly lower than AP8 MIN.

4 Discussion and conclusions

GREEN (Global Radiation Earth ENvironment) is a new model providing fluxes at any location between $L^{\ast }=$ 1 and $L^{\ast }=$ 8 all along the magnetic field lines and for any energy between 1 keV and 10 MeV for electrons and between 1 keV and 800 MeV for protons. This model is composed of global models (AE8 and AP8, and SPM) as well as local models (SLOT model, OZONE and IGE-2006 for electrons, and OPAL and IGP for protons). These local models are used when they are more relevant than AE8 AP8 or SPM. Thus, this version of GREEN is a patchwork of existing models with also some improvements, especially at high energy and low L^∗ values where the AE8 model has been corrected, or in the Slot region with the new version of the SLOT model. Obviously, despite our efforts, some discontinuities exist at the interface of the models but will be removed or at least smoothed in the next versions. The major advantage of GREEN is the dependence of fluxes on the solar cycle. Most of models included in GREEN are solar cycle dependent, which allows it to have a better estimation of fluxes according to the duration of the mission vs. solar cycle. Indeed, fluxes provided by the GREEN model are different for each of the 11 years of the solar cycle. Concerninga GREEN-p, which is less finalized than GREEN-e, the major advantage is in geostationary orbit with the IGP model and at low altitude when OPAL is available, with not only the dependence on the year of the solar cycle but also directly the dependence on the radio flux F10.7 of the Sun and the magnetic field of the given year. In the next versions of GREEN-p, future studies will allow the magnetic field to be predicted for up to several decades and thus will have a better estimation of the proton fluxes at low altitude. Moreover, in the near future, some efforts will be made to try to extend the OPAL model to higher altitude and lower energy by using all the available good-quality data (GPS or THEMIS for example), even if we know it will be a hard task.

Another advantage of GREEN is that it is easy to upgrade. Indeed, a cache file system allows switching between models, in order to obtain the most reliable value at each location in space and each energy point. Thus, the way the model is developed is well suited to adding new local developments or to including international partnership.

Finally a perspective of GREEN, other than the improvement of flux accuracy, would be to develop a special “worst-case” version of GREEN in order to adapt it to space industry user needs in the case of short-term missions, typically a few months, such as the case of electric orbit-raising missions.