Magnetic depression and electron transport in an ion-scale flux rope associated with Kelvin–Helmholtz waves

We report an ion-scale magnetic flux rope (the size of the flux rope is ∼ 8.5 ion inertial lengths) at the trailing edge of Kelvin–Helmholtz (KH) waves observed by the Magnetospheric Multiscale (MMS) mission on 27 September 2016, which is likely generated by multiple X-line reconnection. The currents of this flux rope are highly filamentary: in the central flux rope, the current flows are mainly parallel to the magnetic field, supporting a local magnetic field increase at about 7 nT, while at the edges the current filaments are predominantly along the antiparallel direction, which induce an opposing field that causes a significant magnetic depression along the axis direction (> 20 nT), meaning the overall magnetic field of this flux rope is depressed compared to the ambient magnetic field. Thus, this flux rope, accompanied by the plasma thermal pressure enhancement in the center, is referred to as a crater type. Intense lower hybrid drift waves (LHDWs) are found at the magnetospheric edge of the flux rope, and the wave potential is estimated to be ∼ 17 % of the electron temperature. Though LHDWs may be stabilized by the mechanism of electron resonance broadening, these waves could still effectively enable diffusive electron transports in the cross-field direction, corresponding to a local density dip. This indicates LHDWs could play important roles in the evolution of crater flux ropes.

Keywords. Magnetospheric physics (magnetopause, cusp, and boundary layers; solar wind–magnetosphere interactions)

1 Introduction

Magnetic flux ropes, characterized by a reversal of the magnetic field in the cross section, are 3-D helical magnetic structures. The magnetic flux rope is usually regarded as the physical model of the flux transfer event (FTE) (Russell and Elphic, 1978) on Earth's magnetopause, with spatial sizes extending from several ion inertial lengths (d_i) to a few Earth radii (R_E) (e.g., Hasegawa et al., 2010; Eastwood et al., 2016). Recent in situ observations revealed that flux ropes could be flanked by two converging plasma jets, indicating these flux ropes are still active, and possibly generated by multiple, or even sequential, X-line reconnection (Hasegawa et al., 2010; Øieroset et al., 2011; Pu et al., 2013). Such active flux ropes are relatively less often observed in a statistical study (Zhang et al., 2012); thus, X lines flanking flux ropes might be short-lived once these flux ropes convect away from the generation region.

A typical flux rope, with an enhancement of the magnetic field in the core region, can be modeled either as a force-free structure or a non-force-free structure, where magnetic pressure is balanced by plasma thermal pressures (e.g., Lundquist, 1950; Elphic and Russell, 1983; Zhang et al., 2008; Farrugia et al., 2016; Zhao et al., 2016). There are also some flux ropes with a decrease in magnetic field strength in the center, which are referred to as crater flux ropes (e.g., Farrugia et al., 1988; Sibeck et al., 2008). Zhang et al. (2010) proposed that these crater flux ropes are initial stages of typical flux ropes, and they would evolve into typical flux ropes with a reduction of central plasma pressure resulting from the transport of plasma along their axes. Therefore, they are modeled as a non-force-free structure (Zhang et al., 2010).

The Magnetospheric Multiscale (MMS) mission (Burch et al., 2016) with its unprecedented high-resolution plasma measurements provides a good opportunity to study the structure of ion-scale flux ropes with a duration of a few seconds in the data (e.g., Alm et al., 2018; Eastwood et al., 2016; Teh et al., 2017; Wang et al., 2017), which present observations of current filaments, nonideal ion behaviors, wave activities and even flux rope coalescence. An ion-scale crater-like flux rope has also been resolved by MMS, which is interpreted as a result of the depression of transverse magnetic fields in a flux rope simulation (Teh et al., 2017).

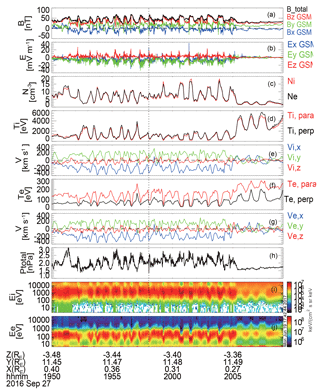
Figure 1 Overview of KH waves observed by MMS on 27 September 2016. From the top, panels show (a) the magnetic field, (b) the electric field, (c) the plasma density, (d, e) the ion temperature and velocity, (f, g) the electron temperature and velocity, (h) the total pressure (sum of the thermal and magnetic pressures) and (i, j) the ion and electron omnidirectional energy flux.

Small-scale flux ropes, identified primarily by magnetic bipolar structures, have been observed at the trailing edges of Kelvin–Helmholtz (KH) waves (e.g., Eriksson et al., 2009; Nakamura et al., 2013), where local conditions could be favorable for magnetic reconnection (Hasegawa et al., 2009). However, due to the limitation of temporal resolutions, such observations had been unable to provide direct and conclusive evidence. The first direct evidence of ongoing magnetic reconnection at the trailing edges of KH waves, where the local magnetic shear is enlarged and the current sheet is compressed to ion scale, is recorded by MMS (Eriksson et al., 2016; Li et al., 2016), and the MMS observations confirm previous studies from both field and particle measurements. But whether such reconnection can result in the generation of flux ropes has not been further examined by MMS. In this study, we report an ion-scale flux rope at the trailing edge of KH waves probably due to multiple X-line reconnection. The reported flux rope, with a size of ∼ 8.5 d_i, presents a depression of the magnetic field and an enhancement of the plasma thermal pressure in the core region, which is taken as a feature of a crater-like flux rope. We also analyze the lower hybrid drift waves (LHDWs) and their possible roles in plasma transport at the magnetospheric side of this flux rope.

2 Observation

The MMS observations were made at the dusk flank of the Earth's magnetopause on 27 September 2016. The four MMS spacecraft were located approximately at (0.3, 11.5, −3.4) R_E in geocentric solar magnetospheric (GSM) coordinates, and the spacecraft were in a tetrahedron formation with a separation of ∼ 10 km. At this scale, data from individual satellites appear almost identical, and we primarily present the data from MMS1. We use plasma data from the fast plasma investigation (FPI) (Pollock et al., 2016), magnetic field data from the fluxgate magnetometer (FGM) and the search coil magnetometer (SCM) (Russell et al., 2014; Le Contel et al., 2014), and electric field data from the electric field double probes (EDP) (Lindqvist et al., 2014; Ergun et al., 2014).

Figure 1 shows an overview of the fast survey between 19:50 and 20:09 UT, when the solar wind is relatively steady and presents an extended northward interplanetary magnetic field (IMF) from OMNI data: $n_{\mathrm{sw}}=\mathrm{8.5}\pm \mathrm{0.5}$ cm⁻³, V_sw = $[-\mathrm{600.0}\pm \mathrm{5.8},-\mathrm{5.2}\pm \mathrm{11.6},-\mathrm{42.5}\pm \mathrm{9.3}]$ km s⁻¹, $P_{\mathrm{dyn}}=\mathrm{6.2}\pm \mathrm{0.4}$ nPa and $B_{\mathrm{IMF}}=[-\mathrm{4.6}\pm \mathrm{1.4},\mathrm{2.6}\pm \mathrm{3.7},\mathrm{7.9}\pm \mathrm{1.6}]$ nT in GSM. During this time interval, MMS was initially located in the magnetospheric boundary layer, characterized by slow plasma velocities (Fig. 1e and g), and a mixture of magnetospheric ions (> 10 keV) and magnetosheath ions (∼ 1 keV) from ion energy–time spectrograms (Fig. 1i). Then it was followed by significant variations of field and plasma parameters during the boundary layer crossings and, occasionally, MMS recorded relatively cold and dense plasma with a large tailward speed, indicating it had entered into the sheath region. After 20:05 MMS returned into the magnetosphere again.

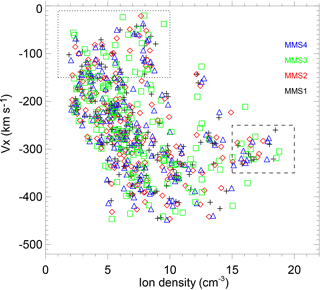
Figure 2 A scatter plot of V_X versus ion density from all four MMS spacecraft from 19:52:00 to 20:05:00 UT. The data points inside the dotted and dashed box present the magnetosphere and magnetosheath ions, respectively.

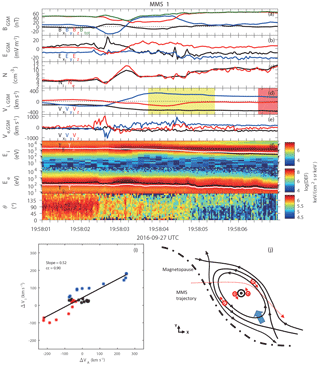
Figure 3 Summary plot of the flux rope at the trailing edge of the KH wave. From the top, the panels show (a) the magnetic field, (b) the electric field, (c) the plasma density, (d, e) the ion and electron velocity, (f, g) the ion and electron omnidirectional energy flux, (h) the electron pitch angle spectrum for the energy larger than 3 keV, (i) scatter plots of the Walén test and (j) the sketch of the observed flux rope.

Table 1 The magnetic field and plasma parameters at the magnetosphere and magnetosheath side during the wave interval, which are averaged from the dashed and dotted boxes in Fig. 2.

These quasi-periodic fluctuations near the magnetic equator can be excited by internal or external mechanisms, one of which is the KH instability. Figure 1h shows the total pressure perturbations (sum of the thermal and magnetic pressures) and the strong total pressure minimum, created inside the waves, is evident for KH instability (Moore et al., 2016). Another indicator for the roll-up of the KH vortex is the low-density and faster-than-sheath signature (Hasegawa et al., 2006). Figure 2 shows a scatter plot of V_X versus ion density from all four MMS spacecraft between 19:52 and 20:05 UT, and the x direction here is redefined to be tangential to the average magnetopause, following Hasegawa et al. (2006). The data points inside the dotted box are magnetospheric ions, characterized by low densities and slow speeds, and the magnetosheath ions are located in the dashed box, identified by the highest ion number densities. There are some data points in the lower-left region presenting a low-density and faster-than-sheath feature, which is consistent with rolled-up KH vortex. Meanwhile, the magnetic field and plasma parameters at both sides, averaged from data points in the boxes of Fig. 2, are shown in Table 1. The boundary conditions are KH unstable based on the linear theory (Chandrasekhar, 1961), and the dominant period of these KH waves is ∼ 44 s (ΔT_KH) from ion density and magnetic field perturbations. At the trailing edges of these surface waves, the magnetic shear could suddenly increase, providing favorable conditions for magnetic reconnection, which has been reported in another KH event on 8 September 2015 (Eriksson et al., 2016; Li et al., 2016). In this event, signatures of reconnection at waves' trailing edges are also revealed, and furthermore several bipolar structures are detected by MMS. We will focus on one of them, marked by the vertical dotted line in Figure 1, and investigate its properties in details.

Figure 3 shows the marked zoom-in plot of the KH wave trailing edge crossing from the magnetospheric side to the magnetosheath during the interval 19:58:01–19:58:07 UT, indicated by the gradual disappearance of the magnetospheric ions (Fig. 3f). The y component of the magnetic field presented a bipolar signature with a significant depression of the magnetic field in the z direction, suggesting a flux rope (Fig. 3a), and its duration is about 2.7 s (ΔT_FR). The axis direction of this flux rope is consistent with previous full kinetic simulations, which showed flux ropes were formed along the periphery of the vortex (Nakamura et al., 2013). The field magnitude dip at the center of this flux rope suggests it is a crater flux rope, which is accompanied by a plasma density peak (Fig. 3c) at the B_Y reversal region around 19:58:03.2 s.

At the magnetospheric side of the flux rope (prior to 19:58:02.5 s), a dawnward ion flow was observed (Fig. 3d). As suggested by Korotova et al. (2011), this flow could be attributed to the passage of the flux rope, which pushes the surrounding plasma to the side, generating flows opposite to its motion on the flank. Inside the flux rope, another duskward ion flow faster than the sheath plasma flow was detected, and then we test the Walén relation to check if it is a reconnection jet (Sonnerup et al., 1981; Phan et al., 2013). Taking the magnetosheath plasma parameters as reference (the shaded red region), we compare two vectors $\mathrm{\Delta }{\mathit{V}}_{\mathrm{i}}={\mathit{V}}_{\mathrm{i}}-{\mathit{V}}_{i,\mathrm{MSH}}$ and $\mathrm{\Delta }{\mathit{V}}_A={\mathit{V}}_A-{\mathit{V}}_{A,\mathrm{MSH}}$ in the shaded yellow region (19:58:03.7–19:58:05.4 UT) and show the scatter plot in Fig. 3i: Though the ion velocity changes across the magnetosheath side of the flux rope, the observed velocity change (ΔV_i) is about 52 % of the predicted flow change (ΔV_A). Therefore, additional evidence from the ion distributions should be used to classify if it is a reconnection jet (Phan et al., 2013). Figure 4 shows the ion velocity distribution functions at 19:58:04.042 and 19:58:06.892 UT in the plane defined by the local B and E×B vectors. The flow in the sheath region is almost along the E×B direction (Fig. 4b) but, crossing the current sheet, the ions have a field-aligned component, suggesting they are transmitted ion flows (Fig. 4a). The bulk velocity is close (∼ 77 %) to the flow velocity predicted by the Walén relation (marked by the black dot). This indicates that this jet was a consequence of magnetic reconnection and the X line is located dawnward of the flux rope. The possible reason why the slope of the Walén test is relatively poor could be attributed to the structure of the flux rope, which modified the flow speeds when ions propagated away from the X line.

Figure 3h shows the pitch angle spectrum of energetic electrons with energies > 3 keV. Inside the flux rope, almost-isotropic energetic electrons were clearly identified, while the energy flux intensity is weaker than that in the magnetosphere, consisting of the re-closure of the field lines in the flux rope. This is different with large-scale flux rope situations, in which both trapped and untrapped electrons can be observed, suggesting different topologies of magnetic field lines (Pu et al., 2013; Roux et al., 2015). At the sheath side (from 19:58:05.0 to 19:58:06.2 s), energetic electrons only in the antiparallel directions were detected, suggesting the existence of another X line on the north-dusk side to generate these open field lines, and also this X line was formed earlier than the one at the dawn side. In addition, the bulk electron velocity could reach up to 1200 km s⁻¹ at the magnetospheric side where a local density dip was revealed (Fig. 3e).

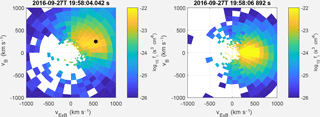
Figure 4 The two-dimensional cuts of ion velocity distributions in the plane formed by the local B and E×B vectors. The black dot denotes the predicted velocity by the Walén relation.

A sketch of the observed flux rope in the equator plane is inferred and summarized in Fig. 3j. At the trailing edge of KH waves, a flux rope is detected at the distorted magnetopause by MMS, whose relative trajectory is shown by red dotted lines. The projection of the magnetic field lines is shown by solid black lines, while the red arrows present the direction of current flows. Circles with a “dot” and “cross” denote the magnetic field (black) and the current (red) is directing out of or into the plane of paper. The ion jets are marked by a blue arrow. The current flows will be explained later.

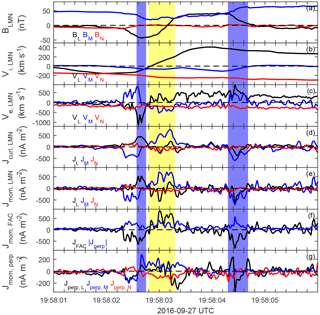
Figure 5 The current density inside the flux rope. (a) The magnetic field, (b, c) the ion and electron velocity, (d) current density computed from the curlometer method, (e) current density computed from plasma moments, (f) the parallel and perpendicular currents, and (g) the perpendicular current in LMN. The vertical yellow and blue bars indicate the current filaments in the core region and at edges of the flux rope.

To better illustrate the structure of the flux rope in detail, we transform the observations into a local boundary normal (LMN) coordinate by performing a minimum variance analysis on the magnetic field (MVAB) from the interval 19:58:02.0 to 19:58:05.5 UT, which yields $\mathbf{L}=[-\mathrm{0.22},\mathrm{0.94},-\mathrm{0.25}]$, $\mathbf{M}=[\mathrm{0.06},\mathrm{0.27},\mathrm{0.96}]$ and $\mathbf{N}=[\mathrm{0.97},\mathrm{0.19},-\mathrm{0.11}]$ in GSM. The four-spacecraft timing analysis of the burst mode electric field data leads to the direction normal to the boundary ${\mathbf{N}}^{\prime }=[\mathrm{0.97},\mathrm{0.22},\mathrm{0.06}]$ in GSM, with a velocity $V_{\mathrm{N}}=-\mathrm{225}$ km s⁻¹. Since the difference of the normal direction between MVAB and the timing method is ∼ 10^∘, the size of the flux rope in the normal direction is estimated to be 610 km, or 8.5 d_i, considering that the nearby magnetosheath density is ∼ 10.2 cm⁻³. The currents calculated from the curlometer method and direct particle measurements are presented in Fig. 5d and e. Good agreement is found between two measures, both showing considerable structure and variability in the current density of the flux rope with a maximum value of ∼ 900 nA m⁻², while the current from plasma measurements is more structured, as shown by Phan et al. (2016). Therefore, this current is transformed to the directions parallel and perpendicular to the magnetic field (Fig. 5f). We find these currents are highly filamentary: in the core region of the flux rope (shaded by the yellow color), the current is parallel to the magnetic field, and at the two edges (shaded by the blue color), it is predominately antiparallel to the magnetic field. The azimuthal component (j_L) of the central parallel current changes from negative to positive (19:58:02.90–19:58:03:10 UT). By applying a simple thin planar current approximation, the local magnetic field change can be estimated by ΔB_M=μ₀I_L, where I_L is the integrated j_L inside the current sheet. From either the positive I_L or negative I_L component, the central current pair could raise the magnetic field in the M direction from about 7.2 to 11.2 nT, which is in good agreement with a local B_M peak in Fig. 5a, with a ∼ 7 nT increase. This provides further evidence that the observed structure is a flux rope. The other j_L current pair with an opposite polarity at edges is also revealed, which is co-located with the depression of the magnetic field in the M direction (19:58:02.57–19:58:02.75 UT and 19:58:04.30–19:58:04.65 UT). The integrated filamentary current density (I_L) is also compared with the decrease in the magnetic B_M component at the magnetospheric edge (17.9 mA m⁻¹ and 24.1 nT) and the sheath edge (16.3 mA m⁻¹ and 26.6 nT), and they are roughly consistent with each other. Thus, the overall result is that the observed magnetic field is depressed inside the flux rope compared to the ambient magnetic field. It is worth noting that most of the current component (j_L) at the edges should be part of the field-aligned current, for its maximum value (> 500 nA m⁻²) is larger than the perpendicular current (∼ 250 nA m⁻²) shown in Fig. 5g. This is different from small-scale magnetic holes, which are supported by electron currents perpendicular to the magnetic field (Gershman et al., 2016; Goodrich et al., 2016).

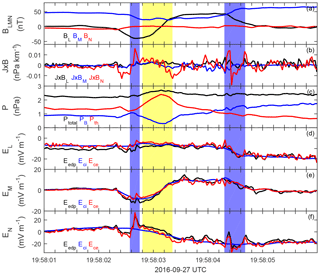
Figure 6 The measured electric field and plasma convective electric field. (a) The magnetic field; (b) J×B force; (c) the plasma thermal, magnetic and total pressures; (d, f) the measured electric field (black), the ion convective electric field (blue) and the electron convective electric field (red) in the L, M and N direction, respectively. The color shaded region is the same as in Fig. 5.

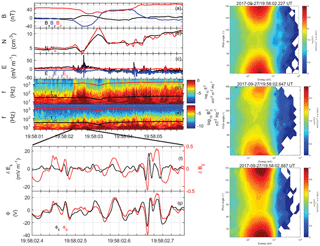
Figure 7 Wave activities in the observed flux rope. (a) The magnetic field, (b) the plasma density, (c) the electric field in burst mode, (d) the electric field spectral power density and (e) the magnetic field spectral power density. The black and red lines present the local lower hybrid frequency and electron cyclotron frequency. (f) Band-pass filtered electric and magnetic field at frequencies 10 Hz < f < 300 Hz from 19:58:02.40–19:58:02.75 UT. (g) The Φ_E (black) and Φ_B (red) for the lower hybrid drift waves. The right panels show electron pitch angle distributions of differential energy flux at 19:58:02.227, 19:58:02.647 and 19:58:02.887 UT.

Though the perpendicular current is relatively small in magnitude, the corresponding J×B force is not negligible (Fig. 6b). The normal component of this force is much larger, and its magnitude varies from −0.015 to 0.015 nPa km⁻¹. To check if it is a force-balanced structure, we plot the pressure profile in Fig. 6c. Though the magnetic pressure and the plasma thermal pressure (ions and electrons) vary obviously during the flux rope crossings, the total pressure stays almost unchanged. This suggests this flux rope is not magnetically force-free but still in force balance with the magnetic field and plasma pressures (Zhao et al., 2016). Since the magnetic field is always depressed in such crater flux ropes, a nonzero pressure gradient force is required to balance the J×B force to maintain the force balance, meaning the crater flux rope should intrinsically be a non-force-free structure.

To test if particles are frozen-in in this flux rope, we compare the electric field measured from EDP (E_edp) with the fluid convective electric field (${\mathit{E}}_{\mathrm{ci},\mathrm{ce}}=-{\mathit{V}}_{i,e}\times \mathit{B}$). Since ${\mathit{E}}_{\mathrm{ce}}={\mathit{E}}_{\mathrm{ci}}+\mathit{J}\times \mathit{B}/n_{\mathrm{e}}$ (Dai et al., 2017) and the $\mathit{J}\times \mathit{B}/n_{\mathrm{e}}$ term is not negligible as shown in Fig. 6b, it is expected that not all fluid convective electric fields are consistent with the measured electric field. This comparison in LMN among E_edp (in black), E_ci (in blue) and E_ce (in red) is presented in Fig. 6d–f. Overall, good agreement of these three lines is found during the selected time interval. The agreement between E_edp and E_ce is extremely good when disregarding some small systematic constant offsets at a few mV m⁻¹, indicating that the electrons are largely frozen-in throughout the encounter with the flux rope. In contrast to the electrons, there are intervals where there is significant deviation in the ions. For example, at the magnetospheric edge, the difference of E_ci and other electric fields exceeds 20 mV m⁻¹, meaning ions cannot move as fast as electrons, which remain frozen-in as pointed out. These deviations are consistent with the changing of J×B and can be found inside the flux rope and at the edges, while they are more obvious at the magnetospheric side due to smaller densities. This indicates the decoupled motions of ions and electrons are not rare in a crater flux rope.

Various wave activities, for instance ion-scale magnetosonic waves and ion acoustic-like waves, have been revealed during KH wave periods, which play a role in plasma transport and heating (Moore et al., 2016; Wilder et al., 2016). In the presence of the pressure (density) gradient in the non-force-free flux rope reported in this study, lower hybrid drift waves can be excited, as shown in Fig. 7. Figure 7c presents the electric field fluctuation in burst mode, whose maximum amplitude can reach ∼ 80 mV m⁻¹, corresponding to a broadband spectrum covering the lower hybrid frequency (Fig. 7d). Magnetic perturbations parallel to the background magnetic field in the lower hybrid frequency range are also clear and presented in Fig. 7e. In this study, we mainly focus on LHDWs on the magnetospheric edge from 19:58:02.40 to 19:58:02.75 UT. Figure 7f presents the fluctuations of the electric field in the wave propagation direction (δE_k) and parallel magnetic field ($\mathit{\delta }{B}_{\left|\right|}$) with a band-pass filtering for frequencies 10 Hz < f < 300 Hz. Then the wave potential is estimated by ${\mathrm{\Phi }}_B=(B_{\mathrm{0}}/n_{\mathrm{e}}e{\mathit{\mu }}_{\mathrm{0}})\mathit{\delta }{B}_{\left|\right|}$ (Norgren et al., 2012; Divin et al., 2015), which peaks at ∼ 20 eV as shown in Fig. 7g. The phase velocity v of the lower hybrid drift waves is found by fitting ${\mathrm{\Phi }}_E=\int \mathit{E}\mathrm{d}t\cdot \mathit{v}$ to Φ_B. The best fitted Φ_E agrees well with Φ_B, with a correlation coefficient 0.83, and the phase speeds v is estimated at 498 × [−0.51, 0.40, −0.75] km s⁻¹ in GSM. The good agreement between Φ_E and Φ_B suggests the constant phase speed is still acceptable, although the background magnetic field changes significantly. The wave length is then about 16.6 km, or equivalently kρ_e≥0.2, where ρ_e is the electron thermal gyroradius. This suggests LHDWs may have a larger wave length in a finite β plasma (Daughton, 2003).

It is worth noting that the ratio of LHDW potential to the electron temperature (eΦ∕k_BT_e) is ∼ 17 %, suggesting that the electrons could be effectively scattered by the wave electric field. We plot the electron pitch angle distributions of differential energy flux at 19:58:02.227, 19:58.02.647 and 19:58.02.887 UT. In the second panel when LHDWs are active, we find a significant decrease in electron energy flux from a few tens of eV to about 200 eV, especially at 0 and 180^∘ pitch angle, which is associated with a local plasma density dip. This result suggests LHDWs could play important roles in plasma transport by this simple wave scattering picture.

The cross-field diffusion coefficient of LHDWs (D_⟂) can be estimated from the quasi-linear theory (Treumann et al., 1991), which is given by

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{D}_{⟂}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\mathit{\rho }}_{\mathrm{ce}}^{\mathrm{2}}{\mathit{\nu }}_{\mathrm{an}}\left(\mathrm{1}+{\displaystyle \frac{T_{\mathrm{i}}}{T_{\mathrm{e}}}}\right)\approx {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\mathit{\rho }}_{\mathrm{ce}}^{\mathrm{2}}{\left({\displaystyle \frac{\mathit{\pi }}{\mathrm{8}}}\right)}^{\frac{\mathrm{1}}{\mathrm{2}}}\\ \text{(1)}& {\displaystyle }& {\displaystyle }{\mathit{\omega }}_{\mathrm{LH}}{\displaystyle \frac{m_{\mathrm{i}}}{m_{\mathrm{e}}}}\left(\mathrm{1}+{\displaystyle \frac{{\mathit{\omega }}_{\mathrm{pe}}^{\mathrm{2}}}{{\mathrm{\Omega }}_{\mathrm{e}}^{\mathrm{2}}}}\right){\displaystyle \frac{\mathcal{E}}{n{T}_{\mathrm{i}}}}\left(\mathrm{1}+{\displaystyle \frac{T_{\mathrm{i}}}{T_{\mathrm{e}}}}\right),\end{array}$$

where ${\mathit{\nu }}_{\mathrm{an}},{\mathit{\rho }}_{\mathrm{ce}},{\mathit{\omega }}_{\mathrm{LH}},{\mathit{\omega }}_{\mathrm{pe}},{\mathrm{\Omega }}_{\mathrm{e}}$ and $\mathcal{E}={\mathit{\epsilon }}_{\mathrm{0}}\mathit{\delta }{E}^{\mathrm{2}}/\mathrm{2}$ are the anomalous collision frequency, electron gyroradius, lower hybrid frequency, electron plasma frequency, electron gyrofrequency and the wave electric field energy density, respectively. Its value is about 1 ×10⁸ m² s⁻¹. This implies a diffusion time of about 2.6 s over a diffusion region with its width at one wave length, which is sufficient for the observed local plasma transport. It is worth noting that the transport due to LHDWs may be only important at edges of the observed flux rope, as the estimated diffusion coefficient is about 1 order of magnitude smaller for the diffusive buildup of the magnetopause boundary layer and also smaller than that in the magnetopause reconnection region (Graham et al., 2017).

The electron transport efficiency of LHDWs is determined by its saturation level. There are several candidate saturation mechanisms, which have been reviewed by Carter et al. (2002). Considering T_e<T_i and $V_{\mathrm{i}}<v_{\mathrm{th},i}$ (V_i, v_th,i are the ion bulk and thermal velocity) in a finite β plasma, the electron resonance broadening model is more suitable here (Huba et al., 1978; Gary and Sanderson, 1979), which predicts

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{\mathcal{E}}{n{T}_{\mathrm{i}}}}\approx {\displaystyle \frac{\mathrm{2}}{\mathrm{5}}}{\displaystyle \frac{m_{\mathrm{e}}}{m_{\mathrm{i}}}}{\displaystyle \frac{{\mathrm{\Omega }}_{\mathrm{e}}^{\mathrm{2}}}{{\mathit{\omega }}_{\mathrm{pe}}^{\mathrm{2}}}}{\left({\displaystyle \frac{T_{\mathrm{i}}}{T_{\mathrm{e}}}}\right)}^{\mathrm{1}/\mathrm{4}}{\left({\displaystyle \frac{V_{\mathrm{i}}}{v_{\mathrm{th},i}}}\right)}^{\mathrm{2}}.\end{array}$$

We estimate the normalized fluctuating electric field energy density (ℰ∕nT_i) from observations to be ∼ 4 × 10⁻⁷, which is comparable to the predicted value (∼ 2 × 10⁻⁷). Thus, the LHDWs are damped as a larger number of electrons are permitted to involve the electron-wave resonance. This process also results into significant energy dissipations, which would be another aspect for the anomalous transport properties of LHDWs.

Another possible explanation for the observed electron distribution is the parallel acceleration, meaning the electrons can resonate with LHDWs. This requires the phase speed of LHDWs to be comparable to the local electron thermal speed (v_th,e). The resonant condition is written as $v_{\left|\right|}={\mathit{\omega }}_{\mathrm{LH}}/k_{\left|\right|}=m_{\mathrm{i}}/m_{\mathrm{e}}\times {\mathit{\omega }}_{\mathrm{LH}}/k_{⟂}$ (Graham et al., 2014). However, the estimated $v_{\left|\right|}$ is far larger than v_th,e. This suggests the parallel acceleration is not the dominant process for the observed electron pitch angle distributions compared to wave scattering.

3 Discussion and conclusions

In this study, an ion-scale magnetic flux rope at the trailing edge of KH waves observed by MMS has been investigated, which is probably generated by multiple X-line reconnection. Highly filamentary currents in this flux rope and their induced magnetic field are discussed: in the core region, a local increase in the magnetic field is supported by the parallel currents, and the current filaments at the edges induce a larger opposing field that causes overall $\left|B\right|$ depressions interior to the flux rope. As the magnetic field is depressed inside this flux rope, plasma thermal pressures increase towards the center to maintain the force balance, corresponding to a non-force-free structure. Decoupling of electron and ion motions is also observed inside the current sheet. Intense LHDWs are also found at the magnetospheric edge of the flux rope, whose wave potential reaches to ∼ 17 % of the electron temperature. Therefore, these waves could effectively cause diffusive electron transport, with an estimated diffusion coefficient at ∼ 1. × 10⁸ m² s⁻¹, consisting of the local plasma density dip. This indicates LHDWs can play a role in the plasma transport in a crater flux rope.

Though we have presented the relation between the magnetic variations and current filaments, and the role of LHDWs in transporting electrons inside a crater-type flux rope, the later evolution of the flux rope is still not well understood. In addition, the reported flux rope is located at the trailing edges of the KH vortex, which will be gradually rolled-up with time. Thus, the following the evolution of this flux rope with the KH vortex still requires further investigations.