the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Three-dimensional density and compressible magnetic structure in solar wind turbulence
Yasuhito Narita
C.-Philippe Escoubet
The three-dimensional structure of both compressible and incompressible components of turbulence is investigated at proton characteristic scales in the solar wind. Measurements of the three-dimensional structure are typically difficult, since the majority of measurements are performed by a single spacecraft. However, the Cluster mission consisting of four spacecraft in a tetrahedral formation allows for a fully three-dimensional investigation of turbulence. Incompressible turbulence is investigated by using the three vector components of the magnetic field. Meanwhile compressible turbulence is investigated by considering the magnitude of the magnetic field as a proxy for the compressible fluctuations and electron density data deduced from spacecraft potential. Application of the multi-point signal resonator technique to intervals of fast and slow wind shows that both compressible and incompressible turbulence are anisotropic with respect to the mean magnetic field direction and are sensitive to the value of the plasma beta (β; ratio of thermal to magnetic pressure) and the wind type. Moreover, the incompressible fluctuations of the fast and slow solar wind are revealed to be different with enhancements along the background magnetic field direction present in the fast wind intervals. The differences in the fast and slow wind and the implications for the presence of different wave modes in the plasma are discussed.
Keywords. Interplanetary physics (MHD waves and turbulence)
- Article
(549 KB) - Full-text XML
- BibTeX
- EndNote
The solar wind is a collisionless, magnetised plasma originating from the Sun and is often observed to be in a state of fully developed turbulence (Tu and Marsch, 1995; Bruno and Carbone, 2013; Alexandrova et al., 2013). In contrast to a neutral fluid that can be regarded as isotropic where vorticities are randomly oriented (Frisch, 1995), the presence of a large-scale magnetic field causes anisotropic fluctuations in the plasma (Shebalin et al., 1983). Several observations have demonstrated the anisotropies of variance (Belcher, 1971), wave vectors (Chen et al., 2010a; Roberts et al., 2013, 2017b), spectral index (Horbury et al., 2008; Wicks et al., 2010; Roberts et al., 2017c) and the fluctuation power (Bieber et al., 1996; Chen et al., 2010a), see also reviews by Horbury et al. (2012) and Oughton et al. (2015).
To study the anisotropy, correlation lengths in the directions parallel and perpendicular to the magnetic field B0 have often been calculated. These revealed correlation lengths longer in the parallel direction than in the perpendicular direction implying a wave vector anisotropy (Matthaeus et al., 1990). Furthermore, when solar wind intervals are classed according to their bulk speed Vsw into fast wind (Vsw>500 km s−1) and slow wind (Vsw<400 km s−1), the fast wind was found to contain more parallel fluctuations than the slow wind (Dasso et al., 2005). This was interpreted to be due to the slow wind being older, having more time to develop before being observed at the spacecraft which are predominantly located at 1 AU in the ecliptic. Moreover, study of other parameters such as plasma velocity, density and temperature show that the geometries of fluctuations in these parameters also exhibit similarities to the magnetic field (Smith et al., 2013). Such studies at kinetic scales are more problematic since plasma data with sufficiently high time resolution are often unavailable. As such, the majority of progress in the study of kinetic turbulence has come from magnetic field measurements, which at proton scales is dominated by incompressible fluctuations (e.g. Kiyani et al., 2009).
The solar wind plasma is also weakly compressible (e.g. Hnat et al., 2005; Chen et al., 2012a; Kiyani et al., 2013; Roberts et al., 2017b, 2018). However, detailed investigations at kinetic scales are typically hampered by the low time resolution of plasma instruments, and thus fluctuations in the magnitude of the magnetic field have often been used as a proxy for the compressible fluctuations provided that fluctuation amplitudes are small (). One novel method to obtain density fluctuations is to use the calibrated spacecraft potential (Pedersen et al., 2001; Kellogg and Horbury, 2005). This allows the electron density to be determined with a high enough time resolution for proton kinetic scales to be investigated.
Several studies of the density power spectrum have highlighted the importance of plasma β (ratio of thermal to magnetic pressure) for the shape of the power spectrum of density fluctuations. Smaller values of β are associated with flattening of the power spectrum near ion scales (Chen et al., 2012b). This has been modelled as being due to two competing processes: a cascade which is passive to the Alfvénic turbulence at large scales, i.e. the compressible component cannot interact with the incompressible component. This is followed in the kinetic range by an active cascade where both components can interact (Chandran et al., 2009; Schekochihin et al., 2009). Further evidence of this hypothesis was found in Roberts et al. (2017b). The dispersion relation diagrams of the compressible components of the turbulence were found to be significantly broadened compared to the vector magnetic field, which is a marker of increased wave–wave interactions (Narita and Motschmann, 2017). The value of plasma β has also been shown in multi-point measurements and direct numerical simulations to affect the level of anisotropy in the plasma (Comişel et al., 2014).
Several different approaches can be taken to investigate the spatial structure of the plasma. Often, much of the information gained about solar wind turbulence comes from single spacecraft measurements. Should the fluctuations evolve slowly compared to the time it takes them to advect over the spacecraft, spatial information can be gained along the sampling direction, by assuming Taylor's hypothesis (Taylor, 1938). This hypothesis assumes that the intrinsic fluctuation timescale is slow compared to the time it takes the fluctuation to advect over the measurement point such that a one-dimensional spatial cut through the plasma is obtained by the spacecraft. The hypothesis has been shown to be a good approximation at fluid scales; however, at proton scales the quality of the estimation often decreases (Narita, 2017; Perri et al., 2017a, b), especially when flow speed is low or fluctuations have large intrinsic speeds (Howes et al., 2014; Klein et al., 2014a). By assuming Taylor's hypothesis, spatial information can be gleaned by investigating different intervals when the orientations of the magnetic field with respect to the sampling direction are different provided that Taylor's hypothesis is satisfied. Several studies have showed that the spectral index of fluctuations when a radial field is present (Vsw∥B0) is steeper than the typical scaling when the field makes an angle θBV>30∘ with the flow direction (Horbury et al., 2008; Podesta, 2009; Wicks et al., 2010; Forman et al., 2011) in agreement with the prediction for a “critically balanced” turbulent cascade (Goldreich and Sridhar, 1995) or alternatively a non-elliptic geometry of the fluctuations (Narita, 2015). However, single-point measurements do not make a simultaneous measurement of the spectral index in k∥ and k⟂, rather different times (or orientations of the magnetic field) are investigated.
In the study of Chen et al. (2012c) Ulysses magnetic field data from fast streams of solar wind were investigated up to the inertial range where the sampling rate of the magnetic field measurement is 1 Hz. The structure functions in directions parallel and perpendicular to the local magnetic field directions were used to derive the three-dimensional structure. The trace magnetic fluctuations (used as a proxy for the incompressible fluctuations) were found to evolve towards being 3-D anisotropic at smaller scales, while fluctuations in the magnetic field magnitude were found to be more anisotropic than the incompressible ones.
Given modern computer processing power, an alternative to using Taylor's hypothesis is to investigate the spatial structure of plasma through direct numerical simulations. Several different schemes have been employed including magnetohydrodynamic (MHD) at large scales (e.g. Verdini and Grappin, 2015; Mallet et al., 2016; Pezzi et al., 2017a, b), Hall MHD for scales at the transition between proton and electron scales (Pucci et al., 2016; Pezzi et al., 2017a, b), hybrid Vlasov (e.g. Perrone et al., 2013; Franci et al., 2015a, b; Valentini et al., 2016; Cerri et al., 2016, 2017; Pezzi et al., 2017a, b) or hybrid particle in cell (Comişel et al., 2014) for proton kinetic scales, finally full particle in cell descriptions can be used to investigate sub-ion scales (Camporeale and Burgess, 2011; Haynes et al., 2014; see also the review by Servidio et al., 2014). Recently the same structure function analysis in Chen et al. (2012c) were applied to simulated magnetohydrodynamic data by Verdini and Grappin (2015) and Mallet et al. (2016) yielding a similar structure of the turbulence.
A final possibility to overcome the difficulties and ambiguities associated with studying turbulence with a single spacecraft are to use multi-spacecraft missions such as the Cluster mission (Escoubet et al., 1997, 2001), as well as specialised analysis techniques which have been developed. Two different techniques have often been used to investigate the anisotropy of solar wind turbulence, the first being based on differences in the fluctuations between pairs of spacecraft (e.g. cross correlation or structure functions) and the second being the use of a multi-spacecraft k-filtering/wave telescope (Pincon and Lefeuvre, 1991; Motschmann et al., 1996) and other derived techniques. While the former requires an assumption of a modified Taylor's hypothesis (e.g. Horbury, 2000; Osman and Horbury, 2009), and can use a “local” magnetic field (e.g. Chen et al., 2010a), the latter requires weak stationarity and that the signal can be described as a superposition of plane waves with random phases with a small component of incoherent noise (e.g. Tjulin et al., 2005; Roberts et al., 2014), and use a global magnetic field. Although due to the short data intervals investigated (∼ tens of minutes for proton scales), the difference between a local and global field is small, and intervals can be selected where the magnetic field direction does not vary much.
The multi-point signal resonator technique (MSR; Narita et al., 2011c) is a derivative of wave telescope/k-filtering methods which estimate the four-dimensional power distribution in wave-number space P(ωsc,k) with an improved signal-to-noise ratio. This improvement is essential for investigating the morphology at small scales. Several studies on the solar wind have been performed by looking at the peaks in the four-dimensional spectra revealing a strong wave-vector anisotropy at MHD and proton kinetic scales in the incompressible magnetic field (Sahraoui et al., 2010b; Narita et al., 2011c; Roberts et al., 2013; Roberts and Li, 2015; Perschke et al., 2016; Narita and Motschmann, 2017), as well as in the compressible fluctuations (Roberts et al., 2017b). The three-dimensional morphology of the total magnetic fluctuations in wave-number space, , has also been investigated by Narita et al. (2010, 2011a, b, 2014). These studies revealed that the vector magnetic fluctuations (which are dominated by incompressible fluctuations) display anisotropy in the direction perpendicular to the magnetic field and also in the direction perpendicular to the bulk flow velocity.
An interesting result from the aforementioned works of Narita et al. (2010, 2011a, b, 2014) as well as in Saur and Bieber (1999), Chen et al. (2012c) and Roberts et al. (2017a) is that axial asymmetry was revealed with respect to the background magnetic field B0. Extensions to the power in wave space were also seen in the direction of the convective electric field . The role of solar wind expansion and the influence of the convective electric field were hypothesised to play a role in forming the observed axial asymmetry (Narita et al., 2014). Alternatively Turner et al. (2011) demonstrated that a sampling effect could account for the non-axisymmetry seen in methods that invoked Taylor's hypothesis, and argued that it would also apply to wave telescope/k-filtering methods since frequency filtering is performed in the spacecraft frame.
In this paper we present a new study of the three-dimensional structure of the turbulence in the solar wind, and this will be investigated using the MSR technique (Narita et al., 2011a, c, 2014). However, in addition to using the vector magnetic field as an input as in these previous studies, we will also use the fluctuations in the magnitude of the magnetic field B∥ as well as fluctuations in electron number density ne to investigate the three-dimensional structure of the compressive fluctuations at the ion inertial and ion kinetic ranges. The ability to estimate the power in three-dimensional space, as well as collapsing the power into one-dimensional spectra as a function of wave number, allow us to make a detailed study of both the power anisotropy and the anisotropy of the spectral index.
Multi-point data from the solar wind are provided from the Cluster mission (Escoubet et al., 1997, 2001) when the angles between the magnetic field direction are greater than 60∘ indicating that the spacecraft were magnetically unconnected to the foreshock. Magnetic field data are used from the fluxgate magnetometer (FGM) instrument (Balogh et al., 2001), which has a sampling frequency of 22 Hz. High time resolution density measurements are obtained by calibrating the spacecraft potential (e.g. Pedersen et al., 2001; Kellogg and Horbury, 2005; Pedersen et al., 2008) obtained from the electric field and waves instrument (Gustafsson et al., 1997) to electron density measurement performed by the WHISPER instrument (Decreau et al., 1997). The spacecraft potential data are subject to a strong spin effect at 0.25 Hz, as well as charging effects at 0.5 Hz and other higher harmonics. We use the method described in the appendix of Roberts et al. (2017b) to remove these various effects. The spurious fluctuations are removed by constructing a statistical model of the spacecraft charging as a function of the spacecraft spin phase angle. This can then be subtracted from the spacecraft potential for a given spin phase, and calibrated to give a density measurement with a sampling frequency of 5Hz.
In total four intervals are analysed, where we have magnetic field and spacecraft potential data available for all intervals. These intervals were chosen as there is no connection to the foreshock and the Cluster spacecraft configuration has inter-spacecraft distances of ∼200 km in a nearly regular tetrahedral configuration with low values of the planarity and elongation parameters (Robert et al., 1998). This allows the investigation of the proton kinetic scales without bias due to inhomogeneous spatial sampling. Parameters of the four intervals are given in Table 1. These include intervals of fast and slow wind with various different values of plasma β.
As the MSR technique is a global technique (based on Fourier analysis), we use the mean magnetic field in the interval to define the parallel direction, whereas the perpendicular direction is defined as the mean over all angles which are perpendicular to the mean direction. It is important to note that anisotropy has been measured to be related to the local magnetic field direction, therefore intervals are selected so that there are no large changes in the magnetic field direction. The times are selected to be sufficiently short so that the local magnetic field at proton scales and the global magnetic field are approximately similar while having enough data points for sufficient averaging required for the MSR technique. Should a much longer time interval be used, then the global and local magnetic field directions might differ significantly and results may not be representative.
To estimate P(k) we use the MSR technique (Narita et al., 2011c), while the same global peak is recovered by the MSR technique and wave telescope/k-filtering methods (e.g. Narita et al., 2011c). The MSR technique improves on wave telescope/k-filtering by making use of the multiple signal classification algorithm (Schmidt, 1986) to improve the signal-to-noise ratio, with an extension to the cases in which the number of sources is unknown (Choi et al., 1993). The improvement in the solution that the MSR technique offers compared to the k-filtering/wave telescope techniques is important for investigating the three-dimensional distribution, since it significantly reduces the background power allowing the morphology of the spectrum to be better determined.
The main advantage of the MSR technique is that it does not require assuming Taylor's hypothesis, but does assume that the fluctuations can be described as a superposition of incoherent plane waves (random phases), and that the signal can be decomposed into separate signal and noise components (Narita et al., 2011c). The method has also been validated by Roberts et al. (2014) and Perrone et al. (2017) for intermittent signals more characteristic of coherent structures which are also often present in the solar wind plasma (e.g. Osman et al., 2011; Perri et al., 2012; Roberts et al., 2016; Perrone et al., 2016, 2017).
Typically when applying the MSR technique to magnetic field data, 12 time series have been used as inputs: three components of the magnetic field at four spacecraft. Additionally for the vector magnetic field data, the solution can be constrained by using the divergence-free nature of the magnetic field. In this study we will investigate the three-dimensional incompressible turbulence by using the vector magnetic field (12 time series) which we use as a proxy for the incompressible fluctuations in the solar wind. The compressible component of the turbulence will be investigated by using the magnitude of the magnetic field and the electron number density which both take an input of four time series each. The technical details of the method and its application to a scalar time series are discussed in detail and tested for simulated and real data in Roberts et al. (2017b). The lack of a divergence-free condition and the smaller number of time series makes identifying multiple peaks in the distribution difficult; however, similar morphologies were found when comparing the full magnetic field with the constraining condition to a single magnetic field component at each spacecraft without the constraining condition.
One important issue is that the presence of a constraining condition has the effect of eliminating any mathematical solutions which do not satisfy the condition. Conversely the absence of a constraining condition makes the possibility of spatial aliasing occur more likely when two wave vectors cannot be differentiated between each other, e.g. . It is technically possible for aliasing to occur in two ways: the first being that an unphysical wave vector is recovered rather than a larger physical wave vector. This is unlikely for turbulence as the power is larger at smaller wave numbers. The second way in which aliasing can occur is that an unphysical wave with a large wave number is recovered instead of the physical wave with a smaller wave number. While it is impossible to remove this effect, we can mitigate its effect by limiting the frequency range in the spacecraft frame appropriately. To curtail this effect we limit the frequency range studied to a conservative range between 0.06–0.8 Hz. These limits are set by the spacecraft separations where the maximum wave number is set as where d is the average spacecraft separation. A minimum wave number of such that we can determine the peak in wave-vector space with accuracy greater than 10 % (Sahraoui et al., 2010a; Roberts et al., 2017b). These wave number limits correspond to spacecraft frequencies of fsc∼0.06 and fsc∼1.6 Hz when Doppler shifted. However, to avoid instrumental noise, especially from the spacecraft potential measurement, we set a more conservative upper limit for the frequency of 0.8 Hz in the spacecraft frame. To investigate the three-dimensional distribution of power at inertial range and proton kinetic scales the energy distributions are integrated over the frequencies between 0.06 and 0.8 Hz in the spacecraft frame.
3.1 Anisotropy
To display the results of the four-dimensional P(ω,k) obtained from the MSR technique they are integrated in frequency , and then averaged over azimuthal angles with respect to the mean magnetic field ϕ. This gives a measure of the total power anisotropy with respect to the mean magnetic field direction.
The total magnetic field which is dominated by incompressible fluctuations is given in Fig. 1c, f, i, l. For the total magnetic fluctuations, the divergence-free condition can also be used to improve the solution. The result for the compressible components relating to electron density and magnetic field magnitude are given in Fig. 1a, d, g, j and Fig. 1b, e, h, k, respectively. The total magnetic field is given in Fig. 1c, f, i, l and the additional divergence-free constraint is used which is dominated by incompressible fluctuations.
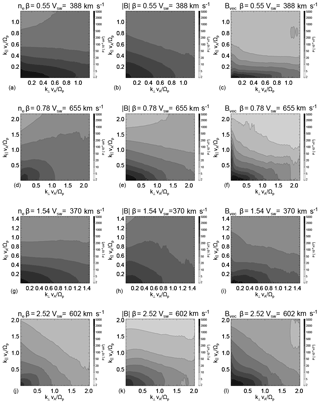
Figure 1Reduced two-dimensional spectra which have been integrated in frequency and integrated azimuthally as described in Eq. (1). For three different intervals, the morphology is investigated for the compressible density fluctuations (a, d, g, j), the compressible (magnitude) of the magnetic field (b, e, h, k) and the total magnetic field which we use as a proxy for the incompressible fluctuations (c, f, i, l).
It is clear for the incompressible components of all intervals that there is an anisotropy in the direction perpendicular to the magnetic field direction, in agreement with the vast amount of literature at MHD scales to proton kinetic scales (e.g. Shebalin et al., 1983; Matthaeus and Goldstein, 1982; Sahraoui et al., 2010b; Narita et al., 2011c; Chen et al., 2012c; Roberts et al., 2015). Additionally, this anisotropy is also present in the compressible magnetic field and in the density although the amount of anisotropy varies somewhat in different components.
One interesting feature in the incompressible component of the fast wind intervals is that there is a distinct enhancement along the magnetic field direction up to around in Fig. 1f, i. This component is significantly weaker in the slow wind interval Fig. 1c, when compared to the two fast wind intervals in Fig. 1f, i. Similar enhancements have been seen in the study of Narita et al. (2014) and was attributed to the increase in plasma β. The intervals studied in Narita et al. (2014) included two intervals of higher plasma β (β>1), which did show enhancements in the parallel direction; however, these were also intervals of fast wind (vsw>600 km s−1).
Another interesting feature is that this parallel component shows no associated counterpart in either compressible component suggesting that these parallel wave vectors are not very compressive, ruling out that the components at these scales are parallel magnetosonic waves which have higher compressibility (Gary, 1986; Sahraoui et al., 2012). One interpretation to explain the fluctuations is that these are ion cyclotron waves (ICWs). This interpretation is supported by two reasons: the extension in the parallel direction is smaller than the perpendicular direction as is expected since the damping rate for ICWs is larger. There is also a lack of compressible power in the parallel direction suggesting that these fluctuations are more ICWs rather than parallel magnetosonic waves as for quasi-parallel propagation magnetosonic waves are more compressible than ICWs, e.g. Gary (1986). The results here also complement the studies of the magnetic helicity (He et al., 2011; Podesta and Gary, 2011; Klein et al., 2014b; Roberts et al., 2015; Bruno and Telloni, 2015; Woodham et al., 2018), which have shown a signature consistent with ICWs for intervals of fast solar wind. Bruno and Telloni (2015) also demonstrated the reduction and disappearance of this component as the velocity transitioned from fast to slow. This may be due to the fast solar wind being in a less developed “younger” state than compared to the slow wind which takes longer to arrive to 1 AU than the fast wind.
To quantify the degree of anisotropy in both cases for the compressible and incompressible components, we use the anisotropy index (Shebalin et al., 1983; Saito et al., 2008) in Eq. (2). The index is equal to 1 for isotropy while values A<1 and A>1 indicate when parallel or perpendicular wave vectors dominate, respectively.
The range of physical scales are limited by the spacecraft separation (which was roughly 200 km in 2004), but are also limited by the plasma parameters giving slightly different ranges (in normalised units) for the spectra in Fig. 1. To compare different intervals with one another, we calculate the value of the anisotropy index up to a maximum value of . These indices are plotted against the mean value of plasma β in the interval in Fig. 2a, and as a function of the bulk speed in Fig. 2b. All components show anisotropy A>1 indicating that power in the perpendicular direction dominates for all of the studied parameters. The dashed line in Fig. 2a denotes the empirical relation derived from the numerical simulations of Comişel et al. (2014), and the dot dashed line at A=1 denotes isotropy. It is important to note that this relation was derived for the total magnetic field fluctuations and were performed over a plasma β range of [0.05,2]. Any empirical relation deriving from direct numerical simulation between the anisotropy index and the β for the compressible components is not known but will be the subject of a future work. The main source of error in determining the anisotropy index is the change in the spacecraft positions over time. To estimate the contribution of the error we run the analysis three times where we use the initial and final spacecraft positions to determine the error bars and the value of the anisotropy index uses the mean value of the positions.
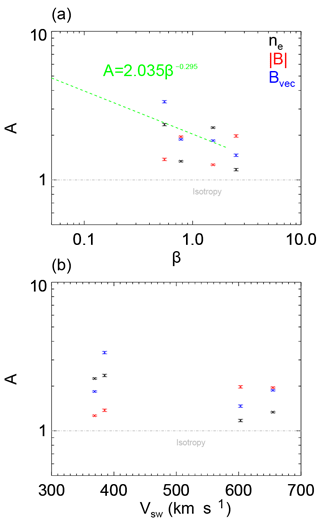
Figure 2(a) Evolution of the anisotropy index with plasma β. Black, red and blue denote the anisotropy indices obtained from density, compressible magnetic and total magnetic field, respectively. The green line denotes the empirical relationship between the anisotropy index and the β (Comişel et al., 2014). (b) The value of the anisotropy index as a function of solar wind speed.
Generally all of the incompressible points follow the empirical law obtained in Comişel et al. (2014). In the two intervals of fast solar wind, the compressible magnetic fluctuations are the most anisotropic followed by the incompressible magnetic fluctuations and the most isotropic being the density fluctuations. This agrees with the results at the inertial range presented by Chen et al. (2012c), where compressible magnetic turbulence was found to be more anisotropic than the trace fluctuations in their intervals of fast wind with β∼1. The higher anisotropy in the compressible magnetic components has been interpreted to be due to fluctuations that are slow-wave-like in nature, exhibiting anti-correlations with the density (e.g. Howes et al., 2012), which are damped proportionally to k∥. Correspondingly only the fluctuations with the smallest k∥ (or the most perpendicular propagating fluctuations) survive. This leads to a stronger anisotropy of the compressible component. However, our results also show that in the fast wind, the density is more isotropic than either of the magnetic components.
In the two intervals of slow wind the compressible magnetic field is the least anisotropic, with one interval showing the incompressible fluctuations (β<1) being the most anisotropic and the other (β>1) showing density fluctuations being the most anisotropic. The compressible components also vary as a function of β; however, it is much less marked than for the incompressible component. The weak β dependence shown here is compatible with the interpretation that wave damping may have a role. For high β plasmas the kinetic slow wave undergoes significantly stronger damping than for a lower β plasma (Narita and Marsch, 2015). One possible scenario is that at lower β kinetic slow waves are damped less and can survive to ion kinetic scales at oblique angles and that in these cases the compressible magnetic component is formed of a superposition of kinetic Alfvén waves (KAWs) and oblique kinetic slow waves giving a smaller anisotropy relative to the incompressible components. However, at higher β, oblique kinetic slow waves cannot survive to these scales and is damped leaving only the most perpendicular kinetic slow and KAWs, and consequently a higher anisotropy than the incompressible component.
There is also a difference between the two compressible components (density and magnitude of the magnetic field). This suggests that a single wave mode cannot be used to describe the fluctuations present in the solar wind. For example, should the turbulence only contain slow waves, both compressible components would be expected to have similar shapes and anisotropies by virtue of the strong anti-correlation of both compressible fluctuations. KAWs also exhibit similar anti-correlations; however, the fluctuations have smaller amplitudes. For the fast wind, where ICWs are seen, there is little to no correlation and any compressible fluctuations are likely to be too small to be measured effectively (Klein et al., 2012), which could contribute to the fact that the anisotropies of compressible fluctuations are different. Alternatively, coherent structures or discontinuities may exist where the magnitude of the magnetic field does not change but changes in density are present.
The results suggest that both the value of the plasma β and the type of solar wind (fast vs. slow) have implications for the three-dimensional structure of the turbulence and the level of the anisotropy in both the compressible and incompressible components. The presence of the parallel component in the fast wind reduces the value of the anisotropy index for the fast intervals in the incompressible component, while the anisotropy of the compressible magnetic components is larger in some cases due to the lack of this parallel component. The anisotropy of the vector magnetic field also decreases as a function of plasma β as do the fluctuations in density, it increases with plasma β for the compressible magnetic component.
Recent studies have found a tendency towards isotropy at sub-ion scales (Kiyani et al., 2013; Lacombe et al., 2017; Roberts et al., 2017a). Although the focus of this work is at ion kinetic scales, future work should investigate the variation in the anisotropy with scale. This is possible from scales of 10 000 down to 100 km with Cluster and down to smaller scales of the order of 10 km with the Magnetospheric Multiscale (MMS) mission and will be the subject of a future work.
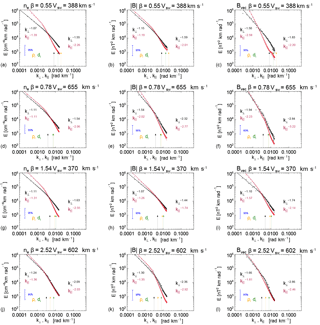
Figure 31-D integrations of the two-dimensional spectra presented in Fig. 1, the labels correspond to the same spectra. Power laws are fitted to the spectra at the scales where the lines are present, the spectral index for the power law fits are given for the parallel and the perpendicular components. The 95 % confidence level is also presented.
3.2 One-dimensional spectra
In Fig. 3, the two-dimensional spectra presented in Fig. 1 are integrated along one direction to produce a 1-D spectrum in wave-number space for the parallel and perpendicular directions, the power is then divided by the wave vector and normalised to the variance assuming the ergodicity of the signal. The spectra are fitted individually with two power laws. The blue bar denotes the 95 % confidence interval (Jenkins and Watts, 1969). The spectra for the density are given in panels (a, d, f, i), the magnitudes of magnetic field are given in panels (b, d, g, j) and finally total magnetic field are given in panels (c, e, h, k). It can be seen that the fluctuations along the magnetic field direction k∥ are steeper than in the k⟂ direction as is expected from critical balance (Goldreich and Sridhar, 1995) or alternatively by a non-elliptic wave-vector anisotropy (Narita, 2015). By assuming the wave vector is along vsw, then for different orientations of B0 with respect to the bulk flow will give different 1-D snapshots through the plasma. Several studies have investigated the anisotropy of the spectral index in this way (Horbury et al., 2008; Podesta, 2009; Wicks et al., 2010; Forman et al., 2011), and give scalings compatible with either critical balance or the non-elliptic model (Narita, 2015). However, these studies analyse different intervals of solar wind which are classified by their geometry. Here through the multi-spacecraft capabilities of Cluster, we are able to present parallel and perpendicular spectra simultaneously for the same time interval (e.g. Roberts et al., 2017c).
The perpendicular magnetic field at inertial range scales with a Kolmogorov power law of , or an Iroshnikov–Kraichnan scaling of and a parallel scaling related to the perpendicular one by the relation . This gives a steeper power law of −2 in the parallel direction when the perpendicular scaling is . At smaller proton kinetic range scales a kinetic Alfvén, or a magnetosonic wave cascade would be expected to have a scaling of in the perpendicular direction and −5 in the parallel direction based on two fluid MHD (Chen et al., 2010b). Meanwhile, a critically balanced kinetic magnetosonic cascade gives scalings of and −9 (Narita, 2016). However, a scaling of is the most commonly observed, e.g. Alexandrova et al. (2012). The departure from the expectation for a critically balanced scaling of to the often observed spectral index of has been explained by the presence of intermittency (Boldyrev, 2006) or Landau damping of KAWs (Howes et al., 2008).
For the density spectra, similar power laws are often observed to have a Kolmogorov-like inertial range followed by a flattening in the spectra between inertial and kinetic ranges, which is sensitive to the value of the plasma β (e.g. Chen et al., 2012b; Chandran et al., 2009).
The total magnetic fluctuations perpendicular slopes show similar scalings at inertial range and kinetic range scales in line with previous studies of the trace magnetic fluctuations (Smith et al., 2006; Alexandrova et al., 2012) apart from one interval which is flatter (Fig. 3i). Spectral slopes for almost all components show that at inertial scales, the parallel spectrum is steeper than the perpendicular spectrum and the break occurs earlier in the parallel direction than the perpendicular direction. The compressible magnetic and density fluctuation typically show flatter spectra than the incompressible fluctuations giving a spectral index near −1 before steepening. This may be due to the transition range between inertial and kinetic scales as the steepest density spectra is the one with the highest β, which would be the least affected.
The orange and green arrows denote the 1∕ρi (inverse Larmor radius) and 1∕di (inverse inertial length), respectively, and the black arrow denotes their sum . There is a weak tendency that the spectral break between the inertial range and proton kinetic scales appears closer to the largest of these scales in accordance with Chen et al. (2014) who used the Taylor-shifted proton characteristic scales to relate the power spectra in the spacecraft frequency to the length scales. This tendency was also seen in numerically simulated data (Franci et al., 2016). Although the plasma β values are much less extreme than the cases reported in Chen et al. (2014), we demonstrate that such a study is currently possible in the wave-vector domain with multi-point measurements. However, the break in the parallel component is closer to the combined inertial and gyro scales suggesting that cyclotron damping may be important (Roberts and Li, 2015; Woodham et al., 2018).
The spectra for all components are shown to be steeper in the parallel direction and the break scale for the different directions is at a different location with the parallel break being at larger scale than the perpendicular direction. A rough agreement is found for some intervals with the spectral indices expected for critical balance at fluid scales for the incompressible components (e.g. Fig. 3l); however, at kinetic scales the slopes in the parallel direction are too shallow. This could be due to a number of reasons: (1) that the critical balance hypothesis is not valid for kinetic scales, (2) that the fluctuation amplitudes are small, (3) in avoiding connection to the foreshock and selecting intervals where θBV>60∘ gives a projection effect (e.g. Roberts et al., 2015), and (4) that the use of a global magnetic field makes resolving the parallel component more difficult especially at smaller scales.
In this paper we have sought to investigate the morphology and the shape of incompressible and compressible turbulence in the solar wind with multi-point measurements as well as the one-dimensional spectra as a function of wave number. It is clear that density and compressible magnetic field fluctuations display the same power anisotropy as the incompressible magnetic field with the power being elongated in the perpendicular direction. However, in accordance with previous studies we see that the value of plasma β plays a role in shaping the morphology of the fluctuations with smaller values leading to larger anisotropies (Comişel et al., 2014).
The anisotropy is also shown to be different in the fast and slow wind, where extensions in power are seen in the k∥ direction which in turn lower the value of the anisotropy index. The compressible components' behaviour is more complex and seems very sensitive to the wind type and weakly sensitive to β. In the fast wind, the compressible magnetic components are the most anisotropic, and the density is the least anisotropic; however, in the slow wind the relative anisotropy of different components varies for the two intervals surveyed. We hypothesise that the observed anisotropies due to β dependence may be partially explained by the properties of some linear wave solutions. The presence of kinetic slow waves can give a reduction or an increase in anisotropy depending on the value of β. In the high β case, they could lead to an increase in the anisotropy as they are heavily damped; however, in the low β case, where damping is not as severe, they could propagate at oblique angles decreasing the anisotropy. Further study with a larger number of intervals or with a direct measurement of the density (which is possible with MMS) may give some further insights.
The multiple spacecraft of Cluster also allow a simultaneous measurement of the spectral index in the parallel and perpendicular directions, and revealed that the spectral index is steeper in the parallel direction for the total magnetic field, the magnitude of the magnetic field and the density in some cases; the spectra of the vector magnetic field are approximately consistent with the predictions of a critically balanced cascade at fluid scales. However, at kinetic scales the agreement is weaker.
To conclude, we have shown that the anisotropy is a function of the plasma β, the solar wind type and is also likely to vary with the scale also. Further work should explore the influence of scale with MMS and also study a large number of intervals at high and low solar wind speeds and plasma β.
All Cluster data are obtained from the ESA Cluster Science Archive: http://www.cosmos.esa.int/web/csa (last access: 22 March 2018).
OWR contributed to the analysis of the data, the writing and co-ordination; YN and CPE contributed to the interpretation of the data and general improvements to the manuscript.
The authors declare that they have no conflict of interest.
All Cluster data are obtained from the ESA Cluster Science Archive. We thank
the FGM, CIS, WHISPER, EFW and PEACE instrument teams and the ESA Cluster
Science Archive. Owen W. Roberts is funded by a ESA Science
Fellowship.
The topical editor, Minna
Palmroth, thanks two anonymous referees for help in evaluating this paper.
Alexandrova, O., Lacombe, C., Mangeney, A., Grappin, R., and Maksimovic, M.: Solar Wind Turbulent Spectrum At Plasma Kinetic Scales, Astrophys. J., 760, 121, https://doi.org/10.1088/0004-637X/760/2/121, 2012. a, b
Alexandrova, O., Chen, C. H. K., Sorriso-Valvo, L., Horbury, T. S., and Bale, S. D.: Solar Wind Turbulence and the Role of Ion Instabilities, Space Sci. Rev., 178, 101–139, https://doi.org/10.1007/978-1-4899-7413-6_3, 2013. a
Balogh, A., Carr, C. M., Acuña, M. H., Dunlop, M. W., Beek, T. J., Brown, P., Fornacon, K.-H., Georgescu, E., Glassmeier, K.-H., Harris, J., Musmann, G., Oddy, T., and Schwingenschuh, K.: The Cluster Magnetic Field Investigation: overview of in-flight performance and initial results, Ann. Geophys., 19, 1207–1217, https://doi.org/10.5194/angeo-19-1207-2001, 2001. a
Belcher, J. W.: Alfvenic wave pressures and the solar wind, Astrophys. J., 168, 509–524, 1971. a
Bieber, J. W., Wanner, W., and Matthaeus, W. H.: Dominant two-dimensional solar wind turbulence with implications for cosmic ray transport, J. Geophys. Res., 101, 2511–2522, 1996. a
Boldyrev, S.: Spectrum of Magnetohydrodynamic Turbulence, Phys. Rev. Lett., 96, 115002, https://doi.org/10.1103/PhysRevLett.96.115002, 2006. a
Bruno, R. and Carbone, V.: The Solar Wind as a Turbulence Laboratory, Living Rev. Sol. Phys., 10, 2, https://doi.org/10.12942/lrsp-2013-2, 2013. a
Bruno, R. and Telloni, D.: Spectral Features of Magnetic Fluctuations at Proton Scales from Fast to Slow Solar Wind, Astrophys. J., 2, L17, https://doi.org/10.1088/2041-8205/811/2/L17, 2015. a, b
Camporeale, E. and Burgess, D.: The dissipation of solar wind turbulent fluctuations at electron scales, Astrophys. J., 730, 114, https://doi.org/10.1088/0004-637X/730/2/114, 2011. a
Cerri, S. S., Califano, F., Jenko, F., Told, D., and Rincon, F.: Subproton-Scale Cascades in Solar Wind Turbulence: Driven Hybrid-Kinetic Simulations, Astrophys. J., 82, L12, https://doi.org/10.3847/2041-8205/822/1/L12, 2016. a
Cerri, S. S., Servidio, S., and Califano, F.: Kinetic cascade in solar-wind turbulence: 3D3V hybrid-kinetic simulations with electron inertia, Astrophys. J. Lett., 846, L18, https://doi.org/10.3847/2041-8213/aa87b0, 2017. a
Chandran, B. D. G., Quataert, E., Howes, G. G., Xia, Q., and Pongkitiwanichakul, P.: Constraining Low-Frequency Alfvenic Turbulence in the Solar Wind using Density-Fluctuation Measurements, Astrophys. J., 707, 1668–1675, 2009. a, b
Chen, C. H. K., Horbury, T. S., Schekochihin, A. A., Wicks, R. T., Alexandrova, O., and Mitchell, J.: Anisotropy of Solar Wind Turbulence between Ion and Electron Scales, Phys. Rev. Lett., 104, 255002, https://doi.org/10.1103/PhysRevLett.104.255002, 2010a. a, b, c
Chen, C. H. K., Wicks, R. T., Horbury, T. S., and Schekochihin, A. A.: Interpreting Power Anisotropy Measurements in Plasma Turbulence, Astrophys. J., 711, L79–L83, https://doi.org/10.1088/2041-8205/711/2/L79, 2010b. a
Chen, C. H. K., Salem, C. S., Bonnell, J. W., Mozer, F. S., and Bale, S. D.: Density Fluctuation Spectrum of Solar wind Turbulence between ion and electron scales, Phys. Rev. Lett., 109, 035001, https://doi.org/10.1103/PhysRevLett.110.225002, 2012a. a
Chen, C. H. K., Howes, G. G., Bonnell, J. W., Mozer, F. S., and Klein, K. G.: Kinetic Scale Density Fluctuations in the Solar Wind, Sol. Wind, 13, 1–5, 2012b. a, b
Chen, C. H. K., Mallet, A., Schekochihin, A. A., Horbury, T. S., Wicks, R. T., and Bale, S. D.: Three-Dimensional Structure of Solar Wind Turbulence, Astrophys. J., 758, 1–5, https://doi.org/10.1088/0004-637X/758/2/120, 2012c. a, b, c, d, e
Chen, C. H. K., Sorriso-Valvo, L., Safrankova, J., and Nemecek, Z.: Intermittency of solar wind density fluctuations from ion to electron scales, Astrophys. J., 789, L8, https://doi.org/10.1088/2041-8205/789/1/L8, 2014. a, b
Choi, J., Song, I., and Kim, H. M.: On estimating the direction of arrival when the number of signal sources is unknown, Signal Processing, 34, 193–205, https://doi.org/10.1016/0165-1684(93)90162-4, 1993. a
Comişel, H., Narita, Y., and Motschmann, U.: Wavevector anisotropy of plasma turbulence at ion kinetic scales: solar wind observations and hybrid simulations, Nonlin. Processes Geophys., 21, 1075–1083, https://doi.org/10.5194/npg-21-1075-2014, 2014. a, b, c, d, e, f
Dasso, S., Milano, L. J., Matthaeus, W. H., and Smith, C. W.: Anisotropy in fast and slow solar wind fluctuations, Astrophys. J., 635, 181–184, 2005. a
Decreau, P. M. E., Fergeaue, P., Krannosels'kikh, V., Leveque, M., Martin, P. H., Randriamboarison, O., Sene, F. X., Trotignon, J. G., Canu, P., and Mogensen, P. B.: WHISPER, A Resonance Sounder And Wave Analyser: Performances And Perspectives For The Cluster Mission, Space Sci. Rev., 79, 157–193, https://doi.org/10.1023/A:1004931326404, 1997. a
Escoubet, C. P., Schmidt, R., and Goldstein, M. L.: Cluster – Science and mission overview, Space Sci. Rev., 79, 11–32, 1997. a, b
Escoubet, C. P., Fehringer, M., and Goldstein, M.: Introduction The Cluster mission, Ann. Geophys., 19, 1197–1200, https://doi.org/10.5194/angeo-19-1197-2001, 2001. a, b
Forman, M. A., Wicks, R. T., and Horbury, T. S.: Detailed Fit of “Critical Balance” Theory To Solar Wind Turbulence Measurements, Astrophys. J., 733, 76, https://doi.org/10.1088/0004-637X/733/2/76, 2011. a, b
Franci, L., Landi, S., Matteini, L., Verdini, A., and Hellinger, P.: High-Resolution Hybrid Simulations of Kinetic Plasma Turbulence At Proton Scales, Astrophys. J., 812, 21, https://doi.org/10.1088/0004-637X/812/1/21, 2015a. a
Franci, L., Verdini, A., Matteini, L., Landi, S., and Hellinger, P.: Solar Wind Turbulence From Mhd To Sub-Ion Scales: High-Resolution Hybrid Simulations, Astrophys. J., 804, L39, https://doi.org/10.1088/2041-8205/804/2/L39, 2015b. a
Franci, L., Landi, S., Matteini, L., Verdini, A., and Hellinger, P.: Plasma beta dependence of the ion-scale spectral break of solar wind turbulence: high-resolution 2D hybrid simulations, Astrophys. J., 833, 91, https://doi.org/10.3847/1538-4357/833/1/91, 2016. a
Frisch, U.: Turbulence: The Legacy of A. N. Kolmogorov, Cambridge University Press, 1995. a
Gary, S. P.: Low-frequency waves in a high-beta collisionless plasma polarization, compressibility and helicity, J. Plasma Phys., 35, 431–447, 1986. a, b
Goldreich, P. and Sridhar, S.: Toward a theory of interstellar turbulence. 2: Strong alfvenic turbulence, Astrophys. J., 438, 763–775, 1995. a, b
Gustafsson, G, Boström, R., Holback, B., Holmgren, G., Lundgren, A., Stasiewicz, K., Åhlén, L., Mozer, F. S., Pankow, D., Harvey, P., Berg, P., Ulrich, R., Pedersen, A., Schmidt, R., Butler, A., Fransen, A. W. C., Klinge, D., Thomsen, M., Fälthammar, C.-G., Lindqvist, P.-A., Christenson, S., Holtet, J., Lybekk, B., Sten, T. A., Tanskanen, P., Lappalainen, K., and Wygant, J.: The electric field and wave experiment for the cluster mission, Space Sci. Rev., 79, 137–156, https://doi.org/10.1007/BF00751342, 1997. a
Haynes, C. T., Burgess, D., and Camporeale, E.: Reconnection and electron temperature anisotropy in sub-proton scale plasma turbulence, Astrophys. J., 783, 38, https://doi.org/10.1088/0004-637X/783/1/38, 2014. a
He, J., Marsch, E., Tu, C.-Y., Yao, S., and Tian, H.: Possible Evidence of Alfvén-Cyclotron Waves in the Angle Distribution of Magnetic Helicity of Solar Wind Turbulence, Astrophys. J., 731, 85, https://doi.org/10.1088/0004-637X/731/2/85, 2011. a
Hnat, B., Chapman, S. C., and Rowlands, G.: Compressibility in Solar Wind Plasma Turbulence, Phys. Rev. Lett., 94, 204502, https://doi.org/10.1103/PhysRevLett.94.204502, 2005. a
Horbury, T. S.: Cluster-II Workshop: Multiscale/Multipoint Plasma Measurements, Proceedings of the Workshop held at Imperial College, London, UK, 22–24 September 1999, Paris: European Space Agency (ESA), ESA-SP, Vol. 449, p. 89, 2000. a
Horbury, T. S., Foreman, M., and Oughton, S.: Anisotropic Scaling of Magnetohydrodynamic Turbulence, Phys. Rev. Lett., 101, 175005, https://doi.org/10.1103/PhysRevLett.101.175005, 2008. a, b, c
Horbury, T. S., Wicks, R. T., and Chen, C. H. K.: Anisotropy in space plasma turbulence: Solar wind observations, Space Sci. Rev., 172, 325–342, https://doi.org/10.1007/s11214-011-9821-9, 2012. a
Howes, G. G., Cowley, S. C., Dorland, W., Hammett, G. W., Quataert, E., and Schekochihin, A. A.: A model of turbulence in magnetized plasmas: Implications for the dissipation range in the solar wind, J. Geophys. Res.-Space, 113, A05103, https://doi.org/10.1029/2007JA012665, 2008. a
Howes, G. G., Bale, S. D., Klein, K. G., Chen, C. H. K., Salem, C. S., and TenBarge, J. M.: The Slow-Mode Nature of Compressible Wave Power in Solar Wind Turbulence, Astrophys. J., 753, L19, https://doi.org/10.1088/2041-8205/753/1/L19, 2012. a
Howes, G. G., Klein, K. G., and TenBarge, J. M.: Validity of the taylor hypothesis for linear kinetic waves in the weakly collisional solar wind, Astrophys. J., 789, 106, https://doi.org/10.1088/0004-637X/789/2/106, 2014. a
Jenkins, G. M. and Watts, D. G.: Spectral analysis and its applications, Holden-Day, San Francisco, 1969. a
Kellogg, P. J. and Horbury, T. S.: Rapid density fluctuations in the solar wind, Ann. Geophys., 23, 3765–3773, https://doi.org/10.5194/angeo-23-3765-2005, 2005. a, b
Kiyani, K. H., Chapman, S. C., Khotyaintsev, Yu. V., Dunlop, M. W., and Sahraoui, F.: Global scale-invariant dissipation in collisionless plasma turbulence, Phys. Rev., 103, 075006, https://doi.org/10.1103/PhysRevLett.103.075006, 2009. a
Kiyani, K. H., Chapman, S. C., Sahraoui, F., Hnat, B., Fauvarque, O., and Khotyaintsev, Yu. V.: Enhanced Magnetic Compressibility and Isotropic Scale Invariance At Sub-Ion Larmor Scales in Solar Wind Turbulence, Astrophys. J., 763, 10, https://doi.org/10.1088/0004-637X/763/1/10, 2013. a, b
Klein, K. G., Howes, G. G., TenBarge, J. M., Bale, S. D., Chen, C. H. K., and Salem, C. S.: Using Synthetic Spacecraft Data To Interpret Compressible Fluctuations in Solar Wind Turbulence, Astrophys. J., 755, 159, https://doi.org/10.1088/0004-637X/755/2/159, 2012. a
Klein, K. G., Howes, G. G., and TenBarge, J. M.: The Violation of the Taylor Hypothesis in Measurements of Solar Wind Turbulence, Astrophys. J., 790, L20, https://doi.org/10.1088/2041-8205/790/2/L20, 2014a. a
Klein, K. G., Howes, G. G., TenBarge, J. M., and Podesta, J. J.: Physical Interpretation of the Angle-dependent Magnetic Helicity Spectrum in the Solar Wind: The Nature of Turbulent Fluctuations near the Proton Gyroradius Scale, Astrophys. J., 785, 138, https://doi.org/10.1088/0004-637X/785/2/138, 2014b. a
Lacombe, C., Alexandrova, O., and Matteini, L.: Anisotropies of the magnetic field fluctuations at kinetic scales in the solar wind: Cluster observations, Astrophys. J., 848, https://doi.org/10.3847/1538-4357/aa8c06, 2017. a
Mallet, A., Schekochihin, A. A., Chandran, B. D. G., Chen, C. H. K., Horbury, T. S., Wicks, R. T., and Greenan, C. C.: Measures of three-dimensional anisotropy and intermittency in strong Alfvénic turbulence, Mon. Not. R. Astron. Soc., 459, 2130–2139, https://doi.org/10.1093/mnras/stw802, 2016. a, b
Matthaeus, W. H. and Goldstein, M. L.: Measurement of the Rugged Invariants of Magnetohydrodynamic Turbulence in the Solar Wind, J. Geophys. Res., 87, 6011–6028, https://doi.org/10.1029/JA087iA08p06011, 1982. a
Matthaeus, W. H., Goldstein, M. L., and Roberts, D. A.: Evidence for the presence of quasi-two-dimensional nearly incompressible fluctuations in the solar wind, J. Geophys. Res., 95, 20673, https://doi.org/10.1029/JA095iA12p20673, 1990. a
Motschmann, U., Woodward, T. I., Glassmeier, K. H., Southwood, D. J., and Pinçon, J. L.: Wavelength and direction filtering by magnetic measurements at satellite arrays: Generalized minimum variance analysis, J. Geophys. Res.-Space, 101, 4961–4965, https://doi.org/10.1029/95JA03471, 1996. a
Narita, Y.: Non-elliptic wavevector anisotropy for magnetohydrodynamic turbulence, Ann. Geophys., 33, 1413–1419, https://doi.org/10.5194/angeo-33-1413-2015, 2015. a, b, c
Narita, Y.: Kinetic Extension of Critical Balance To Whistler Turbulence, Astrophys. J., 831, 83, https://doi.org/10.3847/0004-637X/831/1/83, 2016. a
Narita, Y.: Error estimate of Taylor's frozen-in flow hypothesis in the spectral domain, Ann. Geophys., 35, 325–331, https://doi.org/10.5194/angeo-35-325-2017, 2017. a
Narita, Y. and Marsch, E.: Kinetic Slow Mode in the Solar Wind and Its Possible Role in Turbulence Dissipation and Ion Heating, Astrophys. J., 805, 24, https://doi.org/10.1088/0004-637X/805/1/24, 2015. a
Narita, Y. and Motschmann, U.: Ion-Scale Sideband Waves and Filament Formation: Alfvénic Impact on Heliospheric Plasma Turbulence, Front. Phys., 5, 1–8, https://doi.org/10.3389/fphy.2017.00008, 2017. a, b
Narita, Y., Sahraoui, F., Goldstein, M. L., and Glassmeier, K.-H.: Magnetic energy distribution in the four-dimensional frequency and wave vector domain in the solar wind, J. Geophys. Res., 115, 1–11, https://doi.org/10.1029/2009JA014742, 2010. a, b
Narita, Y., Gary, S. P., Saito, S., Glassmeier, K.-H., and Motschmann, U.: Dispersion relation analysis of solar wind turbulence, Geophys. Res. Lett., 38, L05101, https://doi.org/10.1029/2010GL046588, 2011a. a, b, c
Narita, Y., Glassmeier, K.-H., Goldstein, M. L., Motschmann, U., and Sahraoui, F.: Three-dimensional spatial structures of solar wind turbulence from 10 000-km to 100-km scales, Ann. Geophys., 29, 1731–1738, https://doi.org/10.5194/angeo-29-1731-2011, 2011b. a, b
Narita, Y., Glassmeier, K.-H., and Motschmann, U.: High-resolution wave number spectrum using multi-point measurements in space – the Multi-point Signal Resonator (MSR) technique, Ann. Geophys., 29, 351–360, https://doi.org/10.5194/angeo-29-351-2011, 2011c. a, b, c, d, e, f, g
Narita, Y., Comişel, H., and Motschmann, U.: Spatial structure of ion-scale plasma turbulence, Front. Phys., 2, 1–8, https://doi.org/10.3389/fphy.2014.00013, 2014. a, b, c, d, e, f
Osman, K. T. and Horbury, T. S.: Quantitative estimates of the slab and 2-D power in solar wind turbulence using multispacecraft data, J. Geophys. Res., 114, A06103, https://doi.org/10.1029/2008JA014036, 2009. a
Osman, K. T., Matthaeus, W. H., Greco, A., and Servidio, S.: Evidence for Inhomogeneous Heating in the Solar Wind, Astrophys. J., 727, L11, https://doi.org/10.1088/2041-8205/727/1/L11, 2011. a
Oughton, S., Matthaeus, W. H., Wan, M., and Osman, K. T.: Anisotropy in solar wind plasma turbulence, Philos. T. Roy. Soc. A, 373, 20140152, https://doi.org/10.1098/rsta.2014.0152, 2015. a
Pedersen, A., Décréau, P., Escoubet, C.-P., Gustafsson, G., Laakso, H., Lindqvist, P.-A., Lybekk, B., Masson, A., Mozer, F., and Vaivads, A.: Four-point high time resolution information on electron densities by the electric field experiments (EFW) on Cluster, Ann. Geophys., 19, 1483–1489, https://doi.org/10.5194/angeo-19-1483-2001, 2001. a, b
Pedersen, A., Lybekk, B., André, M., Eriksson, A., Masson, A., Mozer, F. S., Lindqvist, P. A., Décréau, P. M. E., Dandouras, I., Sauvaud, J. A., Fazakerley, A., Taylor, M., Paschmann, G., Svenes, K. R., Torkar, K., and Whipple, E.: Electron density estimations derived from spacecraft potential measurements on cluster in tenuous plasma regions, J. Geophys. Res.-Space, 113, 1–19, https://doi.org/10.1029/2007JA012636, 2008. a
Perri, S., Goldstein, M. L., Dorelli, J., and Sahraoui, F.: Detection of Small-Scale Structures in the Dissipation Regime of Solar-Wind Turbulence, Phys. Rev. Lett., 109, 191101, https://doi.org/10.1103/PhysRevLett.109.191101, 2012. a
Perri, S., Servidio, S., Vaivads, A., and Valentini, F.: Numerical Study on the Validity of the Taylor Hypothesis in Space Plasmas, Astrophys. J. Suppl. Ser., 231, 4, https://doi.org/10.3847/1538-4365/aa755a, 2017a. a
Perri, S., Valentini, F., Sorriso-Valvo, L., Reda, A., and Malara, F.: On the estimation of the current density in space plasmas: Multi- versus single-point techniques, Planet. Space Sci., 140, 6–10, https://doi.org/10.1016/j.pss.2017.03.008, 2017b. a
Perrone, D., Valentini, F., Servidio, S., Dalena, S., and Veltri, P.: Vlasov Simulations of Multi-Ion Plasma Turbulence in the Solar Wind, Astrophys. J., 762, 99, https://doi.org/10.1088/0004-637X/762/2/99, 2013. a
Perrone, D., Alexandrova, O., Mangeney, A., Maksimovic, M., Lacombe, C., Rakoto, V., Kasper, J. C., and Jovanovic, D.: COMPRESSIVE COHERENT STRUCTURES AT ION SCALES IN THE SLOW SOLAR WIND, Astrophys. J., 826, 196, https://doi.org/10.3847/0004-637X/826/2/196, 2016. a
Perrone, D., Alexandrova, O., Roberts, O. W., Lion, S., Lacombe, C., Walsh, A., Maksimovic, M., and Zouganelis, I.: Coherent Structures at Ion Scales in Fast Solar Wind: Cluster Observations, Astrophys. J., 849, 49, https://doi.org/10.3847/1538-4357/aa9022, 2017. a, b
Perschke, C., Narita, Y., Motschmann, U., and Glassmeier, K.-H.: Observational Test for a Random Sweeping Model in Solar Wind Turbulence, Phys. Rev. Lett., 116, 1–5, https://doi.org/10.1103/PhysRevLett.116.125101, 2016. a
Pezzi, O., Parashar, T. N., Servidio, S., Valentini, F., Vasconez, C. L., Yang, Y., Malara, F., Matthaeus, W. H., and Veltri, P.: Colliding Alfvenic wave packets in magnetohydrodynamics Hall and kinetic simulations, J. Plasma Phys., 83, 905830105, https://doi.org/10.1017/S0022377817000113, 2017a. a, b, c
Pezzi, O., Parashar, T. N., Servidio, S., Valentini, F., Vásconez, C. L., Yang, Y., Malara, F., Matthaeus, W. H., and Veltri, P.: Revisiting a Classic: the Parker–Moffatt Problem, Astrophys. J., 834, 166, https://doi.org/10.3847/1538-4357/834/2/166, 2017b. a, b, c
Pincon, J. L. and Lefeuvre, F.: Local characterization of homogeneous turbulence in a space plasma from simultaneous measurements of field components at several points in space, J. Geophys. Res., 96, 1789–1802, 1991. a
Podesta, J. J. and Gary, S. P.: Magnetic Helicity Spectrum of Solar Wind Fluctuations As a Function of the Angle With Respect To the Local Mean Magnetic Field, Astrophys. J., 734, 15, https://doi.org/10.1088/0004-637X/734/1/15, 2011. a
Podesta, J. J.: Relationship Between the Shell-Averaged Energy Spectrum and the Frequency Spectrum Measured By a Single Spacecraft in the Solar Wind, Astrophys. J., 69, 1213–1217, https://doi.org/10.1088/0004-637X/696/2/1213, 2009. a, b
Pucci, F., Vásconez, C. L., Pezzi, O., Servidio, S., Valentini, F., Matthaeus, W. H., and Malara, F.: Special Section: From Alfvén waves to kinetic Alfvén waves in an inhomogeneous, J. Geophys. Res.-Space, 1, 7349–7352, https://doi.org/10.1002/2015JA022216, 2016. a
Robert, P., Roux, A., Harvey, C., Dunlop, M., Daly, P., and Glassmeier, K.-H.: Tetrahedron Geometric Factors, in: Anal. Methods Multi-spacecr. Data, edited by: Paschmann, P. and Daly, G., chap. 13, 323–348, 1998. a
Roberts, O. W. and Xing, L.: Evidence of the ion cyclotron resonance at proton kinetic scales in the solar wind, Astrophys. J., 802, 1–11, https://doi.org/10.1088/0004-637X/802/1/1, 2015. a, b
Roberts, O. W., Li, X., and Li, B.: Kinetic Plasma Turbulence in the Fast Solar Wind Measured By Cluster, Astrophys. J., 769, 58, https://doi.org/10.1088/0004-637X/769/1/58, 2013. a, b
Roberts, O. W., Li, X., and Jeska, L.: Validation of the k-filtering technique for a signal composed of random-phase plane waves and non-random coherent structures, Geosci. Instrum. Method. Data Syst., 3, 247–254, https://doi.org/10.5194/gi-3-247-2014, 2014. a, b
Roberts, O. W., Li, X., and Jeska, L.: A statistical study of the solar wind turbulence at ion kinetic scales using the k-filtering technique and cluster data, Astrophys. J., 802, 1–13, https://doi.org/10.1088/0004-637X/802/1/2, 2015. a, b, c
Roberts, O. W., Li, X., Alexandrova, O., and Li, B.: Observation of an MHD Alfvén vortex in the slow solar wind, J. Geophys. Res.-Space, 121, 3870–3881, https://doi.org/10.1002/2015JA022248, 2016. a
Roberts, O. W., Narita, Y., and Escoubet, C. P.: Direct Measurement of Anisotropic and Asymmetric Wave Vector Spectrum in Ion-scale Solar Wind Turbulence, Astrophys. J., 851, L11, https://doi.org/10.3847/2041-8213/aa9bf3, 2017a. a, b
Roberts, O. W., Narita, Y., Li, X., Escoubet, C. P., and Laakso, H.: Multipoint analysis of compressive fluctuations in the fast and slow solar wind, J. Geophys. Res.-Space, 122, 6940–6963, https://doi.org/10.1002/2016JA023552, 2017b. a, b, c, d, e, f, g
Roberts, O. W., Alexandrova, O., Kajdič, P., Turc, L., Perrone, D., Escoubet, C. P., and Walsh, A.: Variability of the Magnetic Field Power Spectrum in the Solar Wind at Electron Scales, Astrophys. J., 850, 120, https://doi.org/10.3847/1538-4357/aa93e5, 2017c. a, b
Roberts, O. W., Narita, Y., and Escoubet, C.-P.: Multi-scale analysis of compressible fluctuations in the solar wind, Ann. Geophys., 36, 47–52, https://doi.org/10.5194/angeo-36-47-2018, 2018. a
Sahraoui, F., Belmont, G., Goldstein, M. L., and Rezeau, L.: Limitations of multispacecraft data techniques in measuring wave number spectra of space plasma turbulence, J. Geophys. Res., 115, 1–10, https://doi.org/10.1029/2009JA014724, 2010a. a
Sahraoui, F., Goldstein, M. L., Belmont, G., Canu, P., and Rezeau, L.: Three dimensional anisotropic k spectra of turbulence at subproton scales in the solar wind, Phys. Rev. Lett., 105, 1–4, https://doi.org/10.1103/PhysRevLett.105.131101, 2010b. a, b
Sahraoui, F., Belmont, G., and Goldstein, M. L.: New Insight Inot Short-Wavelength Solar Wind Fluctuations From Vlasov Theory, Astrophys. J., 748, 100, https://doi.org/10.1088/0004-637X/748/2/100, 2012. a
Saito, S., Gary, S. P., Li, H., and Narita, Y.: Whistler turbulence: Particle-in-cell simulations, Phys. Plasmas, 15, 102305, https://doi.org/10.1063/1.2997339, 2008. a
Saur, J. and Bieber, J. W.: Geometry of low-frequency solar wind magnetic turbulence: Evidence for radially aligned Alfvénic fluctuations, J. Geophys. Res., 104, 9975, https://doi.org/10.1029/1998JA900077, 1999. a
Schekochihin, A. A., Cowley, S. C., Dorland, W., Hammett, G. W., Howes, G. G., Quataert, E., and Tatsuno, T.: Astrophysical Gyrokinetics: Kinetic and Fluid Turbulent Cascades in Magnetized Weakly Collisional Plasmas, Astrophys. J. Suppl. Ser., 182, 310–377, https://doi.org/10.1088/0067-0049/182/1/310, 2009. a
Schmidt, R.: Multiple emitter location and signal parameter estimation, IEEE Trans. Antennas Propag., 34, 276–280, https://doi.org/10.1109/TAP.1986.1143830, 1986. a
Servidio, S., Valentini, F., Perrone, D., Greco, A., Califano, F., Matthaeus, W. H., and Veltri, P.: A kinetic model of plasma turbulence, J. Plasma Phys., 81, 325810107, https://doi.org/10.1017/S0022377814000841, 2014. a
Shebalin, J. V., Matthaeus, W. H., and Montgomery, D.: Anisotropy in MHD turbulence due to a mean magnetic field, J. Plasma Phys., 29, 525–547, 1983. a, b, c
Smith, C. W., Hamilton, K., Vasquez, B. J., and Leamon, R. R.: Analysis of multi-dimensional correlation functions in the solar wind, Astrophys. J., 645, L85–L88, https://doi.org/10.1086/506151, 2006. a
Smith, C. W., Vasquez, B. J., and Stemkowski, M. R.: Analysis of multi-dimensional correlation functions in the solar wind, 271, 271–274, https://doi.org/10.1063/1.4811040, 2013. a
Taylor, G. I.: The Spectrum of Turbulence, P. Roy. Soc. A, 164, 476–490, https://doi.org/10.1098/rspa.1938.0032, 1938. a
Tjulin, A., Pincon, J. L., Sahraoui, F., André, M., and Cornilleau-Wehrlin, N.: The k-filtering technique applied to wave electric and magnetic field measurements from the Cluster satellites, J. Geophys. Res., 110, 1–17, https://doi.org/10.1029/2005JA011125, 2005. a
Tu, C.-Y. and Marsch, E.: MHD structures, waves and turbulence in the solar wind: Observations and theories, Space Sci. Rev., 73, 1–210, https://doi.org/10.1007/BF00748891, 1995. a
Turner, A. J., Gogoberidze, G., Chapman, S., Hnat, B., and Müller, W.-C.: Nonaxisymmetric Anisotropy of Solar Wind Turbulence, Phys. Rev. Lett., 107, 095002, https://doi.org/10.1103/PhysRevLett.107.095002, 2011. a
Valentini, F., Perrone, D., Stabile, S., Pezzi, O., Servidio, S., De Marco, R., Marcucci, F., Bruno, R., Lavraud, B., De Keyser, J., Consolini, G., Brienza, D., Sorriso-Valvo, L., Retinò, A., Vaivads, A., Salatti, M., and Veltri, P.: Differential kinetic dynamics and heating of ions in the turbulent solar wind, New J. Phys., 18, 125001, https://doi.org/10.1088/1367-2630/18/12/125001, 2016. a
Verdini, R. and Grappin, A.: Imprints of Expansion on the Local Anisotropy of Solar Wind Turbulence, Astrophys. J., 808, L34, https://doi.org/10.1088/2041-8205/808/2/L34, 2015. a, b
Wicks, R. T., Horbury, T. S., Chen, C. H. K., and Schekochihin, A. A.: Power and spectral index anisotropy of the entire inertial range of turbulence in the fast solar wind, Mon. Not. R. Astron. Soc. Lett., 407, L31–L35, https://doi.org/10.1111/j.1745-3933.2010.00898.x, 2010. a, b, c
Woodham, L. D., Wicks, R. T., Verscharen, D., and Owen, C. J.: The Role of Proton-Cyclotron Resonance as a Dissipation Mechanism in Solar Wind Turbulence: A Statistical Study at Ion-Kinetic Scales, https://doi.org/10.3847/1538-4357/aab03d, 2018. a, b