Tripolar electric field Structure in guide field magnetic reconnection

It has been shown that the guide field substantially modifies the structure of the reconnection layer. For instance, the Hall magnetic and electric fields are distorted in guide field reconnection compared to reconnection without guide fields (i.e., anti-parallel reconnection). In this paper, we performed 2.5-D electromagnetic full particle simulation to study the electric field structures in magnetic reconnection under different initial guide fields (B_g). Once the amplitude of a guide field exceeds 0.3 times the asymptotic magnetic field B₀, the traditional bipolar Hall electric field is clearly replaced by a tripolar electric field, which consists of a newly emerged electric field and the bipolar Hall electric field. The newly emerged electric field is a convective electric field about one ion inertial length away from the neutral sheet. It arises from the disappearance of the Hall electric field due to the substantial modification of the magnetic field and electric current by the imposed guide field. The peak magnitude of this new electric field increases linearly with the increment of guide field strength. Possible applications of these results to space observations are also discussed.

Keywords. Space plasma physics (magnetic reconnection)

1 Introduction

Magnetic reconnection is a ubiquitous fundamental phenomenon that transfers magnetic energy into plasma kinetic and thermal energy (Yamada et al., 2010). It is initiated in a small-scale region, named the diffusion region. The diffusion region consists of two-scale structures: the ion diffusion region (ions are demagnetized while electrons are still magnetized on the ion inertial scale) and the electron diffusion region (both ions and electrons are demagnetized on the electron inertial scale) (e.g., Sonnerup, 1979; Birn et al., 2001). The relative motion of ions and electrons results in the Hall currents, the quadrupolar out-of-plane magnetic fields and bipolar electric field pointing toward the center of the current sheet around the ion diffusion region (e.g., Priest and Forbes, 2000). These signatures have frequently been used to locate/identify the ion diffusion regions in the Earth's magnetosphere (e.g., Deng and Matsumoto, 2001; Huang et al., 2010, 2012; Paschmann et al., 2013).

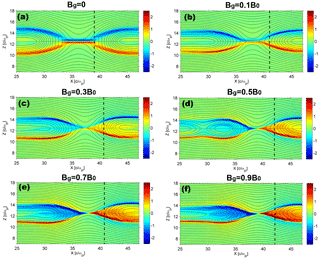
Figure 1 The structure of E_z in reconnection with different guide fields (B_g=0, 0.1B₀, 0.3B₀, 0.5B₀, 0.7B₀, 0.9B₀) at tω_ci=32 in the x–z plane. Solid black curves display the magnetic field lines. Vertical dashed lines in each panel mark the position of $\mathit{\delta }x=\mathrm{3}c/{\mathit{\omega }}_{\mathrm{pi}}$, where δx is the horizontal distance to the X point.

A guide field, which is perpendicular to the reconnection plane (the guide field usually points in the GSM Y direction in the magnetotail), usually exists in reconnection in laboratory, space, and astrophysical plasmas. Many magnetic reconnection events with guide fields in the Earth's magnetotail have been reported. Øieroset et al. (2001) identified an ion diffusion region with a guide field of about 20 % of the field strength in the lobe region. Nakamura et al. (2008) showed that a large guide field (up to 80 % of the lobe field) exists within the magnetic reconnection region. Comparing the simulation results with satellite observation, Eastwood et al. (2010) found that the structure of the diffusion region is altered by a moderate guide field (∼20 % of the lobe field). The Hall electromagnetic fields are asymmetric across the current sheet. Zhou et al. (2014) identified a super-Alfvénic electron jet extended to 30 s ion inertial length away from the X line in a reconnection region with a weak guide field. This jet was deflected from the neutral sheet owing to the Lorentz force j_L×B_g; here, j_L is the electric current in the outflow direction and B_g is the guide field. In the Earth's magnetopause, component reconnections (with a non-negligible guide field) are suggested as important processes during solar-wind–magnetosphere interactions because the interplanetary magnetic fields (IMFs) have a variety of shear angles relative to the Earth's dipole field (Fuselier et al., 2011).

Although great efforts have been made to understand the guide field reconnection, and we have already known that the Hall magnetic and electric field are distorted in the presence of a guide field, the detailed structure of electric fields in guide field reconnection remains an open question. In this paper, we performed a series 2.5-D particle-in-cell simulation to study the electric field structures within magnetic reconnection in the presence of different guide fields. We focus on the electric fields near the X point. The simulation results show that the conventional bipolar Hall electric field is replaced by a tripolar electric field when a sufficient large guide field is imposed (B_g≥0.3B₀), while the conventional bipolar Hall electric field exists only in the small guide field regime. We further analyzed the generalized Ohm law to understand the origin of the new electric field.

2 Simulation results

Our 2.5-D fully electromagnetic full particle code has been used to study the electric field structures inside the magnetic island, density cavity, and sub-structures of the separatrix near and/or within the magnetic reconnection region (Zhou et al., 2011, 2012a, b, 2014; Huang et al., 2014, 2015). In this model, ions and electrons are regarded as individual particles. The Maxwell equation set is solved to advance the electromagnetic fields, while the Lorentz equation is solved to advance particles.

The initial magnetic field is given by two Harris current sheets: $B_x=B_{\mathrm{0}}\tanh \left(\right(z-L_z/\mathrm{4})/L_{\mathrm{0}})-B_{\mathrm{0}}\tanh \left(\right(z-\mathrm{3}{L}_z/\mathrm{4})/L_{\mathrm{0}})-B_{\mathrm{0}}$, where B₀ is the asymptotic magnetic field amplitude, L_z is the box size in the z direction, and L₀ is the initial half-width of the current sheets which is set to 0.5d_i ($d_{\mathrm{i}}=c/{\mathit{\omega }}_{\mathrm{pi}}$ is the initial ion inertial length based on the density n₀ in the center of the current sheets). Reconnection occurs in the x–z plane (+x points right and +z points upward; +y points inward in the out-of-plane direction). We apply periodic boundary conditions in the x and z directions for both particles and fields. A small system size flux perturbation is added initially to boost the system entering the nonlinear stage. Details of this model have been discussed in Zhou et al. (2012b).

The simulation box is 50c∕ω_pi in the x direction and 50c∕ω_pi in the z direction, where c is the speed of light and ω_pi is the ion plasma frequency in the central current sheet. The whole simulation box consists of 2000×2000 grids; that is, each grid is equivalent to 0.025c∕ω_pi. The magnetic field is normalized by B₀, the electric field is normalized by B₀V_A, the velocity is normalized by V_A, and the electric current density is normalized by qn₀V_A, where q is the unit charge and V_A is the Alfvén speed based on B₀ and n₀. The mass ratio used is $m_{\mathrm{i}}/m_{\mathrm{e}}=\mathrm{100}$. Uniform guide fields with different values are added initially in the −y direction.

Figure 2 Profiles of electric field E_z at $\mathit{\delta }x=\mathrm{3}c/{\mathit{\omega }}_{\mathrm{pi}}$ marked by vertical dashed lines in Fig. 1.

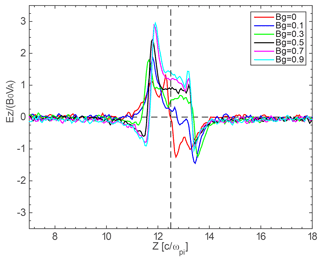
For convenience, we selected one of the two current sheets to illustrate our results. Electric fields E_z in the presence of different initial guide fields at tω_ci=32, when the reconnection rates reach their peak, are displayed in Fig. 1. In the case of a zero guide field, the Hall electric field normal to the current sheet exhibits a typical symmetric bipolar structure (Fig. 1a). When a small guide field (B_g=0.1B₀, Fig. 1b) is added in the system, the structure of a Hall electric field becomes asymmetric with respect to the current sheet though the bipolar structure is retained. With the increase in a guide field, thin current layers in the vicinity of the X points deflect toward the separatrix and magnetic islands are generated within the outflow, and sub-structures of the electric field also appear around the separatrix (Fig. 1c–f), i.e., a positive electric field E_z above the upper left separatrix and negative E_z beneath the lower right separatrix. There is only a negative E_z at and near the upper separatrix and positive E_z around the bottom separatrix in the case without a guide field (Fig. 1a). This difference indicates that the guide field brings some new features to electric fields besides causing the asymmetry.

To further illustrate how the guide fields affect the structure of E_z, six profiles of E_z along δx=3d_i in simulations of different guide fields are shown in Fig. 2. Here δx is the horizontal distance to the X point. Vertical dashed lines in Fig. 1 mark the locations of δx. The red line shows the E_z in the case without a guide field, which exhibits a centrosymmetric bipolar structure with positive E_z below $z=\mathrm{12.5}c/{\mathit{\omega }}_{\mathrm{pi}}$ and negative E_z above $z=\mathrm{12.5}c/{\mathit{\omega }}_{\mathrm{pi}}$. Here $z=\mathrm{12.5}c/{\mathit{\omega }}_{\mathrm{pi}}$ is the location of a neutral sheet where B_x=0. This is the typical Hall electric field as it is convergent toward the neutral sheet because electrons move faster than the ions (Sonnerup, 1979; Priest and Forbes, 2000). With the increase in the guide field, E_z is no longer centrosymmetric with respect to $z=\mathrm{12.5}c/{\mathit{\omega }}_{\mathrm{pi}}$. Positive E_z occupies a larger area than the negative E_z, and it no longer resides beneath the neutral sheet but extends to above the neutral sheet. This is consistent with Eastwood et al. (2010) in that the Hall electric field is asymmetric and shunted away from the neutral sheet in guide field reconnection. We noticed that there is a small negative excursion of E_z on the left-hand side of the enlarged positive E_z region in the cases with B_g≥0.3B₀. Thus, E_z exhibits a tripolar structure instead of a bipolar structure when the initial guide field is larger than 0.3B₀. The negative electric field ranges from 10.4 to 11.4 in the case of B_g=0.3B₀. It occupies a larger region in the case of B_g=0.5B₀. The size of the negative electric field seems to increase with the increment of the guide field. We also noticed that the amplitude of this negative E_z increases with the increment of the guide field, which is further discussed later.

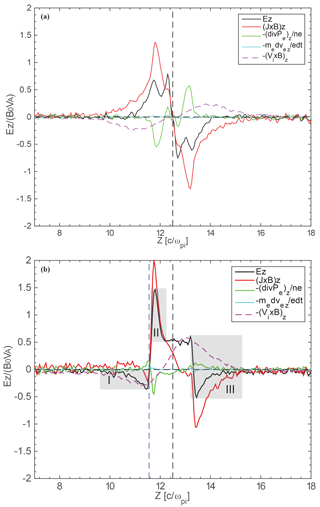
Figure 3 The contributions of each term in the generalized Ohm law to E_z. The upper panel shows the result with a zero guide field, while the lower panel shows the results for guide field B_g=0.5B₀. The three gray shades in the lower panel mark the three peaks of E_z in guide field reconnection.

To reveal the origin of this negative electric field, we examined the generalized Ohm law:

$$\mathit{E}=-{\mathit{V}}_{\mathrm{i}}\times \mathit{B}+{\displaystyle \frac{\mathit{J}\times \mathit{B}}{ne}}-{\displaystyle \frac{\mathrm{\nabla }\cdot \mathit{P}}{ne}}-{\displaystyle \frac{m_{\mathrm{e}}}{e}}{\displaystyle \frac{d{\mathit{V}}_{\mathrm{e}}}{\mathrm{d}t}}+\mathit{\mu }\mathit{J}.$$

The terms on the right-hand side (RHS) are the convective term, Hall term, divergence of the electron pressure tensor, electron inertial term, and resistivity term, respectively. The resistivity term is not evaluated in our simulations. In Fig. 3, we depict the relative contribution of each term on the RHS of the above equation to E_z. Upper panel shows the case with a zero guide field, while the lower panel shows the case with guide field B_g=0.5B₀. For the zero guide field case, peaks of E_z (at approximately z=11.5, 12.4, 12.6, and 13.5c∕ω_pi) are mainly balanced by the Hall terms (red) and the divergences of the electron pressure tensor (green), with the Hall terms dominating. The convective term (purple) is smaller than these two terms around the peak of E_z. For the guide field case, E_z is constituted by different terms in different regions. E_z (black) in regions II and III (marked by the gray shaded area in Fig. 3b) is primarily balanced by the combination of the Hall term, convective term, and divergence of the electron pressure tensor, while in region I, the negative E_z (black) is mainly balanced by the convective term (purple). This implies that this new electric field is a convective electric field instead of a Hall electric field.

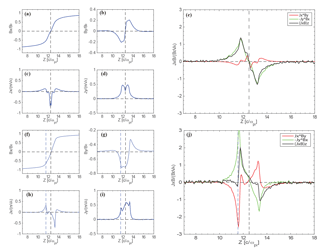
Figure 4 Subitems of the Hall term (J×B)_z. Panels from (a) to (e) display $B_x,B_y,J_x,J_y$ and two components of the Hall term, respectively, for the zero guide field case. Panels from (f) to (j) are similar to (a) to (e) but for the case of guide field B_g=0.5B₀. Black dashed lines in each plot mark the neutral sheet, while blue dashed lines in (f) to (j) mark the inflection points of E_z.

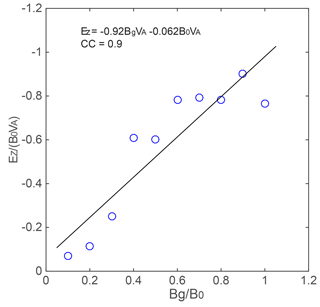
Figure 5 The relation between guide field strength and the peak of the newly emerged electric field. The black line indicates the linear fitting by the least square method.

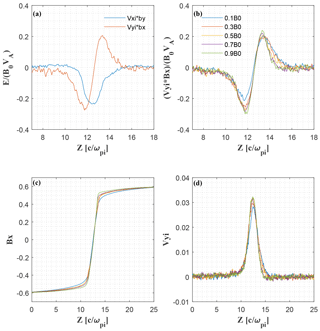
Figure 6 Subitems of the convection electric field V_yB_x−V_xB_y. (a) V_xB_y and V_yB_x for B_g=0.5B₀; (b) V_yB_x for different guide fields; (c) B_x for different guide fields; (d) V_y for different guide fields.

One may ask how the convective electric field emerges in the presence of the guide field. From Fig. 3 one can see that, although the convective term is asymmetric across the neutral sheet in the presence of a guide field, the amplitude does not change too much between the two cases. Nevertheless, the Hall term is substantially different between the two cases. The inflection point (where the Hall term reverses sign) of the Hall term is exactly the same as the inflection point of the convective term in non-guide field reconnection. However, in guide field reconnection, the Hall term is distorted with respect to the neutral sheet. It has been shown that the Hall term is the main factor leading to the distortion of the electric field E_z (Lai et al., 2015). The region with a positive Hall term shrinks compared to the case without a guide field; hence, a region with only a convective term emerges.

In addition, we divide the Hall term into two subitems, i.e., $(\mathit{J}\times \mathit{B}{)}_z=J_x{B}_y-J_y{B}_x$, as is shown in Fig. 4. The electric current density J_x, J_y and the magnetic field B_x, B_y are also shown in Fig. 4. One can see that the profiles of B_x are more or less similar in both cases, while the other three parameters vary much between the two cases. For the non-guide field case (Fig. 4e), J_y has a bifurcation structure with the minimum current density at the neutral sheet. For the guide field case, J_y has three peaks across the current sheet, with one peak located at B_x=0. J_x reaches its peak around B_x=0 without a guide field, while it moves toward the edge of the current sheet in the guide field case. This is consistent with the result of Zhou et al. (2014) that the outflow electron jet is deflected away from the neutral sheet as a result of the in-plane Lorentz force. The profile of B_y also varies significantly because of the superposition of the guide field. Therefore, the Hall term also varies much correspondingly. It is mainly provided by J_yB_x (green) around the peak value, while J_xB_y (red) is negligible compared to J_yB_x in the zero guide field case. This is because J_x and B_y are smaller than J_y and B_x around the peak of the Hall term, the location of which is away from the neutral sheet. In the presence of the guide field (Fig. 4j), the magnitude of J_xB_y increases significantly compared to the case without a guide field. This is because the imposed uniform guide field B_g and the deflected J_x increase the magnitude of J_xB_y. The two peaks of J_xB_y, one of which is around z=13.5 and the other around z=11.6, counterbalance the peaks of J_yB_x, which reduces the Hall electric field. The latter peak corresponds to the location of the newly emerged electric field.

Figure 5 displays the relation between the guide field B_g and the peak magnitude of the negative electric field E_z at δx=3d_i. We see that there is roughly a linear relation between guide field and electric field. The correlation coefficient is about −0.9. We fitted the results with a linear equation by the least square method: $E_z=-\mathrm{0.92}{B}_{\mathrm{g}}{V}_{\mathrm{A}}-\mathrm{0.062}{B}_{\mathrm{0}}{V}_{\mathrm{A}}$. This relation can be understood as follows. We have shown that E_z is mainly contributed by the convective term in the generalized Ohm law, i.e., $E_z\sim V_y{B}_x-V_x{B}_y$. Figure 6a and b show that the negative E_z is mainly balanced by V_yB_x, the magnitude of which increases with the increment of guide field strength. The variation of V_yB_x as a function of B_g is mainly caused by the variation of B_x as shown in Fig. 6c and d. We see that V_y does not vary obviously with the change in the guide field B_g, while B_x at the location of the negative E_z correlates well with B_g; i.e., the larger the $\left|B_{\mathrm{g}}\right|$, the larger the $\left|B_x\right|$. This is because the guide field decreases the width of reconnecting current sheet.

3 Discussion and summary

Eastwood et al. (2010) have pointed out that the moderate guide field causes considerable asymmetry in the Hall fields. Our simulations show that when there is a moderate guide field, the normal electric field will not only become asymmetric, but also evolve to a tripolar structure; i.e., a new negative electric field emerges. This new electric field is not a Hall electric field, but a convective electric field. It is negative and below the neutral sheet with a negative guide field. We can easily deduce that the new electric field appears above the neutral sheet with a positive value once the guide field is positive. It becomes significant because the Hall electric field in that location is small due to the cancellation of J_xB_y and J_yB_x as a result of the enhanced $\left|B_y\right|$ and $\left|J_x\right|$ due to the imposed guide field. The peak magnitude of the new electric field increases linearly with the increment of guide field strength.

Our finding may have applications in space observations. For instance, it may be used to infer the strength of a guide field, which is usually difficult to pinpoint solely from magnetic field measurements. The strength of a guide field is important because it determines the degree of electron magnetization as well as the electron energization efficiency in the vicinity of the diffusion region (Pritchett, 2006; Scudder and Daughton, 2008). With the measurement of this new convective electric field, we may be able to deduce the guide field strength based on the linear relation derived in this study. Hence this could be a supplemental way to infer the guide field strength.

The bipolar normal electric field structure is widely used as evidence of an ion diffusion region in space observations. When a spacecraft crossed the ion diffusion along the normal direction in anti-parallel reconnection, it would observe a bipolar E_N field (N is the current sheet normal; in our simulation it is z). However, according to this study, the spacecraft would record a tripolar E_N when crossing the ion diffusion region in the presence of a moderate guide field. Therefore, one must be cautious not to eliminate the crossing as a possible ion diffusion region based on the fact that a tripolar but not a bipolar E_N field is observed.

Recently Malakit et al. (2013) found a new electric field in asymmetric magnetic reconnection. This electric field is named the “Larmor electric field” because it is associated with the finite ion Larmor radius effect and hence is distinct from the Hall electric field. This electric field is also balanced by the convective term in the generalized Ohm law, which is similar to our simulation. This electric field structure in asymmetric reconnection may be complicated by a guide field, and this issue will be studied in future.