Ultrafast Kelvin waves in the MLT airglow and wind, and their interaction with the atmospheric tides

Airglow and wind measurements from the Brazilian equatorial region were used to investigate the presence and the effects of the 3–4-day ultrafast Kelvin waves in the MLT. The airglow integrated intensities of the OI557.7 nm, O₂b(0-1) and OH(6-2) emissions, as well as the OH rotational temperature, were measured by a multichannel photometer, and the zonal and meridional wind components between 80 and 100 km were obtained from a meteor radar. Both instruments are installed in the Brazilian equatorial region at São João do Cariri (7.4^∘ S, 36.5^∘ W). Data from 2005 were used in this study. The 3–4-day oscillations appear intermittently throughout the year in the airglow. They were identified in January, March, July, August and October–November observations. The amplitudes induced by the waves in the airglow range from 26 to 40 % in the OI557.7 nm, 17 to 43 % in the O₂b(0-1) and 15 to 20 % in the OH(6-2) emissions. In the OH rotational temperature, the amplitudes were from 4 to 6 K. Common 3–4-day oscillations between airglow and neutral wind compatible with ultrafast Kelvin waves were observed in March, August and October–November. In these cases, the amplitudes in the zonal wind were found to be between 22 and 28 m s⁻¹ and the vertical wavelength ranges from 44 to 62 km. Evidence of the nonlinear interaction between the ultrafast Kelvin wave and diurnal tide was observed.

Keywords. Atmospheric composition and structure (airglow and aurora) – meteorology and atmospheric dynamics (middle atmosphere dynamics; waves and tides)

1 Introduction

The planetary-scale waves along with the atmospheric tides strongly influence the large-scale dynamics in the mesosphere and lower thermosphere (MLT) region. In the equatorial MLT, many studies aimed to investigate the contribution of such waves to the total dynamics budget of that region. In this context, the 3–4-day ultrafast Kelvin wave (UFKW) has been investigated due to its effects on the MLT neutral dynamics and ionosphere. The UFKW is the third Kelvin wave mode, in addition to the slow and fast Kelvin wave modes. According to the linear theory, the Kelvin waves are equatorially trapped waves that propagate eastward and upward and that present only perturbation in the zonal direction (Andrews, 1987). Salby et al. (1984) observed the UFKW for the first time in satellite measurements. The first reports of the UFKW activity in the MLT region go back to the 1990s (Vincent and Lesicar, 1991; Vincent et al., 1993). The UFKW presents zonal phase speed ranging approximately from 100 to 130 m s⁻¹, and the zonal wavenumber one is dominant (e.g., Salby et al., 1984; Kovalam et al., 1999; Forbes et al., 2009). The UFKW is believed to play an important role in the well-known intraseasonal (ISO), semiannual (SAO) and quasibiennial (QBO) oscillations by depositing eastward momentum into the mean flow (e.g., Andrews, 1987; Miyoshi and Fujiwara, 2006). Deposition of momentum is found to induce zonal mean flow acceleration of up to 5 m s⁻¹ day⁻¹ (Riggin et al., 1997; Kovalam et al., 1999; Sridharan et al., 2002; Davis et al., 2012).

The effects of the Kelvin waves on the atmospheric composition occur through the transport of constituents and temperature-induced variations, which affects the production and loss in photochemical reactions. Investigations of the effects of the Kelvin waves on the stratospheric ozone revealed their influence on the fluctuations of the ozone concentrations and temperature (Timmermans et al., 2004, 2005). Forbes (2000) predicted in his dynamical model that the effects of the UFKW on the composition and temperature should affect the airglow emissions coming from 90 and 110 km altitudes. From ground-based airglow measurements, Takahashi et al. (2002) associated, possibly for the first time, the 3–4-day airglow variability with an UFKW. Afterwards, Lichstein et al. (2002), using the wave field from the Forbes (2000) model in an unidimensional chemistry–dynamical model, demonstrated that 3–4-day oscillations in the airglow reported by Takahashi et al. (2002) were consistent with the signature of an UFKW. Moreover, they showed that vertical winds are the dominant contributor to the UFKW-induced airglow variations. Buriti et al. (2005) extended the study of Takahashi et al. (2002) and found a year-to-year variation in the frequency of occurrence of the 3–4-day oscillations in the airglow.

Experimental measurements and numerical modeling have shown the influence of the UFKW in the day-to-day variability of the equatorial ionosphere (Takahashi et al., 2007; England et al., 2012; Onohara et al., 2013). One possible way for the planetary-scale waves to communicate their signatures to the ionosphere is through modulations of the atmospheric tides, which are able to penetrate into the ionosphere. Such modulations can occur due to the nonlinear interaction between the tides and planetary-scale waves. Theoretical predictions and observational evidence have shown that the nonlinear interaction between tides and planetary-scale waves can dramatically affect both neutral and ionized atmosphere dynamics (Teitelbaum and Vial, 1991; Pancheva, 2001; Pedatella and Liu, 2013). Recent advances have pointed out the potential of the secondary waves to induce variability in the ionosphere. For example, from a modeling perspective, Gan et al. (2017) showed that secondary waves generated by the nonlinear interaction of the diurnal and semidiurnal solar migrating tides with the 6-day planetary wave contribute to the shorter-term variability in the ionosphere. They observed that the relatively large magnitude and vertical wavelengths of two secondary waves (21 h period westward zonal wavenumber 2 and 13 h period westward zonal wavenumber 1) in the E-region zonal wind are favorable for an efficient dynamo modulation and responsible for the prominent signals of the respective waves in the vertical ion drift and peak electron densities. Yue et al. (2016), also from a modeling perspective, indicated that secondary waves resulting from the nonlinear interaction between the migrating diurnal tide and the quasi-2-day planetary wave induce corresponding oscillations in the vertical ion drift and ionospheric electron densities. Most of these studies address the nonlinear interaction between tides and the 2-day, 5-day and 16-day planetary waves. Concerning the UFKW, England et al. (2012) investigated the nonlinear interaction between them and the tides in the MLT and its effects in the ionosphere. Their findings show that the nonlinear interaction of the UFKW with the diurnal tide is seen between 82 and 88 km, and a resultant 3-day periodicity in the diurnal tide is seen to propagate up to altitudes of approximately 150 km. This could have a significant impact on the ionosphere via modulation of the E-region dynamo and it would carry the 3-day periodicity to higher altitudes. Effects of such interactions in the composition, however, have been little studied.

Airglow measurements can provide information about the composition and temperature of the MLT and, along with wind measurements, have the potential to expand the view of the MLT dynamics. In this study, we investigate the presence of 3–4-day oscillations associated with the UFKW in the MLT airglow and wind. Additionally, we examine the interaction between the UFKW and diurnal tide and its effects on the airglow variability.

2 Methodology and data set

The airglow intensities have been measured in the Brazilian equatorial region at São João do Cariri (7.4^∘ S, 36.5^∘ W) (hereafter Cariri) by a multichannel photometer, denominated MULTI-3. The MULTI-3 uses tilting interference filters to select the airglow wavelengths to be measured. The five interference filters enable the measurement of the airglow integrated intensities of the atomic oxygen green (OI557.7 nm) and red (OI630.0 nm) lines, molecular oxygen O₂b(0-1), Meinel OH(6-2) band, and the sodium NaD (589.0 nm) line. Additionally, from the OH and O₂b(0-1) spectra the rotational temperatures of these molecules are inferred. Additional details about the instrument can be found elsewhere (Takahashi et al., 2002). The airglow measurements are performed only during nighttime and usually occur during 13 nights centered in the new Moon phase. For this study we analyzed the OI557.7 nm (hereafter OI5577), O₂b(0-1) (hereafter O₂) and OH(6-2) (hereafter OH) emissions, and the OH(6-2) rotational temperature (hereafter TOH) measured during 2005. We analyze only months with at least 8 nights of observations, which makes it possible to observe two cycles of the 3–4-day periodic oscillations. Additionally, each night must have at least 3 h of continuous data. Table 1 shows the number of nights for each month in 2005 that met the former criteria.

Table 1 Number of nights per month with airglow observations in 2005.

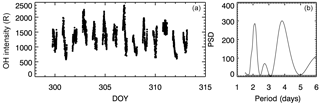
Figure 1 Example of the nightly OH airglow intensity between 26 October and 8 November 2005 (a) and its corresponding Lomb–Scargle periodogram (b).

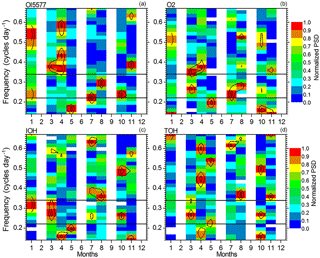
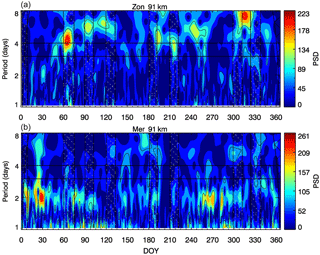
Figure 2 Monthly normalized Lomb–Scargle periodogram of OI5577 (a), O2b(0-1) (b) and OH(6-2) (c) emissions as well as OH (d) temperature. Horizontal black lines delimit the period range from 3 to 4 days and contoured black lines identify peaks in the periodogram.

To search for the 3–4-day periodic variations in the airglow we applied the Lomb–Scargle periodogram (Lomb, 1976; Scargle, 1982) (hereafter LS periodogram), which is suitable to search for periodic variations in nonregularly sampled data as the airglow. The airglow time series, corresponding to an entire period of observation, are built up by putting in sequence all the nights with measurements. Afterwards, the mean intensity for the corresponding time interval is subtracted from the original time series and the LS periodogram is calculated for the residuals. This procedure is performed for each emission and for each period of observation. Figure 1 shows an example of the OH intensity measured between 26 October and 8 November in 2005 and its corresponding LS periodogram, which shows the periodicities present in the data. Each group of data corresponds to one night of observation.

The neutral-wind components are calculated by using measurements performed by the meteor radar also installed at Cariri observatory. The radar operates at 35.24 MHz frequency and uses one transmitter antenna and an array of five receiving ones. The radar transmits pulses of 12 kW peak power, which is partially reflected back by the ionized trail produced during meteor ablation. From reflected echoes, zonal and meridional wind components are retrieved. For this study, we calculated the zonal and meridional winds in layers centered at 82, 85, 88, 91, 94 and 98 km altitudes at a time resolution of 2 h. The planetary wave dominant periodicities in zonal and meridional wind were identified by means of the Morlet wavelet transform (Torrence and Compo, 1998), which also works as a band-pass filter. Additionally, harmonic analysis based on the least mean squared fitting was used to extract the amplitude and phases of the planetary waves periodicities in the wind and airglow.

Figure 3 Wavelet spectra of the zonal (a) and meridional (b) wind at 91 km in 2005.

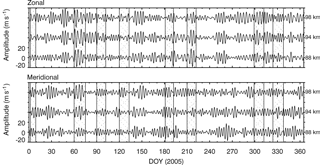
Figure 4 Band-passed zonal and meridional wind at 88, 94 and 98 km. Cutoff periods are from 2.8 to 4.5 days.

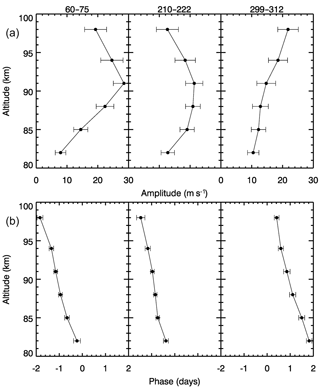
Figure 5 Vertical amplitude (a) and phase profiles (b) of the 3–4-day common oscillations in the zonal wind and airglow. Numbers on the top panels indicate the days of the year.

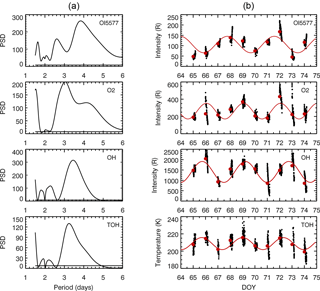
Figure 6 Lomb–Scargle (LS) spectra (a) of the OI557.7 nm, O2(0-1) and OH(6-2) emissions as well as OH rotational temperature (TOH) calculated with data acquired between 00:00 and 05:00 LT, along with its respective time variability from 5 to 14 March 2005 (b). The red curve represents a harmonic fitting corresponding to each peak identified in the LS periodogram.

3 Results and discussion

3.1 Wind and airglow spectral analysis

The airglow and OH rotational temperature time series have been analyzed by applying the LS periodogram as described in the previous section. Figure 2 shows the normalized LS spectra of OI5577, O₂ and OH emissions as well as TOH for all months with observations in 2005. For each parameter, all monthly LS spectra were grouped to produce a 2-D plot, which provides an entire year's view. In this case, the spectrum of each month is exhibited without the blank space due to the interval in which there is no airglow measurements because of the Moon phase. The blank spaces correspond to the months without data. The vertical axis represents the frequency in cycles per day and covers a period range from 1.5 to 7 days. The power spectral density (PSD) higher than 0.4 indicates a confidence level of 95 %, and black line contours identify the spectral peaks in the periodogram. The horizontal black lines delimit the period range from 3 to 4.5 days. The spectra show the presence of periodic variations in the airglow and rotational temperature at frequencies corresponding to the periods near 2, 3–4 and 5–7 days. These periodic variations are observed simultaneously in more than one parameter throughout the year. Such periodic variations in the MLT can be explained due to the presence of the planetary-scale waves passing though the emission layers. The 3–4-day oscillation associated with the UFKW will be the focus of this study.

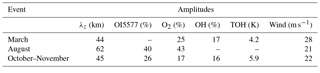
The 3–4-day periodic variations in the airglow and temperature are observed in all seasons. They appear in January, March, July, August and November. We call attention to the 3–4-day periodic variation in March, which is known for its effects on the ionosphere (see Takahashi et al., 2007). Despite being well characterized, this oscillation does not appear in the OI5577 emission. As will be discussed later, this may be related to effects of the atmospheric tides. The amplitude of variation, relative to the mean intensity, induced by the 3–4-day oscillations are 18–45 % in OI5577, 17–43 % in O₂ and 16–28 % in OH. In the OH temperature, they are between 4 and 6 K. These values are similar to those presented previously by Takahashi et al. (2002) and Buriti et al. (2005). Other planetary waves observed at middle latitudes, e.g., over time periods of 2, 5, 10 and 16 days, induce even higher amplitudes in the airglow intensities. For example, Takahashi et al. (2013) reported amplitudes of 57, 51 and 29 % induced by a 10-day planetary wave in the OI5577, O₂ and OH emissions, respectively, at middle latitudes. Nevertheless, the amplitudes in the OI5577 and O₂ emissions are systematically higher than in the OH emission. In addition to possible amplitude growth due to energy conservation, as pointed out by Egito et al. (2017), such behavior may be related to the dependence of each emission on the atomic oxygen concentration, which is approximately cubic, squared and linear in the OI5577, O₂ and OH emissions, respectively.

The presence of 3–4-day oscillations in the airglow in all seasons agrees with previous reports based on MLT wind and satellite-borne temperature measurements. This way, investigations concerning the variability of the 3–4-day induced oscillations in the MLT wind indicate the presence of semiannual variations in their occurrence, with intensification around equinoxes (Yoshida et al., 1999; Tsuda et al., 2002; Davis et al., 2012). Additionally, based on the temperature measurements of the SABER/TIMED satellite, Forbes et al. (2009) showed that the UFKW exists intermittently at amplitudes of the order of 3–10 K between 80 and 120 km during all months of the year, with variability at periods typically in the 20–60-day range.

To complement the information about the 3–4-day oscillations observed in the airglow, we searched for common periodic oscillations in the MLT neutral wind. Figure 3 shows the periodic oscillations in the MLT zonal and meridional wind at 90 km revealed by means of the wavelet transform. The zonal wind spectrum is marked by periodic oscillations at periods between 3 and 4 days and periods from 5 to 8 days. However, the meridional wind spectrum is primarily dominated by quasi-2-day oscillations, which are particularly strong during the austral summer in January, although they are also observed around spring equinox. The white hatched areas delimited by vertical black lines indicate the intervals with coincident airglow measurements. From the airglow LS periodogram and the wind wavelet spectra, Figs. 2 and 3, respectively, one can identify common oscillations at periods near 2 days, 3–4 and 5–7 days on several occasions throughout the year. In the 3–4-day period range, the wind power spectrum indicates the presence of common oscillations in the airglow and in the zonal wind in March (days 60 to 80) and August (days 210 to 230). Although there are other signal enhancements in the 3–4-day band present in the wind spectra, none of them entirely matches with those observed in the airglow. That is the case of the 3–4-day oscillations identified in the airglow in January (days 2 to 9), July (days 210 to 225) and October–November (days 300 to 320).

To investigate additional features of the 3–4-day oscillations in the winds, Fig. 4 shows the filtered zonal and meridional winds at 88, 94 and 98 km altitudes, which correspond approximately to the nominal altitude peaks of the OH, O₂ and OI5577 emissions, respectively. Cutoff frequencies correspond to the periods from 2.8 to 4.2 days. The hatched areas delimited by vertical black lines indicate intervals with airglow observations. The filtered zonal and meridional winds exhibit bursts of amplitude intensification throughout the year. Significant amplitudes (at least 10 m s⁻¹) are observed in the zonal and meridional wind during intervals with coincident airglow observations. In spite of being observed in both components, the amplitude intensifications are higher in the zonal wind component and reach up to 20 m s⁻¹. Comparing the 3–4-day oscillations in the filtered wind and in the airglow, one can see that in addition to the cases of March and August previously identified in the wavelet spectra, the case of October–November (days 299–312) also exhibits coincident enhancements in the zonal wind amplitudes. In March (days 60–75) the zonal wind presents high amplitudes in the 3–4-day band in all altitudes and reaches 20 m s⁻¹ at 94 km. Although the amplitudes in the meridional wind are not negligible, they are lower than in the zonal wind. In the case of the 3–4-day oscillations in August (days 210–222) and in October–November (days 299–312) in the airglow, the wind is characterized by significant amplitudes in the zonal component, while amplitudes in the meridional wind component are much lower. As predicted by the linear theory, Kelvin waves present perturbations only in the zonal direction. This suggests that the aforementioned cases of the common 3–4-day oscillations in the airglow and wind are compatible with the presence of the UFKW.

The zonal and meridional band-passed winds indicate that the other two cases (January and July) with 3–4 oscillations observed in the airglow do not exhibit the characteristics of an UFKW. In January, significant amplitudes are observed in the meridional wind at 94 and 98 km, while in the zonal wind component the amplitudes are much lower. Considering the case of July, during almost the entire period of airglow measurements the amplitudes in the meridional wind are higher than in the zonal wind. Just at the end of the airglow observations, the 3–4-day amplitudes increase in the zonal wind. Younger and Mitchell (2006) investigated the wind-field variability in the equatorial MLT at Ascension Island (8^∘ S, 14^∘ W) and observed relatively high activity of the 3–4-day wave in the meridional wind. They explained the presence of the 3–4-day waves in the meridional wind due to the presence of mixed Rossby–gravity waves and long-period inertia–gravity waves. As Ascension Island and Cariri latitudes are similar, the presence of the 3–4-day oscillations in the airglow in January and July may be explained due to the penetration of mixed Rossby–gravity waves or long-period inertia–gravity waves.

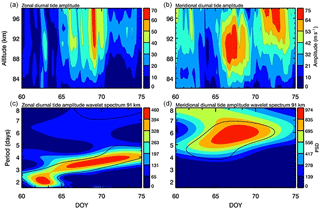
Figure 7 Diurnal tide amplitude in the zonal (a) and meridional (b) wind. Wavelet spectrum of the zonal and meridional diurnal tide amplitudes at 91 km.

To provide additional evidence for an UFKW interpretation of the common 3–4-day oscillation in the airglow and wind, we investigate their vertical structures. From harmonic analysis, we extracted the amplitudes and phases of the 3–4-day oscillation in the zonal wind observed in March, August and October–November. Figure 5 shows the results. The numbers on the top indicate the time interval (days of year) analyzed. Amplitudes are found to increase from near 10 m s⁻¹ at 82 km altitude to 28, 21 and 15 m s⁻¹ at 91 km in events of March, August and October–November, respectively. While in the first two events the amplitudes decrease above this altitude, in the third one the amplitude increases up to 22 m s⁻¹ at 98 km. All the three cases exhibit downward phase propagation, indicating an upward wave propagation and energy flux. From the phase lag among the wind layers, we estimated the vertical wavelengths. The values are 44 ± 4 km for March, 62 ± 7 km for August and 45 ± 5 km for October–November. The vertical wavelengths inferred from wind measurements associated with UFKW in the MLT range from 35 to 85 km, and typical values are around 40 km (Vincent, 1993; Younger and Mitchell, 2006; Davis et al., 2012). Then our results reinforce that the three common 3–4-day oscillations observed in the airglow and wind are consistent with an UFKW interpretation. Table 2 summarizes the characteristics of the 3–4-day common oscillations in the airglow and zonal wind observed in March, August and October–November.

Table 2 Characteristics of the 3–4-day oscillations observed simultaneously in the airglow and wind.

3.2 Interaction between the UFKW and the diurnal tide

The 3–4-day oscillation observed in March in the airglow presents some interesting features that are worthy of investigation. From the spectra in Fig. 2, one can see that the peaks in the LS periodogram correspond to periodic oscillations of about 3.5 days in the OH and O₂ emissions and in the TOH. However, the OI5577 emission does not present the same signature. Instead, there is a signature of a 2.7-day oscillation. During this time interval, the 3–4-day oscillation is quite well defined and its structures in the horizontal wind and the vertical wavelengths are consistent with an UFKW. Additionally, the airglow observations present good continuity with almost no spurious data. The question is why the 3–4-day oscillation does not appear in the OI5577 emission. To investigate this point we performed additional analysis of the simultaneous airglow and wind measurements. The 3–4-day oscillation in August was not observed in the OH emission and temperature. In this case, its background emission was relatively high and variable during the observations, which may have influenced its identification in the data.

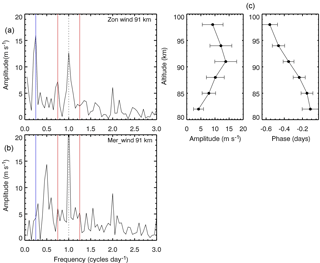
Figure 8 Fourier amplitude spectrum of the zonal (a) and meridional (b) wind between days 60 and 75 of 2005 and vertical structure of amplitude and phase of the 0.75 cycles day⁻¹ secondary wave in the zonal wind (c).

The LS periodograms of Fig. 2 were obtained using the airglow data acquired during the whole night. We performed additional LS periodogram analysis without considering the entire airglow nightly measurements. Instead, we take the airglow data only within specific time intervals during the night. This is because it is well established from ground-based and satellite-borne measurements and modeling studies that the atmospheric tides strongly affect the MLT equatorial airglow and exhibit pronounced nocturnal variation (e.g., Shepherd et al., 1995; Yee et al., 1997; Takahashi et al., 1998). In addition, the tides can interact with other waves (e.g., Teitelbaum and Vial, 1991; Pancheva, 2001; England et al., 2012; Alves et al., 2013), leading to changes in their amplitudes and phases, which in turn could affect the airglow emissions. As there was a 1-day gap on 4 March in the airglow data, we take for this particular analysis the data from 5 to 14 March, which present excellent quality and continuity, and are still long enough to allow the study of the 3–4-day oscillations. First we analyzed the airglow time series built only with data obtained between 18:00 and 00:00 LT. In this case, the periodicities in the 3–4-day band exhibit essentially the same features as those observed in the LS periodogram built with the whole-night data presented in Fig. 2; i.e., the OH and O₂ emissions as well as OH temperatures present oscillations of approximately 3.5 days, while the OI5577 emission presents a 2.8-day oscillation. Next, we performed the LS spectral analysis of the airglow and OH temperature with only the data acquired between 00:00 and 05:00 LT. Figure 6 shows the results. In the right panels are the LS periodograms of the airglow emissions and OH temperature and in the left panels are the respective airglow intensities and OH temperature, along with their respective nightly average (red dots). The red curve represents a fitting corresponding to the 3–4-day harmonic identified in the LS analysis in each parameter. It is interesting to note that in this case the OI5577 emission exhibits a very well-defined 3.5-day oscillation, as well the other two emissions and the OH temperature. In other words, now all the emissions and the temperature exhibit the same periodic pattern, and in the OI5577 emission, the effects of the 3.5-day wave are very prominent.

The time of acquisition of the data can affect the observed airglow and inferred temperature variability, which is related to effects of the atmospheric tides (e.g., Reisin and Scheer, 2017). The influence of the solar tides in the MLT airglow is well known. This way, in the equatorial region, the airglow variability induced by the tides is strong before local midnight, particularly in the OI5577 emission, and after this time, their effects are weaker (Shepherd et al., 2005). Then, the variability of the tides on the scale of days could affect the airglow emissions. The source of variability of the atmospheric tides include, as well as other factors, the nonlinear interaction with planetary-scale waves. As proposed by Teitelbaum and Vial (1991), when a nonlinear interaction between a tide and planetary wave takes place, the result is the generation of secondary waves whose frequencies are the sum and difference of the primary waves (tide and planetary wave) frequencies. As well as this, the amplitude of the tides are modulated in the periods of the planetary waves. Previous investigations of England et al. (2012) using meteor radar, incoherent scatter radar and satellite wind data, along with satellite-borne temperature data, reported the evidence of the nonlinear interaction between the UFKW and the diurnal tide in the MLT and its effects in the E-region of the ionosphere. To investigate a possible interaction between the UFKW and atmospheric tides, we analyzed the amplitudes of the diurnal tide in the zonal and meridional wind during the presence of the 3–4-day UFKW in March. The amplitudes of the diurnal and semidiurnal tides were extracted by applying the harmonic analyses to a 2-day long moving window and stepped forward by 1 day. As the diurnal tide is dominant at Cariri latitude (e.g., Lima et al., 2007), only the amplitudes of the diurnal tide in the zonal (Fig. 7a) and meridional (Fig. 7b) winds together with the wavelet spectra of the zonal (Fig. 7c) and meridional (Fig. 7d) diurnal tide amplitudes at 91 km are plotted. The amplitudes of the diurnal tide in the zonal wind are weak between days 60–65 and 70–75. Additionally, they present a quasiperiodic enhancement of about 4 days between days 65 and 70 around 92 km. The amplitude of the diurnal tidal in the meridional wind also exhibits a similar decrease during days 60–65 and quasiperiodic enhancement between days 65 and 75, but in this case, it is longer than 5 days. The wavelet spectra of both zonal and meridional diurnal tide amplitudes at 91 km confirm the presence of the aforementioned periodic variations.

Figure 8 shows the Fourier amplitude spectra of the zonal (a) and meridional (b) wind at 91 km using data from days 60 to 75. The zonal and meridional wind spectra present clear signatures of the diurnal tide. As expected, the diurnal tide is stronger in the meridional wind. The UFKW signature appears as a peak at the frequency of 0.25 cycles day⁻¹ (4-day period) and it is seen only in the zonal wind as was also expected. In the meridional wind, there is a signature of a 2-day wave (0.5 cycles day⁻¹). The red vertical lines indicate the frequencies of the predicted secondary waves that would be generated by the nonlinear interaction between the diurnal tide and UFKW. Among the four predicted frequencies in the zonal and meridional wind, only that at 0.75 cycles day⁻¹ in the zonal wind is clearly distinguished and strong.

Secondary waves generated from the nonlinear interaction between tides and planetary waves may propagate upward and induce ionospheric variability (e.g., England et al., 2012; Yue et al., 2016; Gan et al., 2017). This way, we investigated the amplitude and phase vertical structures of the 0.75 cycles day⁻¹ secondary wave shown in Fig. 8c. Its amplitude profile is similar to the UFKW seen in Fig. 5. It increases from 4 m s⁻¹ at 82 km to 14 m s⁻¹ at 91 km and afterwards decreases to 9 m s⁻¹ at 98 km. Its phase vertical structure exhibits downward progression, which indicates an upward flux of energy and momentum. From the phase lag we estimated a vertical wavelength of approximately 44 km. This relatively long vertical wavelength (Forbes, 2000; Gan et al., 2017) may allow the secondary wave to penetrate into the E-region dynamo and induce variability in the ionosphere. Such investigation, however, is outside the scope of this study.

The periodic variations in the tidal amplitudes and the presence of the predicted 0.75 cycles day⁻¹ secondary wave may be an indication of a nonlinear interaction between the diurnal tide and UFKW during March 2005 at Cariri. To investigate in more detail the effects of the nonlinear interaction on the airglow and atmospheric composition, especially on the atomic oxygen, a modeling study with a complete atmospheric model is in progress.

4 Conclusions

In this study, we investigated the presence and the effects of the 3–4-day oscillations in the equatorial MLT airglow and wind. The 3–4-day oscillations in the OI557.7 nm, O₂b(0-1) and OH(6-2) emissions, as well as in the OH rotational temperature were identified in January, March, July, August and October–November. Three events of common 3–4-day oscillations in the airglow and wind compatible with the signature of ultrafast Kelvin waves were identified in March, August and October–November. In these cases the amplitudes in the airglow range 40–43 % in OI557.7 nm, 17–43 % in O₂b(0-1), 16–17 % in OH(6-2) emissions and 4–6 K in OH rotational temperatures. The amplitudes in the zonal wind were found to be at their maximum around 90 km and their highest magnitudes range between 22 and 28 m s⁻¹. Vertical wavelengths exhibited typical values for UFKW and range between 44 and 62 km. Evidence of a nonlinear interaction between the UFKW and the diurnal tide was observed in the March event.