Electron mirror branch: observational evidence from “historical” AMPTE-IRM and Equator-S measurements

Based on now “historical” magnetic observations, supported by few available plasma data, and wave spectra from the AMPTE-IRM spacecraft, and also on “historical” Equator-S high-cadence magnetic field observations of mirror modes in the magnetosheath near the dayside magnetopause, we present observational evidence for a recent theoretical evaluation by Noreen et al. (2017) of the contribution of a global (bulk) electron temperature anisotropy to the evolution of mirror modes, giving rise to a separate electron mirror branch. We also refer to related low-frequency lion roars (whistlers) excited by the trapped resonant electron component in the high-temperature anisotropic collisionless plasma of the magnetosheath. These old data most probably indicate that signatures of the anisotropic electron effect on mirror modes had indeed already been observed long ago in magnetic and wave data, though they had not been recognised as such. Unfortunately either poor time resolution or complete lack of plasma data would have inhibited the confirmation of the required pressure balance in the electron branch for unambiguous confirmation of a separate electron mirror mode. If confirmed by future high-resolution observations (like those provided by the MMS mission), in both cases the large mirror mode amplitudes suggest that mirror modes escape quasilinear saturation, being in a state of weak kinetic plasma turbulence. As a side product, this casts as erroneous the frequent claim that the excitation of lion roars (whistlers) would eventually saturate the mirror instability by depleting the bulk temperature anisotropy. Whistlers, excited in mirror modes, just flatten the anisotropy of the small population of resonant electrons responsible for them, without having any effect on the global electron-pressure anisotropy, which causes the electron branch and by no means at all on the ion-mirror instability. For the confirmation of both the electron mirror branch and its responsibility for trapping of electrons and resonantly exciting high-frequency whistlers, also known as lion roars, high time- and energy-resolution observations of electrons (as provided for instance by MMS) are required.

1 Introduction

Within the past 4 decades, observations of magnetic mirror modes in the magnetosheath and magnetotail of Earth's magnetosphere, and occasionally also elsewhere, have been ubiquitous (see Tsurutani et al., 2011, and Sulem, 2011 for reviews on observation and theory, respectively). They were, however, restricted to the ion-mirror mode and the detection of electron-cyclotron waves (lion roars), which propagate in the whistler band deep inside the magnetic mirror configuration and are caused by trapped resonant anisotropic electrons. (Baumjohann et al., 1999; Breuillard et al., 2018; Constantinescu et al., 2003; Czaykowska et al., 1998; Luehr and Kloecker, 1987; Maksimovic et al., 2001; Remya et al., 2014; Smith and Tsurutani, 1976; Treumann et al., 1990; Tsurutani et al., 1982; Zhang et al., 1998). These observations confirmed their theoretical prediction based on fluid (Baumjohann and Treumann, 1996; Chandrasekhar, 1961; Hasegawa, 1969; Southwood and Kivelson, 1993; Thorne and Tsurutani, 1981; Treumann and Baumjohann, 1997) and the substantially more elaborated kinetic theory (Pokhotelov et al., 2000, 2002, 2004), which essentially reproduces the linear fluid results, while including some additional higher-order precision terms (like, for instance, finite Larmor radius effects). An attempt to model the final state of mirror modes by invoking pressure balance can be found in Constantinescu (2002).

Recently, this theory has been extended to the inclusion of the effect of anisotropic non-resonant electrons on the evolution of mirror modes (Noreen et al., 2017) in the linear and quasilinear regimes. Though in principle a rather simple matter, the more interesting finding (when numerically solving the more complicated linear dispersion relation) was that Larmor radius effects are fairly unimportant, while the electrons do indeed substantially contribute to the evolution of mirror modes and in the restriction to quasilinear theory (as it is of the lowest order and therefore believed to be the dominant non-linear term) as well as to their quasilinear saturation, albeit in rather different wavenumber and frequency or growth rate regimes.

This finding leads immediately to the question of observation of such effects in the mirror modes in real space, and especially to the question whether signatures of the electron mirror branch had already been present in any now historical spacecraft observations of mirror modes. Here we suggest that, based on more than 3-decade-old AMPTE-IRM observations in the magnetosheath near the dayside magnetopause and 2-decade-old Eq-S magnetic high-resolution observations in the equatorial magnetosheath, both mirror mode branches (the ion and the electron branch) most probably had indeed already been detected in the data, though, at that time, the electron branch found only recently in linear theory by Noreen et al. (2017) had remained completely unrecognised. However, the same observations also prove that quasilinear theory as a saturation mechanism does not apply to real mirror modes, at least not to mirror modes evolving under the conditions of the magnetosheath to large amplitudes where the former measurements had been performed – and probably also not to those observed in the solar wind. All those observations indicate that the mirror mode amplitudes by far exceed those predicted by quasilinear theory.

2 Observations

Figure 1 shows a typical sequence of magnetosheath mirror modes lasting longer than 6 min during an AMPTE-IRM passage on 21 September 1984. The lower panel shows variation of the magnitude of the magnetic field that is caused by the (ion) mirror mode with amplitude $\left|\mathit{\delta }B\right|\sim \mathrm{0.5}\left|B\right|$. The upper panel is the wave electric power spectrogram. The wavy white line is the electron cyclotron frequency f_ce which maps the magnetic field from the lower panel into the frequency domain. Resonant whistlers (dubbed lion roars) emitted in the central mirror mode minima are indicated for two cases. As was shown a decade later (Baumjohann et al., 1999) by visualising their magnetic wave packet form from high-resolution magnetic field measurements on the Equator-S (Eq-S) spacecraft, and thereby directly confirming their electromagnetic nature, lion roars do indeed propagate in the whistler band parallel to the magnetic field with central frequency roughly f_lr∼0.1f_ce of the local central cyclotron frequency. Though barely recognised, these observations were very important for both these reasons. The origin of the other sporadic intense lion roar emissions centred around f∼0.5–0.7 kHz remained unclear. They are not related to the mirror mode minima. They occur at the mirror mode flanks, being of more broadband nature, more temporarily irregular, and of higher frequency. For being in the whistler band they require the presence of a trapped resonant anisotropic electron component which is difficult to justify at those locations where they appear. In addition there are irregular high-frequency broadband electric signals above f_ce, reaching up to the local plasma frequency at f_e∼60–70 kHz. Their spiky broadband nature, being independent of the presence of the cyclotron frequency, suggests that they are related to narrow structures or boundaries of which such broadband Fourier spectra are typical (Dubouloz et al., 1991). The broad unstructured (green) quasi-stationary noise below roughly 2  Hz propagates in the electrostatic ion-acoustic band and is of little interest here as its presence is well-known and is typical for the magnetosheath, being completely independent from the evolution of the mirror mode.

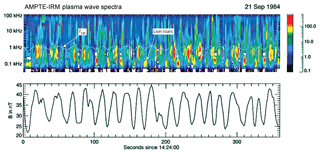
Figure 1 AMPTE-IRM observations of mirror modes in the magnetosheath and related plasma wave power spectra (see the colour bar on the right for relative log-scale intensities). Indicated are the electron cyclotron frequency f_ce (white trace mimicking the mirror mode magnetic field in the lower panel) and lion roar emissions in the mirror mode minima (Baumjohann et al., 1999) at frequency f_lr∼0.1f_ce (Treumann et al., 2004a). The higher-frequency sporadic emissions below the electron cyclotron frequency are related to the flanks of the ion-mirror mode and are interpreted as high-frequency lion roars (high-frequency whistlers) caused by resonant electrons trapped in the electron mirror branch oscillations, which develop in the ion-mirror mode and are caused by the bulk electron temperature anisotropy of the magnetosheath plasma. The weak broadband signals extending in frequency above and beyond f_ce are broadband electrostatic noise (most clearly seen, for instance, around 150 s). They are most probably related to the steep trapped electron–plasma boundaries which locally form when the electron mirror branch evolves and thus also correlate with high-frequency lion roars. In any case, extension of lion roars beyond f_ce into the purely electrostatic frequency range is a clear indication of the presence of steep electron plasma gradients (Dubouloz et al., 1991). High-frequency electric emissions centred around >3 kHz and above are of different nature. In this range, above plasma and upper hybrid frequencies, they are mostly sporadic electromagnetic noise in the magnetosheath plasma turbulence.

In order to prove that the above sequence of magnetic fluctuations is indeed mirror modes, Fig. 2 shows another nearly identical sequence of AMPTE-IRM observations, including plasma data. (Unfortunately, of the former historical sequence no plasma data are available anymore, while in the data set used in this figure no wave data have survived.) The maximum time resolution of the magnetic field on AMPTE-IRM was ∼30 ms (32 Hz). We show a 120 s long full-resolution excerpt from a long magnetic record. The similarity between the magnetic data in Figs. 1 and 2 is striking both in period and amplitude. Four cases are indicated in Fig. 2 in order to demonstrate the detectable (at these time resolutions) anti-phase behaviour in the magnetic and plasma data in the magnetic amplitude (or magnetic pressure) in panel 1, density in panel 3, and temperature in panel 6. (One may note the logarithmic scale in the temperature.) The anti-correlation is not very well expressed, however, because of the vastly different time resolutions of the magnetic and plasma instruments and the stroboscopic and geometrical effects related to the locations and directions of the plasma detector and magnetometer. However, the four cases shown give an indication of its presence, which is sufficient for our purposes here. On the other hand it is evident that the available instrumental resolutions inhibited any detection of the demanded anti-correlations (pressure balance) between fluctuations in the magnetic field pressure and the electron component, which are considered the dominant signature of mirror modes¹.

We will argue that the broadband sporadic nature of the unidentified emissions, their relation to the flanks of the ion-mirror mode, and intensification below the local cyclotron frequency suggest that they are the signatures of electron-mirror branch structures which are superimposed on the ion-mirror branch which dominates the gross behaviour of the magnetic field.

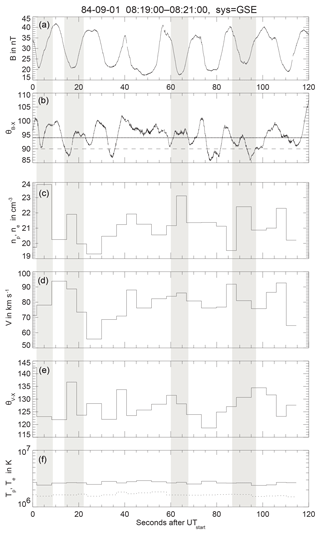
Figure 2 Spin-resolution (∼4 s) AMPTE-IRM plasma observations of mirror modes in the magnetosheath, lacking wave data. (Spin axis was about perpendicular to the ecliptic.) Panel (a) shows the magnitude of the magnetic field and (b) shows the angle of the magnetic vector with sun direction X in GSE coordinates. The mean direction of the field is indicated by the dotted line during the entire long phase of observations of which the 2 min shown are just an excerpt (with field almost in the ecliptic and about tangential to the shock and magnetopause). Panel(c) shows the plasma density in the available spacecraft at spin resolution for a single measurement. Panels (d) and (e) give the mean velocity and direction angle of flow. Panel (f) (in logarithmic scale) shows the plasma temperature, the least reliable due to the resolution. Four cases of mirror troughs are shaded, roughly showing the anti-correlation between magnetic field (or magnetic pressure) and density (or plasma pressure). Though this event is taken at a different occasion, it is similar to the observations in Fig. 1, when no plasma data were available. One may note the small-scale depressions on the average course of the magnetic trace, which indicate decreases in magnitude of the magnetic field and magnetic pressure. Higher resolutions of these will be seen in the Eq-S measurements shown in the next figure. It is these depressions which we take as signatures of the electron mirror branch.

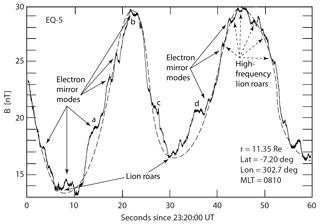
Figure 3 High-resolution Eq-S observations of mirror modes in the magnetosheath near the magnetopause at the high sampling rate of 128 Hz. The dashed line is a low-pass-filtered trace yielding a quasi-sinusoidal approximation to the ion-mirror mode structure. Asymmetries are presumably caused by the obliqueness of the ion-mirror mode structure in combination with the plasma flow, which transports them to pass over the spacecraft. The strong modulation of their shapes on the smaller scale is produced by the superimposed small-scale electron mirror mode structure on the ion-mirror mode. Signatures of low-frequency (f≲0.1f_ce) lion roars are found in the ion-mirror minima (Baumjohann et al., 1999). Higher-frequency lion roars concentrate in the minima of the electron mirror branch structures where they are seen as broadenings of the magnetic trace.

For this purpose we refer to a rare observation by the Eq-S spacecraft at the high magnetic sampling rate of 128 Hz, which is reproduced in Fig. 3. Unfortunately, as had already been noted (Baumjohann et al., 1999), no plasma measurements were available due to failure of the plasma instrument. However, even if the plasma instrument would have worked properly, the resolution of optimum of only ∼3 s spacecraft spin (comparable to the plasma resolution of AMPTE-IRM of ∼4 s) would in any case not have been sufficient for resolving the electron structures in the plasma data and establishing or confirming any pressure balance between the electron fluid (not the resonant electrons responsible for the lion roars) and magnetic field, as was done with the AMPTE observations for the ion-mirror modes. For the identification of the large-amplitude magnetic oscillations as genuine ion-mirror modes, even though no plasma measurements were available on Eq-S, the reader is referred to Lucek et al. (1999a, b), who analysed the whole sequence of magnetic oscillations measured by Eq-S of which our short high-resolution example is just a sample selection. Figure 3 shows this high-resolution record (Baumjohann et al., 1999) of the magnetic field magnitude from this data pool of Eq-S. Just two ion-mirror oscillations of the cycle analysed in Lucek et al. (1999a, b) and used in that paper are shown here. One may note that their period and amplitude is of the same order as in the case of the AMPTE observations, which were approximately at a similar location in the magnetosheath, thereby providing additional independent confidence for them as being ion-mirror modes. One observes the general evolution of the magnetic field, which is reflected in the slight asymmetries of the structures which pass over the spacecraft. These might be caused by temporal evolution of the mode or also by crossing the spatially densely packed mirror mode oscillations (Treumann and Baumjohann, 1997) by the spacecraft under an angle. The maximum of the magnetic field in this case is ∼30 nT with a $\left|\mathit{\delta }B\right|/B\sim \mathrm{50}$ % amplitude oscillation, almost identical to what AMPTE-IRM had observed. The very small-amplitude high-frequency fluctuations of the field in the field minima belong to the lion roars mentioned above and have been investigated in detail (Baumjohann et al., 1999). In the left-hand field minimum at the bottom of the ion-mirror oscillation the small local maximum of the magnetic field (like on the bottom of a wine bottle) can be recognised, to which Baumjohann et al. (1999) refer as an “unexplained” structure which, as shown here, turns out to be the signature of the electron branch caused by the bulk temperature–pressure anisotropy of the ion-mirror trapped electron component.

Figure 4 Four cases (a–d) in Fig. 3 of high-frequency lion roars related to the electron mirror mode branch, extracted and enlarged. Cases a, c, d are at the flanks of the ion-mirror structures, case b is on top in the first absolute magnetic maximum, all causing a broadening of the magnetic trace. At the 128 Hz sampling rate, such oscillations cannot be resolved. It allowed Baumjohann et al. (1999) to analyse the lowest frequencies (f≲0.1f_ce at f_ce≲1 kHz), but inhibits a similar analysis for the higher-frequency lion roars. In a linear sinusoidal oscillation superimposed on the magnetic trace the oscillation would be averaged out. The broadening of the trace thus does not just indicate that lion roars are present; it also shows that the lion roars appear as non-linear wave packets with finite averaged amplitude. Note that the lion roars in the mirror minima had already been identified as occurring in localised large-amplitude non-linear whistler-wave packets.

The importance of the investigations by Baumjohann et al. (1999) for the physics of mirror modes and lion roars lies in the fact that, by measuring the finite magnetic amplitude waveform and non-linear wave-packet form of the lion roar whistler fluctuations δB, frequency, and polarisation, they demonstrated unambiguously that those low-frequency lion roars were indeed electromagnetic waves propagating on the whistler mode. Their spectral analysis proved, in addition, that these waves propagated in large-amplitude spatially confined packets of non-linear whistler waves, a most important achievement as it demonstrated their non-linear evolution. Until then all conclusions concerning lion roar whistlers were based solely on spectral wave electric field measurements δE, like those in the AMPTE-IRM data of Fig. 1 combined with secondary arguments. Earlier magnetic wave instruments than that on Eq-S did not provide any magnetic wave measurements in this low-frequency range. It was, moreover, shown in that work that the occurrence of lion roars was related to the presence of a residual weak resonant anisotropy in the electrons left over after quasilinear saturation of the lion roars. This resonant particle anisotropy was independent of the global pressure anisotropy. The latter remains unaffected by the excitation of lion roars or whistlers².

Three kinds of magnetic variations are visible in this figure. Firstly, we have the large-amplitude ion-mirror mode oscillations of which only two periods are shown. Secondly, superimposed on these are the spiky small-amplitude excursions from the ion-mirror shape which form small peaks and valleys everywhere on the flanks, maxima, and minima in rather irregular or at best quasi-regular sequence. Thirdly and finally, there are very small-amplitude oscillations which, as far as the instrument can resolve them, accumulate mainly in relation to the former medium-frequency and medium-amplitude magnetic modulations. The interesting feature in this high-resolution recording of the magnetic field are these medium-frequency medium-amplitude tooth-like oscillations of the magnetic field in the flanks, in the maxima and also in the minima of the ion-mirror mode. In this respect the high-resolution magnetic field in this figure is quite different from the apparently smooth 4-times-lower resolution and less sensitive course of the mirror field in the AMPTE-IRM magnetosheath observations of Figs. 1 and 2. We repeat that these Eq-S chains of magnetic modulations had indeed been identified as mirror modes by Lucek et al. (1999a), even though no plasma data were available. We also repeat that, even if the plasma instrument on Eq-S would have worked properly, its time resolution of ∼3 s would not have been sufficient to resolve any anti-correlation between the magnetic and plasma pressures in the oscillations which we here and below identify as electron mirror modes. Measuring this anti-correlation would have required a substantially or even much higher time resolution than the spin resolution, which was only available at the times of those spacecraft.

In order to infer the nature of these oscillations we refer to the period of the (ion) mirror mode. This can be read from the figure to be roughly τ_im∼30 s, corresponding to a frequency of f_im∼0.03 Hz. The tooth-like oscillations, for instance at the first steep increase of the magnetic field, have a time period of τ_em∼2–4 s (or frequency f_em∼0.3 Hz), roughly a factor of 10 shorter than the ion-mirror mode. In addition to their steep magnetic boundaries, these structures also exhibit superimposed low-frequency oscillations (appearing as broadenings of the magnetic trace as shown in Fig. 4), which are also present in the modulated maxima of the mirror mode. Since the latter belong to magnetic fluctuations, it is reasonable to assume that they are simply a different kind of lion roar caused by electrons trapped in the local minima of the higher-frequency and shorter-wavelength modulations. Thus their centre frequency should be higher than the lion roar frequency in the ion-mode minima. This suggests identification with the higher-frequency spectral features observed by AMPTE-IRM, while the weak broadband features in the wave spectra may be related to the steep magnetic and plasma (pressure) boundaries of the modulations.

3 Electron mirror branch

If this is the case then it is suggested to identify the small-amplitude modulations in the magnetic field seen by Eq-S and in the wave spectra by AMPTE-IRM with the electron mirror mode which was theoretically predicted (Noreen et al., 2017). These authors put emphasis on the quasilinear evolution of the pure electron (ion) and mixed (electron-ion) mirror modes to numerically show for a number of cases how the normalised magnetic and plasma energy densities evolve and saturate. For our purposes it suffices to consider the mixed linear state, because it is clear from the data in Fig. 3 and as a consequence also in the spectrum of Fig. 1 that the dominant magnetic (and also plasma) structure is the ion-mirror mode while the electron mirror mode just produces some modification. Clearly the ion-mirror mode is a large-scale perturbation on which the quasilinear contribution of the electron mirror mode does not change very much.

For our purposes we need only the simplified purely growing linear growth rate (normalised to the ion-cyclotron frequency ${\mathit{\omega }}_{\mathrm{ci}}=eB/m_{\mathrm{i}}$) for small ion and electron arguments:

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\mathit{\gamma }\left(\mathit{k}\right)}{{\mathit{\omega }}_{\mathrm{ci}}}}\approx {\displaystyle \frac{k_{\Vert }{\mathit{\lambda }}_{\mathrm{i}}}{A_{\mathrm{i}}+\mathrm{1}}}\sqrt{{\displaystyle \frac{{\mathit{\beta }}_{\Vert \mathrm{i}}}{\mathit{\pi }}}}\left[A_{\mathrm{i}}+\sqrt{{\displaystyle \frac{T_{\mathrm{e}⟂}}{T_{\mathrm{i}⟂}}}}{A}_{\mathrm{e}}-{\displaystyle \frac{k^{\mathrm{2}}}{k_{⟂}^{\mathrm{2}}{\mathit{\beta }}_{\mathrm{i}⟂}}}\right],\end{array}$$

with ${\mathit{\lambda }}_{\mathrm{i}}=c/{\mathit{\omega }}_{\mathrm{i}}$ the ion inertial length, ${\mathit{\omega }}_{\mathrm{i}}^{\mathrm{2}}=e^{\mathrm{2}}N/{\mathit{ϵ}}_{\mathrm{0}}{m}_{\mathrm{i}}$ square of ion plasma frequency, $A_j=(T_{⟂}/T_{\Vert }{)}_j-\mathrm{1}>\mathrm{0}$ the temperature anisotropy of species j=i, e, and ${\mathit{\beta }}_{\Vert \mathrm{i}}=\mathrm{2}{\mathit{\mu }}_{\mathrm{0}}N{T}_{\mathrm{i}\Vert }/B^{\mathrm{2}}$ the ratio of parallel ion thermal and magnetic energy densities (Noreen et al., 2017). Wave growth occurs for positive brackets, which provides angular dependent thresholds. The threshold condition for instability can be written in terms of the magnetic field as

$$\begin{array}{}\text{(2)}& {\displaystyle }{\displaystyle }B<B_{\mathrm{crit}}\approx \sqrt{\mathrm{2}{\mathit{\mu }}_{\mathrm{0}}N{T}_{\mathrm{i}⟂}}{\left(A_{\mathrm{i}}+\sqrt{{\displaystyle \frac{T_{\mathrm{e}⟂}}{T_{\mathrm{i}⟂}}}}{A}_{\mathrm{e}}\right)}^{\frac{\mathrm{1}}{\mathrm{2}}}\left|\sin \mathit{\theta }\right|,\end{array}$$

where $\mathit{\theta }={\sin }^{-\mathrm{1}}(k_{⟂}/k)$, and the approximate sign refers to the simplifications made in writing the simplified dispersion relation. Once the local magnetic field drops below this threshold value, instability will necessarily set on. Such a critical value B_crit exists for all combinations of anisotropies which leave the sum under the root positive. It has a deeper physical meaning (Treumann et al., 2004a) corresponding to a classical Meissner effect in superconductivity. This threshold relates to the critical mirror mode angle of Kivelson and Southwood (1996). It sets an angular dependent upper limit on the critical magnetic field which vanishes for parallel and maximises for perpendicular propagation. In both these cases, however, no instability can arise, as follows from the growth rate, and the instability, as is well known, is oblique. The growth rate obtained from the simplified dispersion relation maximises formally at a maximum angle θ_max with

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\sin }^{\mathrm{2}}{\mathit{\theta }}_{\max }\approx {\displaystyle \frac{\mathrm{1}}{\mathrm{2}a}}\left\{\sqrt{\mathrm{1}+\mathrm{8}a}-\mathrm{1}\right\},\\ \text{(3)}& {\displaystyle }& {\displaystyle }\mathrm{1}<a\equiv {\mathit{\beta }}_{\mathrm{i}⟂}\left[A_{\mathrm{i}}+\sqrt{{\displaystyle \frac{T_{\mathrm{e}\perp }}{T_{\mathrm{i}\perp }}}}{A}_{\mathrm{e}}\right].\end{array}$$

For a=2, for instance, this yields θ_max≈45^∘, in accordance with the exact numerical calculation for the ion mode based on the full dispersion relation (Noreen et al., 2017). No maximum exists for a≤1. Folding the growth rate with the threshold condition and maximising yields the optimum unstable range. This gives a third-order equation for x=cos2θ_opt:

$${\displaystyle }{\displaystyle }{x}^{\mathrm{3}}-\left(\mathrm{1}-{\displaystyle \frac{\mathrm{2}}{a}}\right)x\pm {\displaystyle \frac{\mathrm{1}}{a}}=\mathrm{0}\mathrm{for}\left\{\begin{array}{ccc}{\mathit{\theta }}_{\mathrm{opt}}^{\left(\mathrm{1}\right)}& <& \mathit{\pi }/\mathrm{4}\\ {\mathit{\theta }}_{\mathrm{opt}}^{\left(\mathrm{2}\right)}& >& \mathit{\pi }/\mathrm{4}\end{array}\right.$$

depending on the sign of the last term. Expanding near-parallel propagation $x-\mathit{\xi }\approx \mathrm{1}$ for a≳2 and very roughly keeping only the linear term in ξ gives two solutions which approximately fix the range ${\mathit{\theta }}_{\mathrm{opt}}^{\left(\mathrm{1}\right)}<\mathit{\theta }<{\mathit{\theta }}_{\mathrm{opt}}^{\left(\mathrm{2}\right)}$ of maximum growth for the ion mode, corresponding to angles ${\mathit{\theta }}_{\mathrm{opt}}^{\left(\mathrm{1}\right)}\approx \frac{\mathrm{1}}{\mathrm{2}}{\cos }^{-\mathrm{1}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\approx \mathrm{30}$^∘ and ${\mathit{\theta }}_{\mathrm{opt}}^{\left(\mathrm{2}\right)}\approx \frac{\mathrm{1}}{\mathrm{2}}{\cos }^{-\mathrm{1}}\left(\frac{\mathrm{1}}{\mathrm{6}}\right)\approx \mathrm{50}$^∘. These considerations apply to the simplified dispersion relation used in this paper. They do not discriminate between the roles of ion and electron gyro radii. This distinction is contained in the full dispersion relation on which the numerical solution (Noreen et al., 2017) is based, thereby leading to the numerically obtained precise angular ranges for the two branches of the mirror instability to which we refer below.

The pure electron effect which applies to the electron branch is obtained for isotropic ions A_i=0 and $T_{\mathrm{i}\Vert }=T_{\mathrm{i}\perp }\equiv T_{\mathrm{i}}$. On the electron gyroradius scale the ions are unmagnetised, yielding

$$\begin{array}{ll}{\displaystyle }& {\displaystyle \frac{{\mathit{\gamma }}_{\mathrm{e}}\left(\mathit{k}\right)}{{\mathit{\omega }}_{\mathrm{ci}}}}\approx k_{\Vert }{\mathit{\lambda }}_{\mathrm{i}}\sqrt{{\displaystyle \frac{{\mathit{\beta }}_{\mathrm{e}\Vert }}{\mathit{\pi }}}}\left[A_{\mathrm{e}}-{\displaystyle \frac{k^{\mathrm{2}}}{k_{⟂}^{\mathrm{2}}{\mathit{\beta }}_{\mathrm{e}⟂}}}\right]\sqrt{A_{\mathrm{e}}+\mathrm{1}}\\ {\displaystyle }& {\displaystyle }{B}_{\mathrm{crit},\mathrm{e}}\approx \sqrt{\mathrm{2}{\mathit{\mu }}_{\mathrm{0}}{T}_{\mathrm{e}\perp }{A}_{\mathrm{e}}}\left|\sin \mathit{\theta }\right|.\end{array}$$

The perpendicular mirror scale and critical threshold magnetic field are determined by the electron anisotropy A_e and perpendicular electron thermal energy ratio β_e⟂.

Effectively, the electron-mirror branch remains to be a separate branch on the ion-mirror instability with parallel scale determined by the ion inertia, while its perpendicular scale and critical excitation threshold are prescribed by the electron dynamics. The perpendicular scale of the electron branch is much shorter than the ion scale, while the threshold depends only on the electron temperature and anisotropy. Writing the growth rate in pure electron quantities, one has for the isotropic-ion electron branch

$$\begin{array}{ll}{\displaystyle }& {\displaystyle \frac{{\mathit{\gamma }}_{\mathrm{e}}\left(\mathit{k}\right)}{{\mathit{\omega }}_{\mathrm{ce}}}}\approx \sqrt{{\displaystyle \frac{{\mathit{\beta }}_{\mathrm{e}\Vert }}{\mathit{\pi }}}}\left[A_{\mathrm{e}}-{\displaystyle \frac{k^{\mathrm{2}}{e}^{{\mathit{\zeta }}_{\mathrm{e}}}}{k_{⟂}^{\mathrm{2}}{\mathit{\beta }}_{\mathrm{e}⟂}\left[\mathrm{1}-{\mathit{\zeta }}_{\mathrm{e}}/\mathrm{2}\right]}}\right]{\displaystyle \frac{k_{\Vert }{\mathit{\lambda }}_{\mathrm{e}}}{D}}\\ {\displaystyle }& {\displaystyle }D\equiv \mathrm{1}+\sqrt{{\displaystyle \frac{m_{\mathrm{i}}}{m_{\mathrm{e}}}}{\displaystyle \frac{T_{\mathrm{e}⟂}}{T_{\mathrm{i}}}}}{\displaystyle \frac{\exp \left[-\left({\mathit{\zeta }}_{\mathrm{i}}-{\mathit{\zeta }}_{\mathrm{e}}\right)\right]}{{\left(A_{\mathrm{e}}+\mathrm{1}\right)}^{\mathrm{2}}}}\\ \text{(4)}& {\displaystyle }& {\displaystyle }{\mathit{\zeta }}_{\mathrm{e}}=k_{⟂}^{\mathrm{2}}{\mathit{\lambda }}_{\mathrm{e}}^{\mathrm{2}}{\mathit{\beta }}_{\mathrm{e}\perp }\ll \mathrm{1}.\end{array}$$

The ion term D in the nominator acts as a stabilising force on the electron branch though; because of the large square of the ion gyroradius ${\mathit{\zeta }}_{\mathrm{i}}/{\mathit{\zeta }}_{\mathrm{e}}=(m_{\mathrm{i}}/m_{\mathrm{e}})T_{\mathrm{e}\perp }/T_{\mathrm{i}}\gg \mathrm{1}$, the additional term in D is exponentially reduced. The electron inertial scale λ_e enters to replace λ_i. This expression shows the similarity between the ion and electron branches, albeit with different scales and an increased threshold for the electron branch. The electron-branch growth rate depends on the ion temperature. When T_i becomes large, the growth of the electron contribution will be suppressed. In contrast to the magnetosheath this should be the case, for instance, in Earth's magnetotail plasma sheet where one has T_i∼10T_e. Presumably any mirror modes which evolve there will be void of an electron branch.

In the last expressions the direction of anisotropy is with respect to the local magnetic field as the electrons experience it. It can be rather different from that of the main branch of the ion-mirror mode. These effects are still of first order, being independent of any finite Larmor-radius contributions (Pokhotelov et al., 2004) which occur in higher-order approximation, having been shown (Noreen et al., 2017) to be of minor importance. (Though this might not be the last word, because these authors investigate just the linear and quasilinear evolution of mirror modes. Below we comment on this important point.)

It is clear from here that, based on our arguments and the numerical calculations (Noreen et al., 2017), the two branches of the mirror mode grow in separate regions of wavenumber space k_‖, k_⟂, where the indices refer to the directions parallel and perpendicular to the local magnetic field, i.e. in the ion-mirror mode to the average ambient magnetic field which is modulated by the mirror mode, on the electron branch of the local magnetic field. The ion mirror mode magnetic field is modulated at the location where the electron mirror bubble evolves. This main and well expected effect in the combined electron-ion growth rate, found by numerically solving the complete non-simplified growth rate (Noreen et al., 2017) is that, because of the different gyration scales of electrons and protons, the growth rate exhibits its two separate branches and maximises at different angles for the two branches. Since in the linear state the different modes extract their energy from the component of particles to which they belong, the two modes grow separately but not independently because of their inertial coupling and the modification of the local magnetic field by the ion branch. It is this local field and thus mostly reduced field which the electrons feel. Only in the quasilinear state an exchange in energy takes place (Noreen et al., 2017).

Their linear numerical calculations demonstrate clearly that in absolute numbers the electron branch growth rate (measured in ion cyclotron frequencies) is about an order of magnitude larger than that of the ion-mirror mode. It grows faster and, as a consequence, saturates readily, such that one expects it to be of comparably small final amplitude. The ion-mirror mode growth rate maximises at $k_{\Vert \mathrm{i}}\approx k_{⟂\mathrm{i}}$, which corresponds to an angle of ∼45^∘ with respect to the ambient magnetic field direction, while the electron branch mode is nearly perpendicular ($k_{\Vert \mathrm{e}}\approx \mathrm{0.1}{k}_{⟂\mathrm{e}}$); i.e. it is of much shorter perpendicular than parallel wavelength. On the other hand, the maximum unstable parallel wavelengths are comparable ($k_{\Vert \mathrm{e}}\approx \mathrm{3}{k}_{\Vert \mathrm{i}}$), while the maximum unstable perpendicular wavelengths are different: $k_{⟂\mathrm{e}}/k_{⟂\mathrm{i}}\approx \mathrm{20}$–30 for the parameters investigated (Noreen et al., 2017). The electron mirror branch structure is elongated essentially parallel to the local field, while the ion-mirror branch is oblique to the ambient field. Whereas the ion-mirror mode tends to form large magnetic bubbles, the electron mirror mode forms narrow long bottles on the structure given by the ion-mirror mode. We may assume that this behaviour will not be very different for other parameter choices than those used in the numerical calculation, as it is just what one would expect: the electron mirror mode being somewhat longer in parallel wavelengths and substantially shorter in perpendicular wavelengths than the ion-mirror mode, an effect of the vastly different gyroradii.

4 Discussion

With this information at hand we consult the high-resolution Eq-S observations in Fig. 3. This figure suggests that Eq-S was crossed by the chain of mirror structures almost in the perpendicular direction. Comparing the times of crossing the large-scale ion-mirror mode and the well-expressed small-scale structures on the flank of the first rising boundary, we infer that the ratio of wavelengths between the long and short structures is of the order of roughly a factor of ∼10. Though this is not exactly the above value for this ratio in the perpendicular direction, it is pretty close to the expectation that the small-scale structure is caused by the electron component thus representing the electron mirror mode (indicated already in Sect. 2 by the subscript “em”).

4.1 Reference to Noreen et al.'s (2017) linear theory

There are a number of shorter structures of smaller amplitudes visible, the use of which would come closer to the canonical scales obtained from the numerical calculation of the maximum growth rates (Noreen et al., 2017). However, there are many reasons for staying with this result. The first would be the choice of the parameters chosen by Noreen et al. (2017) for their linear and quasilinear calculation. Another and more important one is that even for those parameters the spread of the domain of maximum growth of both the ion and electron mirror modes (Noreen et al., 2017) is sufficiently large for fitting the spread in the measurements. We may apply the half-maximum condition to the numerical calculation for exponential growth. Inspecting the growth-rate plot, the wave power is one-quarter of its value at maximum growth for wave numbers k_⟂ with growth rate $\mathit{\gamma }\left(k_{⟂}\right)\sim \mathrm{0.3}{\mathit{\gamma }}_{\max }$. With this value the figure implies a spread in k_⟂ for the electron mode of $\mathrm{\Delta }{k}_{⟂}{\mathit{\lambda }}_{\mathrm{i}}\sim \mathrm{5}$, large enough for covering a sufficiently broad interval of electron mirror wavelengths to account for the time or wavelength spread in our Fig. 3. Finally, it is worth mentioning that it is not known from the observations which direction precisely the electron mirror mode would propagate relative to the ion-mirror mode. Theory suggests propagation nearly parallel to the local mean magnetic field. This might become fixed with MMS observations. Hence, the above conclusion, though still imprecise, should suffice as evidence for the observation of both electron and ion-mirror modes in the magnetosheath by Eq-S, with both modes acting simultaneously in tandem. Unfortunately, as noted above, no plasma observations were available such that we are not in the position to provide a more sophisticated investigation, in particular the desired pressure balance between the electron mirror field and electron pressure implicitly contained in the theory. But even if the Eq-S plasma instrument would have worked properly, its poor time resolution of ∼3 s would not have been sufficient for demonstration of any pressure balance.

Since electron mirror branches have so far not been reported, there might be substantial reservation, accepting that they are indeed present. This makes it necessary to provide additional arguments, both theoretical and experimental.

4.2 Theoretical arguments for an electron mirror branch

The short-scale modulations of the magnetic field modulus seen in both the AMPTE-IRM and Eq-S recordings are well below the ion-gyroradius scale. Hence on these scales ions are non-magnetic and thus do not contribute to magnetic oscillations while electrostatic waves do anyway not contribute. From the ion point of view the only wave which could be made responsible is electromagnetic ion-cyclotron waves (electromagnetic ion-Bernstein modes) which at frequencies above the ion cyclotron frequency have rather weak amplitudes. Moreover, if present, they should be seen in the spectra as chains of harmonics. This is not the case. The other possibility would be Weibel modes, which have wavelengths of the order of the ion-inertial scale but barely grow in non-zero magnetic fields. When growing they have finite frequency near the ion cyclotron frequency and very weak amplitudes. Moreover, they require the presence of narrow antiparallel ion beams whose origin would not be known.

Since ion modes are probably not a factor, we are left with electromagnetic electron modes, viz. whistlers or electron-Alfvén waves. The electron-mirror branch propagates on this mode as a long-wavelength oblique whistler with $k_{⟂}>k_{\Vert }$. (For the angular range see our above discussion.) The other possibility is electromagnetic drift waves propagating perpendicular to the magnetic field and the gradients of density and field. Their magnetic component is caused by the diamagnetic currents flowing in these waves and is therefore parallel to the ambient field. Such waves cannot be excluded, which is in contrast to the above-mentioned modes. However, these modes are secondarily excited while the electron branch, as shown by Noreen et al. (2017), is a linear first-order mode and should therefore grow faster and stronger. Nevertheless, the possibility remains that electron-drift waves are observed. The only argument against them is that in several cases they appear in the magnetic minima and maxima where the magnetic and density gradients vanish and they could only be present when propagating into those regions. Still, in all those cases the unanswered question remains as to why those waves have comparably large amplitudes and do not form sinusoidal wave chains. Thus, denying the existence of the electron mirror branch as theoretically inferred in Noreen et al. (2017) simply shifts the explanation of the observed magnetic structures into the direction of some other unexplained effect. This is also unsatisfactory from the point of view that the simple argument that these structures would be incidentally caused being “nothing but” fluctuations does not work. For such stochastic fluctuations their amplitudes are by orders of magnitude too large. Thermal fluctuations (Yoon and López, 2017) are invisible on the magnetic traces both in AMPTE-IRM and Eq-S.

4.3 Experimental arguments

It also makes sense to provide some experimental arguments concerning the observation of what we call high-frequency lion roars (whistlers) in the flanks and on top of the mirror modes, even though by now, after the recent publication of a detailed in-depth investigation (Ahmadi et al., 2018) of those wave modes based on MMS data, this is not required anymore.

Both AMPTE-IRM and Eq-S had their spin axes perpendicular to the ecliptic. On AMPTE-IRM the electric wave antenna was perpendicular to the spin axis and the magnetometer was perpendicular to it though oblique to the field. The average field (Fig. 2, panel 2) was about perpendicular to the Sun–Earth line, parallel to the shock and magnetopause. Hence the antenna measured the transverse electric field of a parallel propagating electromagnetic mode modulated at twice the spin frequency, too slow for resolving the modulation during one short passage across any of the whistler sources. This cannot be directly resolved in Fig. 1 though modulations of the spectral intensity can be seen but are obscured by the stroboscopic effect of the rotating antenna and the occurrence of the electron mirror structures. In the particular range of frequencies below the electron cyclotron frequency in Fig. 1 one should, however, not expect any other waves except the weak almost stationary electrostatic ion-acoustic noise (Rodriguez and Gurnett, 1975) mentioned earlier. This noise propagates parallel and oblique but drops out perpendicular to the magnetic field. The occurrence of the high-frequency intense signals coinciding with some of the dropouts of ion-sound indicate that then the electric field measured was more or less strictly perpendicular to the magnetic field, thus being in the electromagnetic parallel propagating whistler mode. This should be sufficient argument here for parallel propagating whistlers wherever high-frequency lion roars were observed.

Eq-S did not carry any wave instrumentation. Hence the only signatures of lion roars at higher frequencies are the broadenings of the magnetic traces. The wave forms and spectra of Baumjohann et al. (1999) proved that those waves occurred in sharply confined large-amplitude non-linear wave packets. Such spatial packets cause two kinds of signals, the noted broadband high-frequency electric signals (Dubouloz et al., 1991) clearly seen in Fig. 1 exceeding the electron cyclotron frequency and, when time-averaging their magnetic components, broadenings of the magnetic trace. Not being simple sinusoidal oscillations, they contribute an average non-vanishing random mean square amplitude to the ambient field at the spatial location of the non-linear wave packets which causes the broadening of the magnetic traces. This is both seen in Figs. 3 and 4 respectively³.

5 Conclusions

Accepting that Eq-S indeed observed both branches in the magnetosheath, reference to Fig. 3 further suggests that, as suspected, the intense higher-frequency unidentified emissions beneath the electron cyclotron frequency in Fig. 1 represent the equivalent to lion roars in the ion-mirror mode, though they are now on the electron mirror branch. Recently Breuillard et al. (2018) analysed MMS electron and wave data observed high-frequency whistler waves at the edges of mirror mode packets in relation to a perpendicular anisotropy in the electron temperature (Breuillard et al., 2018) which, in the light of our claim, provides another indication for the presence of an electron mirror branch. In fact, it would be most interesting to check whether the high sampling rate of 33.3 Hz on MMS suffices for detecting a pressure balance between electron mirror-scale magnetic oscillations and electron pressure. This should decide whether the electron branch is a bulk-electron-anisotropy-driven branch of the mirror mode or just a magnetic oscillation which is not in pressure balance.

The perpendicular extension of an electron mirror branch, though shorter than the ion inertial length ${\mathit{\lambda }}_{\mathrm{i}}=c/{\mathit{\omega }}_{\mathrm{i}}$, is, for a magnetic field of the order of B≈25 nT as in the measurements of Eq-S, still substantially larger than the electron gyroradius, which is a general condition for the electron mirror branch to exist and grow on magnetised globally anisotropic electrons. Electrons trapped inside those structures on the electron mirror branch will, by the same reasoning (Baumjohann et al., 1999; Thorne and Tsurutani, 1981; Tsurutani et al., 1982, 2011), be capable of exciting the whistler instability and thus produce high-frequency lion roars, still below the local electron cyclotron frequency, which in this case would be around f∼0.5–0.7 kHz, in reasonable agreement with the majority of high intensity emissions below the local electron cyclotron frequency in Fig. 1. (It also corresponds to the MMS observations reported by Breuillard et al., 2018.) These are found to coincide with the walls and maxima of the main ion-mirror structures, and in some cases evolve even on top of the maxima (see the cases indicated in Fig. 3) in the magnetic field strength. Quasilinear quenching of the anisotropy to a low level is no argument against the presence of lion roars. A low level of bulk temperature–pressure anisotropy will always be retained even quasilinearly (Treumann and Baumjohann, 1997). Excitation of whistler waves will occur if an anisotropic resonant electron component is present.

Hence the higher-frequency waves related to the mirror structures are presumably caused by those anisotropic resonant electrons which may become trapped in the secondary electron mirror branch structures (Breuillard et al., 2018), which grow on the background magnetic field and plasma structure of the ion-mirror mode. Considering that mirror modes trap electrons and that there is plenty of reason for the trapped electrons to evolve temperature anisotropies as well as a higher energy resonant electron component, this is quite a natural conclusion. On the other hand, the weak broadband electric emissions exceeding the ambient cyclotron frequency and irregularly related to the ion-mirror structures then presumably result from steep plasma boundaries on the shorter scale electron mirror branch structures, i.e. from their trapped electron component which should be responsible for the maintenance of the (currently otherwise undetectable) local total pressure balance in them, when traversing the spacecraft at the high flow speeds in the magnetosheath. Generation of such broadband signals in steep electron gradients are well known from theory and observation of ion and electron holes.

On this occasion a remark on the saturation of the mirror mode is appropriate. It is sometimes claimed that quasilinear saturation, because of the exponential self-quenching of the growth rate, readily limits the achievable amplitude of a linear instability to rather low values of at most few percent or less. This behaviour is clearly seen in the numerical calculations of the quasilinear mirror saturation level (Noreen et al., 2017). For the mirror mode it results in quasilinear depletion of the global temperature anisotropy (Noreen et al., 2017; Treumann, 1997). The same argument applies to the electron whistler instability (leading to lion roars) which (Kennel and Petschek, 1966; Vedenov et al., 1961) is known to quench the responsible resonant electron temperature anisotropy until reaching a balance between a rudimentary level of anisotropy or resonant particle flux and moderate wave intensity, an argument that also applies to the generation of lion roars.

However, there is an important and striking difference between the two saturation processes in mirror modes, whether on the ion or electron mirror branches, and quasilinear saturation of whistlers. This difference frequently leads to misconceptions. Mirror modes result from macroscopic (fluid) instability the source of which is the global pressure/temperature anisotropy of the bulk of the particle distribution. This anisotropy provides the free energy for the mirror instability. Whistlers and ion-cyclotron waves, on the other hand, take their energy from the presence of a population of anisotropic resonant particles. Depletion of the latter by quasilinear saturation of the whistler instability has little effect on the global temperature anisotropy which drives mirror modes to be unstable; it partially quenches the emission of whistlers (or in a similar way also ion-cyclotron waves). Since, however, quasilinear saturation never completely depletes the initial resonant anisotropy, some amount of anisotropy will remain even in this case (Sydora et al., 2007). Such a rudimentary anisotropy which is located in velocity space around the resonant population may, if large enough, nonetheless contribute to a global anisotropy which then affects the evolution of the mirror instability, in the case of whistlers (lion roars) the evolution of the electron branch, for ion whistlers excited in presence of resonant ions the main mirror mode branch.

Though violent quasilinear suppression of the mirror instability and saturation at a low quasilinear level seem reasonable, they contradict the observation of the $\left|\mathit{\delta }B\right|/B\sim \mathrm{50}$ % amplitudes reported here and elsewhere. Restriction to quasilinear saturation ignores higher-order non-linear interactions. It is well known that in many cases these additional weakly turbulent effects undermine quasilinear saturation such as, for instance, that which occurs in one of the most simple and fundamental instabilities, the gentle-beam–plasma interaction (Yoon, 2018). In fully developed weak plasma turbulence (Davidson, 1972; Sagdeev and Galeev, 1969; Tsytovich, 1977), various mode couplings and higher-order wave–particle interactions erase the process of flat straightforward quasilinear stabilisation. Under weak turbulence, the instability evolves through various stages of growth until finally reaching a quasi-stationary turbulent equilibrium very different from being quasilinear. In the particle picture, this equilibrium state is described by generalised Lorentzian thermodynamics (Treumann, 1999a, b; Treumann and Baumjohann, 2014a; Treumann and Jaroschek, 2008; Treumann et al., 2004b) resulting in the generation of power-law tails on the distribution function which have been observed for decades in all space plasmas.

The weakly turbulent generation of the quasi-stationary electron distribution, the so-called κ distribution (Gell-Mann and Tsallis, 2004; Tsallis, 1988), was anticipated in an electron-photon-bath calculation by Hasegawa et al. (1985), but the rigorous weak-turbulence theory, in this case providing an analytical expression for the power κ as function of the turbulent wave power, was given first by Peter H. Yoon for a thermal electron plasma with stationary ions under weakly turbulent electrostatic interactions, including spontaneous emission of Langmuir waves, induced emission, and absorption (Landau damping) (Yoon, 2014).

Similar electromagnetic interactions take place in weak magnetic turbulence (Yoon, 2007; Yoon and Fang, 2007). At high particle energies this power law becomes exponentially truncated when other effects like spontaneous reconnection (Treumann and Baumjohann, 2015) in magnetically turbulent plasmas or particle–particle collisions ultimately come into play when the lifetime becomes comparable to the collision time (Treumann and Baumjohann, 2014b; Yoon, 2014). Until this final quasi-stationary state is reached, the instability grows steadily in different steps, thereby assuming substantially larger amplitudes than predicted by quasilinear theory.

For magnetic mirror modes no weakly turbulent theory has so far been developed. The observed $\left|\mathit{\delta }B\right|/B\sim \mathrm{50}$ % amplitudes of the ion-mirror modes in Figs. 1 and 2, and the comparably large amplitudes of the inferred electron-mirror branch oscillations recognised in Fig. 3 are much larger than quasilinearly expected (Noreen et al., 2017). The electron-mirror branch amplitude inferred from Fig. 3 amounts to $\langle \mathit{\delta }B\rangle /B\sim \mathrm{5}$ %, 1 order of magnitude less than for the ion mode but still much larger than quasilinearly predicted. Such large amplitudes suggest that both branches, the ion-mirror as well as the electron-mirror branch, do in fact not saturate quasilinearly. Rather they are in their weakly turbulent quasi-stationary state. Presumably they have not yet reached their final state of dissipation and at least not that of their ultimate dissipative or even collisional destruction. In any case, both are irrelevant at the plasma flow times in the magnetosheath.

The question for a weak turbulence theory of mirror modes has so far not been brought up, at least not to our knowledge. It should be developed along the lines which have been formally prescribed by Yoon (2007) for low-frequency isotropic magnetic turbulence. This attempt should be extended to include (global non-resonant) pressure anisotropies for both particle species, protons and electrons, in order to apply to and include mirror modes. It, however, raises the problem of identification of the possible plasma modes which could, in addition to mirror modes, be involved.

Candidates different from the mirror modes themselves are drift-waves excited in the mirror-mode boundaries and ion-cyclotron waves and ion whistlers. Similar to electron whistlers, ion-cyclotron waves propagate almost parallel to the magnetic field. Similar to what is believed of whistlers, they quasilinearly deplete any resonant ion-plasma anisotropy. Under the conditions of the AMPTE IRM and Eq-S observations considered here, their frequency should be roughly ∼1 Hz. They should thus appear about once per second. Inspection of the magnetic trace in Fig. 3 gives no indication of their presence. The waves which we identify as the electron-mirror branch are of lower frequency.

However, any weak turbulence theory of the mirror modes should also take into account their mutual interaction. The linear dispersion relation already indicates that they are not independent. Since quasilinear theory fails in the description of their non-linear saturated state, the non-linear interaction of both the ion and electron mirror branches should also be taken into account in weak turbulence theory. Such a theory should lead to the final saturated state of the mirror modes which we have recently discussed in terms of basic thermodynamic theory (Treumann and Baumjohann, 2018), which in thermodynamic equilibrium should always apply.

It can, however, not unambiguously be excluded that just these waves represent electromagnetic ion-Bernstein or ion-cyclotron waves packets which may have evolved non-linearly to large amplitudes and long wavelengths in the course of weak kinetic turbulence of the ion-cyclotron wave, thereby erasing the quasilinear depletion of the resonant ion anisotropy and, in kinetic mirror turbulence, also contributing to further growth of the mirror modes until they achieve their large amplitudes. Hence, here we detect a possible caveat of our investigation.

The argument against this possibility is that these electromagnetic ion-cyclotron waves (ion whistlers), whether linear or non-linear, should not be in pressure balance nor should they trap any electrons. This means that they should not be related to the excitation of the observed high-frequency whistlers or lion roars. However, even that argument may be weak if the non-linear electromagnetic ion-cyclotron wave packets locally produce enough radiation pressure to deplete plasma from their regions of maximum amplitude. Electrons reflected from those packets could then possibly locally evolve temperature anisotropies and in this way excite high-frequency whistlers.

Thus, one identifiable caveat remains in the possibility that electromagnetic ion-cyclotron waves (in both cases of AMPTE IRM and Eq-S at frequency ∼1 Hz) have become involved into the weakly turbulent evolution of the observed ion-mirror modes (or possibly also other low-frequency electromagnetic drift waves, which could be excited in the magnetic and plasma gradients at the ion-mirror boundaries). As noted above, the effect of those electromagnetic ion-cyclotron waves is believed to quasilinearly diminish the resonant part of the ion anisotropy which probably does not happen when weak kinetic turbulence takes over. In weak turbulence, the non-linear evolution of the electromagnetic ion-cyclotron waves erases the quasilinear quenching and allows further growth of the ion-cyclotron waves until they evolve into the above-mentioned wave packets of sufficiently long wavelength, which may become comparable to the structures identified here as the electron-mirror branch waves. This possibility, though presumably improbable, cannot be completely excluded based on the observations.

There is no final argument against the involvement of such waves, other than that ion whistlers, like whistlers, are immune to pressure balance. As linear waves they do not trap any electrons, which, however, might change when they become strongly non-linear. As long as this does not happen, it would exclude ion whistlers as a source of the lion roars observed in the wave data of Fig. 1.

It will be worth investigating these far-reaching questions with the help of high-resolution plasma, field, and wave observations from more recent spacecraft missions like MMS. It would also be worth investigating whether any electromagnetic short-wavelength (electron) drift modes (Gary, 1993; Treumann et al., 1991) can be detected. Those waves might, in addition to ion-cyclotron and of course also electron-mirror branch modes themselves, become involved in the weak turbulence of ion-mirror modes when excited at short wavelengths comparable to the plasma gradient scales in mirror modes. Their excitation is at the expense of the global pressure balance. In such a case they might directly affect the macroscopic temperature anisotropy and contribute to weak kinetic turbulence of mirror modes while at the same time undermining their quasilinear quenching. Extension of the weak magnetic plasma turbulence theory as developed by Yoon (2007) and including pressure anisotropy, the effect of inhomogeneity caused by the turbulence, and oblique propagation could be a promising way to tackle the important problem of weak kinetic mirror mode turbulence.

Note added in final revision: Ahmadi et al. (2018), in a recent study based on high time- and energy-resolution electron data provided by the MMS mission (paralleled by particle-in-cell simulations), recently confirmed the generation of large-amplitude high-frequency whistlers (lion roars) in the flanks of the magnetosheath ion-mirror modes in correlation with locally trapped resonant energetic electrons. Their results indicate the presence of localised magnetic electron traps like those provided by the electron-mirror branch. Incidentally, a statistical study of lion-roar whistlers in the magnetosheath (Giagkiozis et al., 2018) has also been published recently.