Acoustic–gravity waves and their role in the ionospheric D region–lower thermosphere interaction

The properties of acoustic–gravity waves (AGWs) in the ionospheric D layer and their role in the D layer–lower thermosphere interaction are studied using the dispersion equation and the reflection coefficient. These analytical equations are an elegant tool for evaluating the contribution of upward-propagating acoustic and gravity waves to the dynamics of the lower thermosphere. It was found that infrasound waves with a frequency of ω>0.035 s⁻¹, which propagate almost vertically, can reach the lower thermosphere. Also, gravity waves with a frequency of ω<0.0087 s⁻¹, with a horizontal phase velocity in the range of 159 m s⁻¹ < v_h < 222 m s⁻¹ and a horizontal wavelength of 115 km < λ_p < 161 km, are important for the lower thermosphere dynamics. These waves can cause a temperature rise in the lower thermosphere and have the potential to generate middle-scale travelling ionospheric disturbances (TIDs). The reflection coefficient for AGWs is highly temperature-dependent. During maximum solar activity, the temperature of the lower thermosphere can rise several times. This is the situation where infrasound waves become a prime candidate for the ionospheric D layer–lower thermosphere interaction since strongly reflected gravity waves remain trapped in the D layer. Knowing the temperatures of the particular atmospheric layers, we can also know the characteristics of AGWs and vice versa.

1 Introduction

Acoustic–gravity waves (AGWs) are able to transport energy and momentum between different layers of the atmosphere. Understanding these waves is essential if we want to comprehend the atmosphere as a system where the layers are coupled. The ionosphere is a part of the Earth's atmosphere located between about 60 and 1000 km above the Earth's surface where the charged particles significantly influence its physical and chemical properties (Bothmer and Daglis, 2007). Knowledge about typical AGW characteristics in the ionosphere is important for modelling of interaction between the ionized and the neutral atmosphere. Ionosphere is constantly exposed to various influences from outer space as well as from the terrestrial atmosphere and lithosphere. Non-periodic and sudden events, such as solar flares (Singh et al., 2014; Nina et al., 2017; Chum et al., 2018), coronal mass ejection (Bochev and Dimitrova, 2003; Balan et al., 2008), solar eclipses (Singh et al., 2012), supernova explosions followed by hard X and γ radiation (Inan et al., 2007), and lightnings (Voss et al., 1998), and some processes in the terrestrial lithosphere, such as volcanic eruptions and earthquakes (Nenovski et al., 2010; Argunov and Gotovtsev, 2019), induce space- and time-varying ionospheric perturbations. These disturbances cause numerous complex physical, chemical, and dynamical phenomena in ionosphere (Rozhnoi, 2012; Hayakawa et al., 2010) and may directly affect human activities, especially in the telecommunications.

The atmospheric monitoring depends on the altitude of the considered atmospheric layer. The ionospheric D layer at an altitude of about 60 to 90 km, lies below the area being studied by satellite observations and above the region where balloon measurements find their application. Therefore, its monitoring is based on rocket and radar measurements and on the propagation of very low frequency and low-frequency (VLF/LF) radio waves (Nina and Čadež, 2013). In this way, it is possible to observe a large part of the low ionosphere and detect local perturbations and sudden events.

The ionospheric D layer and lower thermosphere below 140 km, where AGWs with the specific frequencies and wavelengths are detected, are the focus of this article. We considered the conditions for propagation of AGWs in the D ionospheric layer and their reflection/transmission on the plane boundary between this layer and the lower thermosphere. This is a way to study the interaction between the ionosphere and the lower thermosphere and to analyse the influence of AGWs on thermospheric processes and characteristics.

The article is structured as follows: Sect. 2 contains the basic theory of AGWs and the derivation of their dispersion equation. Section 3 presents the analytical equation for the AGW reflection coefficient. In Sect. 4, the propagation of AGWs through the ionospheric D layer as well as their reflection/transmission properties are analysed. The discussion and conclusions are displayed in Sects. 5 and 6, respectively.

2 Basic equations

The D layer is a part of the ionosphere where typical atmosphere models give n_n∼10²¹ m⁻³ for the neutral particle density and n_p∼10⁸ m⁻³ for charged plasma particles and where electric and magnetic effects play a minor role in the local atmosphere dynamics. This is why hydrodynamic (HD) equations rather than magneto-hydrodynamic (MHD) equations can be used to analyse wave propagation. The standard set of HD equations describes the dynamics of adiabatic processes in a neutral atmosphere in the presence of gravity, $\mathit{g}=-g{\mathit{e}}_z$, with constant acceleration of g=9.81 m s⁻².

• The first equation is that of continuity and ideal gas equation:

  $$\begin{array}{}\text{(1)}& {\displaystyle \frac{\partial \mathit{\rho }}{\partial t}}+\mathrm{\nabla }\cdot \left(\mathit{\rho }\mathit{v}\right)=\mathrm{0},p=\mathit{\rho }RT.\end{array}$$

• The second equation is the momentum equation:

  $$\begin{array}{}\text{(2)}& \mathit{\rho }\left({\displaystyle \frac{\partial \mathit{v}}{\partial t}}+\mathit{v}\cdot \mathrm{\nabla }\mathit{v}\right)=-\mathrm{\nabla }p+\mathit{\rho }\mathit{g}.\end{array}$$

• And the final equation is an adiabatic law for a perfect gas:

  $$\begin{array}{}\text{(3)}& {\displaystyle \frac{\partial p}{\partial t}}+\mathit{v}\cdot \mathrm{\nabla }p={\displaystyle \frac{\mathit{\gamma }p}{\mathit{\rho }}}\left({\displaystyle \frac{\partial \mathit{\rho }}{\partial t}}+\mathit{v}\cdot \mathrm{\nabla }\mathit{\rho }\right).\end{array}$$

Here, $R=R_{\mathrm{0}}/M$ is the individual gas constant for molecules with molar mass M, R₀=8.314 J mol⁻¹ K⁻¹ is the universal gas constant, and $\mathit{\gamma }=c_p/c_v=(j+\mathrm{2})/j$ is the ratio of specific heats for gas particles with j=5 degrees of freedom.

Dispersion equation for AGWs

In what follows, we consider waves whose wavelengths are sufficiently small in comparison with the Earth's radius, R_E=6371 km. Therefore, the plane-parallel geometry can be applied in a locally isothermal medium. Under these assumptions, the atmosphere is taken to be vertically stratified, initially in hydrostatic equilibrium, and then perturbed by harmonic waves of small amplitude. This means that Eqs. (1)–(3) can be linearized by taking any physical quantity $\mathit{\psi }(x,y,z,t)$ as a sum of its basic-state unperturbed value ψ₀(z) and a small first-order perturbation $\mathit{\delta }\mathit{\psi }(x,y,z,t)$; i.e. $\mathit{\psi }(x,y,z,t)={\mathit{\psi }}_{\mathrm{0}}\left(z\right)+\mathit{\delta }\mathit{\psi }(x,y,z,t)$, where $\mathit{\delta }\mathit{\psi }(x,y,z,t)={\mathit{\psi }}^{\prime }\left(z\right)e^{i(k_{x}x+k_{y}y-\mathit{\omega }t)}$ and $\left|{\mathit{\psi }}^{\prime }\right|\ll \left|{\mathit{\psi }}_{\mathrm{0}}\right|$. Equations (1)–(3), linearized with these perturbations, reduce to three equations: one for the unperturbed basic state and two for small perturbations. The unperturbed basic state is described by

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}z}}\ln {\mathit{\rho }}_{\mathrm{0}}\left(z\right)+{\displaystyle \frac{\mathrm{1}}{H}}=\mathrm{0},p_{\mathrm{0}}={\mathit{\rho }}_{\mathrm{0}}R{T}_{\mathrm{0}},\text{with}{T}_{\mathrm{0}}=\mathrm{const}.,$$

the solution of which is

$$\begin{array}{}\text{(4)}& {\mathit{\rho }}_{\mathrm{0}}\left(z\right)={\mathit{\rho }}_{\mathrm{0}}\left(\mathrm{0}\right)e^{-z/H}\text{or}{p}_{\mathrm{0}}\left(z\right)=p_{\mathrm{0}}\left(\mathrm{0}\right)e^{-z/H},\end{array}$$

where $H=p_{\mathrm{0}}\left(\mathrm{0}\right)/{\mathit{\rho }}_{\mathrm{0}}\left(\mathrm{0}\right)=v_{\mathrm{s}}^{\mathrm{2}}/\mathit{\gamma }g=\mathrm{const}.$ is the characteristic scale height of the isothermal atmosphere.

The small perturbations are governed by the following equations (Jovanović, 2016):

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{\mathrm{d}{\mathit{\xi }}_z^{\prime }}{\mathrm{d}z}}=C_{\mathrm{1}}{\mathit{\xi }}_z^{\prime }-C_{\mathrm{2}}{p}^{\prime },{\displaystyle \frac{\mathrm{d}{p}^{\prime }}{\mathrm{d}z}}-g{\displaystyle \frac{\mathrm{d}{\mathit{\rho }}_{\mathrm{0}}}{\mathrm{d}z}}{\mathit{\xi }}_z^{\prime }=C_{\mathrm{3}}{\mathit{\xi }}_z^{\prime }-C_{\mathrm{1}}{p}^{\prime },\end{array}$$

where ${\mathit{\xi }}_z^{\prime }=i{v}_z^{\prime }/\mathit{\omega }$ is the z component (i.e. the vertical component) of the fluid displacement, while p^′ is the pressure perturbation. The coefficients in Eq. (5) are

$$\begin{array}{}\text{(6)}& C_{\mathrm{1}}={\displaystyle \frac{g}{v_{\mathrm{s}}^{\mathrm{2}}}},C_{\mathrm{2}}={\displaystyle \frac{{\mathit{\omega }}^{\mathrm{2}}-k_p^{\mathrm{2}}{v}_{\mathrm{s}}^{\mathrm{2}}}{{\mathit{\rho }}_{\mathrm{0}}\left(z\right)v_{\mathrm{s}}^{\mathrm{2}}{\mathit{\omega }}^{\mathrm{2}}}},C_{\mathrm{3}}={\mathit{\rho }}_{\mathrm{0}}\left(z\right)\left({\mathit{\omega }}^{\mathrm{2}}+{\displaystyle \frac{g^{\mathrm{2}}}{v_{\mathrm{s}}^{\mathrm{2}}}}\right).\end{array}$$

The density distribution, ρ₀(z), is given by Eq. (4), and $k_p^{\mathrm{2}}=k_x^{\mathrm{2}}+k_y^{\mathrm{2}}$ designates the square of the horizontal wavenumber. Equations (5)–(6) allow for the following solutions for the vertical displacement, ${\mathit{\xi }}_z^{\prime }$, and the pressure perturbation, p^′:

$$\begin{array}{}\text{(7)}& {\mathit{\xi }}_z^{\prime }\left(z\right)={\mathit{\xi }}_z^{\prime }\left(\mathrm{0}\right)e^{\frac{z}{\mathrm{2}H}}{e}^{i{k}_{z}z},p^{\prime }\left(z\right)=p^{\prime }\left(\mathrm{0}\right)e^{\frac{-z}{\mathrm{2}H}}{e}^{i{k}_{z}z}.\end{array}$$

Equation (5) with solutions from Eq. (7) yields the following dispersion equation for AGWs:

$$\begin{array}{}\text{(8)}& k_z^{\mathrm{2}}={\displaystyle \frac{{\mathit{\omega }}^{\mathrm{2}}({\mathit{\omega }}^{\mathrm{2}}-{\mathit{\omega }}_{\mathrm{co}}^{\mathrm{2}})-k_p^{\mathrm{2}}{v}_{\mathrm{s}}^{\mathrm{2}}({\mathit{\omega }}^{\mathrm{2}}-{\mathit{\omega }}_{\mathrm{BV}}^{\mathrm{2}})}{{\mathit{\omega }}^{\mathrm{2}}{v}_{\mathrm{s}}^{\mathrm{2}}}}.\end{array}$$

Here, k_z is the vertical wavenumber, ${\mathit{\omega }}_{\mathrm{co}}^{\mathrm{2}}={\mathit{\gamma }}^{\mathrm{2}}{g}^{\mathrm{2}}/\mathrm{4}{v}_{\mathrm{s}}^{\mathrm{2}}=v_{\mathrm{s}}^{\mathrm{2}}/\mathrm{4}{H}^{\mathrm{2}}$ is the square of the acoustic-wave cutoff frequency, and ${\mathit{\omega }}_{\mathrm{BV}}^{\mathrm{2}}=(\mathit{\gamma }-\mathrm{1})g^{\mathrm{2}}/v_{\mathrm{s}}^{\mathrm{2}}$ is the square of the Brunt–Väisälä frequency. This equation is quadratic in ω², which indicates the existence of two wave modes in the considered stratified atmosphere: acoustic and gravity modes. Stratification in a vertical direction, caused by gravity and given by Eq. (4), introduces cutoff frequencies – an acoustic cutoff frequency below which acoustic waves cannot propagate and a Brunt–Väisälä frequency above which gravity waves cannot propagate. Therefore, the branches of acoustic and gravity waves are present. Between them are evanescent waves that do not propagate (Fig. 1).

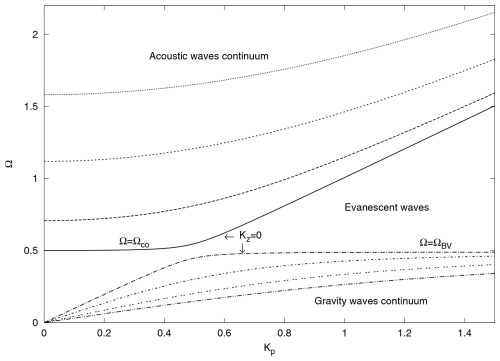
Figure 1 Dispersion curves for AGWs. Two sets of curves are related to acoustic and gravity waves, which cannot propagate below the acoustic cutoff frequency, ${\mathrm{\Omega }}_{\mathrm{co}}={\mathit{\omega }}_{\mathrm{co}}H/v_{\mathrm{s}}$ and above the Brunt–Väisälä frequency, ${\mathrm{\Omega }}_{\mathrm{BV}}={\mathit{\omega }}_{\mathrm{BV}}H/v_{\mathrm{s}}$, respectively.

The dispersion equation, Eq. (8), can be expressed in terms of wavelengths and wave frequency, ω, in the following way:

$$\begin{array}{}\text{(9)}& {\mathit{\lambda }}_z^{\mathrm{2}}\left(\mathit{\omega }\right)={\displaystyle \frac{A_{\mathrm{2}}\left(\mathit{\omega }\right){\mathit{\lambda }}_p^{\mathrm{2}}}{{\mathit{\lambda }}_p^{\mathrm{2}}-A_{\mathrm{0}}\left(\mathit{\omega }\right)}},\end{array}$$

where

$$A_{\mathrm{0}}\left(\mathit{\omega }\right)={\displaystyle \frac{\mathrm{4}{\mathit{\pi }}^{\mathrm{2}}{v}_{\mathrm{s}}^{\mathrm{2}}({\mathit{\omega }}^{\mathrm{2}}-{\mathit{\omega }}_{\mathrm{BV}}^{\mathrm{2}})}{{\mathit{\omega }}^{\mathrm{2}}({\mathit{\omega }}^{\mathrm{2}}-{\mathit{\omega }}_{\mathrm{co}}^{\mathrm{2}})}},A_{\mathrm{2}}\left(\mathit{\omega }\right)={\displaystyle \frac{\mathrm{4}{\mathit{\pi }}^{\mathrm{2}}{v}_{\mathrm{s}}^{\mathrm{2}}}{{\mathit{\omega }}^{\mathrm{2}}-{\mathit{\omega }}_{\mathrm{co}}^{\mathrm{2}}}}.$$

This equation will be useful for further analysis.

The physical quantities in the dispersion equation can be made dimensionless by appropriate scalings: K_p=k_pH, K_z=k_zH, $\mathrm{\Omega }=\mathit{\omega }H/v_{\mathrm{s}}$, ${\mathrm{\Omega }}_{\mathrm{co}}={\mathit{\omega }}_{\mathrm{co}}H/v_{\mathrm{s}}=\mathrm{0.5}$, and ${\mathrm{\Omega }}_{\mathrm{BV}}={\mathit{\omega }}_{\mathrm{BV}}H/v_{\mathrm{s}}=\sqrt{\mathit{\gamma }-\mathrm{1}}/\mathit{\gamma }=\mathrm{0.45}$. Now, the dispersion equation, Eq. (8), for AGWs has the following dimensionless form:

$$\begin{array}{}\text{(10)}& K_z^{\mathrm{2}}={\mathrm{\Omega }}^{\mathrm{2}}-{\mathrm{\Omega }}_{\mathrm{co}}^{\mathrm{2}}-{\displaystyle \frac{K_p^{\mathrm{2}}({\mathrm{\Omega }}^{\mathrm{2}}-{\mathrm{\Omega }}_{\mathrm{BV}}^{\mathrm{2}})}{{\mathrm{\Omega }}^{\mathrm{2}}}}.\end{array}$$

The acoustic waves with a frequency of Ω>Ω_co propagate in the vertical direction if $K_z^{\mathrm{2}}>\mathrm{0}$. This is fulfilled when

$$\begin{array}{}\text{(11)}& K_p^{\mathrm{2}}<{\displaystyle \frac{{\mathrm{\Omega }}^{\mathrm{2}}({\mathrm{\Omega }}^{\mathrm{2}}-{\mathrm{\Omega }}_{\mathrm{co}}^{\mathrm{2}})}{{\mathrm{\Omega }}^{\mathrm{2}}-{\mathrm{\Omega }}_{\mathrm{BV}}^{\mathrm{2}}}},\end{array}$$

i.e. when the dimensionless horizontal phase velocity is

$$\begin{array}{}\text{(12)}& V_{\mathrm{h}}^{\mathrm{2}}={\displaystyle \frac{{\mathrm{\Omega }}^{\mathrm{2}}}{K_p^{\mathrm{2}}}}>{\displaystyle \frac{{\mathrm{\Omega }}^{\mathrm{2}}-{\mathrm{\Omega }}_{\mathrm{BV}}^{\mathrm{2}}}{{\mathrm{\Omega }}^{\mathrm{2}}-{\mathrm{\Omega }}_{\mathrm{co}}^{\mathrm{2}}}}.\end{array}$$

Gravity waves with a frequency of Ω<Ω_BV propagate in the vertical direction if $K_z^{\mathrm{2}}>\mathrm{0}$, i.e. when $K_p^{\mathrm{2}}$ and $V_{\mathrm{h}}^{\mathrm{2}}$ in Eqs. (11) and (12) have the opposite sign.

The AGWs become evanescent if $K_z^{\mathrm{2}}<\mathrm{0}$, i.e. for the frequency of ${\mathrm{\Omega }}_{\mathrm{BV}}<\mathrm{\Omega }<{\mathrm{\Omega }}_{\mathrm{co}}$ (Fig. 1). The boundary between propagating and evanescent regions is given by K_z=0. Acoustic waves with frequencies close to the acoustic cutoff frequency, $\mathrm{\Omega }\approx {\mathrm{\Omega }}_{\mathrm{co}}=\mathrm{0.5}$, are more influenced by gravity than those with high frequencies when Ω≫Ω_co. Hence, gravity–modified acoustic waves and pure acoustic waves coexist in the stratified atmosphere (Mihalas and Mihalas, 1984). Equation (10) shows that the vertical wavenumber K_z has a maximum value for K_p=0; i.e. the following applies:

$$\begin{array}{}\text{(13)}& K_{zmax}=K=\sqrt{{\mathrm{\Omega }}^{\mathrm{2}}-{\mathrm{\Omega }}_{\mathrm{co}}^{\mathrm{2}}}.\end{array}$$

This equation describes acoustic waves that propagate only in the vertical direction.

Gravity waves, in contrast to acoustic waves, are not able to travel vertically with K_p=0, which means there are no pure vertically propagating gravity waves (Mihalas and Mihalas, 1984). Therefore, they propagate obliquely through the stratified atmosphere in accordance with Eq. (10). For the very low frequencies, when $\mathrm{\Omega }\ll {\mathrm{\Omega }}_{\mathrm{BV}}=\mathrm{0.45}$, gravity waves propagate with

$$\begin{array}{}\text{(14)}& K_z\approx {\displaystyle \frac{K_p{\mathrm{\Omega }}_{\mathrm{BV}}}{\mathrm{\Omega }}},\text{i.e.}{\displaystyle \frac{{\mathit{\lambda }}_p}{{\mathit{\lambda }}_z}}\approx {\displaystyle \frac{{\mathit{\omega }}_{\mathrm{BV}}}{\mathit{\omega }}}.\end{array}$$

Dimensionless equations are used because they are valid in each stratified medium, like the Earth, planets, or solar atmosphere. When we rewrite them using characteristic frequencies and temperatures, we obtain the equations for particular atmospheric layers as done in Sect. 4 for the ionospheric D layer.

3 Reflection coefficient of AGWs

The considered basic state in the stratified atmosphere is composed of two half-spaces with constant sound speeds separated by a horizontal plane boundary, z=0. The two regions are characterized by the corresponding neutral atmosphere densities, ρ₀₁ and ρ₀₂, adjacent to the lower and upper side of the boundary z=0. The unperturbed density profile can be expressed as follows:

$$\begin{array}{}\text{(15)}& \begin{array}{lll}{\mathit{\rho }}_{\mathrm{0}}\left(z\right)={\mathit{\rho }}_{\mathrm{01}}{e}^{-z/H_{\mathrm{1}}},& z<\mathrm{0},& \text{region 1},\\ {\mathit{\rho }}_{\mathrm{0}}\left(z\right)={\mathit{\rho }}_{\mathrm{02}}{e}^{-z/H_{\mathrm{2}}},& z>\mathrm{0},& \text{region 2},\end{array}\end{array}$$

where $H\left(n\right)=v_{\mathrm{s}n}^{\mathrm{2}}/\mathit{\gamma }g$, $n=\mathrm{1},\mathrm{2}$. There is a density, pressure, and temperature jump across z=0. The boundary condition that has to be applied at z=0 in the basic state is the continuity of the unperturbed pressure, p₀, at z=0 (Jovanović, 2016), which yields the following:

$$\begin{array}{}\text{(16)}& {\displaystyle \frac{{\mathit{\rho }}_{\mathrm{02}}}{{\mathit{\rho }}_{\mathrm{01}}}}={\displaystyle \frac{v_{\mathrm{s}\mathrm{1}}^{\mathrm{2}}}{v_{\mathrm{s}\mathrm{2}}^{\mathrm{2}}}}={\displaystyle \frac{T_{\mathrm{1}}}{T_{\mathrm{2}}}}=s=\mathrm{const}.\end{array}$$

The boundary conditions for perturbations are continuity of both the vertical fluid displacement ${\mathit{\xi }}_z^{\prime }$ and the pressure perturbation $p^{\prime }-g{\mathit{\rho }}_{\mathrm{0}}\left(z\right){\mathit{\xi }}_z^{\prime }$ at the boundary z=0. Also, the energy density of the perturbations has to diminish to zero as $\left|z\right|$ tends to infinity.

The harmonic wave, which propagates through regions (1) and (2), does not change its frequency and the horizontal wave vector component, K_p, parallel to the boundary z=0. However, the vertical wave vector component, K_z, has a discontinuity at the boundary z=0, where it changes from K_z1 to K_z2 according to the dispersion equation, Eq. (10). We assume that a wave propagates from the lower region, region 1, upward towards the boundary z=0, and that the waves continuing past it are absorbed with no reflection in the upper region, region 2. In this case, in the lower region, the perturbations are the superposition of the incident and reflected waves, while in the upper region, there is only the transmitted wave. The reflection coefficient of AGWs is defined as the square of the absolute value of the reflection amplitude. Using dimensionless physical values for brevity, the reflection coefficient can be written as follows (see details in Jovanović, 2014):

$$\begin{array}{}\text{(17)}& \begin{array}{rl}R& ={\left[{\displaystyle \frac{\begin{array}{c}{\left[\left(\mathrm{1}-\frac{\mathit{\gamma }}{\mathrm{2}}\right)\left(\frac{\mathrm{1}}{V_{\mathrm{h}}^{\mathrm{2}}-\mathrm{1}}-\frac{s^{\mathrm{2}}}{s{V}_{\mathrm{h}}^{\mathrm{2}}-\mathrm{1}}\right)+\frac{(s-\mathrm{1})}{V_{\mathrm{h}}^{\mathrm{2}}}\right]}^{\mathrm{2}}\\ +\frac{{\mathit{\gamma }}^{\mathrm{2}}{\mathrm{\Omega }}^{\mathrm{2}}}{V_{\mathrm{v}\mathrm{1}}^{\mathrm{2}}}\left(\frac{V_{\mathrm{v}\mathrm{1}}^{\mathrm{2}}}{V_{\mathrm{v}\mathrm{2}}^{\mathrm{2}}}\cdot \frac{s^{\mathrm{2}}}{(s{V}_{\mathrm{h}}^{\mathrm{2}}-\mathrm{1}{)}^{\mathrm{2}}}-\frac{\mathrm{1}}{(V_{\mathrm{h}}^{\mathrm{2}}-\mathrm{1}{)}^{\mathrm{2}}}\right)\end{array}}{\begin{array}{c}{\left[\left(\mathrm{1}-\frac{\mathit{\gamma }}{\mathrm{2}}\right)\left(\frac{\mathrm{1}}{V_{\mathrm{h}}^{\mathrm{2}}-\mathrm{1}}-\frac{s^{\mathrm{2}}}{s{V}_{\mathrm{h}}^{\mathrm{2}}-\mathrm{1}}\right)+\frac{(s-\mathrm{1})}{V_{\mathrm{h}}^{\mathrm{2}}}\right]}^{\mathrm{2}}\\ +\frac{{\mathit{\gamma }}^{\mathrm{2}}{\mathrm{\Omega }}^{\mathrm{2}}}{V_{\mathrm{v}\mathrm{1}}^{\mathrm{2}}}{\left[\frac{V_{\mathrm{v}\mathrm{1}}}{V_{\mathrm{v}\mathrm{2}}}\cdot \frac{s}{s{V}_{\mathrm{h}}^{\mathrm{2}}-\mathrm{1}}+\frac{\mathrm{1}}{V_{\mathrm{h}}^{\mathrm{2}}-\mathrm{1}}\right]}^{\mathrm{2}}\end{array}}}\right]}^{\mathrm{2}}\\ & +{\left[{\displaystyle \frac{\frac{\mathrm{2}\mathit{\gamma }\mathrm{\Omega }}{V_{\mathrm{v}\mathrm{1}}(V_{\mathrm{h}}^{\mathrm{2}}-\mathrm{1})}\left[\left(\mathrm{1}-\frac{\mathit{\gamma }}{\mathrm{2}}\right)\left(\frac{\mathrm{1}}{V_{\mathrm{h}}^{\mathrm{2}}-\mathrm{1}}-\frac{s^{\mathrm{2}}}{s{V}_{\mathrm{h}}^{\mathrm{2}}-\mathrm{1}}\right)+\frac{(s-\mathrm{1})}{V_{\mathrm{h}}^{\mathrm{2}}}\right]}{\begin{array}{c}{\left[\left(\mathrm{1}-\frac{\mathit{\gamma }}{\mathrm{2}}\right)\left(\frac{\mathrm{1}}{V_{\mathrm{h}}^{\mathrm{2}}-\mathrm{1}}-\frac{s^{\mathrm{2}}}{s{V}_{\mathrm{h}}^{\mathrm{2}}-\mathrm{1}}\right)+\frac{(s-\mathrm{1})}{V_{\mathrm{h}}^{\mathrm{2}}}\right]}^{\mathrm{2}}\\ +\frac{{\mathit{\gamma }}^{\mathrm{2}}{\mathrm{\Omega }}^{\mathrm{2}}}{V_{\mathrm{v}\mathrm{1}}^{\mathrm{2}}}{\left[\frac{V_{\mathrm{v}\mathrm{1}}}{V_{\mathrm{v}\mathrm{2}}}\cdot \frac{s}{s{V}_{\mathrm{h}}^{\mathrm{2}}-\mathrm{1}}+\frac{\mathrm{1}}{V_{\mathrm{h}}^{\mathrm{2}}-\mathrm{1}}\right]}^{\mathrm{2}}\end{array}}}\right]}^{\mathrm{2}}.\end{array}\end{array}$$

Here, V_v1 and V_v2 are the vertical phase velocities of AGWs in regions 1 and 2, respectively, given by the following equations:

$$\begin{array}{}\text{(18)}& V_{\mathrm{v}\mathrm{1}}={\displaystyle \frac{\mathrm{\Omega }}{K_{z\mathrm{1}}}}={\displaystyle \frac{V_{\mathrm{h}}\mathrm{\Omega }}{\sqrt{V_{\mathrm{h}}^{\mathrm{2}}({\mathrm{\Omega }}^{\mathrm{2}}-{\mathrm{\Omega }}_{\mathrm{co}}^{\mathrm{2}})-({\mathrm{\Omega }}^{\mathrm{2}}-{\mathrm{\Omega }}_{\mathrm{BV}}^{\mathrm{2}})}}}\end{array}$$

and

$$\begin{array}{}\text{(19)}& V_{\mathrm{v}\mathrm{2}}={\displaystyle \frac{\mathrm{\Omega }}{K_{z\mathrm{2}}}}={\displaystyle \frac{V_{\mathrm{h}}\mathrm{\Omega }}{\sqrt{s{V}_{\mathrm{h}}^{\mathrm{2}}({\mathrm{\Omega }}^{\mathrm{2}}-s{\mathrm{\Omega }}_{\mathrm{co}}^{\mathrm{2}})-({\mathrm{\Omega }}^{\mathrm{2}}-s{\mathrm{\Omega }}_{\mathrm{BV}}^{\mathrm{2}})}}},\end{array}$$

while V_h is the horizontal phase velocity given by Eq. (12). If $V_{\mathrm{v}\mathrm{1}}^{\mathrm{2}}$ and $V_{\mathrm{v}\mathrm{2}}^{\mathrm{2}}$ are positive, AGWs propagate through regions 1 and 2, respectively. If $V_{\mathrm{v}\mathrm{1}}^{\mathrm{2}},V_{\mathrm{v}\mathrm{2}}^{\mathrm{2}}<\mathrm{0}$, these waves are evanescent and not of interest to this study.

4 Results

In this section, the analytical equations derived in Sects. 2 and 3 are used to analyse the propagation of AGWs and their reflection/transmission properties in the ionospheric D layer.

4.1 AGWs in the ionospheric D layer

Acoustic–gravity waves which propagate in the lower ionosphere below 90 km can be generated from below, where hydrodynamic motions can be induced by atmospheric convective motions (Sindelarova et al., 2009); in the lithosphere (Nina et al., 2021; Boudjada et al., 2024); and from above due to sunrise and sunset effects (Afraimovich et al., 2009; Nina and Čadež, 2013; Nina et al., 2017). These perturbations may result in various patterns of either eigenmodes or driven linear waves in the atmosphere. The focus of this research is on the driven AGWs and their role in the ionosphere and the lower thermosphere interaction. Therefore, propagation of AGWs in the vertical direction is particularly important.

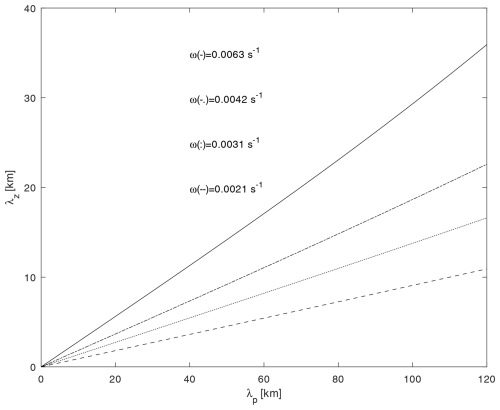
For the considered isothermal ionospheric D layer with a temperature of T=250 K and γ=1.4, the sound velocity is $v_{\mathrm{s}}=\sqrt{\mathit{\gamma }RT}=\mathrm{317}$ m s⁻¹, and H=7317 m. This is in accordance with Lizunov and Hayakawa (2004). For a gravity–modified acoustic wave with a frequency near the acoustic cutoff frequency of ω=0.022 s⁻¹ ≥ ω_co=0.021 s⁻¹, Eq. (13) enables the calculation of ${\mathit{\lambda }}_z\ge {\mathit{\lambda }}_{zmin}\approx \mathrm{460}$ km. For the pure acoustic wave, with a frequency much greater than acoustic cutoff frequency (ω≫ω_co, i.e. $\mathit{\omega }=\mathrm{10}\cdot {\mathit{\omega }}_{\mathrm{co}}=\mathrm{0.21}$ s⁻¹), this value is ${\mathit{\lambda }}_z\ge {\mathit{\lambda }}_{zmin}\approx \mathrm{9.2}$ km. It can be noticed that gravity–modified acoustic waves have much longer vertical wavelengths than pure acoustic waves. Therefore, acoustic waves with frequencies near the acoustic cutoff frequency, ω_co, have the best chance for vertical propagation through the ionospheric D layer towards the lower thermosphere. Acoustic waves in Fig. 2 are detected in the ionospheric D layer using VLF waves (Nina and Čadež, 2013).

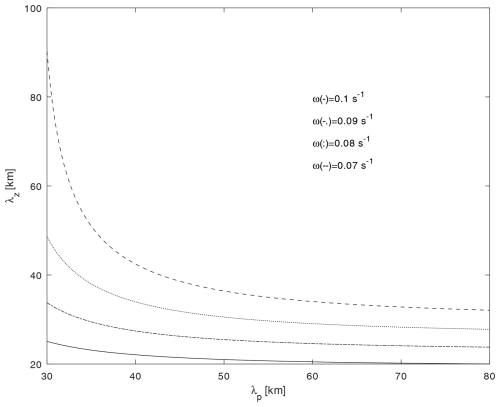
Figure 2 Vertical wavelength, λ_z, of acoustic waves from the dispersion equation, Eq. (9), as a function of the horizontal wavelength λ_p, for a given frequency of $\mathit{\omega }>{\mathit{\omega }}_{\mathrm{co}}=\mathrm{0.021}$ s⁻¹.

Gravity waves with a high frequency, ω≈ω_BV, and with a low frequency, ω≪ω_BV, are presented in Figs. 3 and 4, respectively. Equation (14) shows that low-frequency gravity waves have much longer horizontal than vertical wavelengths; i.e. they propagate more horizontally than vertically (Fig. 4). In addition, for a given λ_p, the vertical wavelengths of low-frequency gravity waves are shorter than those of gravity waves with a frequency that is close to the Brunt–Väisälä frequency (Figs. 3) and (4). The vertical phase velocities of these waves are smaller than those of high-frequency gravity waves. Therefore, high-frequency gravity waves propagate faster upward through the ionospheric D layer towards the lower thermosphere. Figures 3 and 4 show gravity waves that were found in the ionospheric D layer (Nina and Čadež, 2013). They can be induced in situ at sunrise and sunset due to motions of the solar terminator. Low-frequency gravity waves are observed near the OH layer at an altitude of about 87 km and near the O₂ layer at an altitude of about 94 km by the mesospheric temperature mapper (Yuan et al., 2016). Their frequencies are ω=0.0011 s⁻¹ and ω=0.0014 s⁻¹, respectively, and are even lower than the gravity wave frequencies in Fig. 4.

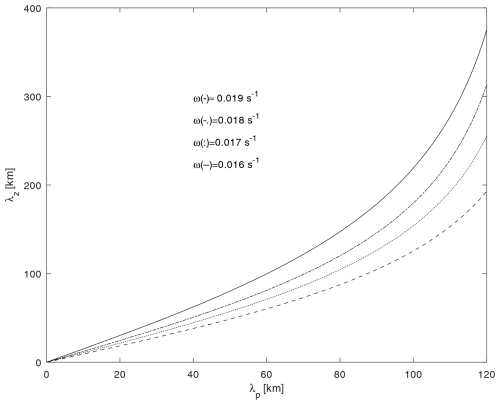
Figure 3 Vertical wavelength, λ_z, of gravity waves from the dispersion equation, Eq. (9), as a function of the horizontal wavelength, λ_p, for a given frequency of $\mathit{\omega }\approx {\mathit{\omega }}_{\mathrm{BV}}=\mathrm{0.0195}$ s⁻¹.

Figure 4 Vertical wavelength, λ_z, of gravity waves from the dispersion equation, Eq. (9), as a function of the horizontal wavelength, λ_p, for a given frequency of $\mathit{\omega }\ll {\mathit{\omega }}_{\mathrm{BV}}=\mathrm{0.0195}$ s⁻¹.

4.2 Reflection coefficient of AGWs at the D layer–lower thermosphere boundary

We assume that z=0 (Eq. 15) is the plane boundary between the ionospheric D layer at an altitude of 60–90 km, i.e. region 1, and lower thermosphere at an altitude of 90 to about 140 km, i.e. region 2. At this boundary, AGWs coming from below can be reflected in the D layer or transmitted into the lower thermosphere. The temperature of the D layer is T₁=250 K, while the temperature of the lower thermosphere is T₂=500 K. Therefore, Eq. (16) gives s=0.5. The reflection coefficients of acoustic and gravity waves will be analysed separately.

4.2.1 Reflection coefficient of the acoustic waves

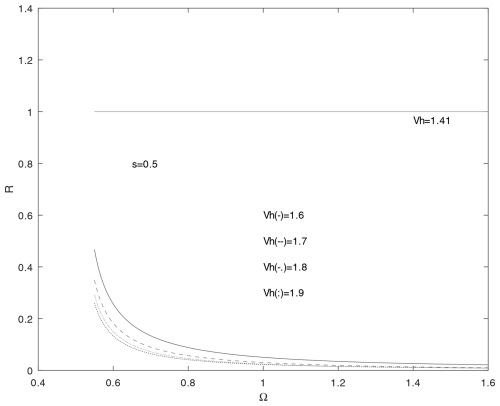
Figure 5 shows the reflection coefficient as a function of frequency, Ω>Ω_co, for acoustic waves at the D layer–lower thermosphere plane boundary, z=0, when s=0.5. Acoustic waves in the frequency range ${\mathrm{\Omega }}_{\mathrm{co}}<\mathrm{\Omega }<\mathrm{0.8}$ are reflected on this boundary to a somewhat greater extent. The reflection coefficient strongly decreases with increasing frequency, and acoustic waves with a frequency of Ω>0.8, i.e. ω=0.035 s⁻¹, can easily propagate through the D layer–lower thermosphere boundary. These waves could affect the thermospheric temperature and dynamics by depositing their momentum and energy in the lower thermosphere. The value of the horizontal phase velocity, V_h, does not significantly affect the reflection coefficient, except in the case when $V_{\mathrm{h}}=\mathrm{1}/\sqrt{s}=\mathrm{1.41}$, i.e. for the horizontal phase velocity of the acoustic waves, $v_{\mathrm{ph}}=\mathrm{1.41}{v}_{\mathrm{s}}=\mathrm{447}$ m s⁻¹, when total internal reflection occurs. Waves with this horizontal velocity cannot penetrate the thermosphere. Acoustic waves with horizontal phase velocity V_h>1.41 can propagate through the D layer–lower thermosphere boundary and extend further into the thermosphere, especially if Ω>1. Their reflection coefficient slowly decreases with the increase in V_h for a given frequency Ω.

Figure 5 Reflection coefficient for acoustic waves at the D layer–lower thermosphere plane boundary, z=0, as a function of frequency, Ω, and parameter s=0.5. If $V_{\mathrm{h}}=\mathrm{1}/\sqrt{s}=\mathrm{1.41}$, the reflection coefficient is R=1, and total internal reflection occurs.

4.2.2 Reflection coefficient of the gravity waves

The reflection coefficient for gravity waves with Ω<Ω_BV increases when the frequency Ω increases and decreases with increasing horizontal phase velocity, V_h, for a given frequency Ω (Fig. 6). These waves can propagate in both regions, in the ionospheric D layer and in the lower thermosphere, if their frequencies are lower than the cutoff frequency $\mathrm{\Omega }=\sqrt{s}{\mathrm{\Omega }}_{\mathrm{BV}}=\mathrm{0.32}$ or ω=0.014 s⁻¹ and their horizontal phase velocities are lower than $V_{\mathrm{h}}={\mathrm{\Omega }}_{\mathrm{BV}}/{\mathrm{\Omega }}_{\mathrm{co}}=\mathrm{0.9}$, i.e. $v_{\mathrm{h}}=\mathrm{0.9}{v}_{\mathrm{s}}=\mathrm{285}$ m s⁻¹. Gravity waves with frequencies much lower than the Brunt–Väisälä frequency and with high horizontal phase velocities are candidates for crossing the D layer–lower thermosphere boundary. Contrary to this, gravity waves with frequencies near the cutoff frequency of $\mathrm{\Omega }=\sqrt{s}{\mathrm{\Omega }}_{\mathrm{BV}}$ are strongly reflected at the D layer–lower thermosphere boundary. For the horizontal phase velocity of V_h=0.9, total internal reflection occurs, and the reflection coefficient is equal to unity.

Figure 6 Reflection coefficient for gravity waves at the D layer–lower thermosphere plane boundary, z=0, as a function of frequency, Ω, and parameter s=0.5. If $V_{\mathrm{h}}={\mathrm{\Omega }}_{\mathrm{BV}}/{\mathrm{\Omega }}_{\mathrm{co}}=\mathrm{0.9}$, the reflection coefficient is R=1, and total internal reflection occurs.

5 Discussion

It is known that high-frequency acoustic waves are strongly absorbed by the atmosphere (Sindelarova et al., 2009). The rate of absorption is proportional to the wave frequency squared. Therefore, only acoustic waves with low frequencies (infrasound) may propagate through the ionospheric D layer and eventually through the lower thermosphere. Indeed, it was found that only acoustic waves with periods of less than 4 min, i.e. Ω>0.6, or ω>0.026 s⁻¹ propagating almost vertically are able to reach the lower thermosphere (Blanc, 1985; Schulthess, 2022). In Fig. 5, the reflection coefficient for infrasound waves is presented since the dimensionless frequency Ω=1.6 corresponds to the frequency of ω=0.069 s⁻¹, i.e. $\mathit{\nu }=\mathit{\omega }/\mathrm{2}\mathit{\pi }=\mathrm{0.01}$ Hz. These waves, with a horizontal phase velocity of v_h>447 m s⁻¹ and with a minimum vertical phase velocity of $v_{\mathrm{v}min}>\mathrm{317}$ m s⁻¹ have the best chance of reaching the thermosphere if they propagate almost vertically with an infrasound frequency of ω>0.035 s⁻¹. Although infrasound waves dissipate their energy in the lower thermosphere, they are not the first option for raising its temperature. Namely, the influence of acoustic wave energetics into the ionosphere/lower thermosphere is weak (Lizunov and Hayakawa, 2004). It appears that the temperature in the thermosphere is increased by low-frequency gravity waves coming from below (Sindelarova et al., 2009). Their reflection coefficient for the ionospheric D layer–lower thermosphere boundary is shown in Fig. 6. Gravity waves with a horizontal phase velocity of V_h<0.5 are easily reflected from the boundary between the D layer and lower thermosphere and will likely remain trapped at lower altitudes. Only waves with a horizontal phase velocity within $\mathrm{0.5}<V_{\mathrm{h}}<\mathrm{0.7}$, i.e. 159 m s⁻¹ < v_h < 222 m s⁻¹, and with a low frequency of Ω<0.2 or ω<0.0087 s⁻¹ are important for the dynamics of the middle atmosphere. Horizontal wavelengths for these waves are in the range of 115 km < λ_p < 161 km. This is consistent with the results known from the scientific literature (Fritts et al., 2014; Bakhmetieva et al., 2019), which emphasize that gravity waves with periods as short as 10 min (i.e. Ω<0.24 or ω<0.01 s⁻¹) can carry significant momentum flux vertically. These waves with a wavelength of λ_p ≈ 100–200 km play an important role in the interaction between the ionospheric D layer and the lower thermosphere. They are responsible for the generation of middle-scale travelling ionospheric disturbances (TIDs) with periods from 15 min to 3 h, velocities from 100 to 250 m s⁻¹, and horizontal wavelength of approximately a few hundred kilometres (Lizunov and Hayakawa, 2004). It seems that they are causing a rise in temperature in the lower thermosphere through the process of gravity wave breaking and dissipation due to kinematic viscosity and thermal diffusivity (Vadas, 2007; Sindelarova et al., 2009; Yuan et al., 2016). A similar situation can be found in the solar atmosphere (Fleck et al., 2021) and on the photosphere–chromosphere boundary (Marmolino et al., 1993; Jovanović, 2014), with the parameter s=0.6.

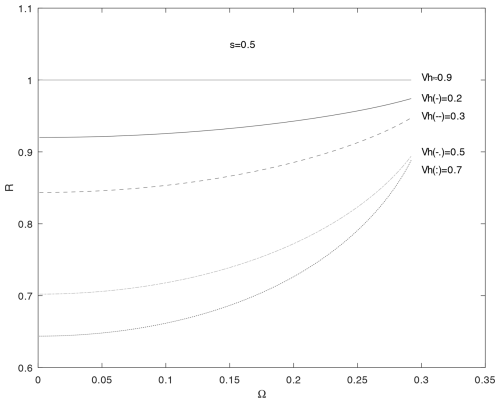
Gravity waves dissipate their energy contributing to local heating of the thermosphere at higher altitudes during extreme solar minimum since the kinematic viscosity is much smaller in warmer than in colder thermosphere at the same altitude (Sindelarova et al., 2009). During extreme solar minimum, the lower thermosphere is relatively cold of T≈500 K, while during active solar conditions, the temperature in thermosphere can be T≈2000 K (Vadas, 2007). The current, 25th solar cycle, which began in December 2019, is expected to have maximum activity in July 2025. This solar activity could increase the temperature in the lower thermosphere several times. The reflection coefficient for acoustic waves in active solar conditions varies with the frequency, Ω, and the parameter s = 250 K/2000 K = 0.125 as depicted in Fig. 7. The reflection coefficient decreases in the frequency range ${\mathrm{\Omega }}_{\mathrm{co}}<\mathrm{\Omega }<\mathrm{1.5}$. Acoustic waves with $V_{\mathrm{h}}\ge \mathrm{1}/\sqrt{s}\approx \mathrm{2.83}$ are the best candidates to pass through the D layer–lower thermosphere boundary and propagate further into the thermosphere. Acoustic waves with $V_{\mathrm{h}}\gg \mathrm{1}/\sqrt{s}$ are the most susceptible to reflection. This is the opposite situation compared to the reflection coefficient for acoustic waves with s=0.5 (Fig. 5), where the waves with $V_{\mathrm{h}}\approx \mathrm{1}/\sqrt{s}$ are the ones that are most prone to reflection. For a frequency of Ω>1.5, the reflection coefficient decreases very slowly and remains almost constant.

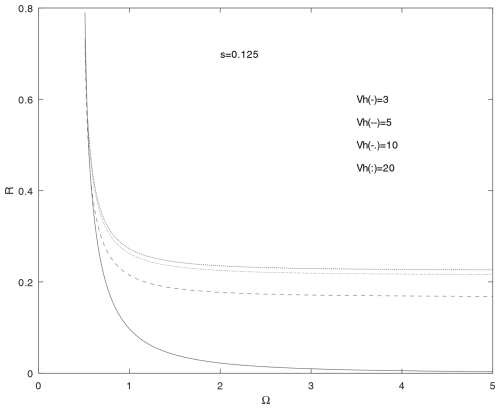
Figure 7 Reflection coefficient for acoustic waves at the D layer–lower thermosphere plane boundary, z=0, as a function of frequency, Ω, and parameter s=0.125.

The reflection coefficient for gravity waves in active solar conditions as a function of frequency, Ω, and the parameter s=0.125, is shown in Fig. 8. It has very high values for all gravity waves propagating with the allowed V_h<0.9. These waves can hardly pass the boundary between the ionospheric D layer and the lower thermosphere. It seems that they are trapped in the ionospheric D layer and cannot propagate through the thermosphere. Therefore, infrasound can play a significant role in the interaction between the ionospheric D layer and lower thermosphere during solar maximum activity.

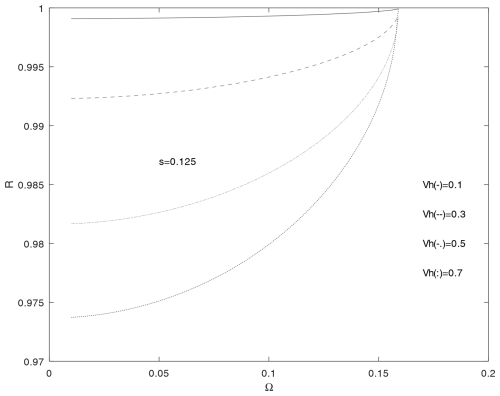
Figure 8 Reflection coefficient for gravity waves at the D layer–lower thermosphere plane boundary, z=0, as a function of frequency, Ω, and parameter s=0.125.

The conditions for AGW propagation, as well as their reflection coefficient, strongly depend on the temperature through v_s and parameter s (Eqs. 8 and 17). Therefore, any change in temperature can affect the propagation of AGWs and their reflection and transmission features. This means that the detection of these waves depends on the current temperature in the region being observed. A similar situation exists with the detection of AGWs by lidar or any other instrument because their positions relative to the wave source region will determine which AGW characteristic can be observed (Yuan et al., 2016).

One of the important effects of AGWs and especially gravity waves is their influence on the concentration of charged particles in the ionospheric E layer embedded in the lower thermosphere at an altitude of 90–140 km. Namely, the concentration of charged particles becomes time-dependent in the presence of waves. The changed characteristics of this layer affect the reflection of radio waves and telecommunication connections (Zawdie et al., 2022). A similar situation is seen in strong natural hazards when earthquakes of magnitude $M_{\mathrm{v}}=\mathrm{5.5}+$ are studied by VLF/LF radio waves. A physical interpretation is based on atmospheric gravity waves which could alter the ionospheric E layer and modulate the height of the VLF/LF wave reflection (Eichelberger et al., 2024).

An interesting approach to the study of linear AGWs has been made by Cheremnykh et al. (2020). They suggest that AGWs in an isothermal atmosphere can be considered a superposition of oscillations that occur simultaneously at two natural frequencies – acoustic and gravitational – for a fixed wavelength.

AGWs driven from the Earth's surface or troposphere are typically characterized as primary or higher order (e.g. secondary) depending on how they propagate to thermospheric altitudes (Zawdie et al., 2022). Primary AGWs propagate directly through the thermosphere and can be modelled using linear theory. Klymenko et al. (2021) proposed a method for recognizing the types of linear AGWs in the atmosphere from satellite measurements. Higher-order AGWs are created when primary AGWs break in the upper atmosphere; nonlinear propagation theory is required to simulate them (Vadas and Crowley, 2010; Gavrilov and Kshevetskii, 2014; Gavrilov et al., 2018; Dong et al., 2022). Considerable attention has recently been paid to the study of so-called secondary AGWs that arise as a result of instability and nonlinear interactions of primary wave modes propagating from atmospheric sources, among themselves, and with the mean flow. Gavrilov and Kshevetskii (2023) separated the horizontal spatial spectra of primary and secondary AGWs at fixed altitude levels in the middle and upper atmosphere at different time moments using a three-dimensional nonlinear high-resolution model AtmoSym. This separation of the spectra of primary and secondary AGWs makes it possible to estimate the relative contribution of secondary AGWs at different altitudes, at different times, and with a different stability of background temperature and wind profiles in the atmosphere. These issues are important for future research, and numerical models could be a good tool for them.

6 Conclusions

In this article, analytical equations are used to study AGWs propagation through the ionospheric D layer and the D layer–lower thermosphere interaction. The dispersion equation and the reflection coefficient show that infrasound waves with a frequency of ω>0.035 s⁻¹ that propagate almost vertically can reach the lower thermosphere. Gravity waves propagate in both regions – the ionospheric D layer and the lower thermosphere – if their frequency is ω<0.014 s⁻¹ and their horizontal phase velocity is v_h<285 m s⁻¹. Gravity waves with frequencies much lower than the Brunt–Väisälä frequency, ω_BV=0.0195 s⁻¹, propagate more horizontally than vertically because λ_p≪λ_z. These waves have lower vertical phase velocities than high-frequency gravity waves with ω≈ω_BV, which travel faster through the ionospheric D layer towards the lower thermosphere. The reflection coefficient is the smallest for the gravity waves with the frequency of ω<0.0087 s⁻¹, horizontal phase velocity of 159 m s⁻¹ < v_h < 222 m s⁻¹, and horizontal wavelength of 115 km < λ_p < 161 km, which is in accordance with the results known in the scientific literature (Lizunov and Hayakawa, 2004; Fritts et al., 2014; Bakhmetieva et al., 2019). These waves can generate the middle-scale TIDs and cause temperature rise in the lower ionosphere.

The reflection coefficient is highly temperature-dependent. It changes significantly during the pronounced solar maximum when the temperature in the lower thermosphere can rise several times. A strong increase in the reflection coefficient for gravity waves indicates that they cannot pass the D layer–lower thermosphere boundary. Therefore, infrasound waves are better interaction instruments.

There is broad scientific interest in the future study of AGWs. This is particularly attributed to the study of natural hazards, telecommunications and navigation, and space weather. Due to the complex nature of this process, differences between model results and observations are expected (Klymenko et al., 2021).