Multi-Global Navigation Satellite System (GNSS) real-time tropospheric delay retrieval based on state-space representation (SSR) products from different analysis centers

The troposphere plays an important role in a range of weather and various climate changes. With the development of the Global Navigation Satellite System (GNSS), the zenith tropospheric delay (ZTD) retrieval using GNSS technology has become a popular method. Research on ZTD accuracies of state-space representation (SSR) corrections from different analysis centers derived from real-time precise point positioning (RT-PPP) is important for Earth observation correction, meteorological disaster forecasting, and warning with the increasing abundance of state-space representation (SSR) products obtained by the International GNSS Service (IGS) analysis center. Therefore, accuracies and availability of real-time orbits and clock errors obtained by the Chinese Academy of Sciences (CAS), GMV Aerospace and Defense (GMV), Centre National d'Etudes Spatiales (CNE), and Wuhan University (WHU) are evaluated, and the RT positioning performance and ZTD accuracies are analyzed for Global Positioning System (GPS), Galileo (GAL), and BeiDou Navigation Satellite System-3 (BDS3) satellites. The results indicate that CAS has the higher satellite availability, providing SSR corrections for 82 GPS, Galileo, and BDS3 satellites. The accuracies of GPS, Galileo, and BDS3 orbits are best at WHU, CAS, and WHU with values of 5.57, 5.91, and 11.77 cm, respectively; the standard deviations (SDs) of clock error are all better than 0.22, 0.19, and 0.55 ns, and the root mean square errors (RMSEs) are better than 0.54, 0.32, and 1.46 ns. CAS has the best signal-in-space ranging errors (SISREs) followed by WHU, while CNE and GMV are worse. In the RT-PPP test, convergence times for CAS and WHU are 14.9 and 14.4 min, respectively, with 3D positioning accuracy for both of around 3.3 cm, which is better than for CNE and GMV. Among them, WHU SSR has the higher accuracy of RT-PPP-derived ZTD, with an RMSE of 6.06 mm and desirable availability with a completeness rate of 89 %.

1 Introduction

Zenith tropospheric delay (ZTD) can be used for Earth observation error correction (Kinoshita, 2022; Xiong et al., 2019; Zhu et al., 2022), including the Global Navigation Satellite System (GNSS), very long baseline interferometry, interferometric synthetic aperture radar, and warning and forecasting of extreme natural disasters (H. B. Li et al., 2022; Li et al., 2021; S. Li et al., 2023; Yao et al., 2018). Besides, satellite signals are affected by refraction during their pass through the troposphere, causing delay errors (Gao et al., 2021). The tropospheric delay can also be converted to obtain atmospheric precipitation water vapor, facilitating the research on scientific issues such as global atmospheric radiation, energy balance, and water cycle (Edokossi et al., 2020; Lin et al., 2018; Ma et al., 2021; Pipatsitee et al., 2023). Therefore, real-time (RT) and high-precision ZTD can be used to provide rapid and accurate tropospheric correction services in space geodesy while benefiting weather forecasting and climate change research (Crocetti et al., 2024; He et al., 2024).

GNSS is an important means of water vapor detection and is increasingly important in short-term and near-space forecasting (Eugenia Bianchi et al., 2016; Li et al., 2023; Li et al., 2015; Sha et al., 2024). GNSS-ZTD retrieval has an excellent prospect for development due to the advantages of all-weather, RT, and high-accuracy measurements (Hadas et al., 2020; Li et al., 2023; Lu et al., 2016; Pan et al., 2024). The double-difference algorithm through GNSS networking and precise point positioning (PPP) is commonly used for ZTD retrieval (Stêpniak et al., 2022). PPP has a broader range of applications, including timing, atmospheric modeling, and deformation monitoring, due to the lower cost and one GNSS receiver (Ge et al., 2021; Liu et al., 2018; Wang et al., 2023). However, the PPP technology relies on high-precision GNSS orbit and clock error products, typically released as final precise post-processing products to the public (B.-F. Li et al., 2022). A working group was established by the International GNSS Service (IGS) analysis center to study GNSS RT data, and it launched an RT data service in 2013 for high-precision RT-PPP applications (Gu et al., 2022). GNSS RT orbits and clock corrections are made available to users based on the Internet through the Networked Transport of Radio Technical Commission for Maritime Services (RTCM) via Internet Protocol (NTRIP) (Shu et al., 2024; L. Wang et al., 2018; Z.-Y. Wang et al., 2018). The orbit accuracy of IGS real-time products is better than 5 cm, with a satellite clock error RMSE of approximately 0.15 ns, which is about 10 times better than the predicted portion of ultra-rapid clock deviations (Di et al., 2020). State-space representation (SSR) products have led to a remarkable 50 % improvement in RT-PPP positioning accuracy compared to IGS ultra-fast products (Elsobeiey and Al-Harbi, 2016). SSR products are becoming increasingly abundant with the rapid development of computer arithmetic and the increasing demand for real-time high-precision GNSS applications. X.-X. Li et al. (2022) conducted a comprehensive evaluation of SSR products from 10 analysis centers' multi-GNSS and performed RT dynamic PPP, which showed the most complete and highest-quality products obtained by Centre National d'Etudes Spatiales (CNE) and Wuhan University (WHU). Furthermore, it has also been applied to RT deformation monitoring, RT atmospheric detection, and other fields (R.-H. Li et al., 2023). Capilla et al. (2016) applied RT-PPP to deformation monitoring, demonstrated that the technique has a monitoring accuracy of 2 cm, and proved that RT-PPP was full of potential for deformation monitoring applications. Li et al. (2015) investigated the ZTD solution and integrated water vapor retrieval of multi-GNSS RT-PPP. They compared RT-PPP-derived ZTD with data from concurrent radiosonde stations and very long baseline interferometry, which demonstrated that the performance of the multi-GNSS RT-PPP-derived ZTD can reach the millimeter level and has potential in the application of meteorology.

Researchers have assessed the accuracy of single-system RT-PPP-derived ZTD and multi-GNSS RT-PPP-derived ZTD. Lu et al. (2015) found that the retrieval accuracy of atmospheric water vapor can be improved by several millimeters when a combined Global Positioning System (GPS) and BeiDou Navigation Satellite System (BDS) solution is used. Li et al. (2015) obtained RT-PPP-derived ZTD using GPS, BDS2, Galileo (GAL), and GLONASS PPP, demonstrating higher accuracy and greater ZTD availability than a single-system PPP. Jiao et al. (2019) analyzed the results of PPP and multi-GNSS PPP, noting that the positioning accuracy and convergence were significantly improved with the inclusion of the BDS3 satellite system. The accuracy of BDS3-derived ZTD is improved by 20.5 % versus that of BDS2. Alcay and Turgut (2021) compared the GPS, GPS–GLONASS, and GPS–GLONASS–Galileo–BDS PPP solutions and found that the ZTD difference between the three schemes was less than 20 mm. Lu et al. (2017) compared the accuracy of the RT-PPP-derived ZTD using the different SSR products, and the multi-GNSS RT-PPP-derived ZTD based on GFZC2 SSR products showed the highest accuracy.

The ongoing discussion primarily centers on the influence of single- and multi-GNSS RT-PPP on the accuracy of RT ZTD. Yet there is a limited discourse on the influence of the different analysis-center-based SSR corrections on the accuracy of RT ZTD. The quality of GNSS SSR products has improved with the increasing abundance of SSR products provided by IGS. Most studies have focused on BDS2 (Lu et al., 2015; Pan and Guo, 2018), while BDS3 needs to be sufficiently studied. Moreover, evaluating the influence of different GNSS SSR products for the accuracy of RT-PPP-derived ZTD is an important reference value for achieving high-precision and high-availability in RT-PPP-derived ZTD with the growth of SSR products. In this study, positioning performance and ZTD accuracy are estimated using the RT-PPP based on multi-GNSS from eight Interactive Gravity and Magnetic Application System (IGMAS) stations from day of year (DOY) 355 in 2023 to DOY 14 in 2024. Our primary objective is to compare the RT-PPP positioning performance, RT-PPP-derived ZTD accuracy and availability based on SSR products from different analysis centers. The findings serve as a valuable reference for selecting SSR products in RT-PPP-derived ZTDs and hold significant importance for applications such as Earth observation correction and meteorological disaster prediction.

2 The method of RT-PPP-derived ZTDs

2.1 Data collection

IGS was established to bolster geodetic and geodynamic research, officially launching its operations on 1 January 1994. IGS offers worldwide access to GNSS satellite observations from various tracking stations and products, including satellite ephemerides, clock errors, Earth orientation parameters, and atmospheres,. (Geng et al., 2021; Griffiths, 2019). IGMAS was established under the leadership of China in 2012. Its primary purpose is establishing an information platform equipped with data acquisition, storage, analysis, management, and release functions for the global RT tracking network of the four major satellite navigation systems with full arcs and multiple coverage observations. The leading indicators and operational status of GNSS are tested and assessed to generate products such as high-precision ephemerides, satellite clock errors, geotropic parameters, tracking station coordinates and rates, and global ionospheric delays (Li et al., 2022; Zhang et al., 2023).

Figure 1 The workflow of this study.

Figure 2 The distribution of IGMAS stations and IGS stations.

Table 1 Location information of IGMAS stations.

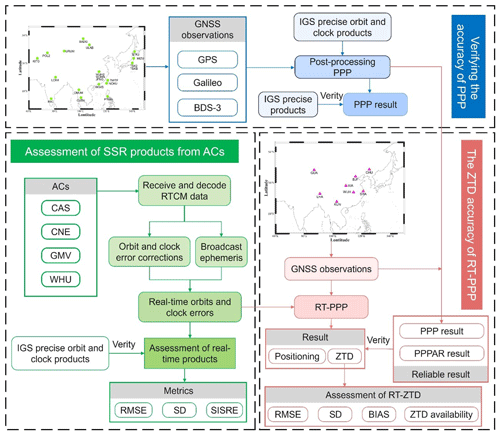
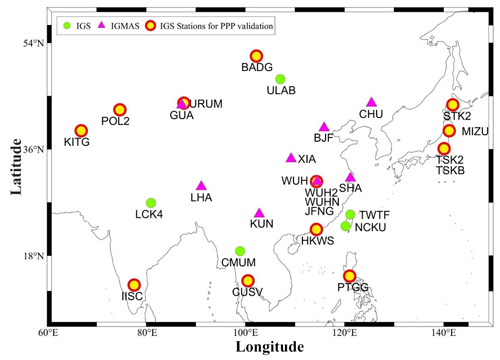
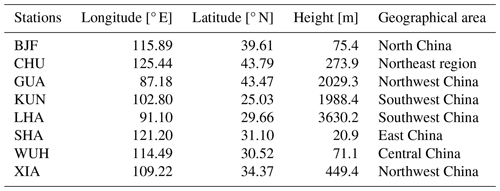
The workflow of this study is shown in Fig. 1 and includes three parts: verifying the performance of PPP, assessing different SSR products, and verifying the performance of RT-PPP using the results obtained by post-processing PPP and Positioning Racers to Image and Decipher the Earth (PRIDE) PPP-AR, where AR stands for ambiguity resolution. PRIDE PPP-AR is a multi-GNSS real-time PPP open-source software developed by the PRIDE Laboratory at Wuhan University. The software supports the post-processing of multi-system GNSS data and can be applied to various fields, including geodesy, seismic analysis, photogrammetry, and gravity measurement. In the first part, the position and ZTD are estimated using the multi-GNSS post-processing PPP technique from IGS stations in Asia–Pacific to verify the performance of multi-GNSS post-processing PPP. A total of 20 stations are selected in countries such as Mongolia, Russia, Japan, India, and Thailand. The 14 IGS sites with the highest availability are selected from the IGS sites for experimental analysis according to the number of observation documents. In the second part, the accuracies of SSR products from four analysis centers are evaluated. In the third part, the position and ZTD are estimated using a multi-GNSS RT-PPP technique from eight IGMAS stations in China. Data from DOY 355 in 2023 to DOY 14 in 2024 are utilized. GPS, Galileo, and BDS3 can be received at these stations simultaneously. The solutions obtained by PRIDE PPP-AR and post-processing PPP are considered the reliable position and ZTD to verify the performance of RT-PPP. Figure 2 displays the distribution information of the selected IGS and IGMAS sites in this study and the information of IGMAS stations is shown in Table 1. It should be noted that “IGS” refers to all IGS stations in China and the surrounding areas, while “IGS stations for PPP validation” refers to the specific IGS stations selected for study.

2.2 Recovering real-time products

IGS RT satellite orbit correction includes the position correction $\mathrm{d}O={\left[\begin{array}{ccc}\mathit{\delta }{O}_{\mathrm{r}}& \mathit{\delta }{O}_{\mathrm{a}}& \mathit{\delta }{O}_{\mathrm{c}}\end{array}\right]}^T$ and velocity correction $\mathrm{d}\stackrel{\mathrm{‾}}{O}={\left[\begin{array}{ccc}\mathit{\delta }{\stackrel{\mathrm{‾}}{O}}_{\mathrm{r}}& \mathit{\delta }{\stackrel{\mathrm{‾}}{O}}_{\mathrm{a}}& \mathit{\delta }{\stackrel{\mathrm{‾}}{O}}_{\mathrm{c}}\end{array}\right]}^T$ at the reference moment t₀; then, the orbital correction at moment t is

$$\begin{array}{}\text{(1)}& \mathit{\delta }O=O+\mathrm{d}\stackrel{\mathrm{‾}}{O}(t-t_{\mathrm{0}}).\end{array}$$

The orbital corrections from the spacecraft body-fixed system should be transformed to the Earth-centered, Earth-fixed system by means of a coordinate transformation. Since the positioning is usually done in the Earth-centered, Earth-fixed system, the following applies:

$$\begin{array}{}\text{(2)}& X=\left[\begin{array}{ccc}\frac{\stackrel{\mathrm{‾}}{r}}{\left|\stackrel{\mathrm{‾}}{r}\right|}\times \frac{r\times \stackrel{\mathrm{‾}}{r}}{\left|r\times \stackrel{\mathrm{‾}}{r}\right|}& \frac{\stackrel{\mathrm{‾}}{r}}{\left|\stackrel{\mathrm{‾}}{r}\right|}& \frac{r\times \stackrel{\mathrm{‾}}{r}}{\left|r\times \stackrel{\mathrm{‾}}{r}\right|}\end{array}\right]\mathit{\delta }O,\end{array}$$

where r=X_brdc refers to satellite positions from broadcast ephemeris. $\stackrel{\mathrm{‾}}{r}={\stackrel{\mathrm{‾}}{X}}_{\text{brdc}}$ refers to velocity from broadcast ephemeris. The X_pre refers to precise satellite position, which can be calculated by

$$\begin{array}{}\text{(3)}& X_{\text{pre}}=X_{\text{brdc}}-\mathit{\delta }X.\end{array}$$

The RT correction of the clock error refers to the difference in precision clock error, δt_pre versus broadcast clock error, δt_brdc, which is similar to RT orbital correction. However, the SSR clock error correction is represented by c₀, c₁, and c₂ of the reference time, t₀, unlike orbital corrections, and the RT correction, δc, is obtained by fitting c₀, c₁, and c₂. The RT correction, δc, of the clock error at moment t is

$$\begin{array}{}\text{(4)}& \mathit{\delta }c=c_{\mathrm{0}}+c_{\mathrm{1}}(t-t_{\mathrm{0}})+c_{\mathrm{2}}(t-t_{\mathrm{0}}{)}^{\mathrm{2}}.\end{array}$$

Eventually, the precision clock error, δt_pre, is obtained by

$$\begin{array}{}\text{(5)}& \mathit{\delta }{t}_{\text{pre}}=\mathit{\delta }{t}_{\text{brdc}}-{\mathit{\delta }}_{\mathrm{c}}/C_{\text{light}},\end{array}$$

where δt_brdc and C_light refers to clock error from broadcast ephemeris and speed of light.

2.3 PPP functional model

The impacts of satellite orbits and clock errors are mitigated by employing RT satellite orbits and clock errors recovered by SSR in the PPP technique. ZTD is solved as an unknown parameter of the equation. The principle is to construct two observation equations based on the ionosphere-free (IF) combinations of pseudo-range and carrier-phase observation (Ju et al., 2022; Ke and Shuanggen, 2020). The basic observation equations can be expressed as follows:

$$\begin{array}{}\text{(6)}& \left\{\begin{array}{ll}{P}_{\mathrm{r},\mathrm{i}}^{\mathrm{s}}=& {\mathit{\rho }}_{\mathrm{r},\mathrm{i}}^{\mathrm{s}}+C_{\text{light}}({\text{dt}}_{\mathrm{r}}-{\text{dt}}^{\mathrm{s}})+I_{\mathrm{r},\mathrm{i}}^{\mathrm{s}}+T_{\mathrm{r}}^{\mathrm{s}}+b_{\mathrm{r},\mathrm{i}}\\ & +b_{\mathrm{r},\mathrm{i}}^{\mathrm{s}}+{\mathit{\epsilon }}_{\mathrm{r},\mathrm{P}}^{\mathrm{s}},\\ L_{\mathrm{r},\mathrm{i}}^{\mathrm{s}}=& {\mathit{\rho }}_{\mathrm{r}}^{\mathrm{s}}+C_{\text{light}}({\text{dt}}_{\mathrm{r}}-{\text{dt}}^{\mathrm{s}})-I_{\mathrm{r},\mathrm{i}}^{\mathrm{s}}+T_{\mathrm{r}}^{\mathrm{s}}+{\mathit{\lambda }}_{\mathrm{i}}{N}_{\mathrm{r},\mathrm{i}}^{\mathrm{s}}\\ & +{\mathit{\delta }}_{\mathrm{r},\mathrm{i}}-{\mathit{\delta }}_{\mathrm{r},\mathrm{i}}^{\mathrm{s}}+{\mathit{\epsilon }}_{\mathrm{r},\mathit{\phi }}^{\mathrm{s}},\end{array}\right.\end{array}$$

where s refer to the satellites. r refers to the receiver, and i refers to the frequency. $L_{\mathrm{r},\mathrm{j}}^{\mathrm{s}}$ and $P_{\mathrm{r},\mathrm{j}}^{\mathrm{s}}$ are the carrier-phase and pseudo-range observation from receiver r to satellite S, respectively. ρ refers to the satellite–receiver geometric distance. dt_r is the receiver clock error, and dt^s is the satellite clock error. I is the ionospheric delay. $T_{\mathrm{r}}^{\mathrm{s}}$ refers to the tropospheric delay. λ is the wavelength. δ and b denote the phase delays and the code bias, respectively. N is the integer ambiguity. ${\mathit{\epsilon }}_{\mathrm{r},\mathrm{P}}^{\mathrm{s}}$ is the pseudo-range observation noise. ${\mathit{\epsilon }}_{\mathrm{r},\mathrm{L}}^{\mathrm{s}}$ is the carrier-phase observation noise.

The dual-frequency IF combination model is constructed and simplified from Eq. (6):

$$\begin{array}{}\text{(7)}& \left\{\begin{array}{l}{P}_{\text{IF}}=\mathit{\rho }-\text{cdt}+T_{\mathrm{r}}^{\mathrm{s}}+{\mathit{\epsilon }}_{r,s}^{\mathrm{s}},\\ L_{\text{IF}}=\mathit{\rho }-\text{cdt}+T_{\mathrm{r}}^{\mathrm{s}}+{\mathit{\lambda }}_{\mathrm{1}}{N}_{\text{IF}}+{\mathit{\epsilon }}_{\mathrm{r},\mathit{\phi }}^{\mathrm{s}},\end{array}\right.\end{array}$$

where L_IF is the carrier-phase observation. P_IF is the pseudo-range observation. The unknown parameters can be estimated in IF-PPP as follows:

$$\begin{array}{}\text{(8)}& X=\left[\begin{array}{cccc}x& \text{cd}{\stackrel{\mathrm{‾}}{t}}_{\mathrm{r}}& Z& {\stackrel{\mathrm{‾}}{N}}_{\text{IF}}^{\mathrm{s}},\end{array}\right]\end{array}$$

where x is the position of the receiver. $\text{cd}{\stackrel{\mathrm{‾}}{t}}_{\mathrm{r}}$ refers to receiver clock error. Z refers to the tropospheric delay. ${\stackrel{\mathrm{‾}}{N}}_{\text{IF}}^{\mathrm{s}}$ refers to the integer-phase ambiguity.

2.4 Accuracy evaluation

Two methods are used to evaluate the accuracy of RT-PPP-derived ZTD at IGMAS stations. The first is our post-processing PPP based on RTKLIB for secondary development, and the other one is PRIDE PPP-AR from Geng et al. (2021) of Wuhan University. The consistency between the solution data and the IGS precision products is used to evaluate the positioning and ZTD accuracy of post-processing PPP for IGS stations. Gross errors and outages in the RT clock error products will lead to an unreliable accuracy assessment of the RT clock error products. The accuracy statistics of clock error may be affected if a single satellite's clock error is used as the reference. Therefore, the average satellite clock error at the current epoch is used as a reference to eliminate system errors in this study (Yao et al., 2017). The root mean square error (RMSE), standard deviation (SD), and bias of the differences are used to evaluate SSR products and positioning and ZTD of RT-PPP. The three metrics are calculated as follows (Su et al., 2023):

$$\begin{array}{}\text{(9)}& \left\{\begin{array}{l}\text{RMSE}=\sqrt{\frac{\mathrm{1}}{N}{\sum }_{i=\mathrm{1}}^N{\mathrm{\Delta }}^{\mathrm{2}}},\\ \text{SD}=\sqrt{\frac{\mathrm{1}}{N}{\sum }_{i=\mathrm{1}}^N(\mathrm{\Delta }-{\mathrm{\Delta }}_{\text{ave}}{)}^{\mathrm{2}}},\\ \text{BIAS}=\frac{\mathrm{1}}{N}{\sum }_{i=\mathrm{1}}^N\mathrm{\Delta },\end{array}\right.\end{array}$$

where N is the sample number. Δ is the difference of the SSR products versus the IGS precision products. Δ_ave is the average Δ.

The Pearson correlation coefficient (R) is also used to evaluate the consistency of reliable ZTD and RT-PPP-derived ZTD. R is calculated as follows:

$$\begin{array}{}\text{(10)}& R={\displaystyle \frac{\begin{array}{c}{\sum }_{i=\mathrm{1}}^N\left({\text{ZTD}}_{\mathrm{i}}^{\text{der}}-\stackrel{\mathrm{‾}}{{\text{ZTD}}_{\mathrm{i}}^{\text{der}}}\right)\\ \times \left({\text{ZTD}}_{\mathrm{i}}^{\text{der}}-\stackrel{\mathrm{‾}}{{\text{ZTD}}_{\mathrm{i}}^{\text{ref}}}\right)\end{array}}{\sqrt{\begin{array}{c}{\sum }_{i=\mathrm{1}}^N{\left({\text{ZTD}}_{\mathrm{i}}^{\text{der}}-\stackrel{\mathrm{‾}}{{\text{ZTD}}_{\mathrm{i}}^{\text{der}}}\right)}^{\mathrm{2}}\\ \times {\sum }_{i=\mathrm{1}}^N{\left({\text{ZTD}}_{\mathrm{i}}^{\text{der}}-\stackrel{\mathrm{‾}}{{\text{ZTD}}_{\mathrm{i}}^{\text{ref}}}\right)}^{\mathrm{2}}\end{array}}}},\end{array}$$

where ${\text{ZTD}}_{\mathrm{i}}^{\text{der}}$ is the PPP solution results and ${\text{ZTD}}_{\mathrm{i}}^{\text{ref}}$ refers to the tropospheric delay used as a reference. $\stackrel{\mathrm{‾}}{{\text{ZTD}}_{\mathrm{i}}^{\text{der}}}$ and $\stackrel{\mathrm{‾}}{{\text{ZTD}}_{\mathrm{i}}^{\text{ref}}}$ denote the mean of ${\text{ZTD}}_{\mathrm{i}}^{\text{der}}$ and ${\text{ZTD}}_{\mathrm{i}}^{\text{ref}}$, respectively.

$$\begin{array}{}\text{(11)}& \begin{array}{rl}& E_{\text{SISRE}}\\ & =\sqrt{\begin{array}{c}{\left[\text{RMSE}({\mathit{\omega }}_{\mathrm{R}}\mathrm{\Delta }{r}_{\mathrm{R}}-C_{\text{light}}\mathrm{\Delta }C)\right]}^{\mathrm{2}}\\ +{\mathit{\omega }}_{\mathrm{A},\mathrm{C}}^{\mathrm{2}}\left\{{\left[\text{RMSE}\left(\mathrm{\Delta }{r}_{\mathrm{A}}\right)\right]}^{\mathrm{2}}+{\left[\text{RMSE}\left(\mathrm{\Delta }{r}_{\mathrm{C}}\right)\right]}^{\mathrm{2}}\right\}\end{array}},\end{array}\end{array}$$

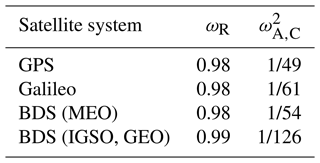
where E_SISRE refers to the signal-in-space ranging errors (SISREs); ΔC is the difference of the RT clock error versus the IGS precision products in each epoch; ${\mathrm{\Delta }}_{r_{\mathrm{R}}}$, ${\mathrm{\Delta }}_{r_{\mathrm{A}}}$, and ${\mathrm{\Delta }}_{r_{\mathrm{C}}}$ are orbital errors in the radial, along-track, and cross-track (R, A, and C) direction in each epoch, respectively. ω_R and ${\mathit{\omega }}_{\mathrm{A},\mathrm{C}}^{\mathrm{2}}$ are weighting factors that convert the orbital errors in the R, A, and C direction to the orbital errors in the line-of-sight direction (Kazmierski et al., 2020). Different satellite systems have different SISRE weighting factors, as shown in Table 2.

Table 2 Weight factors of SISREs.

Table 3 RTCM SSR mount point description. CoM stands for center of mass.

Figure 3 Epoch availability of SSR corrections during the experiment.

3 Accuracy evaluation of SSR products

The stability of SSR streams can be influenced by various factors, including the receiving software, network stability, and broadcasting organization. In this study, RTKNAVI software is used to receive the SSR products in the same network environment from the mount points of SSRC00CAS0, SSRC00CNE0, SSRC00GMV0, and SSRC00WHU0. Since the real-time data from other analysis centers are incomplete during the DOY 355 in 2023 to DOY 14 in 2024, the SSR data from four analysis centers are used in this study. The SSR product information for each subsystem center is shown in Table 3.

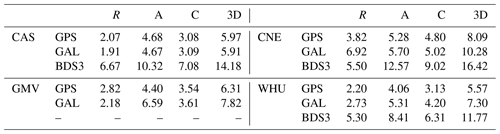
Table 4 The mean accuracies of GPS, Galileo, and BDS3 RT precise products from different analysis centers (in cm).

Figure 4 The RMSE values in R, A, and C directions of GPS RT orbit from different analysis centers.

Figure 5 The RMSEs and SDs of GPS RT clock errors from different analysis centers.

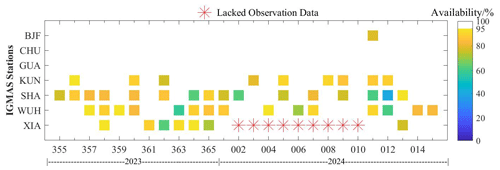
3.1 SSR product availability

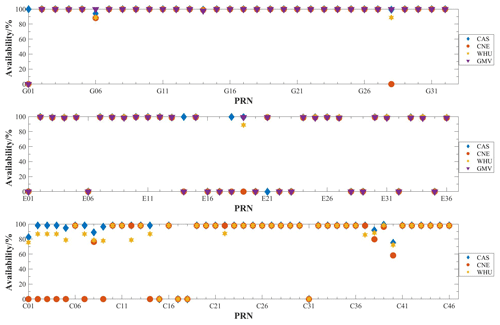
The SSR product completeness rates for the four analysis centers are assessed for 26 d, from DOY 355 in 2023 to DOY 14 in 2024, as illustrated in Fig. 3. Notably, this study excludes the unhealthy satellite G01 from consideration. Since SSR corrections for 31 GPS satellites, 24 Galileo satellites, and 27 BDS3 satellites can be obtained, the Chinese Academy of Sciences (CAS) has the higher satellite availability. WHU offers SSR corrections for 31 GPS satellites, 23 Galileo satellites, and 27 BDS3 satellites. CNE demonstrates lower availability, providing 30 GPS satellites, 22 Galileo satellites, and 27 BDS3 satellites. GMV Aerospace and Defense (GMV) provides SSR corrections for 31 GPS satellites and 23 Galileo satellites. BDS SSR products obtained by GMV are unavailable due to software decoding issues with GMV SSR products during the experimental data period of this study, which resulted in pseudo-random noise and issue of data ephemeris errors for its BDS satellites. Although the variation of epoch availability for GPS, Galileo, and BDS3 SSR corrections from different analysis centers is different, the average epoch availability of the SSR products provided by the four analysis centers is above 97.5 %.

3.2 Accuracy of SSR products

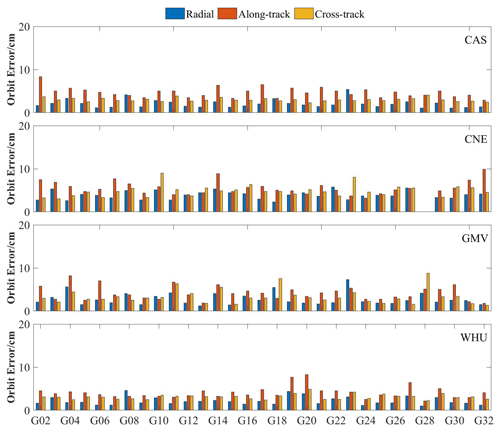
IGS precision products are chosen as references to evaluate different SSR products. The RMSEs of GPS RT orbits in the R, A, and C directions for the four analysis centers are shown in Fig. 4. The average RMSEs of GPS, Galileo, and BDS3 RT orbits in the R, A, and C directions are shown in Table 4. Figure 4 and Table 4 show that the RMSEs of orbit products in the R direction are mostly smaller than in the C direction, with the RMSEs of orbit products in the R direction being the largest due to the observation being mainly centered around the R direction. The accuracies of GPS, Galileo, and BDS3 RT orbits from different analysis centers are individually evaluated. The accuracies of GPS RT orbits from four analysis centers reach the centimeter level, and WHU has the best accuracy followed by CAS and GMV. GPS RT orbits from CNE are relatively worse with 8.09 cm. Galileo RT orbits from CAS exhibit the lowest error followed by WHU and GMV, with CNE showing relatively worse accuracy of 10.28 cm. The accuracies of BDS3 RT orbits from four analysis centers are better than 17 cm. The accuracy of BDS3 RT orbits from WHU is the best; CAS is the second with 14.18 cm, and the products from CNE are worse at 16.42 cm. Overall, Galileo RT orbits from CAS display the best accuracy at 5.91 cm, while WHU has the best accuracies of GPS and BDS3 RT orbits of 5.57 and 11.77 cm, respectively.

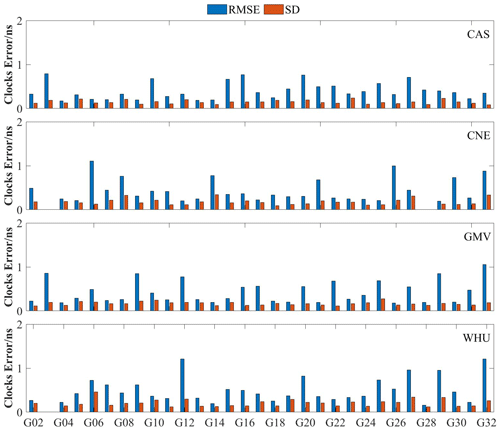
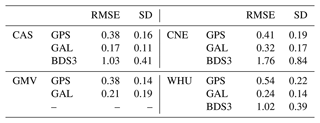
Figure 5 displays the RMSEs and SDs of GPS RT clock errors from four analysis centers. Table 5 shows the RMSEs and SDs of GPS, Galileo, and BDS3 RT clock errors. The RT clock errors in G03 provided by CNE and WHU are excluded from this study due to their gross errors. The remaining GPS satellites are commonly used. The mean SDs of GPS RT clock errors from CAS, GMV, and CNE are 0.16, 0.19, and 0.14 ns, respectively, with the largest SD from WHU being 0.22 ns. For Galileo, CAS RT clock errors display the best accuracy, with a mean SD of 0.11 ns. For BDS3, WHU RT clock errors have the best accuracy with SD of 0.39 ns. Overall, the mean SDs of GPS, Galileo, and BDS3 from the three analysis centers are better than 0.22, 0.19, and 0.55 ns, respectively, and the mean RMSEs of GPS, Galileo, and BDS3 from these analysis centers are better than 0.54, 0.32, and 1.46 ns, respectively.

Table 5 The mean accuracies of GPS, Galileo, and BDS3 RT precise products from different analysis centers (in cm).

3.3 Accuracy of SISREs

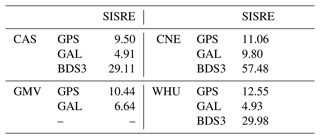
Table 6 shows the average SISREs of GPS, Galileo, and BDS3 from four analysis centers. For GPS, the order of magnitude of SISREs for different analysis centers is WHU > CNE > GMV > CAS. For Galileo, CAS and WHU have the better SISREs of around 5 cm, and CNE has the worst SISRE with 9.80 cm. For BDS3, the SISREs of CAS and WHU are significantly better than the SISRE of CNE, and they are 29.11, 29.98, and 57.48 cm, respectively. Overall, CAS has the best SISREs of GPS, Galileo, and BDS3 followed by WHU as the second, while CNE and GMV exhibit the worst accuracy.

Table 6 Mean SISRE of GPS, BDS, and BDS3 satellite of SSR products from different analysis centers (in cm).

Figure 6 RMSEs and SDs of the positioning performance and ZTD accuracy of post-processing PPP, respectively.

4 Result

4.1 Performances of multi-GNSS PPP at IGS stations

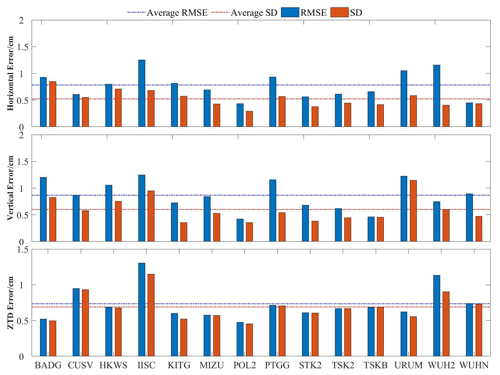
IGS post-processed precise position and ZTD products are used to evaluate the multi-GNSS post-processing PPP performance at 14 IGS sites in and around China. The average convergence time of all stations is less than 20 min. The station coordinates from the IGS SINEX files and the ZTD from the IGS ZPD files are used as references. Positioning performance and ZTD accuracy of post-processing PPP are shown in Fig. 6. The RMSEs of horizontal and vertical errors are within 15 mm for all sites. The RMSEs of ZTD are within 10 mm for most sites, with an average RMSE of 7.4 mm. The abovementioned results suggest that post-processing PPP demonstrates good performance in both positioning and ZTD and can be used to verify the performance of RT-PPP.

4.2 RT-PPP with SSR products from different analysis centers in the IGMAS station

4.2.1 Convergence time of RT-PPP

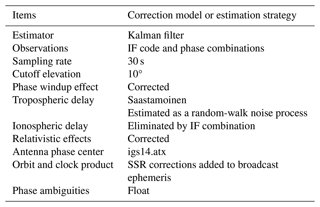
To assess the accuracy of four SSR products, the eight IGMAS stations are selected for RT-PPP after verifying the performance of post-processing PPP. The testing period spans from DOY 355 in 2023 to DOY 14 in 2024. The LHA station is excluded due to a low number of observations among the eight IGMAS stations. The IF model is used. A larger cutoff elevation than the usual cutoff angle can be used when using multi-system PPP (Teunissen et al., 2014). Therefore, the 10° is selected as the cutoff elevation in this study. The Kalman filter is used to estimate parameter, and additional positioning strategies are presented in Table 7.

Table 7 Strategies for RT-PPP.

Figure 7 RT-PPP errors in different analysis centers at seven IGMAS stations.

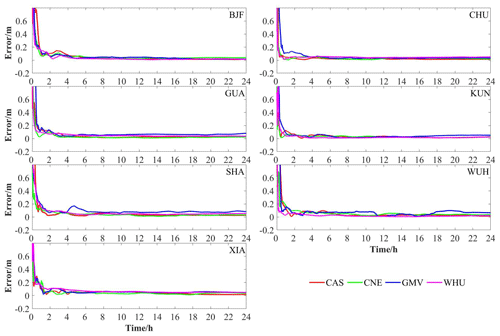
The convergence time, positioning, and ZTD accuracies for multi-GNSS RT-PPP are assessed based on the different SSR products. The convergence time is the initial epoch, where the errors in horizontal and vertical direction are both less than 10 cm, holding for 20 epochs. Figure 7 shows multi-GNSS RT-PPP positioning errors in the 3D direction using the SSR products from the four analysis centers at seven stations on DOY 12, 2024. The results of RT-PPP from different analysis centers are represented by distinct colors, respectively, and the seven sub-figures represent the seven IGMAS sites, respectively. The sub-figures are set with the same range of vertical axes for comparison, and the X direction is the hour since the start of the solution. The average convergence time of four analysis centers is less than 30 min, and the 3D positioning accuracies of four analysis centers are better than 10 cm after completing the convergence process.

Figure 8 Box plot of the convergence time of different analysis centers at IGMAS stations.

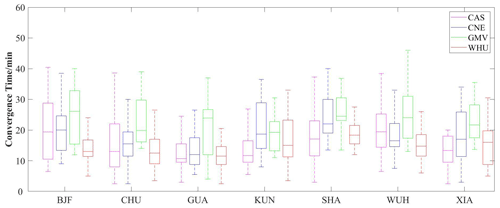
Table 8 The max, min, and mean of the convergence time derived from RT-PPP of different analysis centers (in min).

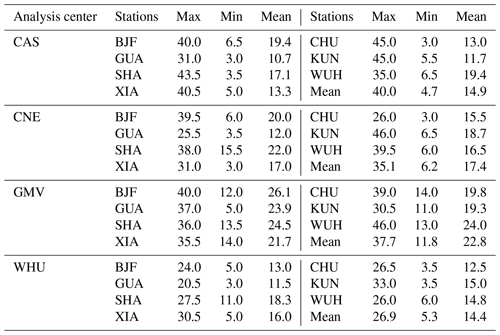
The convergence time for seven stations over 26 d from four analysis centers is counted. Figure 8 shows box plots of the convergence time, including the median, 25 % quantile, and 75 % convergence time. Table 8 provides a detailed breakdown of convergence time statistics for four analysis centers. The average convergence time at all sites based on CAS, WHU, and CNE is less than 20 min, while the one based on GMV is 22.8 min. The discrepancy in the convergence time from GMV and other analysis centers may be because RT-PPP based on GMV SSR products only uses GPS and Galileo, with fewer satellites than the other analysis centers. The average convergence time for CAS and WHU is similar with 14.9 and 14.4 min, respectively, and for CNE, it is 17.4 min, which is slightly longer than CAS and WHU because CNE has fewer satellites available than CAS and WHU.

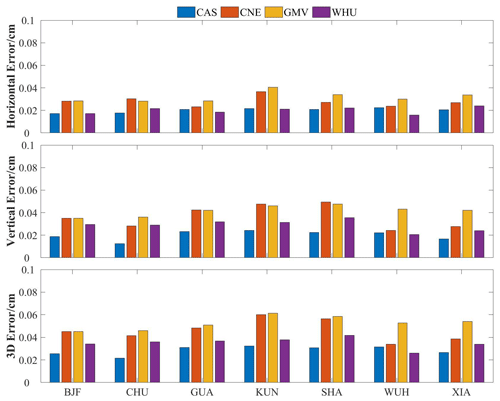
Figure 9 The positioning accuracies in horizontal, vertical, and 3D directions of different analysis centers at seven IGMAS stations.

Figure 10 RT-PPP, post-processing PPP, and PRIDE PPP-AR-derived ZTDs at IGMAS stations.

Table 9 The accuracies of RT-PPP-derived ZTDs from different analysis centers at seven IGMAS stations (in mm).

4.2.2 Positioning accuracy of RT-PPP

The positioning accuracies of RT-PPP for each analysis center at the seven IGMAS stations are evaluated. Figure 9 shows the positioning accuracies in horizontal, vertical, and 3D directions. CAS exhibits the highest accuracy, with 2.1, 2.4, and 3.2 cm in three aspects, respectively. Then, WHU shows a 3.3 cm accuracy in the 3D direction, which is similar to the positioning accuracy of CAS. Since the RMSEs of the SSR products from CNE are higher than those of CAS and WHU, the PPP performance based on CNE is unsatisfactory compared with CAS and WHU. The positioning accuracy with GMV is the worst compared with other analysis centers. The positioning performances of RT-PPP based on GMV SSR products are 3.2 cm in horizontal directions and 4.2 cm in vertical directions. The mean RMSE of 3D positioning accuracy exceeds 5 cm, which is higher than those of the remaining three analysis centers. Therefore, the combination with the BeiDou satellite can improve the positioning performance of RT-PPP.

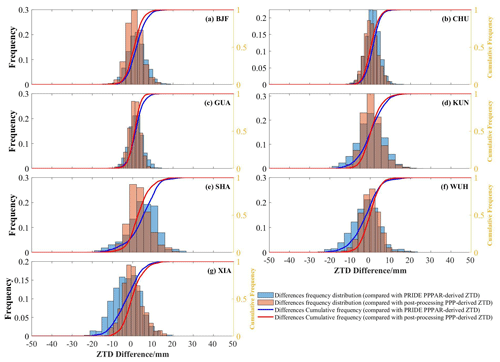
Figure 11 The difference distribution of RT-PPP-derived ZTDs compared with post-processing PPP and PRIDE PPP-AR-derived ZTDs.

Table 10 The availability of RT-PPP-derived ZTDs from different analysis center products at IGMAS stations (in %).

Figure 12 The difference distribution of RT-PPP-derived ZTDs based on four analysis centers.

4.3 Accuracy of RT-PPP-derived ZTDs

4.3.1 Accuracy of RT-PPP-derived ZTDs obtained by different SSR products

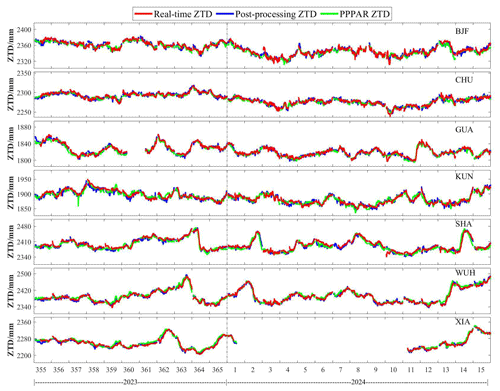
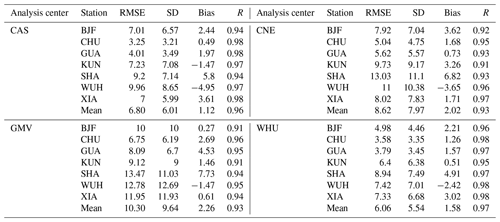
RT-PPP-derived ZTDs based on four analysis center SSR products are compared with post-processing PPP and PRIDE PPP-AR-derived ZTDs, respectively, to verify the accuracy of RT-PPP ZTD retrieval. Figure 10 shows timing diagrams for RT-PPP-derived ZTDs obtained by WHU SSR products alongside those of PRIDE PPP-AR and post-processing PPP-derived ZTDs. RT-PPP, post-processing PPP, and PRIDE PPP-AR-derived ZTDs have a similar trend. Table 9 shows the differences of RT-PPP-derived ZTDs versus PRIDE PPP-AR-derived ZTDs for each analysis center at the seven IGMAS stations. The GUA station lacked observation data from 07:00 LT on DOY 360 to 07:00 LT on DOY 361 in 2023. And the XIA station lacked observation data from 13:00 LT on DOY 1 to 05:00 LT on DOY 11 in 2024. The “breakpoints” in Fig. 10 are caused by occasional disconnections between the local network and the mount point, which result in data loss. RT-PPP-derived ZTD accuracies for GMV can reach the centimeter level. Furthermore, the average accuracies of RT-PPP-derived ZTDs for CAS, WHU, and CNE reach the millimeter level. RT-PPP-derived ZTDs based on WHU have the highest ZTD accuracy, with an RMSE of 6.06 mm. CAS and WHU exhibit similar ZTD accuracies with 6.80 mm. The accuracy of RT-PPP-derived ZTDs based on GMV SSR products is the worst with 10.30 mm. The accuracy of RT-PPP-derived ZTDs based on GMV is worse than that of the other analysis centers, probably because GMV does not provide BDS3 SSR products. The SDs of each analysis center are similar to the RMSEs, with WHU being the best, CAS being slightly inferior, and GMV being the worst. The bias of four analysis centers exhibits minimal differences at around 2.30 mm. The average R of four analysis centers exceeds 0.9, with values of 0.96, 0.93, 0.93, and 0.97 for CAS, CNE, GMV, and WHU, respectively, indicating that RT-PPP-derived ZTD strongly correlates with PRIDE PPP-AR-derived ZTD. The result of RT-PPP-derived ZTD versus post-processing PPP-derived ZTD is similar. The order of RMSEs and SDs for different analysis centers is GMV > CNE > CAS > WHU. The average R of four analysis centers also exceed 0.9 with 0.96, 0.95, 0.91, and 0.97, respectively. In summary, the accuracy of RT-PPP ZTD retrieval obtained by WHU SSR products is the best.

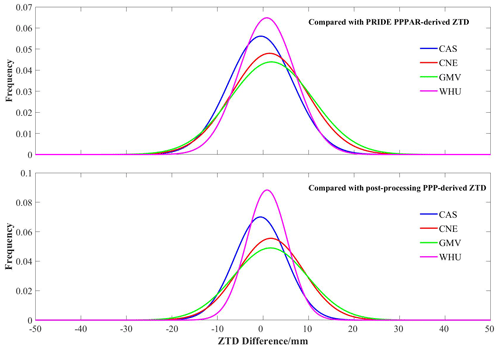
The differences of RT-PPP-derived ZTD versus PRIDE PPP-AR and post-processing PPP-derived ZTD are counted separately to further analyze the ZTD consistency. Figure 11 shows the difference distribution of RT-PPP compared with PRIDE PPP-AR and post-processing PPP-derived ZTDs, respectively, where the bar graph shows the difference frequency distribution and the curve shows the difference cumulative frequency. The difference frequency of RT-PPP-derived ZTDs versus PRIDE PPP-AR and post-processing PPP-derived ZTDs at the seven stations are normally distributed, respectively. The bias of RT-PPP-derived ZTDs at all stations is nearly 0 mm. The difference distribution of RT-PPP-derived ZTDs based on the other analysis centers are also counted, and the bias is nearly 0 mm. Figure 12 shows the error distribution for the four analysis centers. It is evident that the error distributions of ZTD inversion from all four centers follow a normal distribution, with the SDs of the ZTD derived from WHU being notably smaller than that of the other centers. Therefore, the measure of the dispersion of RT-PPP-derived ZTDs based on WHU is lower than CAS, CNE, and GMV. RT-PPP-derived ZTD-based WHU SSR products have the best ZTD retrieval accuracy. The result is consistent with the conclusion of Sect. 4.2.1.

Figure 13 The availability of RT-PPP-derived ZTDs from WHU SSR products at seven IGMAS stations (in %).

4.3.2 RT-ZTD availability

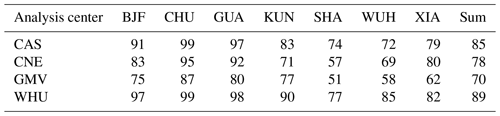
The availability of RT-PPP-derived ZTD is assessed. RT-PPP-derived ZTD in the epoch is considered unavailable if the differences of RT-PPP-derived ZTD versus PRIDE PPP-AR and post-processing PPP-derived ZTD in arbitrary epoch are more than 10 mm, respectively. The daily availability of RT-PPP-derived ZTD based on WHU SSR products is calculated (Fig. 12). Daily ZTD availability of sites with less ZTD variation can be maintained at more than 95 %, such as BJF, CHU, and GUA. Daily ZTD availability of sites with large ZTD variations can basically be maintained at more than 80 %. A similar result also appears in the comparison between RT-PPP-derived ZTD and post-processing PPP-derived ZTD. Table 10 shows the availability of RT-PPP-derived ZTD for the four SSR products at the seven stations using PRIDE PPP-AR-derived ZTD as references. RT-PPP-derived ZTDs based on WHU SSR products have the highest availability, with an average availability of 89 % at all stations. The ZTD availability of CAS is slightly lower at 85 %, and CNE is lower than CAS and WHU at 78 %. GMV shows the worst availability at 70 %. The ZTD availability is positively correlated with the SISRE of SSR products from different analysis centers. Therefore, the SSR products provided by WHU effectively support high-precision RT-PPP ZTD retrieval.

5 Conclusions

Evaluating the accuracies of RT-PPP-derived ZTD based on SSR products from different analysis centers is crucial in warning and forecasting extreme natural disasters and Earth observation error correction. In this study, the accuracies of GPS, Galileo, and BDS3 RT satellite orbit and clock error products from four analysis centers are evaluated. Then, the positioning performance and ZTD accuracies for multi-GNSS RT-PPP are assessed. The following conclusions are obtained. The average epoch availability of SSR corrections provided by four analysis centers exceeds 97.5 %, and CAS SSR products have the highest satellite availability. CAS has the best SISREs of GPS, Galileo, and BDS3 followed by WHU, while CNE and GMV exhibit the worst performance. The results of multi-GNSS RT-PPP indicate that WHU achieves the shortest average convergence times with 14.4 min followed by CAS and CNE. The average convergence time of GMV is 22.8 min, significantly lower than other analysis centers. The accuracies of RT-PPP-derived ZTD obtained by four analysis centers are better than 11 mm, and RT-PPP-derived ZTD is in good conformity with PRIDE PPP-AR-derived ZTD. Among the four analysis centers, WHU has the best accuracy of RT-PPP-derived ZTD with an average RMSE of 6.1 mm, and RT-PPP-derived ZTD based on WHU SSR products has the highest availability with 89 %. This study is essential for selecting SSR products from different analysis centers for RT-PPP ZTD retrieval.