Comparison of gravity wave propagation directions observed by mesospheric airglow imaging at three different latitudes using the M-transform

We developed user-friendly software based on Matsuda et al.'s (2014) 3D-FFT method (Matsuda-transform, M-transform) for airglow imaging data analysis as a function of Interactive Data Language (IDL). Users can customize the range of wave parameters to process when executing the program. The input for this function is a 3-D array of a time series of a 2-D airglow image in geographical coordinates. We applied this new function to mesospheric airglow imaging data with slightly different observation parameters obtained for the period of April–May at three different latitudes: Syowa Station, the Antarctic (69^∘ S, 40^∘ E); Shigaraki, Japan (35^∘ N, 136^∘ E); and Tomohon, Indonesia (1^∘ N, 122^∘ E). The day-to-day variation of the phase velocity spectrum at the Syowa Station is smaller and the propagation direction is mainly westward. In Shigaraki, the day-to-day variation of the horizontal propagation direction is larger than that at the Syowa Station; the variation in Tomohon is even larger. In Tomohon, the variation of the nightly power spectrum magnitude is remarkable, which indicates the intermittency of atmospheric gravity waves (AGWs). The average nightly spectrum obtained from April–May shows that the dominant propagation is westward with a phase speed <50 m s⁻¹ at the Syowa Station and east-southeastward with a phase speed of up to ∼80 m s⁻¹ in Shigaraki. The day-to-day variation in Tomohon is too strong to discuss average characteristics; however, a phase speed of up to ∼100 m s⁻¹ and faster is observed. The corresponding background wind profiles derived from MERRA-2 indicate that wind filtering plays a significant role in filtering out waves that propagate eastward at the Syowa Station. On the other hand, the background wind is not strong enough to filter out relatively high-speed AGWs in Shigaraki and Tomohon and the dominant propagation direction is likely related to the distribution and characteristics of the source region, at least in April and May.

1 Introduction

Atmospheric gravity waves (AGWs) or buoyancy waves are oscillations caused by the vertical displacement of an air parcel, which is restored to its initial position by buoyancy. These waves, which primarily originate in the lower atmosphere, propagate into the upper mesosphere and lower thermosphere (e.g., Lindzen, 1981; Matsuno, 1982; Fritts, 1984; Fritts and Alexander, 2003). The study of AGWs is important because these waves transport energy and momentum vertically and drive the general circulation up to ∼100 km. The AGWs greatly affect the global temperature structure through general circulation. Therefore, improved understanding of AGWs characteristics and their implementation in numerical models, such as climate models, is very important to improve such models and increase their precision. However, quantitative observational studies are progressing slowly, partly because of the difficulties related to investigating global AGW characteristics. One difficulty is that AGWs cover a very broad spectrum (the wave periods range from minutes to hours and spatial scales extend up to thousands of kilometers). Although satellite observations can provide a global view of AGW phenomena, they are limited to the portion of AGWs with a large scale because of the low horizontal and/or vertical resolutions of the instruments (Alexander, 1998; Wright et al., 2016). Therefore, studies using ground-based measurements with high horizontal and/or vertical resolutions are essential to reveal the global characteristics of AGWs.

Among various ground-based observations, airglow-imaging observations have been proven to be very effective in determining both the energy and propagation characteristics. In the last few decades, airglow imagers have been deployed at various latitudes to study AGWs in equatorial, midlatitude, and polar regions (e.g., Shiokawa et al., 2009; Suzuki et al., 2007; Matsuda et al., 2014, 2017). Such long-term observations provide a huge amount of data. However, the lack of sophisticated analysis methods prevents quantitative studies based on complete worldwide datasets that have been collected with great effort.

A new analysis algorithm has been developed by the National Institute of Polar Research (NIPR) group to obtain the power spectrum in the horizontal phase velocity domain from long-series data of airglow imagers, as shown in Matsuda et al. (2014; Matsuda-transform, here M-transform). The M-transform method transforms airglow-intensity image data to a power spectrum in the horizontal phase velocity domain. This method can handle a huge amount of data. Therefore, the time consumption and manpower required for the analysis of such a huge amount of airglow data are reduced. This method has been successfully applied to Antarctic Gravity Wave Instrument Network (ANGWIN) imagers that are used to study the characteristics of mesospheric AGWs over Antarctica, as reported by Matsuda et al. (2017). Takeo et al. (2017) and Tsuchiya et al. (2018) applied this method to 16-year airglow imaging data from Shigaraki (35^∘ N, 136^∘ E) and Rikubetsu (44^∘ N, 144^∘ E), Japan, to study the horizontal phase speed and propagation direction at midlatitudes.

Despite the high success of this method's application, several subroutines must be separately executed in the original program, which is not user-friendly. Therefore, we developed a simple user-friendly function based on Matsuda et al.'s (2014) method that can be handled by users with different backgrounds and programming skills. We encourage AGW research groups to use the program for the analysis of their data and produce results in a uniform format (power spectrum in the phase velocity domain). This will make it easier to compare the AGW phase velocities and energy distributions of different locations, that is, of different latitudes and longitudes. This paper is organized as follows. Section 2 describes the M-transform function and its use. Section 3 shows the comparison of phase speed spectra obtained with the M-transform application for different airglow datasets with different observation parameters recorded at different latitudes: Syowa Station (69^∘ S, 40^∘ E), Shigaraki (35^∘ N, 136^∘ E), and Tomohon Observatory (1^∘ N, 122^∘ E). The conclusions of this paper are provided in Sect. 4.

2 M-Transform function

The M-transform function is a 3-D FFT function using Interactive Data Language (IDL; http://www.exelisvis.com/ProductsServices/IDL.aspx, last access: 15 September 2018), which is used to analyze airglow imaging data based on the method developed by Matsuda et al. (2014). This method requires time series of airglow images in 3-D array format, which have been preprocessed to have fixed intervals of image pixels (dx, dy) and time (dt). These preprocessed images should be obtained through common airglow image preprocessing, that is, (1) star removal, (2) correction of the Van Rijhin effect if necessary, and (3) projection onto a geographical coordinate system in equal distances in latitudinal and longitudinal directions (e.g., Kubota et al., 2001; Suzuki et al., 2007). It is also recommended to normalize the airglow intensity values to compare the power spectral values of different datasets. For this purpose, ($(I-\stackrel{\mathrm{‾}}{I})/\stackrel{\mathrm{‾}}{I}$), where I is the image intensity of each pixel, should be used in the input array. Our M-transform code applies 2-D prewhitening to the images to reduce the contamination of higher wavenumbers with lower-wavenumber peaks of the red AGW spectrum. It also applies the 2-D Hanning window to reduce the harmonics of the window function in the horizontal direction (Coble et al., 1998). Matsuda et al.'s (2014) new method transforms the power spectrum density (PSD) in the wave number domain (k, l, ω) to the phase velocity domain (ν_x, ν_y, ω) based on the following equations:

$$\begin{array}{}\text{(1)}& {\displaystyle }& {\displaystyle }{v}_x=\mathit{\omega }k/(k^{\mathrm{2}}+l^{\mathrm{2}}),\text{(2)}& {\displaystyle }& {\displaystyle }{v}_y=\mathit{\omega }l/(k^{\mathrm{2}}+l^{\mathrm{2}}),\end{array}$$

where v_x and v_y are the orthogonal projections of the phase velocity onto zonal and meridional axes, respectively ($({\mathit{\nu }}_x,{\mathit{\nu }}_y)=c(\sin \mathit{\phi },\cos \mathit{\phi })$, where c and φ are the phase speed and azimuth (east from north) of the phase velocity). Note that ν_x and ν_y are not the phase velocities in the zonal or meridional directions or cross sections; ω is the frequency; and k and l are the zonal and meridional wavenumbers, respectively. Finally, the phase velocity spectrum is integrated over the frequency and results in a 2-D phase velocity spectrum.

Table 1 Description of M-transform function on IDL.

The original program developed by Matsuda et al. (2014) consisted of several subroutines, which were used to calculate the 3-D FFT, create an interpolation table, perform the interpolation, and separately plot the results. The users had to set the wave parameters in each subroutine and had to run it one by one, making the process complicated and inefficient. Furthermore, once the users failed to compile one of the subroutines, the program failed to run and the users had to check the subroutine one by one again. Therefore, a simple, hassle-free one-line-command software with adjustable input keywords is necessary to efficiently apply this method.

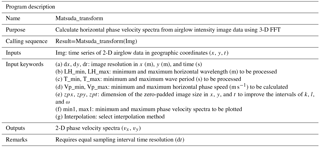
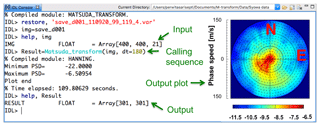
Table 1 shows the description of the M-transform function and Fig. 1 shows how to run the program. To run this function, the user can simply use the calling sequence “Result=Matsuda_transform(Img)”, where “Img” is the 3-D array of the preprocessed images in geographic coordinates (x, y, t). The image resolutions (dx, dy, dt), wave parameters (horizontal wavelength, LH), wave period (T), phase speed (Vp), and size of zero padding (zpx, zpy, zpt) can be adjusted by setting input parameter keywords. The default image resolution is 1 km in both zonal (dx) and meridional (dy) directions. The default image interval time (dt) is 60 s. The default minimum and maximum values of the wave parameters are $\mathrm{5}\le \mathrm{LH}\le \mathrm{100}$ km, $\mathrm{8}\le T\le \mathrm{60}$ min, and $\mathrm{0}\le \mathrm{Vp}\le \mathrm{150}$ m s⁻¹. The default output of this program is a 2-D phase velocity spectrum. The default interpolation method of this new function is the Delaunay triangulation method (e.g., Dwyer, 1987; Su and Scot Drysdale, 1997). One restriction of this program is that it requires an equal time interval (dt). This may not be the case for practical observations, where filter rotations or background (or dark) images for the calibration are obtained from the observation sequence. In that case, users have to interpolate the image to obtain a constant dt interval before applying this function. More details on the function development are provided elsewhere.

Figure 1 Flow chart showing the input, how to run the program, and the output format.

Figure 2 shows an example of the use of the M-transform function. The input consists of airglow data over the Syowa Station obtained on 20 September 2011 (the same dataset as used in Matsuda et al., 2014), which have the following dimensions: x=400 km, y=400 km, t=21 min (×3 min). Because the image time resolution was 3 min, the dt input keyword was set to dt=180 s. The default values were used for the other wave parameters. The IDL console shows the input, calling sequence, total calculation time, and output. The output is a 2-D phase velocity spectrum (right panel). The horizontal axis is v_x, the vertical axis is v_y, and the color bar shows the PSD on a logarithmic scale. The phase velocity spectrum shows dominant propagation in the southwestward direction, which agrees with the wave propagation observed in the airglow preprocessed image movie in the Supplement as that reported by Matsuda et al. (2014). The total calculation time of the M-transform function for 21 images with 400×400 pixels was ∼1.4 min using a personal computer. The calculation was performed on a MacBook Pro with a dual core 2.8 GHz Intel Core i7 processor with 4 MB cache size and 16 GB memory, while the program was single-threaded.

Table 2 Summary of airglow imagers used in this study.

Figure 2 Example of how to use the Matsuda-transform (M-transform) program, showing the input, calling sequence, total calculation time, and output as 2-D phase velocity spectrum.

3 Comparison of the phase velocity spectra obtained with the M-transform function for different airglow datasets at three different latitudes

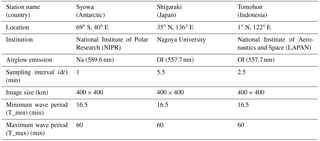
We applied this new M-transform function to various airglow datasets obtained at three different latitudes. Table 2 shows the summary of each airglow imager used in this analysis. Syowa Station (69^∘ S, 40^∘ E) data represent airglow data in the polar region, while Shigaraki (35^∘ N, 136^∘ E) and Tomohon (1^∘ N, 122^∘ E) data represent the midlatitude and equatorial regions, respectively. We used the Na (589.6 nm) airglow emission obtained at the Syowa Station and OI (557.7 nm) airglow emission recorded in Shigaraki and Tomohon.

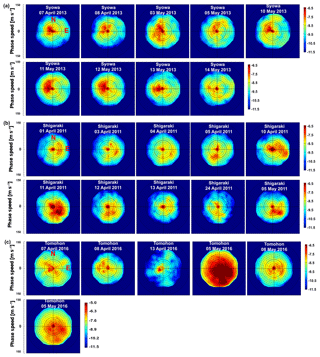
Figure 3 Day-to-day variation of 2-D phase velocity spectra for April–May 2013 at the Syowa Station (a), in Shigaraki (2011) (b), and in Tomohon (2016) (c). Panel (c) is the same as that for 5 May 2016, but with a different color bar level to better visualize the dominant wave propagation direction.

We observed 9 clear-sky nights at the Syowa Station from April to May 2013, 10 clear-sky nights in Shigaraki from April to May 2011, and 5 clear-sky nights in Tomohon from April to May 2016. The Syowa data were the same dataset as that reported by Matsuda et al. (2017). The image size for each observation site was 400×400 km and the sampling intervals (dt) were 1 min (Syowa), 5.5 min (Shigaraki), and 2.5 min (Tomohon). The different sampling intervals limit the maximum phase velocity to be analyzed; that at Shigaraki was the smallest. To avoid an aliasing effect on the 2-D phase velocity spectrum, we selected the period minimum (T_min) to be at least 2 times larger than the sampling interval (2×dt). In this study we set T_min to 3×dt. Because the dt of Shigaraki data was 5.5 min, we set the T_min to 16.5 min for all datasets to obtain the same frequency range. This setting can be easily altered by changing the input keyword (T_min) when running the function. The defaults were used for the other wave parameters.

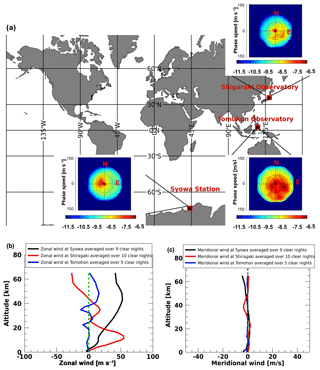
Figure 4 (a) Average day-to-day variation of the 2-D phase velocity spectrum of AGWs observed at Syowa, in Shigaraki, and in Tomohon. (b) Average zonal wind profiles (positive: eastward) and (c) average meridional wind profiles (positive: northward) of GWs observed during clear nights from MERRA-2 data.

Figure 3 shows the day-to-day variation of 2-D phase velocity spectrum results for (a) Syowa Station, (b) Shigaraki, and (c) Tomohon. The top and left represent the north and east respectively. The day-to-day plot at Syowa Station shows a lack of eastward gravity wave (GW) propagation and a dominant westward propagation, which is probably due to the filtering effect by the eastward polar night jet, as described in Matsuda et al. (2014). However, the azimuth direction with large power spectral density was not always the same; a much narrower azimuth distribution was observed on 13 and 14 May. This suggests that the distribution of the GW sources was limited on these days and changed from day to day. On the contrary, the 2-D phase velocity spectrum for Shigaraki shows a lack of westward propagation and dominant eastward and southward propagations. The strong spectrum based on Shigaraki data has a much larger day-to-day azimuth variation than that for Syowa, suggesting that the distribution of the wave source region varied more in Shigaraki, at least in this season's April and May. The day-to-day variation of the propagation direction was even stronger in Tomohon. At the same time, a significant day-to-day variation of the magnitude of the power spectrum was observed. The power was the weakest on 13 April; it was much stronger on 5 May and is overscaled in the plot. The last panel in Fig. 3c was plotted with the maximum color level; it is ∼30 times larger than the others. Such a significant day-to-day variation indicates the intermittency of the GWs.

Figure 4a shows the average nightly spectrum at each observation site plotted on the world map. The average phase velocity spectrum at the Syowa Station shows a distinct westward propagation with a phase speed below 50 m s⁻¹. In Shigaraki, AGWs propagate dominantly in the east-southeastward direction and reach phase speeds up to ∼80 m s⁻¹. The AGWs in Tomohon show a preferred propagation direction, that is, they are moving southeastward with phase speeds of up to ∼100 m s⁻¹. It should be noted that the plot for Tomohon is highly affected by a single day, 5 May. This also indicates the intermittency of GWs, which suggests that the net momentum transportation highly depends on the very strong GWs with smaller occurrence frequency.

One can discuss the AGW propagation by comparing the 2-D phase velocity spectrum and background conditions along the propagation path. Figure 4b and c show the zonal and meridional wind profiles, respectively, obtained from Modern-Era Retrospective Analysis for Research and Applications (MERRA-2; Gelaro et al., 2017) for each observation site. The profiles were averaged over the clear nights of the observed AGWs. The zonal wind over the Syowa Station, which was averaged over nine clear-sky nights, shows strong eastward wind up to ∼50 m s⁻¹ around ∼50 km, which could filter out the waves propagating eastward. A similar conclusion was reported by Matsuda et al. (2017), who applied a GW blocking diagram (Taylor et al., 1993; Tomikawa, 2015) by using horizontal wind data from MERRA and the medium-frequency (MF) radar to discuss the preferred wave propagation direction observed in the phase velocity spectrum. They concluded that eastward-propagating AGWs are restricted to propagating up to the mesopause due to critical-level filtering.

In contrast to the strong zonal wind at the Syowa Station, the average zonal wind profile in Shigaraki over 10 clear nights shows relatively weak westward wind with a speed of up to ∼30 m s⁻¹ at ∼50 km altitude. Previous studies of the seasonal directionality of AGWs in Shigaraki showed that east–west propagation anisotropy is usually caused by wind filtering of the mesospheric jet (e.g., Nakamura et al., 1999; Ejiri et al., 2003; Takeo et al., 2017). However, the westward wind in our current case for April–May 2011 is not stronger than 30 m s⁻¹ above the stratosphere; it is not strong enough to filter out all GWs with westward propagation. The average tropopause eastward jet is as strong as 60 m s⁻¹. If the GW source is associated with such an eastward jet structure, the horizontal phase velocity distribution of generated GWs should shift eastward. This could also be the reason for the lack of westward-propagating AGWs, especially those with higher phase velocities such as over 40 m s⁻¹.

The average zonal wind in Tomohon is small (<20 m s⁻¹) and likely has a limited impact on the much faster AGW phase speed (∼100 m s⁻¹). However, Fig. 4a shows that the GWs over Tomohon have a dominant southeastward propagation. As already discussed, this distribution is affected by the spectrum of a single day and should be highly affected by the location of the strong wave source on that day. Haffke et al. (2016) reported that the Intertropical Convergence Zone (ITCZ) is located above the Equator between March and April and starts to move north of the Equator in May, which could explain the dominant southward propagation of AGWs observed on 5 May 2016 (Fig. 3c). The scenario in which the distribution of the source location has a more significant effect on the AGW propagation direction than the background wind in the equatorial region agrees well with results reported by Nakamura et al. (2003). They reported AGW characteristics for Tanjungsari, Indonesia (107.9^∘ E, 6.9^∘ S) and based on the analysis of Geostationary Meteorological Satellite (GMS) data they concluded that the distribution of tropospheric clouds that are located mainly in the opposite direction of the wave propagation plays a more significant role than the relatively weak background wind. The meridional wind at each observation site has a weak velocity (<5 m s⁻¹) and likely has almost no impact on the wave propagation direction.

4 Conclusion

We developed a user-friendly IDL function based on Matsuda et al.'s (2014) 3-D FFT method for airglow data analysis. This function efficiently deals with extensive amounts of imaging data obtained in different years and at various observation sites without bias caused by the analysis by different research groups and treats the dynamical and physical effect of AGWs by precisely reflecting the amplitude, area, and lifetime of each AGW event with a reasonable execution time. It can also be applied for airglow data with different observation parameters such as the image sampling interval. This new function was applied to airglow imaging data obtained from April–May of selected years at three different latitudes: Syowa Station (69^∘ S, 40^∘ E), Shigaraki (35^∘ N, 136^∘ E), and Tomohon (1^∘ N, 122^∘ E). By comparing the 2-D phase velocity spectra of each site, we found that the day-to-day variation in Shigaraki is larger than that at the Syowa Station. The day-to-day variation in Tomohon has an even greater variability than the other two sites, which suggests that the distribution of the source region in Shigaraki and Tomohon is likely more variable than at the Syowa Station. We also found that the day-to-day variation in Tomohon includes a significant variation of the phase spectrum magnitude, which indicates the intermittency of AGWs. The average nightly spectrum shows a dominant westward wave with a phase speed <50 m s⁻¹ at the Syowa Station and an east-southeastward propagation with a phase speed of up to <80 m s⁻¹ in Shigaraki. Southeastward propagation was observed in Tomohon; however, this result is highly affected by a single day with an extremely strong power spectrum. The phase speed in Tomohon reaches up to ∼100 m s⁻¹, which is larger than that at the other two sites. The comparison of the 2-D phase velocity spectra with background wind profiles derived from MERRA-2 data revealed that wind filtering plays a more significant role in filtering out eastward-propagating waves at the Syowa Station. On the other hand, the background winds in Shigaraki and Tomohon are not strong enough to filter out AGWs that propagate in the opposite direction of the observed wave propagation. This shows that the dominant propagation directions observed in Shigaraki and at the Tomohon Observatory are likely related to the distribution and characteristics of the source region. We demonstrated the distinct difference in the GW propagation characteristics at three different latitudes based on the phase velocity spectra. These results indicate the usefulness of phase velocity spectra for the characterization and comparison of GW characteristics at different sites and the effectiveness of the new M-transform function for airglow imaging data obtained at these locations. The comparison made in the current study is limited to the period of April–May, for which enough preprocessed clear-night data were available. In the future, we plan to extend this comparison and include data for all seasons and months with more global coverage.