Estimating ocean tide model uncertainties for electromagnetic inversion studies

Over a decade ago the semidiurnal lunar M2 ocean tide was identified in CHAMP satellite magnetometer data. Since then and especially since the launch of the satellite mission Swarm, electromagnetic tidal observations from satellites are increasingly used to infer electric properties of the upper mantle. In most of these inversions, ocean tidal models are used to generate oceanic tidal electromagnetic signals via electromagnetic induction. The modeled signals are subsequently compared to the satellite observations. During the inversion, since the tidal models are considered error free, discrepancies between forward models and observations are projected only onto the induction part of the modeling, e.g., Earth's conductivity distribution. Our study analyzes uncertainties in oceanic tidal models from an electromagnetic point of view. Velocities from hydrodynamic and assimilative tidal models are converted into tidal electromagnetic signals and compared. Respective uncertainties are estimated. The studies main goal is to provide errors for electromagnetic inversion studies. At satellite height, the differences between the hydrodynamic tidal models are found to reach up to 2 nT, i.e., over 100 % of the local M2 signal. Assimilative tidal models show smaller differences of up to 0.1 nT, which in some locations still corresponds to over 30 % of the M2 signal.

1 Introduction

The study of electromagnetic (EM) oceanic tidal signals (EMOTS) has a long history (Larsen, 1968; Sanford, 1971). For over a decade, EMOTS from the M2 are detectable in CHAMP satellite magnetometer observations (Sabaka et al., 2015; Tyler et al., 2003). Since the Swarm satellite mission launch in 2013, satellite magnetometer observations became more precise and extended. Already, weaker ocean tides like the N2 may be detectable from space (Sabaka et al., 2016). In most cases, EMOTS are removed from the EM observations before further analysis (Guzavina et al., 2018; Larsen, 1991). However, an increasing number of studies use EMOTS to infer EM properties of Earth's subsystems. Kuvshinov et al. (2006) studied the sensitivity of EMOTS to lithosphere resistance. The strategy is to use discrepancies between observed and modeled EMOTS (Schnepf et al., 2014) to infer lithosphere and upper mantle resistance (Schnepf et al., 2015). Magnetometer satellites allow us to conduct these studies with global coverage. Grayver et al. (2016, 2017) use EMOTS from satellite observations to constrain lithosphere, mantle conductivity, and water content profiles. Saynisch et al. (2016, 2017) propose to use EMOTS to detect changes in oceanic conductance due to salinity and temperature changes.

Many of these approaches compare or propose to compare observed and modeled EMOTS. The found discrepancies are subsequently used to update prior conductivity assumptions. Consequently, flaws of the used tidal model are inevitably projected onto the conductivity updates. Many of these inversion studies use a single tidal model (Kuvshinov, 2008; Kuvshinov et al., 2006; Schnepf et al., 2014). Grayver et al. (2016) compare two tidal models and state that the difference between radial magnetic field components calculated from both tidal models is below the current noise level of current satellite EM observations. However, Grayver et al. (2016) note further that both models use very similar data to estimate tidal flow and that systematic shifts cannot be fully ruled out.

Stammer et al. (2014) compared sea surface heights (SSH) and sea water velocities from 15 tidal models to observations. The authors report rms errors from modern tidal models for the M2-SSH of 0.5–0.7 cm over the open ocean. On the shelf and in high-latitudes, the errors amount to several centimeters. Compared to coastal tide gauges, the rms errors can reach 15.7 cm. Comparison of modeled M2 velocities revealed rms errors of 0.8–1.5 cm s⁻¹.

The reported errors cannot directly be translated into errors of EMOTS. Tidal velocities interact with Earth's background magnetic vector field to generate tidal electric currents. This process is mathematically described by a cross product where local ocean depth and oceanic conductance have to be taken into account. The tidal electric currents subsequently generate tidal magnetic signals by EM induction. This latter process is described by Maxwell's equations. Here, the conductances of ocean, sediments, conductivity of lithosphere, and upper mantle have to be taken into account.

As in Stammer et al. (2014), our study uses an ensemble of tidal models to estimate the uncertainties in EMOTS predictions. The whole modeling chain from the respective tidal velocities to the EMOTS is subject to several uncertainties and modeling choices. Quantizing all of them is beyond the scope of this study. The choice of the induction solver (e.g., 2-D vs. 3-D, frequency domain vs. time domain, galvanic coupling or perfect insulating mantle) and the model's resolution may influence the calculated EMOTS (Kuvshinov, 2008). The same is true for errors in the oceanic conductance (Cabanes et al., 2013; Irrgang et al., 2016), the mantle conductance, or the core field including secular variation (Gillet et al., 2010; Lesur et al., 2008; Sabaka et al., 2015; Thébault et al., 2015). By using a realistic EM induction modeling setup, this manuscript presents only that part of the EMOTS error budget that arises due to the uncertainties in the tidal sources only. In other words, the described EMOTS errors would still persist if the induction processes would be modeled perfectly.

The findings should help to evaluate, weight, and improve EMOTS-based inversions that incorporate model to observation comparisons.

In Sect. 2, the tidal models and the solver for the Maxwell equations are described. Section 3 presents and discusses the model-to-model differences with respect to EMOTS. The paper closes with summary and conclusions in Sect. 4.

2 Models

Stammer et al. (2014) identify two relevant categories of tidal models. First, forward models, which are physically consistent and model tides due to the forces generated by Earth's rotation and the movements of the respective celestial bodies. Second, empirical models, which assimilate observation data. We follow this twofold approach and study the following currently used tidal models.

2.1 Forward models

OMCT (Dobslaw and Thomas, 2007): global baroclinic model with 1^∘ resolution. The forcing is based on the lunisolar ephemerides. Loading and self-attraction (LSA) is parameterized. Tides are calculated in combination with the global general circulation (Thomas et al., 2001). The general circulation is forced with 3-hourly fields of wind stress and freshwater flux.

STORMTIDE (Müller et al., 2012): global baroclinic model of 0.1^∘ resolution. The forcing is based on the ephemerides. LSA is parameterized. Tides are calculated in combination with the global general circulation. The general circulation is forced with daily wind fields from a climatological year.

Since the models are forced with full lunisolar potentials, the M2 signal has to be separated in the model output by harmonic analysis. To do this, the tidal frequencies are fitted to the data. This approach has similarities to the filtering of tidal signals in real observations.

2.2 Assimilative models

HAMTIDE (Taguchi et al., 2014): linearized barotropic global model with a spatial resolution of 0.125^∘. LSA is included. A variational data assimilation scheme is used that is based on a generalized inverse. Output from the Empirical Ocean Tide Model (DGFI-Report No.89: Savcenko R, 2012) is used as data constraints. EOT is based on multi-mission satellite altimetry.

TPXO8-atlas (Egbert and Erofeeva, 2002): global barotropic $\mathrm{1}/\mathrm{30}{}^{\circ }$ model that uses the representer approach to assimilate data from multi-mission satellite altimetry and tide gauges.

FES2014 (Lyard et al., 2006): non-linear barotropic $\mathrm{1}/\mathrm{16}{}^{\circ }$ global tidal model with unstructured grid. Maximal resolution of a few kilometers. FES2014 uses ensemble optimal interpolation in the frequency domain to assimilate observations. Multi-mission satellite altimetry data are used as constraints.

Figure 1 Differences in radial tidal magnetic field at satellite height. STORMTIDE minus OMCT amplitudes, i.e., two forward models. (a) Absolute differences. (b) Relative differences (regions of tidal signal strength below 0.1 nT are grayed out).

2.3 Induction model

For better comparison, tidal transports from the above-mentioned tidal models are regridded to an identical $\mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$ grid. Note that the choice of a (reasonable) resolution had no influence on the presented results (not shown).

Where tidal transports are not provided the given tidal velocities are integrated using the respective model's bathymetry. A 2-D annual mean depth-averaged oceanic conductivity was derived from the OMCT ocean model. OMCT oceanic conductivity ($\stackrel{\mathrm{‾}}{\mathit{\sigma }}$), tidal transports (U), and Earth's background magnetic field (Thébault et al., 2015) are combined to estimate electric sheet current densities (J):

$$\begin{array}{}\text{(1)}& \mathit{J}=\stackrel{\mathrm{‾}}{\mathit{\sigma }}(\mathit{U}\times {\mathit{B}}^{\mathrm{m}}).\end{array}$$

The J force Maxwell's equations, which are solved by the 3-D induction solver of Kuvshinov (2008). X3DG calculates magnetic fields in frequency space using a volume integral equation approach. In our configuration, a thin ocean and sediment layer of spatially variable electric conductance is used (Everett et al., 2003; Laske and Masters, 1997). In addition, a 1-D spherically symmetric mantle conductivity (Püthe et al., 2015) is used.

3 Results and discussion

The study is restricted to tidal magnetic amplitudes of the semidiurnal lunar tide, M2. M2 has the largest magnetic amplitude and is used in the most recent satellite magnetometer-based inversion (Grayver et al., 2017). Only the radial M2 component of the oceanic magnetic field is presented throughout the paper.

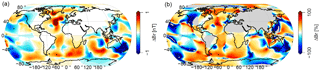
Figure 1 shows the differences between the two hydrodynamic, i.e., the forward, models. Globally, large discrepancies of up to ±2 nT occur, e.g., +1.5 nT in the Gulf Stream region and −2 nT around New Zealand (Fig. 1a). These differences are comparable in size to the actual tidal amplitudes, e.g., 80 % in the Gulf Stream region and over −100 % around New Zealand (Fig.1b).

Assimilation models are better at reproducing observed tidal SSH anomalies (Stammer et al., 2014). This is not astonishing since these models assimilate SSH observations (Egbert and Erofeeva, 2002; Lyard et al., 2006; Taguchi et al., 2014). However, the SSH anomalies themselves are not very relevant for the magnetic signal. SSH anomalies of a few meter have to be related to the entire water depth. Consequently, SSH anomalies are only important in very shallow areas. Important to the magnetic signals are the tidal velocities. Stammer et al. (2014) also compare modeled and observed tidal velocities. The results show that assimilative models are closer to the observations. However, with 56 moorings and 3 acoustic tomography soundings, the comparison under-represents large parts of the global ocean.

In contrast to the assimilative models and in contrast to the comparisons in Stammer et al. (2014), the presented differences of Fig. 1 include baroclinic components. In addition, signals of the general wind-driven circulation are included that directly modulate or became aliased into the M2 tidal signal during the tidal harmonic analysis (see Sect. 2). Both contributions are included in real observations of EMOTS and should be considered in the comparison. Consequently, even if a perfect barotropic tidal model exists, it will show differences to EMOTS observations. Respective contributions are expected to reach 5–10 % (Mueller et al., 2014; Müller et al., 2012; Richet et al., 2017; Thomas et al., 2001). A corresponding inversion strategy would nonetheless project these differences, e.g., on lithospheric resistivity.

Figure 2 shows the comparison of the two tidal models that were compared in Grayver et al. (2016), HAMTIDE and TPXO8-atlas. At satellite height, the two assimilative models show weak large-scale differences of around 0.03 nT (Fig. 2a). However, locally the differences are larger. Especially around the Antarctic Peninsula (−0.3 nT) and in the Arctic Ocean (+0.2 nT), the discrepancies are larger than Swarm's nominal noise level (Friis-Christensen et al., 2006). These higher values are not present in the comparison of Grayver et al. (2016). The reason can only be guessed to be a result of recent updates in the HAMTIDE or TPXO data sets.

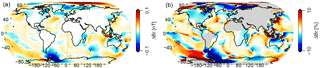
Figure 2 Differences in radial tidal magnetic field at satellite height. HAMTIDE minus TPXO amplitudes, i.e., two assimilative models. (a) Absolute differences. (b) Relative differences (regions of tidal signal strength below 0.1 nT are grayed out).

The relative differences between the HAMTIDE and TPXO8-atlas amount to 10–30 % in higher latitudes and around 5 % elsewhere (Fig. 2b). Please note that all signals below 0.1 nT, i.e., the nominal Swarm precision, are grayed out in the right-side plots. In these areas, even small model differences generate large relative error values. As a consequence, the plotted errors of 5–30 % relate to significant, i.e., measurable tidal magnetic fields, only.

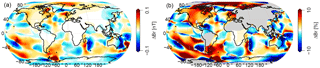
Figure 3 Differences in radial tidal magnetic field at satellite height. FES2014 minus HAMTIDE amplitudes, i.e., two assimilative models. (a) Absolute differences. (b) Relative differences (regions of tidal signal strength below 0.1 nT are grayed out).

If a third assimilative model (FES2014) is taken into account, additional high discrepancies occur in other parts of the globe. Figure 3 compares the M2 signals of FES2014 and HAMTIDE. High differences over 0.1 nT occur in the central Pacific, the North Atlantic, and the Indian Ocean (Fig. 3a). However, the fit in the Arctic Ocean is better than in Fig. 2. The relative values (Fig. 3b) show differences above 30 % globally. Again, small signals below 0.1 nT are not considered for the relative deviations.

Considering the mostly small values in Fig. 2, it is not astonishing that apart from the already mentioned Antarctic Peninsula and the Arctic Ocean, the differences between FES2014 and TPXO-atlas are very similar to the differences between FES2014 and HAMTIDE Fig. 3.

Compared to the forward models (Fig. 1), the assimilative models show smaller discrepancies (Fig. 3). This is a direct result of the assimilation of the same data, i.e., satellite height observations (Egbert and Erofeeva, 2002; Lyard et al., 2006; Taguchi et al., 2014). However, can the smaller magnetic tidal differences among assimilative models be interpreted as better magnetic signals too? The assimilative models fit better to tide gauge data although these observations are only assimilated into TPXO8-atlas (Stammer et al., 2014). However, tide gauge data and satellite altimetry are closely related. The relevant properties for the EM signals, tidal velocities, are not assimilated into these models. A possible answer to the question can be found in comparisons of modeled and observed barotropic tidal velocities (Stammer et al., 2014). Here, the assimilative models also show a better fit than the forward models. However, in this comparison major parts of the oceans and the baroclinic contributions are not considered (Stammer et al., 2014).

Comparing the assimilative models directly with the forward models reveals large discrepancies of around ±1 nT (not shown). Consequently, these differences are smaller than the differences between the forward models alone. In most parts of the globe, the tidal magnetic field amplitudes of the assimilative models lie between the two forward models.

4 Summary and conclusions

The main goal of this study is to provide errors for inversion studies that use tidal observations from satellite magnetometers (Grayver et al., 2016, 2017; Saynisch et al., 2016, 2017; Schnepf et al., 2014, 2015).

Five momentarily used oceanic tidal models are compared with respect to their electromagnetic (EM) signal of the semidiurnal lunar tide M2. The model range includes two baroclinic, hydrodynamic forward models. Here, the tide calculation is coupled to the general circulation and is based on ephemeris forcing. Furthermore, the model range includes three barotropic assimilative models. These models rely heavily on satellite altimetry data.

All models provide M2 velocities or transports. These are combined with a mean 2-D oceanic conductance and Earth's background magnetic field to generate electric sheet current densities. The sheet current densities are interpolated onto a $\mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$ grid and solved for their magnetic signal with a 3-D induction solver (Kuvshinov, 2008).

At satellite height the forward tidal models globally show large-scale differences of up to ±2 nT. In most areas, the differences are larger or on the same order of the actual M2 signal. In comparison, the differences in the assimilative tidal models are smaller. Nonetheless, large scale inter-model differences over 0.1 nT occur that correspond to 30 % or more of the actual M2 signal.

The differences between forward models and assimilative models are slightly smaller but on the same order as the forward model differences.

Depending on the tidal model used in an inversion approach, the respective error budgets should be included. Locally, e.g., in polar regions, up to 30 % of M2 tidal model error may be assumed.

Identifying a best tidal model for EM inversions is beyond the scope of this study. However, a follow-up study will try to derive and compile tidal EM signals from insular, coastal and bottom magnetometers (Kuvshinov et al., 2006; Love and Rigler, 2014; Maus and Kuvshinov, 2004; Schnepf et al., 2014) as well as telecommunication cables (Baringer and Larsen, 2001; Thomson et al., 1986) to answer this question if possible. Such a study could simultaneously assess if modern tidal models are lacking physical processes that are relevant to tidal EM generation but which are not evident in the modeled SSH anomalies.